Study of Route Optimization Considering Bottlenecks and Fairness

Among Partial Paths

Toshihiro Matsui

, Marius Silaghi

, Katsutoshi Hirayama

, Makoto Yokoo

and Hiroshi Matsuo

Nagoya Institute of Technology, Gokiso-cho Showa-ku Nagoya 466-8555, Japan

Florida Institute of Technology, Melbourne FL 32901, U.S.A.

Kobe University, 5-1-1 Fukaeminami-machi Higashinada-ku Kobe 658-0022, Japan

Kyushu University, 744 Motooka Nishi-ku Fukuoka 819-0395, Japan

Keywords:

Bottleneck, Fairness, Dynamic Programming, Search, A*, Route Optimization.

Abstract:

Route optimization is an important problem for single agents and multi-agent systems. In route optimization

tasks, the considered challenges generally belong to the family of shortest path problems. Such problems are

solved using optimization algorithms, such as the A* algorithm, which is based on tree search and dynamic

programming. In several practical cases, cost values should be as evenly minimized for individual parts of

paths as possible. These situations are also considered as multi-objective problems for partial paths. Since dy-

namic programming approaches are employed for the shortest path problems, different types of criteria which

can be decomposed with dynamic programming might be applied to the conventional solution methods. For

this class of problems, we employ a leximax-based criterion, which considers the bottlenecks and unfairness

among the cost values of partial paths. This criterion is based on a similar criterion called leximin for multi-

objective maximization problems. It is also generalized for objective vectors which have variable lengths.

We address an extension of the conventional A* search algorithm and investigate an issue concerning on-line

search algorithms. The inﬂuence of the proposed approach is experimentally evaluated.

1 INTRODUCTION

Route optimization is a critical problem for single

agents and multi-agent systems. Several tasks are

based on the optimization of routes, such as route

navigation for drivers, delivery services, and planning

for mobile robots. The goal of the route optimiza-

tion of agents is generally minimization of the total

cost on the optimal route. The A* search algorithm

is a fundamental path ﬁnding method that is based

on best-ﬁrst search and dynamic programming (Hart

and Raphael, 1968; Hart and Raphael, 1972). On the

other hand, in several practical problems, improving

bottlenecks and fairness among the cost values of the

individual parts in the optimal path might be an is-

sue. This is also a multi-objective optimization prob-

lem where each objectivecorrespondsto an individual

part of a path. Several criteria, which select a solu-

tion to a multi-objective problem, are known as social

welfare or scalarization functions (Sen, 1997; Marler

and Arora, 2004). Leximin is a criterion that con-

siders bottlenecks and fairness among the objectives

for multi-objectivemaximization problems (Bouveret

and Lemaˆıtre, 2009; Greco and Scarcello, 2013). This

criterion is based on the dictionary order of vectors

whose values are sorted in ascending order. Maxi-

mization on the leximin criterion maximizes the min-

imum objective and improves fairness. This approach

has been applied to resource allocation problems with

multiple objectives (Dritan and Pioro, 2008). For the

minimization problems, similar a criterion where the

objective values are sorted in descending order can be

applied.

In this study, we focus on a property that a prob-

lem which is deﬁned with this criterion can be decom-

posed into subproblems in ways similar to dynamic

programming (Matsui et al., 2014; Matsui et al.,

2015). Since the A* search algorithm is based on dy-

namic programming, we can employ a criterion that

resembles leximin. Therefore, in this work we ad-

dress the route optimization methods that improvethe

bottlenecks and the fairness of paths based on this

type of criterion. We apply a modiﬁed leximax cri-

terion that resembles leximin to the A* search algo-

rithm. We also investigate the possibility of incre-

mental optimization approaches for the exploration

Matsui, T., Silaghi, M., Hirayama, K., Yokoo, M. and Matsuo, H.

Study of Route Optimization Considering Bottlenecks and Fairness Among Partial Paths.

DOI: 10.5220/0006589000370047

In Proceedings of the 10th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2018) - Volume 1, pages 37-47

ISBN: 978-989-758-275-2

1 2 3

4 5 6

7 8 9

1 1

211

Figure 1: Lattice graph.

of agents in environments. In this investigation, we

note that the proposed operations have a characteris-

tic property where the lower bounds of the optimal

path might not converge to the optimal values under

the equation of the optimal principle. On the other

hand, the upper bounds converge to the optimal ones.

We address how this property can be mitigated in in-

cremental optimization methods.

The rest of this paper is organized as follows.

The next section introduces the backgrounds of this

study, including path ﬁnding problems, related so-

lution methods, and several concepts about bottle-

necks and fairness. Then we present our proposed ap-

proach where a modiﬁed leximax criterion is applied

to the A* search algorithm in Section 3. Section 4

describes approaches for the exploration of agents in

environments. The proposed approach is experimen-

tally evaluated in Section 5. Then several discussions

and conclusions are shown in Sections 6 and 7.

2 PRELIMINARIES

2.1 Route Optimization Problems

Route optimization problems are generally based on

the shortest path problem. We address a fundamental

problem, which is deﬁned with a weighted and undi-

rected graph G = hV, Ei. V and E are sets of ver-

tices and edges, respectively. We assume the edges

are undirected. For each edge e

i, j

∈ E, which is con-

nected to s

, s

∈ V, its cost value w

i, j

= ω(e

i, j

) is de-

ﬁned with function ω : e

i, j

→ Z+, where Z+ is a set

of positive integer values.

Path P is deﬁned as a sequence of vertices

, s

, ··· , s

) ∈ V

, where edge e

i,i+1

∈ E exists be-

tween each pair of vertices s

, s

i+1

∈ V. The cost of

path P is evaluated as

∑

n−1

i, j

. The shortest path

from start node s

∈ V to goal node s

∈ V is deﬁned

as the path with the minimum cost value among the

paths from s

to s

. Such a shortest path is considered

the optimal route.

In general settings, the aggregation of the cost val-

ues is deﬁned with a summation operator to evaluate

the total summation of the cost values in a path. The

goal of the route optimization problem is to minimize

the cost of the routes for the same pair of start and

goal nodes.

In this work, we assume that the cost values take

a small number of integer values, such as {1, 2} or

{1, ··· , 10}. The cost values basically represent levels

of unfavorableness.

In the following, we interchangeably use vertices

and nodes. In addition, we mainly address lattice

graphs, as shown in Fig. 1, for simple discussions of

such issues as heuristic distances. Here, the numbers

of the nodes correspond to identiﬁers of them. The

numbers for the edges correspond to their cost values.

2.2 Path Finding Algorithm based on

Dynamic Programming

A* search (Hart and Raphael, 1968; Hart and

Raphael, 1972) is a path ﬁnding algorithm based on

best-ﬁrst search and dynamic programming. This al-

gorithm performsa search process from a start node to

a goal node. In the process, the estimated cost values

(distances) of the optimal path are updated for the vis-

ited nodes by dynamic programming. When the goal

node is found, the optimal path is determined from

the stored information. In the exploration process, a

search method extends the nodes based on their esti-

mated cost values.

For each node s

∈ V, its estimated cost value of

optimal path f (s

) is deﬁned:

f(s

) = g(s

) + h(s

). (1)

Here g(s

) is the estimated cost value from the start

node to s

, and h(s

) is the estimated cost value from

to the goal node. While g(s

) is updated based

on dynamic programming in the exploration process,

h(s

) is given as a heuristic value

. h(s

) is admis-

sible when it is a correct lower bound value. For

lattice graphs, h(s

) can be deﬁned based on several

distance functions, such as the Manhattan and Euclid

distances, considering the lower bound cost values of

the edges.

The algorithm consists of two phases based on a

dynamic programming manner. In the ﬁrst phase, an

optimal and complete version of best-ﬁrst search is

performed from the start node s

updating each f(s

After the goal node s

is extracted, the second phase

is performed from the goal node to the start node to

compose the shortest path. See (Hart and Raphael,

1968; Hart and Raphael, 1972; Russell and Norvig,

2003) for details of the algorithm.

The actual algorithm maintains f(s

) as well as g(s

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

2.3 Real-time Search Algorithm

Real-time search algorithms are also path ﬁnding

methods based on search methods and dynamic pro-

gramming. Here the solution methods are designed so

that an agent employs exploration and exploitation in

a path ﬁnding. Initially, the agent is placed at the start

node with estimated cost values (e.g. h(s

) = 0 for all

∈ V). It explores in the environment and learns the

estimated optimal cost value of each node. Based on

these estimated cost values, the agent searches for the

goal node. After the agent arrives at the goal node, it

starts its next tour with the updated values.

An important point of this approach is that dy-

namic programming is assumed to be the agent’s

learning process. With an appropriate strategy and

learning rule, the estimated optimal cost value of each

node is improved by the number of tours. Learning

Real-Time A* (LRTA*) is such an algorithm. With it,

an agent performs the following steps at each node s

in a tour:

1. For all nodes s

adjacent to s

, the agent evaluates

estimated cost value f(s

) = w

i, j

+ h(s

2. The agent updates the estimated cost value so that

h(s

) ← min

f(s

3. It moves to the next node so that s

←

arg min

f(s

Note that in the above rule, the h(s

) value is both

the estimation value to be optimized and the penalty

value that is employed to escape from cyclic paths.

See (Barto et al., 1995) for details of this algorithm.

2.4 Bottlenecks and Fairness Among

Edges

Next we investigate the improvement of bottlenecks

and fairness among edges. In the example in Fig. 1,

let the start node be s

= 1 and the goal node be s

= 9.

In the minimization of conventional total cost values,

one optimal path is (1, 2, 3, 6, 9) and its cost is 5. On

the other hand, for minimization where the edges of

the maximal cost values are reduced, one optimal path

is (1, 2, 3, 6, 5, 8, 9), and its cost is 6. Note that there

are no edges with cost value 2 on this path. Here the

goal of the problem is not only to reduce the number

of edges with the maximum cost values but also to

reduce the total cost value by improving the fairness

among edges, if possible. Such paths might be inves-

tigated when an appropriate route must avoid highly

unsatisfactory speciﬁc residents and extra loads of

bottleneck facilities.

2.5 Multi-objective Optimization

Problems

In the class of multi-objective optimization prob-

lems, multiple objectives are simultaneously opti-

mized. The above route optimization problem with

bottlenecks and fairness is also a multi-objective op-

timization problem. Here we consider the following

multi-objective optimization problem: MOP.

Deﬁnition 1 (MOP). MOP is deﬁned with hX, D, Fi.

X is a set of variables, D is a set of domains of vari-

ables, and F is a set of objective functions. Variable

∈ X takes value from ﬁnite and discrete set D

∈ D.

For set of variables X

⊆ X, function f

∈ F is de-

ﬁned as f

i,1

, ··· , x

i,k

) : D

i,1

× ···× D

i,k

→ N, where

i,1

, ··· , x

i,k

∈ X

. f

i,1

, ··· , x

i,k

) is simply denoted by

). The goal of the problem is to simultaneously

optimize the objective functions under a criterion.

A combination of the values of the objective func-

tions is represented as an objective vector.

Deﬁnition 2 (Objective vector). Objective vector v

is deﬁned as [v

, ··· , v

]. For assignment A to the

variables in X

, v

is deﬁned as v

= f

↓X

Here the ideal goal is to maximize all the values

of the objective functions. However, in general cases,

the goal cannot be achieved since there are trade-

offs between the objectives. Therefore, based on the

Pareto dominance between objective vectors, one of

the Pareto optimal solutions is selected (Sen, 1997;

Marler and Arora, 2004).

2.6 Leximin

Since there are many Pareto optimal solutions in gen-

eral cases, several social welfare criteria and scalar-

ization functions are employed to select a solu-

tion (Sen, 1997; Marler and Arora, 2004).

Summation

∑

j=1

), which is found in con-

ventional social welfare, considers the efﬁciency of

the objectives. While maximization on the summation

achieves Pareto optimality, fairness among the objec-

tives is ignored. Maximin maximizes minimum objec-

tive value min

j=1

). Even though this improves

the worst case value among the objectives, the solu-

tion is not Pareto optimal. To ensure Pareto optimal-

ity, such additional tiebreaker criteria as summation

are necessary. Moreover, since only the minimum ob-

jective value is improved, other objective values are

not distinguished.

Leximin is deﬁned as the dictionary order on ob-

jective vectors whose values are sorted in ascending

order (Bouveret and Lemaˆıtre, 2009; Greco and Scar-

cello, 2013; Matsui et al., 2014; Matsui et al., 2015).

Study of Route Optimization Considering Bottlenecks and Fairness Among Partial Paths

Deﬁnition 3 (Sorted objective vector). The values of

sorted objective vector v are sorted in ascending or-

der.

Deﬁnition 4 (Leximin). Let v = [v

, ··· , v

] and v

′

, ··· , v

′

] denote the sorted objective vectors whose

length is K. The order relation, denoted with ≺

leximin

is deﬁned as follows. v ≺

leximin

′

if and only if

∃t, ∀t

′

< t, v

′

= v

′

∧ v

< v

′

Leximin is a criterion that repeats the comparison

between the minimum values in the vectors. Since

maximization on leximin is a subset of maximin, it

improves the worst case values. In addition, this max-

imization relatively improves the fairness and ensures

Pareto optimality.

The addition of two sorted objective vectors is de-

ﬁned with concatenation and resorting.

Deﬁnition 5 (Addition of sorted objective vec-

tors). Let v and v

′

denote vectors [v

, ··· , v

] and

′

, ··· , v

′

], respectively. The addition of two vectors,

v⊕ v

′

, is represented as v

′′

= [v

′′

, ···v

′′

K+K

′

], where v

′′

consists of all the values in v and v

′

. In addition, the

values in v

′′

are sorted in ascending order.

For the addition of sorted objective vectors, the

following invariance exists (Matsui et al., 2014).

Proposition 1 (Invariance of leximin on addition).

Let v and v

′

denote sorted objective vectors of the

same length. In addition, v

′′

denotes another sorted

objective vector. If v ≺

leximin

′

, then v ⊕ v

′′

≺

leximin

′

⊕ v

′′

Based on this invariance, dynamic programming

can be applied to solve optimization problems with

the leximin criterion (Matsui et al., 2014; Matsui

et al., 2015). However, we assume that the original

problem is decomposed into subproblems with objec-

tive vectors of the same length.

Moreover, a sorted objective vector can be repre-

sented as a vector of the sorted pairs of an objective

value and the count of the value (Matsui et al., 2014).

This representation corresponds to run-length encod-

ing and a sorted histogram. The comparison and the

addition of two sorted objective vectors can be di-

rectly performed on this representation.

2.7 Theil Index

As addressed above, several criteria, including sum-

mation and leximin, ensure Pareto optimality. Pareto

optimality is important in situations with selﬁsh mem-

bers; however, other measurements of inequality are

also critical. To evaluate the paths shown in later sec-

tions, we employ the Theil index, a well-known mea-

surement of inequality.

Deﬁnition 6 (Theil Index). For n objectives, Theil in-

dex T is deﬁned as

T =

∑

¯v

log

¯v

(2)

where v

is the utility or the cost value of an objective

and ¯v is the mean utility value for all the objectives.

The Theil index takes a value in [0, logn]. When

all utilities or cost values are identical, the Theil in-

dex value is zero. Inequalities on different number of

members can be compared using it. Note that the min-

imization on the leximin criterion does not assure the

decrement of the Theil index value, since it is basi-

cally a sequence of improvements of the worst value.

3 ROUTE OPTIMIZATION

CONSIDERING BOTTLENECKS

AND FAIRNESS

We address the route optimization problems that

consider bottlenecks and fairness among individual

edges. As shown in the previous section, the opti-

mization problem with the leximin criterion is decom-

posed with dynamic programming. Therefore, we in-

vestigate the approach that replaces the aggregation

of the cost values in the A* algorithm from the sum-

mation to a leximin-like criterion. Assuming the new

criterion for this optimization, the problem is rede-

ﬁned as follows.

The shortest path ﬁnding problem is deﬁned with

a weighted and undirected graph G = hV, Ei. The sets

V, E, weight values of edges, and Path P are deﬁned

similar to the original deﬁnition. The cost of path

P is aggregated as a objective vector instead of the

summation. Then the cost is compared based on a

criterion which is similar to the leximin, while it is

designed for minimization problems and the variable

length of vectors. The shortest path from start node

∈ V to goal node s

∈ V is deﬁned as the path with

the minimum cost value based on this criterion. Such

a shortest path is considered the optimal route.

The following two modiﬁcations must be ad-

dressed to employ the approach for maximization on

the leximin criterion.

• The maximization on leximin is replaced by the

minimization on leximax.

• The operations are extended for the subproblems

of different lengths of vectors.

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

3.1 Minimization on Leximax

For minimization problems, maximization on leximin

is replaced by the minimization of leximax. Although

leximax is similarly deﬁned as leximin, the ordering

of the values in the objective vectors is inverted.

Deﬁnition 7 (Descending sorted objective vector).

The values of a descending sorted objective vector are

sorted in descending order.

Deﬁnition 8 (Leximax). Let v = [v

, ··· , v

] and

′

= [v

′

, ··· , v

′

] denote descending objective vectors

whose lengths are K. The order relation, denoted with

≺

leximax

, is deﬁned as follows. v ≺

leximax

′

if and only

if ∃t, ∀t

′

< t, v

′

= v

′

∧ v

< v

′

With this modiﬁcation, the worst case values are

inverted to maximum cost values. Thus the objective

of the problem is also inverted to the minimization of

the aggregated objective values. While the addition of

two descending sorted objective vectors is similarly

deﬁned as the leximin, the ordering of the values in

each concatenated vector is the opposite.

3.2 Comparison of Vectors with

Different Lengths

In route optimization problems, when the path lengths

are different, the lengths of the corresponding objec-

tive vectors are also different. Therefore, we employ

the variable-length leximax, vleximax, whose deﬁ-

nition is extended for objective vectors of different

lengths.

Deﬁnition 9 (Vleximax). Let v = [v

, ··· , v

] and

′

= [v

′

, ··· , v

′

] denote descending sorted objective

vectors whose lengths are K and K

′

, respectively. For

K = K

′

, ≺

vleximax

is the same as ≺

leximax

. In other

cases, zero values are appended to one of the vectors

so that the both vectors have the same number of val-

ues. Then the vectors are comparedbased on ≺

leximax

Intuitively, this comparison is based on two modi-

ﬁed vectors which have the same sufﬁcient length by

padding blanks with zeros. Consider the two modiﬁed

vectors of inﬁnite length assuming the cost of zero for

each unused edge, which can contain the extra edges

outside of the system. Since the comparison of lexi-

max is based on tie-breaks from the beginning of the

both vectors, the redundant parts of zeros in both the

vectors can be ignored.

In the A* search algorithm for comparing two

paths based on vleximax, the corresponding descend-

ing sorted objective vector should be appropriately

aggregated.

3.3 Heuristic Distance Function

In the A* search algorithm, estimated cost value h(v

which is given by a heuristic distance function, should

be a lower bound value that does not exceed the op-

timal cost value. For example, in the case of lattice

graphs, such a heuristic function can be deﬁned with

the lower bound cost value for all the edges and the

Manhattan distance. For minimization on the summa-

tion, a heuristic value is the product of the Manhattan

distance and the lower bound cost value.

For minimization on the vleximax, such a heuris-

tic value is an objective vector that consists of dupli-

cates of the lower bound cost values, where the vector

length is identical to the Manhattan distance.

3.4 Correctness and Complexity of

Solution Method

When the objective vector of estimated cost h(v

) of

a heuristic distance function is a correct lower bound

one, the A* search algorithm selects one of the op-

timal paths. For lattice graphs, the Manhattan dis-

tance from a node to the goal node is the minimum

length of the possible vector. Therefore, the objec-

tive vector whose length is the same as the Manhattan

distance and whose values are duplicates of the low-

est cost value for all the edges is a lower bound for

the remaining optimal path. On the other hand, in

general cases, designing efﬁcient heuristic functions

might not be easy.

In addition, for minimization on summation,

heuristic cost value h(v

) can be simply deﬁned as

zero. Similarly, for minimization on leximax, an

empty vector can be employed as h(v

The comparison of two vectors of different lengths

based on vleximin activates a tiebreaker, where the

shorter vector is selected when the two vectors are

identical on their parts of the same length. In this case,

fewer edges are preferred. Since the estimation cost

is a lower bound, no incorrect path can be selected as

the optimal path, even if the lengths of the descending

sorted objective vectors are different. Therefore, the

solution method returns one of the optimal paths.

Even though the overhead of the computation re-

lated to vleximax is signiﬁcantly larger than that of

the summation and the comparison on scalar val-

ues, it is polynomial with the length of each vector.

When the sorted objective vector is represented as

run-length encoding or a histogram, the space com-

plexity of each vector is O(n) for n types of objective

values. If an array is employed for this vector repre-

sentation, the addition of two vectors increments the

Study of Route Optimization Considering Bottlenecks and Fairness Among Partial Paths

1 2 3

4 5 6

7 8 9

1 2

1 1

111

Figure 2: Lattice graph with walls.

count values whose complexity is O(n). The com-

plexity for the comparison of two vectors is also O(n).

4 INCREMENTAL

OPTIMIZATION

Next we focus on how the real-time search algorithm

can be generalized with the leximax criterion. Un-

fortunately, this is impossible due to a problematical

monotonicity on cyclic paths.

Consider the case shown in Fig. 2, where the

agents start from node 1. For the nodes adjacent to

node 1, h(2) + w

1,2

= [ ] + [1] = [1] and h(4) + w

1,4

[ ] + [2] = [2]. With the vleximax and the rules based

on the LRTA* shown in Section 2.3, the agent moves

to node 2 and updates h(1) to [1]. Then for the nodes

adjacent to node 2, h(1) + w

1,2

= [1] + [1] = [1, 1],

h(3) + w

2,3

= [ ] + [2] = [2], and h(5) + w

2,5

= [ ] +

[2] = [2]. Therefore, the agent returns to node 1 and

updates h(2) to [1, 1]. In the third step, for the nodes

adjacent to node 1, h(2)+ w

1,2

= [1, 1] +[1] = [1, 1, 1]

and h(4) + w

1,4

= [ ] + [2] = [2]. Therefore, the agent

returns to node 2 again and repeats this round-trip for-

ever to add cost value 1 to h(1) and h(2).

The above example reveals the necessity of other

approaches for exploration in the case of sorted ob-

jective vectors with variable lengths when there can

be cyclic paths. Such cyclic paths can be detected

with a threshold length. Then some such incorrect

vectors can be replaced by appropriate vectors that

break the cyclic movements. However, such an ap-

proach might be problematic, since the invariance of

vleximin does not hold and may affect the correctness

of the dynamic programming.

4.1 Episode-based Approach

Here we address more safe approaches with a rela-

tively direct extension of conventional search algo-

rithms. Since the dynamic programming is correct,

we employ episode-based learning, where the learn-

ing phases are separated from the exploration phase.

This approach is also called off-line learning.

Assume that a complete path between the start and

goal nodes was obtained from an exploration phase.

Cyclic paths are allowed to increase the learning op-

portunities.

Then the path is scanned from the goal node to the

initial start node by updating corresponding estimated

values h(s

) except the goal node. Note that here s

denotes the k

value from the initial start node on a

path:

1. The agent evaluates f(s

k+1

) = w

i, j

+ h(s

k+1

where w

i, j

corresponds to edge e

i, j

between s

and

k+1

2. If h(s

) has not been updated yet, it is up-

dated by f(s

k+1

). Otherwise, it is updated by

min( f(s

k+1

), h(s

)).

In the example of Fig. 2, assume that an episode

of nodes (1, 2, 3, 6, 5, 2, 3, 6, 9) has been performed in

the initial trial. Since the node 9 is the goal node,

h(9) holds empty vector []. Then h(6) is updated by

f(9) = [] + [1] = [1]. Similarly, for their previous part

of nodes (5, 2, 3), h(3) = [1, 1], h(2) = [1, 1, 2], h(5) =

[1, 1, 2, 2] are updated. However, for their previous

node 6, h(6) holds its vector by min( f(5), h(6)) =

min([1, 1, 1, 2, 2], [1]) = [1]. h(3) = [1, 1] and h(2) =

[1, 1, 2] are also unchanged for the previous part of

nodes (3, 2). Finally, h(1) is updated by [1, 1, 1, 2].

The above h(s

) is the upper bound of the optimal

cost value from s

to the goal node, since it is up-

dated by the propagation from the goal node. When

the agent’s explorations are sufﬁcient, h(s

) converges

to the optimal value, since the algorithm exactly per-

forms partial updates of the dynamic programming.

4.2 Boundaries of Paths

While the above episode-based approach needs com-

plete paths to the goal nodes, it converges with ap-

propriate exploration strategies. The other problem of

the above simple update rule is that it does not employ

the information of neighborhood nodes which are not

on the path. Also, the algorithm cannot evaluate the

lower bound cost values which can be employed by

best-ﬁrst strategies.

Here we address the lower bound of optimal cost

value h

) and the upper bound value h(s

). The

boundaries h

) and h(s

) of the estimated cost val-

ues are initialized as follows:

1. Except for the goal node, h

) and h(s

) are ini-

tialized to [ ] and [⊤···⊤], respectively, where ⊤

denotes the maximum cost value. h(s

) must con-

tain a sufﬁcient number of duplicates of the maxi-

mum cost value to exceed the other objective vec-

tors in the manner of vleximin.

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

2. On the other hand, for the goal node, the initial

value of h(s

) and h(s

) is [ ].

Except for the goal node, node s

updates its h

)

and h(s

) as follows:

h(s

) ← max(h(s

), min

i, j

+ h(s

))) (3)

h(s

) ← min(h(s

), min

i, j

+ h(s

))), (4)

where s

denotes all the nodes adjacent to s

. Here we

update h

) and h(s

) at the same time.

When a path is obtained from an exploration

phase, the following operations are performed.

1. The path is scanned from the goal node to the ﬁrst

node.

2. Except for the goal node, each node s

on the path

updates its h

) and h(s

With the above boundaries the exploration and

learning phases perform parts of dynamic program-

ming. We consider that the boundaries of node s

have

converged when h

) ≥ h(s

). In the case of the con-

ventional summation, the boundaries eventually con-

verge. However, in the case of the vleximax, the con-

vergence is not guaranteed. Consider the example

shown in Fig. 2 again. Assuming that h

(3), h(4), and

(5) take zero, from the initial state, h(1) and h(2)

increase such that [ ], [1], [1, 1], [1, 1, 1], ··· , [1, · · · , 1]

by turns. These vectors never overcome a vector

[2]. Similar cases occur in actual propagations even

if an episode does not contain cyclic paths. For a non

cyclic path (1, 2, 3, 6, 9), the lower bounds are updated

for the sequence of nodes 1 and 2 in reverse order.

If other paths of different episodes contain these two

nodes, they are repeatedly updated in a way that is

similar to the above manner.

This situation resembles LRTA* which is not eas-

ily generalized with vleximax. In this problem, the

upper bounds of cost vectors still follow the principle

of optimality. On the other hand, the lower bounds

might not converge to the optimal vectors, while their

lengths monotonically increase. This property also

resembles that of negative cyclic paths. The A* al-

gorithm dose not affected by this property, since it is

based on the propagation of cost values from the node

of zero cost. In addition, the algorithm does not as-

sume cyclic paths. However, LRTA* is affected by

the property, since its behavior is completely based

on the lower bounds. Therefore, the on-line search

might be caught by cyclic paths.

To mitigate such situations, we revise the cor-

rupted lower bound as follows.

1. When the length of h

) exceeds the number of

edges, h

) is replaced by f (s

) which is the sec-

ond smallest value: f

) = secondmin

i,k

h(s

)). If such all values are corrupted, it means

that there is no information to ﬁx the boundaries.

Therefore, the agent do nothing and wait for fu-

ture propagations from outside.

2. This modiﬁcation may cause the situation of

) 6≤ h(s

) as a result of propagations. In this

case, h

) is replaced by h(s

This approach is not exact but based on the im-

mediate convergence of upper bounds. Since we em-

ploy an off-line learning which updates both upper

and lower bounds simultaneously from the node of

zero cost (i.e. the goal node), the convergence of up-

per bounds will be faster than the lower bounds in

general cases. In addition, the revision of a broken

lower bound vector is performed when its length ex-

ceeds a threshold. It also delays the convergence of

the lower bounds. When these assumptions are suf-

ﬁciently satisﬁed, it is expected that the solution will

resemble the one of A*.

4.3 A Heuristic Exploration

The exploration strategies should cover all solutions

with boundaries. Even though arbitrary exploration

strategies can be employed, we employ a heuristic ex-

ploration strategy as follows. We added the following

information to each node s

• the counter vstcnt

of visits to the node in each

tour. The counter is reset to zero in the beginning

of each exploration process.

• the last visit time lasttime

to the node. This infor-

mation is stored through the optimization process.

We employ a logical time which is incremented

after it is stored to a lastime

. In the initial state,

all lasttime

are set to zero.

Similarly, the following information is added to

each edge.

• the counter selcnt

i, j

of selection of the edge e

i, j

in each tour. The counter is reset to zero in the

beginning of each exploration process.

With the above information, the following rules

are applied to an agent on s

adjacent to nodes s

1. If s

is the goal node, s

has the ﬁrst priority.

2. For s

and an edge e

i, j

, if h

) 6= h(s

) and

selcnt

i, j

= 0, s

has the second priority. This rule

assures to evaluate unexplored edges even if those

cost values are relatively high.

3. The node s

who has a smaller vstcnt

has the third

priority. With this rule, the agent will avoid cyclic

paths if possible.

Study of Route Optimization Considering Bottlenecks and Fairness Among Partial Paths

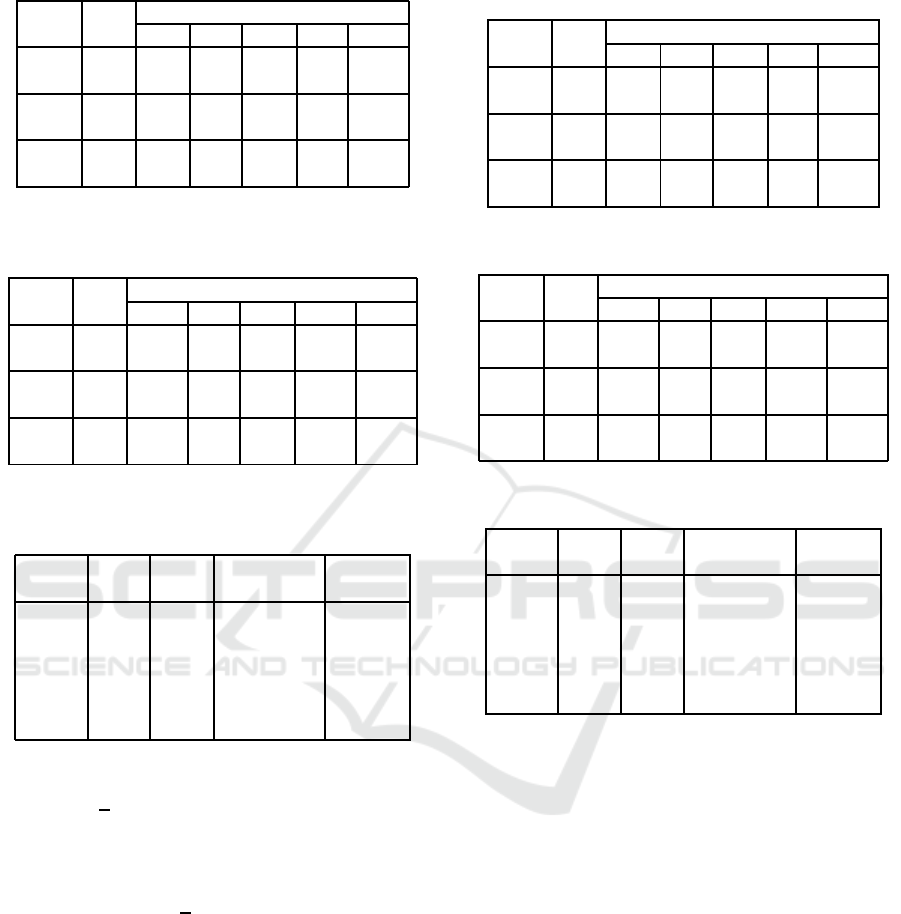
Table 1: Solution qualities: lattice graph of 10× 10 nodes.

Cost Alg. Solution quality

sum. min. max. len. theil

[1, 2] sum. 20.7 1 2 18 0.039

lxm. 21.9 1 2 19.6 0.032

[1, 5] sum. 34.3 1 4 18 0.135

lxm. 41.3 1 3.4 22.4 0.095

[1, 10] sum. 58.6 1 7.7 18.4 0.223

lxm. 74.4 1 6.6 23.2 0.147

Table 2: Solution qualities: Lattice graph of 100 × 100

nodes.

Cost Alg. Solution quality

sum. min. max. len. theil

[1, 2] sum. 213.2 1 2 198 0.025

lxm. 286.9 1 2 282.8 0.006

[1, 5] sum. 346.1 1 5 199.6 0.132

lxm. 446.7 1 3.6 275.6 0.085

[1, 10] sum. 580.8 1 9.5 202.8 0.215

lxm. 960.3 1 6.8 350 0.128

Table 3: Computational cost: lattice graph of 100 × 100

nodes.

cost alg. iter. num. of exec.

opn. nodes time [s]

[1, 2] sum. 7217 7537 0.022

lxm. 8359 8883 0.070

[1, 5] sum. 9989 9996 0.020

lxm. 9497 9923 0.078

[1, 10] sum. 9996 9999 0.019

lxm. 8468 9182 0.172

4. When vstcnt

are identical, the node s

who has

a lower h(s

) has the fourth priority. This is the

best-ﬁrst strategy, which is guided by the above

rules.

5. When vstcnt

and h

) are are identical, respec-

tively, then the node s

with older lasttime

has

the ﬁfth priority. With this rule, ties will be ex-

plored deterministically.

Due to the above boundaries and the heuristic ex-

ploration, the resulting solution method might be an

inexact method; however they ﬁt particular intuitions

based on our experience. As the ﬁrst study, we experi-

mentally employ the aboveapproach assuming simple

graphs. The necessity of such a guided approach for

the vleximax criterion reveals the difﬁculty of design-

ing an on-line optimization algorithm for this class of

problems.

Table 4: Solution qualities: lattice graph of 10 × 10 nodes

(start nodes in the middle).

cost alg. solution quality

sum. min. max. len. theil

[1, 2] sum. 11.8 1 2 10 0.045

lxm. 12.5 1 1.8 11 0.037

[1, 5] sum. 20 1 3.7 10 0.133

lxm. 26.4 1 3.4 14.2 0.096

[1, 10] sum. 34.5 1.2 7.1 10.4 0.199

lxm. 50.6 1.1 6.3 15.4 0.134

Table 5: Solution qualities: Lattice graph of 100 × 100

nodes (start nodes in the middle).

cost alg. solution quality

sum. min. max. len. theil

[1, 2] sum. 108.5 1 2 100 0.027

lxm. 149.5 1 1.8 147 0.006

[1, 5] sum. 178.5 1 4.9 100.8 0.132

lxm. 223.2 1 3.4 135 0.087

[1, 10] sum. 301 1 9 103.2 0.213

lxm. 592.1 1 6.3 214.8 0.130

Table 6: Computational cost: lattice graph of 100 × 100

nodes (start nodes in the middle).

cost alg. iter. num. of exec.

opn. nodes time [s]

[1, 2] sum. 1993 2182 0.004

lxm. 7013 7371 0.066

[1, 5] sum. 4702 4860 0.009

lxm. 9214 9702 0.105

[1, 10] sum. 7023 7217 0.016

lxm. 7759 8402 0.175

5 EVALUATION

We experimentally evaluated the proposed approach.

First, we evaluated the modiﬁed A* search algorithm.

The example problems are based on lattice graphs that

consist of 10 × 10 and 100 × 100 nodes. Start node

and goal node s

are the left-top and right-bottom

nodes. Each edge has an integer cost value in [1, 2],

[1, 5], or [1, 10]. The cost value is randomly set based

on uniform distribution. Ten problem instances are

averaged for each set of parameters. We experimen-

tally compared the conventional method based on the

summation ‘sum.’ and the proposed method based

on leximax (vleximax) ‘lxm.’. The experiment was

performed on a computer with a Core i7-3930K CPU

(3.20 GHz), 16-GB memory, Linux 2.6.32, and g++

(GCC) 4.4.7.

Tables 1 and 2 show the solution qualities. The

cost values in each solution are evaluated with the

summation, the minimum value, the maximum value,

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

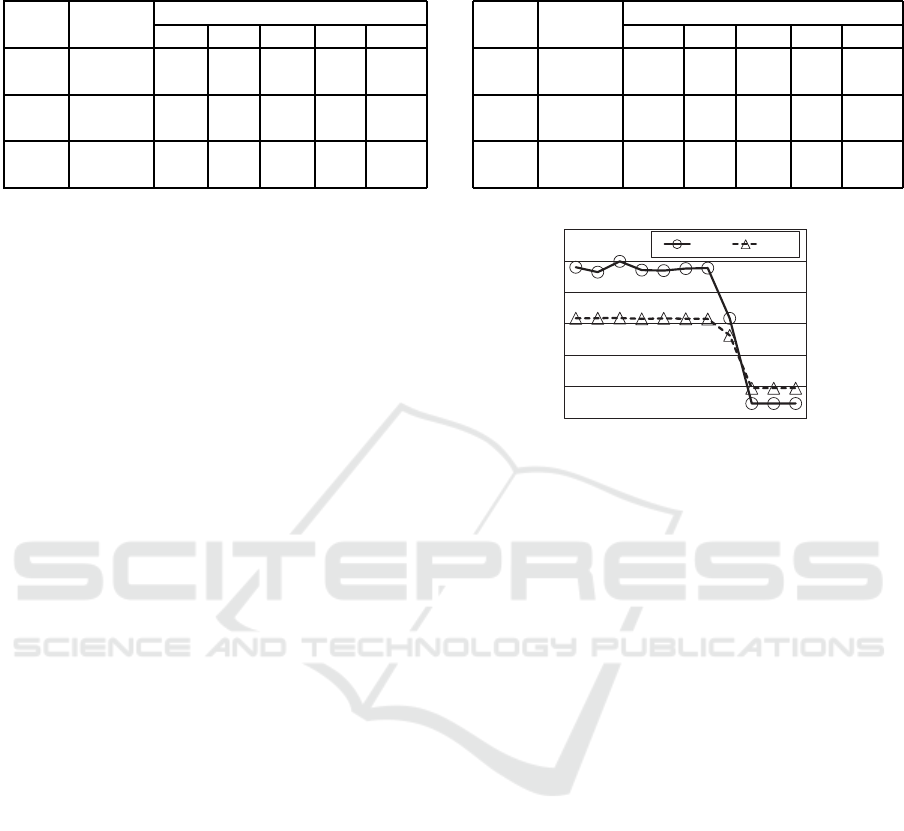
Table 7: Solution qualities: lattice graph of 10× 10 nodes

(lxm) (A* and learning).

cost alg. solution quality

sum. min. max. len. theil

[1, 2] lxm. A* 21.9 1 2 19.6 0.032

lxm. lrn. 21.9 1 2 19.6 0.032

[1, 5] lxm. A* 41.3 1 3.4 22.4 0.095

lxm. lrn. 41.3 1 3.4 22.4 0.095

[1, 10] lxm. A* 74.4 1 6.6 23.2 0.147

lxm. lrn. 74.4 1 6.6 23.2 0.147

the number of values (len.), and the Theil index

(theil). The Theil index is a criterion of unfairness,

where smaller values represent less unfairness. The

results show that the solution method ‘lxm.’ reduced

bottlenecks and unfairness with trade-offs between

them and the summation. It also reduced the Theil in-

dex on average. In addition, the maximum cost value

was reduced whenever possible.

Table 3 shows the computational cost. We eval-

uated the computational cost as the number of oper-

ations for the nodes (iter.), the number of extended

nodes (num. of opn. nodes), and the execution

time. The result reveals that the heuristic cost func-

tion based on the Manhattan distance on the grids is

not very efﬁcient. While most of the nodes were ex-

tended, there were several opportunities for pruning,

even for the solution method ‘lxm.’ The execution

time of ‘lxm.’ signiﬁcantly exceeded that of ‘sum.’

due to the operations on the sorted objective vectors

and vleximax. But overhead might be allowed in rel-

atively small problems.

With the same set of graphs, we evaluated the

cases where a start node s

is almost in the center of

a graph, while a goal node is the right-bottom node.

Tables 4 and 5 show the solution qualities. The results

resemble the cases of the previous setting. Similarly,

Table 6 shows the computational cost. In this result,

the number of extracted nodes is relatively less than

that of the previous setting. It is considered as the

effect of the heuristic distance function of the A* al-

gorithm. On the other hand, the reduction for ‘lxm.’

is relatively small. This reveals the difﬁculty of de-

signing heuristic distance functions for the criterion.

We also evaluated the optimization methods for

the exploration agents. Here 10 × 10 and 20 × 20

lattice graphs with left-top start nodes s

and right-

bottom goal nodes s

are employed. The A* algo-

rithm based on vleximax (‘lxm. A*’) and the incre-

mental solution method (‘lxm. lrn.’) were evaluated.

With preliminary experiments, we set appropriate pa-

rameters so that the incremental solution method ob-

tains episodes and the solution quality converges. Ta-

Table 8: Solution qualities: lattice graph of 20 × 20 nodes

(lxm) (A* and learning).

cost alg. solution quality

sum. min. max. len. theil

[1, 2] lxm. A* 46.8 1 1.9 44.8 0.016

lxm. lrn. 46.8 1 1.9 44.8 0.016

[1, 5] lxm. A* 77.4 1 3.4 45.4 0.102

lxm. lrn. 77.4 1 3.4 45.4 0.102

[1, 10] lxm. A* 145.7 1 6.6 50.6 0.145

lxm. lrn. 145.7 1 6.6 50.6 0.145

0.05

0.1

100

200

300

400

500

600

100 300 500 700 900 1100

theil

sum.

trial

sum theil

Figure 3: Incremental optimization with vleximax: 20× 20

nodes, w

i, j

= [1, 2].

bles 7 and 8 shows the solution quality. Since both

methods obtain similar results, it is considered that

the heuristic approaches of the incremental solution

method are relatively reasonable.

Figures 3-5 show the learning progress of the in-

cremental solution methods. Each graph shows the

anytime curves of the summation and the Theil in-

dex for an actual result. The samples are averaged

for every 100 trials. Note that the results can vary

for instances, since we employed a relatively exhaus-

tive exploration based on best-ﬁrst search. The results

show that the summation and the Theil index were

gradually improved and converged. In addition, the

Theil index was relatively small in early trials when

the range of cost values was also narrow.

6 DISCUSSION

Since maximization on (v)leximax improves the

worst case values, the summation of the cost values

is increased as a trade-off. When the range of the

cost values is relatively large, the trade-off is empha-

sized, and hence the increment of the summation of

the cost values grows. The length of the optimal vec-

tor, namely the number of edges in the optima path,

also grows. Additional approaches, such as limita-

tions on the ranges of the cost values or controls of

Study of Route Optimization Considering Bottlenecks and Fairness Among Partial Paths

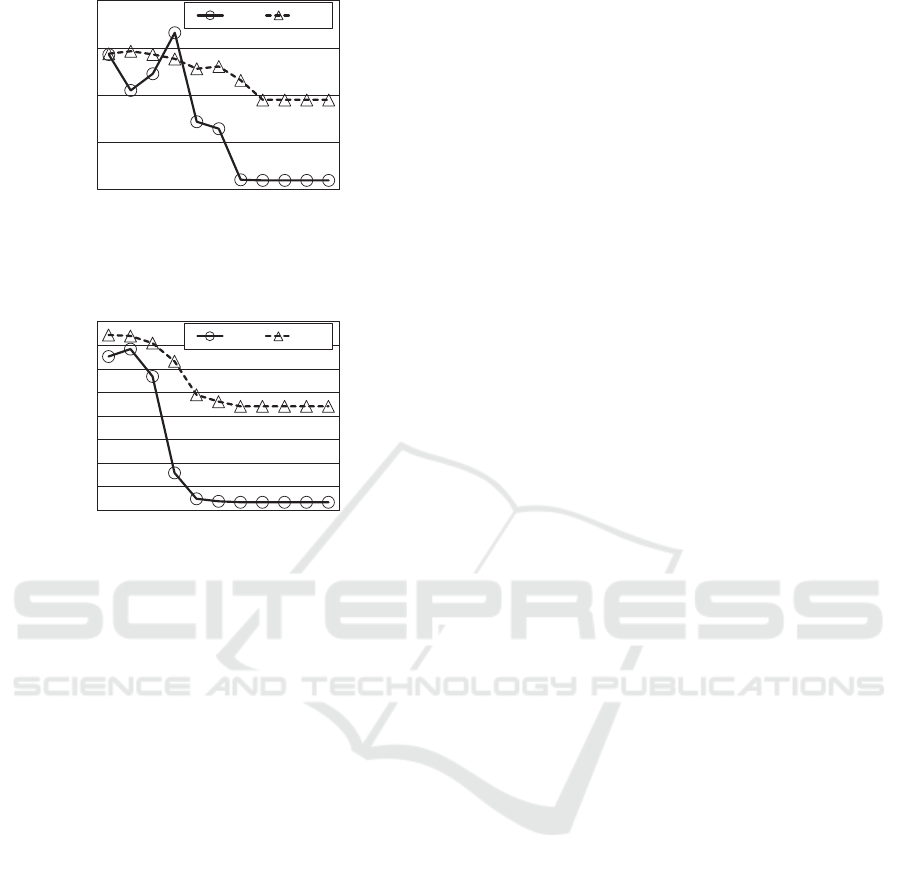
0.05

0.1

0.15

0.2

500

1000

1500

2000

100 300 500 700 900 1100

theil

sum.

trial

sum theil

Figure 4: Incremental optimization with vleximax: 20× 20

nodes, w

i, j

= [1, 5].

0.05

0.1

0.15

0.2

500

1000

1500

2000

2500

3000

3500

4000

100 300 500 700 900 1100

theil

sum.

trial

sum theil

Figure 5: Incremental optimization with vleximax: 20× 20

nodes, w

i, j

= [1, 10].

criteria, are necessary to reduce the trade-offs. On the

other hand, the proposed method’s solution can pro-

vide an analysis based on a criterion that addressed

bottlenecks and fairness.

In this work, we assumed lattice graphs and em-

ployed a distance function based on the Manhattan

distance, which relays the possible minimum length

of the vectors. For other topologies of the graphs and

more efﬁcient estimations, additional considerations

are necessary.

In general, most criteria that strictly address fair-

ness cannot be easily decomposed into parts based on

dynamic programming. In this study, we focused on

how leximin/leximax-based criteria can be applied to

dynamic programming methodsfor path ﬁnding prob-

lems. Even though the aggregation and the compari-

son of the criteria can almost be directly applied, the

exploration process needs other methods to avoid in-

correct results due to the problematical monotonicity

of lower bound vectors on cyclic paths.

In addition, leximin/leximax is different from

summation in several aspects. For example, when the

two neighboring edges are aggregated into an edge,

the resulting edge can be related to the aggregation of

the two original cost values. While the resulting cost

value is still a scalar value for the summation, a vec-

tor of two values is necessary to maintain the original

information for the leximin/leximax. Such general-

ization needs more investigation.

Since this criterion is simply deﬁned without pa-

rameters, the trade-offs among bottleneck, fairness

and effectiveness are ﬁxed. Several modiﬁcations or

different criteria that can be decomposed with dy-

namic programming will be necessary to maintain the

trade-offs.

7 CONCLUSION

We addressed route optimization methods that con-

sider bottlenecks and fairness on optimal paths using

maximization on leximax criteria. The experimental

results shows that our proposed approach reduced the

cases of the worst cost values and relatively improved

the fairness in the optimal path. Future work will

improve the solution methods including better heuris-

tic functions and investigations about similar criteria

with more appropriate tunings of trade-offs between

efﬁciency and fairness. The opportunities of on-line

learning and reinforcement learning will also be inter-

esting issues.

ACKNOWLEDGEMENTS

This work was supported in part by JSPS KAKENHI

Grant Number JP16K00301.

REFERENCES

Barto, A. G., Bradtke, S. J., and Singh, S. P. (1995). Learn-

ing to act using real-time dynamic programming. Ar-

tiﬁcial Intelligence, 72(1-2):81–138.

Bouveret, S. and Lemaˆıtre, M. (2009). Computing leximin-

optimal solutions in constraint networks. Artiﬁcial In-

telligence, 173(2):343–364.

Dritan, N. and Pioro, M. (2008). Max-min fairness and its

applications to routing and load-balancing in commu-

nication networks - a tutorial. IEEE Communications

Surveys and Tutorials, 10(4):5–17.

Greco, G. and Scarcello, F. (2013). Constraint satisfac-

tion and fair multi-objective optimization problems:

Foundations, complexity, and islands of tractability.

In Proc. 23rd International Joint Conference on Arti-

ﬁcial Intelligence, pages 545–551.

Hart, P., N. N. and Raphael, B. (1968). A formal basis

for the heuristic determination of minimum cost paths.

IEEE Trans. Syst. Science and Cybernetics, 4(2):100–

107.

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

Hart, P., N. N. and Raphael, B. (1972). Correction to ’a for-

mal basis for the heuristic determination of minimum-

cost paths’. SIGART Newsletter, (37):28–29.

Marler, R. T. and Arora, J. S. (2004). Survey of

multi-objective optimization methods for engineer-

ing. Structural and Multidisciplinary Optimization,

26:369–395.

Matsui, T., Silaghi, M., Hirayama, K., Yokoo, M., and Mat-

suo, H. (2014). Leximin multiple objective optimiza-

tion for preferences of agents. In 17th International

Conference on Principles and Practice of Multi-Agent

Systems, pages 423–438.

Matsui, T., Silaghi, M., Okimoto, T., Hirayama, K., Yokoo,

M., and Matsuo, H. (2015). Leximin asymmetric mul-

tiple objective DCOP on factor graph. In 18th In-

ternational Conference on Principles and Practice of

Multi-Agent Systems, pages 134–151.

Russell, S. and Norvig, P. (2003). Artiﬁcial Intelligence: A

Modern Approach (2nd Edition). Prentice Hall.

Sen, A. K. (1997). Choice, Welfare and Measurement. Har-

vard University Press.

Study of Route Optimization Considering Bottlenecks and Fairness Among Partial Paths