CARS - A Spatio-temporal BDI Recommender System:

Time, Space and Uncertainty

Amel Ben Othmane

, Andrea Tettamanzi

, Serena Villata

and Nhan Le Thanh

Universit

e C

ote d’Azur, ADEME, Inria, CNRS, I3S, France

Universit

e C

ote d’Azur, CNRS, Inria, I3S, France

Keywords:

Region Connection Calculus, Allen’s Intervals, Fuzzy Sets.

Abstract:

Agent-based recommender systems have been exploited in the last years to provide informative suggestions

to users, showing the advantage of exploiting components like beliefs, goals and trust in the recommenda-

tions’ computation. However, many real-world scenarios, like the trafﬁc one, require the additional feature of

representing and reasoning about spatial and temporal knowledge, considering also their vague connotation.

This paper tackles this challenge and introduces CARS, a spatio-temporal agent-based recommender system

based on the Belief-Desire-Intention (BDI) architecture. Our approach extends the BDI model with spatial

and temporal information to represent and reason about fuzzy beliefs and desires dynamics. An experimental

evaluation about spatio-temporal reasoning in the trafﬁc domain is carried out using the NetLogo platform,

showing the improvements our recommender system introduces to support agents in achieving their goals.

1 INTRODUCTION

Agent-based recommender systems (Casali et al.,

2008a; Chen and Cheng, 2010; Batet et al., 2012;

Othmane et al., 2016b) have been proposed in the last

years in different scenarios, like tourism, health-care,

and trafﬁc, to provide suggestions and support users

to achieve their goals. The advantage of such sys-

tems is that of encoding users’ beliefs and goals in

the system to return a recommendation which is as

close as possible to their needs, with the possibility to

include additional information like the conﬁdence in

the source. In addition, several application scenarios

require to formalize knowledge about the time and the

location in which the action is taking place. This in-

formation often needs to be considered as a whole, as

in the case of the trafﬁc scenario, where a trafﬁc jam

is identiﬁed by its location and the time it is occurring

during the day, and require to encode a certain degree

of vagueness as well.

In this paper, we answer the following research

question:

• how to represent and reason about fuzzy spatial-

temporal knowledge to provide useful recommen-

dations?

To answer this question, we introduce CARS,

a spatio-temporal Cognitive Agent-based Recom-

mender System, extending with spatio-temporal in-

formation the system proposed by (Othmane et al.,

2016b). Based on the extension principle of fuzzy set

theory (Zadeh, 1975), we deﬁne a fuzzy counterpart

of Allen’s intervals (Allen, 1983) to model temporal

knowledge, while fuzzy topological relations are de-

ﬁned in terms of a fuzzy extension of the region con-

nection calculus (Randell et al., 1992), whereby re-

gions are represented as fuzzy sets. These two com-

ponents, namely spatial and temporal information, are

combined together based on the assumption that the

degree to which a spatio-temporal belief is true is

the minimum between the conﬁdence degrees of the

spatial belief and temporal one, respectively. Spatio-

temporal knowledge is thus exploited by agents to

update their beliefs following the other agents’ rec-

ommendations, with the aim to reach their goals. To

show the advantages of the proposed agent-based rec-

ommender system, we address an empirical evalua-

tion in a simulated environment using the NetLogo

platform. In particular, we consider the trafﬁc sce-

nario, where the goal of the agents is to reach a cer-

tain point of interest in the fastest way as possible.

The results of the simulations show that CARS allows

agents to faster reach their own destinations with re-

spect to the baseline, where no recommendation to the

agents is provided.

To the best of our knowledge, CARS is the ﬁrst

Othmane, A., Tettamanzi, A., Villata, S. and Thanh, N.

CARS - A Spatio-temporal BDI Recommender System: Time, Space and Uncertainty.

DOI: 10.5220/0006590700480057

In Proceedings of the 10th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2018) - Volume 1, pages 48-57

ISBN: 978-989-758-275-2

agent-based recommender system taking into account

at the some time i) spatial and temporal knowledge,

and ii) the vagueness and incompleteness typical of

these components. Related work considers either

spatial or temporal knowledge without providing a

unique reasoning model (Jarvis et al., 2005), or does

not take into account the fuzzy connotation of spatio-

temporal knowledge (Schuele and Karaenke, 2010;

Behzadi and Alesheikh, 2013).

The rest of the paper is organized as follows. After

some preliminaries, Section 3 formally introduces the

spatio-temporal fuzzy representation of the agents’

beliefs as well as their update mechanism. Section 4

describes the experimental setting and discusses the

results. The discussion of the related work and con-

clusions end the paper.

2 PRELIMINARIES

In this section, we provide some background about

the formalisms we adopt to introduce our spatio-

temporal fuzzy representation of beliefs and goals.

2.1 Region Connection Calculus

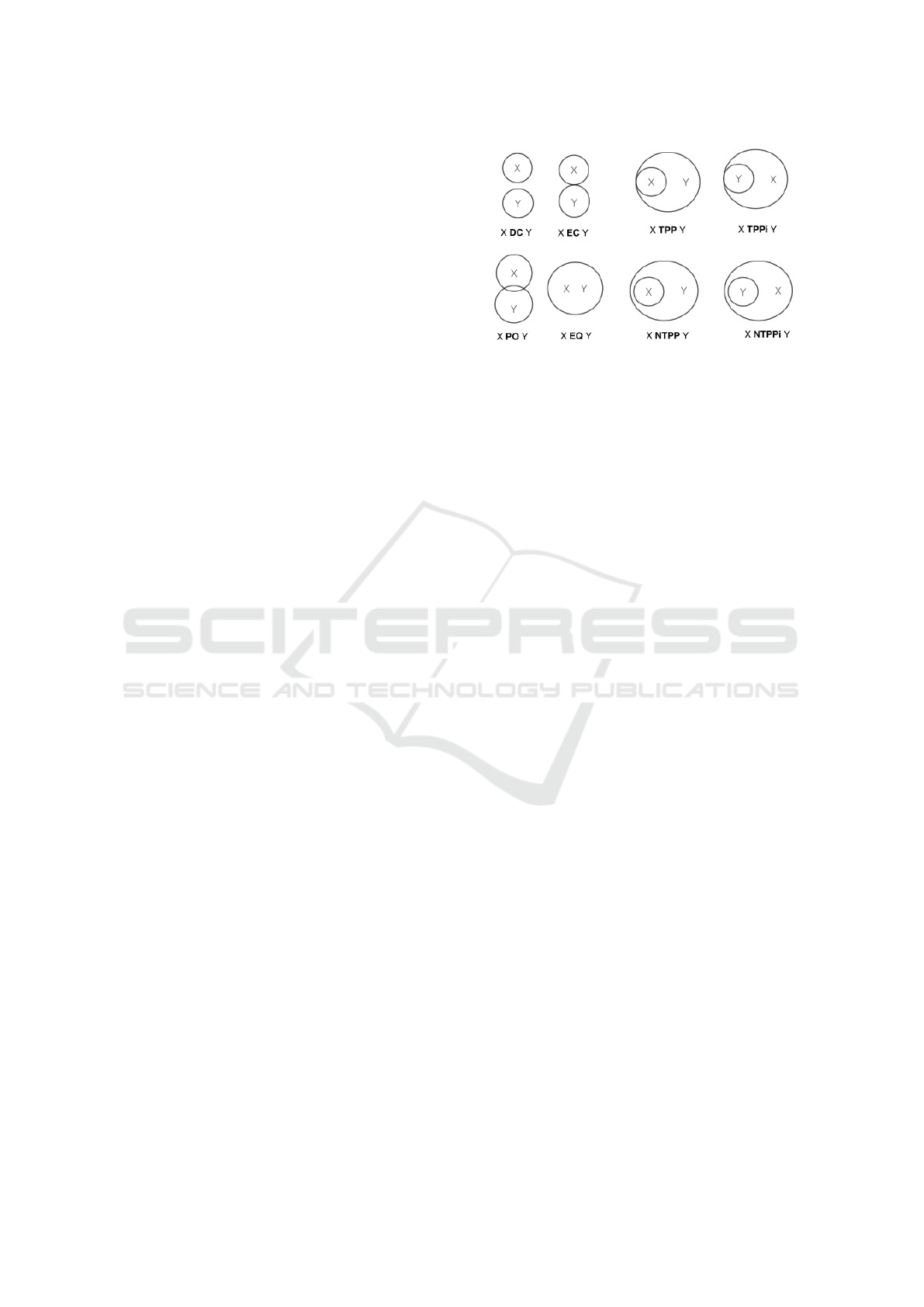
One of the most important formalisms for topologi-

cal relationships is the Region Connection Calculus

(RCC) (Randell et al., 1992). The RCC is an ax-

iomatization in ﬁrst order logic of certain spatial con-

cepts and relations. The basic theory assumes just one

primitive dyadic relation: C(x,y), to be read as “x con-

nects with y”. RCC has eight basic relations (illus-

trated in Figure 1): DC (DisConnected), EC (Exter-

nally Connected), PO (Partial Overlap), EQ (EQual),

TPP (Tangential Proper Part), NTPP (Non Tangential

Proper Part) and their converse relations TPPi (TPP

inverse) and NTPPi (NTPP inverse). The formal def-

inition of the spatial relation entailed in the RCC is

given in Table 1 for reference. For further details

about RCC, we refer the reader to (Randell et al.,

1992).

2.2 Allen’s Intervals Algebra

Allen’s Interval Algebra (Allen, 1983) is an alge-

bra of binary relations on intervals for representing

and reasoning about qualitative temporal information.

Allen’s approach is based on the notion of time inter-

vals and binary relations among them. A time inter-

val X is an ordered pair hX

−

i such that X

−

< X

where X

−

and X

are interpreted respectively as the

starting and ending points of the interval. Allen in-

troduces thirteen basic interval relations, illustrated in

Figure 1: The main RCC-8 relations.

Table 2: ≺ (before), m (meets), o (overlaps), d (dur-

ing), s (starts), f (ﬁnishes), their converse relations

(, m

, o

, d

, s

, f

), and = (equal), where each basic

relation can be deﬁned in terms of relations involv-

ing its endpoints. For example, the interval relation-

ship X

Y (interval X occurs during interval Y) can be

expressed as (X

−

> Y

−

) ∧ (X

< Y

). We refer the

reader to (Allen, 1983) for a more detailed discussion.

2.3 Fuzzy set Theory

Fuzzy set theory (Zadeh, 1965) deals with sets or cat-

egories whose boundaries are blurred or gradual. A

fuzzy set is a set of objects whose membership to the

set takes a value between zero and one. Each fuzzy

object can have partial or multiple memberships. A

fuzzy set A in universe of discourse X is mathemati-

cally characterized by a membership function µ

(x),

which associates with each x in X a real number in the

interval [0,1], with the membership value at x repre-

senting the “degree of membership” of x in A.

Let X be a set of objects, called the the universe,

whose elements are denoted x. A membership in a

fuzzy subset A of X is deﬁned by the membership

function µ

from A to {0,1} such that

(x) =



1 iff x ∈ A

0 iff x /∈ A

The closer the value of µ

(x) is to 1, the more x

belongs to A. A is a subset of X that has no sharp

boundary and is characterized by a set of pairs A =

{(x,µ

(x)),x ∈ X }. When X is a ﬁnite set {x

,...,x

a fuzzy set is expressed as A =

∑

i=1

)/x

; when x

is not ﬁnite, we write A =

(x)/x.

2.4 The Extension Principle

The extension principle (Zadeh, 1975) provides a way

to extend non-fuzzy mathematical concepts to deal

CARS - A Spatio-temporal BDI Recommender System: Time, Space and Uncertainty

Table 1: Deﬁnition of spatial relations entailed in the RCC. U is the universe of all regions; x and y are variables denoting

arbitrary elements of U, i.e. regions.

Name Relation Deﬁnition

Disconnected DC(x,y) ¬C(x,y)

Part P(x,y) ∀z ∈ U,C(z,x) → C(z,y)

Proper Part PP(x,y) P(x,y) ∧ ¬P(y,x)

Equals EQ(x,y) P(x,y) ∧ P(y,x)

Overlaps O(x,y) ∃z ∈ U, P(z, x) ∧ P(z,y)

Discrete DR(x,y) ¬O(x,y)

Partially Overlaps PO(x,y) O(x,y) ∧ ¬P(x, y) ∧ ¬P(y,x)

Externally connects EC(x,y) C(x, y) ∧ ¬O(x,y)

Tangential Proper Part T PP PP(x,y) ∧ (∃z ∈ U, EC(z, x) ∧ EC(z, y))

Non-Tangential Proper Part NT PP(x, y) PP(x, y) ∧ ¬(∃z ∈ U,EC(z,x) ∧ EC(z,y))

Table 2: Allen’s thirteen time relations.

Relation Converse Pictorial Example Endpoint Relations

X ≺ Y X  Y X

< Y

−

XmY Xm

Y X

= Y

−

XoY Xo

Y X

−

< Y

−

, X

> Y

−

, X

< Y

XdY Xd

Y X

−

> Y

−

, X

< Y

XsY Xs

Y X

−

= Y

−

, X

< Y

X fY X f

Y X

−

< Y

−

, X

= Y

X = Y X = Y X

−

= Y

−

, X

= Y

with fuzzy quantities. It is deﬁned by the following

equation:

A∗B

(z) = sup

z=x∗y

min{µ

(x),µ

(y)} (1)

where ∀x,y ∈ X , µ

(x) ∈ [0,1] and µ

(y) ∈ [0,1] are

membership functions deﬁning the degree of mem-

bership of the elements of X to the fuzzy subsets A

and B, respectively. Symbol ∗ denotes any crisp op-

erator. Some of the consequences of applying a fuzzy

function to logical operators are the following:

X∧Y

= min(µ

,µ

)

X∨Y

= max(µ

,µ

)

¬X

= 1 − µ

The union ∪ and the intersection ∩ of ordinary subsets

of X can be extended such that:

∀x ∈ X , µ

A∪B

= max (µ

(x), µ

(x)) (2)

∀x ∈ X , µ

A∩B

= min (µ

(x), µ

(x)) (3)

where µ

A∪B

and µ

A∩B

are respectively the membership

functions of A ∪ B and A ∩ B.

2.5 T-Norms and T-Conorms

T-norms and T-conorms (Deschrijver et al., 2004) are

used to calculate the membership values of intersec-

tion and union of fuzzy sets, respectively. A T-norm

is a binary operation T : [0,1]

→ [0,1] satisfying the

following axioms for all x,y,z ∈ [0,1]:

(i) T (x, y) = T (y,x) (commutativity),

(ii) T (x, y) ≤ T (x,z),i f y ≤ z (monotonicity),

(iii) T (x, T (y, z)) = T (T (x, y), z) (associativity),

(iv) T (x,1) = x

Some common T-norms (and respectively, their cor-

responding T-conorms) are the minimum T

), the

product T

) and Łukasiewicz T

), deﬁned as

follows:

• T

(x,y) = min(x,y), S

(x,y) = max(x,y);

• T

(x,y) = x.y, S

(x,y) = x + y + xy;

• T

(x,y) = max(0,x + y − 1), S

(x,y) =

min(1,x + y).

Implicators generalize the logical implication to the

unit interval and are deﬁned by I

(x,y) = S(1 − x, y)

for x and y in [0,1], e.g., the implicator for S

is de-

ﬁned by I

(x,y) = max(1 − x,y). For more details,

we refer the reader to (Schweizer and Sklar, 1960;

Schweizer and Sklar, 1983).

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

3 SPATIO-TEMPORAL BELIEF

REPRESENTATION AND

REASONING

In this section, we describe the the main features of

our formal representation of fuzzy spatio-temporal

beliefs. Since we extend the multi-agent BDI recom-

mender systems proposed by (Othmane et al., 2016b;

Othmane et al., 2016a) with the formal representation

of fuzzy spatio-temporal information, we begin by re-

calling our multi-context framework, which handles

information uncertainty using possibility theory.

3.1 A Multi-Context Recommender

Agent

Using cognitive agents architecture such as the belief-

desire-intention model as a base of a recommender

system is relevant especially in real-world applica-

tions (Casali et al., 2008b). Casali et al. (Casali et al.,

2008a) and (Othmane et al., 2016b) proposed similar

multi-agent BDI recommender systems that handles

information uncertainty using possibility theory. We

decided to extend the approach proposed in (Othmane

et al., 2016b) because it proposes already a mecha-

nism for beliefs and intentions update compared to

(Casali et al., 2008a). In (Othmane et al., 2016b),

a BDI agent visualized in Figure 2 is deﬁned using

multi-context systems (Parsons et al., 2002) as fol-

lows:

Ag = ({BC,DC,GC,SC,PC,IC,CC},∆

)

where BC, DC, GC represent respectively the Be-

lief Context, the Desire Context and the Goal Context

which model an agent mental attitude. PC, IC and CC

are functional contexts that represent respectively the

Planning Context, the Intention Context and the Com-

munication Context. SC is for the Social Context, and

it models social inﬂuence between agents. Authors

of (Othmane et al., 2016b) assume a trust relation-

ship between agents and trustworthiness of an agent

towards agent a

about an information φ is inter-

preted as a necessity measure τ ∈ [0,1]. The behavior

of these contexts is handled by means of internal de-

duction rules ∆

and axioms L

. The overall behavior

of the system is handled by bridge rules like Rule (2)

(shown in Figure 2) linking GC to DC, and expressed

as follows:

(2)GC : G(a

,φ) = δ

→ DC : D

,φ) = δ

It can be read as follows: if an agent a

has as

goal φ with a satisfaction degree δ

in a GC then it

positively desires φ with the same degree δ

in a DC.

Figure 2: A global view of the multi-context agent compo-

nents.

For more details about this agent model, we refer the

reader to (Othmane et al., 2016b).

Indeed, the work of (Othmane et al., 2016b) has

shown how autonomous BDI agents (Othmane et al.,

2016a) can evolve and move within a dynamic envi-

ronment, this work lacks from a spatial and temporal

reasoning in order to match the needs of a real-world

application.

A spatio-temporal belief is an event deﬁned as

a spatial relation holding in a temporal interval. A

spatio-temporal belief consists then of a sequence of

snapshots of an entity taken at speciﬁc time points:

at t

, b

at t

,..., b

at t

where t

,...,t

∈ T and

,...,b

are spatio-temporal beliefs concerning a

moving spatial object (e.g. car, moving person, etc..).

3.2 Fuzzy Sets for Representing

Imprecise Spatio-temporal Beliefs

Spatio-temporal data are often affected by impreci-

sion and uncertainty (Galton, 2009) due to several

reasons. Spatial uncertainty refers to positional ac-

curacy (e.g., location of an individual or a car). Tem-

poral uncertainty states whether temporal information

describes well a spatial phenomena. A fuzzy set, be-

cause of its ability to represent degrees of member-

ship, is more suitable for modeling geographical en-

tities. In a GIS database, real world objects can be

represented by the degrees of membership to multiple

classes or objects.

Representing only the spatial or the temporal di-

mension is not sufﬁcient to model and analyze such

phenomena. Modeling change involves incorporat-

ing both dimensions simultaneously. In this work,

CARS - A Spatio-temporal BDI Recommender System: Time, Space and Uncertainty

Figure 3: Fuzzy time membership function.

we adopt a dual representation of dynamic spatial

information proposed by Bordogna et al. (Bordogna

et al., 2003). In this approach, they introduce two

representations: i) a precise spatial reference and in-

determinate or vague time reference (e.g., if I leave

home now, I should be at work around 8 pm), and

ii) a precise time reference and a fuzzy spatial one

(e.g., an accident has just occurred in between Route

A and Route B). According to (Bordogna et al.,

2003), a spatial dynamic object can be represented

in the ﬁrst case as a set of pairs (τ

): o

{(τ

),..,(τ

),...,(τ

)}, where τ

is the time

fuzzy validity range associated with the spatial object

. The semantics of τ

is deﬁned by a triangular mem-

bership function centred in t

(see Figure 3). In the

same way, a spatial object with precise time reference

is deﬁned by a set of pairs (t

,σ

), where σ

stands

for the spatial validity of the observed phenomenon at

time instant t

represented as a triangular membership

function. In order to reason about such information,

we need a mechanism to represent also qualitative re-

lationships between spatio-temporal entities. For this

reason, we propose a fuzzy RCC-8 and an extension

to Allen’s intervals to support fuzziness.

3.3 Fuzzy Allen’s Intervals

The twelve relations deﬁned by Allen for simple time

intervals presented in Section 2.2 are generalized for

modeling fuzzy time relations. Each basic relation

can be deﬁned in terms of endpoint relations deﬁned

in Table 2. Using the extension principle, a fuzzy tem-

poral relation is deﬁned. For example, the fuzzy rela-

tion d

is introduced for the simple temporal relation

d (during), as follows:

Y ⇔ (X

−

) ∧ (X

)

and the corresponding degree of conﬁdence, using the

extension principle, can be expressed as:

= min(µ

−

,µ

)

All the values X and Y can be generalized to fuzzy

values and represented by fuzzy triangular numbers.

Based on the extension principle, we deﬁne ﬁrst the

conﬁdence degrees of the fuzzy relations ≥

and ≤

in order to deduce respectively the one of >

, <

and =

. Suppose we have two fuzzy intervals A and

B deﬁned by triangular fuzzy functions as follows:

A = (a

) and B = (b

). By applying

the extension principle, we can deduce the following

fuzzy relations:

A≤







0 if a

> b

−a

−b

if a

≤ b

< a

1 if a

≤ b

(4)

A≥







0 if b

> a

−b

−a

if b

≤ a

> a

1 if b

≤ a

(5)

From Equations 4 and 5, we can deduce the

conﬁdence degree of relations >

, <

and =

follows:

A <

B = A ≤

B ∧ ¬(A =

A >

B = A ≥

B ∧ ¬(A =

(A =

B) = A ≤

B ∧ A ≥

Let us consider, for instance, A = (8,9,10) and

B = (8.5,9.5,10.5) representing two fuzzy time-

points. We can compute the degree of conﬁdence

of this fuzzy temporal relation “A occurs at ap-

proximately the same time as B” using Equation 4

and Equation 5 as follows: µ

= µ

A≤

B∧A≥

min(µ

A≤

,µ

A≥

) = min(1,0.75) = 0.75.

3.4 Fuzzy Topological Relations

The eight binary topological predicates for simple

regions (Section 2.1) are generalized for modeling

fuzzy topological relations. Based on the approach

proposed by Schockaert et al. (Schockaert et al.,

2009) and the deﬁnition of the RCC relations in Ta-

ble 2, we present here an approach for modelling im-

precise spatial information when regions are repre-

sented as fuzzy sets. Let U be a nonempty set (rep-

resenting regions), and C a reﬂexive and symmetric

binary fuzzy relation on it modeling connection. Sev-

eral other topological relations can be deﬁned based

on this relation. These include the RCC8 basic rela-

tions DC, EC, PO, EQ, TPP, NTPP, and the converses

of TPP and NTPP (see Table 3 for their deﬁnitions).

Note that we adopt, following (Schockaert et al.,

2006), the Łukasiewicz-norm T

and its correspond-

ing implicator I

to generalize the standard logical

conjunction and implication. In addition, we chose

this logic for its convenience, especially regarding

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

Table 3: Fuzzy RCC deﬁnitions

Name Deﬁnition Fuzzy Deﬁnition

DC(x,y) ¬C(x,y) 1 −C(x,y)

P(x,y) ∀z ∈ U,C(z,x) → C(z,y) inf

z∈U

(C(z, x),C(z,y))

PP(x,y) P(x,y) ∧ ¬P(y, x) min(P(x,y),1 − P(y,x))

EQ(x,y) P(x,y) ∧ P(y, x) min((P(x,y),P(y,x))

O(x,y) ∃z ∈ U, P(z, x) ∧ P(z,y) sup

z∈C

(P(z,x),P(z,y))

DR(x,y) ¬O(x,y) 1 − O(x, y)

PO(x,y) O(x,y) ∧ ¬P(x, y) ∧ ¬P(y,x) min (O(x,y),1 − P(x, y), 1 − P(y,x)))

EC(x,y) C(x, y) ∧ ¬O(x,y) min(C(x,y),1 − O(x,y))

NT P(x,y) ∀z ∈ U,C(z,x) → O(z,y) inf

t∈U

(C(z, x), O(z, y))

T PP(x, y) PP(x,y) ∧ ¬NT P(x, y) min(PP(x,y),1 − NT P(x, y))

NT PP(x,y) PP(x,y) ∧ NT P(x,y) min(1 − P(x, y), NT P(x, y))

the implication function. The implicator correspond-

ing to the Łukasiewicz t-norm is deﬁned by: I

min(1,1 − x + y). In fact, the minimum operator does

not eliminate values arbitrarily, leaving thus more un-

certainty. For simplicity, we write I

instead of I

the remainder of the paper.

Using this formalism, we can, for example, calcu-

late a fuzzy spatial relation “p is precisely located far

from q”. Knowing the location of p and q, we can

calculate their fuzzy position using Equation 6. We

can then calculate the degree to which those two lo-

cations are connected, and consequently, their degree

of disconnection: DC(p,q) = 1 −C(p,q).

3.5 Fuzzy Spatio-temporal Belief

Representation and Reasoning

In order to represent an imprecise spatio-temporal be-

lief or desire such as “An accident occurred around 8

PM between road A and road B” or “I want to be at

work before 9 AM”, we combine the RCC spatial re-

lations with Allen’s temporal relations. The degree to

which this belief is true is computed using the mini-

mum between the degrees of conﬁdence of the spatial

belief and the temporal one, respectively. For repre-

senting a spatio-temporal belief, we annotate spatial

formulas with temporal information, meaning that a

spatial formula is true during a time interval or at a

speciﬁc time point. In other words, it can be written

as follows:

XDC

Y,Y PO

where X and Y represent two different regions or

moving objects, and I and J are time intervals. This

formula means that X is disconnected from Y during

time interval I, and Y is part of Z during time inter-

val J.

Let us consider again the belief “An accident (A)

occurred around 8 PM (t

) between road A (R

) and

road B (R

)”. This can be formalized as follows:

(A PO

) ∧ (A PO

Its degree of belief is:

B((A PO

) ∧ (A PO

)) =

= min{B(A PO

),B(A PO

)}.

Later, one can reason about temporal intervals or

time-points to infer relevant information such as be-

ing at the same time nearby the accident place. This

spatio-temporal belief is essential for an agent to de-

cide or not to reconsider its intention in case the de-

gree of conﬁdence of this belief is high. However, this

belief is no longer useful after a certain time period,

or if the accident is not placed on the agent’s route

(i.e., intentions).

4 EVALUATION

In this section, we present the evaluation of the

CARS recommendation system equipped with the

fuzzy spatio-temporal belief representation. The pur-

pose of the evaluation is to quantify the gain of agents,

in terms of execution and limited waiting time, to

reach their goals, by exchanging spatio-temporal be-

liefs and desires. To this aim, we propose to test

the proposed model in a real-world scenario where

spatio-temporal knowledge represents a crucial factor

in the user decision making process. In this evalu-

ation, different agent’s strategies are considered, fol-

lowing the ideas proposed by (Othmane et al., 2016a):

• individual agent strategy: agents behave individ-

ually without taking into account any information

coming from other agents. Only information from

external resources are considered in this case, e.g.,

data from the Trafﬁc Message Channel (TMC).

CARS - A Spatio-temporal BDI Recommender System: Time, Space and Uncertainty

• social agent strategy: agents are part of a social

network and communicate with the other agents

in the network by exchanging their own beliefs

and desires. Agents fully trust all other agents in

the network.

• social distrustful agent strategy: agents are part of

a social network, but they consider also the trust-

worthiness degree of the other agents, when they

exchange messages. Agents accept information

only from trustworthy agents. An agent is consid-

ered as deceitful if the information it provides is

repeatedly proven to be false.

4.1 Scenario

In order to evaluate the applicability of the proposed

model in a real-world application, we propose the fol-

lowing scenario. Agent a

uses an electric car, and

needs to reach an electric public charging point. Like

most road users, a

usually consults web-based or

mobile mapping services before the trip to determine

the nearest charging station and to avoid possible traf-

ﬁc jams. Knowing where to get to and estimating the

time needed for the journey, a

can plan its trip. Thus,

it selects a course of actions that will result in reach-

ing its destination before the battery of its car goes

out of charge. It chooses a route to follow and a time

to leave so that it can arrive by a desired arrival time.

Once the trip is planned, it can be executed. As long

as a

has not found any obstacle within the journey, it

can keep executing its original plan. However, it just

found that a certain road on its route is closed due to

an accident (other city events such as soccer games

or music concerts can be considered as well). As a

is not able to drive through that road anymore, it has

to reconsider its options and ﬁnd an alternative route

to reach its destination while taking into account its

battery life (hence its arrival time).

4.2 Implementation

In agent-based systems with spatial reasoning and so-

cial behavior, a visual output is needed to display the

agents’ movements and interactions in two- or three-

dimensional spaces. NetLogo

is a multi-agent pro-

gramming language and modeling environment for

simulating natural and social phenomena particularly

suited for modeling complex systems evolving over

time.

To implement our scenario, we decided to use

NetLogo, as it also provides support for the BDI ar-

chitecture and the FIPA Agent Communication Lan-

guage. The spatial module is implemented using the

https://ccl.northwestern.edu/netlogo/

Geographic Information Systems (GIS) extension for

Netlogo

. We used data about the road network and

Electric Vehicle (EV) charging points from the Nice

city open geographical database

in shapeﬁle format

(i.e., the format supported by the GIS Netlogo exten-

sion). The resulting environment of agents is shown

in Figure 4.

In order to adapt a fuzzy topological relation to a

GIS vector data model, we assume that crisp regions

are a set of trapezoidal shapes containing a ﬁnite se-

quence of line segments. To simplify the representa-

tion, we use a Gaussian function distribution as an ap-

proximation of the trapezoidal distribution. Then, the

membership function µ(x,y) of a spatial object with

coordinates (x, y) is deﬁned by the following equa-

tion:

x,y

= e

−k

|(x−x

)+(y−y

, (6)

where x

and y

are the coordinates of a landmark

point, and k

corresponds to a ﬂattening coefﬁcient

deﬁned according to the user description (d) of a be-

lief. We deﬁne then different coefﬁcients for k

precisely

approximately

, k

near

, k

around

. An example of this distri-

bution run is visualized in Figure 5.

Figure 5: Example of the Gaussian distribution

Agents in this simulation are spatial entities (mov-

ing cars) in an environment (the road network of the

Nice city) which may change their location and at-

tributes as time goes by

. At the beginning of the

simulation, each agent has a desire. As deﬁned in

our scenario, the desire of an agent is to go to the

nearest EV recharge point. A recommended plan is

proposed to the agent following the multi-context ap-

proach to the deliberation of agent behavior proposed

by (Othmane et al., 2016b; Othmane et al., 2016a).

https://ccl.northwestern.edu/netlogo/docs/gis.html

http://opendata.nicecotedazur.org/data/

The simulation code is available at this link:

http://modelingcommons.org/browse/one model/4832

#model tabs browse info.

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

Figure 4: The user interface of the agent-based simulation in NetLogo. The central part shows the agent’s environment

constituted of roads. Blue points represent Electric Vehicle charging stations. An agent is represented by a car. Red squares

represent accidents. Labels represent an agent intention, which consists of two elements: the name, mapped to a NetLogo

command, and a done-condition, mapped to a NetLogo reporter. Intentions are stored in a stack, and are popped out when

they are to be executed. If the done-condition is satisﬁed, the intention is removed and the next intention is popped out

consecutively. The ﬁgure shows also, on the right-hand side, how the graphs are updated dynamically as the program runs.

The left-hand pane shows some setup parameters.

Once the agent starts executing its plan, we trigger

at different random times in different random places

spatio-temporal events, i.e., accidents. If the agent re-

ceives information, it adds it to its belief base and, if

the accident is on its route, it updates its intentions,

if possible. Agents applying the individual strategy

have no knowledge from the other agents, thus they

update their route only when they encounter a closed

route in their plan.

4.3 Results and Discussion

The experiments were conducted as a version of the

scenario proposed in Section 4.1, with the adoption of

the three different strategies described in Section 4.

The scenario is executed with 10, 50, 100, and 150

agents as part of the environment in three different

experiments. We measured the time it took an agent

to reach its destination. Results of the average time

for agents to reach their destination for the different

cases are reported in Figure 6-[a]. The average time

for all agents to reach their destination increases as

the number of agents increases. This can be explained

by the trafﬁc overload, which cannot be avoided due

the number of cars on the road network. However,

it is worth noticing that the time decreases when the

two social agent strategies are exploited, in contrast

to the individual agent strategy. Notice also that so-

cial agents using trust-based information to judge the

reliability of the recommendations they receive have

better performance than purely social ones. As a

conclusion, the results show that exchanging spatio-

temporal beliefs among agents enhances the overall

performance of the agent network.

It is worth observing that some agents adopting

the individual strategy do not even reach their desti-

nation (i.e., they cannot satisfy their goals). There-

fore, the average time reported in the diagrams keeps

rising indeﬁnitely. In contrast, social agents always

achieve their goals and reach their destination, with

an even more limited time interval observed for those

agents exploiting trust-based information. These re-

sults show that exchanging fuzzy spatio-temporal be-

liefs helps agents to achieve their goals by anticipat-

ing the consequences of their intentions. In other

words, agents can anticipate and change their inten-

tions to avoid huge waiting time. Taking into account

spatio-temporal beliefs coming only from trustworthy

agents avoids agents to be mislead and hence to waste

time. Figure 6-[b] reports the average waiting time of

agents. Within social agents, results are slightly bet-

ter for those exploiting trust-based information, ex-

cept when the number of agents is 150. This is due

to the time required to process such information for

the whole agent network, as more processing time is

needed to verify agents’ reliability.

5 RELATED WORK

Few approaches exist to represent and reason about

spatio-temporal beliefs, desires and intentions’ dy-

CARS - A Spatio-temporal BDI Recommender System: Time, Space and Uncertainty

(a) (b)

Figure 6: Experimental results (selﬁsh agents: blue, social agents: red, social distrustful agents: green): (a) average time

required by the agents to reach a destination, and (b) average waiting time for the agents.

namics. (Jonker et al., 2003) propose a formal spatio-

temporal state language to deﬁne the spatio-temporal

behavior of an agent in a dynamic environment. Al-

though their approach provides an interesting formal-

ism for predicting agent spatial behavior, many ques-

tions concerning beliefs, desires and intentions dy-

namics are left open. For example, no mechanism

for updating beliefs, desires and intentions in this for-

malism is presented. Male

s and colleagues (Male

and

Zarni

c, 2011) use modal logic to deﬁne an agent

capable of updating its mental attitude according to

spatio-temporal relations considered as events. They

deﬁne a language for events in which spatio-temporal

knowledge is deﬁned under the form of predicates,

with an example in the trafﬁc scenario. Nevertheless,

the proposed framework is still in a preliminary stage

and presents some drawbacks, e.g., lack of a mech-

anism to update such spatio-temporal beliefs and de-

sires. (Schuele and Karaenke, 2010) propose a spatial

model to enable BDI agents to move autonomously

and collision-free in a spatial environment. Authors

assume that in a spatial context, the agents’ knowl-

edge about their environment is uncertain. However,

this problem is not handled through a qualitative ap-

proach for spatial reasoning. Time reasoning is not

handled neither. Other relevant approaches for spa-

tial reasoning in BDI models are discussed in (Vahid-

nia et al., 2015). However, none of them consider

the imprecision and vagueness that characterise spa-

tial knowledge. So far, to the best of our knowledge,

many approaches to reason about time in the BDI

agent model are proposed in the literature (among

them, see (Jarvis et al., 2005; Fisher, 2005; Sierra and

Sonenberg, 2005) but none of them deals with time

information imprecision. Unlike the aforementioned

approaches, our approach besides combining spatial

and temporal reasoning within the BDI model, it ad-

dresses the open challenge of spatio-temporal infor-

mation vagueness and fuzziness that strongly charac-

terizes such a kind of knowledge.

6 CONCLUSIONS

In this paper, we have introduced and evaluated

the CARS agent-based recommender system, where

fuzzy spatio-temporal beliefs are formally repre-

sented and updated. Answering the need to represent

spatio-temporal information to provide recommenda-

tions in the trafﬁc scenario, we deﬁne spatio-temporal

knowledge annotating spatial formulae (formalized

through fuzzy RCC) with temporal information (for-

malized through fuzzy Allen’s time intervals). The

goodness of the proposed formal framework is vali-

dated through an empirical evaluation simulating the

agents’ behaviour in the trafﬁc scenario. Results show

that the time required by the agents to reach a certain

point of interest sensibly decreases when the CARS

model is applied.

Several open challenges have to be tackled as fu-

ture research. First of all, further qualitative relations

about directions should be introduced concerning spa-

tial reasoning to allow the representation of a model

closer to reality. Second, on the simulation side, ex-

tending the evaluation introducing new metrics to fur-

ther reduce the processing time is also part of our fu-

ture research.

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

REFERENCES

Allen, J. F. (1983). Maintaining knowledge about temporal

intervals. Communications of the ACM, 26(11):832–

843.

Batet, M., Moreno, A., S

anchez, D., Isern, D., and Valls, A.

(2012). Turist@: Agent-based personalised recom-

mendation of tourist activities. Expert Systems with

Applications, 39(8):7319–7329.

Behzadi, S. and Alesheikh, A. A. (2013). Introducing a

novel model of belief–desire–intention agent for ur-

ban land use planning. Engineering Applications of

Artiﬁcial Intelligence, 26(9):2028–2044.

Bordogna, G., Carrara, P., Chiesa, S., and Spaccapietra,

S. (2003). A dual representation of uncertain dy-

namic spatial information. In International Fuzzy

Systems Association World Congress, pages 652–659.

Springer.

Casali, A., Godo, L., and Sierra, C. (2008a). A tourism

recommender agent: from theory to practice. Revista

Iberoamericana de Inteligencia Artiﬁcial, 12(40):23–

38.

Casali, A., Godo, L., and Sierra, C. (2008b). Validation

and experimentation of a tourism recommender agent

based on a graded bdi model. In CCIA, pages 41–50.

Chen, B. and Cheng, H. (2010). A review of the applica-

tions of agent technology in trafﬁc and transportation

systems. IEEE Trans. Intell. Transp. Sys., 11(2):485–

497.

Deschrijver, G., Cornelis, C., and Kerre, E. E. (2004). On

the representation of intuitionistic fuzzy t-norms and

t-conorms. IEEE Tran. on fuzzy systems, 12(1):45–61.

Fisher, M. (2005). Temporal development methods for

agent-based. JAAMAS, 10(1):41–66.

Galton, A. (2009). Spatial and temporal knowledge repre-

sentation. Earth Science Informatics, 2(3):169–187.

Jarvis, B., Corbett, D., and Jain, L. C. (2005). Reason-

ing about time in a BDI architecture. In Int. Conf. on

Knowledge-Based and Intell. Inf. and Eng. Sys., pages

851–857.

Jonker, C. M., Terziyan, V., and Treur, J. (2003). Temporal

and spatial analysis to personalise an agents dynamic

belief, desire, and intention proﬁles. In Int. Work.

on Cooperative Information Agents, pages 298–315.

Springer.

Male

s, L. and

Zarni

c, B. (2011). A spatiotemporal model

of events within a bdi. In Int. Conf. on Computer as a

Tool, pages 1–4. IEEE.

Othmane, A. B., Tettamanzi, A., Villata, S., and Thanh,

N. L. (2016a). A multi-context BDI recommender

system: From theory to simulation. In 2016

IEEE/WIC/ACM International Conference on Web In-

telligence, WI 2016, pages 602–605.

Othmane, A. B., Tettamanzi, A., Villata, S., Thanh, N. L.,

and Buffa, M. (2016b). An agent-based architecture

for personalized recommendations. In Agents and Ar-

tiﬁcial Intelligence - 8th Int. Conf., volume 10162 of

LNCS, pages 96–113.

Parsons, S., Jennings, N. R., Sabater, J., and Sierra, C.

(2002). Agent speciﬁcation using multi-context sys-

tems. In Foundations and Applications of Multi-Agent

Systems, pages 205–226. Springer.

Randell, D. A., Cui, Z., and Cohn, A. G. (1992). A spatial

logic based on regions and connection. KR, 92:165–

176.

Schockaert, S., Cornelis, C., De Cock, M., and Kerre, E. E.

(2006). Fuzzy spatial relations between vague regions.

In 3rd Int. IEEE Conf. Intell. Systems, pages 221–226.

Schockaert, S., De Cock, M., and Kerre, E. E. (2009). Spa-

tial reasoning in a fuzzy region connection calculus.

Artiﬁcial Intelligence, 173(2):258–298.

Schuele, M. and Karaenke, P. (2010). Qualitative spatial

reasoning with topological information in BDI agents.

In 2nd Work. on Artif. Intell. and Logistics, pages 7–

12.

Schweizer, B. and Sklar, A. (1960). Statistical metric

spaces. Paciﬁc J. Math., 10(1):313–334.

Schweizer, B. and Sklar, A. (1983). Probabilistic metric

spaces. North Holland series in probability and ap-

plied mathematics. North Holland.

Sierra, C. and Sonenberg, L. (2005). A real-time negotiation

model and a multi-agent sensor network implementa-

tion. JAAMAS, 11(1):5–6.

Vahidnia, M., Alesheikh, A., and Alavipanah, S. K. (2015).

A multi-agent architecture for geosimulation of mov-

ing agents. J. of Geographical Systems, 17(4):353–

390.

Zadeh, L. A. (1965). Fuzzy sets. Information and control,

8(3):338–353.

Zadeh, L. A. (1975). The concept of a linguistic variable

and its application to approximate reasoning. Infor-

mation sciences, 8(3):199–249.

CARS - A Spatio-temporal BDI Recommender System: Time, Space and Uncertainty