
Deep Learning Policy Quantization
Jos van de Wolfshaar, Marco Wiering and Lambert Schomaker
∗
Institute of Artificial Intelligence and Cognitive Engineering, University of Groningen, The Netherlands
Keywords:
Reinforcement Learning, Deep Learning, Learning Vector Quantization, Nearest Prototype Classification,
Deep Reinforcement Learning, Actor-Critic.
Abstract:
We introduce a novel type of actor-critic approach for deep reinforcement learning which is based on learning
vector quantization. We replace the softmax operator of the policy with a more general and more flexible
operator that is similar to the robust soft learning vector quantization algorithm. We compare our approach
to the default A3C architecture on three Atari 2600 games and a simplistic game called Catch. We show that
the proposed algorithm outperforms the softmax architecture on Catch. On the Atari games, we observe a
nonunanimous pattern in terms of the best performing model.
1 INTRODUCTION
Deep reinforcement learning (DRL) is the marriage
between deep learning (DL) and reinforcement learn-
ing (RL). Combining the two enables us to create self-
learning agents that can cope with complex environ-
ments while using little or no feature engineering. In
DRL systems, the salient features in the data are ex-
tracted implicitly by a deep neural network (DNN).
After the first major successes in DRL with deep Q-
learning (Mnih et al., 2013; Mnih et al., 2015), many
alternative approaches have been explored which are
well summarized in (Li, 2017).
On a coarse-grained level, decision making as
done by RL agents can be related to classification.
One particular class of classification algorithms is
known as nearest prototype classification (NPC). The
most prominent NPC algorithm is learning vector
quantization (LVQ) (Kohonen, 1990; Kohonen, 1995;
Kohonen et al., 1996). As opposed to linearly sepa-
rating different kinds of inputs in the final layer of a
neural network, LVQ chooses to place possibly mul-
tiple prototype vectors in the input space X . Roughly
speaking, a new input~x is then classified by looking at
the nearest prototypes in X . This particular classifica-
tion scheme could in principle be used for reinforce-
ment learning with some modifications. More specif-
ically, we will look at how it can be used to frame
the agent’s decision making as an LVQ problem. In
∗
This project has received funding from the European
Union’s Horizon 2020 research and innovation programme
under grant agreement No 662189 (Mantis).
that case, the prototypes will be placed in a feature
space H ⊆ R
n
in which we compare the prototypes to
nearby hidden activations
~
h of a DNN.
Recently, the asynchronous advantage actor-critic
(A3C) algorithm was introduced. The actor-critic al-
gorithm uses a softmax operator to construct its pol-
icy approximation. In this paper, we explore an alter-
native policy approximation method which is based
on LVQ (Kohonen, 1990; Kohonen, 1995; Kohonen
et al., 1996). We accomplish this by replacing the
softmax operator with a learning policy quantization
(LPQ) layer. In principle, the proposed method al-
lows for a more sophisticated separation of the fea-
ture space. This, in turn, could yield a superior policy
when compared to the separation that a softmax oper-
ator can accomplish.
We explore several variations to the LPQ layer
and evaluate them on two different kinds of domains.
The first domain is a self-implemented version of the
Catch game (Mnih et al., 2014). The second domain
consists of three Atari 2600 games. We show that the
LPQ layer can yield better results on Catch, whereas
the results on Atari 2600 are not unanimously in favor
of any of the approaches.
We now provide an outline of this paper. First, we
discuss relevant literature in Section 2. We then cover
basic reinforcement learning definitions in Section 3.
Then, we describe the workings of LPQ in Section 4.
Our experiments are covered in Section 5. Finally, we
reflect on the outcomes and we provide suggestions
for future work on LPQ in Section 6.
122
Wolfshaar, J., Wiering, M. and Schomaker, L.
Deep Learning Policy Quantization.
DOI: 10.5220/0006592901220130
In Proceedings of the 10th International Conference on Agents and Artificial Intelligence (ICAART 2018) - Volume 2, pages 122-130
ISBN: 978-989-758-275-2
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

2 RELATED WORK
This section covers related work in the field of deep
reinforcement learning. More specifically, we discuss
the asynchronous advantage A3C algorithm and LVQ.
2.1 Asynchronous Advantage
Actor-critic
Despite the significant successes that have been ob-
tained through the usage of a DQN with different
kinds of extensions, the replay memory itself has
some disadvantages. First of all, a replay memory
requires a large amount of computer memory. Sec-
ond, the amount of computation per real interaction
is higher and third, it restricts the applicable algo-
rithms to be off-policy RL methods. In (Mnih et al.,
2016), the authors introduce asynchronous algorithms
for DRL. By running multiple agents in their own in-
stance of the environment in parallel, one can decor-
relate subsequent gradient updates, which fosters the
stability of learning. This opens the way for on-policy
methods such as Sarsa, n-step methods and actor-
critic methods. Their best performing algorithm is
the asynchronous advantage actor-critic method with
n-step returns.
A major disadvantage of single step methods such
as DQN is that in the case of a reward, only the value
of the current state-action pair (s,a) is affected di-
rectly, whereas n-step methods directly incorporate
multiple state-action pairs into a learning update. In
(Mnih et al., 2016), it is shown that the A3C algorithm
outperforms many preceding alternatives. Moreover,
they explore the A3C model in other domains such
as a Labyrinth environment which is made publicly
available by (Beattie et al., 2016), the TORCS 3D car
racing simulator (Wymann et al., 2000) and MuJoCo
(Todorov et al., 2012) which is a physics simulator
with continuous control tasks. The wide applicabil-
ity of their approach supports the notion that A3C is a
robust DRL method.
In (Jaderberg et al., 2016), it is shown that the per-
formance of A3C can be substantially improved by in-
troducing a set of auxiliary RL tasks. For these tasks,
the authors defined pseudo-rewards that are given for
feature control tasks and pixel control tasks. The in-
clusion of these auxiliary tasks yields an agent that
learns faster. The authors show that reward predic-
tion contributes most to the improvement over A3C,
whereas pixel control had the least effect of improve-
ment.
2.2 Learning Vector Quantization
LVQ algorithms were designed for supervised learn-
ing. They are mainly used for classification tasks.
This section will briefly discuss LVQ and the most
relevant features that inspired us to develop LPQ.
2.3 Basic LVQ
We assume we have some feature space H ⊆ R
n
.
Let
~
h be a feature vector of a sample in H . Now
given a set of prototypes {~w
1
,~w
2
,. ..,~w
N
} and cor-
responding class assignments given by the function
c : H 7→{0,1,... ,#classes−1}, we update prototypes
as follows:
~w
i
←~w
i
+ η(t)(
~
h −~w
i
), (1)
~w
j
←~w
j
−η(t)(
~
h −~w
j
), (2)
where ~w
i
is the closest prototype of the same class
as
~
h (so c(~w
i
) = c(
~
h)), and ~w
j
is the closest proto-
type of another class (so c(~w
j
) 6= c(
~
h)). Similar to the
notation in (Kohonen, 1990), we use a learning rate
schedule η(t). In LVQ 2.1, these updates are only
performed if the window condition is met, which is
that min{d
i
/d
j
,d
j
/d
i
} > `, where ` is some prede-
fined constant. Here d
i
= d(~w
i
,
~
h) is the distance of
the current vector
~
h to the prototype ~w
i
. The same dis-
tance function is used to determine which prototypes
are closest.
Unseen samples are classified by taking the class
label of the nearest prototype(s). Depending on the
specific implementation, a single or multiple nearby
prototypes might be involved. Note that the set of pro-
totypes might be larger than the number of classes.
This is different from a softmax operator, where the
number of weight vectors (or prototypes) must corre-
spond to the number of classes.
2.4 Generalized Learning Vector
Quantization
One of the major difficulties with the LVQ 2.1 al-
gorithm is that the prototypes can diverge, which
eventually renders them completely useless for the
classifier. Generalized learning vector quantization
(GLVQ) was designed to overcome this problem
(Sato and Yamada, 1996). Sato and Yamaha define
the following objective function to be minimized:
∑
i
Φ(µ
i
) with µ
i
=
d
(i)
+
−d
(i)
−
d
(i)
+
+ d
(i)
−
, (3)
Deep Learning Policy Quantization
123

where Φ : R 7→ R is any monotonically increasing
function, d
(i)
+
= min
~w
i
:c(~w
i
)=c(
~
h)
d(
~
h,~w
i
) is the dis-
tance to the closest correct prototype and d
(i)
−
=
min
~w
i
:c(~w
i
)6=c(
~
h)
d(
~
h,~w
i
) is the distance to the closest
prototype with a wrong label. In (Sato and Yamada,
1996) it is shown that for certain choices for the dis-
tance function, the algorithm is guaranteed to con-
verge.
2.5 Deep Learning Vector Quantization
Recently, (De Vries et al., 2016) proposed a deep
LVQ approach in which the distance function is de-
fined as follows:
d(
~
h,~w) = kf (x;
~
θ
π
) −~wk
2
2
, (4)
where f is a DNN with parameter vector
~
θ
π
and
~
h =
f (~x;
~
θ
π
). Their deep LVQ method serves as an alter-
native to the softmax function. The softmax function
has a tendency to severely extrapolate such that cer-
tain regions in the parameter space attain high confi-
dences for certain classes while there is no actual data
that would support this level of confidence. Moreover,
they propose to use the objective function as found
in generalized LVQ. They show that a DNN with a
GLVQ cost function outperforms a DNN with a soft-
max cost function. In particular, they show that their
approach is significantly less sensitive to adversarial
examples.
An important design decision is to no longer de-
fine prototypes in the input space but in the feature
space. This saves forward computations for proto-
types and can simplify the learning process as the fea-
ture space is generally a lower-dimensional represen-
tation compared to the input itself.
2.6 Robust Soft Learning Vector
Quantization
Rather than having an all-or-nothing classification,
class confidences can also be modelled by framing
the set of prototypes as defining a density function
over the input space X . This is the idea behind robust
soft learning vector quantization (RSLVQ) (Seo and
Obermayer, 2003).
3 REINFORCEMENT LEARNING
BACKGROUND
In this paper we consider reinforcement learning
problems in which an agent must behave optimally in
a certain environment (Sutton and Barto, 1998). The
environment defines a reward function R : S 7→R that
maps states to scalar rewards. The state space consists
of all possible scenarios in the Atari games. This im-
plies that we are dealing with a discrete state space. In
each state, the agent can pick an action a from a dis-
crete set A. We say that an optimal agent maximizes
its expected cumulative reward. The cumulative re-
ward of a single episode is also known as the return
G
t
=
∑
∞
k=0
γ
k
R
t+k
, where R
t
is the reward obtained at
time t. An episode is defined by a sequence of states,
actions and rewards. An episode ends whenever a ter-
minal state is reached. For Atari games, a typical ter-
minal state is when the agent is out of lives or when
the agent has completed the game. An agent’s policy
π : S ×A 7→ [0,1] assigns probabilities to all state-
action pairs.
The state-value function V
π
(s) gives the expected
reward for being in state s and following policy π
afterwards. The optimal value function V
∗
(s) maxi-
mizes this expectation. The state-action value func-
tion Q
π
(s,a) gives the expected reward for being in
state s, taking action a and following π afterwards.
The optimal state-action value function maximizes
this expectation. The optimal policy maximizes the
state-value function at all states.
For reinforcement learning with video games, the
number of different states can grow very large due to
the high dimensionality of the environment. There-
fore, we require function approximators that allow us
to generalize knowledge from similar states to unseen
situations. The function approximators can be used
to approximate the optimal value functions or to ap-
proximate the optimal policy directly. In deep rein-
forcement learning, these function approximators are
DNNs, which are typically more difficult to train ro-
bustly than linear function approximators (Tsitsiklis
et al., 1997).
The A3C algorithm is a policy-based model-free
algorithm. This implies that the agent learns to be-
have optimally through actual experience. Moreover,
the network directly parameterizes the policy, so that
we do not require an additional mechanism like ε-
greedy exploration to extract a policy. Like any other
actor-critic method, A3C consists of an actor that ap-
proximates the policy with π(s,a;
~
θ
π
) and a critic that
approximates the value with V (s;
~
θ
V
). In the case of
A3C, both are approximated with a single DNN. In
other words, the hidden layers of the DNN are shared
between the actor and the critic. We provide a detailed
description of the A3C architecture in Section 5.2.
ICAART 2018 - 10th International Conference on Agents and Artificial Intelligence
124

4 LEARNING POLICY
QUANTIZATION
This section introduces a new kind of actor-critic al-
gorithm: learning policy quantization (LPQ). It draws
inspiration from LVQ (Kohonen, 1990; Kohonen,
1995; Kohonen et al., 1996). LVQ is a supervised
classification method in which some feature space H
is populated by a set of prototypes W = {~w
i
}
W
i=1
.
Each prototype belongs to a particular class so that
c(~w
i
) gives the class belonging to ~w
i
.
To a certain extent, the parameterized policy of a
DNN in A3C, denoted π(s,a;
~
θ
π
), draws some paral-
lels with a DNN classifier. In both cases, there is a
certain notion of confidence toward a particular class
label (or action) and both are often parameterized by
a softmax function. Moreover, both can be optimized
through gradient descent. We will now generalize the
actor’s output to be compatible with an LVQ classifi-
cation scheme. Let us first rephrase the softmax func-
tion as found in the standard A3C architecture:
π(s,a;
~
θ
π
) =
exp
~w
>
a
h
L−1
+ b
a
∑
a
0
exp
~w
>
a
0
h
L−1
+ b
a
0
, (5)
where h
L−1
is the activation of the last hidden layer,
b
a
is a bias for action a and ~w
a
is the weight vector for
action a. Now consider the more general definition:
π(s,a;
~
θ
π
) =
∑
i:c(~w
i
)=a
exp
ς(~w
i
,h
L−1
)
∑
j
exp
ς(~w
j
,h
L−1
)
, (6)
where ς is a similarity function. Now, we allow mul-
tiple prototypes to belong to the same action by sum-
ming the corresponding exponentialized similarities.
In this form, the separation of classes in the feature
space can be much more sophisticated than a normal
softmax operator. We have chosen to apply such ex-
ponential normalization similar to a softmax function
which makes the output similar to RSLVQ (Seo and
Obermayer, 2003). This provides a clear probabilistic
interpretation that has proven to work well for super-
vised learning.
We also assess the LPQ equivalent of generalized
LVQ. The generalized learning policy quantization
(GLPQ) output is computed as follows:
π(s,a;
~
θ
π
) =
∑
i:c(~w
i
)=a
exp
τ
ς
i
−ς
⊥
i
ς
i
+ς
⊥
i
∑
j
exp
τ
ς
j
−ς
⊥
j
ς
j
+ς
⊥
j
(7)
=
∑
i:c(~w
i
)=a
exp(τµ
i
)
∑
j
(τµ
j
)
, (8)
where we have abbreviated ς(~w
i
,h
L−1
) with ς
i
and
where ς
⊥
i
= max
j6=i
ς
j
. Using the closest proto-
types of another class (ς
⊥
) puts more emphasis on
class boundaries. During our initial experiments, we
quickly noticed that the temperature τ was affecting
the magnitude of the gradients significantly, which
could lead to poor performance for values far from
τ = 1. We compensated for this effect by multiplying
the policy loss used in gradient descent with a factor
1/τ. We will explain the importance of this τ param-
eter in Section 4.2.
4.1 Attracting or Repelling without
Supervision
Note that there is a subtle yet important difference in
the definition of Equation (7) compared to the defini-
tion in Equation (3). We can no longer directly deter-
mine whether a certain prototype ~w
a
is correct as we
do not have supervised class labels anymore.
The obvious question that comes to mind is: how
should we determine when to move a prototype to-
ward some hidden activation vector
~
h? The answer
is provided by the environment interaction and the
critic. To see this, note that the policy gradient the-
orem (Sutton et al., 2000) already justifies the follow-
ing:
∆
~
θ
π
← ∆
~
θ
π
−∇
~
θ
π
logπ(a
t
|s
t
;
~
θ
π
)(G
(n)
t
−V (s
t
;
~
θ
V
)),
(9)
where G
(n)
t
=
∑
n−1
k=0
γ
k
R
t+k
+ γ
n
V (s
t+n
;
~
θ
V
) is the n-
step return obtained through environment interaction
and V (s
t
;
~
θ
V
) is the output of the critic. This expres-
sion accumulates the negative gradients of the actor’s
parameter vector
~
θ
π
. When these negative gradients
are plugged into a gradient descent optimizer such as
RMSprop (Tieleman and Hinton, 2012), the result-
ing behavior is equivalent to gradient ascent, which
is required for policy gradient methods. It is impor-
tant to realize that all prototypes ~w
a
are included in
the parameter vector
~
θ
π
. The factor (G
(n)
t
−V(s
t
;
~
θ
V
))
is also known as the advantage. The advantage of a
certain action a gives us the relative gain in expected
return after taking action a compared to the expected
return of state s
t
. In other words, a positive advantage
corresponds to a correct prototype, whereas a nega-
tive advantage would correspond to a wrong proto-
type. Intuitively, applying Equation (9) now corre-
sponds to increasing the result of µ
i
(that is by attract-
ing ~w
i
and repelling ~w
⊥
i
) whenever the advantage is
positive and decreasing the result of µ
i
(that is by re-
pelling ~w
i
and attracting ~w
⊥
i
) whenever the advantage
is negative.
Hence, the learning process closely resembles that
of GLVQ while we only modify the construction of
π(s,a;
~
θ
π
). Note that a similar argument can be made
Deep Learning Policy Quantization
125

for LPQ with respect to RSLVQ (Seo and Obermayer,
2003).
4.2 Temperature for GLPQ
An interesting property of the relative distance mea-
sure as given by µ
i
, is that it is guaranteed to be in the
range [−1,1]. Therefore, we can can show that the
maximum value of the actor’s output is:
maxπ(s, a;
~
θ
π
) =
exp(2τ)
exp(2τ)+ |A|−1
, (10)
where we have assumed that each action has exactly k
prototypes. Alternatively, one could determine what
the temperature τ should be given some desired max-
imum p:
τ =
1
2
ln
−
p(|A|−1)
p −1
. (11)
Hence, we can control the rate of stochasticity
through the parameter τ in a way that is relatively sim-
ple to interpret when looking at the value of p. For
further explanation regarding Equations (10) and (11)
see the Appendix. We will use Equation (11) to deter-
mine the exact value of τ. In other words, τ is not part
of our hyperparameters, whereas p is part of it.
5 EXPERIMENTS
This section discusses the experiments that were per-
formed to assess different configurations of LPQ. We
first describe our experiment setup in terms of envi-
ronments, models and hyperparameters. Finally, we
present and discuss our results.
5.1 Environments
We have two types of domains. The first domain,
Catch, is very simplistic and was mainly intended to
find proper hyperparameter settings for LPQ, whereas
the second domain, Atari, is more challenging.
5.1.1 Catch
For testing and hyperparameter tuning purposes, we
have implemented the game Catch as described in
(Mnih et al., 2014). In our version of the game, the
agent only has to catch a ball that goes down from
top to bottom, potentially bouncing off walls. The
world is a 24 ×24 grid where the ball has a vertical
speed of v
y
= −1 cell/s and a horizontal speed of
v
x
∈ {−2,−1, 0,1,2}. If the agent catches the ball by
moving a little bar in between the ball and the bottom
Figure 1: Screenshot of the Catch game that is used in our
experiments.
of the world, the episode ends and the agent receives
a reward of +1. If the agent misses the ball, the agent
obtains a zero reward. With such a game, a typical
run of the A3C algorithm only requires about 15 min-
utes of training time to reach a proper policy. For our
experiments, we resize the 24 ×24 world to have the
size of 84 ×84 pixels per frame. See Figure 1 for an
impression of the game.
5.1.2 The Arcade Learning Environment
To assess the performance of our proposed method
in more complex environments, we also consider a
subset of Atari games. The Arcade Learning Envi-
ronment (Bellemare et al., 2013) is a programmatic
interface to an Atari 2600 emulator. The agent re-
ceives a 210 ×160 RGB image as a single frame. The
observation is preprocessed by converting each frame
to a grayscale image of 84 ×84. Each grayscale im-
age is then concatenated with the 3 preceding frames,
which brings the input volume at 84 ×84 ×4. In be-
tween these frames, the agent’s action is repeated 4
times.
We have used the gym package (Brockman et al.,
2016) to perform our experiments in the Atari do-
main. The gym package provides a high-level Python
interface to the Arcade Learning Environment (Belle-
mare et al., 2013). For each game, we considered
the version denoted XDeterministic-v4, where X is the
name of the game. These game versions are available
since version 0.9.0 of the gym package and should
closely reflect the settings as used in most of the DRL
research on Atari since (Mnih et al., 2013). We have
run our experiments on Beam Rider, Breakout and
Pong.
5.2 Models
In our experiments, we compare three types of agents.
The first agent corresponds to the A3C FF agent of
(Mnih et al., 2016), which has a feed-forward DNN.
It is the only agent that uses the regular softmax op-
erator, so we refer to it as A3C Softmax from hereon.
The other two agents are A3C LPQ and A3C GLPQ,
ICAART 2018 - 10th International Conference on Agents and Artificial Intelligence
126

which correspond to agents using the output operators
as defined in Equation (6) and Equation (7) respec-
tively. Note that the A3C FF agent forms the basis
of our models, meaning that we use the exact same
architecture for the hidden layers as in (Mnih et al.,
2016). Only the output layers differ among the three
models. The first convolutional layer has 32 kernels
of size 8 ×8 with strides 4 ×4, the second convolu-
tional layer has 64 kernels of size 4 ×4 with strides
2×2 and the final layer is a fully connected layer with
256 units. All hidden layers use a ReLU nonlinearity
(Nair and Hinton, 2010).
Learning takes place by accumulating the gradi-
ents in minibatches of t
max
steps. The policy gradients
are accumulated through Equation (9) minus an en-
tropy factor ∇
~
θ
π
0
βH(π(s
i
;
~
θ
π
)) added to the right hand
side. The β parameter controls the relative impor-
tance of the entropy. The entropy factor encourages
the agent to explore (Williams and Peng, 1991).
The critic’s gradients are accumulated as follows:
∆
~
θ
V
← ∆
~
θ
V
+ ∇
~
θ
V
1
2
(G
(n)
t
−V (s
t
;
~
θ
V
))
2
. (12)
After a minibatch of t
max
steps through Equation (9)
and (12), the accumulated gradients are used to update
the actual values of θ
π
and θ
V
. This is accomplished
by adding these terms together for any weights that
are shared in both the actor and the critic and adap-
tively rescaling the resulting gradient using the RM-
Sprop update:
~m ←α~m + (1 −α)∆
~
θ
2
, (13)
~
θ ←
~
θ −η
~
∆θ/
√
~m + ε, (14)
where ~m is the vector that contains a running average
of the squared gradient and ε > 0 is a numerical stabil-
ity constant, α is the decay parameter for the running
average of the squared gradient and η is the learning
rate (Tieleman and Hinton, 2012). It is important to
realize that
~
theta contains the parameters of both the
actor and the critic. The squared gradients are initial-
ized at a zero vector and their values are shared among
all threads as proposed by (Mnih et al., 2016).
5.3 Hyperparameters
The reader might notice that a lot of parameters must
be preconfigured. We provide an overview in Table
1. Note that the weight initialization’s U refers to a
uniform distribution and ρ =
1
√
f an
in
. The f an
in
cor-
responds to the number of incoming connections for
each neuron. The temperature τ is determined through
p
t
using Equation (11). We linearly increase p
t
from
p
0
to p
T
max
. As is customary ever since the work by
(Mnih et al., 2013), we anneal the learning rate lin-
early between t = 0 and t = T
max
to zero.
Table 1: Overview of default settings for hyperparameters.
Name Symbol Value
Learning rate η 7 ·10
−4
Discount factor γ 0.99
RMSprop decay α 0.99
RMSprop stability ε 0.1
Entropy factor β 0.01
Steps lookahead t
max
20
Total steps ALE T
max
1 ·10
8
Total steps Catch T
max
1 ·10
6
Frames per observation NA 4
Action repeat ALE NA 4
Action repeat Catch NA 1
Number of threads NA 12
Prototypes per action NA 16
Similarity function ς(
~
h,~w) −
∑
i
(h
i
−w
i
)
2
Max π GLPQ t = 0 p
0
0.95
Max π GLPQ t = T
max
p
T
max
0.99
Weight initialization NA U [−ρ, ρ]
Bias initialization NA 0
5.4 Results
For all our experiments, a training epoch corresponds
to 1 million steps for Atari and 50,000 for Catch.
Note that a step might result in multiple frames of
progress depending on the action repeat configura-
tion. At each training epoch, we evaluate the agent’s
performance by taking the average score of 50 envi-
ronment episodes.
5.4.1 Catch
First, we consider the Catch game as described in Sec-
tion 5.1.1. To get a better insight into the robustness
of each model, we consider a learning rate sweep in
which we vary the learning rate by sampling it from a
log-uniform distribution between 10
−6
and 10
−2
.
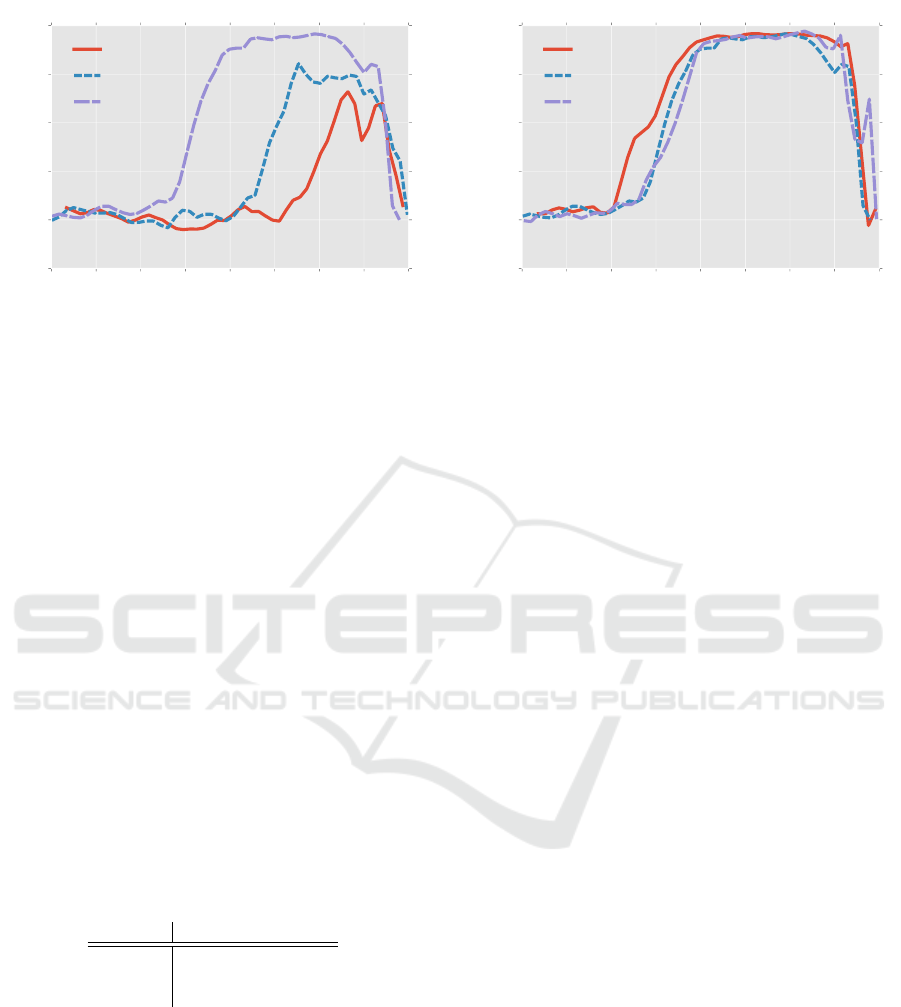
Similarity Functions. Figure 2 shows the aver-
age score for the learning rate sweep with different
similarity functions combined with the LPQ layer.
We looked at the Euclidean similarity ς(
~
h,~w) =
−
q
(
~
h −~w)
>
(
~
h −~w), the squared Euclidean similar-
ity ς(
~
h,~w) = −(
~
h −~w)
>
(
~
h −~w) and the Manhattan
similarity ς(
~
h,~w) = −
∑
i
|h
i
−w
i
|.
It is clear that the squared Euclidean similarity
works better than any other similarity function. More-
over, it attains good performance for a wide range of
learning rates. Hence, this is the default choice for
the remainder of our experiments. The second best
performing similarity measure is the Manhattan sim-
ilarity. This result corresponds with the theoretical
findings in (Sato and Yamada, 1996).
Deep Learning Policy Quantization
127
−6.0 −5.5 −5.0 −4.5 −4.0 −3.5 −3.0 −2.5 −2.0
log
10
(η)
0.0
0.2
0.4
0.6
0.8
1.0
Mean score final 5 evaluations
Similarity functions
Euclidean
Manhattan
Squared Euclidean
Figure 2: Comparison between different similarity func-
tions for the LPQ model: performance score as a function
of the learning rate. The lines are smoothly connected be-
tween the evaluations of different runs. Note that for re-
porting each of these scores, we took the average evaluation
result of the final 5 training epochs. A training epoch corre-
sponds to 50,000 steps.
Softmax, LPQ and GLPQ. Figure 3 displays the
learning rate sweep with a softmax architecture, an
LPQ architecture and a GLPQ architecture. We can
see that especially for lower learning rates between
10
−5
and 10
−4
, the GLPQ model seems to outper-
form the softmax and LPQ models. This could be
caused by the fact that the relative distance measure
puts more emphasis on class boundaries, which leads
to larger gradients for the most relevant prototypes.
The average across all learning rates between
10
−5
and 10
−2
is shown in Table 2, which also con-
firms that the GLPQ model outperforms the others.
GLPQ attains a score of 0.81 on average on the last 5
runs for any learning rate. This corresponds to catch-
ing the ball about 4 out of 5 times.
Table 2: Average final evaluation scores across the full
learning rate sweep for LPQ, GLPQ and A3C with standard
deviations.
Model Score average (±σ)
Softmax 0.73 ±0.28
LPQ 0.72 ±0.28
GLPQ 0.81 ±0.21
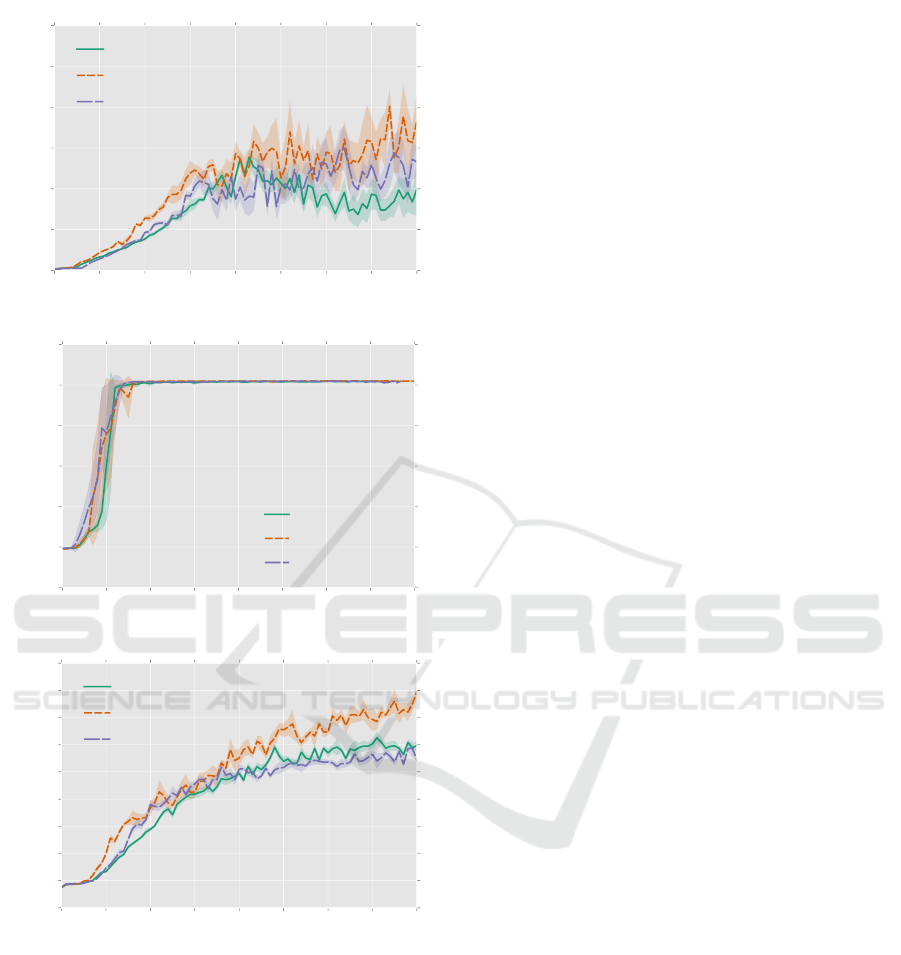
5.4.2 Atari
The results are shown in Figure 4. We have only
considered 3 games due to constraints in terms of
resources and time. It can be seen that GLPQ and
LPQ generally train slower than the default architec-
ture for Beam Rider and Breakout. For Breakout, the
final performance for LPQ and A3C softmax is simi-
lar. For Beam Rider, GLPQ starts improving consid-
erably slower than LPQ and FF, but surpasses LPQ
−6.0 −5.5 −5.0 −4.5 −4.0 −3.5 −3.0 −2.5 −2.0
log
10
(η)
0.0
0.2
0.4
0.6
0.8
1.0
Mean score final 5 evaluations
Softmax, LPQ and GLPQ
GLPQ
LPQ
Softmax
Figure 3: Comparison between softmax, LPQ and GLPQ
for the A3C algorithm on Catch. The lines are smoothly
connected between the evaluations of different runs. Note
that for reporting each of these scores, we took the average
evaluation result of the final 5 training epochs. A training
epoch corresponds to 50,000 steps.
eventually. For Pong, we see that the onset of im-
provement in policy starts earlier on average. This
game is a relatively simple problem for the agent to
truly optimize. This is confirmed by realizing that the
maximum score is 21, which is reached after about 10
training epochs.
Based on these three games, one should still pre-
fer the softmax operator, but it is interesting to see
how the LPQ and GLPQ models would perform on
other games in the ALE which we leave for future
research because of limited time and resources. A
possible explanation for the poor performance by the
LPQ models is that the hyperparameters are far from
optimal. The hyperparameters were tuned based on
the Catch game, which might not reliably reflect the
difficulty and complexity of the Atari games. More-
over, it might be that the (generalized) LPQ’s reduced
tendency to extrapolate when compared to the soft-
max operator limits the domain over which it can gen-
eralize. This could result in deteriorated performance,
especially when new phases of the game arise later in
the learning process that the agent has not encoun-
tered yet. For example, in Breakout, the ball tends to
move faster when more hard-to-reach blocks are de-
stroyed, which the agent typically only reaches after
about 20 training epochs.
6 DISCUSSION
In this paper, we have described a new algorithm for
reinforcement learning which is inspired by the LVQ
algorithm. The new LPQ algorithm was combined
with a DNN and tested on a simple Catch game and on
ICAART 2018 - 10th International Conference on Agents and Artificial Intelligence
128
0 10 20 30 40 50 60 70 80
Epoch
0
50
100
150
200
250
300
Score
Breakout
A3C GLPQ
A3C softmax
A3C LPQ
0 10 20 30 40 50 60 70 80
Epoch
−30
−20
−10
0
10
20
30
Score
Pong
A3C softmax
A3C LPQ
A3C GLPQ
0 10 20 30 40 50 60 70 80
Epoch
0
500
1000
1500
2000
2500
3000
3500
4000
4500
Score
BeamRider
A3C GLPQ
A3C softmax
A3C LPQ
Figure 4: Results on three Atari (Breakout, Pong and Beam
Rider) games where we compare the performance of GLPQ
and LPQ with a softmax operator. Each epoch corresponds
to 1 million steps. For each run, the agent is evaluated by
taking the average score of 50 episodes after every 1 million
steps. The plot displays the average of 5 separate runs.
three games in the Atari domain. We have shown that
the squared Euclidean distance function is most ap-
propriate based on the outcomes on the Catch game.
The best results on the Catch game seem to sug-
gest that the GLPQ algorithm performs slightly bet-
ter than LPQ for lower learning rates and competitive
for others when using a temperature scheme which is
based on the decisiveness of a single prototype vector.
Because of limited time and computational resources,
we were unable to further improve our parameters and
our understanding thereof. The best results obtained
with GLPQ on Catch seem to outperform the softmax
layer.
Both GLPQ and LPQ yielded competitive or even
superior results for the Catch game when compared to
a softmax layer, but they result in slightly worse per-
formance on two of the three Atari games. Given the
limited amount of experiments, it is difficult to make
general claims about the difference in performance of
these algorithms for the full Atari domain, let alone
outside the ALE. We can speed up further evaluation
and parameter tuning by using the recently introduced
parallel advantage actor-critic algorithm (Clemente
et al., 2017), which has proven to be a much more
efficient implementation of a parallel actor-critic.
The novel application of LVQ to actor-critic al-
gorithms opens up the door for a wide array of fur-
ther research. For example, one could look into more
advanced strategies for softmax temperature settings,
the proper initialization of prototypes, dynamically
adding or removing prototypes, alternative distance
functions, adding learning vector regression for value
function approximation and more. It is also worth-
while to study the extension of a neighborhood func-
tion to gradually focus more on the direct neighbors
instead of directly summing all similarities in the nu-
merator of the LPQ operator. The work on supervised
neural gas already mentions such a mechanism for
supervised learning (Hammer et al., 2005). Further
improvement of the LPQ algorithms will potentially
yield a better alternative to the default A3C algorithm.
REFERENCES
Beattie, C., Leibo, J. Z., Teplyashin, D., Ward, T., Wain-
wright, M., K
¨
uttler, H., Lefrancq, A., Green, S.,
Vald
´
es, V., Sadik, A., Schrittwieser, J., Anderson, K.,
York, S., Cant, M., Cain, A., Bolton, A., Gaffney,
S., King, H., Hassabis, D., Legg, S., and Petersen, S.
(2016). DeepMind Lab. CoRR, abs/1612.03801.
Bellemare, M. G., Naddaf, Y., Veness, J., and Bowling, M.
(2013). The arcade learning environment: An evalua-
tion platform for general agents. Journal of Artificial
Intelligence Research, 47:253–279.
Brockman, G., Cheung, V., Pettersson, L., Schneider, J.,
Schulman, J., Tang, J., and Zaremba, W. (2016). Ope-
nAI Gym.
Clemente, A. V., Castej
´
on, H. N., and Chandra, A. (2017).
Efficient Parallel Methods for Deep Reinforcement
Learning. ArXiv e-prints.
Deep Learning Policy Quantization
129

De Vries, H., Memisevic, R., and Courville, A. (2016).
Deep learning vector quantization. In European Sym-
posium on Artificial Neural Networks, Computational
Intelligence and Machine Learning.
Hammer, B., Strickert, M., and Villmann, T. (2005). Su-
pervised neural gas with general similarity measure.
Neural Processing Letters, 21(1):21–44.
Jaderberg, M., Mnih, V., Czarnecki, W. M., Schaul, T.,
Leibo, J. Z., Silver, D., and Kavukcuoglu, K. (2016).
Reinforcement learning with unsupervised auxiliary
tasks. arXiv preprint arXiv:1611.05397.
Kohonen, T. (1990). Improved versions of learning vector
quantization. In 1990 IJCNN International Joint Con-
ference on Neural Networks, pages 545–550 vol.1.
Kohonen, T. (1995). Learning vector quantization. In Self-
Organizing Maps, pages 175–189. Springer.
Kohonen, T., Hynninen, J., Kangas, J., Laaksonen, J., and
Torkkola, K. (1996). LVQ PAK: The learning vec-
tor quantization program package. Technical report,
Technical report, Laboratory of Computer and Infor-
mation Science Rakentajanaukio 2 C, 1991-1992.
Li, Y. (2017). Deep reinforcement learning: An overview.
arXiv preprint arXiv:1701.07274.
Mnih, V., Badia, A. P., Mirza, M., Graves, A., Lillicrap, T.,
Harley, T., Silver, D., and Kavukcuoglu, K. (2016).
Asynchronous methods for deep reinforcement learn-
ing. In Proceedings of The 33rd International Con-
ference on Machine Learning, volume 48 of Pro-
ceedings of Machine Learning Research, pages 1928–
1937, New York, New York, USA. PMLR.
Mnih, V., Heess, N., Graves, A., et al. (2014). Recurrent
models of visual attention. In Advances in neural in-
formation processing systems, pages 2204–2212.
Mnih, V., Kavukcuoglu, K., Silver, D., Graves, A.,
Antonoglou, I., Wierstra, D., and Riedmiller, M.
(2013). Playing atari with deep reinforcement learn-
ing. arXiv preprint arXiv:1312.5602.
Mnih, V., Kavukcuoglu, K., Silver, D., Rusu, A. A., Veness,
J., Bellemare, M. G., Graves, A., Riedmiller, M., Fid-
jeland, A. K., Ostrovski, G., et al. (2015). Human-
level control through deep reinforcement learning.
Nature, 518(7540):529–533.
Nair, V. and Hinton, G. E. (2010). Rectified linear units
improve restricted boltzmann machines. In Proceed-
ings of the 27th international conference on machine
learning (ICML-10), pages 807–814.
Sato, A. and Yamada, K. (1996). Generalized learning vec-
tor quantization. In Advances in neural information
processing systems, pages 423–429.
Seo, S. and Obermayer, K. (2003). Soft learning vector
quantization. Neural Computation, 15(7):1589–1604.
Sutton, R. S. and Barto, A. G. (1998). Reinforcement learn-
ing: An introduction, volume 1. MIT press Cam-
bridge.
Sutton, R. S., McAllester, D. A., Singh, S. P., and Mansour,
Y. (2000). Policy gradient methods for reinforcement
learning with function approximation. In Solla, S. A.,
Leen, T. K., and M
¨
uller, K., editors, Advances in Neu-
ral Information Processing Systems 12, pages 1057–
1063. MIT Press.
Tieleman, T. and Hinton, G. (2012). Lecture 6.5-rmsprop:
Divide the gradient by a running average of its recent
magnitude. COURSERA: Neural networks for ma-
chine learning, 4(2):26–31.
Todorov, E., Erez, T., and Tassa, Y. (2012). Mujoco:
A physics engine for model-based control. In 2012
IEEE/RSJ International Conference on Intelligent
Robots and Systems, pages 5026–5033.
Tsitsiklis, J. N., Van Roy, B., et al. (1997). An analy-
sis of temporal-difference learning with function ap-
proximation. IEEE transactions on automatic control,
42(5):674–690.
Williams, R. J. and Peng, J. (1991). Function optimiza-
tion using connectionist reinforcement learning algo-
rithms. Connection Science, 3(3):241–268.
Wymann, B., Espi
´
e, E., Guionneau, C., Dimitrakakis, C.,
Coulom, R., and Sumner, A. (2000). Torcs, the
open racing car simulator. Software available at
http://torcs. sourceforge. net.
APPENDIX
We now discuss some technical details concerning the
GLPQ temperature.
Theorem 1. Consider a GLPQ output operator with
µ
i
=
ς
i
−ς
j
ς
i
+ς
j
. Also assume that each action has k corre-
sponding prototypes.
We then know that
max
∑
i:c(~w
i
)=a
exp(τµ
i
)
∑
j
(τµ
j
)
=
exp(2τ)
exp(2τ)+ |A|−1
(15)
Proof. We automatically know that the output is max-
imized for some action a if for all prototypes for
which c(~w
i
) = a we have that ~w
i
=
~
h. In such cases,
we obtain µ
i
= 1 and µ
j
= −1 for j 6= i. Therefore,
the resulting maximum value of the policy is
k exp(τ)
k exp(τ)+ k(|A|−1)exp(−τ)
=
exp(2τ)
exp(2τ)+ |A|−1
(16)
Corollary 1. Let p be the maximum value of the pol-
icy, we then have that
p =
exp(2τ)
exp(2τ)+ |A|−1
(17)
⇒ pexp(2τ) + p(|A|−1) = exp(2τ) (18)
⇒ exp(2τ) = −
p(|A|−1)
p −1
(19)
⇒ τ =
1
2
ln
−
p(|A|−1)
p −1
, (20)
ICAART 2018 - 10th International Conference on Agents and Artificial Intelligence
130
