
Hierarchical Reinforcement Learning for Real-Time Strategy Games
Remi Niel
1
, Jasper Krebbers
1
, Madalina M. Drugan
2
and Marco A. Wiering
1
1
Institute of Artificial Intelligence and Cognitive Engineering, University of Groningen, The Netherlands
2
ITLearns.Online, The Netherlands
Keywords:
Computer Games, Reinforcement Learning, Multi-agent Systems, Multi-layer Perceptrons, Real-Time
Strategy Games.
Abstract:
Real-Time Strategy (RTS) games can be abstracted to resource allocation applicable in many fields and indus-
tries. We consider a simplified custom RTS game focused on mid-level combat using reinforcement learning
(RL) algorithms. There are a number of contributions to game playing with RL in this paper. First, we combine
hierarchical RL with a multi-layer perceptron (MLP) that receives higher-order inputs for increased learning
speed and performance. Second, we compare Q-learning against Monte Carlo learning as reinforcement learn-
ing algorithms. Third, because the teams in the RTS game are multi-agent systems, we examine two different
methods for assigning rewards to agents. Experiments are performed against two different fixed opponents.
The results show that the combination of Q-learning and individual rewards yields the highest win-rate against
the different opponents, and is able to defeat the opponent within 26 training games.
1 INTRODUCTION
Games are a thriving area for reinforcement learning
(RL) which have a long and mutually beneficial re-
lationship (Szita, 2012). Evolution Chamber for ex-
ample uses an evolutionary algorithm to find build-
orders in the game of Starcraft 2. Temporal-difference
learning, Monte Carlo learning and evolutionary RL
(Wiering and Van Otterlo, 2012) are among the most
popular techniques within the RL approach to games
(Szita, 2012). Most RL research is based on the
Markov decision process (MDP) that is a sequential
decision making problem for fully observed worlds
with the Markov property (Markov, 1960). Many
RL techniques use MDPs as learning problems with
stochastic nature; in multi-agent systems (Littman,
1994) the environment is also non-stationary.
As an alternative to RL, the AI opponents in to-
day’s games work mostly via finite state machines
(FSMs) which cannot develop new strategies and are
thus predictable. A higher difficulty is usually mod-
elled by increasing gather-, attack- and hit-point mod-
ifiers of AI (Buro et al., 2007). The FSM behaviour
is solely based on fixed state-transition tables. There-
fore, in the past dynamic scripting has been proposed
which can optimize performance and therefore the
challenge (Spronck et al., 2006), but it is still depen-
dent on a pre-programmed rule-base.
The real-time strategy (RTS) genre is a game
played in real-time, where both players make moves
simultaneously. Moves in RTS games can generally
be seen as actions, such as move to a certain posi-
tion, attack a specific unit, construct this building etc.
These actions can be performed by units which are
semi-autonomous agents. These agents come in dif-
ferent types with their own attributes and actions they
can perform. The player can control all agents that are
on his/her team via mouse and keyboard. The game
environment is often seen from above with an angle
that shows depth, and teams are indicated by colour.
The RTS genre is a particularly hard nut to crack
for RL. In RTS games, the game-play consists of
many different game-play components like resource
gathering, unit building, scouting, planning and com-
bat, which have to be handled in parallel in order to
win (Marthi et al., 2005). In this paper we propose
the use of hierarchical reinforcement learning (HRL)
that allows RL to scale up to more complex problems
(Barto and Mahadevan, 2003) to play an RTS game.
Hierarchical reinforcement learning allows for a di-
vide and conquer strategy (van Seijen et al., 2017),
which significantly simplifies the learning problem.
Towards the top of the hierarchy, the problem con-
sist of selecting the best macro actions that take more
than a single time step. The Semi-Markov decision
process (SMDP) theory for HRL allows for actions
470
Niel, R., Krebbers, J., Drugan, M. and Wiering, M.
Hierarchical Reinforcement Learning for Real-Time Strategy Games.
DOI: 10.5220/0006593804700477
In Proceedings of the 10th International Conference on Agents and Artificial Intelligence (ICAART 2018) - Volume 2, pages 470-477
ISBN: 978-989-758-275-2
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

that last multiple time steps (Puterman, 1994).
Our RTS approach focusses on the sub-process
of mid-level combat strategy. Neural network im-
plementations of low-level combat behaviour have al-
ready shown reasonable results in (Patel, 2009; Buro
and Churchill, 2012). Agents in the game of Counter
Strike were given a single task and a neural network
was used to optimize performance accomplishing this
task. Our method uses task selection: instead of giv-
ing the neural network a single task for which it has to
optimize, our neural network optimizes task selection
for each unit. The unit then executes an order, like
defend the base or attack that unit. The implementa-
tion of the behavior is executed via an FSM. Abstract
actions reduce the state space and the number of time
steps before rewards are received. The reduction is
beneficial for RTS games due to the many options and
the need for real-time decision-making.
For learning to play RTS games, we use HRL with
a multi-layer perceptron (MLP). The combination of
RL and MLP has already been successfully applied
to game-playing agents (Ghory, 2004; Bom et al.,
2013). RL and MLP have for example been suc-
cessfully used to learn the combat behavior in Star-
craft (Shantia et al., 2011). The MLP receives higher-
order inputs, an approach where only a subset of (pro-
cessed) inputs is used that has been successfully ap-
plied to improve speed and efficiency in the game Ms.
Pac-man (Bom et al., 2013). Two RL methods, Q-
learning and Monte Carlo learning (Sutton and Barto,
1998), are used to find optimal performance against
a pre-programmed AI and a random AI. Since play-
ing in an RTS game involves a multi-agent system,
we compare two different methods for assigning re-
wards to individual agents: using individual rewards
or sharing rewards by the entire team.
We developed a simple custom RTS where every
aspect is controlled to reduce unwanted influences or
effects. The game contains two bases, one for each
team. A base spawns one of three types of units until
it is destroyed, the goal of these units is to defend their
own base and to destroy the enemy base. All decision-
making components are handled by FSMs except for
the component that assigns behaviours to units, and
this is the subject of our research.
2 REAL-TIME STRATEGY GAME
The game is a simple custom RTS game that focuses
on the mid-level combat behaviour. A lot of RTS
game-play features such as building construction and
resource gathering are omitted, while other aspects
are controlled by FSMs and algorithms to reduce un-
wanted influences and effects. An example is the A
∗
search algorithm which is used for path finding, while
unit building is done by an FSM that builds the unit
that counters the most enemies for which there is not
a counter already present. A visual representation of
the game can be found in Figure 1.
Figure 1: Visual representation of the custom RTS game.
The game consists of tiles; black tiles are walls
and can’t be moved through and white tiles are open
space. The units can move in 4 directions. We use the
Manhattan distance to determine the distance between
2 points. Although units do not step as large as a tile,
our A
∗
path finding algorithm computes a path from
tile to tile for speed. When a unit is within a tile of the
target, the unit moves directly towards it.
The goal of the game is to destroy the opponent’s
base and defend the own base. The bases are indicated
by large blue and red squares in Figure 1. The game
finishes when the hit-points of a base reach zero be-
cause of the units attacking it. Depending on the unit
type a base has to be attacked at least 4 times before it
is destroyed. The base is also the spawning point for
new units of a team, the spawning time depends on
the cool-down time of the previously produced unit.
There are three different types of units: archer,
cavalry and spearman. Each unit has different statis-
tics (stats) for attack, attack cool-down, hit-point,
range, speed and spawning time. Spearmen are the
default units with average stats. Archers have a
ranged attack but move and attack speed is lowered.
Cavalry units are fast and have high attack power but
take longer to build. All units also have a multiplier
that doubles their damage against one specific type.
The archer has a multiplier against the spearman, the
cavalry has a multiplier against the archer, and the
spearman has a multiplier against the cavalry. This
resembles a rock, paper, scissors mechanism, which
is commonly applied in strategy games.
The most basic action performed by a unit is mov-
ing. Every frame, a unit can move up, down, left, right
or stand still. If after moving, the unit is within attack-
ing range of an enemy building or enemy unit, the unit
deals damage to all the enemies that are in its range.
The damage dealt is determined by the unit’s attack
Hierarchical Reinforcement Learning for Real-Time Strategy Games
471

power and the unit-type multiplier. When a unit is
damaged, its movement speed is halved for 25 frames
(0.5s in real-time), which prevents units rushing the
enemy base while enemy units cannot stop them in
time. To make sure units do not die immediately they
also have an attack cooldown after each attack, so that
they cannot attack for a few turns after attacking.
2.1 Behaviours
The computer players do not directly control their
units in our game, instead they give the units orders in
the form of behaviours (goals). Four such behaviours
are available: evasive invade, defensive invade, hunt
and defend base. Units that are currently using a spe-
cific behaviour follow rules that correspond to that
behaviour to determine their moves. All behaviours
make use of an A* algorithm to either find the opti-
mal paths to other assets/locations, or to compute the
distance between locations. There is also an ”idle”
behaviour which means the unit does nothing. This
behaviour is used when the unit is awaiting an order.
2.1.1 Defend Base
When starting the defend base behaviour, the unit se-
lects a random location within 3 tiles of its base as its
guard location such that not all guards stay at the same
spot. If an enemy comes close to the base (within 3
tiles), the unit moves towards and attacks that enemy.
If no enemies have come close to the base for 100
frames (2s in real time), the unit stops this behaviour,
and goes to the idle state awaiting a new order. The
pseudo-code can be found in Algorithm 1.
2.1.2 Evasive Invade
The unit takes a path to the enemy base that is at most
a map length longer than the shortest path. The unit
then chooses the path with the least enemy resistance
of all the possible paths. While moving along the
path, the unit also attacks everything in range includ-
ing the enemy base hoping to find a weakness in the
enemy defence and to exploit it. If the unit is dam-
aged while in this behaviour, the unit returns to ’idle’
until a new order is received. If the unit was damaged,
the unit clearly failed to attack the enemy base while
evading the enemy unit. This behaviour can be seen
in the pseudo-code in Algorithm 2.
2.1.3 Defensive Invade
The unit takes a path to the enemy base that is at most
a map length longer than the shortest path. The unit
then chooses the path with the most enemy resistance
Algorithm 1: Defend Base.
if not within 3 tiles of the base then
move back to own random guard location
else
target = NULL
for enemy in list of enemy units do
distance=distance(base,enemy)
if distance < minDistance then
minDistance = distance
target = enemy
end if
end for
if target != NULL then
move towards and attack target
else
move back to own random guard location
if frame count > 100 then
state = ”idle”
end if
end if
end if
Algorithm 2: Evasive Invade.
if Damaged then
state=”idle”
return
end if
lowest resistance= ∞
for path in find path to enemy base do
if resistance < lowest resistance then
lowest resistance = path resistance
best path = path
end if
end for
walk best path
of all the possible paths, to perform a counter attack
on the strongest enemy front. After every step the unit
attempts to attack everything around it. The idea here
is to either destroy invading enemy units or at least
slow them down, while still putting pressure on the
enemy base defences. The behaviour does not default
to the ”idle” state since the termination condition is ei-
ther the destruction of the enemy base or the death of
the unit. The behavior is similar to the evasive invade
behaviour and therefore we omitted its pseudo-code.
2.1.4 Hunt
The unit moves towards and attacks the closest enemy
asset (enemy unit or base) it can find. The unit pur-
sues the enemy asset until either it or the enemy asset
is dead. If the enemy asset dies, the unit defaults back
ICAART 2018 - 10th International Conference on Agents and Artificial Intelligence
472

Algorithm 3: Hunt.
if target=NULL then
minDistance=∞
for enemy in list of enemy assets do
if enemy distance < distance then
minDistance = enemy distance
target = enemy
end if
end for
else
if target health > 0 then
find path to target
walk path
else
target = NULL
state = ”idle”
end if
end if
to an ”idle” state, which is represented in Algorithm
3 by the target having 0 or less health.
3 HIERARCHICAL
REINFORCEMENT LEARNING
In this section, we describe how we use reinforce-
ment learning to teach the neural network how to play
our RTS game. A reinforcement learning system con-
sists of five parts, a model, an agent, actions, a re-
ward function and a value function (Sutton and Barto,
1998). Here, the model is the game itself, our neural
network is the agent, the policy determines how states
are mapped to actions using the value function, the re-
ward function defines rewards for specific states and
finally the value function reflects the expected sum
of future rewards for state-actions pairs. This value
takes into account both short term rewards and future
rewards. The goal of the agent is to reach states with
high values. In most reinforcement learning systems
it is assumed that future rewards can be predicted us-
ing only the information in the current state: past ac-
tions / history are not needed to make decisions. This
is called the Markov property (Markov, 1960).
3.1 The Reward Function
The reward function is fixed and based on the zero-
sum principle, points are distributed according to
what would be prime objectives in RTS games: killing
enemy units and destroying the enemy base which re-
sults in winning the game. The rewards are received
the moment a unit destroys the enemy base or kills an
enemy unit. Dying or losing the game is punished, dy-
ing is not punished harsher than the reward for killing
because units are expendable given that they at least
take out 1 enemy unit before dying. The reward func-
tion for our RTS game can be found in Table 1. If
multiple rewards are given while a specific behaviour
is active they are simply summed and the total reward
is taken as the reward for taking the chosen behaviour.
We created two different ways of distributing the
rewards, individually and shared. For individual re-
wards the units get only the reward they caused them-
selves and so the only shared reward is the ”Lose” re-
ward. We assume that all units are responsible for los-
ing. With shared rewards the moment a unit achieves
a rewarding event all units from the same team get
the reward. The exception here is that the step-reward
is still only applied once per time-step to prevent ex-
treme time-based punishments, when there are many
units in the environment.
Table 1: List of events and their corresponding rewards.
Event Reward Description
Enemy killed 100 Unit has killed enemy unit
Died -100 Unit died
Win 1000 Unit has destroyed the enemy base
Lose -1000 The unit’s base has been destroyed
Step -1 Time step
3.2 The Exploration Strategy
We use the ε-greedy exploration strategy, this means
that we choose the action with the highest state-action
value all but ε of the time where 0 ≤ ε ≤ 1. In the
cases ε-greedy does not act greedily, it will select a
random behavior. We start with an ε of 0.2 and lower
it over time to 0.02. We do this because intuitively the
system knows very little in the beginning so it should
explore, while over time the system should have more
knowledge and therefore act more greedily.
3.3 Learning Strategies
From the various learning algorithms that can be
used to learn the value-function, we have selected Q-
learning and Monte Carlo methods (Sutton and Barto,
1998). From here on a state at time t is referred to as
s
t
and an action at time t as a
t
. The total reward re-
ceived after action a
t
and before s
t+1
is noted as r
t
.
The time that r
t
spans can be arbitrarily long.
Monte Carlo methods implement a complete
policy evaluation, this means that for every state
we sum the rewards from that point onward, with a
discount factor for future rewards, and use the total
sum of discounted rewards to update the expected
Hierarchical Reinforcement Learning for Real-Time Strategy Games
473

reward of that state-action pair. The general Monte
Carlo learning rule is:
Q(s
t
, a
t
) = Q(s
t
, a
t
) + α · (
∑
∞
i=0
(λ
i
· r
t+i
) − Q(s
t
, a
t
))
Where α is the learning rate and λ the discount
factor. The learning rate determines how strongly the
value function is altered, while the discount factor de-
termines how strongly future rewards are weakened
compared to immediate rewards.
As opposed to Monte Carlo learning, Q-learning
uses step by step evaluation. This means Q-learning
uses the reward it gets after an action (can take
arbitrary amount of time) and adds the current
maximal expected future reward to determine how to
update the action-value function. To get the expected
future rewards the current value-function is used to
evaluate the possible state-actions pairs. The general
Q-learning rule is:
Q(s
t
, a
t
) = Q(s
t
, a
t
) + α · (r
t
+ λ · max
a
Q(s
t+1
, a)− Q
t
(s
t
, a
t
))
3.4 The Neural Network Component
The neural network contains one different output unit
for every behavior, which represents the Q-value for
selecting that behavior given the game input for that
unit. For updating the network, we use the back-
propagation algorithm where the target value of the
previously selected behavior of a unit is given by one
of our learning algorithms. The back-propagation al-
gorithm takes a target for a specific input-action pair
and then updates the network such that given the same
input, the output is closer to the given target. When
using RL, the target is given by a combination of the
reward(s), discount factor and in case of Q-learning
the value of the best next state-action pair. We use
3 different formulas to determine the target-value to
train the neural network. The first function is used
when this is the last behaviour of the unit, both learn-
ing methods share this formula:
T (s
t
, a
t
) = r
t
In other states Monte Carlo learning uses the fol-
lowing formula to determine the target-value:
T (s
t
, a
t
) =
∞
∑
i=0
(λ
i
· r
t+i
)
While for Q-learning the following formula is
used to determine the target-value:
T (s
t
, a
t
) = r
t
+ λ · max
a
Q(s
t+1
, a)
Table 2: Inputs used to represent a state.
Unit specific inputs
Amount of hit-points left
Boolean (0 or 1) value ”is spearman”
Boolean (0 or 1) value ”is archer”
Boolean (0 or 1) value ”is cavelry”
Minimal travel distance to enemy base
Minimal travel distance to own base
Resistance around the unit
Game specific inputs
Amount of defenders
Amount of attackers
Amount of hunters
Amount of enemy spearmen
Amount of enemy archers
Amount of enemy cavelry
Minimal travel distance between base and enemy unit
3.5 State Representation
The neural network does not directly perceive the
game, and receives as input numeric variables that
represent the game-state. These variables contain the
most important information to make the best deci-
sions. Including more information generally means
deploying larger networks that make use of the infor-
mation. Hence, the method would become slower and
takes longer to train. The neural network receives 14
inputs, see Table 2. Half of the inputs are about the
unit for which the behaviour has to be decided while
the other half contains information about the current
state of the game.
Unit specific inputs contain first of all basic infor-
mation: the amount of hit-points the unit has left and
which type it is (in the form of 3 boolean values). A
unit also contains 2 inputs which give distance val-
ues namely the minimal travel distances to the enemy
base and its own base. The final unit specific informa-
tion contained in the inputs is the ’enemy resistance’
around the unit, this counts all enemy units in a 5 × 5
square around the unit where the unit type it is strong
against is counted as a half unit. Then the amount of
friendly units in the same square is subtracted from
this number. The result gives an indication how dan-
gerous the current location is for the unit.
Game-wide inputs provide information about the
owner of the units: the amount of defenders, attack-
ers and hunters the owner already has. Note that
for attackers the aggressive and evading invaders are
summed. The inputs about the enemy contain the
composition of the enemy army, so the amount of
archers, cavalry and spearmen. This can be used to
prevent for example hunting behaviour if the enemy
has a lot of archers while the unit in question is a
ICAART 2018 - 10th International Conference on Agents and Artificial Intelligence
474
spearman. Given that a spearman cannot perform
ranged attack and is not very fast, the spearman would
be taken out before achieving anything. The last in-
put gives the distance between the owner’s base and
the enemy unit closest to it.
4 EXPERIMENTS AND RESULTS
We compare our methods in all configurations: shared
vs individual rewards, and Q-learning vs Monte Carlo
methods.
4.1 Testing Setup
We test the algorithms against two pre-programmed
opponents: 1) a random AI which simply chooses a
random behaviour whenever it needs to make a deci-
sion, and 2) a classic AI which we programmed our-
selves to follow a set of rules we thought to be logical.
We also tested these two opponents against each other
and found that they never tied and all games ended
within 4500 frames. The classic AI wins about 46.5%
of the games. Making a deterministic AI that plays
well against the random AI as well as other opponents
is quite difficult since the random AI is hard to pre-
dict, and countering the random AI specifically could
result in the AI equivalent of over fitting where it wins
from the random AI but loses from other opponents.
Each configuration has been ran for 100 trials
where each trial is 26 epochs (games) long. Each ini-
tial neural network was stored on disk and after each
game the network was again stored on disk. All stored
networks were then tested for 40 games against the
same AI opponent against which they were trained.
During these 40 games, training and exploration is
disabled to determine the network’s performance. We
then stored the win, lose and tie percentages. A tie
is a game that is not finished after 4500 frames (90
seconds real-time).
The neural networks consist of 14 inputs and 4
outputs. After several parameter-sweeps for all con-
figurations we found that the best performance was
achieved with the following parameter settings. We
used 2 hidden layers with layer sizes of 100 and 50
hidden units and a learning-rate which starts at 0.005
and that is multiplied with 0.7 after each game de-
grading to a minimum of 10
−6
. The exploration rate
also degrades from a start exploration rate of 20%
to a final exploration rate of 2%. The discount fac-
tor is 0.9. Since most units have a relatively small
amount of behaviours before dying we discount future
rewards relatively harshly. Finally, we added momen-
tum to the training algorithm of the neural network,
this means that the previous change of the network
is used to adjust how the network should change. In
our case 40% of the previous change is added to the
current change of a weight in the network.
4.2 Results
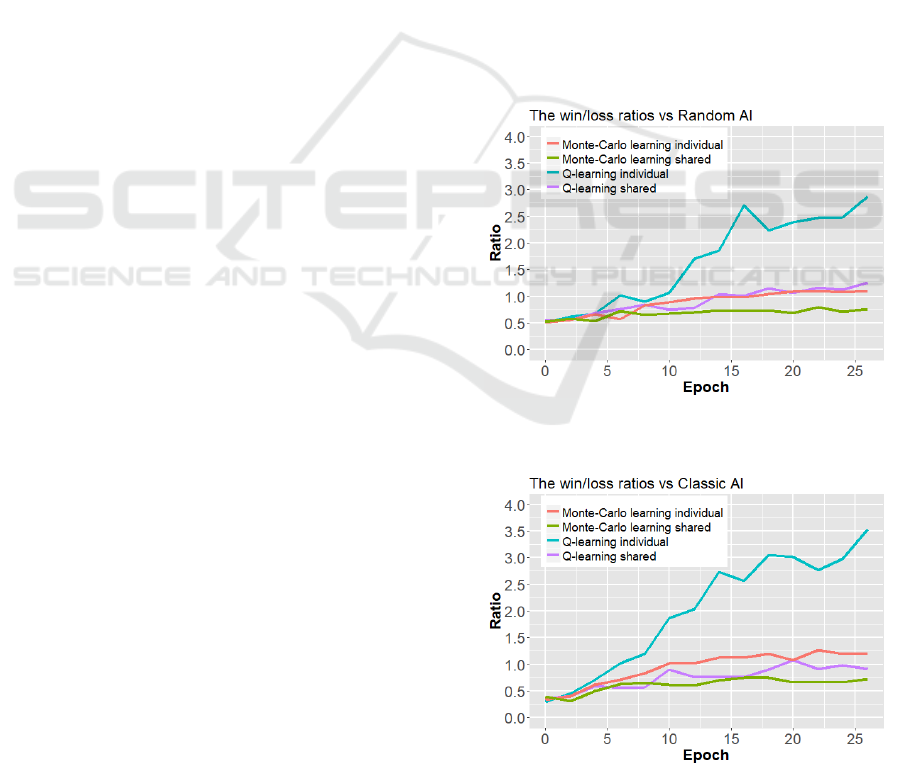
The results that were gathered are plotted in Figures
2 - 5. Figure 2 and Figure 3 contain the mean ratio
between wins and losses after X amount of epochs
(games) for different combinations of learning al-
gorithms and reward applications. Figure 2 shows
the ratios of every configuration playing against the
random AI, while Figure 3 shows the ratios for ev-
ery configuration playing against the classic (pre-
programmed) AI. The win-loss ratio shows how well
the neural network performs in comparison to the op-
ponent, a value of 1 represents equal performance. A
value higher than 1 such as the Q-learning individ-
ual rewards result in Figure 2 represents better perfor-
mance than the opponent, while a value lower than 1
represents worse performance than the opponent.
Figure 2: Graph that shows the ratio between wins and
losses for all configurations against the random AI.
Figure 3: Graph that shows the ratio between wins and
losses for all configurations against the classic AI.
Hierarchical Reinforcement Learning for Real-Time Strategy Games
475
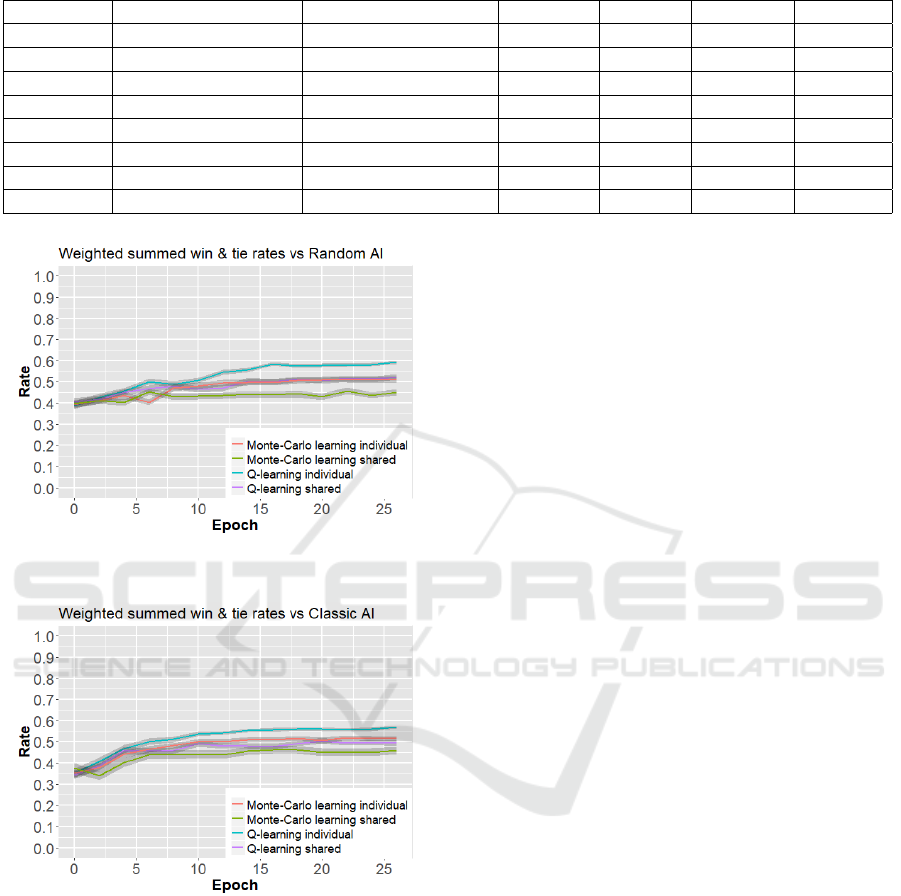
Table 3: Mean performance after 26 epochs (games).
Opponent Method Reward Application Win-rate Tie-rate Loss-rate Win:loss
Classic Q-learning Individual 19.5% 75.0% 5.5% 7:2
Classic Q-learning Shared 13.2% 72.3% 14.4% 9:10
Classic Monte Carlo method Individual 18.0% 67.0% 15.0% 6:5
Classic Monte Carlo method Shared 21.9% 48.0% 30.0% 7:10
Random Q-learning Individual 28.6% 61.5% 10.0% 3:1
Random Q-learning Shared 23.5% 57.8% 18.8% 5:4
Random Monte Carlo method Individual 28.8% 45.1% 26.2% 11:10
Random Monte Carlo method Shared 32.0% 26.2% 41.9% 3:4
Figure 4: Graph that shows the summed ratios of wins and
ties for all configurations against the random AI.
Figure 5: Graph that shows the summed ratios of wins and
ties for all configurations against the classic AI.
The results shown in Figure 4 and Figure 5 contain
the weighted sum of the mean win- and tie-rates for
all different combinations of learning algorithms and
reward applications. The win-rate has a weight of 1,
loss-rate a weight of 0 and the tie-rate has a weight of
0.5. The lines indicate the mean weighted sum while
the gray area indicates the standard deviation.
In all figures, all lines increase over time, meaning
that all configurations improve their performance dur-
ing training. One can clearly see that the combination
of Q-learning with individual rewards outperforms all
other configurations significantly. After training, this
method achieves a final win:loss ratio which is ap-
proximately 7:2 against the classic AI and 3:1 against
the random AI, roughly 3 times higher than the sec-
ond best configuration. The weighted sum of its win-
and tie-rates are also significantly higher than all other
combinations. It is noticeable that Q-learning out-
performs Monte Carlo learning in both performance
measures given that the other factors are equal and
individual rewards outperforms shared rewards given
the other factors are equal.
All the results measured show considerable tie-
rates. Against the classic AI the tie-rates are mostly
in the region of 65-75% and against the random AI
they are mostly between 45-65% as shown in Table
3. The exceptions for both opponents are the results
of Monte Carlo methods using a shared reward func-
tion, for which the tie-rate converges to around 50%
against the classic AI, while the tie-rate converges to
around 25% against the Random AI. This might seem
favourable, but the decrease of the tie-rate has an al-
most one to one inverse relation with the loss-rate and
is thus an overall worse result.
4.3 Discussion
The results show that individual rewards outperform
shared rewards. We suspect the reason for this that
predicting the sum of all future unit rewards is much
harder for a unit than to learn to predict its own re-
ward intake. Furthermore, Q-learning outperforms
the Monte Carlo learning method. It is known that
Monte Carlo methods have a higher variance in the
updates, which makes the learning process harder.
The encountered relatively high tie-rates that were
encountered in the measured results can be explained
as follows. A round is deemed a tie when a time-limit
of 90 seconds is reached. This feature is implemented
to reduce stagnating behaviour and allow for faster
data collection. Increasing the time limit should lower
the amount of ties.
There are several facets which deserve a closer
ICAART 2018 - 10th International Conference on Agents and Artificial Intelligence
476

look following our experiences during this research,
especially the use of different modules and the multi-
plicative effects they can have. The unit builder is a
great example. We found that having a more intelli-
gent unit builder significantly improves performance.
Even though the unit builder is now handled by an
FSM, it implies that adding a module to the AI that
can learn which units to build would likely increase
the performance as a whole significantly. The result
of a neural network using a smart unit builder (FSM)
against our classic AI with a random unit builder can
be observed in Figure 6. One can clearly see that
the win-rate approaches 90%, which shows the im-
portance of an intelligent unit builder for this game.
Figure 6: Graph of the performance for Q-learning with
individual rewards where it has an improved unit building
algorithm compared to the opponent’s random choice.
5 CONCLUSIONS
We described several different reinforcement learning
methods for learning to play a particular RTS game.
The use of higher-order inputs and hierarchical rein-
forcement learning leads to a system which can learn
to play the game within only 26 games. The results
also show that Q-learning is better able to optimize
the team strategy than Monte Carlo methods. For as-
signing rewards to individual agents, the use of in-
dividual rewards is better than sharing the rewards
among all team members. This is most probably be-
cause predicting the intake of all shared rewards is
difficult to learn for an agent given its own higher-
level game representation as input to the multi-layer
perceptron.
In future work, we would like to study the use-
fulness of more game-related input information in the
decision making process of the agents. Furthermore,
we want to use reinforcement learning techniques to
not only learn the mid-level combat strategy, but also
other tasks commonly present in an RTS game.
REFERENCES
Barto, A. and Mahadevan, S. (2003). Recent advances in
hierarchical reinforcement learning. Discrete Event
Dynamic Systems, 13:341–379.
Bom, L., Henken, R., and Wiering, M. (2013). Reinforce-
ment learning to train Ms. Pac-Man using higher-order
action-relative inputs. In Adaptive Dynamic Program-
ming and Reinforcement Learning (ADPRL), 2013
IEEE Symposium on, pages 156–163.
Buro, M. and Churchill, D. (2012). Real-time strategy game
competitions. AI Magazine, 33(3):106.
Buro, M., Lanctot, M., and Orsten, S. (2007). The second
annual real-time strategy game AI competition. Pro-
ceedings of gameon NA.
Ghory, I. (2004). Reinforcment learning in board games.
Department of Computer Science, University of Bris-
tol, Tech. Rep.
Littman, M. L. (1994). Markov games as a framework for
multi-agent reinforcement learning. In Proceedings
of the eleventh international conference on machine
learning, volume 157, pages 157–163.
Markov, A. A. (1960). The theory of algorithms. Am. Math.
Soc. Transl., 15:1–14.
Marthi, B., Russell, S. J., Latham, D., and Guestrin, C.
(2005). Concurrent hierarchical reinforcement learn-
ing. In IJCAI, pages 779–785.
Patel, P. (2009). Improving computer game bots behavior
using Q-learning. Master’s thesis, Southern Illinois
University Carbondale, San Diego.
Puterman, M. L. (1994). Markov decision processes. 1994.
John Wiley & Sons, New Jersey.
Shantia, A., Begue, E., and Wiering, M. (2011). Con-
nectionist reinforcement learning for intelligent unit
micro management in Starcraft. In Neural Networks
(IJCNN), The 2011 International Joint Conference on,
pages 1794–1801. IEEE.
Spronck, P., Ponsen, M., Sprinkhuizen-Kuyper, I., and
Postma, E. (2006). Adaptive game AI with dynamic
scripting. Machine Learning, 63(3):217–248.
Sutton, R. S. and Barto, A. G. (1998). Reinforcement learn-
ing: An introduction, volume 1. MIT press Cam-
bridge.
Szita, I. (2012). Reinforcement learning in games. In Rein-
forcement Learning State-of-the-Art, pages 539–577.
Springer.
van Seijen, H., Fatemi, M., Romoff, J., Laroche, R.,
Barnes, T., and Tsang, J. (2017). Hybrid reward ar-
chitecture for reinforcement learning. arXiv preprint
arXiv:1706.04208.
Wiering, M. and Van Otterlo, M. (2012). Reinforcement
Learning State-of-the-Art, volume 12. Springer.
Hierarchical Reinforcement Learning for Real-Time Strategy Games
477
