Hijacked Smart Devices

Methodical Foundations for Autonomous Theft Awareness based on Activity

Recognition and Novelty Detection

Martin J

anicke

, Viktor Schmidt

, Bernhard Sick

, Sven Tomforde

and Paul Lukowicz

Intelligent Embedded Systems Group, University of Kassel, Wilhelmsh

oher Allee 73, 34121 Kassel, Germany

German Research Center for Artiﬁcial Intelligence, Trippstadter Straße 122, 67663 Kaiserslautern, Germany

Keywords:

Smart Devices, Gaussian Mixture Model, Organic Computing, Self-Awareness, Probabilistic Theft Detection.

Abstract:

Personal devices such as smart phones are increasingly utilised in everyday life. Frequently, Activity Recogni-

tion is performed on these devices to estimate the current user status and trigger automated actions according

to the user’s needs. In this article, we focus on improving the self-awareness of such systems in terms of

detecting theft: We equip devices with the capabilities to model their own user and to, e.g., alarm the legal

user if an unexpected other person is carrying the device. We gathered 24hours of data in a case study with

14 persons using a Nokia N97 and trained an activity recognition system. Based on it, we developed and

investigated an autonomous novelty detection system that continuously checks if the observed user behav-

ior corresponds to the initial model, and that gives an alarm if not. Our evaluations show that the presented

method is highly successful with a successful theft detection rate of over 85% for the trained set of persons.

Comparison experiments with state of the art techniques support the strong practicality of our approach.

1 INTRODUCTION

More and more smart devices are available nowadays,

interconnected and always trying to improve our daily

lives. Their automated support ranges from reminders

for meetings via navigational assistance to analyzing

and improving our running style. Their ubiquitous

assistance is completely pervading our personal en-

vironments. It is also common that users have more

than one smart device, as old ones are rarely dis-

posed or sold. Unfortunatly, the monetary value of

such devices is also very high, so that thefts are quite

common, especially in urban areas. Even though it

is possible to track a stolen device afterwards, an

active involvment of the user in particular is neces-

sary – and often happens when it is already too late.

The major challenge with such approaches is that

theft and the discovery of the theft might be hours

apart. So instead, we envision an approach, where

the device itself recognizes whether it was stolen or

not, autonomously, based on internal sensors. Such

self-aware systems can then trigger counteractions or

alarms timely, even before the legitimate user misses

the device. In terms of developing such self-* prop-

erties, the proposed approach augments the concept

of initiatives such as Autonomic Computing (Kephart

and Chess, 2003) or Organic Computing (Tomforde

et al., 2017). In particular, we aim at providing capa-

bilities to autonomously observe the user behaviour

and estimate whether the device itself is still carried

by the owner or not. In case a severe deviation of ex-

pected behaviour is noticed, the owner can be notiﬁed

immediately on a backup-channel or sensible infor-

mation can be secured even stronger.

Our proposal uses methods from the ﬁeld of Ac-

tivity Recognition (AR) to model the characteristics

of users activities. Methods from the ﬁeld of Nov-

elty Detection (ND) are then used to detect, whether

a carrier’s activities still match that model or deviate

from the expected behavior. So far, such a combina-

tion of approaches from these different research direc-

tions does not exist. We see our approach as an impor-

tant part towards creating self-awareness in technical

systems, as the detection of environmental changes is

integral to such a task.

In this article, we use a probabilistic, genera-

tive approach based on Gaussian Mixture Models

(GMMs) to classify daily activities from smartphone

data. The evaluation of our method involves a case

study with activity data from 14 users and 5 sessions

of approx. 20 minutes each, so the overall database

comprises of roughly 24h of user data. Even though

Jänicke, M., Schmidt, V., Sick, B., Tomforde, S. and Lukowicz, P.

Hijacked Smart Devices - Methodical Foundations for Autonomous Theft Awareness based on Activity Recognition and Novelty Detection.

DOI: 10.5220/0006594901310142

In Proceedings of the 10th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2018) - Volume 2, pages 131-142

ISBN: 978-989-758-275-2

131

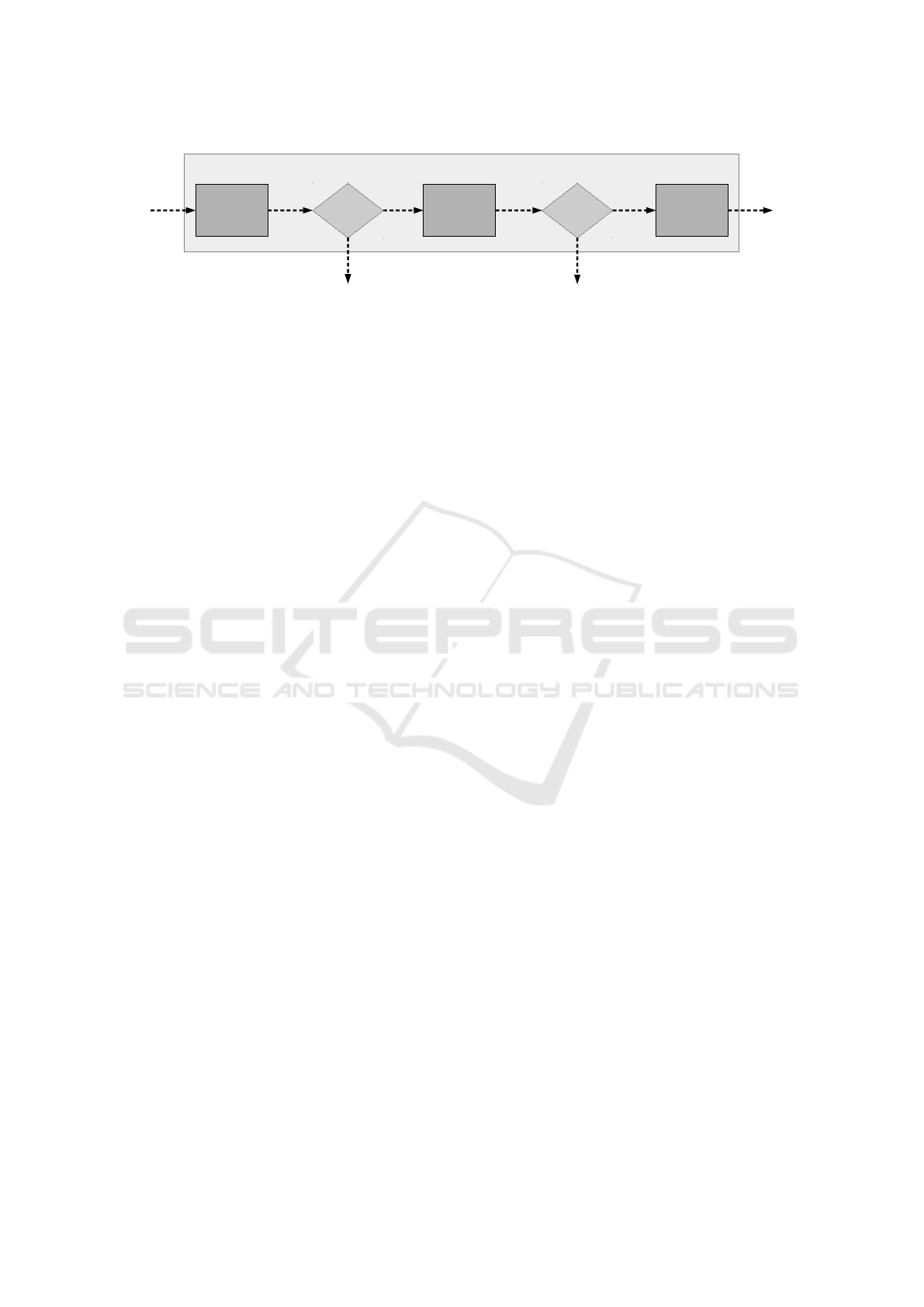
Theft detection

Activity

Recognition

Novelty

Detection

High

Certainty?

Deviation?

Yes

Alarm

Generation

Yes

Figure 1: System parts involved in a theft detection that can run on smart devices. With input being processed by the AR

component (see Section 3 for details), output with high certainty is forwarded to a ND component (see Section 4 for details).

If a deviation to a pre-learned model is measured, an alarm can be generated and further actions taken.

the data uses very basic daily activities, our approach

is not limited to them. The used GMM captures struc-

ture in arbitrary data, so it is not conﬁned to a pre-

deﬁned set of activities. Based on the trained mod-

els, the detection of novel data is investigated and dis-

cussed in depth. By detecting novel / previously un-

known data, it is possible to realize an autonomous

theft detection that works quite well, even with data

from very simple activities. Figure 1 gives an idea,

how such a system can be designed.

The key contributions of our work are 1. the in-

troduction of methods to realize an unobtrusive se-

curity feature for body-worn smart devices and 2. to

realize a theft detection with a very simple and com-

mon sensor, along with easy to compute features of

very basic, daily activities.

The remainder of this article is structured as fol-

lows: In Section 2 our approach is put into perspective

with the work from other groups in the area of ND. In

Section 3, the solution for the AR task based on ac-

celeration data is presented. Based on optimized AR-

models, our approach towards the problem of novelty

detection is addressed in Section 4. Afterwards, in

Section 5, a realization of a smart device with theft

detection capabilities is sketched. This work is then

concluded by a summary in Section 6, discussing the

evaluations and giving an outlook on further work.

2 RELATED WORK

Our related work brieﬂy touches the ﬁeld of Activ-

ity Recognition (AR), but mostly focuses on Novelty

Detection (ND). The term AR was ﬁrst publicly dis-

cussed nearly 20 years ago by Abowd et al. (Abowd

et al., 1999) and has since then gained a lot of pop-

ularity among researchers. The greatest challenge

of inferring a user’s activity from body-worn devices

was pursued since day one (c.f., e.g., (Clarkson et al.,

2000; Gellersen et al., 2002)). A ﬁrst step moved re-

search from visual data (i.e. probands were ﬁlmed) to

movement data from body worn sensors. Those sen-

sors were packed in sensor-nodes and strapped to the

body, on arms, torso, thighs, etc. Later, smartphones

became more popular in research, due to the sensors

of interest being integrated and their increasing com-

puting power. Those two properties led to Machine

Learning (ML)-techniques being implemented on the

devices, so that the recognition could happen effort-

lessly.

Addressing preparations for ML algorithms, Lau

et al. (Lau et al., 2010) focused on various param-

eters that have an inﬂuence on feature computation.

They investigated different sensor sampling frequen-

cies (8, 16 and 32Hz) along with different sliding win-

dow sizes (0.5s, 1s, 2s, 4s) and different sliding win-

dow overlaps (25%, 50%, 75%), with features being

calculated from each sliding window. The results re-

vealed that a sampling frequency of 32Hz, a sliding

window size of 4 seconds (128 measurements) and an

overlap of 75% achieved the most accurate results for

recognizing daily activities. Besides that, similar ac-

tivities (like Walking, Ascending stairs and Descend-

ing stairs) were often mixed up by the classiﬁers un-

der investigation. The work of Franke et al. was also

focused on technical details and preprocessing in rec-

ognizing daily activities (Franke et al., 2009). They

put a lot of effort into recognizing user activities based

on sound samples of a smartphones microphone, that

itself was carried in different pockets. However, they

did not investigate advanced ML-techniques in depth.

The question of how to model recorded data is

following: Which modelling technique(s) should be

used to represent the data? In (Chen et al., 2012)

the authors give an overview of different methods, as

well as approaches based on prior problem knowledge

(so called “Knowledge driven”). An explicit distinc-

tion between discriminative approaches (e.g. Support

Vector Machines (SVMs)) and generative approaches

(e.g. Hidden Markov Models) is made and discussed

in depth. Despite their discussion of different ap-

proaches that were tried for AR scenarios, the authors

neglect the heavy inﬂuence of chosen training algo-

rithms. Our experience showed, that a paradigm can

perform somewhere between excellent and very bad,

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

132

only depending on the training algorithm; sometimes

even only the initialization of the very same train-

ing algorithm. The authors also mentioned, that they

did not discuss inconsistencies and missing values in

training data, but both effects commonly appear in

real life datasets. Even though classiﬁers of various

kinds are investigated, in practical applications, most

common solutions prefer discriminative techniques,

completely neglecting the information that can be ex-

tracted when using generative models (e.g. structural

information of training data). While often superior

in terms of classiﬁcation performance, no further in-

formation other than the class prediction can be ex-

tracted from discriminative models. Contrarily, gen-

erative models approximate the structure of the data

and thus allow the detection of datapoints that do not

ﬁt that structure: outliers. With this huge advantage,

we decided to use a generative representation over a

discriminative one.

Outlier detection or Novelty Detection (ND) fo-

cuses on the detection of data, that does not ﬁt a spe-

ciﬁc data-model. With a trained model at hand, ob-

served data is expected to ﬁt that model, because an

implicit assumption usually is, that training data is

representative and thus the model trained on it is a

good representation of expected data to come. How-

ever, over time, or due to changes in the observed

environment, the distribution of observed data may

change and that assumption is violated. Suppose an

input space with several clusters and, at some point

in time, a new cluster arising, which is not covered

by the data-model. Those datapoints can be seen

as outliers with respect to the model or, as novel,

if never before observations were made in that re-

gion. A ﬁrst categorization of ND approaches was

done by Markou et al. and depicted two groups of

detection mechanisms. One group included statisti-

cal methods, relying on trained models (Markou and

Singh, 2003a). Datapoints were depicted as novel,

if they differed too much from that model. Ac-

cording to the authors, statistical approaches involved

non-parametric models (e.g., k nearest neighbor ap-

proaches or density estimators), as well as parametric

models, for which certain assumptions on the data dis-

tribution are made. The second group was associated

with neural network based approaches (Markou and

Singh, 2003b), however, should not be discussed fur-

ther, as our method clearly is a group one approach.

The authors put a common technique in the second

group, namely the detection of outliers via One-class

SVMs, but to our understanding the approach is not

neural network based. The approach was ﬁrst sug-

gested by (Sch

olkopf et al., 1999) and later applied to

the problem of object recognition based on image data

by (Tax and Duin, 2002). The authors used an artiﬁ-

cial dataset with artiﬁcially added outliers, as well as

images from handwritten digits with artiﬁcially added

outliers. Even though a certain feasibility was shown,

the authors had no real life dataset to proof their con-

cept. Apart from that, the approach was accepted

for outlier detection among researchers and later ap-

plied to, e.g., intrusion detection scenarios ((Li et al.,

2003)) or the detection of abnormal nodes in wire-

less sensor networks ((Zhang et al., 2009)). In both

cases, training data representing a normal situation

were used to train One-class SVMs and the goal was

to detect deviations from it.

The novelty detection mechanism we propose is

based on a Gaussian Mixture Model (GMM) and uses

a state variable to deﬁne the current status of data ﬁt-

ting the model. The parameters associated with the

measure then enable users to inﬂuence the tradeoff be-

tween detection-accuracy and time-to-detection. The

technique was introduced and ﬁrst used by Fisch et al.

in (Fisch et al., 2009).

Related Work in a Nutshell: As noted at the begin-

ning of this section, Activity Recognition based on

body worn sensors, like smartphones, smart watches

or other wearables, is the current way to go in re-

search. Even though preprocessing steps have heavily

been researched, detection algorithms mostly ignore

usable information available in the dataset. So, with

respect to information gained from datasets, there is

room for improvement. Secondly, the ﬁeld of novelty

detection has a broad ﬁeld of techniques at hand, how-

ever, only few were investigated on real life datasets.

To address the ﬁrst point, we see big potential in

the use of probabilistic, generative approaches and

thus investigated the usage of classiﬁers based on

Gaussian Mixture Models and present results in Sec-

tion 3. Building on top of that, we are ﬁrst in the ﬁeld

of theft detection based on such models and discuss

our proposal in depth in Section 4.

3 ACTIVITY RECOGNITION

In Section 1 the overall approach with all neces-

sary steps for a theft detection (Activity Recognition

(AR), followed by Novelty Detection (ND)) were in-

troduced (c.f. Figure 1). In the following section, all

experiments that were performed to reach a most ac-

curate activity prediction are discussed.

The used dataset was recorded at our institute and

comprises of the data of 14 different users. Each user

followed a script that described which activity should

be performed how long and in which order. Each run

of the script was repeated ﬁve times, with a maxi-

Hijacked Smart Devices - Methodical Foundations for Autonomous Theft Awareness based on Activity Recognition and Novelty Detection

133

mum of two sessions on the same day, to reduce self-

similarities in the data. The activites under investi-

gation were Walking, Ascending Stairs, Descending

Stairs, Standing and Sitting. Please note that, while

these activities are very basic, our techniques are not

conﬁned to them and, as will be explained, GMM are

rather powerful modelling approaches that can cap-

ture all kinds of data. The ﬁve basic activities are

chosen exemplatory, for comparison with other stud-

ies (cf., e.g., (Kwapisz et al., 2011; Lau and David,

2010)). All data were three-dimensional acceleration

data recorded on Nokia N97 with a highest possi-

ble frequency of 182Hz. Overall 70 sessions with

an overall length of approximately 1400min were

recorded and labeled.

Preprocessing steps included a resampling to

32Hz (cf. Section 2), a linear interpolation of miss-

ing values, a feature extraction and a standardization.

On our path to train an optimal classiﬁer, we quanti-

ﬁed the inﬂuence of 1. an additional sensor dimen-

sion, 2. different features, 3. optimized parameters

and 4. aggregated classiﬁer outputs.

The ﬁrst step towards improving AR performance

was the addition of the magnitude as additional value.

The values of this new “dimension” were calculated

as the length of the acceleration vector by using the

Euclidean distance:

mag =

+ y

+ z

. (1)

Afterwards, for every dimension the following four

features were extracted:

• mean

µ =

∑

n=1

, (2)

• standard deviation

σ =

N − 1

∑

n=1

− µ)

, (3)

• energy of Fourier transformation

energy =

∑

n=1

fft

, (4)

• information entropy of Fourier transformation

entropy =

−1

log(N)

∑

n=1

fft

· log(fft

), (5)

with fft

being the magnitude of the n-th Fourier

coefﬁcient.

All features are extracted by a sliding window ap-

proach (which is quite common in AR, cf., e.g., (Lau

et al., 2010; Sun et al., 2010)) with a size of 128 val-

ues and an offset of 32 (followingly 75% overlap);

aggregating 4 seconds of data, for one classiﬁcation

prediction each second.

The generative approach we used as a classiﬁer is

also used as a basis for the novelty detection mecha-

nism later (see Section 4), as the detailed modeling of

data enables a well working outlier detection. Gener-

ative approaches model the given data by means of a

density model; so that after training, data generated

by this model would underly the same distribution

as the original training data. We focus on a Clas-

siﬁer based on Gaussian Mixture Models (CMM),

trained by a realization of Variational Bayesian Infer-

ence (VI), a method proposed in (Bishop, 2006a).

The second optimization step was a better compu-

tation of features to allow a better discrimination be-

tween Ascending stairs, Descending stairs and Walk-

ing. As it turned out, the most vivid combination was

the replacement of the Fourier coefﬁcient based fea-

tures by a high-pass-ﬁltered version, where mean and

standard deviation of that coefﬁcients are used. The

great performance of this replacements is no coin-

cidence, but was previously observed by others (cf.

(Junker et al., 2008)), stating that “simple” features

(mean and standard deviation) perform very well most

of the time.

The next step was the optimization of classiﬁer pa-

rameters. A popular method from the domain of ML

is a parameter grid search, so that an optimal conﬁgu-

ration for the classiﬁer can be used in a practical appli-

cation. However, a detailed grid search is exhaustive,

since it tests every possible parameter combination.

It also comes at very high computational costs, with

respect to time and resources. We used four out of

ﬁve sessions for the parameter search, while keeping

one session to use as test data for the evaluation. The

parameter optimization was also carried out in a ﬁve-

fold cross-validation, with four parts being used for

training and the ﬁfth part being used for parameter-

validation. This leads us to have 70 (14 users, 5 ses-

sions each) different models, each one with the need

for a grid search on three of the four VI-parameters

(cf. (Bishop, 2006a)). To ﬁnd optimized parameters

for CMM we use an initialization heuristic with initial

centers being placed farthest apart from each other as

described by Bishop (Bishop, 2006b), with an initial

number of 50 components. Convergence criterion for

the training algorithm was a Likelihood function, with

a convergence threshold of 0.01 between two consec-

utive steps. The parameter α was varied between 0.1

– 0.5, β between 0.1 – 1.0 and w between 0.01 – 1.0

(names of aprameters as given by (Bishop, 2006b)).

As known from comparable scenarios, these regions

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

134

are most interesting. Every possible combination of

the points is evaluated by a ﬁve-fold cross-validation

(overall 17920 classiﬁer trainings), with the classiﬁ-

cation error of the validation data being the compar-

ison measure and the lowest error denoting the best

ﬁtting model.

As a last step to improve the classiﬁcation per-

formance, a short term memory is added right after

the classiﬁer. This is motivated by the fact that users

are unlikely to change their current activity for just

a short period of time. E.g. with our preprocessing,

every second a class prediction is made; but Walking,

Sitting, Walking is a highly implausible chain of ac-

tivities. The size of this memory, which was realized

as a FIFO buffer, had varying sizes between 2 and 10,

storing the last activity predictions. The classiﬁer as

we used it before, is not affected in any way. The

ﬁnal system prediction is determined by a simple ma-

jority vote on the buffer. If there is no majority, the

last majority decided value will be taken and if the

buffer is not ﬁlled yet, the classiﬁer output will be as

usual. Please note that whith each real activity transi-

tion, there is a delay in system output. However, num-

bers clearly indicate that those few misclassiﬁcations

(which only occur on activity transitions) compensate

the greater number of (otherwise misclassiﬁed) “out-

liers” during normal operation.

Buffer sizes 2, 3 and 5 are favorable, depending

on whether recognition speed is important to an ap-

plication or not. In our case, a buffer size of 5 implies

a prediction delay of 3 seconds between activities.

Taking all optimizations into accout on a per-

user-basis, the overall improvement based on ﬁve-

fold cross-validations, leads to an average classiﬁca-

tion error of 6.99% ± 2.79%, which is an error re-

duction of 7.63%. It is also worth mentioning, that

wisely chosen features lead to the greatest improve-

ment (3.55%), whereas a parameter optimization of

the training algorithm reveals a surprisingly low im-

provement (0.17%). This results are summarized in

Table 1.

Table 1: Classiﬁcation errors of test data with one additional

optimization added in each step, showing one step per line.

The last line represents the setting with all optimizations

active. Mean ± Standard Deviation are evaluated by ﬁve-

fold cross-validations and aggregated across all 14 users.

The best results are shaded gray.

Dimensions CMM E

[%]

baseline 14.62 ± 5.00

+ additional dimension 12.52 ± 5.06

+ better features 8.97 ± 3.20

+ grid search 8.80 ± 3.26

+ short term memory 6.99 ± 2.79

4 NOVELTY DETECTION

The Novelty Detection mechanism of choice is de-

scribed in this section, along with the performed pa-

rameter optimization and experiments. The measure

is based on CMMs and was ﬁrst proposed by Fisch et

al. in (Fisch et al., 2009). It is bound to [0.0, 1.0] and

based on a penalty/rewards scheme, i.e., with each

new observation a variable is either increased (data-

point ﬁts the model) or decreased (datapoint seems

to be an outlier). The term novelty stems from the

ﬁrst applications of this measure, where data (that is

unknown to a generative model, cf. Section 2) rep-

resented novel processes in the input space. Follow-

ingly, a “dissatisfaction” of the measure with the cur-

rent model was the result: There were more penal-

ties than rewards for the observations and thus the

measure fell, eventually below a predeﬁned thresh-

old. Please note that the detection mechanism can be

applied to GMMs of any kind. Here, the pretrained

models from Section 3, that are based on basic daily

activities, are used for all evaluations.

4.1 Parameter Optimization

The novelty detection mechanism has two parame-

ters (α, η) and once the measure falls below a given

threshold, it indicates a difference between observa-

tions and data-model. The parameter α describes the

fraction of datapoints that should be seen as “normal”

with respect to the model, with 1 - α denoting the

fraction of outliers that is acceptable. Values from

the interval [0.75, 0.95] were chosen in 0.05 steps.

Other values were not investigated, as data with more

than 25% outliers (α = 0.75) or less than 5% outliers

(α = 0.95) might appear in data – but to our under-

standing, would only be so extreme due to bad mod-

els. The parameter η describes a kind of sensitivity,

i.e., the magnitude of the measure’s punishment and

reward factors. As in comparable datasets, tested val-

ues were chosen from the interval [0.001, 0.1] in 100

equidistant steps. Finally, the threshold γ allows for

statements about data-to-model ﬁtment: If the mea-

sure stays above that threshold for every datapoint

(more reward than punishment), the current data and

the training data seem to underly the same distribu-

tion. Hence, the model covers the data well and the

novelty measure stays up. In contrast, data that un-

derly a different distribution than the training data,

will reduce the novelty value until it falls below γ. It is

obvious that η and γ are connected: a lower threshold

can be reached within the same number of datapoints

as a higher one, if the sensitivity is increased. Further-

more, the adaption of one parameter can be compen-

Hijacked Smart Devices - Methodical Foundations for Autonomous Theft Awareness based on Activity Recognition and Novelty Detection

135

sated by changing the value of the other parameter,

resulting in the same effects. Due to this, γ was ﬁxed

before η was adjusted independently for each user.

In our experiments, the goal is to ﬁnd an η for

each investigated α, so that no novelty is detected for

the own user, but for all other users, as fast as possi-

ble. For γ, 8 equidistant values from the interval [0.0,

0.7] were investigated. If more than one η fulﬁlling

the condition during validation was found, it was av-

eraged for ﬁnal testing. For a detailed description of

the parameters please refer to (Fisch et al., 2009). For

all evaluation scenarios two graphs were generated.

The ﬁgures for success rates show the reached val-

ues, illustrated by a bar for each α and γ combination

for a ﬁtting η, which was determined by the respec-

tive method. The success rate is composed of user

data (bottom), where no novelty should be detected

and data from other users (top), for which the mea-

sure should fall below γ for success.

Because there is more data from other users than

from the actual user (Ratio 13 to 1), the results are

weighted accordingly to have a maximum af 50%

each, so that the overall maximum is 100%. The av-

erage time needed for a novelty detection is displayed

by a line chart. This time is only determined by the

number of successfully detected novelties. Displayed

values of both graphs are averaged results of ﬁve-fold

cross-validations from each user.

When looking at working combinations of α and

γ, successful detections mean that a ﬁtting η was

found during our experiments.

One way to conﬁgure the η parameter for each

user, would be the usage of the training data to op-

timize the parameters. In other words, the optimiza-

tion takes place with data, which “is known” to the

models. However, a major concern for this scenario is

overﬁtting: If the data was used to create the model,

how representative would an optimization on its basis

be?

As we wanted to use unknown, but user-ﬁtting

data to ﬁnd a speciﬁc η, additional validation data was

necessary. To address this issue, models were trained

with only three out of ﬁve user-sessions, with one of

the remaining sessions being a parameter validation

set and the other one being the parameter test set (V-

VAL).

The model parameters themselves were optimized

via grid search on α and η.

The optimization was aiming at an η, that made

the novelty measure sensitive enough to reach a value

in the interval [0.74, 0.76] for the correct user at least

once, however, the measure was not allowed to fall

below that interval. This speciﬁc interval can also be

interpreted as follows: The target was to adjust the

α = 0.75 α = 0.80 α = 0.85 α = 0.90 α = 0.95 user thief

0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7

Success Rate in %

(a)

250

275

300

325

350

375

400

425

450

475

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7

α = 0.75

α = 0.80

α = 0.85

α = 0.90

α = 0.95

Avg. Time in Sec.

(b)

Figure 2: Success rates (a) and average times (b) of a nov-

elty detection with various conﬁgurations of the novelty

measure (V-VAL). For further description please refer to

Section 4.1.

sensitivity, so that a 25% deviance on the current

user’s validation data was allowed with a tolerance

of 1% (0.75 ± 0.01). With that condition satis-

ﬁed, all other test-users should be detected by the so

parametrized measure.

Figure 2 visualizes the evaluation: The higher the

demanded recognition threshold γ, the lower is the

rate of successfully detected novelties. Everything

considered, this means that for a predeﬁned thresh-

old (γ) the chance of ﬁnding a suitable sensitivity (η)

decreases when the fraction of tolerated outliers is re-

duced (α is risen).

It can also be seen that for different γ the success

rate hardly differs; basically proving the dependence

between γ and η: for nearly every threshold, a sen-

sitivity can be found. A ﬁrst signiﬁcant drop of the

success rate can be recognized for a γ of 0.60. The

best average detection time was reached for α-values

of 0.75 and 0.80.

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

136

4.2 Ensemble-based Approach

As three out of four training datasets are used to train

the model on which novelty parameters are validated

with the fourth session, four different models can also

be stored and used as an ensemble for novelty de-

tection. With several models, a number of ensemble

members have to agree on the type of a datapoint (out-

lier or model-compatible), before the dataset under in-

vestigation can be identiﬁed as fraud.

α = 0.75 α = 0.80 α = 0.85 α = 0.90 α = 0.95 user thief

0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7

Success Rate in %

(a)

100

125

150

175

200

225

250

275

300

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7

α = 0.75

α = 0.80

α = 0.85

α = 0.90

α = 0.95

Avg. Time in Sec.

(b)

Figure 3: Success rate (a) and average detection time (b) of

novelty detections based on ENS with a majority of 1 out

of 4 members (ENS

). For further details please refer to

Section 4.2.

Four novelty detections were run in parallel for

one test session. Deviating data is detected, as soon as

a predeﬁned majority of the ensemble detects a nov-

elty (ENS).

In Figures 3 to 6 the evaluation results are visual-

ized. A majority of one (Figures 3a and 3b) results in

a rather sensitive ensemble, that seems to be overcau-

tious, the higher the detection threshold is selected.

This means that novelty is easily detected, but also

that the rightious user is more often falsely detected

as non ﬁtting the data. This can be seen in the suc-

cess rate for data from other users, which is nearly at

the maximum of 50% for each α. However, in turn

the success rate on legitimate user data is way below

50%; with γ = 0.70 even around 10% for each α. A

γ of 0.20 seems to be a practical value, because the

success rate on the user’s data starts to drop from 0.30

onwards. With this low γ, an α of 0.80 reveals the best

success rate and the second best detection time.

For each threshold, a majority of two increases the

detection performance (Figures 4a and 4b). A γ of

0.60 and an α of 0.95 are a good choice here, as the

success rate is high and the detection time fast.

α = 0.75 α = 0.80 α = 0.85 α = 0.90 α = 0.95 user thief

0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7

Success Rate in %

(a)

175

200

225

250

275

300

325

350

375

400

425

450

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7

α = 0.75

α = 0.80

α = 0.85

α = 0.90

α = 0.95

Avg. Time in Sec.

(b)

Figure 4: Success rate (c) and average detection time (d) of

novelty detections based on ENS with a majority of 2 out

of 4 members (ENS

For a majority of three (Figures 5a and 5b), the

success rate for novelty detection is slightly rising

with an increased γ, while the false alarm rate also

increases (user success rate decreases). In order to

keep the detection time low, a γ of 0.7 and an α of

0.75 seem to be a good choice.

The majority of four is yet another special case

(Figures 6a and 6b). The insensitivity against deviat-

ing data is rather high and takes comparatively long,

even with high thresholds (e.g. γ = 0.60 or 0.70). Out-

put from this model can be interpreted as very reli-

able, however, successful detections take a very long

time. A γ of 0.70 is the only meaningful value here.

Hijacked Smart Devices - Methodical Foundations for Autonomous Theft Awareness based on Activity Recognition and Novelty Detection

137

α = 0.75 α = 0.80 α = 0.85 α = 0.90 α = 0.95 user thief

0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7

Success Rate in %

(a)

300

325

350

375

400

425

450

475

500

525

550

575

600

625

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7

α = 0.75

α = 0.80

α = 0.85

α = 0.90

α = 0.95

Avg. Time in Sec.

(b)

Figure 5: Success rate (e) and average detection time (f) of

novelty detections based on ENS with a majority of 3 out

of 4 members (ENS

Due to the lowest detection time with such an en-

semble, an α of 0.75 would be an appropriate choice.

4.3 One-class SVM

For a comparison we decided to focus on One-Class

SVMs, which are commonly used for outlier/anomaly

detection ((Fernndez-Francos et al., 2013; Amer

et al., 2013; Guerbai et al., 2015)). Positive data

(in our case data from the actual user) is often used

to train a discriminative function, which then outputs

whether data belongs to the positive class (“+”) or not

(“-”). For that purpose, ν-SVMs with a Radial Basis

Function (RBF)-kernel (γ

RBF

= 0.10) were trained in

the same manner as before, i.e., three out of ﬁve ses-

sions were used for training, a parameter-optimization

was done on a fourth session (validation session) and

the evaluation was done with the remaining session

(test session). For the optimization step, the overall

number of positive outputs from the validation set was

used: The more positive predictions a certain parame-

ter value caused, the better the trained SVM (and thus

the current ν) was considered.

α = 0.75 α = 0.80 α = 0.85 α = 0.90 α = 0.95 user thief

0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7

Success Rate in %

(a)

625

650

675

700

725

750

775

800

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7

α = 0.75

α = 0.80

α = 0.85

α = 0.90

α = 0.95

Avg. Time in Sec.

(b)

Figure 6: Success rate (g) and average detection time (h) of

novelty detections based on ENS with a majority of 4 out

of 4 members (ENS

As ν can be interpreted as a maximum accepted

fraction of datapoints outside the region of interest,

it is comparable to the parameter α from our novelty

measure and thus, values {.05, .10, .15, .20, .25, .30

} were investigated. Cross-validated over all users, ν

= 0.05 turned out to be the best available parameter,

i.e., the maximum number of accepted datapoints was

reached for that parameter.

The next challenge on ν-SVMs is the creation of a

mechanism for novelty detection, so that outliers are

recognized with a speciﬁc certainty: Our method of

choice was the short term memory technique as in-

troduced for the AR-task in Section 3. The neces-

sary majority for outliers within a window was ﬁxed

to being greater than 50%. For each user, a speciﬁc

window length was found. Starting with a window

length of 3, the size was incremented up to the point,

where all other users where recognized as being dif-

ferent (had more outliers in the sliding window than

accepted datapoints), which corresponds to the fastest

possible reaction time in terms of novelty detection.

Given an optimal sliding window length, the follow-

ing criteria had to be met for a working conﬁguration:

1. the dataset of the current user has to cause less than

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

138

50% outlier predictions, while 2. for each other user,

the fraction of outlier predictions was greater than

50%.

Still, as a result, only 328 out of 930 (14 users

with 13 datasets from other users and 5 sessions of

each other user being tested) novelties were actually

detected. Results are summarized in Table 2.

Table 2: Comparison of the success rates and average detec-

tion times of all users using parameter optimized ν-SVMs.

Average values in the shaded line are given in the form mean

± standard deviation.

User

Success Rate [%] Avg.

user

non-

total

Time

owner [s]

1 80.00 13.85 46.93 1182

2 100.00 38.46 69.23 1262

3 80.00 60.00 70.00 1117

4 80.00 27.69 53.85 1114

5 60.00 27.69 43.85 1198

6 100.00 33.85 66.93 1075

7 80.00 80.00 80.00 858

8 80.00 33.85 56.93 1018

9 80.00 40.00 60.00 1109

10 80.00 27.69 53.85 901

11 100.00 16.92 58.46 1322

12 100.00 4.62 52.31 1032

13 80.00 3.08 41.54 1212

14 80.00 96.92 88.46 442

84.29 36.04 60.17 1060

∅

± 11.58 ± 26.87 ± 13.48 ± 204

From the table can clearly be seen that the accep-

tance of user data by the trained ν-SVM is rather high,

however, the detection rate of non-owner-data is very

bad: Out of 65 possible detections (13 other users,

5 sessions each) at most 62 (in the case of user 14th

SVM) and at least 2 (in the case of user 13th SVM)

were detected as not-ﬁtting. Furthermore, the average

detection time is quite high. Overall can be stated,

that a One-Class SVM seems unsuitable for novelty

detection tasks in AR-scenarios. This statement is

supported by the fact, that the average detection ac-

curacies have a very high standard deviation.

4.4 Discussion

In Table 3 a comparison of our new techniques along

the commonly accepted One-class SVM approach is

visualized.

Parameters α and η for our novelty detection ap-

proach were optimized by means of a grid search. In

the SVM-case, ν was chosen by detection accuracy,

with the radius of the kernel functions γ

RBF

ﬁxed to

0.10 and the majority of the necessary sliding window

content ﬁxed at 50%. Whereas the SVM struggles

most with an overall working detection, our approach

is working and can even be parametrized to the user’s

needs: The tradeoff between accuracy and detection

speed is the biggest issue and should be handled with

care, depending on, e.g., whether false alarms are ac-

ceptable or not. In all investigated scenarios, the SVM

delivers a mostly bad performance for novelty detec-

tion, while offering a rather acceptable performance

for identifying the correct user. The inﬂuence of novel

data however, leads to a seemingly random behaviour.

Furthermore, the SVM-based approach is completely

inappropriate in terms of fast detections.

When false alarms (the actual users data is de-

tected as foreign) should be avoided at all costs, an

ensemble with a majority of 4 out of 4 (ENS

) seems

to be the method of choice. It has the highest suc-

cess rate (85.71%) for correctly identifying the owner,

however, this comes 1. at the cost of the lowest detec-

tion rate for non-owner-data and 2. also a long de-

tection time of more than 10 minutes (611 seconds).

It should also be noted that GMM-based approaches

allow for a more precise statement, be it on user- or

non-user-data. This seems to be a manifestation of the

generative property those models possess.

If a good trade-off between success rates for user

and novelty detection is targeted, an ensemble with a

majority with 3 (ENS

) is the best choice, with the

highest total success rate of 85.55% and a rather ac-

ceptable detection time of 284 seconds in average.

5 THEFT DETECTION

To train an autonomic theft detection for smart de-

vices, it is necessary to train user models, that are

as speciﬁc as possible.In terms of high quality data-

descriptions, estimations via GMMs are very suitable.

AR-datasets as used in this study of feasibility can

be collected explicitly or implicitly while a user fol-

lows his regular routine. With the goal of detecting

unknown data (e.g., data from non-owners), please

note that our modelling approach is not limited to a

labeled dataset, but instead models the data distribu-

tion, no matter if classes are available or not. Labeled

data just provides additional information, so that the

false alarm rate can be minimized (see below). The

techniques are also not limited to the simple activi-

ties chosen for this study, and the techniques can be

adapted to more complex activities. Of course, sev-

eral sessions of data, as used here, allow for a better

ﬁne-tuning of the models and are thus advisable.

Hijacked Smart Devices - Methodical Foundations for Autonomous Theft Awareness based on Activity Recognition and Novelty Detection

139

Table 3: Comparison of the success rates and detection times for theft detection methods with suggested novelty conﬁgurations

as described in Section 4.1 and Section 4.2 and a parameter optimized ν-SVM. Total success rate is calculated as the mean of

user and thief success rates. Time is calculated as the mean of the successfully detected thefts.

Parameter Success Rate Time

Method α γ user [%] non-owner [%] total [%] [s]

V-VAL 0.80 0.4 75.71 79.45 77.58 325

ENS

0.80 0.2 68.57 96.59 82.58 219

ENS

0.95 0.6 70.00 96.04 83.02 246

ENS

0.75 0.7 77.14 93.96 85.55 284

ENS

0.75 0.7 85.71 69.34 77.53 611

One-Class SVM ν = 0.05 84.29 36.04 60.17 1060

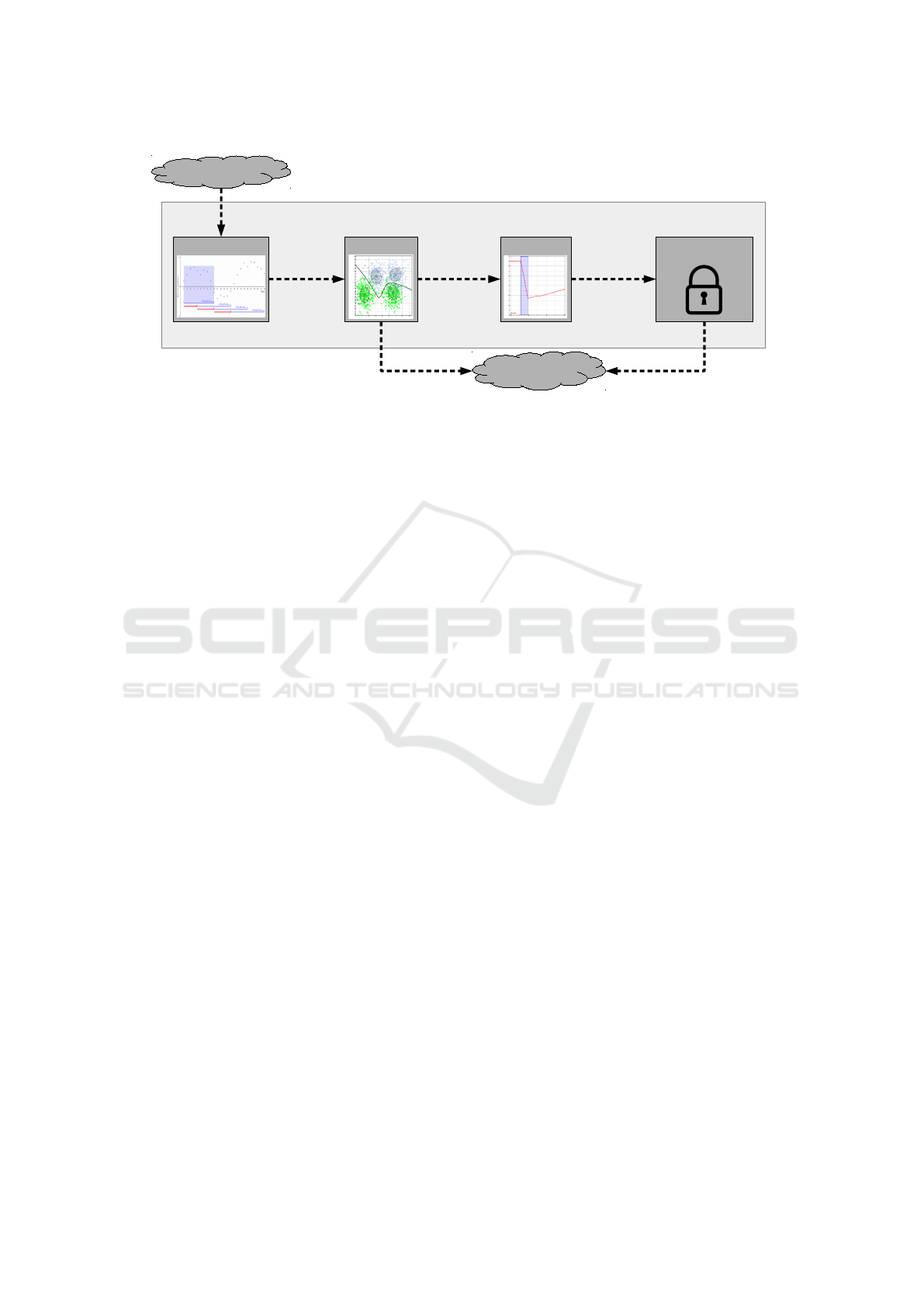
In Figure 7 such a system with all it’s compo-

nents is sketched. Visualized are involved compo-

nents (dark gray rectangles), the data ﬂow (dashed ar-

rows), input source (the environment) and resulting

output source (the smartphone’s operating system).

Suppose that the overall system is consisting of a

classiﬁcation component and a detection component.

Even though other algorithms might be eligible, the

following explanations focus on a CMMs as model in

conjunction with a penalty/reward-based Novelty De-

tection in the same manner as described in Section 4.

As the classiﬁer is a probabilistic one, information

about certainty for each output are available. When-

ever the classiﬁer is certain enough about an activity

prediction, the observed sample can be forwarded to

the detection part of the system. In that part, the mea-

sure is updated and compared to the given threshold γ.

Whenever the measure falls below that threshold, the

device could sample a soundclip and gps-annotated

picture (or video) footage and transmit it to a prede-

ﬁned location, server, backup- or rescue-address for

the owner to review. Next actions could, e.g., be the

shutoff of the device, the request for a pin, the activa-

tion of cryptographic code to secure sensible data or

alike.

Two unknown numbers were just mentioned, one

was a certain enough class prediction, the other one

was a given threshold for novelty (or in this case theft-

) detection. Concrete values are highly application

speciﬁc, but usually a user would not want a hyper-

sensitive smart device, but instead a very reliable theft

detection (cf. Section 4.4). So one goal is a minimal

false alarm rate, which can be achieved by deﬁning a

high class prediction certainty, along with a threshold,

that matches the novelty detections sensitivity param-

eter η.

Those parameter estimations need data from non-

owners, otherwise the adaptation to the user might not

be speciﬁc enough (cf. Section 4.3, with a good de-

tection of the rightful user but no more). Such data is

usually not available on a user’s device, but with cloud

connected devices everywhere, it would be possible

to push user-models into the cloud anonymously and

make it available for other users. Especially when you

think of a new device generation and only a fraction

of users participating in this setup, everyone would

beneﬁt, as the novelty detection parameters could be

adjusted very user-speciﬁc. In such a manner, every

device of that new generation could be secured and

autonomuously react to detected thefts.

A technical implementation of the overall system

needs to make sure, that the following points are cov-

ered:

1. Initialization. The cold start phase of the system,

is crucial for correct functioning. While the per-

sonalization and adaptation to the user is impor-

tant, an average model (e.g., data collected by the

manufacturer prior to release) for detecting every-

day activities can be used as a good starting point.

For a correct initialization, the system should also

occasionally question the user for feedback, as,

e.g., done in the Active Learning domain (cf., e.g.,

(Atlas et al., 1990)). During initialization, a set of

activities that can be detected reliably for the de-

vice’s user, should be ﬁxed.

2. Online operation. After a successful initial-

ization, the theft detection can start to work.

Parameter-tweaking can be done via, e.g., non-

owner models that are provided via the manu-

facturers or even a public cloud with movement

models. To avoid confusion of the system or a

watering of the model precision, the novelty de-

tection should only receive data, when the clas-

sifying component is very certain. Again, this is

a strong argument for the usage of simple activi-

tiesm which can be detected very reliably.

3. Detection action. As soon as the novelty measure

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

140

Environment

Smartphone OS

Autonomous theft detection

Classifier Detector Privacy Guard

Sensory

Data

Non-Owner Data

Detected

Predicted Activity

−2.5

−2.25

−2

−1.75

−1.5

−1.25

−1

−0.75

−0.5

−0.25

0.25

0.5

0.75

1.25

1.5

1.75

2.25

2.5

−2 −1.5 −1 −0.5 0 0.5 1 1.5 2

Dimension 0

Dimension 1

#components: 4

test error: 0.08

train error: 0.10

−0.1

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1.1

0 2 5 50 75 100 12 5 150

novelty

step

novelty

Securing action

Prediction with

high certainty

Extracted

features

Preprocessing

Figure 7: Schematic visualization of theft detection on a smartphone. Sensors signals come from effects in the environment

(acceleration, sound, etc.) and are preprocessed. Prepared features are put into a classiﬁer for activity recognition and into

a detection unit. While the classiﬁer predicts the user’s current activity only, the detector identiﬁes foreign data (based on

the data model of the classiﬁer) and triggers a privacy protecting guard if necessary. As a result, sensible information on the

smartphone can be locked and made inaccessible to a thief.

is below the predeﬁned threshold, the user action

that was conﬁgured, should be taken. This could

range from locking the device, via requesting a se-

cure pin or answering a secret question to wiping

all data, depending on the user’s initial conﬁgura-

tion.

6 SUMMARY & OUTLOOK

In this article, we based a novelty detection on top

of an Activity Recognition (AR) process to realize a

prototypical theft detection. Even though our experi-

ments were based on ﬁve simple activities, the CMM

is based on the structure of data and thus not conﬁned

to these exact activities. Followingly, the exact classes

only play a role for the activity recognition part, but

not for modelling a user by means of his data. This

is very advantegous, because no matter how precise

how many activities can be recognized: thefts can be

detected based on very simple activities, that can be

predicted very well and are nowadays included in ev-

ery smartphone and ﬁtness tracker from factory.

In Section 4 several techniques for detecting novel

data in the input space were investigated and com-

pared to a One-class SVM approach. The comparison

revealed that there is no overall best technique, but

that an implementation should be chosen with respect

to an application speciﬁc requirement: the always

present trade-off between detection accuracy and de-

tection speed. Even though One-class SVMs are com-

monly used for the task of anomaly detection, even

with a parameter optimization, we were not able to get

the SVM to function comparably well as our GMM

based novelty detection approach. A recommendation

can be made for ensemble based techniques due to

several reasons: First, each part of the ensemble can

be trained independently, which allows for a speed up

by parallelization. Second, less data is necessary to

train each competetive ensemble member. And ﬁ-

nally, even small ensembles (three members) reveal

a very good and robust performance, when compared

to other models that were trained on larger datasets or

with higher computational effort. Based on the ability

to detect data that deviates from a learned model, we

sketched the usage of an autonomuous theft detection

to secure user data in Section 5. Most remarkable is

the fact, that even with just ﬁve daily activities, the

detection works very well.

In general, SVMs perform reasonably well in Ac-

tivity Recognition scenarios and are a good approach

that could be focused more intensively (Lau et al.,

2010). As an alternative to our performed grid search,

better techniques like a Bayesian Optimization on

training parameters might be worth considering. To-

wards theft detection, an even further spanned input

space would be interesting, e.g. by incorporating

more available sensors. Taking the theft detection to-

wards a realization, it is necessary to conduct experi-

ments with data not only from smartphones, but also

from other smart devices (smart watches, smart in-

frastructure, ...). Finally, another interesting research

question should aim at the structure of detected out-

liers: Are they random or do they form a new cluster

in the input space? While random points might be a

result of sensor noise, coherent points might be the

result of something else. This question can be ad-

dressed by methods like CANDIES, as described in

(Gruhl and Sick, 2016).

Hijacked Smart Devices - Methodical Foundations for Autonomous Theft Awareness based on Activity Recognition and Novelty Detection

141

ACKNOWLEDGEMENTS

The authors would like to thank the German

research foundation (Deutsche Forschungsgemein-

schaft, DFG) for the ﬁnancial support in the context

of the “Organic Computing Techniques for Runtime

Self-Adaptation of Multi-Modal Activity Recognition

Systems” project (SI 674/12-1).

REFERENCES

Abowd, G., Dey, A., Brown, P., Davies, N., Smith, M., and

Steggles, P. (1999). Towards a better understanding

of context and context-awareness. In Proc. of HUC,

pages 304–307. Springer.

Amer, M., Goldstein, M., and Abdennadher, S. (2013). En-

hancing one-class support vector machines for unsu-

pervised anomaly detection. In Proceedings of the

ACM SIGKDD Workshop on Outlier Detection and

Description, ODD ’13, pages 8–15, New York, NY,

USA. ACM.

Atlas, L. E., Cohn, D. A., and Ladner, R. E. (1990). Train-

ing connectionist networks with queries and selective

sampling. In Touretzky, D. S., editor, Advances in

Neural Information Processing Systems 2, pages 566–

573. Morgan-Kaufmann.

Bishop, C. M. (2006a). Pattern Recognition and Machine

Learning, chapter 10 Variational Inference, pages 461

– 486. Springer, New York, NY.

Bishop, C. M. (2006b). Pattern Recognition and Machine

Learning. Springer, New York, NY.

Chen, L., Hoey, J., Nugent, C. D., Cook, D. J., and Yu,

Z. (2012). Sensor-based activity recognition. IEEE

Transactions on Systems, Man, and Cybernetics, Part

C (Applications and Reviews), 42(6):790–808.

Clarkson, B., Mase, K., and Pentland, A. (2000). Recog-

nizing user context via wearable sensors. In Proc. of

ISWC, pages 69–75.

Fernndez-Francos, D., Martnez-Rego, D., Fontenla-

Romero, O., and Alonso-Betanzos, A. (2013). Au-

tomatic bearing fault diagnosis based on one-class ν-

svm. Computers & Industrial Engineering, 64(1):357

– 365.

Fisch, D., J

anicke, M., Kalkowski, E., and Sick, B.

(2009). Learning by teaching versus learning by do-

ing: Knowledge exchange in organic agent systems.

In Intelligent Agents, 2009. IA’09. IEEE Symposium,

pages 31–38. IEEE.

Franke, T., Lukowicz, P., Kunze, K., and Bannach, D.

(2009). Can a mobile phone in a pocket reliably rec-

ognize ambient sounds? In Wearable Computers,

2009. ISWC’09. International Symposium on, pages

161–162. IEEE.

Gellersen, H., Schmidt, A., and Beigl, M. (2002). Multi-

sensor context-awareness in mobile devices and

smart artifacts. Mobile Networks and Applications,

7(5):341–351.

Gruhl, C. and Sick, B. (2016). Detecting novel pro-

cesses with CANDIES - an holistic novelty detec-

tion technique based on probabilistic models. CoRR,

abs/1605.05628.

Guerbai, Y., Chibani, Y., and Hadjadji, B. (2015).

The effective use of the one-class {SVM} classi-

ﬁer for handwritten signature veriﬁcation based on

writer-independent parameters. Pattern Recognition,

48(1):103 – 113.

Junker, H., Amft, O., Lukowicz, P., and Trster, G. (2008).

Gesture spotting with body-worn inertial sensors to

detect user activities. Pattern Recognition, 41(6):2010

– 2024.

Kephart, J. and Chess, D. (2003). The Vision of Autonomic

Computing. IEEE Computer, 36(1):41–50.

Kwapisz, J., Weiss, G., and Moore, S. (2011). Activity

recognition using cell phone accelerometers. ACM

SIGKDD Explorations Newsletter, 12(2):74–82.

Lau, S. and David, K. (2010). Movement recognition using

the accelerometer in smartphones. In Future Network

and Mobile Summit, 2010, pages 1–9. IEEE.

Lau, S., K

onig, I., David, K., Parandian, B., Carius-D

ussel,

C., and Schultz, M. (2010). Supporting patient moni-

toring using activity recognition with a smartphone. In

Wireless Communication Systems (ISWCS), 2010 7th

International Symposium on, pages 810–814. IEEE.

Li, K.-L., Huang, H.-K., Tian, S.-F., and Xu, W. (2003). Im-

proving one-class svm for anomaly detection. In Ma-

chine Learning and Cybernetics, 2003 International

Conference on, volume 5, pages 3077–3081. IEEE.

Markou, M. and Singh, S. (2003a). Novelty Detection: a

review – part 1: statistical approaches. Signal Pro-

cessing, 83:2481–2497.

Markou, M. and Singh, S. (2003b). Novelty Detection: a re-

view – part 2: neural network based approaches. Sig-

nal Processing, 83:2499–2521.

Sch

olkopf, B., Williamson, R. C., Smola, A. J., Shawe-

Taylor, J., Platt, J. C., et al. (1999). Support vector

method for novelty detection. In NIPS, volume 12,

pages 582–588.

Sun, L., Zhang, D., Li, B., Guo, B., and Li, S. (2010). Activ-

ity recognition on an accelerometer embedded mobile

phone with varying positions and orientations. Ubiq-

uitous Intelligence and Computing, pages 548–562.

Tax, D. and Duin, R. (2002). Uniform Object Generation

for Optimizing One-class Classiﬁers. The Journal of

Machine Learning Research, 2:155–173.

Tomforde, S., Sick, B., and M

uller-Schloer, C. (2017).

Organic Computing in the Spotlight. arXiv.org.

http://arxiv.org/abs/1701.08125.

Zhang, Y., Meratnia, N., and Havinga, P. (2009). Adap-

tive and online one-class support vector machine-

based outlier detection techniques for wireless sen-

sor networks. In 2009 International Conference on

Advanced Information Networking and Applications

Workshops, pages 990–995.

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

142