3D Orientation Estimation of Industrial Parts from 2D Images using

Neural Networks

Julien Langlois

1,2

, Harold Mouchère

, Nicolas Normand

and Christian Viard-Gaudin

University of Nantes, Laboratoire des Sciences du Numérique de Nantes, UMR 6004, France

Multitude-Technologies a company of Wedo, France

Keywords:

Neural Networks, 3D Pose Estimation, 2D Images, Deep Learning, Quaternions, Geodesic Loss, Rendered

Data, Data Augmentation.

Abstract:

In this paper we propose a pose regression method employing a convolutional neural network (CNN) fed with

single 2D images to estimate the 3D orientation of a speciﬁc industrial part. The network training dataset

is generated by rendering pose-views from a textured CAD model to compensate for the lack of real images

and their associated position label. Using several lighting conditions and material reﬂectances increases the

robustness of the prediction and allows to anticipate challenging industrial situations. We show that using a

geodesic loss function, the network is able to estimate a rendered view pose with a 5

◦

accuracy while inferring

from real images gives visually convincing results suitable for any pose reﬁnement processes.

1 INTRODUCTION

Pose estimation of objects has recently gained lots of

interest in the literature for its wide application possi-

bilities such as robotic grasping for bin picking. Nev-

ertheless, this task remains challenging in the case of

industrial parts, usually texture-less and not appropri-

ate for key-points and local descriptors. Moreover,

in a non-controlled and unfriendly industrial environ-

ment many issues have to be tackled akin to low lu-

minosity or cluttered scenes. To be embedded in a bin

picking process, any pose estimation module requires

high precision recognition while offering acceptable

execution speed not to penalize the following indus-

trial treatments. It is even more arduous when the part

needs to be precisely placed on an assembly module

afterwards.

Estimating the position of any 3D objects in a scene

has gained interest in the past years thanks to neural

networks and their abilities to extract relevant features

for a given task. However, this task remains challeng-

ing when handling industrial parts because of their of-

ten black and glossy plastic material: in hostile plant

conditions this material is known to constrain the pre-

diction capabilities of image-based algorithms.

Many works have been conducted with a depth infor-

mation allowing algorithms to learn spatial features to

recognize (Bo et al., 2012) or estimate the positions of

objects within an image (Hodan et al., 2015) (Shot-

ton et al., 2013). In this paper we show that a simple

2D information is enough to predict the rotations of a

part given a certain conﬁdence score using a CNN and

quaternions. However, the training dataset creation

based on real images appears to be a painful process.

Thereby, we also propose a dataset generation frame-

work using rendered views from a CAD (Computer-

Aided Design) model as a way to offset the lack of

real images labeled with the accurate object position

(Su et al., 2015). Using an alpha channel (trans-

parency) offers the possibility to add backgrounds and

rotations without any image cropping. Scene param-

eters (lightening, scale, reﬂectance...) must be deci-

sive for a relevant feature learning to infer from real

images thus we choose them according to the part ap-

pearances in real views (Mitash et al., 2017).

When directly regressing the pose of an object, the

Euclidean distance is often employed as a loss func-

tion to approximate the distance between quater-

nions (Melekhov et al., 2017) (Kendall et al., 2015)

(Doumanoglou et al., 2016). In this paper we pro-

pose a geodesic distance-based loss function using

the quaternion properties. Operations of the quater-

nion algebra are a combination of simple derivable

operators which can be used in a gradient-based back-

propagation. We achieve to get a network which of-

fers a great pose estimation with a low uncertainty

over the data. With a wide variety of scene param-

eters, the network is able to estimate the pose of the

Langlois, J., Mouchère, H., Normand, N. and Viard-Gaudin, C.

3D Orientation Estimation of Industrial Parts from 2D Images using Neural Networks.

DOI: 10.5220/0006597604090416

In Proceedings of the 7th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2018), pages 409-416

ISBN: 978-989-758-276-9

409

object in a real image with a sufﬁcient accuracy to be

fed into a pose reﬁnement process.

2 RELATED WORK

2.1 Local Features Matching

Local features extraction has been widely studied in

the literature as it easily gives matching pair opportu-

nities between two views. These features were ﬁrst

constructed from parametric shapes isolated within

the image contours (Honda et al., 1995). The indus-

trial parts need to have speciﬁc shape singularities

to be properly localized, though. More recently, the

well known SIFT local descriptor was employed to

get a pose description of an object (Lowe, 2004). In

(Gordon and Lowe, 2004) a matching between the ex-

tracted SIFT with the pose description of the object

is performed to get a camera pose estimation. Be-

cause of the high dimension of the features vector,

the S IFT severely impacts the algorithm computa-

tion time. Later, the SURF local descriptors, faster

to extract, were introduced. However, they appear to

be less robust to rotation and image distorsion than

SIFT (Bay et al., 2008). To be computed, the local

descriptors often rely on the object texture, one el-

ement absent from industrial parts. Moreover, they

suffer from high luminosity and contrast variations

which make them improper to be used in a challeng-

ing plant environment. Using the depth channel of

RGB-D images, (Lee et al., 2016) proposes an ICP al-

gorithm fed with 3D SURF features and Closed Loop

Boundaries (CLB) to estimate the pose of industrial

objects. However, the system can not deal with oc-

clusions likely to happen inside a bin.

2.2 Template Matching

To tackle the issue of texture-less objects, template

matching methods are employed to assign more com-

plex feature pairs from two different points of view.

Prime works built an object descriptor composed of

different templates hierarchically extracted from an

object point of view and later compared with an input

image through a distance transform (Gavrila, 1998).

To handle more degrees of freedom in the camera

pose estimation, the recent machine learning tech-

niques are used to learn the object templates and

the associated camera pose to infer the position and

then reﬁne it using the distance transform. However,

the algorithms still need a contour extraction pro-

cess which is not suitable for low contrasted, noisy

or blurred images. In (Hinterstoisser et al., 2010) the

discretized gradient directions are used to build tem-

plates compared with an object model through an en-

ergy function robust to small distorsion and rotation.

This method called LINE is yet not suitable for clut-

tered background as it severely impacts the computed

gradient. A similar technique is proposed in (Muja

et al., 2011). The arrival of low-cost RGB-D cameras

led the templates to become multimodal. LINEMOD

presented in (Hinterstoisser et al., 2011) uses a depth

canal in the object template among the gradient from

LINE to easily remove background side effects. The

method is later integrated into Hough forests to im-

prove the occlusion robustness (Tejani et al., 2014).

To deal with more objects inside the database, (Hodan

et al., 2015) proposes a sliding window algorithm ex-

tracting relevant image areas to build candidate tem-

plates. These templates are veriﬁed to get a rough

3D pose estimation later reﬁned with a stochastic op-

timization procedure. The camera pose estimation

problem can be solved with template matching but re-

mains constrained to RGB-D information to achieve

acceptable results. In this paper we propose to use 2D

images without depth information therefore not suit-

able for this type of matching.

2.3 Features Matching from Neural

Networks

Neural networks offer the ability to automatically ex-

tract relevant features to perform a given task. In

a pose estimation problem they use convolutional

neural networks to compute object descriptors as a

database prior to a kNN algorithm to ﬁnd the closest

camera pose in the set (Wohlhart and Lepetit, 2015).

The loss function is fed with a triplet formed with

one sample from the training dataset and two others

respectively close and far from the considered cam-

era position. Forcing the similarity between features

and estimated poses for two close points of view is

also employed in (Doumanoglou et al., 2016) with a

Siamese neural network doing a real pose regression.

Although these methods are quite appealing, they still

take advantage of RGB-D modalities. In (Kendall

et al., 2015) a deep CNN known as PoseNet based

on the GoogLeNet network is built to regress a 6D

camera pose from a 2D image. Whereas slightly dif-

ferent from our work for dealing with urban scenes,

the work shows the continuous 3D space regression

capability of a CNN in an end-to-end manner. Other

works are using pre-trained CNN for object classiﬁ-

cation to estimate a view pose through SVMs. The

depth channel of the RGB-D image is converted into

an RGB image to be fed into a CNN with relevant 3D

features (Schwarz et al., 2015).

ICPRAM 2018 - 7th International Conference on Pattern Recognition Applications and Methods

410

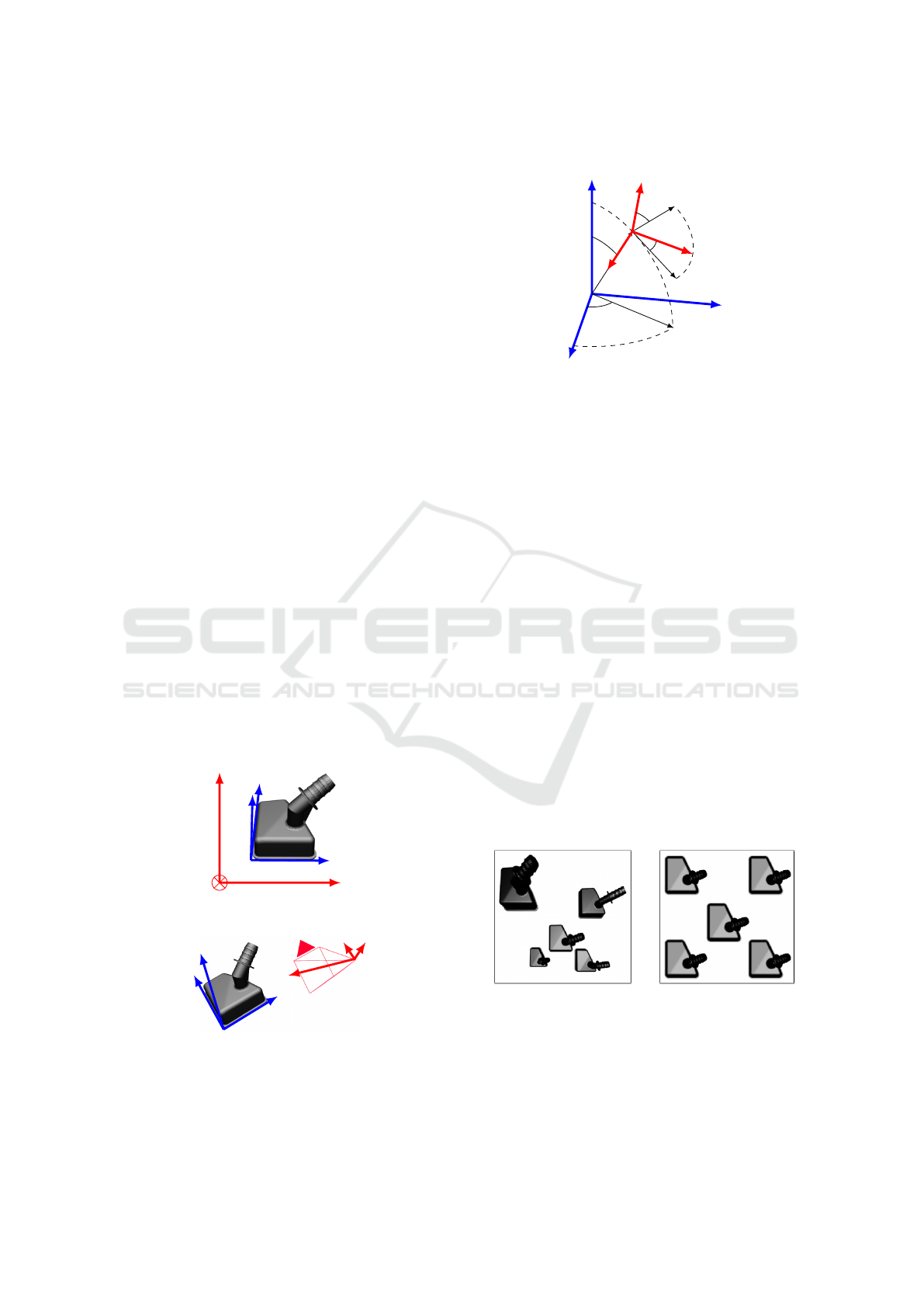
3 POSE REGRESSION

In this section we ﬁrst deﬁne and transform the pose

regression problem as a camera pose estimation prob-

lem using a bounding sphere and quaternions. To gen-

erate the pose views later fed into the CNN, a 3D

pipeline rendering a CAD model seen under several

scene atmosphere conditions is presented. Finally,

the convolutional neural network which regresses the

pose of the object is described from its architecture to

its loss function based on the geodesic distance in the

quaternions space.

3.1 Problem Deﬁnition

An object O is placed in a world scene with its frame

position P

= (x

) and orientation expressed

as the Euler triplet R

= (φ

,θ

,ψ

). The objec-

tive is to retrieve the object orientation from a point

of view given by a ﬁxed top camera. A trivial prob-

lem shift is to consider a ﬁxed object with a mo-

bile camera encompassing the scene localized with

= (φ

,θ

,ψ

) lying on a bounding r-radius sphere

centered on the object’s centroid (Figure 1). Using

the convention Z −Y − Z for the Euler triplet allows

us to easily map the camera position according to the

sphere azimuth and elevation. The third angle ψ

then the camera plane rotation angle (Figure 2).

Any composition of rotations can be written as

an axis-angle rotation according to the Euler’s rota-

tion theorem. Following this equivalence, to avoid

any gimbal locks and improve computation perfor-

mances, the triplet R

is written as the quaternion

Figure 1: Top: The object O placed in the world scene and

its CAD frame (

) viewed from a ﬁxed top-view

camera. Bottom: Finding the O frame is equivalent to a

camera frame (

) evaluation problem in the scene

when the object is ﬁxed.

Figure 2: The camera is placed according to the

(φ

,θ

,ψ

) Euler’s triplet using the Z −Y − Z convention.

= (w

, ~v

) according to the chosen Euler conven-

tion, representing an axis-angle rotation with a vector

expressed as an hypercomplex number. Any camera

orientation is now independent from the Euler’s con-

vention used.

Using a telecentric lens on the camera would allow

us to estimate the position P

and orientation R

of a

part without any perspective effect: two objects sim-

ilarly orientated but widely separated in the world

scene would take the same shape in the top-view cam-

era plane. The side effect is that different Z altitudes

would give identical zooms (subject to magnifying er-

rors) thus misleading the frame position estimation

(Figure 3). It means that the system still needs to

use an entocentric lens to predict the r sphere radius.

Knowing the object centroid in the image plan plus

the estimated r sphere radius is enough to obtain each

object frame position P

among R

from our neural

network prediction. The position estimation P

re-

mains out of this paper scope yet so we suppose the

radius r is known and we only use entocentric render-

ing for the orientation estimation R

Figure 3: Same scene rendered with different camera lens.

Left: entocentric lens rendering different altitude and per-

spectives. Right: telecentric lens giving the same aspect for

every object including scale.

3D Orientation Estimation of Industrial Parts from 2D Images using Neural Networks

411

3.2 Pose Generation

The industrial parts inside a bin have many possible

poses as they can lie on each other. Thereby, creating

a training dataset of real images covering all possibil-

ities is tedious and complex. Moreover, every point

of view will rely on a speciﬁc lightening condition

not necessarily consistent with different bin-picking

module placements in a factory. In this work a CAD

model of the object is available so that a dataset can be

generated during a rendering process. Using a virtual

dataset has several advantages including the anticipa-

tion of different atmosphere conditions, backgrounds,

scene cluttering and occlusions happening in a non-

favorable plant environment.

3.2.1 Camera Placement

A CAD model is placed on the center of a 3D scene

according to its frame then textured to reproduce the

glossy black plastic material of the real part. The

camera positions are evenly picked on an r radius

sphere surface with a speciﬁed number of poses us-

ing a golden spiral algorithm (Boucher, 2006). The

camera frame is computed so that the

Z axis is point-

ing toward the scene center and the

X axis remains

horizontal (meaning ψ

= 0). This results in two an-

gles φ

and θ

positioning and a camera plane rota-

tion ψ

. Notice that this third angle can be generated

by rotating the result image which can be done on the

ﬂy during the training phase thus reducing the dataset

size on the hard drive.

3.2.2 Scene Parameters

For each point of view, the lighting conditions as well

as the material reﬂectance are modiﬁed. This em-

phasizes different areas of the part so that the neural

network can learn different features from the training

dataset (Figure 4). A relevant scene parameter range

Figure 4: Effects of several lightening conditions in the

scene and different object material reﬂectances on the ren-

dered image.

Figure 5: Relevant scene parameters can render realistic

views of the part. Left: the real image pose. Right: the

rendered approximated pose.

comes from the study of real images taken under sev-

eral conditions as shown in Figure 5. However, this

might not always look realistic since the real material

has no constant reﬂectance on its surface and it may

contains blur or timestamp prints as seen in the top-

left image in Figure 5. Finally, to avoid any pixelation

the software antialiasing is applied and the image is

generated with a size of 64 × 64 pixels. This image

resolution is approximately the object bounding box

size inside a bin rendered with an initial camera res-

olution of 1600 × 1200 pixels (which is an industrial

standard) at a working distance of 2 meters.

The scene background is set as an alpha channel (full

transparency) to apply different backgrounds on the

ﬂy during the future training phase (Figure 8). The

background can be deﬁned as a color or a texture

picked within high resolution samples showing mate-

rial such as wood, plastic or metal as we don’t know

the nature of the bin in advance. The RGB image with

the alpha channel leads to a 4-channels image later

ﬂattened to grayscale during the training process.

3.3 Network Architecture

3.3.1 Architecture

To estimate the pose of a single part from an RGB im-

age we use a CNN architecture composed of convo-

lutional and fully connected layers. Our network can

only deal with a speciﬁed object but seen in differ-

ent lighting conditions and with several backgrounds.

In this case, using 2 convolutional layers is enough

to extract shape and reﬂection features. On the other

hand, relations between the extracted features and the

quaternion are quite complex which basically leads to

use at least one massive fully connected (FC) layer.

Inspired by the recent work of (Wohlhart and Lep-

ICPRAM 2018 - 7th International Conference on Pattern Recognition Applications and Methods

412

Image

grayscale

64 × 64

CONV

11×11

POOL

384

CONV

5 × 5

POOL

512

Output

Figure 6: The proposed convolutional neural network archi-

tecture for quaternion regression.

etit, 2015), an efﬁcient way to bypass such compu-

tation time and memory consumption is presented in

(Doumanoglou et al., 2016) using a Siamese archi-

tecture forcing via the loss function a similarity be-

tween features and pose estimations for similar sam-

ples. From these works, we also use a last FC layer

described as the descriptor layer but we propose a net-

work which has an increasing number of ﬁlters per

layer as we handle only one object and thus do not

need a sparse description of the part.

In the following description, CONV (a, b) stands for a

convolution layer with b ﬁlters of size a×a, POOL(a)

for a max pooling layer of size a × a and FC(a) for a

fully connected layer of a hidden neurons. This CNN

is built as follows: CONV(11, 96) − POOL(2) −

CONV(5, 384) − POOL(2) − FC(512) − FC(64) −

FC(4). The network is fed with a 64 × 64 grayscale

image. All layers are using a ReLU activation func-

tion while the output layer uses a tanh function as the

prediction domain is [−1, 1] which is suitable for the

quaternion space. The images are normalized prior to

the input layer.

3.3.2 Loss Function

An object orientation R

can be described with an Eu-

ler’s triplet (φ

,θ

,ψ

). However when using uni-

tary quaternions for rotations, R

can also be de-

scribed by two quaternions : q

and −q

. Thus to es-

timate the discrepancy between two poses, the usual

distance is not suitable since L

,−q

) is not

null. Even if in the end of the learning process the

prediction q

is getting close to the ground truth q

leading the L

distance to be small, the network be-

haviour in the beginning of the learning process is not

clear. Moreover, using the L

norm constrains the net-

work to predict the exact same vector regardless of

the quaternion geometric possibilities. For the quater-

nions are lying on a 3-sphere, we build a loss com-

puted with the geodesic distance θ between q

and

the normalized predicted quaternion

to tackle this

issue (Huynh, 2009). Using the scalar product h.i, we

have:

i = cos





cos(θ) + 1

(1)

With (1) we deﬁne the geodesic loss for the i

ex-

ample in the dataset as:

= 1 − hq

(2)

This loss is suitable for a gradient-based backpropa-

gation for it is made with simple derivable operators.

With this objective function, the network is able to

predict the truth q

but also −q

. To properly use

this loss term, the predicted quaternion is manually

normalized thus, the network does not tend naturally

to predict unitary quaternion (real rotations) when not

fully converged. One simple way to force this is to

add a β weighted penalty when the prediction’s norm

differs from 1.

= β(1 − ||q

||)

(3)

The ﬁnal loss is built with the geodesic error L

(2)

and normalization error L

(3) mean over the samples

i among a L

regularization term weighted by λ to

prevent any overﬁtting:

L =

∑

i=1

+ L

) + λ||w||

(4)

4 EXPERIMENTS

In our experiments we used an industrial black plas-

tic part generated by its CAD model. We ﬁrst pro-

duce the dataset for the neural network according to

a certain number of evenly distributed positions on a

sphere under several scene parameters. During the

training, we process each image to create different

backgrounds and render the third angle.

4.1 Protocol

The training dataset is generated with 1000 evenly

distributed positions on the sphere, 3 material re-

ﬂectances and 2 orthographic camera lens scales to

avoid overﬁtting leading to a training dataset of 6000

images. With a number of 1000 positions, the average

geodesic distance between two close samples is 6.3

◦

The validation and test datasets are made with 1000

random samples extracted from 10000 even positions

on the sphere set with random light conditions and re-

ﬂectances for each one.

The training is performed with minibatches contain-

ing 100 samples. For each sample, a process can

add the third angle ψ

by rotating the image plane

and changing the associated quaternion. The quater-

nion q

modiﬁcation is however not straightforward

as it needs to ﬁrst be converted into a rotation matrix

Rot

then to the corresponding Euler’s triplet using

3D Orientation Estimation of Industrial Parts from 2D Images using Neural Networks

413

Rot

(φ

,θ

,0)

+(0,0, ψ

)

’

Figure 7: Quaternion modiﬁcation when adding a third an-

gle ψ

the proper convention. Once the third angle of the

triplet is modiﬁed, the new quaternion is computed

and placed into the minibatch sample (Figure 7).

A colored or textured background is then applied to

each image sample to remove the alpha channel. The

image color channels do not provide relevant informa-

tion as our parts are made of black plastic. Thereby

each image is ﬂattened to obtain a grayscale picture.

After the image process, the minibatches are normal-

ized and zero-centered.

In a ﬁrst experiment, we only generate and estimate

the two ﬁrst angles φ

and θ

. Learning the third an-

gle requires a strong variability in the dataset so that

the network needs lots of epochs to converge. The

third angle ψ

learning starts with widely separated

angles within the [−180

◦

,180

◦

[ angle space (a 90

◦

step). Through the epochs, the step is reduced to ﬁ-

nally reach 10

◦

(Figure 11).

We introduce two metrics suitable for the angle es-

timation error. First, we retrieve the Euler’s triplet

from the predicted quaternion using the rotation ma-

trix. We deﬁne the angle error vector E = (E

)

as the absolute difference between the angles pre-

dicted and the ground truth. However, the error un-

der each Euler’s axis does not represent how far the

estimated pose if from the truth as they can be cumu-

lated. Yet, we build a second metric G obtained with

Batch (6000) Minibatch (100)

Sample i

Image

Quaternion

Rotate ψ

Image’

Quaternion’

Background

Grayscale

Image”

Sample’ i

Figure 8: Image processing during the minibatch creation:

the third angle ψ

is generated on the ﬂy before the image

is ﬂattened to obtain a gray level matrix.

the geodesic distance between the predicted and the

ground truth quaternion coming from (1).

G = |cos

−1

(2hq

− 1)| (5)

The geodesic distance shows the smallest transforma-

tion needed to align the prediction with the truth and

can be seen as a cumulative Euler angle error for each

sample. Thus it is expected to be higher than any com-

ponents of E.

For the training phase we use a Nesterov momentum

backpropagation with an initial learning rate of 0.001

decreased through the epochs and a 0.9 momentum.

The λ regularization weight is set to 0.001 as well

as β. The implementation is Python-based with a

Theano+Lasagne framework. The training dataset is

build with a Blender rendering pipeline and learned

on a Nvidia Tesla P100 in roughly 10 hours. The

parameters giving the best score for the validation

dataset are kept for the test phase.

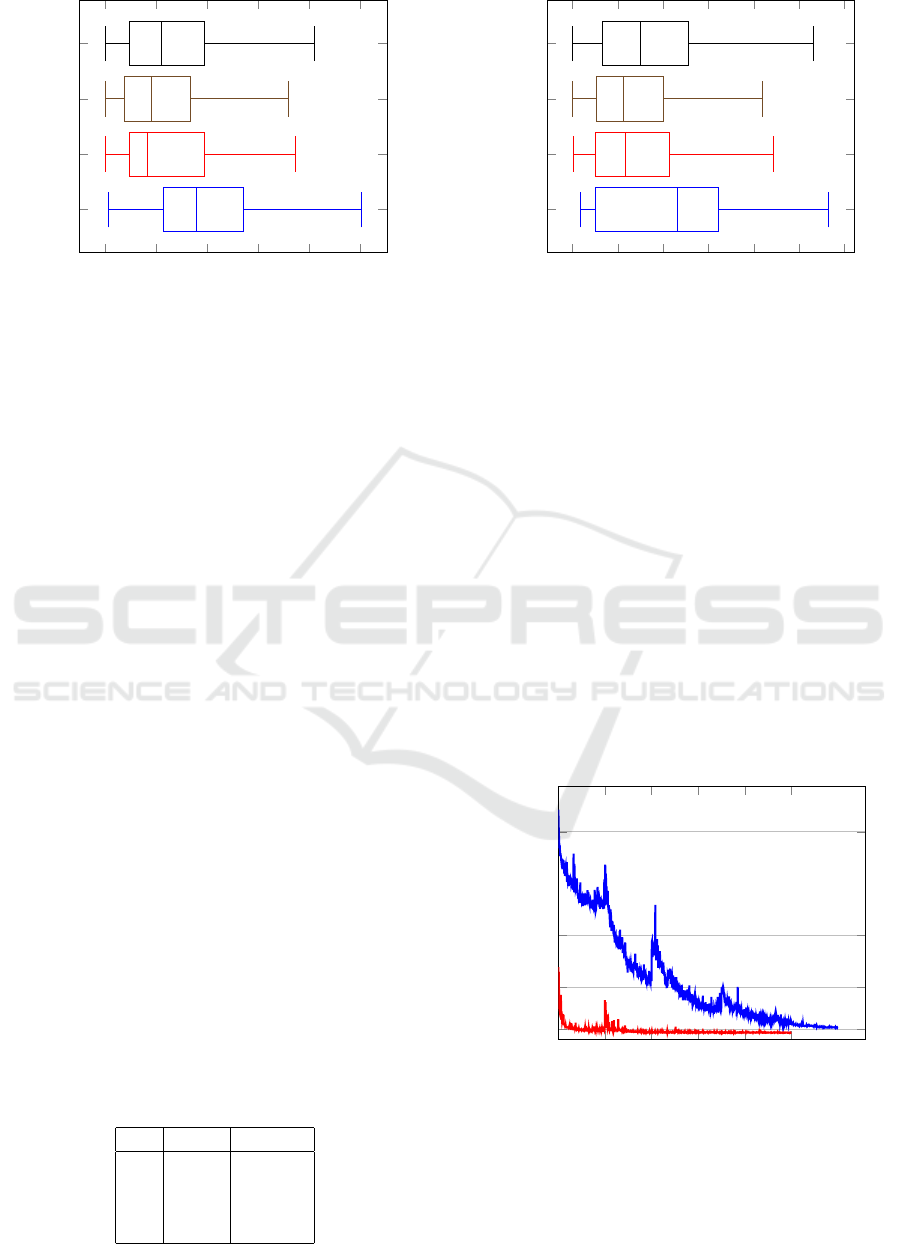
4.2 Results

Looking at the results in Table 1 we are able to es-

timate both φ

and θ

with an average accuracy of

◦

when only the two ﬁrst angles are learned with a

random background. The last estimated angle ψ

can

also be retrieved for an unitary quaternion since it can

represent any rotation composition. However we see

that the mean ψ

value is high because no variability

on it has been seen in the training dataset (Figure 9).

As expected, the geodesic error is the highest because

it represents an Euler angle cumulative error.

When the third angle ψ

is learned, we observe that

its distribution gets a larger prediction uncertainty

than in the two angles scenario but has a lower mean

(Figure 10). With a 6

◦

resolution for φ

and θ

and

◦

for ψ

, the angle error medians are under 3

◦

which shows that the network is performing the ex-

pected regression task and do not tend to classify to

the nearest learned angle (Table ??). It is interesting

to note that in a two angles learning scenario, the net-

work converges really fast at 100 epochs under a 5

◦

error whereas the three angles learning scenario needs

more than 1000 epochs (Figure 11). Some samples

are shown with the associated geodesic error in the

Figure 12. The trained network has two max-pooling

Table 1: Pose estimation angle error with a two angles train-

ing.

mean median

4.39

◦

2.0

◦

1.93

◦

1.46

◦

9.24

◦

1.52

◦

G 3.3

◦

2.8

◦

ICPRAM 2018 - 7th International Conference on Pattern Recognition Applications and Methods

414

0 2 4

8 10

Angle error (

◦

)

Figure 9: Box-plot of the angle estimation errors with two

angles generated (ψ

, θ

layers (Figure 6) which are known to be invariant to

small rotations. Despite their abilities to reduce the

training time and complexity, they tend to constrain

the prediction capacities of the algorithm.

When estimating the object pose from real images,

the task remains challenging for we do not dispose

any telecentric dataset. Only a small number of views

with limited perspective effects can be fed into the

network. With an only rendered-based training, we

are still able to estimate the pose of the object with a

visually convincing precision (Figure 13). Even if we

do not have any ground truth information, the pose of

the object inside the real image can be roughly esti-

mated by the mean of a 3D modeler as in Figure 5.

With this information, the average Euler’s angles er-

ror reaches 22

◦

5 CONCLUSION

In this paper we proposed a convolutional neural net-

work performing a 3D pose regression of a known ob-

ject in a scene. We showed that once the network has

learned from rendered data, it can infer from rendered

images the three Euler’s angles with a 5

◦

accuracy de-

spite the max-pooling layers dropping the third angle

estimation performance.

Inside a real industrial bin, the parts can lie on each

other so that severe occlusions are likely to happen.

Table 2: Pose estimation angle error with a three angles

training.

mean median

6.46

◦

3.0

◦

2.8

◦

2.26

◦

6.56

◦

2.31

◦

G 5.14

◦

4.61

◦

0 2 4

8 10 12

Angle error (

◦

)

Figure 10: Box-plot of the angle estimation errors with

three angles generated (φ

, θ

,ψ

However, our network does not learn how to han-

dle these conﬁgurations. Some works already tackle

this issue with a loss function term handling an occlu-

sion factor (Doumanoglou et al., 2016). In a future

work, occlusions are going to be taken into account

among an instance segmentation algorithm also based

on a convolutional neural network to get an end-to-

end learning process. When the network is fed with

real image containing small perspective effects, the

estimated pose is visually convincing however the ac-

curacy exceeds 22

◦

. There are several factors to be

taken into account to outperform this score: a non-

constant background luminosity, noise, perspective

effects and textured backgrounds. In a future work,

we aim at learning perspective effects by associating

any quaternion estimations to the object (x, y) position

in the image plane.

0 200 400

600

800 1,000

100

Epochs

G angle error (

◦

)

Figure 11: Geodesic error of test batch during the two (red)

and three (blue) angles training phase. For the three angles

training, the third angle steps are reduced at 200, 400, 700

and 900 epochs.

3D Orientation Estimation of Industrial Parts from 2D Images using Neural Networks

415

G = 2.62

◦

G = 4.11

◦

G = 2.75

◦

G = 5.92

◦

G = 2.29

◦

G = 2.85

◦

G = 2.85

◦

G = 2.16

◦

Figure 12: Estimating the object pose from rendered im-

ages. Left: the truth image. Right: the rendered estimated

pose. The geodesic error is printed below.

Figure 13: Estimating the object pose from real images.

Left: the real image. Right: the rendered estimated pose.

The estimation average accuracy reaches 22

◦

REFERENCES

Bay, H., Tuytelaars, T., and Gool, L. V. (2008). Surf :

Speeded up robust features. CVIU.

Bo, L., Ren, X., and Fox, D. (2012). Unsupervised feature

learning for rgb-d based object recognition. ISER.

Boucher, P. (2006). Points on a sphere.

Doumanoglou, A., Balntas, V., Kouskouridas, R., and Kim,

T.-K. (2016). Siamese regression networks with ef-

ﬁcient mid-level feature extraction for 3d object pose

estimation. arXiv:1607.02257.

Gavrila, D. M. (1998). Multi-feature hierarchical template

matching using distance transforms. ICPR.

Gordon, I. and Lowe, D. G. (2004). What and where: 3d

object recognition with accurate pose. ISMAR.

Hinterstoisser, S., Holzer, S., Cagniart, C., Ilic, S., Kono-

lige, K., Navab, N., and Lepetit, V. (2011). Multi-

modal templates for real-time detection of texture-less

objects in heavily cluttered scenes. ICCV.

Hinterstoisser, S., Lepetit, V., Ilic, S., Fua, P., and Navab, N.

(2010). Dominant orientation templates for real-time

detection of texture-less objects. CVPR.

Hodan, T., Zabulis, X., Lourakis, M., Obdrzalek, S., and

Matas, J. (2015). Detection and ﬁne 3d pose estima-

tion of texture-less objects in rgb-d images. IROS.

Honda, T., Igura, H., and Niwakawa, M. (1995). A handling

system for randomly placed casting parts using plane

ﬁtting technique. IROS.

Huynh, D. (2009). Metrics for 3d rotations: comparison

and analysis. JMIV.

Kendall, A., Grimes, M., and Cipolla, R. (2015). Posenet:

A convolutional network for real-time 6-dof camera

relocalization. ICCV.

Lee, S., Wei, L., and Naguib, A. M. (2016). Adaptive

bayesian recognition and pose estimation of 3d indus-

trial objects with optimal feature selection. ISAM.

Lowe, D. G. (2004). Distinctive image features from scale-

invariant keypoints. IJCV.

Melekhov, I., Ylioinas, J., Kannala, J., and Rahtu, E. (2017).

Relative camera pose estimation using convolutional

neural networks. ACIVS.

Mitash, C., Bekris, K. E., and Boularias, A. (2017). A self-

supervised learning system for object detection using

physics simulation and multi-view pose estimation.

IROS.

Muja, M., Rusu, R. B., Bradski, G., and Lowe, D. G. (2011).

Rein-a fast, robust, scalable recognition infrastructure.

ICRA.

Schwarz, M., Schulz, H., and Behnke, S. (2015). Rgb-d

object recognition and pose estimation based on pre-

trained convolutional neural network features. ICRA.

Shotton, J., Glocker, B., Zach, C., Izadi, S., Criminisi, A.,

and Fitzgibbon, A. (2013). Scene coordinate regres-

sion forests for camera relocalization in rgb-d images.

CVPR.

Su, H., Qi, C. R., Li, Y., and Guibas, L. (2015). Render

for cnn: Viewpoint estimation in images using cnns

trained with rendered 3d model views. ICCV.

Tejani, A., Tang, D., Kouskouridas, R., and Kim, T.-K.

(2014). Latent-class hough forests for 3d object de-

tection and pose estimation. ECCV.

Wohlhart, P. and Lepetit, V. (2015). Learning descriptors

for object recognition and 3d pose estimation. CVPR.

ICPRAM 2018 - 7th International Conference on Pattern Recognition Applications and Methods

416