Splitting-merging Clustering Algorithm for Collaborative Filtering

Recommendation System

Nabil Belacel

, Guillaume Durand

, Serge Leger

and Cajetan Bouchard

National Research Council, Information and Communication Technologies, Ottawa, Ontario, Canada

National Research Council, Information and Communication Technologies, Moncton, New Brunswick, Canada

Keywords:

Information Filtering, Recommender Systems, Collaborative Filtering, Clustering, Splitting-merging

Clustering.

Abstract:

Collaborative ﬁltering (CF) is a well-known and successful ﬁltering technique that has its own limits, espe-

cially in dealing with highly sparse and large-scale data. To address this scalability issue, some researchers

propose to use clustering methods like K-means that has the shortcomings of having its performances highly

dependent on the manual deﬁnition of its number of clusters and on the selection of the initial centroids, which

leads in case of ill-deﬁned values to inaccurate recommendations and an increase in computation time. In this

paper, we will show how the Merging and Splitting clustering algorithm can improve the performances of

recommendation with reasonable computation time by comparing it with K-means based approach. Our ex-

periment results demonstrate that the performances of our system are independent on the initial partition by

considering the statistical nature of data. More specially, results in this paper provide signiﬁcant evidences that

the proposed splitting-merging clustering based CF is more scalable than the well-known K-means clustering

based CF.

1 INTRODUCTION

In general, recommendation systems use mainly three

types of ﬁltering techniques: content based ﬁltering

(CBF), collaborative ﬁltering (CF) and hybrid ﬁlte-

ring (the combination of content based ﬁltering and

collaborative ﬁltering)(Burke, 2002). The CBF re-

commendation technique recommends speciﬁc items

that are similar to those that have been already positi-

vely rated in the past by the active user. CBF uses only

the content of the items in order to make a recommen-

dation (Pazzani and Billsus, 2007). The CF recom-

mendation technique recommends items that were

preferred in the past by similar users to the active user.

CF techniques make the assumption that the active

user will be interested in items appreciated by simi-

lar users. Finally, the hybrid based ﬁltering techni-

ques recommend items by combining CF and content-

based ﬁltering (Burke, 2002). CF is widely used in the

ﬁelds of e-commerce (Linden et al., 2003), e-learning

(Bobadilla et al., 2009), e-government (Shambour and

Lu, 2011), TV programs (Zhang et al., 2013), music

(Cohen and Fan, 2000) and books (Benkoussas et al.,

2014). Methods in CF can be either memory-based

or model-based. Memory-based algorithms operate

on the whole user-item rating matrix and make re-

commendations by identifying the neighborhood of

the target user to whom the recommendations will

be made based on his preferences (Herlocker et al.,

1999). The memory based ﬁltering algorithms are

easy to implement and they perform very well in

many real world applications (Lu et al., 2015). Ho-

wever, they face important problems limiting their ap-

plications with sparse and/or large data. Data spar-

sity is common when users rate only a small number

of items creating a very sparse user-item matrix (Su

and Khoshgoftaar, 2009). On the scalability side, the

memory based ﬁltering algorithms do not scale satis-

factory when the users and items in ratings database

increase (Lu et al., 2015). To solve this last scala-

bility issue, model-based techniques were proposed.

Model based techniques use machine learning algo-

rithms on users-rating training data to learn a mo-

del and to make predictions on the users-rating test

data or on real data. Several algorithms have been

used for model based CF. Among the machine lea-

ning algorithms used, let’s list Bayesian networks (Su

and Khoshgoftaar, 2006), matrix factorization (Bokde

et al., 2015), probabilistic latent space models (Hof-

mann and Puzicha, 1999), neural networks(Feng and

Huiyou, 2006) and clustering methods(Salah et al.,

2016). Clustering methods using K-means algorithm

Belacel, N., Durand, G., Leger, S. and Bouchard, C.

Splitting-merging Clustering Algorithm for Collaborative Filtering Recommendation System.

DOI: 10.5220/0006599501650174

In Proceedings of the 10th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2018) - Volume 2, pages 165-174

ISBN: 978-989-758-275-2

165

have been widely used in model based CF because

of K-means simplicity and low complexity. Howe-

ver, the usability of K-means is limited by the fact

that the clustering results are heavily dependent on

the user deﬁned variants, i.e., the selection of the ini-

tial centroids and the number of clusters. In practice,

K-means algorithm conﬁguration difﬁculties can ea-

sily lead to inaccurate recommendation and drama-

tic computation time increases. To avoid the shortco-

mings of the K-means algorithm and at the same time

to solve scalability but also sparsity in CF, we propose

to use an automatic clustering approach. The propo-

sed clustering method can automatically determine a

pseudo-optimal number of clusters according to the

statistical nature of data so that the initial centroids

seeds are not critical to the clustering (Guan et al.,

2003b); (Guan et al., 2003a). This paper proposes a

recommendation method that alleviates the scalability

difﬁculty of CF and improves the K-means CF-based

recommendation approaches proposed in literature by

performing extensive experiments using three diffe-

rent data sets classiﬁed as small, medium and large

from MovieLens(Harper and Konstan, 2015). To the

best of our knowledge, this is the ﬁrst time that large

data with 10 millions entries were used in clustering

based CF. The rest of the article is organized as fol-

lows: Section 2 presents related works on traditional

CF as well as different algorithms including the clus-

tering methods used. Section 3 describes the propo-

sed approach to automatic clustering for CF. Section

4 provides experimental results and Section 5 outlines

conclusions and future work.

2 RELATED WORK

CF relies on past users items ratings. It predicts user

preferences on items that have not been seen yet based

on the historical preference judgments (rating values)

from a community of users. The preference judg-

ments are usually structured as a user-item rating ma-

trix. Note that user rating can be either implicit or ex-

plicit (Jawaheer et al., 2010). CF approach uses only

the past users’ behaviors and does not require any user

proﬁle. It has the advantage of not requiring any ex-

ternal data such as demographic information hence

reducing the time consumed by the recommendation

process ((Su and Khoshgoftaar, 2009)). Techniques

used in CF can be either memory based or model ba-

sed (Su and Khoshgoftaar, 2009).

2.1 Memory based Filtering

Memory based ﬁltering uses the entire user-item data

to generate a prediction. Based on some similarities,

the algorithms ﬁnd a set of users with similar tastes

or preferences, called neighbors, to target user. These

neighbors have a history of agreeing with the target

user.They rate different items similarly. Once neig-

hbors of users are found, the algorithms predict the

preferences on new items for the target user. These

algorithms are known as nearest-neighbor CF.

General Approach of k-nn based CF

The most prevalent algorithms used in collabora-

tive ﬁltering are k nearest neighbor CF. It was

the ﬁrst automated CF system introduced by Grou-

pLens(Resnick et al., 1994). The k nearest neighbor

for collaborative ﬁltering follows three phases to ge-

nerate a recommendation:

2.1.1 Phase 1: Similarity Weighting

The ﬁrst step in k-nn based CF is to weight all users

with respect to similarity. The similarity reﬂects the

correlation, distance or weight among users. Various

approaches have been proposed to compute the simi-

larity sim(a, v) between users a and v based on ratings

of items that both users have rated. Different simila-

rity measures have been proposed and evaluated in the

literature. Among these measures we can list: Cosine

vector, Pearson correlation, Spearman rank correla-

tion, mean squared difference and these are few simi-

larity measures used in CF among others (Al-Shamri,

2014), (Liu et al., 2014). Popular approach for simi-

larity weighting in CF is Pearson correlation. As a

result, we used Pearson correlation in the proposed

modeled based ﬁltering algorithm. In many research

works the Pearson correlation tends to lead to better

results (Ekstrand et al., 2011). The Pearson correla-

tion between the active user a and v is given as fol-

lows:

sim(a,v) =

∑

i∈I

a,i

− ¯r

)(r

v,i

− ¯r

)

∑

i∈I

a,i

− ¯r

)

∑

i∈I

v,i

− ¯r

)

(1)

where I is the set of co-rated items by the two users a

and v. r

a,i

and r

v,i

refer to the rating of the target item

i by the user a and v respectively. ¯r

and ¯r

are the

average rating of the co-rated items of the users a and

v respectively. Pearson correlation can be a problem

when it computes similarities between users who have

rated only few items. To alleviate this difﬁculty some

researchers propose an improved Pearson correlation

by adding a signiﬁcance weighting factor that would

devalue similarity weights based on a small number of

co-rated items (Herlocker et al., 2002). Some experi-

ments have shown a threshold value of 50 to be useful

in improving prediction accuracy. The threshold can

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

166

be applied by multiplying the similarity function by

min{|I

|/50,1}, where |I

| is the number of

co-rated item by the users a and v (Ekstrand et al.,

2011).

2.1.2 Phase 2: Neighborhoods Selection

As shown in different analysis (Herlocker et al.,

1999), a number of k neighbors between 20 and 50

is usually a reasonable starting point in CF. In our ex-

periments we used the best k selected technique. We

tried different number of neighborhood on training set

to ﬁnd the best one.

2.1.3 Phase 3: Prediction

After that the similarities between the active user with

other users are computed and that k neighbors are se-

lected, the CF system combines the items rating from

those k users to predict the user’s preferences for an

item. The formula used to generate prediction is the

weighted average of deviation from the neighbor’s

mean, using the similarity calculated in Eq. (1):

a,i

= ¯r

∑

v=1

v,i

− ¯r

) ∗ sim(a,v)

∑

v=1

sim(a,v)

(2)

where p

a,i

represents the prediction for the active user

a on the target item i. k is the selected number of

neighbors and sim(a,v) is the weighted similarity cal-

culated by Eq. (1). Herlocker et al. (Herlocker et al.,

1999) found that the weighted average deviation of

neighbor’s rating from that neighbor’s mean rating

performs signiﬁcantly better than the non-normalized

ratings approach. In our experiment we chose to use

eq. (2).

2.1.4 Challenges of Memory based

Collaborative Filtering

Memory based CF have been very successful due to

their simplicity and their good performances. Howe-

ver, and as previously mentioned, they suffer from

limitations such as scalability and data sparsity. In

practice recommender systems are used for large

numbers of user-items data. Hence, memory based

CF has difﬁculty scaling for systems such as ama-

zon.com or e-bay e-commerce. These systems con-

tain millions of users and items. In this paper we pro-

pose an approach that can deal with this scalability

issue, and we test it on millions of users and items.

In addition, most recommender systems dealing with

millions of items have active users rating only a small

number of them (sparsity) resulting in a poor recom-

mendation accuracy. Another illustration of the spar-

sity case is when a new user or item occurs, making

difﬁcult to ﬁnd similar neighbors as there is no in-

formation available on them. More details on me-

mory based collaborative ﬁltering challenges can be

found in ((Adomavicius and Tuzhilin, 2005);(Su and

Khoshgoftaar, 2009); (Lu et al., 2015). To overcome

these difﬁculties researchers have proposed model ba-

sed ﬁltering approaches.

2.2 Model based Filtering

Model based ﬁltering ﬁrst builds a model on the trai-

ning set (ofﬂine data set) to predict the items for the

active users on the test set (online). Since the model is

built ofﬂine, the system uses less memory and the pre-

diction time decreases ((Darvishi-Mirshekarlou et al.,

2013), (Gong et al., 2009)). The model based CF pro-

vides more accurate predictions for sparse data and

addresses scalability problems as shown in (Huang

and Yin, 2010), (Birtolo et al., 2011) and (Birtolo and

Ronca, 2013). Several popular model based ﬁltering

approaches are based on probabilistic latent semantic

CF and clustering techniques (Su and Khoshgoftaar,

2009). The goal of the latent semantic analysis is to

discover latent features that explain observed ratings

(Koren, 2010). Techniques of latent semantic analysis

count probabilistic latent space models (Hofmann and

Puzicha, 1999), neural network (Salakhutdinov et al.,

2007) and latent Dirichlet allocation or based on to-

pic modeling (Wilson et al., 2014). The clustering CF

techniques are extensively used to address the scala-

bility and sparsity problems. Researchers including

(Huang and Yin, 2010), (Birtolo et al., 2011), (Roh

et al., 2003) and (Birtolo and Ronca, 2013) show

in their experiments that clustering CF provide more

accurate predictions for sparse data than memory ba-

sed ﬁltering while addressing the scalability issue as

well as the items cold start problems. In the next sub

section, we give an overview on clustering methods

for CF.

2.2.1 Clustering based CF

In CF, the clustering techniques can be used to group

either the items into clusters that have same users’

preferences or users into clusters with similar items

ratings. In users’ CF, users who have same items’ pre-

ferences are grouped in restricted clusters. Therefore,

when a new user is identiﬁed as similar to a user clus-

ter, items liked by that user group are recommended

to the new user ((Tsai and Hung, 2012), (Sarwar et al.,

2002)). In their clustering methods, Ungar and Fos-

ter ((Ungar and Foster, 1998)) clustered users and ra-

ted items separately using variations of K-means with

Expectation Maximization (EM) and Gibbs sampling

Splitting-merging Clustering Algorithm for Collaborative Filtering Recommendation System

167

(Geman and Geman, 1984). Their experiments sho-

wed that the results of EM clustering based CF on

real data were not very promising but when they used

the repeated K-means with Gibbs sampling their re-

sults got better. Moreover, their model could be ea-

sily extended to much complex models and it may

handle clustering with multiple attributes. However,

Gibbs sampling is computationally expensive ((Un-

gar and Foster, 1998)). Kohrs et al. (Kohrs and Me-

rialdo, 1999) applied hierarchy clustering using the

top down approach for CF with sparse rating matrix.

Their approach was more efﬁcient than other traditio-

nal CF when applied to few users and provided high

prediction values even for users who rated only a li-

mited number of items. Hierarchical clustering is par-

ticularly efﬁcient in providing recommendations for

new users who rated only few items. Xue et al. (Xue

et al., 2005) applied the K-means algorithm to clus-

ter users before analyzing the clusters obtained and

choosing an adequate cluster for the active user. They

applied the smoothing strategies to the unseen items

using the same idea used in natural language proces-

sing (Brown et al., 1992) where the cluster is used as

topic in order to alleviate the sparsity difﬁculty. They

showed that their approach outperformed other CF

approaches on small data sets. Sarwar et al.(Sarwar

et al., 2002) addressed the scalability issues by users

clustering and used the user cluster as the neighbor-

hood. (Ma et al., 2016) showed the efﬁciency of their

newly proposed clustering based CF in rating pre-

dictions with addressing the data sparsity and cold

start problems. Rong et al. (Hu et al., 2013) proposed

a clustering method for CF. Their approach was divi-

ded into two phases: clustering and CF. The clustering

method was based on K-means used as pre-processing

for CF. By using clustering techniques, the data size

was reduced so that the online computation time of

CF algorithm decreased signiﬁcantly. One could ar-

gue that the results of their approach depends strongly

on the number of clusters. Unfortunately this number

of clusters is initially unknown. These recent studies

point out that a clustering algorithm computing auto-

matically the cluster numbers could further improve

the performance of the recommendation. This moti-

vated us to develop the CF approach presented in the

next section.

3 GENERAL APPROACH OF

CLUSTERING BASED CF

The main contribution of this paper is to propose a

recommendation method that alleviates the scalabi-

lity and sparsity difﬁculties of CF by introducing the

splitting and merging clustering based on K-means+

algorithm and by performing extensive experiments

using three different data sets classiﬁed as small, me-

dium and large from MovieLens data sets (Harper and

Konstan, 2015). Generally, CF using clustering algo-

rithm is based on the following steps:

• step 1: Cluster users u ∈ U in K clusters using any

clustering algorithm

• step 2: Evaluate the distance between active user

and centroids

• step 3: Choose the closest cluster for the active

user

• step 4: Select the n nearest neighbor from the cho-

sen active user’s cluster

• Step 5: Predict items’ active user preferences.

In this paper the clustering methods used in step 1

for CF are K-means and splitting merging K-means+

clustering algorithm as detailed in the two following

sub-sections.

3.1 K-means Clustering Algorithm for

K-means clustering is the most well-known and com-

monly used partitional clustering method. It is very

simple, fast and straightforward. Many researchers

show that K-means is very efﬁcient for model based

CF ((Dakhel and Mahdavi, 2011), (Xue et al., 2005)).

Algorithm 1 presents the different steps of K-means

clustering method.

Algorithm 1: K-Means algorithm.

Input:U : training users; K: the number of clusters

Output: K centroids, {C

,...,C

}

Step 1: Initialization: Randomly select K users uni-

formly at random from U, as initial starting points. Cal-

culate centroids as the means value of the users for each

cluster.

Alternate steps

repeat

Step 2: assign each user to the cluster with nearest

centroid;

Step 3: update the centroid clusters, i.e., calculate the

mean value of the users for each cluster

until (no user changes its cluster membership or any ot-

her stopping condition is satisﬁed)

K-means is relatively scalable when processing

large data sets as its complexity is O(

× K × t),

where t is the number of iterations, |U| is the total

number of users and K is the number of clusters. It

can also converge to local optimum in a relatively

small number of iterations. However, the usability of

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

168

K-means is limited since clustering results are hea-

vily dependent on the user deﬁned variants, i.e., the

selection of the initial centroids seeds and the num-

ber of clusters. Consequently, these shortcomings

lead to inaccurate recommendation and increase the

computation time of collaborative ﬁltering. To over-

come the K-means algorithm issue and in the same

time to solve both problems scalability and sparsity in

CF, we applied K-means+ ((Guan et al., 2003a),(Guan

et al., 2003b)). K-means+ can automatically deter-

mine a pseudo optimal number of clusters according

to the statistical nature of the data. The initial cen-

troid seeds are not critical to the K-means+ clustering

((Guan et al., 2003b), (Guan et al., 2003a), (Huang

et al., 2005)). K-means is sensitive to outliers and

noise in data since a small number of such data can

substantially inﬂuence the mean value. The resulting

cluster centroids may not be excellent representatives

of their cluster. However, K-means+ can handle noise

and outliers in the data. The clusters with outliers in

K-means+ can be split depending on the data distri-

bution of the cluster. In a sparse matrix as in the case

of CF, data contains outliers that are not appropriate

for clustering algorithms like K-means. In such situa-

tion, K-means can end up with several empty clusters

to which no data points are allocated during the assig-

nment step. Two approaches are proposed to handle

empty clusters: (1) deleting the empty clusters or (2)

replacing the empty cluster with newly created non-

empty clusters. The second approach chooses the

point that is farthest away from its current centroid,

replaces it as the centroid of the empty cluster, and

then perform the re-clustering. This strategy as propo-

sed by (Hansen and Mladenovic, 2001) eliminates the

farthest point that contributes most to the total sum of

squared errors. In our experiments, in case of empty

clusters situation, K-means+ follows the ﬁrst appro-

ach by removing the empty clusters using a splitting

and merging strategy. The second approach was dee-

med too complicated and computationally expensive.

3.2 Proposed Splitting Merging

Clustering Approach for CF

Our proposed collaborative ﬁltering model is based

on K-means+ and is characterized by exploiting the

statistical nature of the data to adjust autonomously

the number of clusters K. K-means+ partitions the

data into an appropriate number of clusters without

requiring an adhoc ﬁxed number of clusters like K-

means. K-means+ considers the statistical nature of

data distribution. By splitting and merging clusters,

it self-adjusts the number of clusters K. If the initial

value of K is too small, the splitting strategy is used to

increase the number of clusters; likewise the merging

strategy reduces the number of clusters in case it is

too large. Algorithm 2 presents the general steps of

the clustering method k-means+ ((Guan et al., 2003a),

(Guan et al., 2003b)).

Algorithm 2: Splitting and merging clustering algorithm.

Input:U : training users; K: the initial number of clusters

Output: K0 clusters of users; K0 centroids,

,...,C

0; K0 is the adjusted number of clus-

ters;

Step 1: Initialization: arbitrarily choose K users uni-

formly at random from U, as initial starting points. Cal-

culate centroids as the means value of the users for each

cluster.

Apply K-means;

Search for an empty Cluster

if (there are empty clusters ) then

delete the empty clusters

end if

hasOutlier ← true

/*Splitting Steps*/

while (hasOutlier) do

search all the clusters

if (there is an outlier) then

hasOutlier ← true

remove the ﬁrst found outlier

Create a new cluster with this deleted outlier

Apply K-means with centroids of new clusters as

initial solution

Search for an empty Cluster

if (there are empty clusters ) then

delete the empty clusters

end if

else

hasOutlier ← f alse

end if

end while

/*merging steps*/

for i = 1 to K0 − 1 do

for j = i + 1 to K0 do

if (cluster

and cluster

can be merged) then

group cluster

and cluster

(Reassign users

in cluster i and users in cluster j to the same cluster)

end if

end for

The algorithm 2 ﬁrst performs k-means on a

random number between 2 and n. The outliers are

detected and removed by a conﬁdent area d1 with ra-

dius of ﬁve standard deviation σ of each cluster. In-

deed, the data points that are far beyond the threshold

d1 = 5σ are considered as outliers and they are remo-

ved from each cluster. Then the removed data are as-

signed as centroids of a new clusters. Once this split-

ting phase is done the adjacent clusters whose overlap

is over the threshold d2 = 1.414(σ

+σ

) are merged.

The threshold d2 represents the correlation coefﬁcient

Splitting-merging Clustering Algorithm for Collaborative Filtering Recommendation System

169

between two different clusters. Hence the clustering

results are not sensitive to the initial partitions and

to the number of clusters. Consequently, the effect

of outliers in K-means+ is well handled. More de-

tails on the signiﬁcance of the two thresholds d1 and

d2 can be found in (Guan et al., 2003a) and (Guan

et al., 2003b). Our proposed clustering based CF met-

hod proceeds into two phases. The ﬁrst phase (ofﬂine

phase) is done on the training set or on the historical

users-items ratings data. In this phase users are clus-

tered in different groups such that users with similar

preferences are grouped in the same cluster. In the se-

cond phase (online phase on testing set), the nearest

neighbor based CF is applied on the active user into

two steps. The ﬁrst step aims at choosing the closest

cluster for the active user by calculating the distance

between the active user and the centroid of the classes.

Therefore, the cluster of the active user is determined

by the closest distance between the active user and

the centroid of the corresponding cluster. The second

step of this phase applies the k-nearest neighbor ba-

sed CF ﬁltering as presented in section 2.1 on active

user’s cluster only (do not include all users data) as in

the classical CF technique. Consequently, the online

execution time (or the testing time) of collaborative

ﬁltering is reduced as well as the resulting sparsity

difﬁculty.

4 EXPERIMENT

4.1 Datasets

In the experimentation we considered three data

sets from the movie rating application MovieLens.

More details on the different MovieLens data sets

can be found in (Harper and Konstan, 2015). The

ﬁrst data set used is MovieLens 100,000 ratings,

we called it SML. It contains 100,000 ratings

provided by 943 users for 1682 movies. Movies are

rated on an integer scale going from 1 (bad) to 5

(excellent) with 0 for not rated movies. The second

data set called MML in the paper is a medium size

MovieLens data set. MML contains slightly more

than 1 million ratings and 209 ratings rated by 6040

users on 3900 movies using the same integer scale

as SML. The third data set called LML is a large

MovieLens data set. LML contains 10 millions and

5 ratings applied to 10681 movies by 71567 users of

the online movie recommender service MovieLens

http://ﬁles.grouplens.org/datasets/movielens/ml-

10m-README.html. The ratings of LML data set

is different from SML and MML. Rates in LML are

made on a 5-stars scale and with half-star increments.

As a result there is 10 rates possibilities ranged from

0.5 to 5 with 0 standing as a not rated item.

4.2 Metrics

To evaluate the quality of our CF algorithm, we used

the Mean Absolute Error (MAE) because of its versa-

tility in CF literature ((Breese et al., 1998), (Herlocker

et al., 2004), (Zahra et al., 2015)). The MAE calcula-

tes the average absolute deviation between predicted

rating provided by CF algorithm and true rating as-

signed by user in the testing data test. It is deﬁned

as:

MAE =

∑

i=1

− r

(3)

where n is the total of ratings provided by the test set,

is the predicted rating provided by the CF algo-

rithm and r

is the actual rating assigned by user to

item i. The lower the MAE, the more accurately the

recommendation engine predicts user ratings.

4.3 Evaluation Methodology

In this study, we used 5 fold cross validation techni-

que to evaluate the developed algorithms for collabo-

rative ﬁltering on SML and MML data set; 20% of

the users were randomly selected to be test set and

the 80% remaining were used for training. From each

user in the test set, ratings for 20% of items were wit-

hheld, and rating predictions were computed for those

withheld items. Finally, the average results on the ﬁve

folds including the MAE cluster numbers and the exe-

cution time were reported. For LML data set we have

divided the data set into two folds. One fold with 80%

of users was used for training and the 20% remaining

were used for testing.

5 RESULTS AND DISCUSSION

To compare the performance of the different algo-

rithms in terms of scalability, we calculated the pre-

dictive accuracy using, as previously mentioned the

MAE but also the execution time to get a prediction

on the test data set. We tested this way the three al-

gorithms: the nearest neighbor based CF, the k-means

(k > 3) clustering based CF and K-means+ clustering

based CF. In this comparative study, different num-

bers of clusters ranging from 3 to 150 have been used

as initial condition for clustering methods. The clas-

sical collaborative ﬁltering is designated in the graph

as k-nn CF with a number of clusters equal to one.

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

170

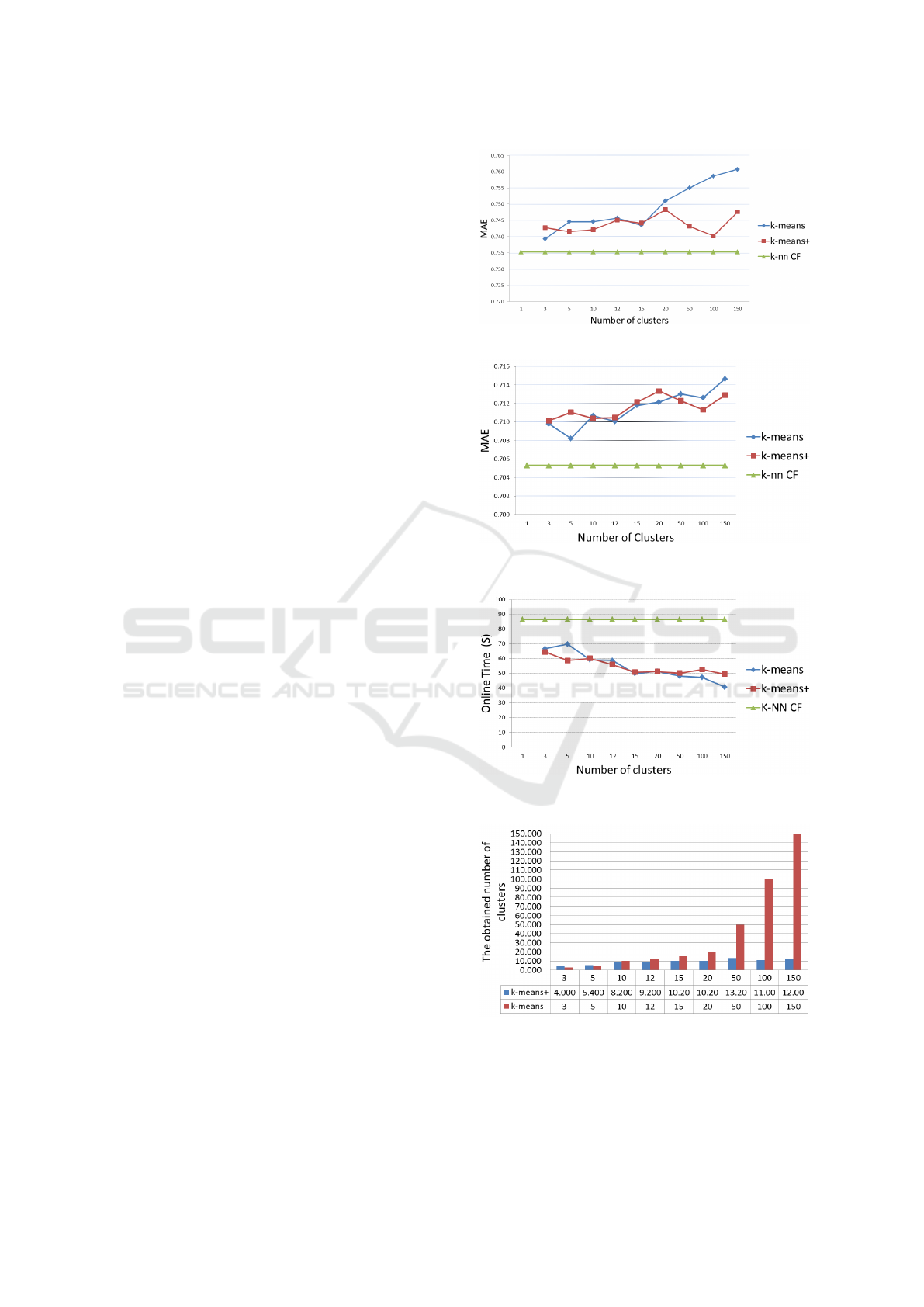
The results over SML dataset in ﬁgure 1 show that

the CF based on splitting and merging clearly out-

performs the CF based K-means algorithm when the

number of clusters is greater than 20 and it is slightly

better with a smaller number of clusters. As shown in

ﬁgure 1, the performances obtained by the classical

CF is slightly better than our proposed clustering ba-

sed CF and much better than k-means based CF spe-

ciﬁcally when the number of clusters is greater than

20. The results over MML dataset in ﬁgure 2 show

that K-means+ outperforms K-means while slightly

not being as good as classical CF. However, it is two

times faster than the classical collaborative ﬁltering

when the initial number of clusters is 150 as presen-

ted in ﬁgure 3. The results over LML data set in table

1 show that K-means+ and K-means based CF have

the same performances as the traditional CF based k-

nn while being faster. As shown in table 1, the online

prediction by K-means based CF is two times faster

than traditional CF and the online prediction by K-

means+ is three times faster than traditional CF and it

is almost two times faster than K-means based CF. As

we mentioned in related work, the CF algorithms suf-

fer from the scalability problem. However, K-means+

based CF is less time consuming than traditional CF

method. As seen in ﬁgure 3 and table 1, our proposed

K-means+ based CF algorithm outperforms K-means

based CF and has almost the same prediction time on

MML data sets. It is also faster than both classical CF

and K-means based CF methods. Our proposed met-

hod with K-means+ takes about one ﬁfth of the tradi-

tional CF average prediction running time. As shown

in ﬁgure 4, on average, the ﬁnal number of clusters

obtained by K-means+ is decreased. For example,

considering the initial number of cluster K=150, on

average the ﬁnal number of clusters is about K=7.

This could explain why the performances of CF ba-

sed K-means+ is better than CF based on K-means.

However, the CPU time for online prediction will in-

crease a little bit because the closest cluster to the

target user will have more users than it would with

K-means. For very large data set (LML), the propo-

sed K-means+ based CF has less online computatio-

nal time on testing data with a comparable prediction

accuracy as shown in table 1.

Figure 5 summarizes our results using different

initial centroids approaches. In this experiment we

have tested two approaches, the ﬁrst one selects K

users from training set uniformly and randomly and

the second one, splits the users in K subsets and then

calculates centroids as the means value of the users

for each subset. As shown in ﬁgure 5, the propo-

sed CF based K-means+ algorithm provides almost

same predictions with different initial centroid seeds

Figure 1: MAE for varying number of clusters on SML data.

Figure 2: MAE for varying number of clusters on MML

data.

Figure 3: Online time in seconds for varying number of

clusters on MML data set.

Figure 4: The average number of clusters obtained by K-

means+ on training set (MML data).

approaches. As a result, CF based K-means+ appro-

ach seems more robust and stable to the initial cen-

troid seeds than K-means.

Splitting-merging Clustering Algorithm for Collaborative Filtering Recommendation System

171

Table 1: Comparative results on LML data set with initial number of clusters K = 100.

K-means K-means+ k-NN CF

Average MAE 0.656199389 0.656794361 0.654921579

Average online time on testing data in seconds 2.211 1.542 7.020

Online prediction time per item in seconds 0.00568455 0.00396411 0.018059

Figure 5: The average MAE of different initial centroids

selection approaches on K-means and K-means+ over the

SML test sets with K=150.

6 CONCLUSION AND FUTURE

WORK

Recommender systems have become an essential

functionality for many E-commerce Web applicati-

ons. Many systems use k nearest neighbor based CF

algorithms that are very efﬁcient in ﬁltering interes-

ting items to users. However, k nearest neighbor ba-

sed CF algorithms have difﬁculties to scale. To ad-

dress this scalability issue, we investigated the appli-

cation of a clustering method based on a splitting and

merging heuristic for model based collaborative ﬁl-

tering. We considered an aspect that is usually ig-

nored in CF, the statistical nature of the data. The

experimental results obtained show that the recom-

mendation method based on splitting and merging

heuristic is a viable approach for scalable collabo-

rative ﬁltering. The comparative results have shown

that splitting-merging clustering algorithm has a lo-

wer prediction error compared to K-means clustering

method especially for large amount of data with high

dimensional space. Moreover, the experimental re-

sults we obtained on Movielens data illustrate the ro-

bustness of the K-means+ clustering algorithm and

the fact that initial centroid seeds are not critical to

the clustering results as they are for K-means. In our

study we considered only user collaborative ﬁltering

but it would be interesting to investigate the applica-

tion of our proposed clustering method to item based

collaborative ﬁltering and to compare the results with

user based collaborative ﬁltering. More precisely, we

will, in future works, apply our proposed clustering

method to the item based ﬁltering method. Once the

items are clustered and the closest cluster to the new

item is determined, the item based CF will be applied

to produce the recommendation to the target user. Be-

sides, we will investigate the application of other type

of Splitting and merging algorithms for CF. Among

the algorithms we would like to test are (Laplante

et al., 2015) and (Wang and Belacel, 2008).

ACKNOWLEDGMENTS

This work is part of the National Research Council

Canada program Learning and Performance Support

Systems (LPSS), which addresses training, develop-

ment and performance support in all industry sectors,

including education, oil and gas, policing, military

and medical devices.

REFERENCES

Adomavicius, G. and Tuzhilin, A. (2005). Toward the

next generation of recommender systems: A survey

of the state-of-the-art and possible extensions. Kno-

wledge and Data Engineering, IEEE Transactions on,

17(6):734–749.

Al-Shamri, M. Y. H. (2014). Power coefﬁcient as a simila-

rity measure for memory-based collaborative recom-

mender systems. Expert Systems with Applications,

41(13):5680–5688.

Benkoussas, C., Hamdan, H., Albitar, S., Ollagnier, A., and

Bellot, P. (2014). Collaborative ﬁltering for book re-

commandation. In In Working Notes for CLEF 2014

Conference, Sheeld, UK, September 15-18, 2014, pa-

ges 501–507.

Birtolo, C. and Ronca, D. (2013). Advances in clustering

collaborative ﬁltering by means of fuzzy c-means and

trust. Expert Systems with Applications, 40(17):6997

– 7009.

Birtolo, C., Ronca, D., Armenise, R., and Ascione, M.

(2011). Personalized suggestions by means of col-

laborative ﬁltering: A comparison of two different

model-based techniques. In Nature and Biologically

Inspired Computing (NaBIC), 2011 Third World Con-

gress on, pages 444–450.

Bobadilla, J., Serradilla, F., and Hernando, A. (2009). Col-

laborative ﬁltering adapted to recommender systems

of e-learning. Know.-Based Syst., 22(4):261–265.

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

172

Bokde, D., Girase, S., and Mukhopadhyay, D. (2015). Ma-

trix factorization model in collaborative ﬁltering algo-

rithms: A survey. Procedia Computer Science, 49:136

– 146. Proceedings of 4th International Conference on

Advances in Computing, Communication and Control

(ICAC3’15).

Breese, J. S., Heckerman, D., and Kadie, C. (1998). Empiri-

cal analysis of predictive algorithms for collaborative

ﬁltering. In Proceedings of the Fourteenth conference

on Uncertainty in artiﬁcial intelligence, pages 43–52.

Brown, P. F., deSouza, P. V., Mercer, R. L., Pietra, V. J. D.,

and Lai, J. C. (1992). Class-based n-gram models of

natural language. Comput. Linguist., 18(4):467–479.

Burke, R. (2002). Hybrid recommender systems: Survey

and experiments. User modeling and user-adapted in-

teraction, 12(4):331–370.

Cohen, W. W. and Fan, W. (2000). Web-collaborative ﬁl-

tering: Recommending music by crawling the web.

Computer Networks, 33(1):685–698.

Dakhel, G. and Mahdavi, M. (2011). A new collaborative

ﬁltering algorithm using k-means clustering and neig-

hbors’ voting. In Hybrid Intelligent Systems (HIS),

2011 11th International Conference on, pages 179–

184.

Darvishi-Mirshekarlou, F., Akbarpour, S., Feizi-Derakhshi,

M., et al. (2013). Reviewing cluster based colla-

borative ﬁltering approaches. International Journal

of Computer Applications Technology and Research,

2(6):650–659.

Ekstrand, M. D., Riedl, J. T., and Konstan, J. A. (2011).

Collaborative ﬁltering recommender systems. Found.

Trends Hum.-Comput. Interact., 4(2):81–173.

Feng, Z. and Huiyou, C. (2006). Employing bp neural net-

works to alleviate the sparsity issue in collaborative

ﬁltering recommendation algorithms [j]. Journal of

Computer Research and Development, 4:014.

Geman, S. and Geman, D. (1984). Stochastic relaxation,

gibbs distributions, and the bayesian restoration of

images. IEEE Transactions on Pattern Analysis and

Machine Intelligence, PAMI-6(6):721–741.

Gong, S., Ye, H., and Tan, H. (2009). Combining memory-

based and model-based collaborative ﬁltering in re-

commender system. In Circuits, Communications and

Systems, 2009. PACCS’09. Paciﬁc-Asia Conference

on, pages 690–693. IEEE.

Guan, Y., Ghorbani, A. A., and Belacel, N. (2003a). An

unsupervised clustering algorithm for intrusion de-

tection. In Advances in Artiﬁcial Intelligence, 16th

Conference of the Canadian Society for Computatio-

nal Studies of Intelligence, AI 2003, Halifax, Canada,

June 11-13, 2003, Proceedings, pages 616–617.

Guan, Y., Ghorbani, A. A., and Belacel, N. (2003b). Y-

means: a clustering method for intrusion detection.

In Electrical and Computer Engineering, 2003. IEEE

CCECE 2003. Canadian Conference on, volume 2,

pages 1083–1086. IEEE.

Hansen, P. and Mladenovic, N. (2001). J-means: a new lo-

cal search heuristic for minimum sum of squares clus-

tering. Pattern Recognition, 34(2):405 – 413.

Harper, F. M. and Konstan, J. A. (2015). The movielens

datasets: History and context. ACM Trans. Interact.

Intell. Syst., 5(4):19:1–19:19.

Herlocker, J., Konstan, J. A., and Riedl, J. (2002). An

empirical analysis of design choices in neighborhood-

based collaborative ﬁltering algorithms. Information

retrieval, 5(4):287–310.

Herlocker, J. L., Konstan, J. A., Borchers, A., and Riedj,

J. (1999). An algorithmic framework for performing

collaborative ﬁltering. In Proceedings of the 22nd An-

nual International ACM SIGIR Conference on Rese-

arch and Development in Information Retrieval, SI-

GIR ’99, pages 230–237, New York, NY, USA. ACM.

Herlocker, J. L., Konstan, J. A., Terveen, L. G., and Riedl,

J. T. (2004). Evaluating collaborative ﬁltering recom-

mender systems. ACM Transactions on Information

Systems (TOIS), 22(1):5–53.

Hofmann, T. and Puzicha, J. (1999). Latent class models

for collaborative ﬁltering. In IJCAI, volume 99, pages

688–693.

Hu, R., Dou, W., and Liu, J. (2013). Clustering-based colla-

borative ﬁltering approach for mashups recommenda-

tion over big data. In Computational Science and En-

gineering (CSE), 2013 IEEE 16th International Con-

ference on, pages 810–817.

Huang, C. and Yin, J. (2010). Effective association clus-

ters ﬁltering to cold-start recommendations. In Fuzzy

Systems and Knowledge Discovery (FSKD), 2010 Se-

venth International Conference on, volume 5, pages

2461–2464. IEEE.

Huang, H., Zhang, R., Xiong, F., Makedon, F., Shen, L.,

Hettleman, B., and Pearlman, J. (2005). K-means+

method for improving gene selection for classiﬁcation

of microarray data. In Computational Systems Bioin-

formatics Conference, pages 110–111. IEEE.

Jawaheer, G., Szomszor, M., and Kostkova, P. (2010). Com-

parison of implicit and explicit feedback from an on-

line music recommendation service. In proceedings

of the 1st international workshop on information he-

terogeneity and fusion in recommender systems, pages

47–51. ACM.

Kohrs, A. and Merialdo, B. (1999). Clustering for collabo-

rative ﬁltering applications. Intelligent Image Proces-

sing, Data Analysis & Information Retrieval, 3:199–

205.

Koren, Y. (2010). Factor in the neighbors: Scalable and

accurate collaborative ﬁltering. ACM Trans. Knowl.

Discov. Data, 4(1):1–24.

Laplante, F., Belacel, N., and Kardouchi, M. (2015). A heu-

ristic automatic clustering method based on hierarchi-

cal clustering. In Revised Selected Papers of the 6th

International Conference on Agents and Artiﬁcial In-

telligence - Volume 8946, ICAART 2014, pages 312–

328, New York, NY, USA. Springer-Verlag New York,

Inc.

Linden, G., Smith, B., and York, J. (2003). Amazon.com re-

commendations: Item-to-item collaborative ﬁltering.

Internet Computing, IEEE, 7(1):76–80.

Liu, H., Hu, Z., Mian, A., Tian, H., and Zhu, X. (2014).

A new user similarity model to improve the accuracy

Splitting-merging Clustering Algorithm for Collaborative Filtering Recommendation System

173

of collaborative ﬁltering. Knowledge-Based Systems,

56:156–166.

Lu, J., Wu, D., Mao, M., Wang, W., and Zhang, G. (2015).

Recommender system application developments: a

survey. Decision Support Systems, 74:12–32.

Ma, X., Lu, H., Gan, Z., and Zhao, Q. (2016). An explora-

tion of improving prediction accuracy by constructing

a multi-type clustering based recommendation frame-

work. Neurocomputing, pages –. In Press.

Pazzani, M. J. and Billsus, D. (2007). Content-based re-

commendation systems. In The adaptive web, pages

325–341. Springer.

Resnick, P., Iacovou, N., Suchak, M., Bergstrom, P., and

Riedl, J. (1994). Grouplens: an open architecture

for collaborative ﬁltering of netnews. In Proceedings

of the 1994 ACM conference on Computer supported

cooperative work, pages 175–186. ACM.

Roh, T. H., Oh, K. J., and Han, I. (2003). The col-

laborative ﬁltering recommendation based on som

cluster-indexing cbr. Expert Systems with Applicati-

ons, 25(3):413–423.

Salah, A., Rogovschi, N., and Nadif, M. (2016). A dynamic

collaborative ﬁltering system via a weighted cluste-

ring approach. Neurocomputing, 175:206–215.

Salakhutdinov, R., Mnih, A., and Hinton, G. (2007). Re-

stricted boltzmann machines for collaborative ﬁlte-

ring. In Proceedings of the 24th International Con-

ference on Machine Learning, ICML ’07, pages 791–

798, New York, NY, USA. ACM.

Sarwar, B. M., Karypis, G., Konstan, J., and Riedl, J.

(2002). Recommender systems for large-scale e-

commerce: Scalable neighborhood formation using

clustering. In Proceedings of the ﬁfth international

conference on computer and information technology,

volume 1, pages 1–5.

Shambour, Q. and Lu, J. (2011). A hybrid trust-enhanced

collaborative ﬁltering recommendation approach for

personalized government-to-business e-services. In-

ternational Journal of Intelligent Systems, 26(9):814–

843.

Su, X. and Khoshgoftaar, T. M. (2006). Collaborative ﬁlte-

ring for multi-class data using belief nets algorithms.

In Tools with Artiﬁcial Intelligence, 2006. ICTAI’06.

18th IEEE International Conference on, pages 497–

504. IEEE.

Su, X. and Khoshgoftaar, T. M. (2009). A survey of col-

laborative ﬁltering techniques. Advances in artiﬁcial

intelligence, 2009:4.

Tsai, C.-F. and Hung, C. (2012). Cluster ensembles in colla-

borative ﬁltering recommendation. Applied Soft Com-

puting, 12(4):1417 – 1425.

Ungar, L. H. and Foster, D. P. (1998). Clustering methods

for collaborative ﬁltering. In AAAI workshop on re-

commendation systems, vol. 1, pp. 114-129. 1998., vo-

lume 1, pages 114–129.

Wang, C. and Belacel, N. (2008). VNSOptClust: A Variable

Neighborhood Search Based Approach for Unsuper-

vised Anomaly Detection, pages 607–616. Springer

Berlin Heidelberg, Berlin, Heidelberg.

Wilson, J., Chaudhury, S., and Lall, B. (2014). Im-

proving collaborative ﬁltering based recommenders

using topic modelling. In Proceedings of the 2014

IEEE/WIC/ACM International Joint Conferences on

Web Intelligence (WI) and Intelligent Agent Techno-

logies (IAT)-Volume 01, pages 340–346. IEEE Com-

puter Society.

Xue, G.-R., Lin, C., Yang, Q., Xi, W., Zeng, H.-J., Yu,

Y., and Chen, Z. (2005). Scalable collaborative ﬁl-

tering using cluster-based smoothing. In Proceedings

of the 28th Annual International ACM SIGIR Confe-

rence on Research and Development in Information

Retrieval, SIGIR ’05, pages 114–121, New York, NY,

USA. ACM.

Zahra, S., Ghazanfar, M. A., Khalid, A., Azam, M. A.,

Naeem, U., and Prugel-Bennett, A. (2015). Novel

centroid selection approaches for kmeans-clustering

based recommender systems. Information Sciences,

320:156 – 189.

Zhang, Y., Chen, W., and Yin, Z. (2013). Collaborative ﬁlte-

ring with social regularization for tv program recom-

mendation. Knowledge-Based Systems, 54:310–317.

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

174