Dynamic Pricing Strategy for Electromobility using Markov Decision

Processes

Jan Mrkos, Anton

ın Komenda and Michal Jakob

Artiﬁcial Intelligence Center, Faculty of Electrical Engineering, Czech Technical University in Prague, Czech Republic

Keywords:

Electric Vehicles, Demand-response, Dynamic Pricing, Charging, MDP, Markov Decision Process.

Abstract:

Efﬁcient allocation of charging capacity to electric vehicle (EV) users is a key prerequisite for large-scale

adaption of electric vehicles. Dynamic pricing represents a ﬂexible framework for balancing the supply and

demand for limited resources. In this paper, we show how dynamic pricing can be employed for allocation of

EV charging capacity. Our approach uses Markov Decision Process (MDP) to implement demand-response

pricing which can take into account both revenue maximization at the side of the charging station provider

and the minimization of cost of charging on the side of the EV driver. We experimentally evaluate our method

on a real-world data set. We compare our dynamic pricing method with the ﬂat rate time-of-use pricing that

is used today by most paid charging stations and show signiﬁcant beneﬁts of dynamically allocating charging

station capacity through dynamic pricing.

1 INTRODUCTION

Electriﬁcation of personal transportation is commenc-

ing. There is a multitude of reasons, primarily en-

vironmental concerns, energy supply independence,

and overall falling costs of production of both elec-

tric vehicles and the needed energy. Hand in hand

with the clear beneﬁts of a wide-spread deployment of

electric vehicles (EVs) come many challenges. One

of the most pressing problems is how to efﬁciently

and cheaply distribute the energy from often unstable

renewable sources to the EVs.

To illustrate the gravity of the situation, let us take

the recent target to charge future EVs by no less than

300kW (Dyer et al., 2013). Provided a charging sta-

tion with ten charging slots, we get to 3MW power

intake if all the slots are charging EVs in parallel. For

a comparison, an average instantaneous power con-

sumption

of a U.S. household is about 1.2kW. The

costs of upgrading the distribution network to cover

such intakes would be extreme, on par with build-

ing the grid for additional three times the number of

households

Based on the 2015 statistics of the U.S. Energy In-

formation Administration: https://www.eia.gov/tools/faqs/

faq.php?id=97&t=3https://www.eia.gov/tools/faqs/faq.php

?id=97&t=3

Based on the IEEE Spectrum article: http://

spectrum.ieee.org/transportation/advanced-cars/speed-

Provided that the charging stations are not perma-

nently fully occupied by EVs, an alternative to up-

grading the grid is to charge stationary batteries at

charging station, which are later used to fast charge

EVs. In this approach, the initial costs of the up-

grade of the grid are transferred to charging station

owners in the cost of stationary batteries. Another

approach is to use grid-centric methods ensuring fair-

ness of charging such as the packetized charging man-

agement (Rezaei et al., 2014). However, such meth-

ods do not guarantee the charging service capacity,

therefore the charging duration can not be guaranteed.

Existing regulations and laws design the overall

mechanism for the allocation of charging resources.

Within the rules of this mechanism, participants in

this mechanism are free to act in a way that pro-

motes their self-interests. These participants are

power distribution service operators, charging service

providers, and EV drivers responsible for charging

their cars. However, self-interested strategies em-

ployed by the participants can be dangerous to the

system as a whole. Multi-agent paradigm is suitable

to efﬁciently balance the supply of the (renewable)

power and EV charging demand. More precisely, the

ﬁeld of multi-agent resource allocation (Chevaleyre

et al., 2006) provides techniques for solving problems

bumps-ahead-for-electricvehicle-charging

http://spectrum.ieee.org/transportation/advanced-cars/

speed-bumps-ahead-for-electricvehicle-charging

Mrkos, J., Komenda, A. and Jakob, M.

Dynamic Pricing Strategy for Electromobility using Markov Decision Processes.

DOI: 10.5220/0006601505070514

In Proceedings of the 10th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2018) - Volume 2, pages 507-514

ISBN: 978-989-758-275-2

507

with self-interested agents.

We base our approach to dynamic pricing on the

pricing of charging services as whole. This means

that we do not consider the charging station to be sell-

ing electricity with price per kWh as is currently the

norm. Instead, in our view, the charging station is sell-

ing a charging service that has multiple parameters

that include time of day, volume of consumed elec-

tricity etc. This approach does not directly depend

on the details of the low-level battery charging pat-

terns and its optimization as proposed in (Cao et al.,

2012). (Li et al., 2014) suggests an idea similar to

our approach in the locational pricing; however, their

method is based on the solution of nonlinear opti-

mization towards the social welfare to get charging

prices. Our approach solves the same problem as a

solution to a set of decentralized Markov Decision

Processes (MDPs), where the resulting decisions are

prices of charging services at various times.

In this paper, we provide an experimental com-

parison of the MDP demand-response pricing strategy

applicable in the context of multi-agent resource allo-

cation for electromobility and today widespread ﬂat

rate time-of-use pricing (Versi and Allington, 2016).

2 DEMAND-RESPONSE PRICING

Economics, revenue management, and supply chain

management have extensively studied demand-

response pricing mechanisms of various kinds of ser-

vices (Albadi and El-Saadany, 2008; McGill and

van Ryzin, 1999). These ﬁelds recognize demand-

response pricing as a critical lever for inﬂuencing

the behavior of buyers. For this quality, we choose

demand-response pricing as a way of dealing with in-

creasing loads on the power grid caused by uptake of

EVs.

To put the charging services pricing into context,

we can view it as pricing of perishable goods, such as

seasonal clothing, hotel rooms or airline tickets (Sub-

ramanian et al., 1999). These goods have value only

until a certain point in time. For clothing, that is the

end of the season, for airline tickets, it is the depar-

ture of the airplane. In the case of charging stations,

the commodity is the charging resources available in

a given time window. With perishable products, the

goal is to sell the available stock for a proﬁt before

the stock expires. Same with the charging services,

charging resources are a missed proﬁt opportunity if

they are left unused at the end of some time window.

Pricing of airline tickets has been extensively

studied in different variations and with focus on vari-

ous aspects of the problem (Chiang et al., 2007). The

Figure 1: Difference between airline pricing and charging

station pricing. Green rectangles show valid bookings. Seat

bookings do not signiﬁcantly affect bookings of other seats

(except for large group bookings). On the other hand, a

booking of short charging sessions and 1:00 and 4:00 blocks

bookings of longer charging sessions shown in red.

ﬁrst step is usually the construction of an approximate

model of user behavior (such as customer price sen-

sitivity, seasonality of demand, no shows, etc.). Next,

airlines need to determine how many tickets at which

price to sell through the maximization of expected

revenue. In brief, optimal rule for accepting or re-

jecting bookings is as follows: “Is the proﬁt from this

booking greater or smaller than the expected proﬁt

from this seat that we could get later? Conﬁrm the

booking now if the proﬁt is bigger than the expected

proﬁt later. If it is smaller, deny this booking.”

However, each accepted or rejected booking can

inﬂuence following bookings as consecutive cus-

tomers are not able to book seats at the same price.

If we include connecting ﬂights and group bookings

into the problem, pricing decisions can have a domino

effect on the pricing in the whole network of an air-

line operator. Although the problem can look simple,

due to this knock-down effect, the survey (McGill and

van Ryzin, 1999) notes the complexity of this issue.

For this reason, most work on this subject restricts the

problem in some way.

In the following sections, we approach the charg-

ing station pricing strategy in a similar way to how

airline revenue management approaches the pricing

of airline tickets. Both problems focus on perish-

able goods where the knockdown effect plays a role

as both bookings of airline tickets and bookings of

charging station can affect following sales.

Similarly to airline revenue management, we do

not directly consider competition between different

service providers. We aggregate charging station cus-

tomers (whose actions are based the options offered

by different service providers as well as individual

circumstances) in an environment model that adjusts

demand as a response to changing price.

An important distinction between the airline pric-

ing and charging station pricing is the interconnected-

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

508

ness of the bookings in the case of charging services;

this is not present with the sales of the airline tick-

ets. In the case of the airline tickets, it is not particu-

larly important which seat (in a given class) was sold

as booking of single seat does not block booking of

surrounding seats. This distinction is illustrated in

Figure 1.

3 PRICING STRATEGY

In the next section, we focus on the formalization and

modeling of the pricing strategies as Markov Decision

Processes (MDP)(Bellman, 1957).

3.1 Demand-response Pricing Strategy

We focus on the demand-response pricing strat-

egy (Albadi and El-Saadany, 2008) for single charg-

ing station. As input, we use a discretization of possi-

ble charging parameters (time, duration and location

of charging), current and historical utilization of sin-

gle charging station and the expected price elasticity

of the demand for charging services.

The goal of the pricing strategy described below is

the maximization of charging station revenue within

particular time horizon. However, other optimization

criteria are possible to achieve different goals. For

example, a publicly owned charging station that is

not concerned with proﬁts may attempt to maximize

charging station utilization or minimize waiting times

at the charging station.

3.2 Problem Formalization

In this section, we formalize the problem of dynamic

pricing of charging station offers. In this formaliza-

tion, our focus is on the offers that use the uniform

discretization of time and some form of discretiza-

tion of the other offer parameters. Regular structur-

ing in time simpliﬁes the formalization. We consider

the set T of times t

, . . . ,t

for which the prices

, p

, . . . , p

need to be determined.

The times in T denote the starting times of time

intervals of the same length that start at time t

and

end at time t

i+1

. For simplicity, we denote both the

time interval and the associated start time with t

. c

is the expected free charging capacity of the charging

station in each time interval t

In this formalization, we use the symbol c

, the ex-

pected free capacity to be the aggregate of all charging

station constraints, such as power grid capacity or the

number of available charging connectors.

Customers may book charging in any future time

interval. Thus, we will denote price and capacity as

functions p(t

, τ) and c(t

, τ), meaning the price or ca-

pacity of ith time interval at time τ ∈ T . Fixing the

time τ, both price and capacity functions are elements

of the space of step functions over real numbers L .

Given an offer, each reservation r

= (r

, r

, τ

) ∈

R is made for one or more consecutive time intervals,

starting at time interval r

and ending in r

. The ar-

rival of a reservation is denoted τ

. The price of the

reservation π(r

) is the sum of prices associated with

the time intervals at the time of the reservation:

π(r

= (r

, r

, τ

)) =

∑

t=r

p(t, τ

)

Reservations arrive randomly according to a de-

mand distribution that is dependent on the price func-

tion as well as external factors. The set of reservations

R depends on the pricing function because changes

to the price inﬂuence demand. Thus, R is a function

R(p) : L × T → 2T × T × T , where 2T × T × T is the

superset of the set of all possible reservations. The

initial free capacity of the time interval relies on the

state of the grid. We model this as stationary distribu-

tion.

The goal of the charging station is to maximize

proﬁts. In each time interval, charging station needs

to cover the ground cost of maintaining the infras-

tructure denoted Γ

. During charging, a charging sta-

tion needs to pay for the electricity consumed from

the grid γ(r

). This cost is unique to each charging

session as it depends on the total charge delivered to

the EV and possibly variable price of electricity and

charging rate. Given that the price π(r

) of a reser-

vation r

, proﬁt or loss at the end of the time horizon,

after n time intervals, can be written as the sum across

all reservations:

Π = −nΓ

∑

∈R

π(r

) − γ(r

)

However, this point of view of the proﬁt is not par-

ticularly useful for optimization. As each price π(r

)

is calculated as the sum of prices of booked time inter-

vals, we can rewrite the proﬁt as a function of pricing

of time intervals:

Π(p) = −nΓ

∑

∈R(p)

∑

t=r

p(t, τ

) − γ(r

)

The optimization goal of the pricing is then:

= argmax

p∈L

Π(p)

Dynamic Pricing Strategy for Electromobility using Markov Decision Processes

509

Finding optimal pricing function is not an easy

task. The pricing function is part of the innermost

sum in the calculation of Π. The sum itself is also de-

pendent on p, as the set of reservations R is dependent

on p. In fact, the set of reservations is dependent on p

through the actions and responses of individual cus-

tomers. However, it would be challenging to model

behavior of each customer to get optimal pricing strat-

egy.

To make the problem tractable, we aggregate be-

havior of a multitude of customers into the probability

distributions that describe the behavior of customers

together. As such, we can no longer maximize the

proﬁt in absolute numbers. Instead, we maximize the

expected proﬁt (in the statistical sense):

= argmax

p∈L

E(Π(p)) (1)

The framework that deals with problems posed

this way is the framework of Markov Decision Pro-

cesses.

3.3 Modeling as a Markov Decision

Process

The described optimization problem is a complex one.

To solve it, we choose to model the charging ser-

vices pricing problem as a Markov Decision Process

(MDP) (Bellman, 1957; Puterman., 1994). First, we

decompose the optimization problem into a sequence

of decisions, where at each time point τ, we need to

select new pricing function p ∈ L . Markov Decision

Processes provide a framework for modeling a broad

range of sequential decision problems, where an agent

must submit a sequence of decisions as responses to

the developing environment.

An MDP is a tuple

S, A, R, P, s

, where S is a ﬁ-

nite set of states, A is a ﬁnite set of actions; P : S×A ×

S → [0, 1] is the transition function forming the transi-

tion model giving a probability P(s

|s, a) of getting to

the state s

from the state s after application of the ac-

tion a; and a reward function R : S ×A × S → R. Start-

ing in initial state s

, any action from A can be chosen.

Based on this action, the system develops and moves

to the next state where another action can be applied.

During the move, the reward can be received based on

the R(s, a, s

) function.

When solving the MDP, the goal is to select a se-

quence of actions that will in expectation lead to the

highest accumulated reward.

For the implementation, we consider a charging

station with integer capacity between 0 and c

max

and

possible prices being integers between 1 and p

max

We consider a single day of 24 time intervals, each

1 hour long. For computational feasibility reasons,

we split the MDP into multiple MDPs, one for each

time window. This splitting gives us 24 MDPs, each

responsible for setting the price of the corresponding

time window. Each MDP generates a decision pol-

icy for its own time window. While these policies are

optimal in a sense that they maximize the reward in

given time window, together they may not maximize

the revenue in the whole day.

MDP-1 is in charge of setting the price between

00:00 and 01:00, MDP-2 for setting the price in the

time window between 01:00 and 02:00 and so on. As

the bookings arrive ahead of the charging, we include

time t to the kth time window in the state of the kth

MDP. For example, in our experiments, at the time

between 13:00 and 14:00, time t to MDP-18 is 4.

State s of MDP-k is thus deﬁned by the capacity,

price and time; s = (c, p,t). The actions are changes

to the price in the kth time interval, that is, a = p

. The

transition model for the kth MDP, P

|s, a) then de-

termines, given the current price, capacity and time to

the kth time interval, whether somebody books charg-

ing (which reduces capacity in the time window.). We

calculate the transition probabilities from the given

price elasticity function P

(p) and discrete historical

probability D

(t) of a booking arriving t ahead of kth

time window:

((c − 1, p

,t − 1)|(c, p, t), p

) =P

(p)D

(t),

c > 0, t > 1

((c, p

,t − 1)|(c, p, t), p

) =1 − P

(p)D

(t),

t > 0

((c

, p

)|(c, p,t), p

) =0 otherwise

(t) give the probability of a booking for charg-

ing during kth time interval arriving t ahead of the kth

time interval.Values of D

(t) are taken from the his-

torical data. The use of D

(t) in the transition func-

tion forms a simpliﬁed demand model that models

the distribution of demand within one day, but one

that is independent of the absolute demand expected

within this day. Price elasticity function P

(p) gives

the probability that given price p a customer will ac-

cept the price of the booking.

Instead of maximizing the proﬁt of the whole day

(in the sense of Equation 1), each MDP factor max-

imizes the proﬁt in given time window. This adjust-

ment is an important omission regarding optimality

of the resulting pricing. As Figure 1 shows, sales of

time windows affect the value of the neighboring time

windows. However, as we will show in Section 4,

even in this factored form with simple demand model,

MDP demand-response pricing can bring some bene-

ﬁts. In the model, splitting of the MDP into MDP

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

510

Table 1: Summary statistics of the E-WALD data for the

selected charging station with three charging points.

CS Dataset Statistics Mean Std

Charging session duration 0.726 h 0.794 h

Charge per charging session 6.72 kWh 5.19 kWh

# of daily charging sessions 2.53 1.49

Figure 2: Histogram of the charging session start times in

the E-WALD dataset for the selected charging station.

factors means that changes to capacity and price do

not affect on the neighboring prices.

We ﬁnd the optimal policies for MDP-1 to MDP-

24 through policy iteration. We implemented all

structures and algorithms in Python, using commonly

used Python packages such as NumPy (van der Walt

et al., 2011) and Pandas (McKinney, 2011). Policy

iteration algorithm that we used is from the pymdp-

toolbox

4 EXPERIMENTS

We evaluate the MDP dynamic pricing algorithm on

real data provided by E-WALD

, EV charging station

provider in Germany. First, we provide summarizing

statistics of the dataset and describe the preprocessing

we performed on the data. Then we describe the ex-

periments we conducted with the data and the results

we obtained.

4.1 Dataset

The dataset contains information on charging sessions

realized at one of the E-WALD charging stations.

This information includes timestamps of the begin-

ning and the end of each charging session, the sta-

tus of the electricity meter at the beginning and the

end of the charging session and anonymized identiﬁer

of a user who activated the charging session. In the

https://github.com/sawcordwell/pymdptoolbox

We would like to thank E-WALD for providing us with

the charging data for this study.

preprocessing step, we remove clearly erroneous data

points, (such as charging sessions with negative du-

ration) and merge some short charging sessions with

following charging sessions if the same customer ini-

tiated both sessions.

The summary statistics of the dataset can be found

in Table 1. Histogram of charging session start times

can be seen in Figure 2.

The particular charging station dataset does not

contain any pricing information about the charging

sessions. However, E-WALD uses only ﬂat rate pric-

ing in all their pricing stations.

4.2 Experimental Setup

In our experiments, we compare the performance of

the ﬂat rate pricing to the MDP based dynamic pric-

ing. To compare their performance we use four met-

rics, charging station revenue, charging station uti-

lization time, charge delivered by the charging station

and price per unit of energy sold by the charging sta-

tion. A detailed description of these metrics is given

in Table 2.

We use the real E-WALD charging station data to

simulate 24 hour period of the charging station oper-

ation. As the data was collected at charging station

with three charging slots, in our experiments we con-

sider our station to have three charging points. That

is, we use c

max

= 3 and p

max

= 5. We consider the

charging points to be capable of realizing any charg-

ing session recorded in our dataset. This means that

at most three charging sessions can be realized at

any point in time. In our simulation, customers book

charging sessions ahead of time. Charging station re-

jects the booking if all three charging points are al-

ready booked for any portion of the requested time.

If the station can realize the booking, pricing scheme

is used to determine the price of the charging session

which the station offers to the customer. Based on

this price, the customer either accepts or rejects the

offer. Price elasticity of demand described below de-

termines whether the offer is accepted or rejected by

the customer.

To make it possible for users to plan their trips in

the environment where the charging capacity may not

be readily available, we use ahead of time bookings

in our simulation. We simulate how much ahead each

customer books the charging session by drawing from

the uniform distribution. The maximum period ahead

of which customer can book a charging session is in

our experiments set to 6 hours. The time of the book-

ings determines the order of the arrival of the book-

ings to the.

The simulation starts by drawing n charging ses-

Dynamic Pricing Strategy for Electromobility using Markov Decision Processes

511

Table 2: Description of evaluation metrics.

Metric Description

CS Revenue Revenue of the charging station is the sum of prices of all charging sessions. We do not

express price in any currency. Instead, we use unit price as a basic unit. Revenue is

directly dependent on the selected pricing scheme.

CS Utilization Measured in hours, it is the added duration of all charging sessions realized by the

charging station. This as a proxy of a social welfare of the EV drivers achieved through

various pricing schemes. The higher the utilization, the more of the EV driver charging

demand was satisﬁed by the charging station.

Delivered Charge Measured in kWh, it is the charge delivered to all of the charging station customers.

Delivered charge is another proxy of a social welfare of the EV drivers realized by various

pricing schemes. The higher the delivered charge, the more of the EV charging demand

was satisﬁed by the charging station. Because of each EV charging with different

charging rate, this information complements the CS Utilization metric.

Energy price Average price per unit of energy across all charging sessions realized by the CS.

sions from the dataset. As can be seen from Table 1,

the mean number of customers at the charging station

is quite small. Also, the dataset does not give us any

information about the unsatisﬁed demand for charg-

ing services. Thus, in most of our experiments, we

use higher values of n so that all demand cannot be

satisﬁed by the given charging station.

Normalized histogram in Figure 2 and the sim-

ulated booking times are the basis of the histori-

cal probability D

(t) of a booking request arriving t

ahead of kth time window.

The MDP dynamic pricing uses different price for

every hour. To get the price of the charging session,

we ﬁrst split the charging session into segments that

correspond to the various dynamic prices. The cor-

responding hourly rate then multiplies the length of

each segment. Adding the partial prices together gets

us the price of the charging session offered to the user.

For the ﬂat rate pricing, the duration of the charging

session in hours is multiplied by the hourly rate.

When the customer receives the offered price, he

can accept or reject the offer. We simulate this using

the price elasticity of demand curve. The price elas-

ticity function we use is P

(x) = e

−Cx

Because we do not know the real price elasticity

of demand for EV charging services and we can not

estimate it from data, we experiment with multiple

values of C. The different values of C and the corre-

sponding shapes of price-elasticity curves are shown

in Figure 3. Having the price of the charging session,

we apply the price elasticity function to this price.

The resulting number is a probability that the cus-

tomer accepts the offer. If the user accepts the of-

fer, the charging session is added to the other already

booked charging sessions. Rejected offer is discarded

and no longer used by the system. For C = 0, we talk

about inelastic demand as the customer will accept

any price. At C = 0.5 the demand is highly elastic as

small changes to the price have a big effect on users

acceptance or refusal of the offer. For comparison,

the price elasticity of demand for gas station services

is usually described as relatively inelastic, meaning

low values of C (Lin Lawell and Prince, 2013).

Figure 3: Price elasticity of demand curves for different val-

ues of the C parameter.

4.3 Results

To compare the performance of the MDP dynamic

pricing and the ﬂat rate pricing, we experimented with

various numbers of customers and various parameters

of price elasticity of these customers. In each experi-

ment, we compare the MDP dynamic pricing that can

set price in each time window to an integer value be-

tween 1 and 5. We compare it to the ﬂat rate pricing

that uses ﬂat rates between 1 and 5.

For the ﬁrst experiment, we ﬁxed the price elas-

ticity parameter to C = 0.1 and varied the number of

customers arriving per day from 2 to 80. For the sec-

ond experiment, we varied the number price elasticity

parameter C through values given in Figure 3. We

ﬁxed the number of booking to 40.

Each data point in Figures 4 and 5 is an average of

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

512

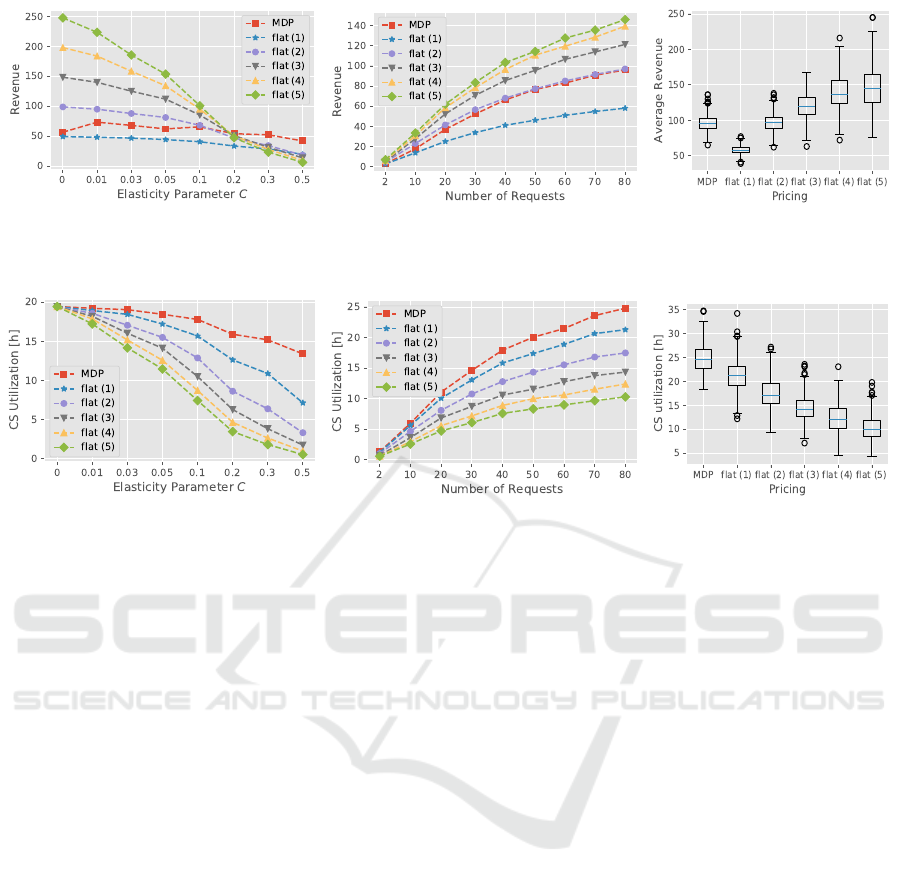
Figure 4: Performance in terms of revenue of the MDP dynamic pricing compared to the performance of the ﬂat rate during

one simulated day. The graphs are based on 400 runs with a random selection of booking requests from the E-WALD dataset.

Price elasticity parameter C = 0.1and n = 40 booking requests in plots where these parameters are not on axis.

Figure 5: Performance in terms of CS utilization of the MDP dynamic pricing compared to the performance of the ﬂat rate

during one simulated day. The graphs are based on 400 runs with a random selection of booking requests from the E-WALD

dataset. Price elasticity parameter C = 0.1and n = 40 booking requests in plots where these parameters are not on axis.

400 runs. In each run, we picked the booking requests

randomly from the full E-WALD dataset. For price

elasticity parameter C = 0.1 and 40 requests we give

the quartiles of the evaluation metrics.

As could be expected, increasing the number of

booking requests increases revenue, utilization and

delivered charge for all pricing schemes. Figure 4 for

revenue and Figure 5 for CS utilization illustrate this,

curves for delivered charge display the same trends as

ﬁgures for utilization.

Note that while the revenue is lower for the MDP

demand-response pricing for the lower price elasticity

curves (C < 0.2), the charging station utilization and

delivered charge are better across all values of C. The

utilization and delivered charge are same for all pric-

ing schemes when C = 0; that is, when the demand

is inelastic, customers always accept the offered price

and the charging capacity is distributed solely on the

ﬁrst come, ﬁrst serve basis.

For the experiment with variable elasticity param-

eter C, the downslope trend of the utilization and

delivered charge with increasing elasticity are to be

expected, given the ﬁxed number of 40 booking re-

quests at average duration 0.726 (the maximal theo-

retical utilization with three charging points would be

3 ∗ 24). As the price elasticity increases, the likeli-

hood of any given customer booking for given price

becomes lower.

Another notable result is that while the MDP price

per kWh is for most values of C comparable to the ﬂat

rate of price 1, the revenue of MDP is consistently

higher than the revenue of the ﬂat rate of 1.

The results show that that in simulation, the MDP

dynamic pricing will return greater revenue than ﬂat

rates with a price higher than one only if the demand

for EV charging is somewhat elastic (elasticity pa-

rameter C ≥ 0.2, Figure 3). However, dynamic pric-

ing improves the utilization and energy delivered by

the charging station across all values of the elastic-

ity parameter C and any number of booking requests,

while keeping the average price per kWh to the cus-

tomer comparable to the ﬂat rate pricing with the low-

est price. Additionaly, these results for the demand-

response MDP pricing are achieved reliably, without

increasing the variance of the observed metrics over

the ﬂat rate pricing.

The runtime of the simulations is in the order of

minutes on the Intel Core i7-3930K CPU @ 3.20GHz

with 32 GB of RAM, with most of the time spent on

pre-calculation of the policies for the MDPs.

5 CONCLUSION

We have shown how to use the Markov Decision

Processes to model the problem of demand-response

Dynamic Pricing Strategy for Electromobility using Markov Decision Processes

513

pricing of charging services for electric vehicles. Us-

ing the factored MDP demand-response pricing, we

aimed at the core objectives of electromobility: dis-

tribution of cost between the grid and EV owners,

signaling of power scarcity or abundance and incen-

tivization of behavior change of the EV drivers.

Experimentally, we have compared the demand-

response pricing strategy with the baseline of cur-

rently most commonly used time-of-use ﬂat rate pric-

ing across a wide range of environmental parame-

ters, that is, the price elasticity of demand and volume

of demand for charging services. While the revenue

generated by the proposed demand-response pricing

method was higher than the ﬂat rate pricing methods

only for speciﬁc values of the environmental param-

eters, our method performed better than any consid-

ered ﬂat rate pricing in the achieved utilization of the

charging station and delivered energy across all con-

sidered scenarios. The improvement of our method

in the utilization of the charging station and delivered

energy over the ﬂat rate pricing of comparable rev-

enue was up to 300%, depending on the price elastic-

ity and the demand.

As we mentioned in the paper, the most obvious

future work is to incorporate dependence of the con-

secutive time windows in the factored MDP model

and improve the demand model. Further, the model is

extendable to a game theoretic setting. Such approach

will, however, need substantial work to provide scal-

ability for practical use of the approach.

ACKNOWLEDGMENTS

This research was funded by the European Union

Horizon 2020 research and innovation programme

under the grant agreement N

◦

713864 and by the Grant

Agency of the Czech Technical University in Prague,

grant No. SGS16/235/OHK3/3T/13.

REFERENCES

Albadi, M. and El-Saadany, E. (2008). A summary of de-

mand response in electricity markets. Electric Power

Systems Research, 78(11):1989 – 1996.

Bellman, R. (1957). A markovian decision process. Journal

of Mathematics and Mechanics, 6:679–684.

Cao, Y., Tang, S., Li, C., Zhang, P., Tan, Y., Zhang, Z.,

and Li, J. (2012). An optimized EV charging model

considering TOU price and SOC curve. IEEE Trans.

Smart Grid, 3(1):388–393.

Chevaleyre, Y., Dunne, P. E., Endriss, U., Lang, J.,

Lema

ıtre, M., Maudet, N., Padget, J. A., Phelps, S.,

Rodr

ıguez-Aguilar, J. A., and Sousa, P. (2006). Issues

in multiagent resource allocation. Informatica (Slove-

nia), 30(1):3–31.

Chiang, W.-C., Chen, J. C., and Xu, X. (2007). An overview

of research on revenue management: current issues

and future research. International Journal of Revenue

Management, 1(1):97–128.

Dyer, C., Epstein, M., and Culver, D. (2013). Station for

rapidly charging an electric vehicle battery. US Patent

8,350,526.

Li, R., Wu, Q., and Oren, S. S. (2014). Distribution lo-

cational marginal pricing for optimal electric vehicle

charging management. IEEE Transactions on Power

Systems, 29(1):203–211.

Lin Lawell, C.-Y. C. and Prince, L. (2013). Gasoline price

volatility and the elasticity of demand for gasoline.

Energy Economics, 38(C):111–117.

McGill, J. I. and van Ryzin, G. J. (1999). Revenue manage-

ment: Research overview and prospects. Transporta-

tion Science, 33(2):233–256.

McKinney, W. (2011). Pandas: a foundational python li-

brary for data analysis and statistics.

Puterman., M. L. (1994). Markov Decision Processes.

Rezaei, P., Frolik, J., and Hines, P. D. H. (2014). Packetized

plug-in electric vehicle charge management. IEEE

Transactions on Smart Grid, 5(2):642–650.

Subramanian, J., Jr., S. S., and Lautenbacher, C. J. (1999).

Airline yield management with overbooking, can-

cellations, and no-shows. Transportation Science,

33(2):147–167.

van der Walt, S., Colbert, S. C., and Varoquaux, G. (2011).

The numpy array: A structure for efﬁcient numerical

computation. Computing in Science & Engineering,

13(2):22–30.

Versi, T. and Allington, M. (2016). Overview of the Electric

Vehicle market and the potential of charge points for

demand response. Technical report, ICF Consulting

Services.

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

514