
Analyzing Frame Conditions in UML/OCL Models
Consistency Equivalence and Independence
Philipp Niemann
1
, Nils Przigoda
2
, Robert Wille
1,3
and Rolf Drechsler
1,4
1
Cyber-Physical Systems, DFKI GmbH, Bremen, Germany
2
Siemens AG, Braunschweig, Germany
3
Institute for Integrated Circuits, Johannes Kepler University Linz, Linz, Austria
4
Group for Computer Architecture, University of Bremen, Bremen, Germany
Keywords:
UML/OCL, Operation Contracts, Frame Conditions, Validation and Verification.
Abstract:
In behavioral modeling using UML/OCL, operation contracts defined by pre- and postconditions describe
the effects on model elements (such as attributes, links, etc.) that are enforced by an operation. However,
it is usually not clearly stated which model elements can be affected and which shall not, although this in-
formation is essential in order to obtain a comprehensive description. A promising solution to this so-called
frame problem is to define additional frame conditions. However, properly defining frame conditions which
complete the model description in the intended way is a non-trivial, tedious and error-prone task. While for
UML/OCL models in general, methods for validation and verification are available, no analysis methods for
frame conditions exist so far that could support the designer in this process. In this work, we close this gap
and propose a set of primary analysis objectives (namely consistency, equivalence, and independence) that
provide substantial information about the correctness and adequateness of given frame conditions. Moreover,
we formalize these objectives as to be able to conduct the corresponding analyses in an automatic fashion
using the deductive power of established approaches for model validation and verification. Finally, we discuss
how the resulting methodology can actually be applied and demonstrate its potential for elaborated analyses
of frame conditions.
1 INTRODUCTION
The design of software as well as hardware systems
has become an increasingly complex task. The in-
troduction of modeling languages aims to aid desig-
ners in this process by providing description means
that abstract from implementation details but remain
precise enough to specifically describe the intended
system. Nowadays, the Unified Modeling Language
(UML) Rumbaugh et al. (1999) is one of the standard
modeling languages which allows, e. g., the descrip-
tion of a design by means of class diagrams. Since
UML version 1.1, the respective models can additi-
onally be enriched by descriptions formulated in the
Object Constraint Language (OCL) OMG – Object
Management Group (2014)—a declarative language
that allows to impose additional textual constraints
which further refine properties and relations between
the respective model elements (such as attributes,
links, etc.). Overall, this allows to define valid sy-
stem states by invariants and to describe the behavior
of operations by means of pre- and postconditions—
eventually yielding UML/OCL models that precisely
describe the structure and behavior of the system.
A well-known shortcoming of the resulting decla-
rative descriptions is that pre- and postconditions of-
ten do not make clear enough what may or may not
be modified in a transition between two system sta-
tes. In fact, they only define restrictions of the cal-
ling and the succeeding system state, respectively, but
do not specify precisely what is within the frame that
might be modified by an operation—possibly allo-
wing for unintended behaviour. This so-called frame
problem Borgida et al. (1995) does not only occur
in UML/OCL, but also in many other languages that
use declarative descriptions like, e.g., Eiffel, Z, JML,
VDM, or CML. Consequently, there has been a large
body of research on this problem. A common appro-
ach to cope with it and avoid unintended behaviour
is to provide additional constraints in terms of so-
called frame conditions. While each of the mentio-
ned languages has built-in functionalities for this pur-
Niemann, P., Przigoda, N., Wille, R. and Drechsler, R.
Analyzing Frame Conditions in UML/OCL Models - Consistency Equivalence and Independence.
DOI: 10.5220/0006602301390151
In Proceedings of the 6th International Conference on Model-Driven Engineering and Software Development (MODELSWARD 2018), pages 139-151
ISBN: 978-989-758-283-7
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
139

pose, mechanisms for specifying frame conditions in
UML/OCL have been suggested only recently Kosiu-
czenko (2013); Brucker et al. (2014).
However, while frame conditions are indeed able
to solve the frame problem, properly defining them is
a non-trivial process. Similarly as the definition of the
UML/OCL model itself, it requires a full understan-
ding of the considered system as well as its depen-
dencies. But while the designer is aided by several
tools and methods when defining the UML/OCL mo-
del (see, e. g., Gogolla et al. (2007, 2009); Demuth
and Wilke (2009)), almost no support exists yet for
the proper definition of frame conditions. In fact,
initial approaches providing the designer with pro-
posals for frame conditions and/or a classification of
model elements that may be affected by an opera-
tion have recently been proposed in Niemann et al.
(2015b). But they cannot guarantee that the deri-
ved frame conditions are indeed correct or complete
the specification of the model in the actually inten-
ded way. While for UML/OCL models in general,
corresponding methods for validation and verification
are available (see, e. g., Anastasakis et al. (2007); Ca-
bot et al. (2008, 2009); Brucker and Wolff (2008);
Choppy et al. (2011); Soeken et al. (2011); Hilken
et al. (2014); Przigoda et al. (2015a, 2016b)), no dedi-
cated analysis method for frame conditions exists so
far.
In this work, we close this gap by providing a
methodology for the dedicated analysis of frame con-
ditions in UML/OCL models. To this end, we first
discuss primary objectives for such an analysis—
yielding a notion of consistency, equivalence, and in-
dependence of frame conditions. Based on that, a
method is introduced afterwards, which automatically
analyzes a given set (or sets) of frame conditions with
respect to these objectives. An application of the re-
sulting methodology confirms the benefits of the pro-
posed approach. In fact, designers are aided with a
tool that allows them to efficiently check whether the
derived frame conditions are consistent with the gi-
ven UML/OCL model and complete the specification
of the model in the actually intended way.
The remainder of this paper is structured as fol-
lows: All ideas and concepts covered in this work
are illustrated by means of a simple UML/OCL mo-
del specifying an access control system which serves
as a running example and is introduced in Section 2.
Afterwards, Section 3 briefly reviews the frame pro-
blem as well as the different UML/OCL description
means introduced in the past to define frame conditi-
ons. Based on that, primary objectives for analyzing
the respectively obtained frame conditions are intro-
duced and discussed in Section 4 and an automatic
method for conducting these analyses is described in
Section 5. Finally, an implementation of the resulting
methodology is discussed in Section 6 and the paper
is concluded in Section 7.
2 PRELIMINARIES
In this section, we introduce basic concepts and noti-
ons of UML/OCL by means of the running example
that will also be later on used to illustrate the basic
concepts of frame conditions as well as the proposed
analysis methodology.
The running example, a slightly modified ver-
sion of the one originally presented in Przigoda et al.
(2015b), specifies a control system which grants
access to buildings based on magnetic cards as au-
thentication method. The cards are checked at turn-
stiles at the buildings’ entries and exits. The system
model is given in terms of a UML class diagram enri-
ched with textual OCL constraints and is depicted in
Fig. 1. The pure UML part describes the structure of
the system in terms of classes (e. g., Building, Mag-
neticCard, Turnstile), attributes and available ope-
rations of each class (e. g., Building::inside or
Turnstile::goThrough()) as well as relationships
between the classes in terms of associations. For the
sake of a convenient reference, we will refer to the
union of all attributes (of all classes) together with all
relations of a model as the set of model elements.
In this particular case, there is a single relationship
stating that each turnstile is associated with a unique
building and that each building contains at least two
turnstiles (gates). Such multiplicity constraints—
besides inheritance of classes which is not present in
the running example—are essentially the only con-
straints that can be stated in class diagrams using pure
UML.
To enforce further constraints or properties of
a system, textual OCL constraints are applied. On
the one hand, invariants describe properties such as
the uniqueness of a magnetic card’s ID (invariant
uniqueID), the existence of at least one entry and one
exit for each building (invariants atLeastOneEntry
and atLeastOneExit) or the fact that permanently
either the green or the red light of a turnstile is
lit (invariant eitherGreenOrRedLight). On the
other hand, OCL is employed to formulate so-called
operation contracts Meyer (1992) which comprise
preconditions (denoted by C) that are necessary to
invoke an operation call in the first place as well
as postconditions (denoted by B) that can be taken
for granted after the execution of the operation
has been completed. For instance, the operation
MODELSWARD 2018 - 6th International Conference on Model-Driven Engineering and Software Development
140

Turnstile
greenLightOn: Boolean
redLightOn: Boolean
currentlyAuthorized: Integer
entry: Boolean
checkCard(card : MagneticCard)
goThrough()
Building
authorized: Set(Integer)
inside: Set(Integer)
MagneticCard
id: Integer
gates
2..∗
building
1
inv eitherGreenOrRedLight:
greenLightOn xor redLightOn
inv uniqueID:
MagneticCard.allInstances()->isUnique(id)
context Turnstile::checkCard(card : MagneticCard):
pre: greenLightOn = false
post: greenLightOn =
building.authorized->includes(card.id)
and (entry <> building.inside->includes(card.id))
post: if (greenLightOn = true) then
currentlyAuthorized = card.id
end if
context Turnstile::goThrough():
pre : greenLightOn = true
post : if (entry = true) then
building.inside = building.inside@pre->including(currentlyAuthorized)
else
building.inside = building.inside@pre->excluding(currentlyAuthorized)
end if
post : greenLightOn = false
inv atLeastOneEntry:
gates->exists( t |
t.entry = true)
inv atLeastOneExit:
gates->exists( t |
t.entry = false)
Figure 1: Class diagram of the access control system.
checkCard() can only be invoked on a turnstile
if its green light is not on (precondition). The
state of the green light after the operation has been
executed depends on whether (a) the inserted card
is in principle authorized to enter/leave the building
(building.authorized->includes(card.id))
and whether (b) the card has been inserted on
the “expected” side of the turnstile (entry <>
building.inside->includes(card.id); the se-
cond part has been added in order to prevent multiple
persons from using the same card to enter/leave a
building one after the other). If these checks are
passed, the postconditions enforce that the green light
is lit and the ID of the inserted card is stored in the
attribute currentlyAuthorized.
All these constraints determine which instantiati-
ons of the model (system states) and operation calls
(transitions) are valid and which are not:
• A system state σ is a set of objects together
with attribute values (instantiations of classes) and
interconnecting links (instantiations of associati-
ons). A state σ is termed valid if, and only if, it
satisfies all UML constraints (multiplicity and in-
heritance) as well as all OCL invariants.
• A transition between two system states σ
1
,σ
2
through an operation call ω (i.e., an operation op
ω
called on some object from σ
1
) is termed valid if,
and only if, the preconditions C
ω
of ω are satis-
fied in σ
1
and the associated postconditions B
ω
are satisfied in σ
2
.
1
A valid transition is denoted as σ
1
ω
→ σ
2
and is termed
valid execution scenario if, and only if, also both sy-
stem states σ
1
and σ
2
are valid (which is not required
in the definition of valid transitions).
1
Note that the postconditions might also refer to the pre-
state of the operation (σ
1
) using the suffix @pre as, e.g., for
Turnstile::goThrough() in the running example.
B1:Building
authorized = {1}
inside =
/
0
T1:Turnstile
greenLightOn = false
redLightOn = true
currentlyAuthorized = -1
entry = true
T2:Turnstile
greenLightOn = false
redLightOn = true
currentlyAuthorized = -1
entry = false
M1:MagneticCard
id = 1
B1:Building
authorized = {1}
inside = {42}
T1:Turnstile
greenLightOn = true
redLightOn = false
currentlyAuthorized = 1
entry = true
T2:Turnstile
greenLightOn = true
redLightOn = false
currentlyAuthorized = -1
entry = false
M1:MagneticCard
id = 1
T1.checkCard(M1)
Figure 2: A valid execution scenario for the operation
Turnstile::checkCard(..).
Example 1. Figure 2 shows two valid system sta-
tes comprising a single building with two turnstiles.
In both states, all multiplicity constraints as well as
invariants hold. As indicated, calling the operation
checkCard(M1) on turnstile T1 leads to the transi-
tion from the system state depicted on the top of Fig. 2
to the system state depicted on the bottom of Fig. 2.
This transition is valid since all pre- and postconditi-
ons are satisfied. Overall, Fig. 2 shows a valid execu-
tion scenario for the operation checkCard().
3 FRAME PROBLEM AND
FRAME CONDITIONS
This section briefly reviews the frame problem of be-
havioral models and presents the state-of-the-art for
the specification of frame conditions which are em-
ployed to address this problem. Based on that, the re-
sulting validation gap and the proposed analysis met-
hodology are discussed in detail in Section 4.
In UML/OCL class diagrams, behavior is expres-
sed in terms of operations with pre- and postcondi-
tions. At first glance, these declarative descriptions
of the operation’s behavior ideally fit to the paradigm
of designing systems without the need to provide de-
Analyzing Frame Conditions in UML/OCL Models - Consistency Equivalence and Independence
141

tailed implementations. However, a closer look re-
veals that this may allow for undesired behavior.
Example 2. Consider again the valid execution sce-
nario shown in Fig. 2. Recall that both system states
are valid, i. e. all model constraints are satisfied. Mo-
reover, also the transition from the system state on the
top to the one on the bottom is valid, since for the ope-
ration checkCard(M1) (called on turnstile T1) the
corresponding preconditions (postconditions) are sa-
tisfied in the top (bottom) system state.
More precisely, as intended by the designer, the
green light of turnstile T1 is turned on and the ID of
M1 is stored in the currentlyAuthorized attri-
bute. However, at the same time it is also possible
to turn on the green light of the other turnstile T2 or
to add an arbitrary ID (e. g., 42) to the inside at-
tribute of the building B1 as highlighted in red and
italics in Fig. 2. Although such a behavior is obvi-
ously not intended, it is completely in line with the
postconditions.
In general, the shortcoming of declarative descrip-
tions like pre- and postconditions is that they often
do not make clear enough which model elements are
allowed to change during an operation call. In ot-
her words, they do not specify what is within the
frame that might be modified by an operation—the so-
called frame problem Borgida et al. (1995). As a con-
sequence, the resulting model/description is under-
specified and additional frame conditions need to be
formulated.
To this end, note that the frame problem also ari-
ses in the context of software verification where a sub-
stantial body of research has focused on possible so-
lutions (see, e. g., Beckert and Schmitt (2003)) and
corresponding approaches have been integrated into
several verification tools like Boogie Leino (2008)
or KeY Ahrendt et al. (2005). Unfortunately, these
approaches are not directly applicable to UML/OCL
for various reasons, especially due to the fact that
(a) OCL principally allows one to access arbitrary
objects via allInstances(), (b) associations are
always bi-directional (in contrast to uni-directional
pointers) such that changes to references always af-
fect both ends, and (c) object creation and deletion
can be rather random as we usually do not have a pre-
cise implementation.
Nonetheless, recently there have been several de-
dicated proposals for the specification of frame con-
ditions in UML/OCL models which are inspired by
the above approaches. More precisely, the following
approaches have been suggested:
• Explicit Postconditions: A straightforward ap-
proach is to explicitly specify what is not in
1 context Tu rn sti le :: che ckC ar d ( c ar d : Mag net ic C ar d ):
2 . ..
3 -- FrameConditions for Class Turnstile
4 post : T urn st i le . a ll I ns t an c es () - > f or All ( t |
5 t . en try = t. en t ry @pr e
6 and t. bu i ld ing = t. b ui ldi ng@ pre
7 and (( se lf <> t ) implies
8 ( t . g re enL igh tOn
9 = t. gre enL igh tOn @pr e
10 and t . r ed L ig h tO n
11 = t. re d Li g ht O n@ p re )
12 and t . c urr e nt l yA u tho riz ed
13 = t. cur ren t ly A uth ori z ed @ pre )
14 )
15 )
16 post : Tur ns t il e . al l In s tan ces @pr e ( )
17 = Tur nst il e . al l In s ta n ce s ()
18 -- FrameConditions for Class Building
19 post : B uil di ng . a ll I ns t an c es () - > f or All ( b |
20 b . aut hor iz e d = b . a u th o ri z ed @ pr e
21 and b. in sid e = b . i nsi de @ pr e
22 )
23 post : Bui ld ing . a ll I ns t an c es @ pre ()
24 = Bui ld ing . a ll I ns tan ces ()
25 -- FrameConditions for Class MagneticCard
26 post : M a gn eti cCa rd . a ll I ns t an c es () - > f orAll ( mc |
27 mc . id = mc . id @pre
28 )
29 post : Mag net icC ard . a ll I ns t an c es @ pre ()
30 = M ag net icC ard . a ll I ns tan ces ()
Figure 3: Frame conditions for checkCard(..) using the
explicit postconditions approach.
the frame by extending the postconditions with
constraints like modelElem = modelElem@pre.
The corresponding conditions for the operation
Turnstile::checkCard(..) from the running
example are listed in Fig. 3. This listing, but even
more the case study in de Dios et al. (2014), illus-
trates very impressively the drawback of this ap-
proach: it is time-consuming to manually create
the constraints in the first place and to maintain
them later on in the case of design changes.
• Modifies Only Statements: A complementary
approach has been suggested by Kosiuczenko Ko-
siuczenko (2006, 2013). The idea is to specify the
set of variable model elements, i. e., model ele-
ments that are allowed to be changed during an
operation call, at the same level as pre- and pos-
tconditions in terms of modifies only statements
2
.
These are of the form
modifies only: scope::modelElement.
2
Modifies only statements were originally introduced as
invariability clauses by Kosiuczenko Kosiuczenko (2006).
A variation of this idea is to specify the set of variable model
elements within the postconditions using an OCL primitive
modifiedOnly(Set) Brucker et al. (2014).
MODELSWARD 2018 - 6th International Conference on Model-Driven Engineering and Software Development
142

1 context Tu rn sti le :: che ckC ar d ( c ar d : Mag net ic C ar d ):
2 . ..
3 -- FrameConditions for Class Turnstile
4 modifies only : se lf :: gre enL igh tOn
5 modifies only : se lf :: red Lig ht O n
6 modifies only : se lf :: c ur r en t lyA uth ori z ed
7
8 context Tu rn sti le :: goT hro ug h () :
9 . ..
10 -- FrameConditions for Class Turnstile
11 modifies only : se lf :: gre enL igh tOn
12 modifies only : se lf :: red Lig ht O n
13 modifies only : se lf . bui ld ing :: in sid e
Figure 4: Frame conditions for checkCard(..) and
goThrough() using the modifies only approach.
1 se lf . g ree nLi ght On
2 se lf . b ui ldi ng
3 se lf . b ui ldi ng . a ut h or i ze d
4 ca rd . id <- > M ag n et i cC a rd . id
5 se lf . ent ry
6 se lf . b ui ldi ng . ins id e
7 se lf . c urr e ntl yAu t ho r ize d
Figure 5: List of model elements referenced within the pos-
tconditions of checkCard(..).
For instance, the clause modifies only:
self::greenLightOn expresses that the opera-
tion may only change the attribute greenLightOn
of the turnstile on which the operation is called
(self). Likewise, the complete frame conditions
for the operations Turnstile::checkCard(..)
and Turnstile::goThrough() are shown in
Fig. 4. Note that the scope can also be more com-
plex than just self and may contain navigation
or collections as in Line 13. In addition, it is even
possible to allow objects of a certain class to be
created or deleted during an operation call using
the construct Class::allInstances().
This approach enables the designer to precisely
define frame conditions in a much more comfor-
table, understandable, and maintainable fashion.
Moreover, there exists a methodology to assist the
designer in the initial generation of the frame con-
ditions Niemann et al. (2015a) and an approach
that does most of the work automatically and re-
quests feedback of the designer in ambiguous ca-
ses only Niemann et al. (2015b).
• Nothing Else Changes: Another approach to the
specification of frame conditions is to not write
them down explicitly, but automatically derive
them from the postconditions using a paradigm
such as nothing else changes Cabot (2006, 2007).
Following this paradigm, every model element
that is referenced within the postconditions is
included in the frame of what may change (and
nothing else). In the best case, this implicit
approach requires no additional efforts by the
designer. However, in general, the resulting frame
conditions are often not exactly what the designer
intended and it can be non-trivial to adjust them
manually—which would have to be done by
rewriting the postconditions or adding further
ones. For instance, Fig. 5 lists all model elements
which are referenced within the postconditions
of the operation Turnstile::checkCard(..)
from the running example. Only the very first and
very last of them, i. e., self.greenLightOn
and self.currentlyAuthorized, are
actually meant to be affected. In addi-
tion, both self.greenLightOn and also
self.redLightOn have to be variable in order
to fulfill the invariant eitherGreenOrRedLight.
To make this implicit dependency transparent to
the automatic derivation approach, the particular
invariant is added as another postcondition as
shown in Fig. 6 (Lines 3–4). To fix the values of
the other elements, postconditions as listed in the
remainder of Fig. 6 have to be added. Note that,
as it is not clear which instance of MagneticCard
is used for the card parameter, the id attributes
of all MagneticCards are marked as variable by
the approach and, hence, have to be restricted
manually. Moreover, the additional postcondi-
tions contain calls to Class.allInstances()
(Lines 9 and 16) which again would be interpre-
ted as referenced model elements and allow for
the creation and deletion of objects (of Class).
To avoid this, further postconditions have to be
added (Lines 13 and 19).
Overall, frame conditions are very important for
obtaining complete model descriptions and are a
key ingredient when considering the behavior of
UML/OCL models. Various approaches to their spe-
cification exist, each with complementary strengths
and weaknesses.
4 ANALYSIS OF FRAME
CONDITIONS
While using frame conditions as reviewed above in-
deed solves the frame problem, properly defining
them remains a non-trivial process. To this end, the
designer needs to fully understand the considered mo-
del as well as its dependencies. While initial appro-
aches such as the one proposed in Niemann et al.
(2015b) may aid him or her in this process, they can-
not guarantee that the derived frame conditions are in-
deed correct or complete the specification of the mo-
Analyzing Frame Conditions in UML/OCL Models - Consistency Equivalence and Independence
143

1 context Tu rn sti le :: che ckC ar d ( c ar d : Mag net ic C ar d ):
2 . ..
3 -- Implicit Dependency
4 post : red Li g ht On = not gre en L ig h tO n
5 -- FrameConditions for Class Turnstile
6 post : se lf . en tr y = se lf . ent ry @pr e
7 post : se lf . bu ild in g = self . bui ldi ng@ pre
8 -- FrameConditions for Class Building
9 post : Bu ild in g . all In s ta n ce s ()-> fo rAl l ( b |
10 b . aut hor iz e d = b . a u th o ri z ed @ pr e
11 and b. in sid e = b . i nsi de @ pr e
12 )
13 post : B uil di ng . a llI nst anc e s@ p re ()
14 = Bui ld ing . a ll I ns tan ces ()
15 -- FrameConditions for Class MagneticCard
16 post : Mag ne t ic C ar d . all Ins ta n ce s ( )-> fo rAl l ( mc |
17 mc . id = mc . id @pre
18 )
19 post : M a gn e ti cCa rd . a llI nst anc e s@ p re ()
20 = M ag net icC ard . a ll I ns tan ces ()
Figure 6: Additional postconditions for checkCard(..)
required for the nothing else changes approach.
del in the actually intended way. In this work, we
propose a methodology for the dedicated analysis of
frame conditions in UML/OCL models with the parti-
cular aim to check their correctness and adequateness.
Here, we distinguish between three primary objecti-
ves:
1. Most importantly, to judge the correctness of
frame conditions it is essential to investigate their
consistency with the originally given UML/OCL
model (i.e., do the obtained frame conditions still
allow for a valid execution of an operation?).
2. On top of that, an analysis of the effect of different
sets of frame conditions, i.e., their possible equi-
valence or non-equivalence, is of interest in order
to judge whether they indeed complete the model
in the intended way.
3. Furthermore, for several purposes (e. g., for the
sake of obtaining a small/compact set of frame
conditions or for debugging inconsistent frame
conditions) the designer may be interested in de-
pendencies between different (sub-)sets of frame
conditions, i. e., in analyzing independence of
frame conditions.
In this section, the three above-mentioned analy-
sis objectives are illustrated in more detail and des-
cribed in a formal way in order to allow for an au-
tomatic analysis (which will be discussed in the fol-
lowing section). To this end, we study the impact of
frame conditions on the set of valid execution scena-
rios (cf. Section 2). Recall that this set (in the fol-
lowing denoted by S) is constituted by all valid tran-
sitions σ
1
ω
→ σ
2
between valid system states σ
1
,σ
2
.
A transition is induced by an operation call ω which
σ
1
/C
ω
σ
2
/B
ω
op
ω
=?
∈ S
T
T
σ
1
/C
ω
σ
2
/B
ω
op
ω
= op
∈ S
op
σ
1
/C
ω
σ
2
/B
ω
op
ω
= op
+F
∈ S
F
op
Figure 7: Execution scenarios.
consists of an object o
ω
∈ σ
1
, an operation op
ω
that is
called on it and a (possibly empty) set of parameters.
The transition σ
1
ω
→ σ
2
is termed valid if, and only if,
the preconditions C
ω
of ω are satisfied in σ
1
and its
postconditions B
ω
are satisfied in σ
2
(see the top of
Fig. 7). Note that the particular operation op
ω
can be
arbitrary for the transitions in S.
Now, to focus on individual operations, we clas-
sify the valid execution scenarios of a model by the
corresponding operation op
ω
. This yields a partition
of the set of all valid scenarios of a model into disjoint
subsets S
op
= {σ
1
ω
→ σ
2
∈ S | op
ω
= op} for each
operation op (of any class) of the model (see the cen-
ter of Fig. 7). Note, however, that only pre- and pos-
tconditions, but no frame conditions have been taken
into account so far. Consequently, in order to ana-
lyze a particular set of frame conditions, we further
restrict to those execution scenarios that additionally
satisfy the given frame conditions (denoted by F ) and
consider the corresponding subsets S
F
op
⊂ S
op
(see the
bottom of Fig. 7).
Using this notation, the analysis objectives menti-
oned above can be formalized as follows:
4.1 Consistency
The major criterion for the quality and validity of
well-defined frame conditions is that they are consis-
tent with the (original) contractual specification of the
operation. More precisely, assuming that an operation
contract in terms of pre- and postconditions is free of
contradictions and in principle allows for an execu-
tion of the operation (S
op
6=
/
0), this property shall be
preserved when additionally enforcing the frame con-
ditions (S
F
op
6=
/
0). In other words, frame conditions
can only be considered consistent, if they are compa-
tible with at least one execution scenario.
To strengthen the significance of this objective,
the same compatibility can be required for a set of
pivot scenarios P ⊂ S
op
(provided by the designer)
MODELSWARD 2018 - 6th International Conference on Model-Driven Engineering and Software Development
144
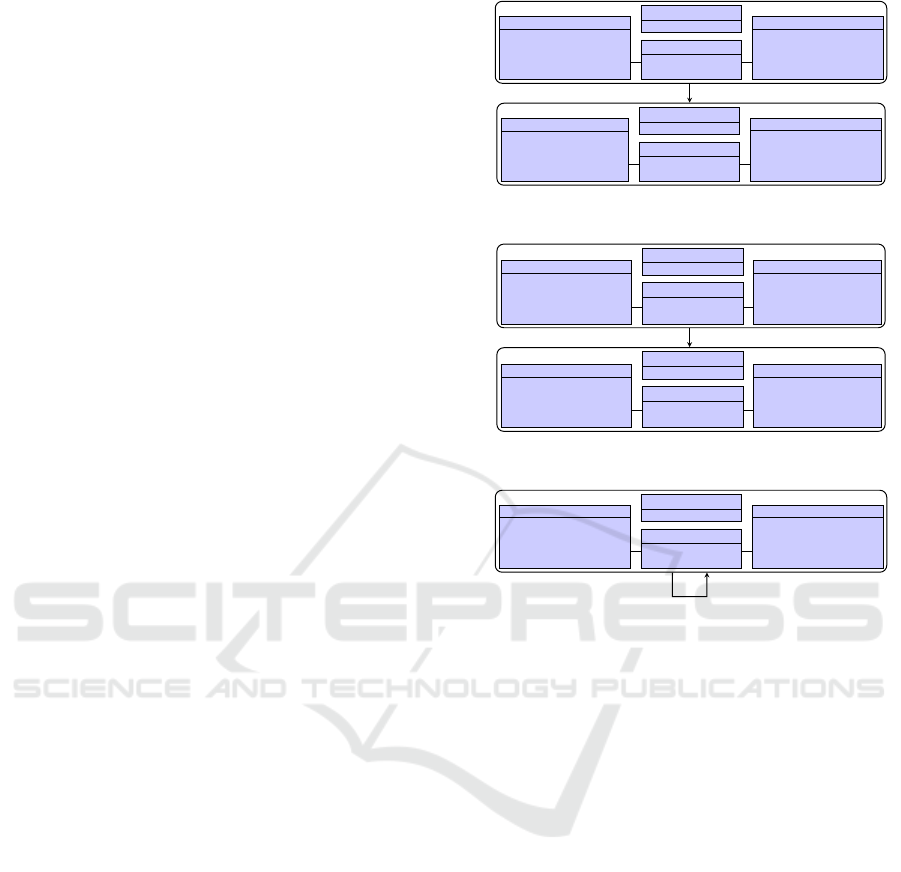
that characterize the intended behavior of the opera-
tion, i. e., we check whether P ⊂ S
F
op
. In a similar
fashion, one may also employ scenarios characteri-
zing unintended behavior and, thus, being incompati-
ble to well-defined frame conditions. For most signi-
ficant results, the pivot scenarios shall cover the ope-
ration’s functionality as comprehensively as possible,
i. e., affect as many model elements as possible, be as
complementary as possible, and desirably also cover
corner-cases.
Example 3. Consider the operation checkCard()
from the running example (Fig. 1) together with the
frame conditions specified in Fig. 3. The operation
contract in principle allows for an execution of the
operation (S
checkCard()
6=
/
0), since the transition
from Fig. 2 (termed ω
0
in the following) is a valid
execution scenario as shown above. However, the
frame conditions do not allow the changes highligh-
ted in red: B1::inside is required to remain con-
stant in Line 21 of Fig. 3 and switching the lights
of T2 is prohibited by Lines 8–11. Overall, this means
ω
0
/∈ S
F
checkCard()
. Nonetheless, the frame conditi-
ons themselves are clearly consistent. For instance,
when refraining from the changes highlighted in red,
i. e., the attributes of B1 and T2 do not change, the
resulting transition (shown in Fig. 8(a)) is still a va-
lid execution scenario and is also compatible with the
frame conditions. A meaningful set of complemen-
tary pivot scenarios would cover the cases of leaving
and entering the building (cf. Figs. 8(a) and 8(b)) as
well as checking an authorized or unauthorized card
(Fig. 8(c)).
4.2 Equivalence
Aiming at the relationship between different sets of
frame conditions, the first important objective is to
check for equivalence. More precisely, given two sets
of frame conditions F
1
and F
2
we are interested to
know whether they lead to the same set of valid exe-
cution scenarios (S
F
1
op
= S
F
2
op
) or, if not, what the rea-
sons for the non-equivalence are. To this end, we aim
to find scenarios that are only compatible with one set
of frame conditions, but not with the other, i. e., scena-
rios from the set S
F
1
op
4S
F
2
op
= (S
F
1
op
\S
F
2
op
)∪ (S
F
2
op
\S
F
1
op
)
(symmetric difference). The check can be performed
on sets of frame conditions that are only slight va-
riations of each other, but also if they are specified
using different approaches/formalisms. Again, pivot
scenarios can be employed to prove equivalence on
a relevant subset of scenarios or to allow for a more
detailed analysis of the differences.
B1:Building
authorized = {1}
inside =
/
0
T1:Turnstile
greenLightOn = false
redLightOn = true
currentlyAuthorized = -1
entry = true
T2:Turnstile
greenLightOn = false
redLightOn = true
currentlyAuthorized = -1
entry = false
M1:MagneticCard
id = 1
B1:Building
authorized = {1}
inside =
/
0
T1:Turnstile
greenLightOn = true
redLightOn = false
currentlyAuthorized = 1
entry = true
T2:Turnstile
greenLightOn = false
redLightOn = true
currentlyAuthorized = -1
entry = false
M1:MagneticCard
id = 1
T1.checkCard(M1)
(a) Entering the building with an authorized card
B1:Building
authorized = {1}
inside = {1}
T1:Turnstile
greenLightOn = false
redLightOn = true
currentlyAuthorized = -1
entry = true
T2:Turnstile
greenLightOn = false
redLightOn = true
currentlyAuthorized = 1
entry = false
M1:MagneticCard
id = 1
B1:Building
authorized = {1}
inside = {1}
T1:Turnstile
greenLightOn = false
redLightOn = true
currentlyAuthorized = -1
entry = true
T2:Turnstile
greenLightOn = true
redLightOn = false
currentlyAuthorized = 1
entry = false
M1:MagneticCard
id = 1
T2.checkCard(M1)
(b) Leaving the building with an authorized card
B1:Building
authorized = {1}
inside =
/
0
T1:Turnstile
greenLightOn = false
redLightOn = true
currentlyAuthorized = -1
entry = true
T2:Turnstile
greenLightOn = false
redLightOn = true
currentlyAuthorized = -1
entry = false
M1:MagneticCard
id = 2
T1.checkCard(M1)
(c) Entering the building with an unauthorized card
Figure 8: Pivot scenarios for the operation checkCard().
Example 4. Consider again the operation
checkCard() from the running example (as
in the previous example). Comparing the frame
conditions from Fig. 3 (specified as explicit postcon-
ditions) and Fig. 4 (specified using modifies only
statements) shows that they are indeed equivalent.
However, if the second modifies only statement
regarding self::redLightOn would have been
forgotten in the specification, an evaluation of the
pivot scenarios from Fig. 8 shows that only the
third one is still compatible, while the first two
scenarios are no longer compatible. A deeper
analyis of the second scenario reveals that only
T2::greenLightOn and T2::redLightOn
are modified which provides a hint on the missing
modifies only statement for self::redLightOn.
4.3 Independence
The second objective aiming at analyzing the relati-
onship between different sets of frame condition ad-
dresses dependencies between individual frame con-
ditions. To this end, two sets of frame conditions
F
1
,F
2
are combined to a set F
1
∪ F
2
whose frame of
change is essentially the union of the respective fra-
Analyzing Frame Conditions in UML/OCL Models - Consistency Equivalence and Independence
145
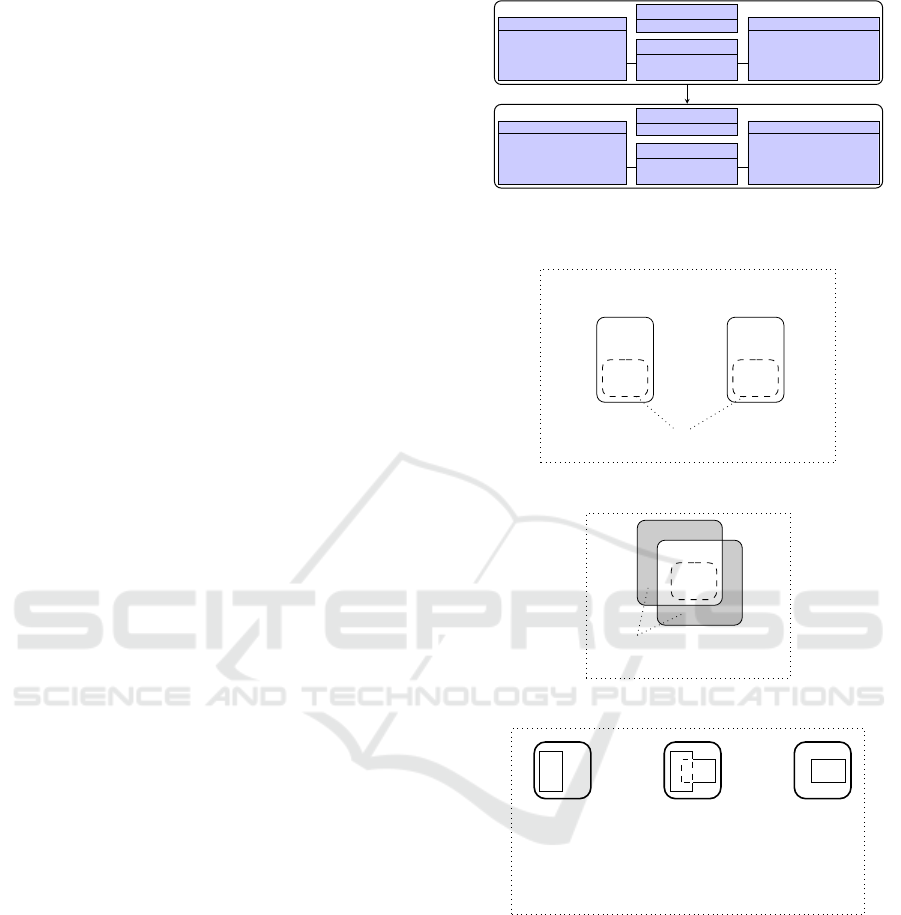
mes of F
1
and F
2
. In other words, a model element
is allowed to be modified according to F
1
∪ F
2
if, and
only if, it is allowed to be modified according to at
least one set of frame conditions.
Then, several different cases are possible:
• F
1
∪ F
2
is consistent (S
F
1
∪F
2
op
6=
/
0), although
neither F
1
nor F
2
(considered separately) are con-
sistent. This means that F
1
and F
2
require each
other.
• F
1
∪ F
2
and F
i
are consistent (i = 1 and/or i = 2).
This means that F
i
is independent from the other
set of frame conditions F
3−i
.
• F
1
∪ F
2
is not consistent (S
F
1
∪F
2
op
=
/
0), although
F
1
or F
2
(considered separately) are consistent.
This means that F
1
and F
2
exclude each other.
• Neither F
1
∪ F
2
, nor F
1
, nor F
2
are consistent.
This only implies that F
1
and F
2
are not sufficient
to obtain complete or consistent frame conditions.
In order to obtain more detailed information about
the particular dependencies, we can go down to the
level of model elements and analyze what happens if
particular model elements are not only allowed to be
modified, but are required to actually be subject to
changes. More precisely, we consider a set of model
elements M = {m
1
,...,m
k
} (all included in the frame
of F
1
) together with another model element m
0
/∈ M
(included in the frame of F
2
). If all elements from
M are actually changed in an execution scenario, m
0
can either (a) be forced to be modified as well, (b)
be forced to remain constant, or (c) be allowed to be-
have either way, i. e., do not have an immediate de-
pendency to the model elements in M.
Example 5. Consider the operation goThrough()
from the running example together with the
modifies only statements as listed in Fig. 4.
Set F
1
to be the first modifies only statement
(self::greenLightOn) and F
2
to contain the
two remaining statements (self::redLightOn
and self.building::inside). Then, F
2
requires F
1
and vice versa. In fact, it can be
shown that a modification of building.inside
and/or self.redLightOn implies that also
self.greenLightOn needs to be modified. On
the contrary, a change to self.greenLightOn
also requires self.redLightOn to be modified,
but not necessarily also building.inside. In
fact, if the ID stored in currentlyAuthorized
is—by incidence—logically already inside/outside
the building, a building can be entered/left with no
change to building.inside (cf. Fig. 9). This
dependency becomes apparent at the level of frame
conditions if one moves the second modifies only
B1:Building
authorized = {1}
inside = {1}
T1:Turnstile
greenLightOn = true
redLightOn = false
currentlyAuthorized = 1
entry = true
T2:Turnstile
greenLightOn = false
redLightOn = true
currentlyAuthorized = -1
entry = false
M1:MagneticCard
id = 1
B1:Building
authorized = {1}
inside = {1}
T1:Turnstile
greenLightOn = false
redLightOn = true
currentlyAuthorized = 1
entry = true
T2:Turnstile
greenLightOn = false
redLightOn = true
currentlyAuthorized = -1
entry = false
M1:MagneticCard
id = 1
T1.goThrough()
Figure 9: Entering a building without changing the attribute
building.inside.
S
op
/
0 6=
P
⇒
!
S
F
op
6=
/
0
P
pivot scenarios
(a) Consistency
S
F
1
op
P
S
F
2
op
S
F
1
op
4S
F
2
op
=
?
/
0
(b) Equivalence
F
1
F
1
∪ F
2
F
2
↓ ↓↓
S
F
1
op
?
=
/
0 S
F
1
∪F
2
op
?
=
/
0 S
F
2
op
?
=
/
0
⇐⇒
(c) Independence
Figure 10: Summary of Analysis Objectives.
statement (self::redLightOn) from F
2
to F
1
.
Then, F
2
still requires F
1
, but not vice versa.
Overall, Fig. 10 summarizes the three proposed
objectives for the analysis of frame conditions. As
already illustrated by the provided examples, the ma-
nual evaluation can be a very elaborate task. Conse-
quently, the objectives need to be evaluated in an auto-
matic fashion in order to be the basis of a really useful
analysis methodology. In the following, we outline
how this aim can be achieved.
MODELSWARD 2018 - 6th International Conference on Model-Driven Engineering and Software Development
146

5 AUTOMATIC ANALYSIS OF
FRAME CONDITIONS
In order to automatically analyze the objectives in-
troduced above, we propose to employ approaches
for automatic reasoning on UML/OCL models. To
this end, we first review corresponding approaches in
Section 5.1. Afterwards, we describe in Section 5.2
how the respective objectives can be formulated on
top of these solutions.
5.1 Automatic Reasoning on UML/OCL
In the recent past, several approaches for automatic
reasoning on UML/OCL models have been proposed
which aim at the validation and verification of struc-
tural as well as behavioral aspects (see, e. g., Anasta-
sakis et al. (2007); Cabot et al. (2008, 2009); Brucker
and Wolff (2008); Choppy et al. (2011); Soeken et al.
(2011); Hilken et al. (2014); Przigoda et al. (2015a,
2016b)). Here, we focus on approaches using solvers
for problems of Boolean Satisfiability (SAT) or Sa-
tisfiability Modulo Theories (SMT), see, e. g., Hilken
et al. (2014); Przigoda et al. (2016b).
The general idea of these approaches is sket-
ched by means of Fig. 11: Instead of explicitly
enumerating all possible system states and operation
calls, they utilize a symbolic formulation of the given
UML/OCL model which allows to consider all possi-
ble sequences of system states and operation calls at
the same time (up to a given sequence length n).
3
For this purpose, the model is expressed as a
set of variables which can describe arbitrary system
states σ
1
,...,σ
n
, i. e., the instantiated objects, their
attributes and associations, as well as arbitrary
transitions—each of which is triggered by a (sin-
gle) operation call ω
1
,...,ω
n−1
. Note that this
formulation in principle also covers invalid system
states as well as invalid transitions. Consequently,
in order to restrict to valid states only, additional
constraints over these variables are applied to enforce
the model’s static constraints such as multiplicity
constraints and OCL invariants. Analogously, in
order to ensure valid transitions, pre-, post-, and
frame conditions of each possible operation call
are also translated to constraints over the state
variables, but are only enforced if the transition ω
i
is
3
In addition to limiting the sequence length, all these
approaches require further problem bounds in order to limit
the search space, i. e., they need to be provided with a fixed
number or at least a range of objects that shall be instantia-
ted as well as a finite domain for all data types.
σ
1
σ
2
σ
n
. . .
ω
1
ω
2
ω
n−1
Figure 11: Symbolic formulation for automated reasoning.
chosen to be the corresponding operation. More pre-
cisely, the following formulation is applied:
4
Formulation 1. For a sequence of system sta-
tes σ
1
,...,σ
n
, let Ω
i
be the set of all operation calls
that are available within system state σ
i
(i = 1,...,n).
Then, for each of the transitions ω
i
(i = 1, . . . , n − 1)
from a system state σ
i
to the succeeding state σ
i+1
it
is required that
^
ω∈Ω
i
(ω
i
= ω) ⇒ (JC
ω
K ∧ JB
ω
K ∧ JF
ω
K)) (1)
holds, where
• JC
ω
K is a constraint enforcing the preconditions
of ω for system state σ
i
,
• JB
ω
K is a constraint enforcing the postconditions
of ω for system state σ
i+1
, maybe by using σ
i
as
well, and
• JF
ω
K is a constraint enforcing the frame conditi-
ons for the entire transition (i. e., for both system
states).
Based on this formulation, afterwards the parti-
cular validation or verification objective can be for-
mulated in terms of further specific constraints. For
instance, in order to check whether a certain opera-
tion Class::op() is executable at all, a constraint
stating that ω
1
= o
1
.op() ∨... ∨ ω
1
= o
k
.op() (where
o
1
to o
k
are the possibly instantiated objects of Class
in σ
1
) needs to be added. Finally, the complete pro-
blem instance is passed to a reasoning engine (solver)
which is supposed to determine a satisfying assign-
ment to all variables, i. e., an assignment that satisfies
all of the constraints. If the solver returns SAT, i. e.,
a satisfying assignment has been determined, a corre-
sponding sequence of valid system states and transiti-
ons (a so-called witness of the problem instance) can
be extracted. Otherwise, if the solver returns UNSAT,
it has been proven that no satisfying assignment exists
(within the specified problem bounds).
5
5.2 Employing the Analysis Objective
In the following, we utilize the reasoning scheme re-
viewed above for the analysis of frame conditions.
4
Note that, in the following, an abstract description is
provided which is sufficient for the purposes of this work.
For a more detailed treatment of the respective formulation,
we refer to Przigoda et al. (2016b).
5
Note that the solver will always conclude at some point
due to the finite search space.
Analyzing Frame Conditions in UML/OCL Models - Consistency Equivalence and Independence
147

1 σ
1
:: T1 :: g ree nLi ght On = fa lse
2 σ
1
:: T1 :: r ed L ig h tO n = t ru e
3 ...
4 σ
1
:: T1 :: b ui ldi ng = σ
1
:: B1
5 ...
6 σ
2
:: T1 :: g ree nLi ght On = tr ue
7 σ
2
:: T1 :: r ed L ig h tO n = f al se
8 ...
9 ω
1
= σ
1
:: T1 . c hec kCa rd (σ
1
:: M1 )
Figure 12: Constraints for the pivot scenario from Fig. 8(a).
For this purpose, we apply as validation or verification
objective the previously proposed analysis objectives,
namely consistency, equivalence, or independence of
frame conditions. To this end, it is important to note
that we may restrict to a single transition between two
system states and also to one particular operation (as
illustrated by the dashed box in Fig. 11). While all
effects that we are interested in are still present in this
restricted scenario, the complexity of the formulation
can be reduced significantly. Taking this into account,
the considered objectives and resulting decision pro-
blems can be formulated as follows.
5.2.1 Consistency
In order to analyze the consistency for given frame
conditions F regarding an operation op, the formula-
tion simply has to ask “Does there exist a valid execu-
tion scenario for operation op?” (S
F
op
6=
/
0). As vali-
dity is ensured implicitly by the general formulation,
this boils down to the question whether the operation
op is executable at all. As already discussed above, no
further constraints have to be applied to answer this
question besides the restriction of ω
1
to the operation
under consideration.
In order to check whether a pivot scenario ω
p
∈ P
given in terms of a pair of a pre- and a poststate is va-
lid (ω
p
∈ S
F
op
), the specified values of attributes, links,
etc. additionally have to be enforced in the correspon-
ding state.
Example 6. In order to enforce the pivot scenario
from Fig. 8(a), the constraints listed in Fig. 12 have
to be added.
If these formulations return SAT, it has been
shown that S
F
op
6=
/
0 or ω
p
∈ S
F
op
, respectively, and
a valid execution scenario can be extracted from the
satisfying assignment. If UNSAT is returned, it has
been proven that no valid execution scenario exists or
that the given scenario ω
p
is not valid, respectively.
Note that it is possible to let the solver check a
set P of multiple alternative pivot scenarios at the
same time. However, in case of SAT, we would not
be able to deduce that P is entirely contained in S
F
op
,
as the found witness only implies that P ∩ S
F
op
6=
/
0.
5.2.2 Equivalence
In order to prove the equivalence of two sets of frame
conditions F
1
and F
2
, (S
F
1
op
= S
F
2
op
), we ask the solver
to find a counterexample ω ∈ (S
F
1
op
\S
F
2
op
)∪(S
F
2
op
\S
F
1
op
),
i. e., a scenario that is only valid when enforcing one
set of frame conditions, but not the other. Using the
standard formulation (cf. Eq. (1)), we can only en-
force either JF
1,ω
K or JF
2,ω
K at the same time. Howe-
ver, as the corresponding constraints are commonly
generated in an automatic fashion from the original
description of frame conditions, there is no reason
why one should not enforce, e. g., ¬JF
i,ω
K instead of
JF
i,ω
K (i = 1,2). Then, only those scenarios would be
considered “valid” by the solver which are not compa-
tible with the respective frame conditions. This can be
exploited for our purpose by enforcing the constraint
(JF
1,ω
K ∧ ¬JF
2,ω
K) ∨ (JF
2,ω
K ∧ ¬JF
1,ω
K)
instead of JF
ω
K in Eq. (1).
If this formulation returns UNSAT, it has been
proven that (S
F
1
op
\S
F
2
op
)∪(S
F
2
op
\S
F
1
op
) =
/
0. This is logi-
cally equivalent to S
F
1
op
= S
F
2
op
, i. e., both sets of frame
conditions are equivalent. If SAT is returned, an exe-
cution scenario can be extracted from the satisfying
assignment which is valid for exactly one set of frame
conditions (but not for the other). This scenario can
then be analyzed further.
Note that equivalence can either be checked for
the frame conditions of a single operation or for all
operations of the considered model at once. Howe-
ver, in the latter case, a possible witness will reveal
only one of possibly multiple operations for which the
frame conditions are not equivalent.
5.2.3 Independence
Determining dependencies between different sets of
frame conditions F
1
and F
2
essentially boils down to
performing consistency checks on F
1
, F
2
and F
1
∪F
2
.
Unfortunately, it is in general not possible to automa-
tically derive the constraint J(F
1
∪F
2
)
ω
K for the frame
conditions F
1
∪ F
2
from the constraints JF
1,ω
K and
JF
2,ω
K. In fact, only when the frame conditions are
specified using modified only statements, the appro-
ach presented in Przigoda et al. (2016a) can be em-
ployed to do this automatically. More precisely, the
constraints JF
1,ω
K and JF
2,ω
K are constructed using
so-called variability maps which store for each mo-
del element whether it may be modified or not. Then,
the logical disjunction of these maps precisely gives
J(F
1
∪F
2
)
ω
K. In all other cases, F
1
∪F
2
is required to
be specified manually which can be a highly elaborate
and non-trivial task.
MODELSWARD 2018 - 6th International Conference on Model-Driven Engineering and Software Development
148

In order to determine dependencies between chan-
ges to model elements from a set M = {m
1
,...,m
k
}
and changes to a model element m
0
/∈ M, the
solver is asked to determine two different exe-
cution scenarios. In these scenarios, all ele-
ments from the set M are required to be mo-
dified using constraints like modelElement <>
modelElement@pre or modelElements->exists(m
| m <> m@pre) (depending on whether a single or
multiple instances of the model element are included
in the frame), while (1) the model element m
0
is re-
quired to be modified with similar constraints in one
scenario and (2) m
0
is required to keep its value (m0
= m0@pre or m0->forAll(m | m = m@pre)) in the
other scenario.
If the solver can determine a valid execution sce-
nario in both cases, there is no dependency. If the sol-
ver can determine a valid execution scenario only in
one case, it follows that m
0
is either forced to change
or to remain constant, respectively. If the solver re-
turns UNSAT in both cases (and the frame conditions
are consistent in principle), one can deduce that there
already has to be a dependency between the model
elements of M such that not all of them may be chan-
ged at once.
Having these problem formulations, the objecti-
ves proposed in the previous section can be evaluated
automatically using approaches for automated reaso-
ning on UML/OCL models. In the following section,
we discuss how the resulting methodology can actu-
ally be applied and, beyond that, additionally allows
for more elaborated analyses on the considered set of
frame conditions.
6 APPLICATION AND FURTHER
POTENTIAL
We implemented the presented concepts and formu-
lations for the analysis of frame conditions on top of
the model verification approach presented in Przigoda
et al. (2016b). Here, the authors propose to translate
the verification task into an instance of a Satisfiabi-
lity Modulo Theories (SMT) problem. The correspon-
ding symbolic formulation is created automatically in
terms of the SMT-LIB bit-vector logic QF_BV. Then,
the problem instance can be solved using so-called
SMT solvers (e. g., Z3 De Moura and Bjørner (2008)).
These solvers allow for an efficient traversal of large
search spaces and, hence, are suitable to determine
precise assignments to the symbolic formulation and,
by this, a sequence of transitions satisfying the consi-
dered verification objective. A big advantage of this
particular approach regarding the analysis of frame
conditions is that it natively supports the nothing else
changes approach as well as modifies only statements
according to the symbolic formulation proposed in Pr-
zigoda et al. (2016a). More precisely, as already in-
dicated above, the constraints JF K that enforce a set
of frame conditions within the symbolic formulation
(cf. Eq. (1)) are realized as variability maps which,
for each model element, store whether it may be mo-
dified by the corresponding operation call or not. By
combining several of these maps for different sets of
frame conditions, the required constraints for analy-
zing equivalence or independence can be generated in
a convenient, automatic fashion.
We successfully employed this implementation
for the automatic analysis of the objectives introdu-
ced above. In fact, the whole analysis presented in
Examples 2 (consistency), 3 (equivalence), and 4 (in-
dependence) could be performed automatically and
the absence or existence of corresponding execution
scenarios could be proven formally. This is especially
remarkable for the equivalence of the frame conditi-
ons provided in Figs. 3, 4 and 6 (cf. Example 3) as the
required proof for the absence of a counterexample is
very elaborate (if not completely infeasible) to be con-
ducted manually. Using the deductive power and effi-
ciency of established reasoning approaches certainly
helped here.
Besides the analysis presented in those examples,
the presented methodology offers a large potential for
further applications:
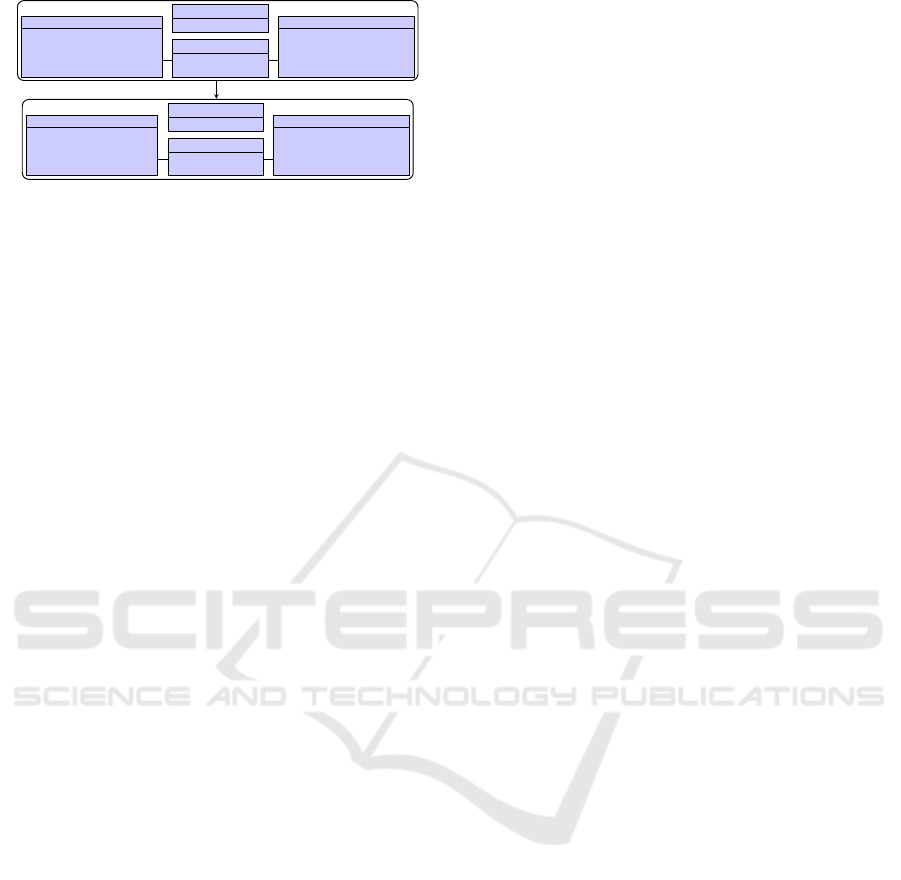
• The employed reasoning approach allows to use
pivot scenarios that are only partially specified,
i. e., values of model elements can be left open
and will be assigned by the solver if, and only if,
there is a possible assignment that belongs to a
valid scenario.
For instance, Figure 13 shows a pivot scenarios
where only a few attribute values are actually spe-
cified, while the majority is not specified (indica-
ted by a “?”). For the corresponding variables, the
solver determines a satisfying assignment (shown
in blue color) which extends the partially specified
scenario to a completely specified scenario that is
valid and compatible with the given frame condi-
tions.
• Frame conditions can be evaluated for aspects like
completeness or minimality, i. e., whether they
precisely describe the intended frame of change
and whether this is done in a somehow optimal
fashion.
For instance, if one considers the frame conditions
specified in Fig. 4 and drops either of the first two
modifies only statements (Line 4 or 5), one obtains
Analyzing Frame Conditions in UML/OCL Models - Consistency Equivalence and Independence
149
B1:Building
authorized = {1}
inside =
/
0
T1:Turnstile
greenLightOn = false
redLightOn = true
currentlyAuthorized = ? (17)
entry = true
T2:Turnstile
greenLightOn = ? (true)
redLightOn = ? (false)
currentlyAuthorized = ? (3)
entry = ? (false)
M1:MagneticCard
id = ? (1)
B1:Building
authorized = {1}
inside =
/
0
T1:Turnstile
greenLightOn = true
redLightOn = ? (false)
currentlyAuthorized = ? 1
entry = ? (true)
T2:Turnstile
greenLightOn = ? (true)
redLightOn = ? (false)
currentlyAuthorized = ? (3)
entry = ? (false)
M1:MagneticCard
id = ? (1)
T1.checkCard(M1)
Figure 13: Partially specified pivot scenario.
frame conditions that are incompatible with any
scenario in which the performed checks succeed
and access is granted. Dropping the third sta-
tement (Line 6) makes it impossible to store the
card’s ID in case of success. Overall, this shows
that the initial set of frame conditions is already
minimal. A similar methodology using consis-
tency and equivalence checks can be applied on
any model.
• The methods can be used to evaluate the proposals
for frame conditions that are automatically gene-
rated from a given model using solutions as pro-
posed in Niemann et al. (2015b).
For instance, for the operation goThrough()
the approach from Niemann et al. (2015b)
suggests to consider the model elements
self.greenLightOn and building.inside
as affected (with high probability) and to
have a more thorough look at self.entry,
self.currentlyAuthorized, and
self.redLightOn (which also occur in the
postconditions or may have a dependency via
invariants, respectively).
Including all mentioned model elements in the
frame of change (e.g., using corresponding modi-
fies only statements) yields consistent frame con-
ditions, but allows for much more changes than
intended by the designer. Consequently, the im-
pact of the individual statements, e.g., on the va-
lidity of pivot scenarios, needs to be analyzed and
unnecessary statements have to be dropped.
Overall, the proposed method allows for an effi-
cient, automatic analysis of frame conditions with re-
spect to the three primary analysis objectives of con-
sistency, equivalence and independence, and also pro-
vides potential for a variety of further applications
beyond that.
7 CONCLUSIONS
In this work, we considered the analysis of frame con-
ditions in UML/OCL models. While several propo-
sals and formalisms for specifying frame conditions
exist, it remains non-trivial to define them properly.
In fact, no corresponding methods or tools have been
developed so far which can guarantee that the deri-
ved frame conditions indeed complete the model des-
cription in the intended way. We addressed this gap
by proposing a set of analysis objectives (consistency,
equivalence, and independence) together with a for-
mulation that allows for performing corresponding
analyses using automated reasoning engines. More-
over, we implemented the proposed concepts on top
of an established approach for model validation and
verification. By this, a method and also a correspon-
ding tool becomes available that allows for the dedi-
cated analysis of frame conditions with a similar per-
formance as many established approaches for the va-
lidation and verification of UML/OCL models in ge-
neral. More precisely, the method benefits from the
same deductive power of automatic reasoning engi-
nes as well as the same efficiency and scalability, but
now additionally targets frame conditions rather than
pure UML/OCL descriptions only.
ACKNOWLEDGMENTS
This work was supported by the German Federal Mi-
nistry of Education and Research (BMBF) within the
project SELFIE under grant no. 01IW16001 and the
German Research Foundation (DFG) within the Rein-
hart Koselleck project under grant no. DR287/23-1.
REFERENCES
Ahrendt, W., Baar, T., Beckert, B., Bubel, R., Giese, M.,
Hähnle, R., Menzel, W., Mostowski, W., Roth, A.,
Schlager, S., and Schmitt, P. H. (2005). The KeY tool.
Software and System Modeling, 4(1):32–54.
Anastasakis, K., Bordbar, B., Georg, G., and Ray, I. (2007).
UML2Alloy: A challenging model transformation. In
MoDELS, pages 436–450. Springer.
Beckert, B. and Schmitt, P. H. (2003). Program verification
using change information. In SEFM, page 91.
Borgida, A., Mylopoulos, J., and Reiter, R. (1995). On
the Frame Problem in Procedure Specifications. IEEE
Trans. Software Eng., pages 785–798.
Brucker, A. D., Tuong, F., and Wolff, B. (2014). Feather-
weight OCL: A Proposal for a Machine-Checked For-
mal Semantics for OCL 2.5. Archive of Formal Proofs.
Brucker, A. D. and Wolff, B. (2008). HOL-OCL: A formal
proof environment for UML/OCL. In FASE, pages
97–100.
Cabot, J. (2006). Ambiguity issues in OCL postconditions.
In OCL Workshop, pages 194–204.
MODELSWARD 2018 - 6th International Conference on Model-Driven Engineering and Software Development
150

Cabot, J. (2007). From Declarative to Imperative
UML/OCL Operation Specifications. In Conceptual
Modeling, pages 198–213.
Cabot, J., Clarisó, R., and Riera, D. (2008). Verification
of UML/OCL Class Diagrams using Constraint Pro-
gramming. In ICST, pages 73–80.
Cabot, J., Clarisó, R., and Riera, D. (2009). Verifying
UML/OCL Operation Contracts. In Integrated For-
mal Methods, pages 40–55.
Choppy, C., Klai, K., and Zidani, H. (2011). Formal Ve-
rification of UML State Diagrams: A Petri Net based
Approach. Softw. Eng. Notes, 36(1):1–8.
de Dios, M. A. G., Dania, C., Basin, D. A., and Clavel, M.
(2014). Model-driven development of a secure ehe-
alth application. In Engineering Secure Future Inter-
net Services and Systems - Current Research, pages
97–118.
De Moura, L. and Bjørner, N. (2008). Z3: An Efficient
SMT Solver. In TACAS, pages 337–340.
Demuth, B. and Wilke, C. (2009). Model and Object Veri-
fication by Using Dresden OCL. In IIT-TP, page 81.
Technical University.
Gogolla, M., Büttner, F., and Richters, M. (2007). USE: A
UML-based specification environment for validating
UML and OCL. Science of Computer Programming,
69(1-3):27–34.
Gogolla, M., Kuhlmann, M., and Hamann, L. (2009). Con-
sistency, Independence and Consequences in UML
and OCL Models. In TAP, pages 90–104.
Hilken, F., Niemann, P., Gogolla, M., and Wille, R. (2014).
Filmstripping and unrolling: A comparison of verifi-
cation approaches for UML and OCL behavioral mo-
dels. In TAP, pages 99–116.
Kosiuczenko, P. (2006). Specification of Invariability in
OCL. In MoDELS, pages 676–691.
Kosiuczenko, P. (2013). Specification of invariability in
OCL - Specifying invariable system parts and views.
Software and System Modeling, 12(2):415–434.
Leino, K. R. M. (2008). This is Boogie 2. Technical report.
Meyer, B. (1992). Applying design by contract. IEEE Com-
puter, 25(10):40–51.
Niemann, P., Hilken, F., Gogolla, M., and Wille, R. (2015a).
Assisted Generation of Frame Conditions for Formal
Models. In DATE, pages 309–312.
Niemann, P., Hilken, F., Gogolla, M., and Wille, R. (2015b).
Extracting frame conditions from operation contracts.
In MoDELS, pages 266–275.
OMG – Object Management Group (2014). Object Con-
straint Language. Version 2.4, February 2014.
Przigoda, N., Filho, J. G., Niemann, P., Wille, R., and
Drechsler, R. (2016a). Frame conditions in symbo-
lic representations of UML/OCL models. In MEMO-
CODE, pages 65–70.
Przigoda, N., Hilken, C., Wille, R., Peleska, J., and Dre-
chsler, R. (2015a). Checking concurrent behavior in
UML/OCL models. In MoDELS, pages 176–185.
Przigoda, N., Soeken, M., Wille, R., and Drechsler, R.
(2016b). Verifying the Structure and Behavior in
UML/OCL Models Using Satisfiability Solvers. IET
Cyber-Physical Systems: Theory & Applications,
1(1):49–59.
Przigoda, N., Stoppe, J., Seiter, J., Wille, R., and Dre-
chsler, R. (2015b). Verification-driven design across
abstraction levels: A case study. In DSD, pages 375–
382. IEEE Computer Society.
Rumbaugh, J., Jacobson, I., and Booch, G., editors (1999).
The Unified Modeling Language reference manual.
Addison-Wesley Longman Ltd., Essex, UK.
Soeken, M., Wille, R., and Drechsler, R. (2011). Verifying
Dynamic Aspects of UML models. In DATE, pages
1077–1082.
Analyzing Frame Conditions in UML/OCL Models - Consistency Equivalence and Independence
151
