
Static Analysis of Conformance Preserving Model Transformation Rules
Fazle Rabbi, Lars Michael Kristensen and Yngve Lamo
Western Norway University of Applied Sciences, Bergen, Norway
Keywords:
Formal Methods for Model Driven Software Engineering, Formal Correctness of Model Transformations,
Meta-modelling, Domain-specific Modeling Languages.
Abstract:
Model transformation is a core element in model driven software engineering and is used for several purposes,
including model migration, model synthesis, and code generation. Application of conformance preserving
transformation rules guarantee that produced output models will conform to its underlying metamodel. Con-
formance persevering rules are therefore important in order to ensure the formal correctness of transforma-
tions. However, to determine if a rule is conformance preserving requires sophisticated analysis techniques.
The contribution of this paper is a new algorithm for checking conformance preserving rules with respect to a
set of graph constraints and to prove the soundness of the algorithm. We apply our technique to homogeneous
model transformations where input and output models must conform to the same meta-model. The algorithm
relies on locality of a constrained graph to reduce the computational cost. We show that the performance of
our algorithm depends on the complexity of the graph constraints and model transformation rules, but that it
is independent of the size of the input model.
1 INTRODUCTION
Model transformation is the process of transforming
a model into another model and plays a key role in
model driven software development. A transforma-
tion rule describes how a target model can be au-
tomatically generated from a source model. Often
these models need to conform to the syntax and se-
mantics of a metamodel. There are various applica-
tions of model transformations such as model migra-
tion, model synthesis, code generation, model sim-
ulation, model execution, and model repair. Formal
development of transformation rules is an important
concern since precisely defined rules can be used to
verify that the automated transformations are correct
(Varr
´
o et al., 2002). Graph transformation is a formal
technique to represent model transformation rules en-
abling reasoning and studying properties of transfor-
mation systems. Depending on the source and target
language, a transformation can be homogeneous or
heterogeneous. In homogeneous model transforma-
tion, input models and output models belong to the
same language. Heterogeneous model transformation
transforms models from one language to another. In
general, the result of the application of a model trans-
formation rule may lead to inconsistency, i.e., the tar-
get model violating constraints defined in its meta-
model. Therefore, the application of a model transfor-
mation rule requires conformance checking of the tar-
get model which is time consuming. To address this
problem, it is of interest to develop techniques to re-
duce the complexity of conformance checking. Since
the application of a conformance preserving transfor-
mation rule preserves the conformance of a model, it
eliminates the need for conformance checking of tar-
get models. This approach is particularly suited for
the development of systems where models produced
in every step of a model transformation are supposed
to be valid i.e., conforming w.r.t a set of constraints.
Current verification approaches for model trans-
formation rules include theorem proving and model
checking. Simone et al. proposed a relational and
logical approach to graph grammars that allow the
analysis of asynchronous distributed systems with in-
finite state spaces (da Costa and Ribeiro, 2012). They
used relational structures to define graph grammars
and first-order logic to model graph transformations.
They provided a semi-automated process to prove
structural properties of reachable graphs using theo-
rem proving. Another theorem proving technique was
presented in (Ribeiro et al., 2010) based on translat-
ing graph grammars into Event-B specifications pre-
serving its semantics and then using theorem provers
available for Event-B for analysis. Automatic veri-
fication of model transformation is gaining popular-
ity and several methods have already been proposed.
152
Rabbi, F., Kristensen, L. and Lamo, Y.
Static Analysis of Conformance Preserving Model Transformation Rules.
DOI: 10.5220/0006602601520162
In Proceedings of the 6th International Conference on Model-Driven Engineering and Software Development (MODELSWARD 2018), pages 152-162
ISBN: 978-989-758-283-7
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Baresi et al. (Baresi and Spoletini, 2006) proposed
a methodology to analyze graph transformation sys-
tems by means of Alloy. Given an initial graph of a
system, the method can be used to check the config-
urations that can be obtained by applying a sequence
of transformation rules. In (Wang et al., 2014), Wang
et al. investigated the use of the Alloy analyzer for
analyzing model transformation systems. A bounded
verification approach was used to check if a model
transformation system is correct w.r.t conformance by
translating a metamodel specification into a relational
logic specification in Alloy. The authors in (Troya
and Vallecillo, 2010) presented a formal semantics of
the ATL model transformation language using rewrit-
ing logic and Maude. Through the formalization it
was possible to simulate and verify model transforma-
tions. Although model checking is an elegant analysis
method, it requires building the complete state space.
This can easily lead to the state explosion problem
thereby limiting its practical applicability. Hackel and
Wagner (Heckel and Wagner, 1995) presented an ap-
proach that ensures the conformance of graph trans-
formations by automatically adding application con-
ditions to rules. Application conditions are derived
by analyzing the constraints individually which can
produce an unnecessary large number of application
conditions.
In our approach, we use characteristics of model
transformation rules and present an algorithm to
check if a transformation rule is conformance pre-
serving w.r.t a given set of constraints. We focus on
homogeneous model transformation. We do not au-
tomatically modify a rule. We provide an algorithm
for checking the conformance preserving property of
a transformation rule that can be used to provide feed-
back to the modeler. The approach is illustrated by an
example from the healthcare domain.
The rest of the paper is organized as follows. Sec-
tion 2 provides background on the theoretical founda-
tion of our approach. Section 3 presents the concept
of conformance preserving rules. Section 4 presents
our algorithm for checking conformance preserving
rules. Section 5 contains a further discussion of re-
lated work, and Section 6 concludes the paper with
directions for future work. We assume that the reader
is familiar with graph transformation systems (Ehrig
et al., 2006).
2 MODELLING SPECIFICATION
IN DPF
We use Diagrammatic Logic (Diskin and Wolter,
2008) and the Diagram Predicate Framework (DPF)
(Rutle, 2010) for the formal development of meta-
model specifications. In DPF, a model is represented
by a diagrammatic specification S = (S,C
S
: Σ) con-
sisting of an underlying graph S together with a set of
atomic constraints C
S
specified by a predicate sig-
nature Σ. A predicate signature consists of a collec-
tion of predicates, each having a name, an arity (shape
graph, α
Σ
(p)), visualization and semantic interpreta-
tion (see Table 1). The underlying graph and arity of
predicates specify type graphs with a data algebra as
in (Ehrig et al., 2006). A predicate is used to spec-
ify a constraint in a model by means of graph homo-
morphisms. DPF provides a general mechanism of
diagrammatic modeling as it supports various kinds
of graph structures. DPF provides a formalization
of multi level meta-modelling by defining the confor-
mance relation between models at adjacent levels of a
meta-modelling hierarchy. DPF has a potentially un-
bounded number of metalevels.
Table 1: Predicates of a signature, Σ.
p Arity Visualization Semantic interpretation
f must have at least n and
at most m instances for
each instance of X
For each instance of f there
exists an instance of g with the
same source node
For each composition of
instances f;g, there exists an
instance of h such that h = f;g
If there are instances of f and g
with the same source node,
then value of Y is less than value
of Z
Instances of f never maps
distinct elements of its domain
to the same element of its
codomain
<mult(n,m)>
<pre-
Condition>
<composite>
<precede>
1
1 2
1 2
3
1
2
3
f
g
h
f
g
f
h
X Y
Z
f
g
X Y
Z
f
g
[pCond]
X
f
Y
[n..m]
[comp]
X Y
Z
f
g
[prcd]
3
f
g
2
1 2
f
X
f
Y
[inj]
<injective>
α (p)
∑
There are two kinds of conformance: typed by and
satisfaction of constraints. Figure 1 (top) shows a
DPF metamodel specification S of an Orthopedic de-
partment of a hospital. The metamodel specification
is constrained by a set of predicates from the signature
Σ. Constraints are added into the specifications by
graph homomorphisms from the arity (shape graph)
of the predicates to the model elements. Below is a
list of constraints specified in S:
• C1. A patient must have exactly one birthdate
(specified by <mult(1,1)>)
• C2. An appointment time-slot (i.e., TS@Dept)
allocated to a patient must belong to that patient’s
assigned doctor (specified by <composite>)
• C3. An imaging order can only be given to a
Static Analysis of Conformance Preserving Model Transformation Rules
153
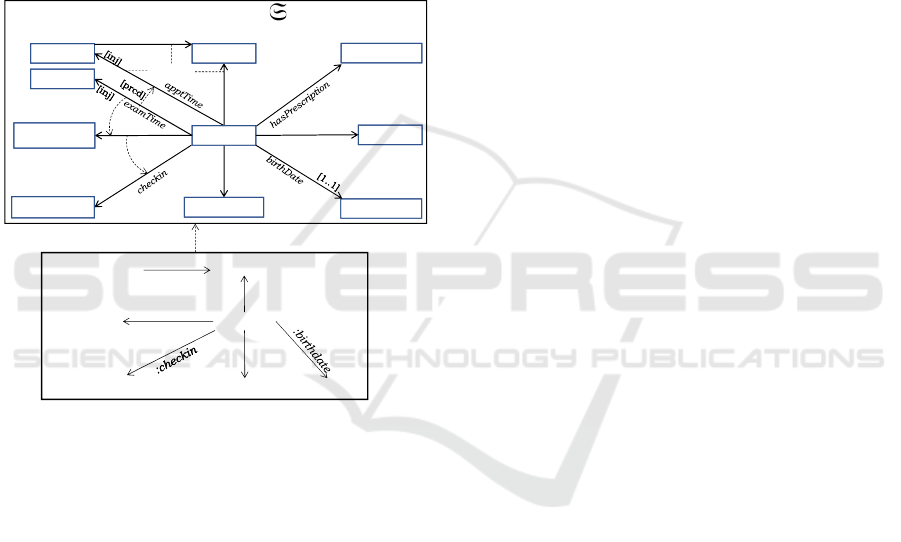
registered patient (specified by <pre-Condition>)
• C4. An exam time-slot (i.e., TS@Lab) can only
be allocated to a patient with an imaging order
(specified by <pre-Condition>)
• C5. An appointment time-slot cannot be al-
located to more than one patient (specified by
<injective>)
• C6. An exam time-slot cannot be allocated to
more than one patient (specified by <injective>)
• C7. Patient’s exam time-slot must be pre-
ceded by the appointment time-slot (specified by
<precede>)
TS@DeptTS@Dept
assigned
Doctor
assigned
Doctor
belongsTobelongsTo
hasOrderhasOrder
admittedToadmittedTo
DoctorDoctor
PatientPatient
DeptDeptRegistrationRegistration
Imaging
Exam
Imaging
Exam
[comp][comp]
PrescriptionPrescription
ReportReport
examReportexamReport
DateDate
[pCond][pCond]
[pCond][pCond]
TS@LabTS@Lab
Typing, lTyping, l
:assigned
Doctor
:assigned
Doctor
:belongsTo:belongsTo
Dr. LoganDr. Logan
0950-1010
@Logan
0950-1010
@Logan
:hasOrder:hasOrder
:admittedTo:admittedTo
BarbaraBarbara
OrthopedicsOrthopedics
:Registration:Registration
:Imaging
Exam
:Imaging
Exam
02.11.199102.11.1991
Instance, (I, )Instance, (I, )
II
II
ll
Metamodel specification, Metamodel specification,
II
Figure 1: Metamodel specification S (top) of an Orthopedic
department and an instance of S (bottom).
Usually orthopedic doctors need to see patient’s
X-ray reports while seeing patients. Therefore or-
thopedic patient’s time-slot for the imaging exam
must be preceded by the appointment time-slot. Fig-
ure 1(bottom) shows an instance (I, ι
I
) of the meta-
model specification S. In the instance (I, ι
I
), Barbara
is a patient admitted to the Orthopedic department;
she is a registered patient and assigned to Dr. Logan;
an order for radiology exam has been given for
Barbara. (I, ι
I
) is also referred to as a model of S and
it is typed by S. Formally, this means that there is a
graph homomorphism from the graph I to the graph
of S, denoted as I : S where S is the underlying graph
of S. We use a compact notation for typed attributed
graph where data nodes are used for the inscription
of graph nodes as depicted in the model (I,ι
I
) in Fig-
ure 1.
2.1 Coupled Graph Constraints
The semantics of a DPF predicate can be specified in
various ways. In this paper, we use graph constraints
to specify the semantics of the predicates. Typically a
graph constraint N
n
←− L
u
−→ R consist of three graphs:
left L, right R and an application condition N (positive
or negative application condition) , and two injective
graph homomorphisms n and u where the graphs are
typed by the underlying graph of the model (Ehrig
et al., 2006). We propose to use graph constraints
which conforms to two syntactic formats ∀L
p
→ ∃R
p
and ∀L
p
→ ¬∃R
p
where the graphs are typed by the
shape graph of the predicates. Therefore we use graph
constraints of the following forms where superscript p
indicates that the constraint is giving the semantics of
a DPF predicate, p. The graph constraints are called
coupled graph constraints as they link to predicates.
• ∀(L
p
: α
Σ
(p)) → ∃(R
p
: α
Σ
(p)), read as “for all
matches of the condition pattern L
p
(typed by
α
Σ
(p)) in a model, there exists a match of the re-
quired pattern R
p
(typed by α
Σ
(p)) in the model”
• ∀(L
p
: α
Σ
(p)) → ¬∃(R
p
: α
Σ
(p)), read as “for
all matches of the condition pattern L
p
(typed by
α
Σ
(p)) in a model, there does not exist a match of
the forbidden pattern R
p
(typed by α
Σ
(p)) in the
model”
Here L
p
and R
p
are typed attributed graphs over
the arity of the predicate p and there exists an inclu-
sion attributed graph morphism m
c
: L
p
→ R
p
. A cou-
pled graph constraint gc may have a post-condition
PC(gc) imposed on R
p
. Table 2 shows the seman-
tics of predicates from signature Σ in terms of graph
constraints. The semantic of the <mult(1,1)> predi-
cate is given by two graph constraints where the pat-
terns are typed by α
Σ
(<mult(1,1)>), i.e., the arity of
the <mult(1,1)> predicate. The graph constraint giv-
ing semantic to the <precede> predicate has a post-
condition which ensures that the time specified in y
must precede the time specified in z.
Let gc ∈ GC(p) be a graph constraint linked to a
predicate p. A match (δ,m
L
) of the condition pattern
(L
p
: α
Σ
(p)) for the graph constraint gc in a model
(I, ι
I
) is given by an atomic constraint δ : α
Σ
(p) → S
and an injective morphism m
L
such that constraint δ
and the injective graph homomorphism m
L
together
with the typing morphisms ι
c
: (L
p
∪R
p
) → α
Σ
(p) and
ι
I
: I → S constitute a commuting square: ι
c
;δ = m
L
;ι
I
as shown in Figure 2(a). If gc has a required pattern
(R
p
: α
Σ
(p)), then for any match (δ,m
L
) of the condi-
tion pattern in (I,ι
I
), a match (δ, m
R
) of the required
pattern must exist, which is given by the commuting
diagram in Figure 2(b). If gc has a forbidden pat-
tern (R
p
: α
Σ
(p)), then for any match (δ,m
L
) of the
MODELSWARD 2018 - 6th International Conference on Model-Driven Engineering and Software Development
154
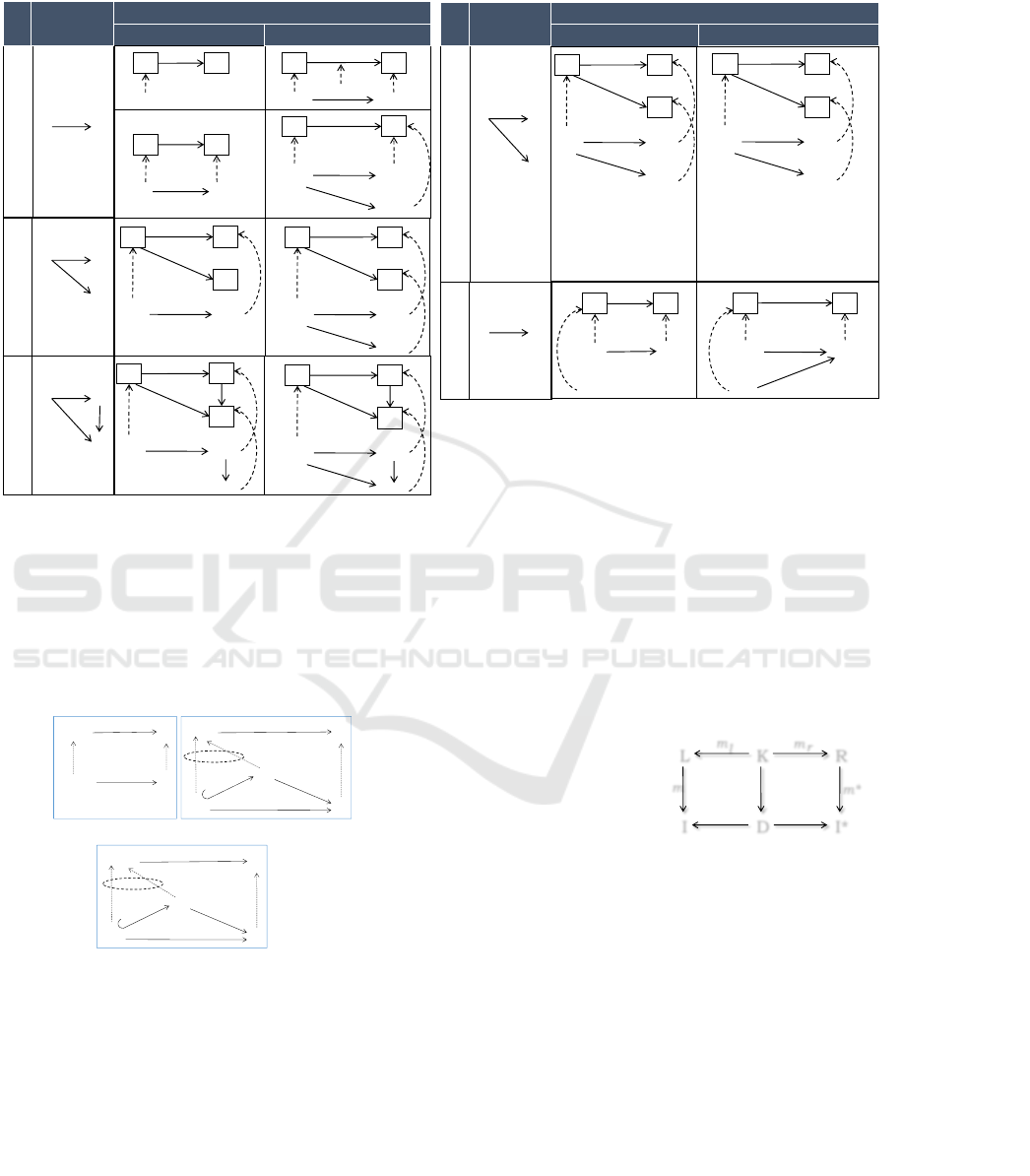
Table 2: A set of graph constraints giving semantics to the predicates in Σ.
p Arity Semantic in Graph Constraint
<mult
(1,1)>
X Y
f
<injective>
X Y
f
L :
p
R :
p
α (p)
∑
x
x
y
¬
e
1
X
Y
f
X
Y
f
x
y
x
y
X
Y
f
X
Y
f
e
1
z
x
y
x
y
X
Y
f
X
Y
f
z
¬
z
α (p)
∑
<pre
-Condition
>
X Y
f
f
x
y
X
Y
z
Z
g
f
x
y
e : f
1
X
Y
Z
g
Z
<composite>
X Y
f
f
x
y
X
Y
z
Z
h
Z
h
g
g
g
e : f
1
e : g
2
e : f
1
e : f
2
e :f
1
e :h
3
e :g
2
f
x
y
X
Y
z
Z
h
g
e :f
1
e :g
2
e : f
1
e : f
2
e : f
1
p Arity Semantic in Graph Constraint
<precede>
L :
p
R :
p
α (p)
∑
α (p)
∑
α (p)
∑
α (p)
∑
X Y
f
Z
g
f
x
y
X
Y
z
Z
g
e :f
1
e :g
2
f
x
y
X
Y
z
Z
g
e :f
1
e :g
2
Post Condition :
`startTime(y) < startTime(z)
ᴧ
endTime(y) < endTime(z)’
condition pattern in (I,ι
I
), a match (δ,m
R
) of the for-
bidden pattern must not exist such that it constitutes
a commuting diagram as shown in Figure 2(c). A
valid model is typed by its metamodel specification
and conforms to the constraints specified in its meta-
model specification. Formally, it states that a valid
model (I,ι
I
) satisfies all the constraints defined in S,
which is written as I |= S.
αα
(p)(p)
∑∑
α
(p)
∑
δδ
ll
LL
pp
cc
SS
ll
II
II
mm
LL
==
αα
(p)(p)
∑∑
α
(p)
∑
δδ
RR
pp
SS
ll
II
II
mm
RR
==
ll
LL
pp
cc
==
(a)(a)
(b)(b)
(c)(c)
mm
LL
mm
cc
δδ
RR
pp
SS
ll
II
II
mm
RR
==
ll
LL
pp
cc
≠≠
mm
LL
mm
cc
αα
(p)(p)
∑∑
α
(p)
∑
Figure 2: (a) match of a condition pattern ; (b) match of a
required pattern; (c) satisfaction of a forbidden pattern.
3 CONFORMANCE PRESERVING
RULES
DPF provides functionality to specify graph-based
model transformations (Rutle et al., 2012). We use
the standard double-pushout (DPO) approach (Ehrig
et al., 2006) for defining transformation rules. A
model transformation rule (r : N
n
←− L
m
l
←− K
m
r
−→ R) has
a matching pattern (L), a gluing graph (K), a replace-
ment pattern (R) and an optional negative application
condition, NAC(n : L → N) where L, K, R, N are typed
by S and m
l
, m
r
, n are injective graph morphisms. We
use a transformation approach where transformation
rules have a set of negative application conditions as
proposed by Lambers et al., in (Lambers et al., 2008).
L
m
K R
I D I*
m*
m
l
m
r
Given a model
(I, ι
I
), a model
transformation
I
r,m
=⇒ I
∗
via a
transformation rule
r : L ← K → R with a set of negative application
conditions NAC
r
and a match m : L → I consists of
the double pushout as shown in the diagram above.
Here, the injective morphism m satisfies each NAC
in NAC
r
, written m |= NAC
r
. When a rule is applied,
some elements from the source model are deleted
and some elements are added to the target model.
The rest of the source model remain unchanged in
the target model. A rule is applied as long as it
satisfies its negative application conditions. Negative
application conditions are typically used in graph
transformation to prohibit an infinite number of rule
applications. Figure 3 shows a model transformation
rule for allocating resources (i.e., appointment
time-slot, exam time-slot) to patients in a model
of the metamodel specification from Figure 1. We
Static Analysis of Conformance Preserving Model Transformation Rules
155
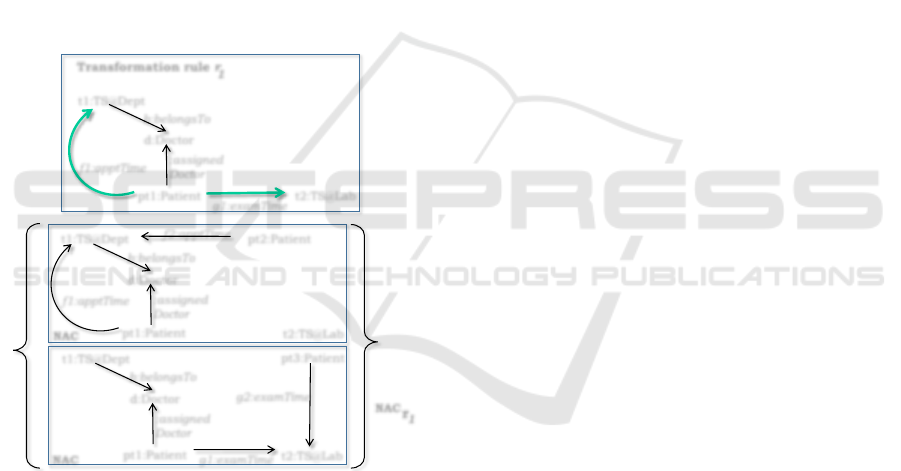
use the concept of ‘time-slot’ for an appointment or
an examination to represent the time assigned for a
scheduled appointment. The transformation rule r
1
encodes the following instructions:
• Allocate appointment time-slot t
1
and exam time-
slot t
2
to patient pt
1
if t
1
belongs to the doctor
whom pt
1
is assigned to and satisfies the follow-
ing conditions:
– Allocate t
1
to pt
1
if t
1
is not allocated to any
other patient pt
2
;
– Allocate t
2
to pt
1
if t
2
is not allocated to any
other patient pt
3
;
The typing information of a modelling element in
r
1
appears after a colon (:). The green color (thick
arrow) is used to represent elements that the rule is
going to produce. The rule r
1
has two negative ap-
plication conditions to make sure that the patients are
assigned using available resources.
pt1:Patient
t1:TS@Dept
pt2:Patient
f2:apptTime
pt1:Patient
t2:TS@Lab
f1:apptTime
b:belongsTo
t1:TS@Dept
g1:examTime
d:Doctor
:assigned
Doctor
f1:apptTime
g1:examTime
pt1:Patient
t2:TS@Lab
pt3:Patient
g2:examTime
Transformation rule r
1
NAC
NAC
NAC
r
1
b:belongsTo
d:Doctor
:assigned
Doctor
b:belongsTo
d:Doctor
:assigned
Doctor
t1:TS@Dept
t2:TS@Lab
Figure 3: Transformation rule r
1
for individual resource al-
location of patients.
One problem with this version of the transforma-
tion rule is that it does not guarantee the conformance
of constraint C4 (an imaging order must be given for
a patient before exam time-slots). The application of
the rule may allocate a radiology exam time-slot to a
patient who does not have an imaging order. Also the
rule does not guarantee the conformance of constraint
C7 (Patient’s exam time-slot must be preceded by the
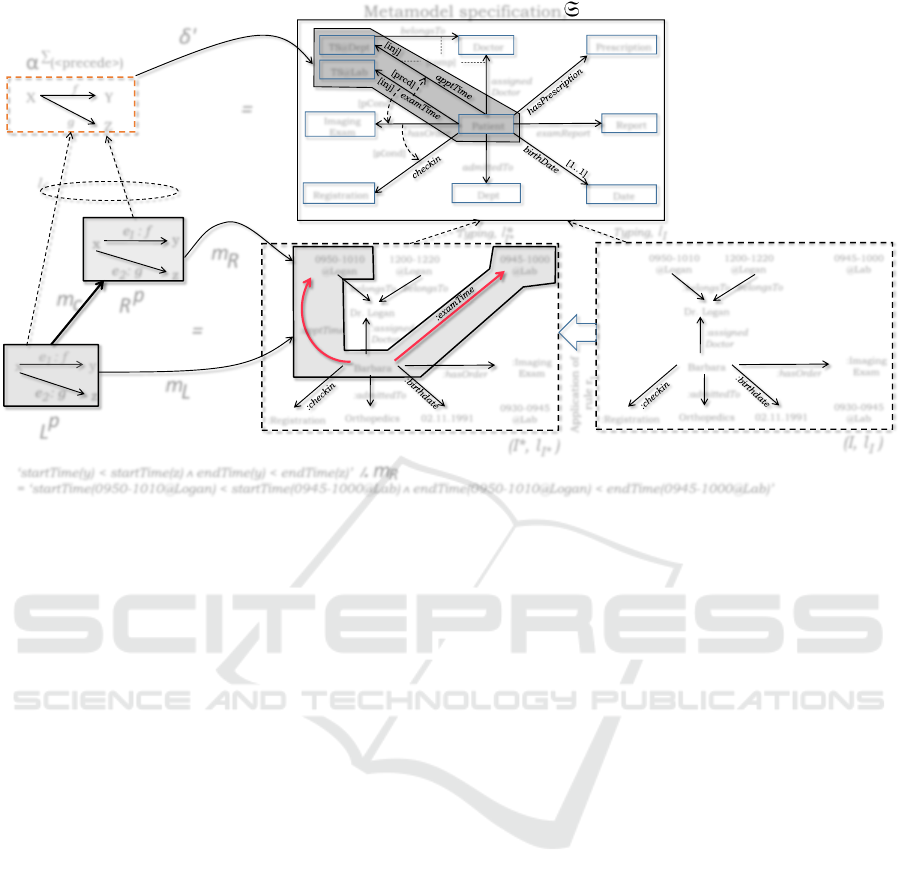
appointment time-slot). To illustrate this, Figure 4
shows a model (I,ι
I
) of S. The rule r
1
of Figure 3
can be applied over (I,ι
I
) in four different ways since
there are four matches. (I
∗
,ι
I
∗
) in Figure 4 shows a
result of the application of rule r
1
giving a resource
allocation where Barbara is assigned the exam time-
slot 0945 − 1000@Lab at the radiology department
and the appointment time-slot 0950 − 1010@Logan
at the orthopedics department with Dr. Logan. Here
(I
∗
,ι
I
∗
) is not conforming to the constraint expressed
by the <precede> predicate. A time-slot t2 which in-
clude information about the start-time and end-time
of a scheduled appointment is preceded by a time-slot
t1 if the start-time and end-time of t2 are less than the
start-time and end-time of t1, respectively. The start-
Time and endTime are two time-functions that specify
the start-time and end-time of an appointment time-
slot. To check if a model conforms to a graph con-
straint which has a post-condition, we use a replace-
ment operator /. (pronounced “slash-dot”) that re-
places the variables of an expression with the image of
a match. Figure 4 illustrates how we check the satis-
faction of the atomic constraint (<precede>,δ
1
) over
model (I
∗
,ι
I
∗
) by its graph constraint. The graph con-
straint used to give the semantics of the <precede>
predicate has a post-condition given by an expres-
sion. To check if the post-condition is satisfied, the
variables of the expression are replaced with elements
from (I
∗
,ι
I
∗
) via a match m
R
: R
p
→ I
∗
. This resource
distribution is not valid as (I
∗
,ι
I
∗
) is not conforming
to the resource constraint C7: Barbara’s exam time-
slot 0945 − 1000@Lab must be preceded by her ap-
pointment time-slot 0950− 1010@Logan. Even if the
rule is applied on a valid model, it does not guaran-
tee that the result will be a valid model conforming
to the metamodel specification. The portion of the
model that is not conforming to the constraints are
highlighted in red (thick arrow) in the figure.
The rule r
1
can be enhanced so that while match-
ing with a model it makes sure that the result will be
a valid model. Since the addition of new instances of
examTime and apptTime in a valid model of S can
possibly violate atomic constraints C2, C4, C5, C6
and C7, we enhance rule r
1
with an additional match-
ing condition to make sure that when applied on a
valid model of S, the addition of new elements does
not violate any of the above mentioned constraints.
The enhanced rule is equipped with an additional
matching condition: ‘startTime(t2) < startTime(t1)
∧ endTime(t2) < endTime(t1)’ which makes sure
that the constraint C7 is not violated. Therefore the
application of the enhanced rule will not require any
further conformance checking. Formally, the appli-
cation of a transformation rule that is equipped with
a set of additional matching conditions is defined be-
low:
Definition 1 (. Application of Transformation Rule)
Let (I, ι) be a model of a metamodel specification
S = (S,C
S
) and r : L ← K → R a rule with a set
MODELSWARD 2018 - 6th International Conference on Model-Driven Engineering and Software Development
156
Metamodel specification,
Typing, l*
X Y
f
α
(<precede>)
∑
δ'
l
m
TS@Dept
assigned
Doctor
belongsTo
hasOrder
admittedTo
Doctor
Patient
DeptRegistration
Imaging
Exam
[comp]
Prescription
Report
examReport
Date
[pCond]
[pCond]
TS@Lab
Z
g
x
y
z
x
y
e : f
1
e : f
1
e : g
2
L
L
p
R
p
m
R
=
I*
m
c
:assigned
Doctor
:belongsTo
:hasOrder
:admittedTo
Dr. Logan
Barbara
Orthopedics
:Registration
:Imaging
Exam
02.11.1991
0945-1000
@Lab
0930-0945
@Lab
0950-1010
@Logan
1200-1220
@Logan
:belongsTo
:apptTime
(I*, l )
I*
e : g
2
z
‘startTime(y) < startTime(z) ᴧ endTime(y) < endTime(z)’
/.
= ‘startTime(0950-1010@Logan) < startTime(0945-1000@Lab) ᴧ endTime(0950-1010@Logan) < endTime(0945-1000@Lab)’
m
R
=
c
:assigned
Doctor
:belongsTo
:hasOrder
:admittedTo
Dr. Logan
Barbara
Orthopedics
:Registration
:Imaging
Exam
02.11.1991
0945-1000
@Lab
0930-0945
@Lab
0950-1010
@Logan
1200-1220
@Logan
:belongsTo
(I, l )
I
Typing, l
I
Application of
rule r
1
Figure 4: Application of rule r
1
over a valid model (I,ι
I
) and the checking for the satisfaction of a graph constraint.
of negative application conditions NAC
r
and a set of
additional matching conditions MC
r
. The rule r is ap-
plicable on (I,ι) if there exists a match m : L → I that
constitute a double pushout diagram and the match
m satisfies all the negative application conditions and
additional matching conditions.
Definition 2 (. Conformance Preserving Rule) Given
a metamodel specification S = (S,C
S
: Σ). A trans-
formation rule r is conformance preserving w.r.t a set
of atomic constraints from C
S
if the application of
r on any valid model (I,ι
I
) |= S always results in a
valid model of S.
4 ANALYSIS FOR CHECKING
CONFORMANCE PRESERVING
RULES
In this section, we present an algorithm to automat-
ically check if a transformation rule is conformance
preserving w.r.t a set of constraints specified in a
metamodel. Automatic check of conformance pre-
serving rules requires that the constraints specified in
a metamodel is processed. To develop an efficient
method for determining if a rule is conformance pre-
serving or not, we need to analyze the possibility of
the rule to make changes that may violate a given con-
straint. If a rule makes changes to only the uncon-
strained portion of a graph, then we can claim that the
rule will preserve conformance by its application. If
a rule makes changes to the constrained portion of a
graph, it is possible that the rule will preserve confor-
mance by its application. We present an algorithm
with the aid of a set of patterns to make sure that
consistency preserving rules exhibit certain desirable
structures.
4.1 A Sufficient Condition for
Conformance
Here we present three conditions to determine if a
transformation rule r : L ← K → R can make changes
to the constrained portion of a graph i.e., if r can pos-
sibly affect an atomic constraint (p,δ):
• Cond 1: r creates an element x of type X where
X is constrained by a predicate p and X is mapped
by the condition pattern of a graph constraint
gc ∈ GC(p) via the typing morphism of L
p
and
the atomic constraint (p,δ), i.e., X ∈ ι
c
;δ(L
p
);
• Cond 2: r deletes an element y of type Y where Y
is constrained by a predicate p and Y is mapped
by the elements from (required pattern, R
p
\
condition pattern, L
p
) via the typing of (R
p
∪L
p
)
and the atomic constraint (p,δ), i.e., Y ∈ ι
c
;δ(R
p
\
L
p
);
• Cond 3: r creates an element x of type X where X
is constrained by a predicate p and X is mapped
by the elements from ( f orbidden pattern, R
p
\
Static Analysis of Conformance Preserving Model Transformation Rules
157

r is a transformation rule and
gc ∈ GC(p) is a graph constraint
If r creates an element x that
partially matches with the
condition pattern of gc
If r deletes an element y that partially
matches with the required pattern of gc
If r creates an element x that partially
matches with the forbidden pattern of gc
r has a NAC that forbids
the existence of a
condition pattern of gc
Otherwise, r is not
conformance preserving
r produces a match with
the condition pattern and
required pattern of gc
r has a NAC that forbids the existence of
a condition pattern of gc
Otherwise, r is not conformance
preserving
r removes a match with the required
pattern of gc; r also removes a match
with the condition pattern of gc
r removes an existing match of a
required pattern of gc but produces
another for replacement
r has a NAC that forbids the
existence of a forbidden
pattern of gc
If gc has a required pattern
i.e., gc is of the form Ɐ (L : α (p) )→ ꓱ (R : α (p) )
If gc has a forbidden pattern
i.e., gc is of the form Ɐ (L : α (p) )→ ¬ꓱ (R : α (p) )
Otherwise, r is not
conformance preserving
Either of
the following
Either of the following
Either of the following
∑
∑
p
p
∑
∑
p
p
Cond 1
Cond 2
Cond 3
P.C1#1
P.C1#2
P.C2#1
P.C2#2
P.C2#3
P.C3#1
Figure 5: Informal description of the algorithm illustrating the intuition.
condition pattern, L
p
) via the typing of (R
p
∪L
p
)
and the atomic constraint (p,δ), i.e., X ∈ ι
c
;δ(R
p
\
L
p
);
Intuitively, Cond 1, 2, and 3 checks if a rule can
create a new match with the condition pattern, delete
an existing match of a required pattern, or create a
new match with the forbidden pattern of a graph con-
straint, respectively.
Lemma 1. Given a metamodel specification S with
a set of constraints C
S
. A transformation rule r is
conformance preserving if it does not satisfy any of
Cond 1-3.
Proof. Let (I, ι) be a valid instance of S and the ap-
plication of r on (I,ι) produces an instance (I
∗
,ι
∗
).
There are three ways (I
∗
,ι
∗
) may violate a constraint
from C
S
: (i) r produces a new match with the condi-
tion pattern L
p
of a graph constraint where the corre-
sponding required pattern is missing; (ii) r deletes an
existing match of a required pattern; (iii) r produces
a new match with the forbidden pattern. However, it
can be seen that if r does not satisfy any of Cond 1-3,
then it does not affect any constraint from C
S
because
of the following reasons:
• r does not satisfy Cond 1; therefore, it does not
produce any new match with the condition pattern
L
p
of a graph constraint.
• r does not satisfy Cond 2; therefore, it does not
delete any existing match of a required pattern.
• r does not satisfy Cond 3; therefore, it does not
produce any new match with the forbidden pat-
terns.
4.2 Desired Patterns for Conformance
A rule r can be conformance preserving if it satisfies
some conditions from Cond 1-3 and complies with
desired patterns described below. Figure 5 illustrates
a diagram representing the intuition of the proposed
method where P.C1#1, P.C1#2,... indicates a pattern
number.
RR
rr
αα
(p)(p)
∑∑
α
(p)
∑
δδ
RR
pp
SS
ll
mm
RRRR
==
ll
LL
pp
cc
==
mm
LRLR
mm
cc
x
ϵ and
x
ϵ and
m ( )m ( )
LRLR
LL
pp
αα
(p)(p)
∑∑
α
(p)
∑
δδ
LL
pp
mm
LNLN
==
ll
cc
x
ϵ
, N ϵ NAC , y
ϵ
s.t. y
ϵ L and y ϵ R
x
ϵ
, N ϵ NAC , y
ϵ
s.t. y
ϵ L and y ϵ R
m ( )m ( )
LNLN
LL
pp
EE
m ( )m ( )
LNLN
LL
pp
P.C1#1P.C1#1
P.C1#2P.C1#2
rr
PC /. m
ϵ MC
PC /. m
ϵ MC
RRRRgcgc
rr
KK
LL
rr
SS
ll
KK
LL
RRNN
Figure 6: Patterns for a conformance preserving rule r that
satisfies Cond 1.
In our approach, if a rule satisfies Cond 1 for a
graph constraint gc, it has to comply with the patterns
specified in Figure 6. Patterns specified in the figure
makes sure that if the creation of an element produces
a new match with the condition pattern of a graph con-
straint, the required pattern must exist (P.C1#1); oth-
erwise a new match with the condition pattern is not
produced by the application of rule r (P.C1#2). Note
MODELSWARD 2018 - 6th International Conference on Model-Driven Engineering and Software Development
158
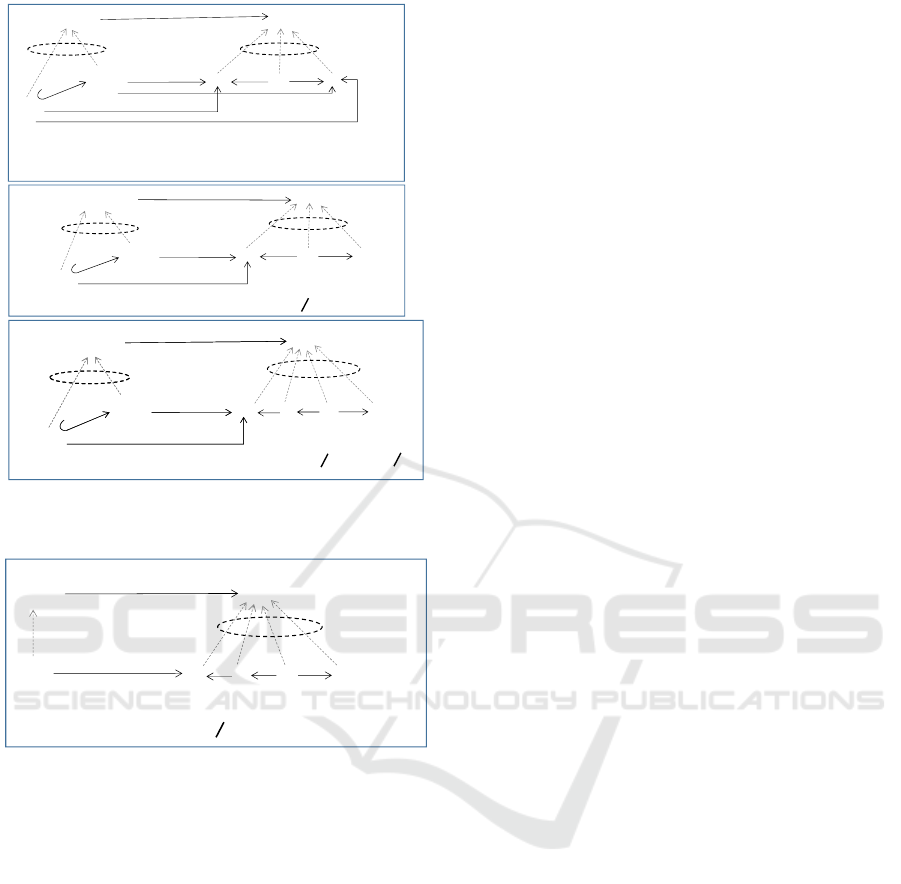
αα
(p)(p)
∑∑
α
(p)
∑
δδ
RR
pp
SS
ll
LL
rr
mm
RLRL
==
ll
LL
pp
cc
mm
LLLL
mm
cc
KK
RR
mm
RRRR
mm
LRLR
αα
(p)(p)
∑∑
α
(p)
∑
δδ
RR
pp
mm
RLRL
==
ll
LL
pp
cc
mm
LLLL
mm
cc
==
y
ϵ
, m ; m = m , m (L ) = m (L ), y
ϵ
, m ; m = m , m (L ) = m (L ),
m ( )m ( )
RLRL
RR
pp
RLRL
cc
LLLL
RRRR
cc
LRLR
LLLL
m ; m = m and PC
/.
m ϵ MC m ; m = m and PC
/.
m ϵ MC
y
ϵ
and z
ϵ
s.t. z
ϵ R
y
ϵ
and z
ϵ
s.t. z
ϵ R
m ( )m ( )
RLRL
RR
pp
EE
m ( )m ( )
LLLL
LL
pp
αα
(p)(p)
∑∑
δ
R
p
m
RN
=
l
L
p
c
m
LN
m
c
=
α
(p)
∑
δ
R
p
m
RN
=
l
L
p
c
m
LN
m
c
=
y
ϵ
, N ϵ NAC , z
ϵ
s.t. z
ϵ L and z ϵ R
y
ϵ
, N ϵ NAC , z
ϵ
s.t. z
ϵ L and z ϵ R
m ( )m ( )
RNRN
RR
pp
EE
m ( )m ( )
LNLN
LL
pp
P.C2#1P.C2#1
P.C2#2P.C2#2
P.C2#3P.C2#3
rr
pp
pp
gcgc
RRRR
rr
LRLR
rr
SS
ll
KK
LL
RR
NN
SS
ll
LL
rr
KK
RR
Figure 7: Patterns for a conformance preserving rule r that
satisfies Cond 2.
x
ϵ m (R )
, N ϵ NAC , m (R ) \ L = Ф ,
w
ϵ
m (R ) s.t. w
ϵ R
x
ϵ m (R )
, N ϵ NAC , m (R ) \ L = Ф ,
w
ϵ
m (R ) s.t. w
ϵ R
αα
(p)(p)
∑∑
α
(p)
∑
δδ
RR
pp
mm
RNRN
==
ll
cc
RNRN
pp
EE
RNRN
pp
rr
RNRN
pp
P.C3#1P.C3#1
rr
SS
ll
KK
LL
RR
NN
Figure 8: Pattern for a conformance preserving rule r that
satisfies Cond 3.
that in the graph patterns, solid arrows are represent-
ing injective graph homomorphisms. Pattern P.C1#1
ensures that if a graph constraint has a post-condition
(PC
gc
), a compliant rule r includes the post-condition
into the set of matching conditions MC
r
by replacing
PC
gc
with the matching elements from r.
The patterns presented in Figure 7 makes sure
that if the deletion of an element removes an exist-
ing match of a required pattern of a graph constraint,
then either the match of the condition pattern is also
removed (P.C2#2) or another match of a required pat-
tern is produced (P.C2#1); otherwise (P.C2#3) makes
sure that the deletion of an existing element does not
remove an existing match of a required pattern.
The pattern P.C3#1 presented in Figure 8 makes
sure that the creation of an element does not produce
a match with the forbidden pattern of a graph con-
straint. P.C3#1 also ensures that the forbidden pattern
of gc is included in the NACs of the rule via the con-
dition m
RN
(R
p
) \ L = φ.
4.3 Algorithm for Checking
Conformance Preserving Rule
Algorithm 1 provides a method for checking the con-
formance preserving property of a rule w.r.t a set of
graph constraints.
Theorem 1 (. Soundness of Algorithm. 1) Let S =
(S,C
S
: Σ) be a metamodel specification and r (typed
by S) a transformation rule which is determined to be
conformance preserving w.r.t C
S
by Algorithm 1. If r
is applied on a valid model (I,ι
I
) |= S then the result
(I
∗
,ι
I
∗
) will be a valid model of S.
Proof. Let GC be a set of constraints giving semantics
to the set of constraints C
S
. To prove the theorem by
contradiction, it is sufficient to show that there exists a
gc ∈ GC such that (I
∗
,ι
I
∗
) does not satisfy gc. There
are three ways in which it is possible for (I
∗
,ι
I
∗
) to
violate the graph constraint:
i gc is of the form ∀(L
p
: α
Σ
(p)) → ∃(R
p
: α
Σ
(p))
and ∃ A ⊆ (I
∗
\ I) such that a new match (δ,m
LI
∗
)
is produced from (L
p
: α
Σ
(p)) to I
∗
but a corre-
sponding match from (R
p
: α
Σ
(p)) to I
∗
is miss-
ing.
ii gc is of the form ∀(L
p
: α
Σ
(p)) → ∃(R
p
: α
Σ
(p))
and B ⊆ (I \ I
∗
) such that a required match from
(R
p
: α
Σ
(p)) to I is removed but a match from
(L
p
: α
Σ
(p)) to I still remains in I
∗
.
iii gc is of the form ∀(L
p
: α
Σ
(p)) → ¬∃(R
p
: α
Σ
(p))
and ∃ A ⊆ (I
∗
\ I) such that a new match is pro-
duced from the forbidden pattern (R
p
: α
Σ
(p)) to
I
∗
.
Case (i): r satisfies Cond 1 since a new match for
the condition pattern is produced. According to Algo-
rithm 1, r must comply with either P.C1#1 or P.C1#2.
The pattern in P.C1#2 has a NAC that prevents the
existence of pattern that matches with (L
p
: α
Σ
(p)).
Since a new match with (L
p
: α
Σ
(p)) is produced in
(i), r must comply with P.C1#1. Therefore, when the
rule is applied, a corresponding match (δ, m
RI
∗
) from
(R
p
: α
Σ
(p)) to I
∗
for the match (δ,m
LI
∗
) must ex-
ist. Therefore (I
∗
,ι
I
∗
) satisfies the graph constraint
gc. Hence we reach to a contradiction.
Case (ii): This case is explained by considering
three matches:
• (δ,m
LI
) : (L
p
: α
Σ
(p)) → (I : S),
• (δ,m
RI
) : (R
p
: α
Σ
(p)) → (I : S),
Static Analysis of Conformance Preserving Model Transformation Rules
159

Algorithm 1: Check for conformance preserving rule.
Require: a coupled transformation rule r, a set of graph constraints GC
C := R \ L of r //set of elements created by r
D := L \ R of r //set of elements deleted by r
for each x in C do
for each gc ∈ GC do
if gc has a required pattern R
p
and r satisfies Cond 1 for x and gc then
if r does not comply with P.C1#1 or P.C1#2 for x then
return ‘‘may not be conformance preserving’’
if gc has a forbidden pattern R
p
and r satisfies Cond 3 for x and gc then
if r does not comply with P.C3#1 for x then
return ‘‘may not be conformance preserving’’
for each y in D do
for each gc ∈ GC do
if gc has a required pattern R
p
and r satisfies Cond 2 for y and gc then
if r does not comply with P.C2#1 or P.C2#2 or P.C2#3
for y then
return ‘‘may not be conformance preserving’’
return ‘‘conformance preserving’’
• (δ,m
LI
∗
) : (L
p
: α
Σ
(p)) → (I
∗
: S)
where m
c
;m
RI
= m
LI
, m
LI
(L
p
) = m
LI
∗
(L
p
) and there
does not exist a corresponding match (δ,m
RI
∗
) : (R
p
:
α
Σ
(p)) → (I
∗
: S) such that m
c
;m
RI
∗
= m
LI
∗
. There-
fore ∃ y ∈ B such that y ∈ (m
RI
(R
p
) \ m
LI
(L
p
)) from
which we obtain Y ∈ ι
c
;δ(R
p
\ L
p
) where Y is the
type of y. Hence, r satisfies Cond 2 and according
to Algorithm 1, r must comply with either P.C2#1,
P.C2#2 or P.C2#3. Pattern in P.C2#3 has a NAC that
prevents the existence of pattern that matches with
(L
p
: α
Σ
(p)). The pattern in P.C2#2 makes sure that
the existence of pattern that matches with (L
p
: α
Σ
(p))
is removed. Since in case (ii), the matching with
the condition pattern remains, the rule r must comply
with P.C2#1. However, pattern P.C2#1 makes sure
that a corresponding match for the required pattern is
produced which contradicts with the second case.
Case (iii): r satisfies Cond 3 since a new match for
the forbidden pattern is produced. According to Algo-
rithm 1, r must comply with P.C3#1. Pattern P.C3#1
has a NAC that prevents the existence of pattern that
matches with (R
p
: α
Σ
(p)). Therefore we reach to a
contradiction.
In all three cases we have shown that if r is applied
on a valid model I |= S then the result (I
∗
,ι
I
∗
) cannot
violate the constraints specified in S.
Complexity of Algorithm 1: The complexity of the
algorithm depends on two factors: (i) the size of graph
patterns of the graph constraints and (ii) the size of
graph patterns in transformation rules. The size of a
graph pattern refers to the number of vertices of the
graph. The performance of the algorithm depends on
injective matching. Finding an injective match from
an n-vertex graph (G) to a m-vertex graph (H) has
complexity 2
O(n log m)
as finding all possible vertex
subsets of H of size at most n is m
O(n)
and for each
subset we need to try all possible mappings from G.
The algorithm avoids processing the models of a sys-
tem, therefore it is expected to analyze the transfor-
mation rules fast because in a typical situation, the
size of graph patterns in graph constraints and trans-
formation rules would be very small compared to the
size of models.
Theorem 2. Given a metamodel specification S =
(S,C
S
: Σ) and a set of conformance preserving rules
R = {r
1
,...r
n
} w.r.t a set of atomic constraints C
S
. If
the rules are applied on a valid model of S a finite
number of times, the result will be a valid model of S.
Proof. The theorem can be proved by induction over
the number of application of the transformation rules
as the results produced in each step are valid models
of S.
MODELSWARD 2018 - 6th International Conference on Model-Driven Engineering and Software Development
160

5 RELATED WORK
There has been a great deal of research related to the
formal analysis of termination, confluence, functional
behaviour of model transformation systems (Her-
mann et al., 2010) (Bruggink et al., 2014) (Heckel
et al., 2002) (Plump, 2010) and tool support (Arendt
et al., 2010) (Taentzer, 2003). One important differ-
ence between our approach and existing approaches
is that our approach rest on diagrammatic logic. Our
approach is closely related to the work of Heckel and
Wagner (Heckel and Wagner, 1995). They ensured
consistency of graph transformations by automati-
cally adding application conditions to single pushout
(SPO) rules. They propose a technique for deriving
application conditions from SPO rules of the form
L
r
−→ R and constraints. Constraints are specified in
the form P
c
−→ Q where P and Q are directed graphs
and c is an injective morphism. In their approach,
a post-condition (i.e., an application condition over
the right hand side of a rule) is constructed as a set
of all right-sided constraints by generating all possi-
ble gluings of the premise P and the graph R. The
post-condition is then used to construct a left-sided
constraint (i.e, an application condition over L) by in-
verse decomposition of pushout diagrams. One is-
sue with this approach is that a post-condition in-
duced by a constraint may include a large number
of right-sided constraints. A simple technique was
presented in (Heckel and Wagner, 1995) to reduce
the number of right-sided constraints from a post-
condition. The idea of the reduction is based on
the removal of right-sided constraints that is obtained
from a gluing R
s
−→ S
p
←− P where the image of P in
S does not depend on elements generated by rule r
i.e., p(P) ∩ s(R − r(L)) =
/
0. This reduction technique
however cannot handle situations where a rule deletes
an element that matches with the required pattern Q
of a constraint c : P → Q (see Cond 2 of Figure 5). To
illustrate this issue, consider an input graph G with
c;m
q
= m
p
where m
p
: P → G and m
q
: Q → G are
two injective morphism. Now consider a rule L
r
−→ R
where p(P) ∩ s(R − r(L)) =
/
0 which means that the
reduction will disregard the constraint c and no left-
sided constraint will be constructed. But it is possible
for the rule to remove an element x from m
q
(Q) which
results in an output not conforming to its metamodel.
Later on, this approach for ensuring consistency
was adapted for a double pushout approaches and
generalized for high level transformation systems
(Ehrig et al., 2006). The approach was further en-
hanced for nested constraints in (Habel and Penne-
mann, 2009). Although the approach presented in
(Ehrig et al., 2006; Habel and Pennemann, 2009) can
deal with situations where a rule add/delete elements,
the construction of application conditions do not in-
clude any reduction technique. This results in a large
number of application conditions. In our approach,
we rely on the modeller to develop transformation
rules and automatically check conformance using our
algorithm. The proposed algorithm filters out triv-
ially conformance preserving rules as described in
section 4.1 before checking the existence of the de-
sired patterns in section 4.2 for optimal performance.
Becker et al. (Becker et al., 2006) developed a
verification technique for structural safety property of
a transformation system which is very similar to our
approach in the sense that their technique is based on
checking the locality of transformation rules against a
set of safety properties. In their approach, the authors
checked if the application of transformation rules can
violate any safety property given as a set of forbid-
den graph patterns. Dyck and Giese (Dyck and Giese,
2015) improved the technique for the automated ver-
ification of structural invariants for graph transforma-
tion systems by extending the expressive power. They
provided support for negative application conditions
in constraints and support for application conditions
in transformation rules. However, both techniques
only check against forbidden patterns while in our ap-
proach we support checking the conformance prop-
erty of transformation rules against both required and
forbidden patterns. Making sure that the application
of a transformation rule does not violate any required
pattern is more complex than checking against a set
of forbidden patterns as it involves more scenarios to
cover for the checking algorithm.
6 CONCLUSION
In this paper, we presented a static analysis technique
for checking the conformance property of transforma-
tion rules. The static analysis technique processes the
semantics of graph constraints and analyzes if a trans-
formation rule exhibits certain structure in order to be
conformance preserving rule w.r.t a set of constraints.
We presented the idea in the context of DPF which
provides a formal framework for metamodelling. Fu-
ture work includes the implementation of the algo-
rithm and undertaking performance evaluation tests.
Also, as part of future work, we plan to adapt the al-
gorithm to more expressive constraint language such
as nested graph constraints.
Static Analysis of Conformance Preserving Model Transformation Rules
161

REFERENCES
Arendt, T., Biermann, E., Jurack, S., Krause, C., and
Taentzer, G. (2010). Henshin: Advanced Concepts
and Tools for In-place EMF Model Transformations.
In Proceedings of the 13th International Conference
on Model Driven Engineering Languages and Sys-
tems: Part I, MODELS’10, pages 121–135. Springer-
Verlag.
Baresi, L. and Spoletini, P. (2006). On the Use of Alloy to
Analyze Graph Transformation Systems, pages 306–
320. Springer.
Becker, B., Beyer, D., Giese, H., Klein, F., and Schilling,
D. (2006). Symbolic invariant verification for systems
with dynamic structural adaptation. In Proceedings
of the 28th International Conference on Software En-
gineering, ICSE ’06, pages 72–81, New York, NY,
USA. ACM.
Bruggink, H. J. S., K
¨
onig, B., and Zantema, H. (2014). Ter-
mination Analysis for Graph Transformation Systems,
pages 179–194. Springer.
da Costa, S. A. and Ribeiro, L. (2012). Verification of graph
grammars using a logical approach. Science of Com-
puter Programming, 77(4):480 – 504.
Diskin, Z. and Wolter, U. (2008). A diagrammatic logic for
object-oriented visual modeling. Electronic Notes in
Theoretical Computer Science, 203(6):19 – 41. Pro-
ceedings of the 2nd Workshop on Applied and Com-
putational Category Theory (ACCAT 2007).
Dyck, J. and Giese, H. (2015). Inductive Invariant Checking
with Partial Negative Application Conditions, pages
237–253. Springer International Publishing, Cham.
Ehrig, H., Ehrig, K., Prange, U., and Taentzer, G.
(2006). Fundamentals of Algebraic Graph Transfor-
mation. Monographs in Theoretical Computer Sci-
ence. Springer.
Habel, A. and Pennemann, K.-h. (2009). Correctness of
high-level transformation systems relative to nested
conditions. Mathematical. Structures in Comp. Sci.,
19(2):245–296.
Heckel, R., K
¨
uster, J. M., and Taentzer, G. (2002). Conflu-
ence of Typed Attributed Graph Transformation Sys-
tems, pages 161–176. Springer.
Heckel, R. and Wagner, A. (1995). Ensuring Consistency
of Conditional Graph Grammars - A Constructive Ap-
proach -. ENTCS, 2(C):118–126.
Hermann, F., Ehrig, H., Orejas, F., and Golas, U. (2010).
Formal Analysis of Functional Behaviour for Model
Transformations Based on Triple Graph Grammars,
pages 155–170. Springer.
Lambers, L., Ehrig, H., Prange, U., and Orejas, F. (2008).
Embedding and Confluence of Graph Transformations
with Negative Application Conditions, pages 162–
177. Springer.
Plump, D. (2010). Checking graph-transformation systems
for confluence. ECEASST, 26.
Ribeiro, L., Dotti, F. L., da Costa, S. A., and Dillenburg,
F. C. (2010). Towards theorem proving graph gram-
mars using event-b. ECEASST, 30.
Rutle, A. (2010). Diagram Predicate Framework: A For-
mal Approach to MDE. PhD thesis, Department of
Informatics, University of Bergen, Norway.
Rutle, A., Rossini, A., Lamo, Y., and Wolter, U. (2012).
A formal approach to the specification and transfor-
mation of constraints in mde. Journal of Logic and
Algebraic Programming, 81(4):422–457.
Taentzer, G. (2003). AGG: A graph transformation envi-
ronment for modeling and validation of software. In
Pfaltz, J. L., Nagl, M., and B
¨
ohlen, B., editors, Ap-
plications of Graph Transformations with Industrial
Relevance, Second International Workshop, AGTIVE
2003, Charlottesville, VA, USA, September 27 - Oc-
tober 1, 2003, Revised Selected and Invited Papers,
volume 3062 of Lecture Notes in Computer Science,
pages 446–453. Springer.
Troya, J. and Vallecillo, A. (2010). Towards a Rewriting
Logic Semantics for ATL, pages 230–244. Springer.
Varr
´
o, D., Varr
´
o, G., and Pataricza, A. (2002). Designing
the automatic transformation of visual languages. Sci.
Comput. Program., 44(2):205–227.
Wang, X., B
¨
uttner, F., and Lamo, Y. (2014). Verification of
graph-based model transformations using alloy. ECE-
ASST, 67.
MODELSWARD 2018 - 6th International Conference on Model-Driven Engineering and Software Development
162
