
Packing Circles and Irregular Polygons using Separation Lines
Jeinny Peralta
1
, Marina Andretta
1
and Jos
´
e Fernando Oliveira
2
1
Instituto de Ci
ˆ
encias Matem
´
aticas e de Computac¸
˜
ao, Universidade de S
˜
ao Paulo, Av. Trabalhador S
˜
ao Carlense, 400,
13566-590, S
˜
ao Carlos, Brasil
2
Faculdade de Engenharia, Universidade do Porto, Rua Dr. Roberto Frias, 4200-590, Porto, Portugal
Keywords:
Irregular Packing Problems, Circle Packing, Separation Lines.
Abstract:
In this paper we propose a nonlinear mathematical model for the problem of packing circles, convex and non-
convex irregular polygons, within a rectangular envelope to be produced, obeying containment constraints and
non-overlapping constraints; the objective of the problem is to minimize the area of the rectangular envelope.
We consider free rotations of the polygons and use separation lines to ensure non-overlapping. Computational
tests were run using instances presented in the literature that deal with circles and polygons simultaneously;
different solutions, in which the area of the rectangular envelope is smaller than or equal to the ones found in
the literature were found in most cases, and the execution time is very low. This indicates that our model is
computationally efficient.
1 INTRODUCTION
In production processes, such as garment manufac-
turing, shoe manufacturing, furniture making, among
others, the optimization of layouts of items of differ-
ent shapes is necessary. These items can be repre-
sented by circles or polygons. In the literature, there
are many works dealing with circle packing problem
(e.g., (Szab
´
o et al., 2007) and (Castillo et al., 2008))
and polygon packing problem (see (Oliveira and Fer-
reira, 1993), (Toledo et al., 2013), and (Jones, 2013)),
but few papers deal with the problem of packing cir-
cles and polygons simultaneously ((Kallrath, 2009;
Stoyan et al., 2012; Mundim et al., 2017)).
In packing problems, items must be positioned
into a certain shape, aiming to optimize an objective
function. In this work, we consider the positioning of
circles and polygons into a rectangle is such a man-
ner that the produced area is minimized. That is, the
objective is to minimize the multiplication of the rect-
angle dimensions which must be determined.
The main constraint in packing problems is the
non-overlapping between items, but it is generally
very complex for a computational program to deter-
mine if two items are overlapping, touching or sep-
arated. When dealing with polygons, there are tools
for solving this issue ((Bennell and Oliveira, 2008)),
such as the raster methods, direct trigonometry, no-fit
polygon, and phi-function. When dealing with cir-
cles, the problem is commonly formulated as a prob-
lem of Euclidean geometry, either in cartesian coordi-
nates (George et al., 1995; Addis et al., 2008) or po-
lar and cartesian coordinates combined (Mladenovi
´
c
et al., 2005; L
´
opez and Beasley, 2013). In this paper,
we use direct trigonometry in cartesian coordinates to
ensure non-overlapping between items.
Both for circle packing problems and polygon
packing problems, different techniques of solution
have been developed: there are heuristics (Liu et al.,
2016; Oliveira and Ferreira, 1993), linear program-
ming models (Galiev and Lisafina, 2013), linear
mixed integer programming models (Toledo et al.,
2013), nonlinear mixed integer programming mod-
els (George et al., 1995), and nonlinear programming
models (Birgin et al., 2013; Stoyan et al., 2016). For
the problem of packing circles and polygons simul-
taneously, there are fewer works, such as (Kallrath,
2009; Stoyan et al., 2012; Mundim et al., 2017). In
(Kallrath, 2009) and (Stoyan et al., 2012), nonlinear
programming models where the items can be both
translated and rotated were proposed. In (Mundim
et al., 2017), two heuristics based on bottom-left
moves and the no-fit raster concept were proposed;
in these, the items can not be freely rotated.
In (Kallrath, 2009) a model for two cases of pack-
ing of circles and convex polygons was developed. In
the first case, the objective is to pack all items pro-
vided minimizing the area of the rectangular enve-
Peralta, J., Andretta, M. and Oliveira, J.
Packing Circles and Irregular Polygons using Separation Lines.
DOI: 10.5220/0006602700710077
In Proceedings of the 7th International Conference on Operations Research and Enterprise Systems (ICORES 2018), pages 71-77
ISBN: 978-989-758-285-1
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
71

lope, as it will be done here. In the second case, the
objective is to pack the items on stocked rectangles
of known geometric dimensions. Separation lines are
used to ensure non-overlapping. In (Kallrath, 2009),
the problem is addressed using Branch&Reduce Op-
timization Navigator (BARON) (Tawarmalani and
Sahinidis, 2005; Sahinidis, 2014) and LindoGlobal
from Lindo Systems, Inc., which is part of the GAMS
22.5 distributions.
In (Stoyan et al., 2012) a model for packing prob-
lem of circles and non-convex polygons into a strip
with prohibited regions was proposed. The objective
of the problem is to maximize space utilization. Fur-
thermore, the authors ensures non-overlapping by us-
ing the phi-function.
In (Mundim et al., 2017) two heuristics for
packing circles and non-convex polygons into two-
dimensional bin in order to minimize one or both di-
mensions of the bin are proposed. These heuristics
are based on bottom-left moves and the no-fit raster
concept. For the development of the heuristics, the se-
quence in which items are packed must be determined
and this is done by a Biased Random Key Genetic Al-
gorithm.
The model proposed here is an extension of the
one presented in (Peralta et al., 2017), which is a non-
linear mathematical model for an irregular strip pack-
ing problem of polygons, which may be convex or
non-convex, that can rotate freely. This model yielded
good solutions for large instances in rather reasonable
execution time, and it should be noted that this model
has a significantly smaller number of variables, when
compared to the model proposed in (Kallrath, 2009).
Here, we propose a nonlinear mathematical model for
a packing problem in which the items are not only
polygons, but also circles. The container is no longer
a strip, but a rectangular envelope; the objective is to
minimize the area of the rectangular envelope. In this
model, we use direct trigonometry, in particular sep-
aration lines, to ensure the non-overlapping between
items. A separation line is a straight line such that,
given two items, one of them is on one side of the line
and the other on the opposite side. A polygon is on
one side of the line if all its vertices are on that side
of the line or on the line. A circle is on one side of the
line if its center is on that side of the line and if the dis-
tance from center to the line is greater than or equal
to its radius. The use of separation lines allows us
to find good solutions, even when dealing with non-
convex polygons, since in this case the non-convex
polygons are partitioned into convex polygons and we
must have lines separating each convex sub-polygon
belonging to the partition of the remaining items.
Both the polygons and the separation lines can ro-
tate freely. We use a code for nonlinear programming
to solve the problem, IPOPT (W
¨
achter and Biegler,
2006).
This paper is organized as follows. In the next sec-
tion we develop a model for packing circles and poly-
gons from one rectangular envelope, which considers
free rotations of the polygons. In Section 3, the nu-
merical results obtained are presented and discussed.
We end up presenting some conclusions in Section 4.
2 MODEL FOR A CIRCLES AND
POLYGONS PACKING
PROBLEM
We assume that n items, which can rotate freely,
should be positioned into one rectangular envelope,
obeying containment constraints and non-overlapping
constraints, in order to minimize the area of the rect-
angular envelope. Items can be circles or irregular
(convex or non-convex) polygons. The ideas used to
model this problem are based in the ones presented in
(Peralta et al., 2017).
If a polygon is non-convex, it is partitioned into
convex polygons. The coordinates of a vertex of a
non-convex polygon P
i
are given by:
(v
l
x
i
k
,v
l
y
i
k
),
with k = 1,..., p
i
and l = 1, . . . , v
i
k
, being p
i
the num-
ber of convex polygons belonging to the partition of
the non-convex polygon P
i
and v
i
k
the number of ver-
tices of the convex polygon P
i
k
.
The problem is modeled using the following vari-
ables: for each circle i, the coordinates of its center
(x
c
i
,y
c
i
); for each polygon i, the coordinates of its ref-
erence point (x
P
i
,y
P
i
) and its angle of rotation θ
i
; for
each separation line, which separates item i from item
j, the coordinates of its reference point (x
`
i, j
,y
`
i, j
) and
its rotation angle α
i, j
; and, the width W and the length
L of the rectangular envelope.
The reference point of a polygon is used to repre-
sent all the vertices of the polygon, even after transla-
tions and/or rotations are undergone; a separation line
is given by two points, one is its reference point and
the other is rewritten in terms of its reference point
(see more details in (Peralta et al., 2017)).
The nonlinear mathematical model which is pro-
posed here, as said before, consists of minimizing the
area (W × L) of the rectangular envelope, subject to
constraints ensuring that all items do not exceed the
bounds of the rectangular envelope (that are presented
in Section 2.1), and others ensuring that the items do
not overlap (that are presented in Section 2.2).
ICORES 2018 - 7th International Conference on Operations Research and Enterprise Systems
72

2.1 Containment Constraints
We have to ensure that all items are fully inside the
rectangular envelope.
To garantee that the circles are inside the rectan-
gular envelope, we require that:
r
i
− x
c
i
≤ 0, (1)
r
i
+ x
c
i
≤ W, (2)
r
i
− y
c
i
≤ 0, (3)
and,
r
i
+ y
c
i
≤ L, (4)
where (x
c
i
,y
c
i
) are the coordinates of the center of cir-
cle i and r
i
is its radius, for i = 1, ..., n
c
, with n
c
the
number of circles to be packed.
To garantee that the polygons are inside the rect-
angular envelope, we require that:
0 ≤ v
l
x
i
k
cosθ
i
− v
l
y
i
k
sinθ
i
+ x
P
i
≤ W, (5)
and,
0 ≤ v
l
x
i
k
sinθ
i
+ v
l
y
i
k
cosθ
i
+ y
P
i
≤ L, (6)
for i = 1,...,n
p
, where n
p
is the number of polygons
to be packed; k = 1,..., p
i
and l = 1, . . . , v
i
k
.
2.2 Non-overlapping Constraints
In the model, separation lines are used to ensure non-
overlapping. The equation that ensures that a line sep-
arates item i from item j is given by:
y = c
i, j
x + d
i, j
, (7)
with
c
i, j
=
(x
k+1
− x
k
)sinα
i, j
+ (y
k+1
− y
k
)cosα
i, j
(x
k+1
− x
k
)cosα
i, j
+ (y
k
− y
k+1
)sinα
i, j
and
d
i, j
= y
`
i, j
− c
i, j
x
`
i, j
,
being (x
k
,y
k
) and (x
k+1
,y
k+1
), the two points that de-
termine the initial separation line; (x
`
i, j
,y
`
i, j
) and α
i, j
,
are the reference point and the rotation angle of the
separation line, respectively. When we are dealing
with non-convex polygons, we must have lines sep-
arating each pair of convex polygons, belonging to
the partition of two different non-convex polygons.
To see more details of how separation lines are used
when it comes to non-convex polygons, see (Peralta
et al., 2017). The non-overlapping constraints are
given below.
2.2.1 Avoiding Overlap Between Circles
In the constraints of non-overlap between circles, the
use of separation lines is not necessary. We ensure
that two circles do not overlap by enforcing that the
distance between their centers are greater than or
equal to the sum of their radii. Therefore, for two cir-
cles C
i
and C
j
, i = 1, . . . , n
c
− 1 and j = i + 1, . . . , n
c
,
the constraint is given by
(x
c
i
− x
c
j
)
2
+ (y
c
i
− y
c
j
)
2
≥ (r
i
+ r
j
)
2
. (8)
2.2.2 Avoiding Overlap Between Polygons
Non-overlap between two polygons P
i
and P
j
is en-
forced by the condition that all vertices of P
i
and P
j
are on different sides of, or on a separation line.
Let
X
l
i
= v
l
x
i
cosθ
i
− v
l
y
i
sinθ
i
+ x
P
i
,
and
Y
l
i
= v
l
x
i
sinθ
i
+ v
l
y
i
cosθ
i
+ y
P
i
,
be the coordinates of vertice l of a polygon P
i
. Then,
the constraints that ensure non-overlap between two
polygons are given by
Y
l
i
− c
i, j
X
l
i
− d
i, j
≤ 0, for l = 1, . . . , v
i
(9)
and
Y
l
j
− c
i, j
X
l
j
− d
i, j
≥ 0, for l = 1, . . . , v
j
. (10)
2.2.3 Avoiding Overlap Between Circles and
Polygons
We ensure that a circle and a polygon are not over-
lapping by using a separation line. A separation line
separates a circle C
i
and a polygon P
j
if (i) all vertices
of P
j
are on one side of (or on) the separation line,
and (ii) the center of C
i
is on the other side of the sep-
aration line and distant from at least the radius of C
i
.
The constraints that ensure non-overlapping between
a circle and a polygon are given by
Y
l
j
− c
i, j
X
l
j
− d
i, j
≥ 0, for l = 1, . . . , v
j
, (11)
y
c
i
− c
i, j
x
c
i
− d
i, j
≤ 0, (12)
and
∆
i, j
≥ r
i
, (13)
with ∆
i, j
=
|c
i, j
x
c
i
− y
c
i
+ d
i, j
|
q
c
2
i, j
+ 1
the distance from the
center of C
i
to the line that separates C
i
from P
j
.
Packing Circles and Irregular Polygons using Separation Lines
73
3 NUMERICAL RESULTS
In this section we present and compare the results ob-
tained when applying our model to solve the prob-
lems presented in (Kallrath, 2009) and (Stoyan et al.,
2012), which pack circles and polygons simultane-
ously. All the numerical experiments have been
performed using a code for nonlinear programming
to solve the problem, IPOPT (W
¨
achter and Biegler,
2006) (an algorithm of interior points type designed
to find local solutions of mathematical optimization
problems), which is part of the COIN-OR (W
¨
achter
and Biegler, 2015), on an Ubuntu 12.04 laptop with an
Intel Core I7-4510U CPU @ 2.1GHz processor and 8
GB of memory.
In (Kallrath, 2009), as here, the items should be
positioned into a rectangular envelope. The rectangu-
lar envelope is subject to lower and upper bounds of
its width and length. We tested all those instances in
(Kallrath, 2009) with circles and polygons which has
data available and used the same bounds presented
there, which are
¯
W = 4 for the upper bound of the
width and
¯
L = 8 for the upper bound of the length for
all instances, except for instance c1p1-3, for which
we have
¯
W = 2.5 and
¯
L = 3, and for instance c6p3,
for which we have
¯
W = 6 and
¯
L = 10.
The results obtained by solving these instances us-
ing the model presented in Section 2 and those pre-
sented in (Kallrath, 2009) are summarized in Table 1.
The names of the instances are presented in the first
column. The number of circles and polygons are
presented in second and third columns, respectively.
From the fourth to the seventh column, the data and
results in (Kallrath, 2009) are presented. From the
eighth to the eleventh column, our data and results
are presented. In these, n is the number of variables
of the model; m is the number of constraints of the
model; CPU is the execution time in seconds; and a is
the area of the rectangular envelope. In all instances,
IPOPT stopped in optimal local solutions. The solu-
tion obtained by the proposed model and the starting
point used to find it, for each instance, are displayed
from Figures 1 to 8.
We can observe that the number of variables and
constraints in our model is significantly smaller than
the number of variables and constraints of the model
presented in (Kallrath, 2009). The execution time is
considerably reduced, which can be attributed, not
only to the reduction of variables and constraints in
the model, but also to the differences in operating sys-
tem, hardware architecture, among others. We can
also observe in our results that the area is smaller
than or equal to the ones obtained in (Kallrath, 2009)
in most instances. This reduction in the number of
4.00
8.00
(a) Starting point
1.00
1.00
(b) Solution
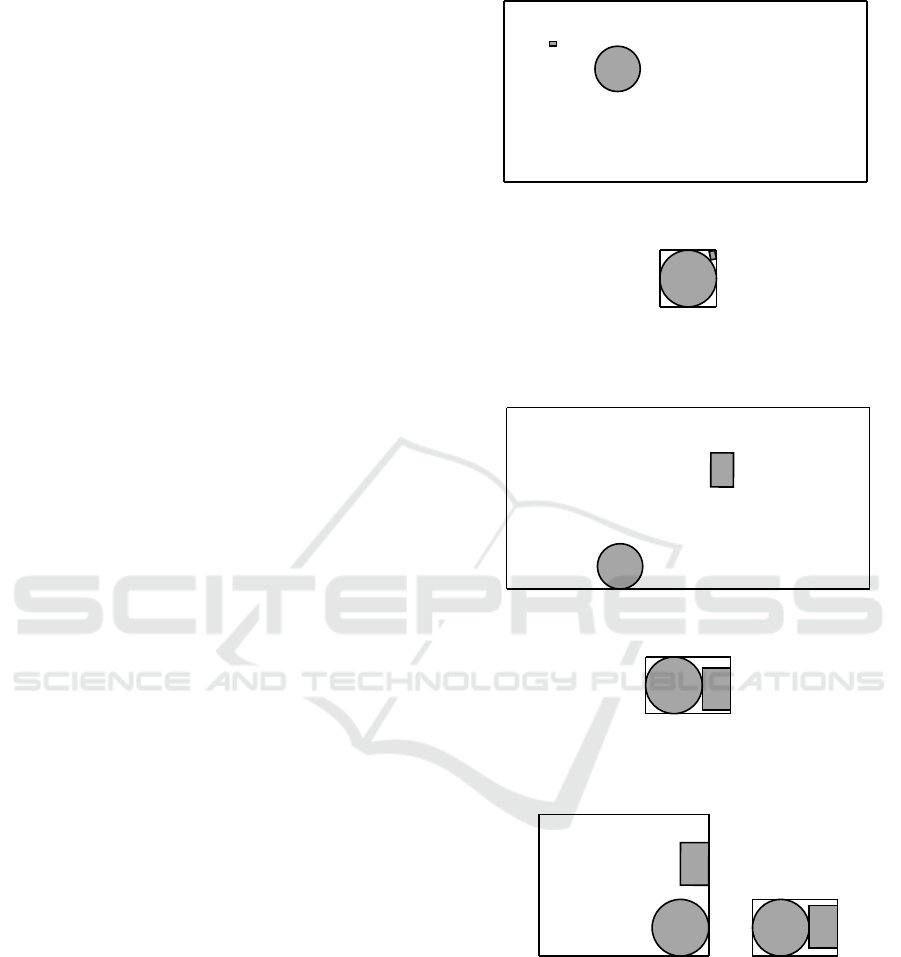
Figure 1: Instance: c1p1-1.
4.00
8.00
(a) Starting point
1.00
1.50
(b) Solution
Figure 2: Instance: c1p1-2.
2.50
3.00
(a) Starting point
1.00
1.50
(b) Solution
Figure 3: Instance: c1p1-3.
variables, constraints and execution time allows us
to solve larger instances, as the ones presented in
(Stoyan et al., 2012).
In (Stoyan et al., 2012), the items should be posi-
tioned into a strip which can have prohibited regions;
only one instance without prohibited regions was pre-
sented in this paper. We use this instance to test our
model, fixing the width W of the strip in the value
ICORES 2018 - 7th International Conference on Operations Research and Enterprise Systems
74

Table 1: Comparison of our results to those in (Kallrath, 2009).
(Kallrath, 2009) Our approach
Instance C P n m CPU a n m CPU a
c1p1-1 1 1 47 54 0.10 1.00 10 26 0.01 1.00
c1p1-2 1 1 47 54 42.00 1.50 10 26 0.02 1.50
c1p1-3 1 1 47 54 368.00 2.50 10 26 0.01 1.50
c1p5a 1 2 767 799 2000.00 15.90 19 80 0.89 11.70
c1p5b 1 5 791 838 1800.00 18.55 64 284 0.06 19.73
c1p6a 1 6 1110 1161 1800.00 20.37 85 376 0.05 20.06
c3p3 3 3 489 516 2000.00 16.75 53 177 0.03 16.86
c6p3 6 3 628 661 33000.00 35.10 86 219 0.04 33.19
4.00
8.00
(a) Starting point
3.90
3.00
(b) Solution
Figure 4: Instance: c1p5a.
4.00
8.00
(a) Starting Point
3.00
6.57
(b) Solution
Figure 5: Instance: c1p5b.
4.00
8.00
(a) Starting point
3.00
6.68
(b) Solution
Figure 6: Instance: c1p6a.
4.00
8.00
(a) Starting point
3.40
4.96
(b) Solution
Figure 7: Instance: c3p3.
Packing Circles and Irregular Polygons using Separation Lines
75

6.00
10.00
(a) Starting point
5.97
5.56
(b) Solution
Figure 8: Instance: c6p3.
presented in the paper, W = 25; for this, we setup the
option of IPOPT “fixed variable treatment” which in-
cludes equality constraints to fix the variable. This
instance consists of 44 polygons, being some non-
convex, and 5 circles of different size. To model this
instance, 19335 variables and 54860 restrictions were
used. In (Stoyan et al., 2012), a length of 33.9 in two
hours of runtime was achieved. We achieved a length
of 36.00 in 521.64 seconds. The layout obtained is
displayed in Figure 10.
4 CONCLUSIONS
This work deals with a mathematical model for a
packing problem of circles and non-convex polygons
with continuous rotations in a rectangular envelope;
the objective of the problem is to minimize the area of
the rectangular envelope. In the model, we use sepa-
ration lines to avoid overlap of the items. The model-
ing of separation lines uses the general equation of the
line. We compare our model with the one presented
in (Kallrath, 2009) for packing problem of circles and
convex polygons, in which separation lines are also
used, but these are modeled using the vector equation
of the line. The vector equation of the line implies the
employment of many variables and constraints. With
the use of the general equation of the line the num-
ber of variables and constraints in the model is sig-
nificantly reduced, and therefore, the execution time
is also reduced; with these reductions, we were able
to extend the model to non-convex polygons and to
solve larger problems.
We tested seven instances of those presented in
(Kallrath, 2009), and to verify the effectiveness of our
model for larger problems with non-convex polygons,
we tested the only instance for packing problem of
circles and polygons without prohibited regions pre-
sented in (Stoyan et al., 2012). We achieved a very
good solution in a short runtime for this instance.
To solve this problem, we use a code for nonlinear
programming, IPOPT (W
¨
achter and Biegler, 2006),
which depends substantially on a starting point. In all
the instances we have tested, we use a random starting
point. We will work on a method that constructs start-
ing points, with which we believe the results could be
improved.
ACKNOWLEDGEMENTS
This research was partially supported by CNPq
(grants 141072/2014-8 and 409043/2016-8) and
FAPESP (grants 2013/07375-0 and 2016/01860-1),
from Brazil.
REFERENCES
Addis, B., Locatelli, M., and Schoen, F. (2008). Efficiently
packing unequal disks in a circle. Operations Re-
search Letters, 36:37–42.
Bennell, J. A. and Oliveira, J. F. (2008). The geometry of
nesting problems: A tutorial. European Journal of
Operational Research, 184:397–415.
Birgin, E. G., Bustamante, L. H., Callisaya, H. F., and
Mart
´
ınez, J. M. (2013). Packing circles within el-
lipses. International Transactions in Operational Re-
search, 20:365–389.
Castillo, I., Kampas, F. J., and Pintr, J. D. (2008). Solving
circle packing problems by global optimization: Nu-
merical results and industrial applications. European
Journal of Operational Research, 191(3):786–802.
Galiev, S. I. and Lisafina, M. S. (2013). Linear models for
the approximate solution of the problem of packing
equal circles into a given domain. European Journal
of Operational Research, 230:505–514.
George, J. A., George, J. M., and Lamar, B. W. (1995).
Packing different-sized circles into a rectangular con-
tainer. European Journal of Operation Research,
84:693–712.
Jones, D. R. (2013). A fully general, exact algorithm for
nesting irregular shapes. Journal of Global Optimiza-
tion, 59:367–404.
ICORES 2018 - 7th International Conference on Operations Research and Enterprise Systems
76

25.00
100.00
Figure 9: Starting point used to solve the instance from (Stoyan et al., 2012).
25.00
35,97
Figure 10: Solution found for the instance from (Stoyan et al., 2012).
Kallrath, J. (2009). Cutting circles and polygons from area-
minimizing rectangles. Journal of Global Optimiza-
tion, 43:299–328.
Liu, J., Zhang, K., Yao, Y., Xue, Y., and Guan, T. (2016).
A heuristic quasi-physical algorithm with coarse and
fine adjustment for multi-objective weighted circles
packing problem. Computers and Industrial Engi-
neering, 101:416–426.
L
´
opez, C. O. and Beasley, J. E. (2013). Packing unequal cir-
cles using formulation space search. Computers and
Operations Research, 40(5):1276–1288.
Mladenovi
´
c, N., Plastria, F., and Urosevi
´
c, D. (2005).
Reformulation descent applied to circle packing
problems. Computers and Operations Research,
32(9):2419–2434.
Mundim, L. R., Andretta, M., and Queiroz, T. (2017). A
biased random key genetic algorithm for open dimen-
sion nesting problems using no-fit raster. Expert Sys-
tems with Applications, 81:358–371.
Oliveira, J. F. and Ferreira, J. S. (1993). Algorithms for nest-
ing problems, applied simulated annealing. In: Vidal,
R.V.V. (Ed.), Lecture notes in econ. and Maths Sys-
tems. Springer Verlag, 396:255–274.
Peralta, J., Andretta, M., and Oliveira, J. F. (2017). Solving
irregular strip packing problems with free rotations us-
ing separation lines. https://arxiv.org/abs/1707.07177.
Sahinidis, N. V. (2014). BARON 14.3.1: Global Optimiza-
tion of Mixed-Integer Nonlinear Programs, User’s
Manual.
Stoyan, Y., Pankratov, A., and Romanova, T. (2016). Cut-
ting and packing problems for irregular objects with
continuous rotations: mathematical modelling and
non-linear optimization. Journal of the Operational
Research Society, 67(5):786–800.
Stoyan, Y. G., Zlotnik, M. V., and Chugay, A. M. (2012).
Solving an optimization packing problem of circles
and non-convex polygons with rotations into a mul-
tiply connected region. Journal of the Operational
Research Society, 63:379–391.
Szab
´
o, P. G., Mark
´
ot, M. C., Csendes, T., Specht, E.,
Casado, L. G., and Garcia, I. (2007). New approaches
to circle packing in a square: with program codes.
Optimization and its Applications.
Tawarmalani, M. and Sahinidis, N. V. (2005). A polyhe-
dral branch-and-cut approach to global optimization.
Mathematical Programming, 103:225–249.
Toledo, F. M. B., Carravilla, M. A., Ribeiro, C., Oliveira,
J. F., and Gomes, A. M. (2013). The dotted-
board model: A new mip model for nesting irregu-
lar shapes. International Journal of Production Eco-
nomics, 145(2):478–487.
W
¨
achter, A. and Biegler, L. T. (2006). On the imple-
mentation of a primal-dual interior point filter line
search algorithm for large-scale nonlinear program-
ming. Mathematical Programming, 106(1):25–57.
W
¨
achter, A. and Biegler, L. T. (2015). COIN OR project.
http://projects.coin-or.org/Ipopt.
Packing Circles and Irregular Polygons using Separation Lines
77
