Information Extraction from High-level Activity Diagrams to Support
Development Tasks
Martin Beckmann, Thomas Karbe and Andreas Vogelsang
Technische Universit
¨
at Berlin, Ernst-Reuter-Platz 7, 10587 Berlin, Germany
Keywords:
UML2 Activity Diagrams, Information Extraction, Activity Semantics.
Abstract:
As the complexity of systems continues to increase, the use of model-driven development approaches becomes
more widely applied. One of our industry partners (Daimler AG) uses UML activity diagrams as the first step
in the development of vehicle functions, mainly for the purpose of communication and overview. However, the
contained information is also valuable for further development tasks. In this paper, we present an automated
approach to extract information from these high-level activities. We put a focus on aspects of activities such as
propositional logic relations, sequences of actions, and differentiability of execution paths. The extracted parts
are needed for the compilation of requirements and the creation of test cases. Also, this approach supports
stakeholders unfamiliar with the notations of activities as implicit information is made explicit and hence
more accessible. For this purpose, we provide a formalism for the kind of activities our industry partner
uses. Based on that formalism, we define properties that express the contained sequences and execution paths.
Furthermore, the formalism is used to derive the underlying propositional logic relations. We show how the
approach is applied to eliminate hundreds of existing quality issues in an existing requirements document.
1 INTRODUCTION
Complex software systems, which, for example, can
be found in distributed embedded systems, require
model-based and system-oriented development ap-
proaches (Broy, 2006). Also, using graphical mod-
els for specification manages complexity and im-
proves reusability and analytical capabilities (Vogel-
sang et al., 2014). One of our industry partners
(Daimler AG) uses UML activity diagrams as a first
step for developing a new function of a vehicle sys-
tem. The activities describe the function’s activation
and deactivation in terms of triggers and conditions
that need to be checked and fulfilled before a function
is activated. By this, the activity diagrams provide an
early overview of the desired function behavior.
Although the main purpose of the diagrams is to
be a means of communication and to ease the over-
all understanding, the contained information is also a
valuable input for following development tasks such
as the elaboration and documentation of detailed re-
quirements (Drusinsky, 2008) or the derivation of test
cases (Kundu and Samanta, 2009). Yet, different
tasks have different information needs and may ben-
efit from making explicit specific information con-
tained in the activity diagrams. We aim at support-
ing downstream development tasks by extracting and
preparing the relevant information from the activity
diagrams. This extraction is additionally helpful for
stakeholders unfamiliar with the notations of acti-
vity diagrams (Arlow and Neustadt, 2004) because it
makes information contained in the activity diagrams
more accessible (Maiden et al., 2005).
In this paper, we focus (1) on the transformation of
activity diagrams to textual specifications by exploit-
ing information on logical activation expressions and
(2) on supporting the derivation of test cases by ex-
ploiting information on minimal execution sequences.
This paper makes the following contributions:
• We define a simplified representation of UML ac-
tivities based on graphs. For this simplified rep-
resentation, we define an algorithm that computes
minimal execution sequences within the activity
and a second algorithm that computes an activa-
tion expression for a function.
• We use the information about minimal execution
sequences to derive test cases from the activities.
• We show how we use the activation expressions
to derive textual requirements specifications from
the activities.
• For both applications, we report on our experi-
ences gained at our industrial partner.
438
Beckmann, M., Karbe, T. and Vogelsang, A.
Information Extraction from High-level Activity Diagrams to Support Development Tasks.
DOI: 10.5220/0006605504380445
In Proceedings of the 6th International Conference on Model-Driven Engineering and Software Development (MODELSWARD 2018), pages 438-445
ISBN: 978-989-758-283-7
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

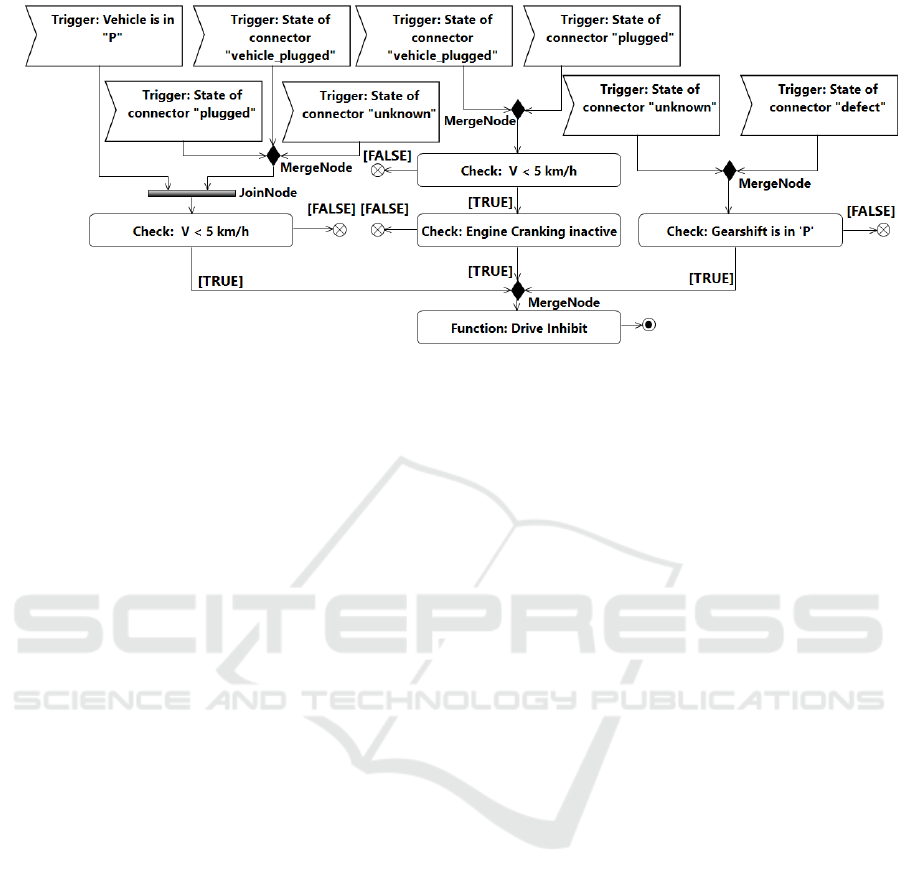
Figure 1: Activity diagram of the function Drive Inhibit.
2 BACKGROUND
Our industry partner uses UML2 activity diagrams
to specify functions of a system. These activity di-
agrams are the first step of the development of a
new system function. They are used to get an early
overview of the desired function behavior. Although
the main focus of the activity is to be a means of com-
munication and to make the understanding easier, it
already contains a number of information that can be
used in the following development phases such as the
elicitation and documentation of requirements and the
derivation of test cases.
Figure 1 shows the activity diagram of the func-
tion Drive Inhibit. The actual behavior of the ac-
tivated function is described in the Action node la-
beled with Drive Inhibit (bottom of the diagram). The
function’s activation is described by a combination
of triggers and checks for conditions. For triggers,
the AcceptEventAction element is used. The checks
are modeled as Action elements. If the condition of
a check is not fulfilled, the flow ends (FlowFinal).
As a consequence, a check acts as an implicit AND.
The triggers and checks are connected by Control-
Nodes such as JoinNodes and MergeNodes. Join-
Nodes act as synchronization points and can be in-
terpreted as AND operators in terms of propositional
logic. MergeNodes represent OR operators. Once the
actual functionality of the function is executed, Acti-
vityFinal elements designate the end of an activity.
Relevant information for our industry partner con-
cerns (amongst others): (minimal) execution paths,
propositional logic relations and sequential or inde-
pendent executability of actions.
Execution paths are of interest for testing and to
facilitate the planning of the system. They are the
basis to derive test cases that ensure that the function
is in fact activated, when certain action are executed.
The execution paths also provide information about
the sequences of execution of actions. This can be
combined with the mapping of the involved actions
to the components of the system (this mapping is not
part of the activity). As a result, it is possible to make
statements on the dependencies between the involved
components. This knowledge is applied during the
planning of the development of the system.
Propositional logic relations are needed to derive
requirements that describe the correct behavior of the
system as well as the test cases that validate these re-
quirements.
3 RELATED WORK
As this paper introduces a formalism for a certain kind
of activities, it is related to work about formal seman-
tics of UML2 activities. The UML2 Specification
describes Activities as Petri net like graphs (Object
Management Group (OMG), 2015, p. 283), but does
not provide formal semantics. Therefore a number
of formal semantics have been proposed, i.a. (St
¨
orrle,
2004). While most approaches try to cover the ca-
pabilities to a full extent, it is considered useful to
express activities in simpler constructs (Lano, 2009).
We use this idea and present a formalism solely de-
voted to derive information about certain aspects in
activities.
Graphical models are the basis for a number of
approaches that derive different software engineer-
ing artifacts from the models. Amongst others, they
are used to automatically generate source code (Us-
man and Nadeem, 2009) and test cases (Kundu and
Information Extraction from High-level Activity Diagrams to Support Development Tasks
439

Samanta, 2009). Using graphical models and espe-
cially UML to generate textual requirements or parts
of requirements documents has already been covered
by a number of research papers (Nicol
´
as and To-
val, 2009). Specifically activities as a source for re-
quirements have already been addressed by Drusin-
sky (Drusinsky, 2008), however, only for UML-1.
Additionally, we take into account propositional logic
relations, execution paths, and allow for queries on
actions about independent executions.
In contrast to the mentioned approaches, our ap-
proach focuses on extracting certain aspects of activi-
ties and does not restrict itself on a single application.
4 EXTRACTING INFORMATION
FROM ACTIVITIES
For the purpose of this paper, we aim at extracting
specific information from activities to facilitate down-
stream development tasks. More specifically, we want
to extract the following information:
Independent Actions. Independent actions within
an activity can be executed without any interrela-
tions. This information is useful for the planning
of the development. Actions are executed by com-
ponents of the system. From the independence of
actions follows that there is no flow of information
between the components and hence development
can progress without considering the component
executing an independent action.
Minimal Execution Paths. A minimal execution
path for a node within an activity is a set of
actions that need to be executed before the node
can be executed. These paths contain all actions
that are logically required for a token to reach an
action. Superfluous actions occurring in parallel
are not part of the minimal execution path. This
information is useful for the creation of test cases.
The test cases verify that a function is executed
due to or in spite of certain conditions. Using
minimal paths ensures that only conditions are
tested that influence the examined executed path.
This leads to a minimal set of tests, which are
necessary to confirm the behavior of a function.
Activation Expressions. An activation expression
for a node within an activity is a propositional ex-
pression that reflects the logical relations between
the preceding actions of the node. The activation
expression abstracts from any order of execution
and can be used to derive textual specifications
corresponding to the activities.
In the following, we present how these informa-
tion can be extracted from the activities.
4.1 Activity Graphs
To extract the information on independent actions and
minimal execution paths, we introduce activity graphs
as a simplified representation of the activities. Acti-
vity graphs focus on expressing whether certain ac-
tions are independent of one another or whether they
have to be executed sequentially. We transform an
activity to an activity graph by mapping the actions
of an activity to nodes of a graph. We assume that
implicit connections in the activity are made explicit
and that ExecutableNodes only appear once in the ac-
tivity. Beckmann et al. have proposed an approach
that we use to remove redundant occurrences of Ex-
ecutableNodes within an activity (Beckmann et al.,
2017a). There may be cycles in the activity.
Each node in the activity graph has a label contain-
ing the text of the corresponding Action of the activity.
They also have one of the following types: Trigger,
Check, Function, Merge, Decision, Join, Fork. More-
over, each node has a set of successors.
Definition 1. Activity Graph
Given a non-empty set of nodes V , an activity graph
T is defined as
T
def
= (V, suc
T
, type
T
, label
T
)
where
1. suc
T
: V → P (V ) is the successor function for
T , where suc
T
(v) denotes the set of all successor
nodes of v ∈ V,
2. type
T
: V → {Trigger,Check, Function, Merge,
Decision, Join, Fork, End} assigns a type to every
node, and
3. label
T
: V → Σ
∗
assigns a label to every node.
Definition 2. Direct Predecessors
Given an activity graph T , the set of direct predeces-
sors of a node v ∈ V is defined as
d pred
T
(v)
def
= {w|v ∈ suc
T
(w)}
In the activity the direct predecessor is the source
node of any incoming edge. There might be more than
one direct predecessor to one node. Since we assume
that all connections were made explicit and there are
no redundant elements, multiple direct predecessors
occur only for JoinNodes and MergeNodes.
Definition 3. Execution Sequence
Given an activity graph T ,
1. A list of nodes s = hv
1
, . . . , v
n
i with v
1
, . . . , v
n
∈ V
is called an execution sequence, and v
i
is called
the i-th execution step of s.
2. An execution step v
i
is a sequence-predecessor of
another execution step v
j
(denoted by v
i
<
s
v
j
) if
i < j.
MODELSWARD 2018 - 6th International Conference on Model-Driven Engineering and Software Development
440

3. The set of all execution sequences of T is denoted
by S.
Considering Figure 1 one possible execution se-
quence might be Trigger: State of connector ”un-
known”, Check: Gearshift is in ’P’, Function: Drive
Inhibit.
Definition 4. Prefix
Given an activity graph T and an execution sequence
s = hv
1
, . . . , v
n
i. For any k with 1 ≤ k ≤ n the k-prefix
(or just prefix) of s is defined by
s
(k)
def
= hv
1
, . . . , v
k
i.
Definition 5. Node Count
Given an activity graph T and an execution sequence
s = hv
1
, . . . , v
n
i. For any node v ∈ V , the node count
of v in s is a function #
v
(s) : S → N and describes the
number of appearances of v in s.
Example:
• #
a
(ha, b, c, a, d, e, a, di) = 3,
• #
e
(ha, b, c, a, d, e, a, di) = 1,
• #
f
(ha, b, c, a, d, e, a, di) = 0.
Definition 6. Valid Execution Sequence
Given an activity graph T and an execution sequence
s = hv
1
, . . . , v
n
i,
1. An execution step v
i
of a sequence s is valid (de-
noted by s `
T
v
i
) if and only if one of the following
cases is true:
(a) d pred
T
(v
i
) =
/
0,
(b) d pred
T
(v
i
) 6=
/
0 ∧type(v
i
) 6= Merge ∧
∀w ∈ d pred
T
(v
i
).#
w
(s
(v
i
)
) ≥ #
v
i
(s
(v
i
)
)
Explanation: A join node is valid when each of
its predecessors appears at least as often as the
join node itself in the prefix before it. Check,
Function, Fork, Decision, and End nodes are
similar, but have only one predecessor. The for-
mula is the same for them.
(c) d pred
T
(v
i
) 6=
/
0 ∧type(v
i
) = Merge ∧
#
v
i
(s
(v
i
)
) <=
∑
w∈d pred
T
(v
i
)
#
w
(s
(v
i
)
)
Explanation: A merge node is valid when all its
predecessors together appear at least as often
as the merge node itself in the prefix before it.
2. An execution sequence s is valid (denoted by `
T
s), when all its execution steps are valid.
3. The set of all valid execution sequences for T is
denoted by S
T
.
Definition 7. Predecessor
Given an activity graph T , a node v
i
∈ V is a prede-
cessor of another node v
j
∈ V (denoted by v
i
<
T
v
j
)
if v
i
is a sequence predecessor of v
j
in every valid se-
quence of T .
v
i
<
T
v
j
⇔ ∀s ∈ S
T
.v
i
<
s
v
j
This definition is used to find dependencies be-
tween actions. In case a node is predecessor of an-
other node, the predecessor has to be executed first.
This also tells us that there is an interaction between
nodes.
Definition 8. Independent Nodes / Parallel Exe-
cutable
Given an activity graph T , two nodes v
i
, v
j
∈ V are
independent (denoted by v
i
k
T
v
j
) if they are not pre-
decessors of each other:
v
i
k
T
v
j
⇔ v
i
≮
T
v
j
∧ v
j
≮
T
v
i
In contrast to the predecessor relation, two inde-
pendent nodes can be executed without any interre-
lations between the involved actions. An example in
Figure 1 are the checks V < 5 km/h and Gearshift is
in ’P’.
Definition 9. Minimal Execution
Given an activity graph T and a node v ∈ V . A
minimal execution sequence s
min,T
(v) = hv
1
, . . . , v
n
i
is a valid execution sequence that ends in v and
for which no i exists for which 1 ≤ i < n and
hv
1
, . . . , v
i−1
, v
i+1
, . . . , v
n
i is valid.
Note, that v
n
= v because the sequence ends in v.
Explanation: An execution sequence is minimal when
no step can be cut out of the sequence.
Every path to the specified node that does not con-
tain unnecessary actions for the activation, is a mini-
mal execution. Since MergeNodes might have multi-
ple predecessors, there can be more than one minimal
execution. The action Check: V < 5 km/h after the
JoinNode in Figure 1 has three minimal executions.
Each path consists of one of the three triggers con-
nected by the MergeNode, the MergeNode itself, the
JoinNode and the action Trigger: Vehicle is in ’P’.
Definition 10. Concatenation of Execution Se-
quences
Given two execution sequences of disjoint nodes
s
1
= hv
1
, . . . , v
n
i and s
2
= hw
1
, . . . , w
m
i. The concate-
nated execution sequence s
1
◦ s
2
is defined as
s
1
◦ s
2
def
= hv
1
, . . . , v
n
, w
1
, . . . , w
m
i
The algorithm to compute a minimal execution is
shown in Algorithm 1. The algorithm works recur-
sively through the graph. In a each step the necess-
ary minimal executions are concatenated to the cur-
rent node. Which executions are necessary depends
on the type of the node. In case a node is neither a
JoinNode nor a MergeNode, the minimal execution
is the concatenation of the minimal execution of its
direct predecessor and itself. For a JoinNode, all pre-
vious minimal executions are needed. For a Merge-
Node, any of the predecessor can be used. Hence,
Information Extraction from High-level Activity Diagrams to Support Development Tasks
441

Algorithm 1: Recursively computing a minimal execution.
Input: Activity Graph T , Node v ∈ V
function MINEX(v)
if d pred
T
(v) =
/
0 then
return {v}
else if type(v
i
) 6∈ {Merge,Join} and
d pred
T
(v) = {w} then
return MINEX(w) ◦ hvi
else if type
T
(v) = Join and
d pred
T
(v) = {w
1
, . . . , w
n
} then
return MINEX(w
1
) ◦ ··· ◦ MINEX(w
n
) ◦ hvi
Note, this step is not deterministic, since depend-
ing on the order of concatenation there are multiple
options. Only one choice is needed.
else if type
T
(v) = Merge and
w ∈ d pred
T
(v) (any predecessor) then
return MINEX(w) ◦ hvi
Note that this step is not deterministic, since mul-
tiple predecessors can exist. Any choice would be
correct.
end if
end function
there are multiple minimal executions. The algorithm
terminates, if there are no predecessors or if a cycle is
detected. Executions containing cycles are discarded,
because they cannot be minimal executions.
4.2 Activation Expressions
Actions that are predecessors of other actions in an ac-
tivity diagram can also be interpreted as logical facts
that need to be fulfilled before an action can be ex-
ecuted. Activation expressions focus on these logi-
cal relations between actions. These relations can be
represented by a propositional logic expression tree.
The algorithm to construct the activation expression
for a node in an activity graph is displayed in Algo-
rithm 2.
The algorithm requires the node for which the ac-
tivation expression shall be computed as input. In our
case, we are especially interested in action nodes that
represent function executions. Some of the activities
of our industry partner contain more than one func-
tion. In that case, multiple trees have to be created
since each function has different triggers and checks,
and thus, the activation expression is also different.
As a second input, the algorithm requires a node of
the tree that is to be created. The input is required
since the algorithm works recursively. When the al-
gorithm is called for the first time, a start node is used
Algorithm 2: Recursively computing an expression tree.
Input: Node v
Act
∈ V
Act
, Node v
Tree
∈ V
Tree
function CREATEEXPTREE(v
Act
, v
Tree
)
if d pred
Act
(v
Act
) =
/
0 then
suc
Tree
(v
Tree
) = suc
Tree
(v
Tree
) ∪ v
Act
else if d pred
Act
(v
Act
) 6=
/
0 and type
Act
(v
Act
) ∈
{Trigger,Check, Function} then
v
Tree
next
def
= createNode(AND)
suc
Tree
(v
Tree
) = suc
Tree
(v
Tree
) ∪ v
Tree
next
suc
Tree
(v
Tree
next
) = suc
Tree
(v
Tree
next
) ∪ v
Act
v
Act
def
= v ∈ d pred
Act
(v
Act
)
v
Tree
def
= v
Tree
next
createExpTree(v
Act
, v
Tree
)
else if d pred
Act
(v
Act
) 6=
/
0 and
type
Act
(v
Act
) = Join then
v
Tree
and
def
= createNode(AND)
suc
Tree
(v
Tree
) = suc
Tree
(v
Tree
) ∪ v
Tree
and
for all v
Act
in
of d pred
Act
(v
Act
) do
v
Act
def
= v
Act
in
v
Tree
def
= v
Tree
and
createExpTree(v
Act
, v
Tree
)
end for
else if d pred
Act
(v
Act
) 6=
/
0 and
type
Act
(v
Act
) = Merge then
v
Tree
or
def
= createNode(OR)
suc
Tree
(v
Tree
) = suc
Tree
(v
Tree
) ∪ v
Tree
or
for all v
Act
in
of d pred
Act
(v
Act
) do
v
Act
def
= v
Act
in
v
Tree
def
= v
Tree
or
createExpTree(v
Act
, v
Tree
)
end for
else if d pred
Act
(v
Act
) 6=
/
0 and
type
Act
(v
Act
) ∈ {Fork, Decision} then
v
Act
def
= v ∈ d pred
Act
(v
Act
)
createExpTree(v
Act
, v
Tree
)
end if
end function
as the root node of the tree. What the algorithm basi-
cally does, is to traverse the activity graph backwards.
It starts from the node that represents the function that
has to be activated. From there the predecessors are
analyzed until the triggers of the function or nodes
without any predecessors are reached. As a conse-
quence, the algorithm terminates as long as there is
no cycle in any of the execution sequences. This can
be automatically ensured beforehand by checking for
MODELSWARD 2018 - 6th International Conference on Model-Driven Engineering and Software Development
442

Figure 2: Expression Tree of the function Drive Inhibit
cycles. Also, for the activities our industry partner
uses, a detected cycle can be ignored. This is possi-
ble, since the repeated execution of actions does not
have any influence on the function activation. If the
actions in the cycle were executed once, the flow of
tokens also continues outside the cycle. Further repe-
titions do not effect that flow.
In each step of the traversal, the type of the current
activity node is examined. Depending on the type, the
nodes that are appended to the tree, differ. In case the
examined node is an Action (e.g., a check), it means
it has to be executed successfully for the flow to con-
tinue. This is depicted in Figure 3a. The traversal
of the activity starts from the function. Before the
function can be executed, a check must be fulfilled.
Besides, there might be other nodes before the check.
As this represents an AND connection, an AND node
is added to the tree, and the found check is added to
that new AND node. The resulting tree is shown in Fi-
gure 4a. The following recursive call uses the added
AND node as the tree node input. The following ac-
tivity nodes are then added to the AND. If a Join-
Node or MergeNode is found in the activity, an AND
or OR node is appended to the tree respectively. In
contrast to a single action, these ControlNodes might
have more than one predecessor. Exemplar activities
for the JoinNode and the MergeNode are shown in Fi-
gure 3b and Figure 3c respectively. All predecessors
are added to these tree nodes. The corresponding ex-
pression trees to the activities in Figure 3b and Fi-
gure 3c are shown in Figure 4b and Figure 4c. There
is no negation operator, since there are no actions that
undo events and hence stop the flow of tokens.
The corresponding expression tree to the activity
in Figure 1 is displayed in Figure 2. The tree nodes
that represent the operators (START, AND, OR) are
displayed in square boxes, while the actual ActivityN-
(a) Checks connected sequentually
(b) Checks connected by a JoinNode
(c) Checks connected by a MergeNode
Figure 3: Different situations in activities.
odes are displayed as oval boxes. As a result of the
algorithm, the ExecutableNodes of the original acti-
vity are the leaves of the tree.
5 APPLICATIONS AND
LIMITATIONS
5.1 Applications
We used the introduced algorithms and definitions to
support different development tasks in practice.
Information Extraction from High-level Activity Diagrams to Support Development Tasks
443

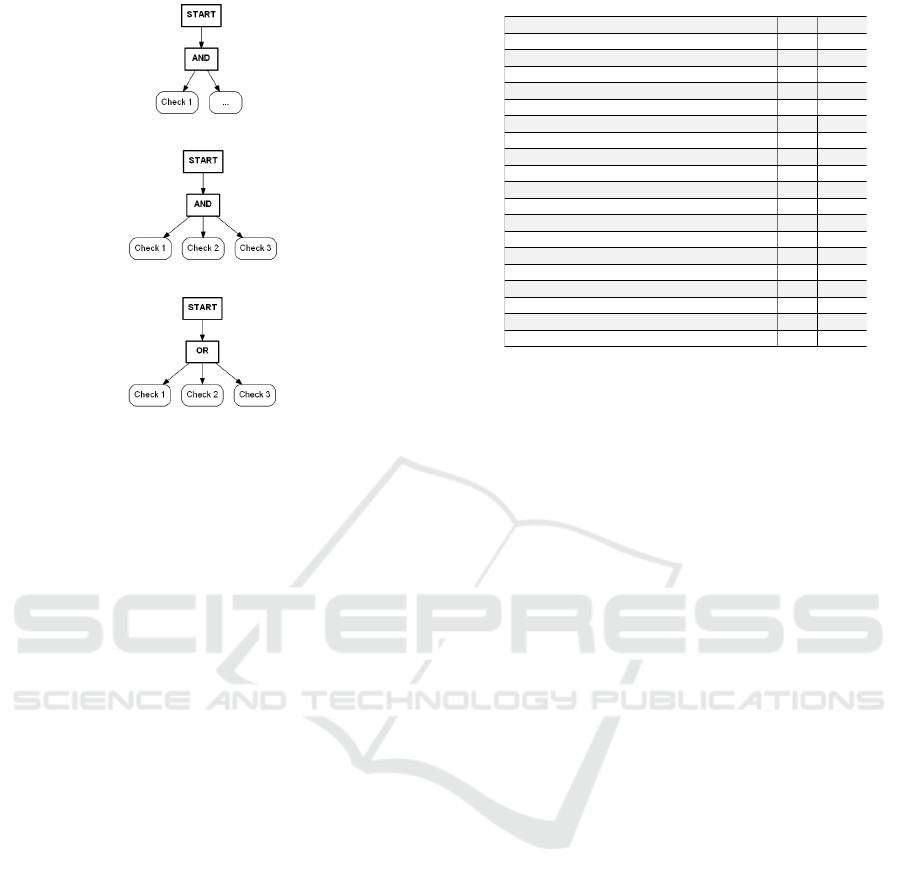
(a) Corresponding expression tree to situation in Figure 3a
(b) Corresponding expression tree to situation in Figure 3b
(c) Corresponding expression tree to situation in Figure 3c
Figure 4: Resulting expression trees.
5.1.1 Transformation of Activity Diagrams to
Textual Specifications
In industry, graphical models such as activity dia-
grams cannot be used as the sole means of speci-
fication. Textual requirements complementing the
activities are needed because of legal considera-
tions (Sikora et al., 2012; Maiden et al., 2005) and
to provide a systematic display of derived informa-
tion (Weber and Weisbrod, 2002). Recent studies
have found that practitioners prefer textual require-
ments specifications that are structured according to
the different logical cases that may lead to a spe-
cific event (Beckmann and Vogelsang, 2017). There-
fore, we used the structure of the activation expression
tree to generate complementing textual requirements
specifications for 36 activity diagrams of our industry
partner. That way, we eliminated hundreds of differ-
ent existing quality issues of a previous version.
Figure 5 shows the textual requirements derived
from the activity of Figure 1. The excerpt shows
explicitly the propositional logic relations by using
the operators AND and OR. All elements connected
by the same operator were placed one level below.
This kind of structure equals the structure of the ac-
tivation expression tree. Hence, we could directly
map the result of the underlying propositional logic
to the document structure. Prior studies have shown
that manual creation and maintenance of textual re-
quirements from diagrams is error-prone and labor-
intensive (Beckmann et al., 2017b). An automatic
model-to-text transformation based on our algorithm
prevents quality issues and may save time.
Text
Level
Type
Drive Inhibit
2
Function
OR 3
-
AND 4
-
Vehicle is in "P" 5
Trigger
OR 5
-
State of connector "plugged" 6
Trigger
State of connector "vehicle_plugged" 6
Trigger
State of connector "unknown" 6
Trigger
V < 5 km/h 5
Check
AND 4
-
OR 5
-
State of connector "plugged" 6
Trigger
State of connector "vehicle_plugged" 6
Trigger
V < 5 km/h 5
Check
Engine Cranking inactive 5
Check
AND 4
-
OR 5
-
State of connector "defect" 6
Trigger
State of connector "unknown" 6
Trigger
Gearshift is in "P" 5
Check
Figure 5: Derived Textual Requirements.
5.1.2 Derivation of Test Cases
The approach was applied to recreate parts of already
existing test cases for the displayed function Drive In-
hibit in an automatic manner as a proof-of-concept.
These parts encompass the name of the test case as
well as templates for the test steps that must be per-
formed to conduct the test case. The test steps must
be added manually as they are not part of the activity
diagram. The test cases ensure that the function is
activated due to certain occurring events and fulfilled
conditions. The necessary states and circumstances
were directly derived from the identified minimal ex-
ecutions. The minimal executions of an action in the
activity contain all necessary actions (i.e., events) that
must appear and conditions that must be fulfilled to
start an execution. As a result, test cases that describe
in which states a function is activated can be directly
derived since a minimal execution only contains these
necessary conditions. Consequently every minimal
execution is used to derive one test case. The cre-
ated test cases can therefore assure that the function
is in fact executed under the intended circumstances.
Hence, using this approach ensures that all necessary
conditions for executions are tested. For example in
Figure 1 this leads to the creation of seven test cases.
Three test cases originate from the three triggers con-
nected to the trigger Vehicle is in ”P” by a JoinNode.
Two test cases are created for each pair of the two
triggers connected by the MergeNodes.
In addition, non-minimal sequences can also be
useful. The execution of superfluous actions makes
sure the function is still activated when the necess-
ary actions were executed. Also, it can be checked
whether the function is activated, although necessary
conditions are not met. In that case necessary actions
are not executed.
MODELSWARD 2018 - 6th International Conference on Model-Driven Engineering and Software Development
444

5.2 Limitations
We focused on the capability of activities to describe
sequences, parallelism, execution paths and proposi-
tional logic relations. Still, activities can be used in
other ways to describe other aspects of behavior. Con-
sequently, it is not possible to foresee every applica-
tion. Thus, it is necessary to restrict oneself to cer-
tain aspects. While the extracted information can be
used for multiple purposes, there are use cases that
require different aspects our approach does not yet
cover. One of these aspects are asynchronous events
that are potentially used to abort the execution of an
activity. These were not part of our work, since our
industry partner does not use them.
Also, this work focuses on the activity diagrams
of our industry partner. These activities only incor-
porate a subset of elements in activities. Still, this
kind of description is quite common to describe func-
tions (Firesmith, 2004). As a result, the approach is
not generally applicable but we think that it provides
a benefit for that kind of graphical descriptions.
6 CONCLUSION AND OUTLOOK
In this paper we presented an approach to extract im-
plicitly contained information from high-level activ-
ities to support downstream development tasks. For
this purpose we introduce activity graphs as a simpli-
fied, yet formal, representation of activity diagrams,
which can be used to make statements about se-
quences and execution paths of activities. We show
in detail how this can be used to derive textual re-
quirements, which both improves the quality of the
resulting requirements document and saves effort in
its creation. Also, the creation of test cases was per-
formed as a proof-of-concept for one function.
Furthermore, it is planned to use the extracted in-
formation for impact analysis. By combining the ac-
tivities with the mapping of the actions to the com-
ponents, dependencies between components are made
more easily accessible. This knowledge will be used
to derive visual architectural views of the whole sys-
tem, which in turn shall facilitate release planning.
As the approach is restricted to a subset of ele-
ments, the approach is not generally applicable to all
activities. Incorporating all elements (such as guards)
of activities into the approach is an open issue. Also,
there are further aspects of activities that are needed
during the development of systems we did not yet
consider. Which aspects need to be included and what
artifacts they might be used for is also worth investi-
gating.
REFERENCES
Arlow, J. and Neustadt, I. (2004). Enterprise patterns and
MDA: Building better software with archetype pat-
terns and UML. Addison-Wesley Professional.
Beckmann, M., Michalke, V., Vogelsang, A., and Schlutter,
A. (2017a). Removal of Redundant Elements within
UML Activity Diagrams. In Conference on Model
Driven Engineering Languages and Systems.
Beckmann, M. and Vogelsang, A. (2017). What is a Good
Textual Representation of Activity Diagrams in Re-
quirements Documents? In Model-Driven Require-
ments Engineering Workshop.
Beckmann, M., Vogelsang, A., and Reuter, C. (2017b). A
Case Study on a Specification Approach using Acti-
vity Diagrams in Requirements Documents. In Inter-
national Requirements Engineering Conference.
Broy, M. (2006). Challenges in automotive software en-
gineering. In Proceedings of the 28th international
conference on Software engineering.
Drusinsky, D. (2008). From UML activity diagrams to
specification requirements. In International Confer-
ence on System of Systems Engineering.
Firesmith, D. (2004). Generating Complete, Unambiguous,
and Verifiable Requirements from Stories, Scenarios,
and Use Cases. Journal of Object Technology.
Kundu, D. and Samanta, D. (2009). A Novel Approach to
Generate Test Cases from UML Activity Diagrams.
Journal of Object Technology.
Lano, K. (2009). UML 2 Semantics and Applications. John
Wiley & Sons.
Maiden, N. A., Manning, S., Jones, S., and Greenwood, J.
(2005). Generating requirements from systems mod-
els using patterns: a case study. Requirements Engi-
neering.
Nicol
´
as, J. and Toval, A. (2009). On the generation of re-
quirements specifications from software engineering
models: A systematic literature review. Information
and Software Technology.
Object Management Group (OMG) (2015). OMG Unified
Modeling Language (OMG UML), Version 2.5.
Sikora, E., Tenbergen, B., and Pohl, K. (2012). Industry
needs and research directions in requirements engi-
neering for embedded systems. Requirements Engi-
neering.
St
¨
orrle, H. (2004). Semantics of UML 2.0 Activities. In
Symposium on Visual Languages and Human-Centric
Computing.
Usman, M. and Nadeem, A. (2009). Automatic Generation
of Java Code from UML Diagrams using UJECTOR.
Journal of Software Engineering and Its Applications.
Vogelsang, A., Eder, S., Hackenberg, G., Junker, M., and
Teufl, S. (2014). Supporting concurrent development
of requirements and architecture: A model-based ap-
proach. In Conference on Model-Driven Engineering
and Software Development.
Weber, M. and Weisbrod, J. (2002). Requirements En-
gineering in Automotive Development - Experiences
and Challenges. In International Conference on Re-
quirements Engineering.
Information Extraction from High-level Activity Diagrams to Support Development Tasks
445