Spectral Analysis of Keystroke Streams: Towards Effective Real-time

Continuous User Authentication

Abdullah Alshehri, Frans Coenen and Danushka Bollegala

Department of Computer Science, University of Liverpool, Liverpool, U.K.

Keywords:

Keystroke Time Series, Continuous Authentication, Keystroke Streams, Behavioral Biometric.

Abstract:

Continuous authentication using keystroke dynamics is signiﬁcant for applications where continuous moni-

toring of a user’s identity is desirable, for example in the context of the online assessments and examinations

frequently encountered in eLearning environments. In this paper, a novel approach to realtime keystroke

continuous authentication is proposed that is founded on a sinusoidal signal based approach that takes into

consideration the sequencing of keystrokes. Three alternative time series representations are considered and

compared: Keystroke Time Series (KTS), Discrete Fourier Transform (DFT) and Discrete Wavelet Transform

(DWT). The proposed process is fully described and analysed using three keystroke dynamics datasets. The

evaluation also includes a comparison with the established Feature Vector Representation (FVR) approach.

The reported evaluation demonstrates that the proposed method, coupled with the DWT representation, out-

performs other approaches to keystroke continuous authentication with a best overall accuracy of 98.24%; a

clear indicator that the proposed keystroke continuous authentication using time series analysis has signiﬁcant

potential.

1 INTRODUCTION

Keystroke dynamics are a form of behavioural bio-

metrics which can be used to authenticate keyboard

(keypad) users (Gaines et al., 1980; Alshehri et al.,

2016b). Broadly, we can identify two forms of

keystroke authentication: (i) static authentication and

(ii) continuous authentication. The ﬁrst is used in the

context of one-time authentication, for example pass-

word or pin number access to a system; thus in the

context of ﬁxed texts. Some examples, from the lit-

erature, concerning this form of authentication can be

found in (Bleha et al., 1990; Killourhy and Maxion,

2009; Syed, 2014). The second form of authentica-

tion is typically applied in the context of continuous

free text where it is desirable to continuously monitor

the identity of a user; examples regarding this form of

authentication can be found in (Shepherd, 1995; Mon-

rose and Rubin, 1997; Dowland and Furnell, 2004;

Gunetti and Picardi, 2005; Ahmed and Traore, 2014).

One application, where continuous authentication is

applicable, is in the case of students completing on-

line assessments as part of distance and online learn-

ing systems.

The focus of the work presented in this paper is con-

tinuous authentication. The reasons for this are as

follows: (i) there is little reported work concerning

continuous authentication using keystroke dynamics

due to the challenges involved, and (ii) the increas-

ing prevalence of internet facilitated distance learning

(eLearning, Massive Open Online Courses and so on)

where continuous authentication is desirable.

In this paper, we introduce a novel mechanism

for keystroke continuous authentication, namely

Keystroke Continuous Authentication based Spectral

Analysis (KCASA) mechanism. The proposed model

is motivated by conceptualising the process of key-

board usage as a continuous stream of keystroke

events, thus as a time series which can be trans-

formed into the spectral domain to extract typing

patterns. More speciﬁcally, the idea is to convert

a given keystroke stream from the temporal domain

(raw data) to the sinusoidal (frequency) domain. The

intuition is that such transformations for time series

streams lead to faster, and more accurate, detection

of patterns (Chan and Fu, 1999; Keogh et al., 2001).

Therefore, keystroke streams can be effectively em-

ployed for real-time/continuous user authentication.

In this study, two types of spectral transform are con-

sidered: (i) Discrete Fourier Transformation (DFT)

and (ii) Discrete Wavelet Transform (DWT).

The remainder of this paper is structured as follows.

Alshehri, A., Coenen, F. and Bollegala, D.

Spectral Analysis of Keystroke Streams: Towards Effective Real-time Continuous User Authentication.

DOI: 10.5220/0006606100620073

In Proceedings of the 4th International Conference on Information Systems Security and Privacy (ICISSP 2018), pages 62-73

ISBN: 978-989-758-282-0

In Section 2 a problem statement is provided to-

gether with a discussion of current issues with respect

to keystroke continuous authentication. This is fol-

lowed. in Section 3, with some deﬁnitions and pre-

liminaries concerning the proposed model. Section

4 then discusses the proposed process for ﬁnding the

similarity between keystroke sinusoidal signals, while

Section 5 presents the proposed KCASA model. The

evaluation of the proposed approach is given in Sec-

tion 6. Finally, the paper is concluded with a summary

of the main ﬁndings, and some recommendations for

further work, in Section 7.

2 PREVIOUS WORK

The fundamental approach of using keystroke dy-

namics for user authentication is founded on two

keystroke timing features: (i) key hold time (KH

the elapsed time between a key press and a key re-

lease; and (ii) ﬂight time (F

), the time between n

consecutive key presses (releases), also sometimes

referred to as ﬂight time latency or simply latency

(Obaidat and Sadoun, 1997). Both can be indexed

using either a temporal or a consecutive numeric ref-

erence. Whatever the case, both ﬂight time and hold

time can be used to construct a distinctive typing pro-

ﬁle associated with individual users (Gaines et al.,

1980). These proﬁles are typically encapsulated using

a feature vector representation of some form. In other

words, typing proﬁles are frequently constructed us-

ing vectors of statistical values, such as the average

and standard deviation of hold times, or the digraph

ﬂight time latency of selected frequently occurring di-

graphs. Authentication is then conducted by compar-

ing the similarity between stored feature vectors rep-

resented typing (reference) proﬁles, which are known

to belong to a speciﬁc user, and a previously unseen

proﬁle that is claimed to belong to a particular user.

Although there has been only limited reported work

directed at keystroke continuous authentication, what

reported work there has been has used a feature vector

representation; this has met with some success.

However, there are some limitations regarding the

utilisation of the feature vector representation in the

context of keystroke continuous authentication. One

of the main limitations is the size of the required fea-

ture vectors; a signiﬁcant number of digraphs and/or

trigraphs has to be considered which is infeasible in

the context of real-time continuous authentication. In

(Monrose and Rubin, 1997) the feature vectors were

composed of the ﬂight time means of all digraphs in

the training dataset. The continuous authentication

was then conducted by repeatedly generating “test”

feature vectors for a given user, one every minute,

and comparing with stored reference proﬁles. If a

statistically similar match was found, then this was

considered to be an indication of user authentication.

Although the typing proﬁle was composed of all di-

graph features, the overall reported accuracy was a

dsappoiting 23%. Similarly, in (Dowland and Fur-

nell, 2004) the mean and Standard Deviation (SD) of

the ﬂight times for all digraphs and trigraphs in the

training dataset were used. Some 6,390 digraphs were

needed to make up a sufﬁcient typing proﬁle.

Some researchers have attempted to use an abstrac-

tion of typing features to decrease the size of the fea-

ture vectors. In (Gunetti and Picardi, 2005) the ﬂight

time, for frequent n-graphs, was used, although the

approach was applied in the context of user identiﬁca-

tion (as opposed to user authentication). Thus, given

a previously unseen sample, the shared n-graphs in

the sample and the stored n-graphs were identiﬁed

and collected in separate arrays. The elements in

the arrays were then ordered according to ﬂight time

and the difference between the arrays computed by

considering the orderings of the elements; a measure

referred to as the degree of disorder was used (an

idea motivated by Spearman’s rank correlation co-

efﬁcient (Zar, 1972)). Identifying a new sample re-

quired comparison with all stored sample (reference)

proﬁles, a computationally expensive process. In the

reported evaluation, 600 reference proﬁles were con-

sidered (generated from 40 users, each with 15 sam-

ples); the time taken for a single match was 140 sec-

onds (using a Pentium IV, 2.5 GHz). However, con-

struction typing proﬁle using the average ﬂight time

of only shared n-graphs contained in the training data

might not be representative of the n-graphs in the sam-

ples to be authenticated. This can, in turn, affect the

authentication accuracy, especially in the context of

real-time continuous authentication where typing pat-

terns are extracted from free text; a substantial num-

ber of n-graphs are required. Furthermore, it can be

observed from the study presented in (Gunetti and Pi-

cardi, 2005) that the authentication of one sample re-

lies on all other samples in the training data. This can

also lead to an efﬁciency issue in the context of con-

tinuous authentication.

In (Ahmed and Traore, 2014) an Artiﬁcial Neural

Network classiﬁer was used to build a prediction

model to overcome the limitation of the work pre-

sented in (Gunetti and Picardi, 2005). Key-down

time was used together with average digraph and

monograph ﬂight times to predict missing digraphs

based on the limited information in the training data;

thus, there was no need to involve a great number of

keystroke features while constructing the typing pro-

Spectral Analysis of Keystroke Streams: Towards Effective Real-time Continuous User Authentication

ﬁle. This mechanism worked reasonably well in the

context of static authentication in a controlled setting;

typing of the same text using the same keyboard lay-

out in an allocated environment. Thus how this would

work in the context of continuous authentication re-

mains an open question. A more general criticism of

the feature vector approach is that the feature vector

values are either typing pattern abstractions (for ex-

ample average hold times) or only represent a subset

of the data (for example only frequently occurring di-

graphs).

It is proposed in this paper that the established fea-

ture vector representation may not be ideally suited

to keystroke continuous authentication. It is argued

that by representing keystroke dynamics as time se-

ries, and transforming these series to the frequency

domain, can lead to a better intepretation of typing

patterns with respect to real-time continuous authenti-

cation. To the best knowledge of the authors, no prior

work in the literature has considered the concept of

the sinusoidal representation of keystroke dynamics

in the context of continuous keyboard authentication.

However, it should be noted that in (Alshehri et al.,

2016b) the authors ﬁrst proposed the idea of keyboard

based user authentication using time series, but with

respect to static text. In (Alshehri et al., 2016a) it was

suggested that this could also be applied in the context

of continuous text, although only hold time was con-

sidered. This paper presents a much more sophisti-

cated implementation of the approach, encompassing:

(i) the concept of transforming keystroke time series

into the sinusoidal (frequency) domain, (ii) utilsing

additional keystroke timing features to enhance au-

thentication effectiveness, (iii) usage of a transformed

sinusoidal sliding windows to achieve authentication,

(iv) a data cleaning process for keystroke dynamic to

be applied prior to any authentication being carried

out and (iv) a dynamic method for bespoke similarity

thresholds applicable to individual users.

3 REPRESENTING KEYSTROKE

DYNAMICS AS TIME SERIES

As already noted, the process of typing produces

a Keystroke time series K

= {e

,...,e

} where

is an independent data event, and n ∈ N is the

length of the time series. Each data event e

rep-

resents a tuple of the form ht

i where: (i) t

a temporal index of some form, and (ii) k

denotes

some associated attribute (feature) value. Thus, K

{ht

i,ht

i,...,ht

i}. Such a time series can

be viewed as a 2D plot with t along the x-axis and

attribute value k along the y-axis (Figure 1). With re-

spect to the work presented in this paper, the value

for t

is set to be a sequential ID number (sequence of

key presses), whilst k records either ﬂight time (F

)

or hold time (KH

). Note also that in this paper only

the univariate time series representation is considered,

that is, in the evaluation section, we consider F

and

as independently and compare their effectiveness

in the context of the proposed model. Figure 1 shows

four pairs of K

sequences, each featuring n = 300

keystrokes, using F

as the keyboard dynamic. The

ﬁgure shows four (random) subjects selected from the

datasets used for evaluation purposes as reported on

in Section 6. Inspection of the ﬁgure clearly indicates

that individual subjects poses distinct keystroke pat-

terns and that these patterns can consequently be used

to generate distinct typing proﬁles.

The generated keystroke time series can be used di-

rectly as described in (Alshehri et al., 2016b). How-

ever, as already noted, the usage of such “raw” time

series is expensive in terms of efﬁciency and storage

capacity (Agrawal et al., 1993). Thus the idea pre-

sented in this paper is to use some forms of trans-

formation of the time series; it is conjectured that

this will yield accurate results more efﬁciently. Two

transformations are considered: the Discrete Fourier

Transform (DFT) and the Discrete Wavelet Transform

(DWT). Each is discussed in further detail in the fol-

lowing two sub-sections.

3.1 The Discrete Fourier Transform

The Discrete Fourier Transform (DFT) has been

widely adopted with respect to time series data of all

kinds (see for example (Agrawal et al., 1993; Vla-

chos et al., 2004)). In this paper, DFT has been used

to transform keystroke time series data from the tem-

poral domain to the frequency domain. The idea is

that this will then allow comparisons of keystroke

times series in a more efﬁcient manner (than if the

transformation had not been conducted) without los-

ing any salient information. The compression is con-

ducted by representing the keystroke stream as a lin-

ear combination of sinusoidal coefﬁcients. Similarity

between the transformed coefﬁcients for any pair of

corresponding signals can then be computed for au-

thentication purposes.

Given a keystroke time series K

= {e

,...,e

where k

∈ e

is either a F

or a KH

value, and n

is the length of the keystroke time series. The DFT

transform compresses K

into a linear set of sinu-

soidal functions with amplitudes p, q and phase w:

∑

i=1

Cos(2πw

) + q

Sin(2πw

)) (1)

ICISSP 2018 - 4th International Conference on Information Systems Security and Privacy

(ms)

Subject 1 Subject 2 Subject 3 Subject 4

a) a) a) a)

b) b) b) b)

Figure 1: Keyboard time series examples (n = 300) for four subjects, two examples per subject, writing unspeciﬁed free text.

The time complexity for transforming (each) K

time

series is O(n log n) using the radix 2 DFT algorithm

(Janacek et al., 2005; Cooley and Tukey, 1965).

Using the DFT transform, the obtained K

is com-

posed of a new magnitude (the amplitude of the dis-

crete coefﬁcients) and phase spectral shape in which

the similarity can be computed between pairs of trans-

formed K

. Similarity measurement will be discussed

in further detail in Section 4. Further detail concern-

ing the DFT can be found in(Harris, 1978).

3.2 The Discrete Wavelet Transform

The Discrete Wavelet Transform (DWT) is an alter-

native form of time series representation that con-

siders the time span over which different frequen-

cies are present in a time series. DWT is some-

times claimed to provide a better transformation than

DFT in that it retains more information (Chan and Fu,

1999). DWT can be applied to time series accord-

ing to different scales, orthogonal (Haar, 1910) and

nonorthogonal (Gabor, 1946). In this paper, an or-

thogonal scale is used for the DWT, more speciﬁcally

the well known Haar transform was adopted (Haar,

1910) as described in (Chan and Fu, 1999). Fun-

damentally, a Haar wavelet is simply a sequence of

functions which together form a wavelet comprised

of a series of square shapes. The Haar transform is

considered to be the simplest form of DWT; however,

it has been shown to offer advantages with respect to

time series analysis where the time series feature sud-

den changes. The transformation is usually described

in terms of Equation 2 where, in the context of this

paper, x is some keystroke dynamic.

φ(x) =







1 if 0 < t <

−1 if

< t < 1

0 otherwise

(2)

The time complexity for transforming (each) K

time

series, using the Haar transform is O(n). Further de-

tail concerning the Haar DWT transform can be found

in (Edwards, 1991) and (Burrus et al., 1997).

4 SIMILARITY MEASUREMENT

Comparison of the transformed keystroke time series,

for the purpose of continuous authentication, requires

some kind of similarity measure. Given two keystroke

time series, S

and S

, of the same length, the sim-

plest manner in which this can be achieved is to com-

pare the sum or average of the Euclidean distances be-

tween all pairs of corresponding points in S

and S

The smaller the sum (average) the more similar the

two time series are; If the sum (average) is 0 then S

and S

are identical. However, this simple approach

does not take into account “offsets” (phase shifts and

amplitude differences) that might exist in the time se-

ries. For the proposed KCASA model, detailed in the

following section, Dynamic Time Warping (DTW)

was therefore adopted. The advantage offered is that

DTW takes into consideration phase shifts between

pairs of signals whereas Euclidean distance does not

(Ye and Keogh, 2009).

In more detail, the operation of DTW can best be de-

scribed by considering two (transformed) keystroke

time series S

= {a

,...,a

} and S

,...,b

}, where x and y are the lengths

of the two series respectively, and (a

and b

) are DFT

or DWT coefﬁcients. A matrix M of size x − 1 ×y − 1

is then constructed whereby the value held at each cell

i j

∈ M is the distance from point a

∈ S

to point

∈ S

i j

− b

)

(3)

The matrix M is used to determine a minimum warp-

ing distance (wd), which is then used as a similarity

measure. A wd is the accumulated sum of the val-

ues associated with a Warping Path (W P) from cell

0,0

to cell m

x−1,y−1

. A warping path is a sequence

of cell locations, W P = {w

,...,w

}, such that

given w

= m

i, j

the follow on location is either m

i+1, j

i, j+1

or m

i+1, j+1

. The wd associated with a particu-

lar W P is then the sum of the values held at the loca-

tions in W P:

Spectral Analysis of Keystroke Streams: Towards Effective Real-time Continuous User Authentication

Top

(a) (b)

Bottom

Figure 2: Warping Path (WP) examples. Top: W Ps obtained from comparing two keystroke sinusoidal signals from the same

subject typing different texts, (a) DFT and (b) DWT. Bottom W Ps obtained from comparing two keystroke sinusoidal signals

from two different subjects writing different texts, (c) DFT and (d) DWT.

wd =

|W P|

∑

i=1

∈ W P (4)

To arrive at a minimum wp, for each location the fol-

lowing location is chosen so as to minimise the ac-

cumulated wd. The“best” warping path is thus that

which serves to minimise the distance from m

0,0

x−1,y−1

. The minimum wd for a pair of time se-

ries can therefore be interpreted as an indicator of the

similarity between the two time series. Note that if

wd = 0 the two keystroke time series in question will

be identical.

To further illustrate the concept of DTW, Figure 2

presents four W Ps, resulting from application of the

DTW process. Figures 2(a) and 2(b) show W Ps ob-

tained when DTW was applied to keystroke sinu-

soidal signals for the same subject writing different

unknown texts; Figure 2(a) using DFT and 2(b) us-

ing DWT. In contrast, Figures 2(c) and 2(d) show the

W Ps obtained when comparing keystroke sinusoidal

signals associated with two different subjects, writing

different texts; Figure 2(c) using DFT and 2(d) using

DWT.

5 KEYSTROKE CONTINUOUS

AUTHENTICATION BASED

SPECTRAL ANALYSIS

(KCASA) OPERATION

The proposed KCASA model operates using a win-

dowing approach, continuously sampling keystroke

stream subsequences K

⊂ K

. The window size w is

predeﬁned by the user. Thus K

= {e

i+1

,...,e

}

where i is a “start” time stamp. The keystroke stream

subsequences can be made up of either ﬂight time (F

)

or hold time (KH

) values and can be processed sim-

ply as a straight forward time series, the Keystroke

Time Series (KTS) representation. Alternatively, as

proposed in this paper, the time series can be trans-

formed, using the DFT or DWT representation as de-

scribed above. In the evaluation presented later in

this paper, the effectiveness of the DFT and DWT

representations is compared with the operation of the

straight-forward KTS representation.

ICISSP 2018 - 4th International Conference on Information Systems Security and Privacy

5.1 User Proﬁle Calculation

A user proﬁle U

is a set of m non-overlapping

keystroke streams (windows), or simply keystroke

sinusoidal windows, U

= {W

,...,W

}, where

each window W has a length of ω. Note that |U

needs to be substantially greater than the window

length ω, so that a number of subsequences (win-

dows) can be extracted. Note also that the generated

windows are prepared for the next transformation us-

ing DFT and DWT.

The value of ω is user deﬁned. For the experiments

reported on later in this paper, a range of ω values was

considered from 25 to 150 key presses increasing in

steps of 25, that is ω = {25,50,75,100,125,150}. By

doing so, we can examine the effect of ω on perfor-

mance in terms of accuracy. It was anticipated that

a small window size would provide efﬁciency gains;

desirable in the context of real-time continuous au-

thentication.

The set U

is also used to generate a bespoke σ

threshold value. This is calculated by comparing all

subsequences in U

using DTW, and obtaining an av-

erage warping distance

wd which is used as the value

for σ:

σ =

wd =

∑

i=2

DTW (W

i−1

) (5)

It has been shown that averaging the warping dis-

tances associated with a set of time series can lead to

effective and more accurate classiﬁcation of stream-

ing data than if only one warping distance is consid-

ered (Niennattrakul and Ratanamahatana, 2009).

5.2 Subsequence Preprocessing and

Noise Reduction

Prior to the commencement of the KCASA authen-

tication process each newly collated keystroke time

series must be “cleaned”. The issue here is that F

values can be substantial, for example when there

is pause in the typing process. A limit is therefore

placed on F

values using a maximum ﬂight time

threshold value ϕ. Given a F

value in excess of

ϕ, the value will be reduced to ϕ. For the evalu-

ation presented later in this paper, a range of val-

ues for ϕ were considered, from 0.750 to 2.00 sec-

onds incrementing in steps of 0.25 seconds, thus:

ϕ = {0.75, 1.00, 1.25, 1.50, 1.75, 2.00}.

With respect to key hold time KH

, the time whereby

a key is held down is normally no longer than 1 sec-

ond. Inspection of the datasets used for evaluation

purposes with respect to the study presented in this

paper indicated that the highest recorded value of KH

was 0.95 seconds. Consequently, it was felt that no

maximum hold time threshold was required.

5.3 The KCASA Algorithm

The pseudo code for KCASA process is presented

in Algorithm 1. As noted earlier in this paper,

the principle idea is that, as typing proceeds, non-

overlapping keystroke sub-series are collected, each

of (window) length ω, and compared to previously

obtained keystroke sub-series. On start up, an ini-

tial requirement is to conﬁrm that the user is who

they say they are by comparing the ﬁrst collected sub-

series with the user proﬁle U

as described in Sub-

section 5.1. As the session proceeds, continuous au-

thentication is undertaken by comparing the most re-

cent sub-series W

with the previously collected sub-

series W

i−1

. Algorithm 1 takes the following inputs:

(i) window size ω, (ii) a similarity threshold σ (de-

rived as described above in Sub-Section 5.1) and (iii)

a ϕ threshold for F

. The process operates continu-

ously in a loop until the typing session is terminated

(the user completes the assessment, times out or logs-

out) (lines 4-6). Values for k are recorded as soon

as the typing session starts (line 7). Note that in the

case of ﬂight time the value will be checked, and if

necessary replaced, according to ϕ (lines 8 to 10).

The k value is then appended to the keystroke stream

. The counter is monitored, and sub-sequences

are extracted whenever ω keystrokes have been ob-

tained. The ﬁrst collected sub-series (W

∈ K

) is the

startup time series; each subsequent sub-series W

then compared, using DTW, with the previous W

i−1

sub-series.

6 EVALUATION

A series of experiments were conducted to evaluate

the proposed KCASA mechanism so as to determine

how well it performed in terms of the detection of im-

personators. Comparisons were also undertaken with

respect to a Feature Vector Representation (FVR), the

established approach from the literature for keystroke

continuous authentication. The metrics used for the

evaluation were: (i) Authentication accuracy (Acc.),

(ii) the False Acceptance Rate (FAR) and (iii) the

False Rejection Rate (FRR). Note that FAR and FRR

are the traditional metrics used to measure the perfor-

mance of Biometric systems (Polemi, 1997). In more

detail, the objectives of the evaluation were:

1. Authentication Performance using the KCASA

Model: To compare the effectiveness of DFT and

Spectral Analysis of Keystroke Streams: Towards Effective Real-time Continuous User Authentication

Table 1: Summary of datasets.

Dataset # Sub. Env. Lang. Features Avg. size SD

ACB 30 Free English F

,KH

4625 1207

GP 31 Free Italian F

7157 1095

VHHS 39 Lab English F

,KH

4853 1021

Algorithm 1: KCASA algorithm.

Input: ω, σ, ϕ.

Output: Continuous authentication reporting

1: counter = 0

2: K

3: loop

4: if termination signal received then

5: break

6: end if

7: k = keystroke feature (e.g. F

or KH

)

8: if Flight time & k > ϕ then

9: k = ϕ  Noise reduction.

10: end if

11: K

= K

∪ hcounter, ki

12: counter + +

13: if REM(counter/ω) == 0 then

14: W

= sub-series {K

counter−ω

...K

counter

}

15: if counter = ω then  Start up situation

16: Trans f orm(W )  Transform W to

(DFT)/(DWT)

17: Start up: authenticate W

w.r.t U

and

σ, and report

18: else

19: Authenticate W

w.r.t. W

i−1

and σ, and

report

20: end if

21: end if

22: end loop

DWT in the context of the proposed KCASA ap-

proach, and the usage of the simple KTS represen-

tation (as proposed in (Alshehri et al., 2016b)), in

terms of accuracy, FAR and FRR.

2. Effect on Authentication Performance using

Different Parameters: To determine the effect of

using different values for ω (the sampling window

size) and ϕ (the maximum ﬂight time threshold

value).

3. Efﬁciency: to compare the run time efﬁciency of

KCASA in the context of the three representations

considered (DFT, DWT and KTS).

4. Comparison with Feature Vector Approach:

To compare the operation of KCASA with the

established feature vector based approach for

keystroke continuous authentication.

Note that the evaluation was conducted using ﬂight

time and hold time so as to also analyse which feature

yielded the better results.

The rest of this section is organised as follows. The

datasets used for the evaluation are introduced in Sub-

section 6.1. The results with respect to the ﬁrst eval-

uation objective are considered in Sub-section 6.2,

while those with respect to the second objective are

considered in Sub-section 6.3. Efﬁciency is consid-

ered in Sub-section 6.4; and the comparison with the

feature vector based approach in Sub-section 6.5.

6.1 Datasets

Three datasets were used with respect to the reported

experiments taken from (Gunetti and Picardi, 2005),

(Vural et al., 2014), and (Alshehri et al., 2016b). For

ease of presentation the three data sets are identiﬁed

using acronyms made up of the authors’ surnames:

GP (Gunetti and Picardi, 2005), VHHS (Vural et al.,

2014) and ACB (Alshehri et al., 2016b).

The GP dataset was used with respect to the work re-

ported on in (Gunetti and Picardi, 2005). The publicly

available version of this dataset comprised 31 sub-

jects typing free text in Italian (that used in (Gunetti

and Picardi, 2005) comprised 40 subjects, however,

the text associated with nine of the subjects was not

included in the public version of the dataset). The

VHHS dataset was collected in laboratory conditions.

The subjects were asked to type both predeﬁned text

and free text in English; only the free text part was

used with respect to the experiments reported on in

this paper. The version of the authors’ ACB dataset

used with respect to the work presented in this pa-

per comprised 30 subjects (an earlier version of the

dataset consisted of only 17 subjects). Each subject

was asked to provide free text samples (in English)

in a simulated online assessment environment; the

aim being to mimic the mode of typing when using

an eLearning environment. Thus, the subjects used

whatever keyboard they had at hand. Note that for the

GP dataset only the F

feature was available, whilst

for the remaining two datasets both F

and KH

were

collected. Therefore the performance of KCASA us-

ing KH

could not be evaluated using the GP dataset.

Table 1 provides a summary of the three datasets

used; the table also includes some statistical measure-

ICISSP 2018 - 4th International Conference on Information Systems Security and Privacy

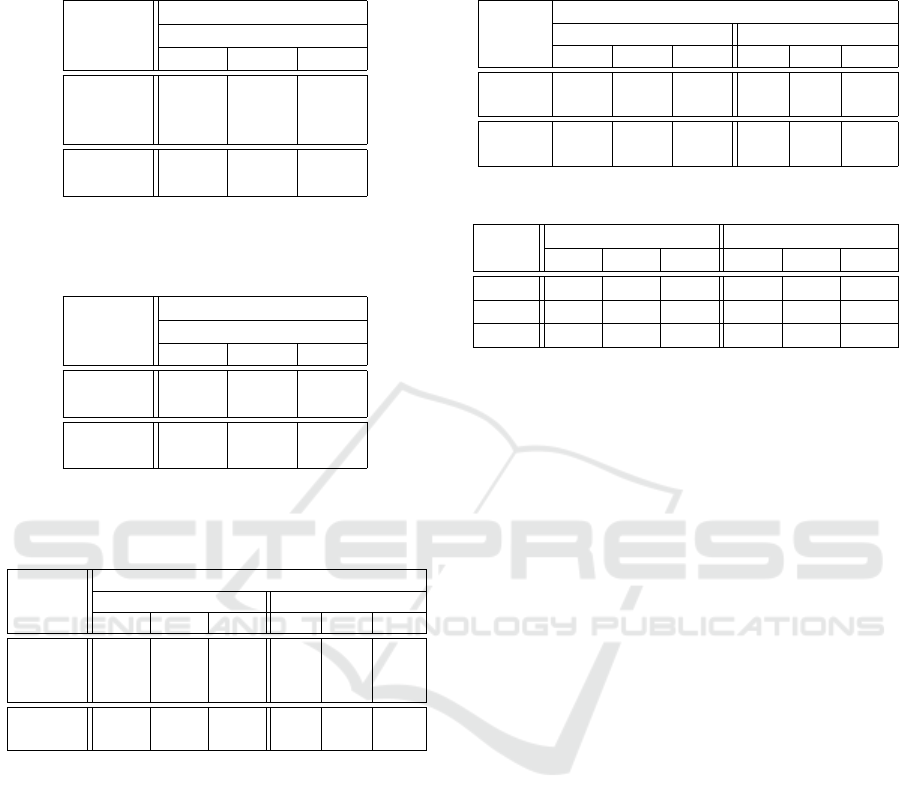
Table 2: Accuracy results obtained using the three different

KCASA representations when using F

(best results in bold

font).

Dataset

Flight time F

Accuracy

KTS DFT DWT

ACB 96.20 97.43 99.22

GP 95.47 96.94 98.41

VHHS 94.83 97.43 97.09

Average 95.50 97.27 98.24

SD 0.68 0.28 1.07

Table 3: Accuracy results obtained using the three different

KCASA representations when using KH

(best results in

bold font).

Dataset

Key hold time KH

Accuracy

KTS DFT DWT

ACB 96.15 97.36 95.09

VHHS 94.33 93.69 95.75

Average 95.24 95.66 95.42

SD 1.29 2.40 0.47

Table 4: FAR and FRR results obtained using the three dif-

ferent KCASA representations when using F

(best results

in bold font).

Dataset

Flight time F

FAR FRR

KTS DFT DWT KTS DFT DWT

ACB 0.050 0.030 0.026 1.96 1.50 1.37

GP 0.039 0.034 0.035 1.98 1.72 1.48

VHHS 0.030 0.022 0.016 1.97 1.85 1.65

Avg. 0.040 0.029 0.026 1.97 1.69 1.50

SD 0.010 0.006 0.010 0.01 0.17 0.14

ments concerning the average length of the time se-

ries in each dataset and associated Standard Devia-

tions (SDs). For evaluation purpose, each record in

each data set was divided into two; the ﬁrst half was

used to generate the typing proﬁle U

and the second

for the continuous authentication evaluation.

6.2 Authentication Performance using

the KCASA Model

The results obtained with respect to the evaluation di-

rected at comparing the DFT, DWT and KTS KCASA

representations, using either F

or KH

, are given

in Tables 2 to 5; Tables 2 and 4 show the accuracy

(Acc.), FAR and FRR results obtained using F

, while

Tables 3 and 5 present the results, using the same met-

rics, obtained using KH

. For the reported experi-

Table 5: FAR and FRR results obtained using the three dif-

ferent KCASA representations when using KH

(best re-

sults in bold font).

Dataset

Key hold time KH

FAR FRR

KTS DFT DWT KTS DFT DWT

ACB 0.06 0.04 0.45 2.01 1.61 1.38

VHHS 0.03 0.02 0.04 1.97 1.91 1.74

Avg. 0.05 0.04 0.25 1.99 1.76 1.56

SD 0.02 0.01 0.29 0.02 0.22 0.25

Table 6: Summary of results presented in Tables 2 to 5.

Metric

Feature KH

Feature

KTS DFT DWT KTS DFT DWT

Acc 95.50 97.27 98.24 95.24 95.66 95.42

FAR 0.040 0.029 0.026 0.05 0.04 0.25

FRR 1.97 1.69 1.50 1.99 1.76 1.56

ments, ω = 75 keystrokes and ϕ = 1.25 seconds were

used as default settings. These parameters were used

because experiments, reported on in the following

sub-section, had indicated that these produced best re-

sults.

From Table 2, it can be observed that the DWT repre-

sentation produced the best overall accuracy (average

accuracy of 98.24% with an associated Standard De-

viation (SD) of 1.07 when using F

. With respect to

FAR we can observe, from Table 4, that DWT also

produced the best results, except in the case of the GP

datasets where DFT was recorded as producing the

best result. It can also be noted, from Table 4, that the

DWT representation gave the best FRR results with

an average of 1.50 and an associated SD of 0.14.

With respect to KH

(Tables 3 and 5), a best average

accuracy of 95.66% was obtained using DFT (with an

associated SD of 2.40). Inspection of Table 5 shows

that the best average FAR result was 0.04 when us-

ing the DFT representation, and the best average FRR

result was 1.56 using DWT. Recall that evaluation us-

ing KH

could not be conducted using the GP dataset

because KH

was not included in the GP dataset.

The results listed in Tables 2 to 5 are presented in

summary form in Table 6. From this summary, it

can be observed that the straightforward KTS repre-

sentation did not perform well compared to the DFT

and DWT representations. Also, from the results pre-

sented in the table, an argument can be made in favour

of the DWT representation, coupled with F

, which

gave the best overall performance in terms of Acc,

FAR and FRR.

Spectral Analysis of Keystroke Streams: Towards Effective Real-time Continuous User Authentication

6.3 Effect on Authentication

Performance using Different

Parameters

The results presented in the previous sub-section as-

sumed a window size ω of 75 and a maximum

threshold value ϕ of 1.25. Recall that the lat-

ter is only applicable in the context of F

. To

evaluate the effect of these parameters, experiments

were conducted using a range of values for ω and

ϕ; {25,50,75,100,125,150} key presses for ω and

{0.75,1.00,1.25,1.50,1.75,2.00} seconds for ϕ.

150

100

125

100

VHHS dataset

DWT

DFT

KTS

Figure 3: The effect of changes in the ω parameter on accu-

racy using KH

feature for VHHS dataset.

150

100

125

100

ACB dataset

DWT

DFT

KTS

Figure 4: The effect of changes in the ω parameter on accu-

racy using KH

feature for ACB dataset.

The accuracy results using KH

, as the keystroke dy-

namic, are shown in the form of 3D bar charts in Fig-

ures 3 and 4 for the VHHS and ACB datasets respec-

tively. From the ﬁgure, it can be seen that ω = 75

produced better accuracy results for the two datasets

in terms of all three KCASA representations, with

the exception of the KTS representation in the ACB

dataset where ω = 100 produced a better accuracy.

The accuracy results obtained using F

as the

keystroke dynamics are presented, again in the form

of 3D bar charts, in Figure 5. From this Figure, it can

be seen that ω and ϕ values of 75 and 1.25, respec-

tively, tended to produce best results, although the se-

lection of ϕ does not seem to have had as much impact

as the selection of ω. Note also that accuracy “levels

off” as ω is increased.

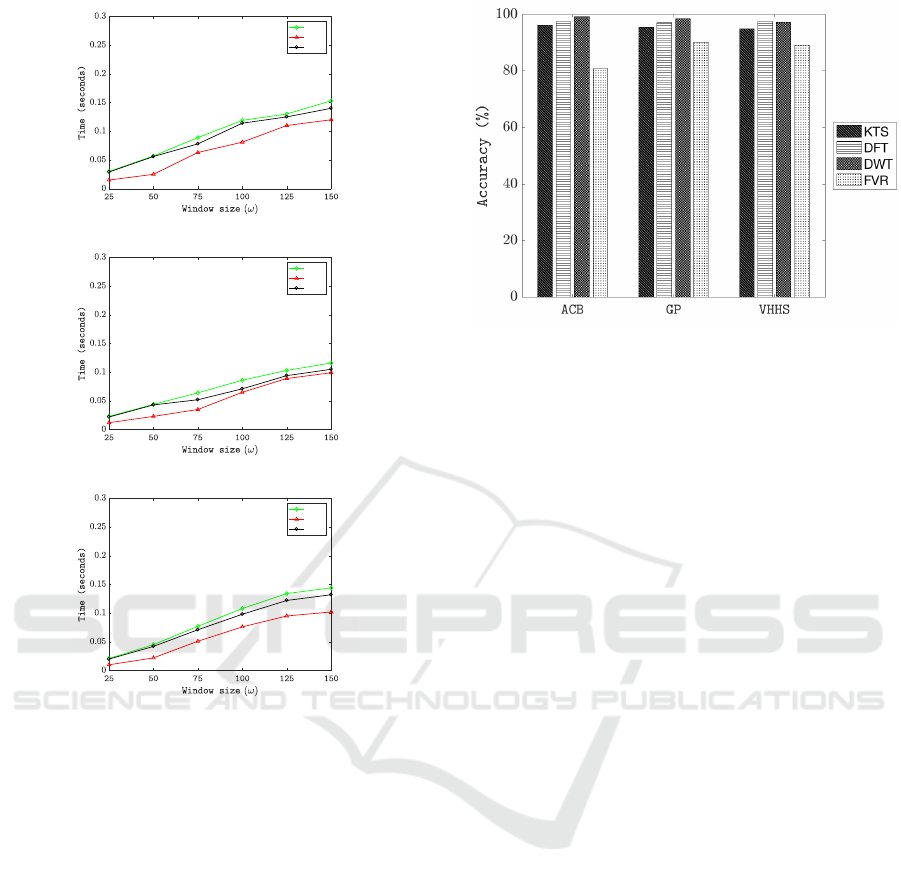
6.4 Efﬁciency

To compare the efﬁciency of the considered KCASA

representations, experiments were conducted in terms

of the time to generate the user proﬁles in each case.

For the experiments, ω was set to a range of values, as

described earlier, whilst ϕ was kept constant at 1.25

because earlier experiments, reported on above, had

demonstrated that the value of ϕ was less signiﬁcant.

The efﬁciency performance using F

is presented in

Figure 6 with respect to each of the three datasets con-

sidered. From the Figure, it can be seen that as ω in-

creased the run time also increased. This was to be ex-

pected because the computation time required by the

DTW process would increase as the size of the win-

dow ω increased. Interestingly, there are well-known

solutions to mitigate against the complexity of DTW

(see for example (Itakura, 1975; Sakoe and Chiba,

1978)); however, no such mitigation was applied with

respect to the experiments reported on in this paper

although this could clearly be done.

Overall the results indicated that when using the pro-

posed transformations efﬁciency gains were made

with respect to the simple KTS representation, with

DFT producing better runtime results than DWT. It

is interesting to note that the time given in (Gunetti

and Picardi, 2005) to construct a user proﬁle was

140 seconds, a signiﬁcant difference compared to the

proposed approach, although in (Gunetti and Picardi,

2005) the computing technology available in 2005

was used. It should also be noted that, in the con-

text of KH

, similar runtime results were produced to

those presented in Figure 6, because both are using

the same DTW similarity measure.

6.5 Comparison with Feature Vector

Approach

From the literature, previous work on keystroke con-

tinuous authentication has frequently been founded

on the Feature Vector Representation (FVR). It has

already been noted that the proposed KCASA model

has signiﬁcant runtime advantages over the feature

vector based approach (see Subsection 6.4). However,

it was felt appropriate to conduct further experiments

comparing the operation of KCASA with the feature

vector based approach in terms of authentication ac-

curacy. Using both F

and KH

appropriate feature

vectors were generated. Consequently, further com-

parison could be made with the approach proposed in

(Gunetti and Picardi, 2005) (see Section 2). The rea-

ICISSP 2018 - 4th International Conference on Information Systems Security and Privacy

GP dataset

150

100

125

KTS

2.00

100

1.75

1.50

1.25

1.00

0.750

150

100

125

DFT

2.00

100

1.75

1.50

1.25

1.00

0.750

150

100

125

DWT

2.00

100

1.75

1.50

1.25

1.00

0.750

VHHS dataset

150

100

125

KTS

2.00

100

1.75

1.50

1.25

1.00

0.750

(a)

150

100

125

DFT

100

2.00

1.75

1.50

1.25

1.00

0.750

(b)

150

100

125

DWT

2.00

100

1.75

1.50

1.25

1.00

0.750

(c)

ACB dataset

150

100

125

KTS

2.00

100

1.75

1.50

1.25

1.00

0.750

150

100

125

DFT

100

2.00

1.75

1.50

1.25

1.00

0.750

150

100

125

DWT

2.00

100

1.75

1.50

1.25

1.00

0.750

Figure 5: The accuracy results obtained for KTS, DFT and DWT using different values ω and ϕ.

son for selecting this approach was that, to the best

knowledge of the authors, the approach had produced

the best reported FAR and FRR results to date. How-

ever, the software for the approach was not publicly

available; thus the authors encoded the mechanism

themselves according to the description given in the

original study. So as to conduct a fair comparison

only F

was considered, because the study in (Gunetti

and Picardi, 2005) used F

values. The average ac-

curacy results obtained, when comparing the opera-

tion of FVR with the KTS, DFT and DWT represen-

tations, in terms of F

, are given in Figure 7. The best

accuracy result obtained for FVR was 90.15%, signif-

icantly worse than the accuracy results obtained using

the KCASA representations which yielded a best ac-

curacy result of 98.24% (when using the DWT repre-

sentation).

7 CONCLUSION

In this paper, a novel mechanism for realtime con-

tinuous keystroke authentication, called Keystroke

Continuous Authentication using Spectral Analysis

(KCASA) has been proposed, whereby authentica-

tion of user typing patterns is conducted by captur-

ing keystroke dynamics in the form of spectral (fre-

quency) streams. KCASA operates efﬁciently using

either ﬂight time F

or hold time KH

keystroke tim-

ing features. Two spectral transformations were con-

sidered to represent keystroke timing features: Dis-

crete Fourier Transform (DFT) and Discrete Wavelet

Transform (DWT). Keystroke spectral streams simi-

larity was conducted using Dynamic Time Warping

(DTW), although alternative time series comparison

techniques could equally well have been applied. The

KCASA model operates by continuously extracting

non-overlapped keystroke sinusoidal signals captured

using a sliding window of size ω. The most appro-

priate size for ω was found to be 75 keystrokes for

both timing features (ﬂight time F

and key hold time

). In the case of ﬂight time, an issue was dis-

covered with excessive ﬂight times; ﬂight times were

thus capped with a maximum value deﬁned by a pa-

Spectral Analysis of Keystroke Streams: Towards Effective Real-time Continuous User Authentication

KTS

DFT

DWT

(a)

KTS

DFT

DWT

(b)

KTS

DFT

DWT

(c)

Figure 6: Runtime (seconds) comparison using ﬂight time

and the three KCASA representations with respect to each

of the three datasets, (a) GP, (b) VHHS and (c) ACB.

rameter ϕ, the most appropriate value for ϕ was found

to be 1.25 seconds. The reported experimentation

and evaluation indicated that the most accurate rep-

resentation was DWT using the F

keystroke feature,

while the most efﬁcient was found to be DFT. Exper-

iments were also reported on indicating that the pro-

posed KCASA model outperformed the feature vec-

tor based approach used by comparator systems such

as that reported in (Gunetti and Picardi, 2005). For

future work, the authors intend to investigate the us-

age of multivariate keystroke time series (incorporat-

ing F

and KH

timing features together) within the

context of the proposed KCASA model. Furthermore,

the time complexity of DTW, in the context of the

proposed representations, remains an open topic for

future work.

Figure 7: The obtained average accuracy using the three

representations (KTS, DFT, DWT and FVR) with respect to

the three datasets used. DWT shows a comparative perfor-

mance with respect to KCASA model.

REFERENCES

Agrawal, R., Faloutsos, C., and Swami, A. (1993). Efﬁcient

similarity search in sequence databases. In Interna-

tional Conference on Foundations of Data Organiza-

tion and Algorithms, pages 69–84. Springer.

Ahmed, A. A. and Traore, I. (2014). Biometric recognition

based on free-text keystroke dynamics. Cybernetics,

IEEE Transactions on, 44(4):458–472.

Alshehri, A., Coenen, F., and Bollegala, D. (2016a). Key-

board usage authentication using time series analy-

sis. In International Conference on Big Data Analytics

and Knowledge Discovery, pages 239–252. Springer.

Alshehri, A., Coenen, F., and Bollegala, D. (2016b). To-

wards keystroke continuous authentication using time

series analytics. In Proc. AI 2016, Research and

Development in Intelligent Systems XXXIII, Springer,

pp275-287., pages 325–338. Springer.

Bleha, S., Slivinsky, C., and Hussien, B. (1990). Computer-

access security systems using keystroke dynamics.

Pattern Analysis and Machine Intelligence, IEEE

Transactions on, 12(12):1217–1222.

Burrus, C. S., Gopinath, R. A., and Guo, H. (1997). Intro-

duction to wavelets and wavelet transforms: a primer.

Chan, K.-P. and Fu, A. W.-C. (1999). Efﬁcient time se-

ries matching by wavelets. In Data Engineering,

1999. Proceedings., 15th International Conference

on, pages 126–133. IEEE.

Cooley, J. W. and Tukey, J. W. (1965). An algorithm for the

machine calculation of complex fourier series. Math-

ematics of computation, 19(90):297–301.

Dowland, P. S. and Furnell, S. M. (2004). A long-term trial

of keystroke proﬁling using digraph, trigraph and key-

word latencies. In Security and Protection in Informa-

tion Processing Systems, pages 275–289. Springer.

Edwards, T. (1991). Discrete wavelet transforms: Theory

and implementation. Universidad de.

ICISSP 2018 - 4th International Conference on Information Systems Security and Privacy

Gabor, D. (1946). Theory of communication. part 1: The

analysis of information. Journal of the Institution of

Electrical Engineers-Part III: Radio and Communica-

tion Engineering, 93(26):429–441.

Gaines, R. S., Lisowski, W., Press, S. J., and Shapiro, N.

(1980). Authentication by keystroke timing: Some

preliminary results. Technical report, DTIC Docu-

ment.

Gunetti, D. and Picardi, C. (2005). Keystroke analysis of

free text. ACM Transactions on Information and Sys-

tem Security (TISSEC), 8(3):312–347.

Haar, A. (1910). Zur theorie der orthogonalen funktionen-

systeme. Mathematische Annalen, 69(3):331–371.

Harris, F. J. (1978). On the use of windows for harmonic

analysis with the discrete fourier transform. Proceed-

ings of the IEEE, 66(1):51–83.

Itakura, F. (1975). Minimum prediction residual principle

applied to speech recognition. IEEETrans. Acoustics,

Speech, and Signal Processing, pages 52–72.

Janacek, G. J., Bagnall, A. J., and Powell, M. (2005). A

likelihood ratio distance measure for the similarity be-

tween the fourier transform of time series. In Paciﬁc-

Asia Conference on Knowledge Discovery and Data

Mining, pages 737–743. Springer.

Keogh, E., Chakrabarti, K., Pazzani, M., and Mehrotra, S.

(2001). Dimensionality reduction for fast similarity

search in large time series databases. Knowledge and

information Systems, 3(3):263–286.

Killourhy, K. S. and Maxion, R. A. (2009). Compar-

ing anomaly-detection algorithms for keystroke dy-

namics. In Dependable Systems & Networks, 2009.

DSN’09. IEEE/IFIP International Conference on,

pages 125–134. IEEE.

Monrose, F. and Rubin, A. (1997). Authentication via

keystroke dynamics. In Proceedings of the 4th ACM

conference on Computer and communications secu-

rity, pages 48–56. ACM.

Niennattrakul, V. and Ratanamahatana, C. A. (2009). Shape

averaging under time warping. In Electrical Engineer-

ing/Electronics, Computer, Telecommunications and

Information Technology, 2009. ECTI-CON 2009. 6th

International Conference on, volume 2, pages 626–

629. IEEE.

Obaidat, M. S. and Sadoun, B. (1997). Veriﬁcation of com-

puter users using keystroke dynamics. Systems, Man,

and Cybernetics, Part B: Cybernetics, IEEE Transac-

tions on, 27(2):261–269.

Polemi, D. (1997). Biometric techniques: review and evalu-

ation of biometric techniques for identiﬁcation and au-

thentication, including an appraisal of the areas where

they are most applicable. Reported prepared for the

European Commision DG XIIIC, 4.

Sakoe, H. and Chiba, S. (1978). Dynamic programming

algorithm optimization fro spoken word recognition.

IEEE Trans. Acoustics, Speech, and Signal Process-

ing, pages 43–49.

Shepherd, S. (1995). Continuous authentication by anal-

ysis of keyboard typing characteristics. In Security

and Detection, 1995., European Convention on, pages

111–114. IET.

Syed, Z. A. (2014). Keystroke and Touch-dynamics Based

Authentication for Desktop and Mobile Devices. PhD

thesis, West Virginia University.

Vlachos, M., Meek, C., Vagena, Z., and Gunopulos, D.

(2004). Identifying similarities, periodicities and

bursts for online search queries. In Proceedings of

the 2004 ACM SIGMOD international conference on

Management of data, pages 131–142. ACM.

Vural, E., Huang, J., Hou, D., and Schuckers, S. (2014).

Shared research dataset to support development of

keystroke authentication. In Biometrics (IJCB), 2014

IEEE International Joint Conference on, pages 1–8.

IEEE.

Ye, L. and Keogh, E. (2009). Time series shapelets: a

new primitive for data mining. In Proceedings of

the 15th ACM SIGKDD international conference on

Knowledge discovery and data mining, pages 947–

956. ACM.

Zar, J. H. (1972). Signiﬁcance testing of the spearman rank

correlation coefﬁcient. Journal of the American Sta-

tistical Association, 67(339):578–580.

Spectral Analysis of Keystroke Streams: Towards Effective Real-time Continuous User Authentication