
Automatic Transformation from Ecore Metamodels towards Gallina
Inductive Types
Jérémy Buisson
1
and Seidali Rehab
2
1
IRISA, Écoles de Saint-Cyr Coëtquidan, Guer, France
2
MISC, University of Constantine 2, Abdelhamid Mehri, Nouvelle Ville Ali Mendjeli, Constantine, Algeria
Keywords:
Model-Driven Engineering, Model Transformation, QVT, Ecore, Xtext, Coq.
Abstract:
When engineering a language (and its compiler), it is convenient to use widespread and easy-to-use MDE
frameworks like Xtext that automatically generate a compiler infrastructure, and even a full-featured IDE. At
the same time, a formal workbench such as a proof assistant is helpful to ensure the language specification is
sound. Unfortunately, the two technical spaces hardly integrate. In this paper, we propose a transformation
from Ecore’s metametamodel to Coq’s language named Gallina/Vernacular. The structural fragment of Ecore
is fully handled. At the cost of not being bijective, our transformation has relaxed constraints over the input
metamodel, in comparison to previous state of the art. To validate, we have used the proposed transformation
with a complete and representative test suite, as well as a proof-carrying code type checker.
1 INTRODUCTION
In the context of designing a formal architecture des-
cription langua ge for system of systems engineerin g,
named SosADL (Oquendo et al., 2016) , the work pre-
sented in this pa per is specifically related to the im-
plementation of supporting tools for this langu age.
On the one side, model-driven engineering pro-
vides effective tools like ASF+SDF (Klint, 1993),
Xtext (Bettini, 2013) or MPS (Voelter, 2013) that
ease the creation of a language and its supporting
infrastructure. From a combined description of a
concrete and/or abstract syntax, a complete editing
environme nt is generated, which includes syntax-
highlighting, auto -completio n, e rror repor ting. These
tools often come with a compilation o r interpretation
framework, which is d e signed to smoothly interact
with the generated editing environment.
On the other side, la nguage theo ry promotes prin-
cipled language design by means of well-established
techniques to specify a language in terms of, e.g.,
semantics and typ e system, then to study this spe-
cification, e.g., proving a type soundness theorem.
Existing literature hints at relevant properties, proof
techniques, and mechanization approaches by m e -
ans of proof assistants like Coq (Bertot and Castran,
2010) or Isabelle/HOL (Nip kow et al., 2002).
In our project, we expect to benefit fr om the two
fields. But model-driven engine e ring tools like Xtext
or MPS hardly integrate with proof assistants. For in-
stance, often, the former use a graph-based formalism
while the latter rely on inductive data types, despite
some exceptions such a s Rascal (Klint and van der
Storm, 2016). Furthermore, the question arises whet-
her the (inform al) implementation, e.g., in the Java
technical space co nforms to the (formal) specifica-
tion, e.g., in the Coq technical space. To address
this issue, we consider the proof-carrying code appro-
ach (Necula, 1997). Figure 1 summarizes this con-
text. From a co ncrete grammar, Xtext generates a
metamodel, and an editor, a parser and a compila-
tion infrastructure. The parser transform s the textual
source into an object-oriented model, which is an in-
stance of the meta model. Thanks to the compilation
infrastructure, we develop a compiler that transforms
the model into output artifacts. Proof-carrying code
appears in the lowest part of th e figure: the compiler
also uses a proof generation infrastructure to produce
a proof, which is an instance of the language’s specifi-
cation, i.e., of the type system or semantics. The proo f
contains terms, which are instances of abstract syntax
type. Furth ermore, term s and models map one each
other, and therefore the metam odel and the abstract
syntax type mu st be consistent.
Our long-term goal is to automatically de rive (part
of) the proof generation infrastructure. In this per-
spective, in this paper, we focus on how we can gene-
rate the abstract syntax type from th e metamodel. In
488
Buisson, J. and Rehab, S.
Automatic Transformation from Ecore Metamodels towards Gallina Inductive Types.
DOI: 10.5220/0006608604880495
In Proceedings of the 6th International Conference on Model-Driven Engineering and Software Development (MODELSWARD 2018), pages 488-495
ISBN: 978-989-758-283-7
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

grammar
editor metamodel
model
source
parser
compilation
infrastructu re
output
artifacts
proof
compiler
term
abstract
syntax type
proof
generation
infrastructu re
type system,
semantics, ...
is transformed into
depends on
is an instance of
is composed of
as usual with Xtext
Figure 1: The big picture of our general approach.
compariso n to the previous state of the art, our contri-
bution is an improved transformation that has relaxed
constraints over the input metamodel, especially with
regard to inh e ritance, at the cost of not being bijective.
Section 2 presents relate d works. Section 3 des-
cribes a running example. Section 4 shows in d e ta ils
how the Ecore metamod el is translated into Gallina
types. Section 5 discusses specific points, notice ably
why we c onsider having a bijective transf ormation is
not that important in our case. Section 6 gives indi-
cations abou t implementation issues. Section 7 sum-
marizes how we validate the transfo rmation. Finally,
section 8 concludes the paper with perspec tives.
2 RELATED WORKS
On the one side, language theory provides back -
ground to specify lang uages (their semantics and their
type systems) as well as what properties of such spe -
cification should be investigated for in order to con-
vince a language specification is sound. In additio n
to bare extraction mechanisms, several approaches in
the field of language theory aims at generating ar-
tifacts from the description of a languag e. In the
K-fram ework (Ro¸su and ¸Serb
˘
anu¸t
˘
a, 2 014), concrete
syntax, operational semantics, type system, and ot-
her static analyses are specified by means of an exe-
cutable semantic framework such that an inte rpreter
and a set of tools are generated from th eir specifica-
tion. Lem (Mulligan et al., 2014) is a domain spe ci-
fic functional programming language, which compi-
les in ductive relations, e.g., an encoding of an opera-
tional semantics o r of a type system, into executable
functions. From the same specification, Lem is able
to generate Coq and Isabelle/HOL ar tifacts along with
L
A
T
E
X documen ta tion. Ott (Sewell et al., 2010) aims
at intuitive notations for inference rules and targets
mainly proof assistant artifacts and documentation. It
supports the generation of Lem code as w ell as b oiler-
plate OCaml code. But none of these works addresses
the u ser programm ing environment.
On the other side, m odel-driven eng ineering fos-
ters the automatic generation of compiler infr a-
structure and user interface from a descrip tion of
the language. Centaur (Borras et al., 198 8) and
ASF+SDF (Klint, 1993) aim at generating a com-
plete programming environment, including user inter-
faces, given a combined abstract and concrete syn-
tax description, along with an executable semantics.
More recently, X text (Bettini, 2013) generates a full-
featured text editor and a c ompilation framework
from the combined defin ition of concrete and abstract
syntax. MPS (Voelter, 2013) introd uces a projection al
editor, i.e., edition is made directly at the level of the
abstract syntax. MPS also provides a declarative lan-
guage for executable type systems. But none of them
allow formal specification and study of langu ages.
There is there fore a ne ed for bridging the gap bet-
ween model-driven engineering and formal methods.
Most of the works in this topic , e.g., (Meyer and
Souquières, 1999; L ano et al., 2004; Barbier and Ca-
riou, 2 012; Cabot et al., 2014) focus on a different is-
sue: verification of proper ties of metamodels. In habi-
Automatic Transformation from Ecore Metamodels towards Gallina Inductive Types
489

tation (or consistency) is for instance a widely-studied
problem, which aims at verifying tha t a metamodel is
contradiction-free, i.e., that some instance exist. Be-
cause of th is focus, the object manipulated in these
works is the me ta model itself. Like depicted in Fi-
gure 1, we aim at b eing able to mechanize semantics
and typ e systems of the language, hence properties of
instances of the metamodel. So the metamodel has to
be transformed into a type, such that terms (or instan-
ces) of that ty pe can be manipulated.
Some p revious works have studied such transfor-
mations: (Djeddai et al., 2012) have defined a bidi-
rectional transformation between Ecore and Isabelle’s
inductive type. To obtain a bijection, they restrict to
single-level single inheritance : each abstract class
A
is map ped to an inductive type
t
; and each concrete
class
C
is tran sf ormed to a constructor
c
of the in-
ductive type
a
mapped from the super c la ss
A
of
C
.
Rascal (Klint and van der Storm, 2016) proposes to
preprocess the metamodel before this scheme is used:
step 1 structural feature s are pushed to c oncrete clas-
ses (same as our step
6
in Figure 3); step 2 refe-
rences are generalized, i.e., references to any class
C
are replaced with a referenc e to
C
’s most general su-
per class. Rascal’s step 2 assumes existence of a most
general super class for any class, but this assumption
does not hold when multiple inheritanc e is used
1
.
The tr ansformation of Section 4 follows the same
principles as those of (Dje ddai et al. , 2012; Klin t and
van der Storm, 2016), but it does n ot require any re-
striction on the input Ecore me ta model. Whe n multi-
ple inheritance is not used , it generates narrower types
than Rascal’s transformation by duplicating co nstruc-
tors, so generating a term from a model is going to
be harder, because the right constructor has to be se-
lected with re spect to the expected type f or the term.
Like Rascal’s one, our transformation is not b ijec tive.
3 A RUNNING EXAMPLE
To illustrate the discussion in subseque nt sections, we
use the meta model for λ terms o f Figure 2. A
File
is composed of
Definition
s, each containing a
Term
.
A term is eithe r an
Abstraction
, an
Application
or
a
Variable
. In order to avoid issues related to na-
ming and scopes, the abstract syntax assumes varia-
bles have already been resolved, hence
Variable
has a
non-containment reference to
Binder
, which is either
an abstraction or a defin ition. Classes are generic such
that terms c a n be annotated, e.g., with types.
1
Unless a predefined super class implicitly generalizes
any class, for instance, like Ecore’s
EObject
class. In this
case, all the reference types are generalized to
EObject
.
File
«abstract»
Binder
boundName
:
EString
Definition
Term
Abstraction
Variable
Application
U
D
A
T
V
B
«bind U» D
«bind U» A
«bind T»
A
«bind T» V
«bind T»
B
0..1
boundType
0..∗
definitions
1..1
term
0..1
type
1..1
body
1..1
binder
1..1
parameter
1..1
function
Figure 2: Ecore metamodel of the example.
We expec t that our transformation generates the
following Coq script (or equivalent), i.e., ind uctive
types such that any mo del that is an instance of the
source metamodel can be written as a ter m whose type
is one resulting from the transformation.
Inductive
Term:
Type
→
Type
:=
|
Term Abstraction: ∀ (A:
Type
) (type: option A)
(
boundName: string) (boundType: option A)
(
body: Ter m A), Term A
| Term Application: ∀ (A:
Type
) (function: Term A)
(
parameter: Term A), Term A
| Term Variable:
∀ (A:
Type
) (binder: URI ( Binder A)), Term A
with
Binder:
Type
→
Type
:=
|
Binder Definition: ∀ (D:
Type
) (boundName: string)
(
boundType: option D) (term: Term D),
Binder D
| Binder Abstraction: ∀ (A:
Type
) (type: option A)
(
boundName: string) (boundType: option A)
(
body: Term A), Binder A.
Inductive
Definition:
Type
→
Type
:=
|
Definition Definition: ∀ (D:
Type
)
(
boundName: string) (boundType: option D)
(
term: Ter m D), Definition D.
Inductive
File:
Type
:=
|
File File:
∀ (definitions: list ( Definition Type)), File.
4 THE TRANSFORMATION
Ecore is an object- oriented language fo r metamodels.
A me ta model consists in some classes, organized into
MODELSWARD 2018 - 6th International Conference on Model-Driven Engineering and Software Development
490

Ecore
metamode l
link
normalize
types
eliminate
behavioral
aspect
eliminate
cross-
referenc e s
introdu ce
constructo rs
percolate
features
remove
inheritance
translate to
inductive
types
schedule
types
translate to
Gallina /
Vernacu la r
text
generation
Coq file
1 2
3
4
56
7
8
9
10
11
Ecore-specific front end
Coq-specific back end
Figure 3: Decomposition of the Ecore-to-Coq transformation.
hierarchically-nested packages, and spread over one
or several Ecore files. A sp ecialization/gen e ralization
relationship provides inheritance and su btyping. Any
class can specialize one or several ge neral classes.
Some classes can be a bstract, mea ning that th ey can-
not be instantiated. Each class con ta ins structural fe-
atures (or fields) which are further refined as either
attributes (store plain-Java objects only) or referen-
ces (stor e Ecore objects only). References can be
containme nt or n on-containment refer ences. A mo-
del, or instanc e of a me ta model, is therefore a tree of
objects (following the containment references) with
additional non-containment references. Derived fea-
tures have their value computed o n-the-fly; transient
features a re omitted f rom XMI serialization; volatile
features are not stored in the in-memory instance. In
this work, we do not consider operations.
Inductive ty pes are mutually-recursive types.
Each type is defined by a set of constructors, each of
which has formal parameters. Each constructor defi-
nes a variant for the type, with its own data structure.
A value of a given type is built by calling one of its
constructo rs with effective parameters. A value is the-
refore a tre e . Types are o rganized in hier a rchically-
nested modules, and each file is a module as well.
Without lack of generality, in the following, we tar-
get Gallina and the Vernacular, Coq’s languages for
terms and for module-level commands.
Following the same principle as (Djeddai et al.,
2012; Klint and van der Storm, 2016), our transfor-
mation maps classes to types, concrete classes to con-
structors, and structural features to constructor pa-
rameters. It ignore s behavioral elements, i. e., ope-
rations, and derived, transient or volatile features.
The novelty of our transformation lies in pre-and-
postprocessing, noticeably to ad dress multiple inheri-
tance. L ike depicted in Figure 3, our transformation is
< LE Packa g e >
< eC l assif i ers
name =
" ecore _EStr i ng " ... / >
< eC l assif i ers
name =
" lambd a_Bin d er "
eSu p erty p es = " // ec o re_EO bject " ... >
< eT y pePar a mete r s name =
" U " / >
< eS t ructu r alFe a t u r e s
name =
" bound Name " ... / >
< eS t ructu r alFe a t u r e s
name =
" bound Type " ... >
< e G ener i cType e T ypeP a rame t er =
" // la m bda_ B inder / U " / >
</ eStr uctur a lFea tu re s >
</ eCla ssifi e rs >
...
</ LEPa ckage >
Figure 4: XMI excerpt after the link step.
decomp osed into 11 steps. Each step targets a specific
issue.
Steps
1
and
2
aim at first simplifying the repre-
sentation of the metamodel. It would be tempting to
map packages to modules. However, consider f or in-
stance an abstract class
A
in pack a ge
p1
, specialized
by concrete class
C
of package
p2
. Class
C
maps to
constructo r
C that belongs to typ e A, which in turn
is mapped from class
A
. If packages w e re mapped
to modules, type
A should be in module P1 and con-
structor C should be in module P2. This is impossible
since constructors belong to types, not to modules. To
avoid this issue, step
1
removes packages and gat-
hers all th e dependencies within a single package.
Figure 4 shows an excerpt of the metamode l of
Figure 2 after step
1
. The metamodel is almost un-
changed. Still, classes fro m the Ecore metamodel are
pulled into the package, starting with
EObject
because
it is used a s the raw type of
type
in
Term
. Because of
boundName
in
Binder
,
EString
is p ulled too. The pr o-
Automatic Transformation from Ecore Metamodels towards Gallina Inductive Types
491

cess is repeated until a ll the dependencies are gathe-
red. To avoid clashes, we use a renam ing scheme.
Due to backward compatibility, Ecore has two
representations of types: non-g e neric types are di-
rect references to classifiers; other types are instan-
ces of
EGenericType
. Figure 4 conta ins examples
of both. To state that
lambda_Binder
specializes the
(non-generic)
ecore_EObject
class,
eSuperTypes
con-
tains the reference string
"//ecore_EObject"
(legacy
representation); while the type of
boundType
is given
by an instance of
EGenericType
, he re th e type para-
meter
U
of
lambda_Binder
. Step
2
translates types to
a simpler unifor m representation.
Since inductive types do not model behaviors,
step
3
erases operatio ns as well as derived, transient
and volatile features from the metamodel. Step
4
re-
places cross r e ferences with attributes of a
_URI
type,
which is intended to stor e an identifier of the refer-
red object. Feature multiplicities are expanded to
appropriate collection types at the same time. For
instance, features with 0..1 multiplicity are mapped
to an
_Option
type.
_URI
,
_Option
and other col-
lection types are suitably interpreted in subsequ ent
steps, such that they are ultimately mapped to Coq
types.
Steps
5
to
7
introdu ce constructors within clas-
ses, before the classes can be turned into inductive
types. At step
5
, a constructor is added to map each
concrete class of the metamodel, like illustrated in Fi-
gure 5. At step
6
, features are percolated through
inheritance down to the constructors, like shown in
Figure 6. When the concrete class is generic, so is
the co nstructor, like the two constructors in Figure 6.
For correct han dling of gener ic classes, type variables
are substituted in the type of the structural features,
like in the type of
type
and
boundType
. At step
7
,
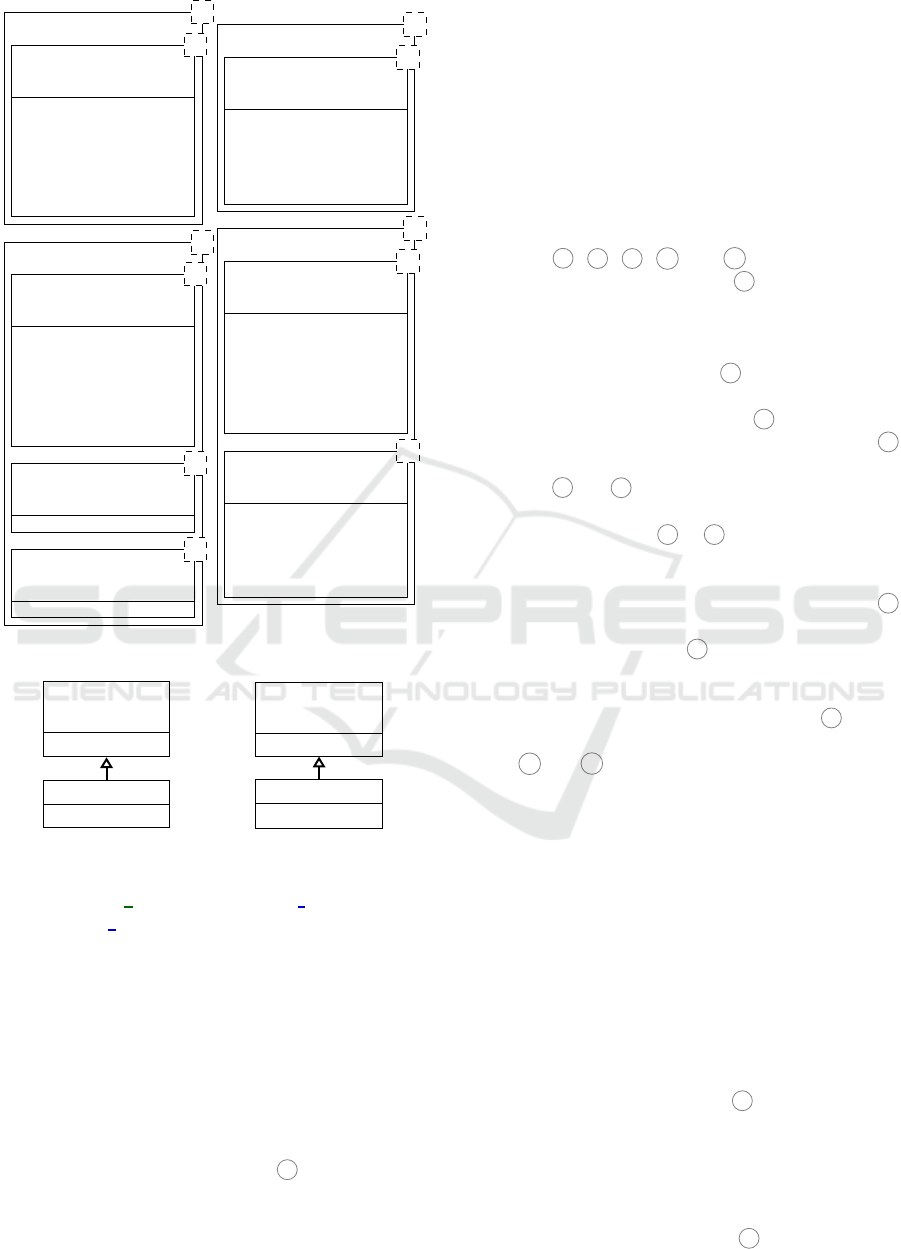
constructo rs are duplicated a t each level of the gene-
ralization relation, like shown in Figure 7. At the end
of step
7
, each class, eith er concrete or abstract, has
a set of constructo rs that corresponds to th e set of all
its specializing concrete subclasses. The generalizati-
on/specialization relation can therefore be d iscarded.
Duplicating co nstructors addresses the fact that a con-
structor be longs to exactly one type, while a class be-
longs to all its super classes. An assignment records
in addition, for each constructor, the precise type of
the built value, to correctly handle generic classes.
Step
8
straightfor ward ly turns each class into an
inductive types, without any further transformation.
Coq disallows r eferencing an inductive type that is
not previously defined or that does n ot belong to the
same group. To satisfy this constrain t, step
9
groups
the inductive types by strongly connected compo-
nents, then sorts them accor ding to a topological or-
«abstract»
Term
type
:
_Option<T>
«abstract»
Binder
boundName
:
EString
boundType
:
_Option<U>
DefinitionAbstraction
«constructor» «constructor»
term
body
U
T
DA
Figure 5: Metamodel excerpt after the introduce steps.
«abstract»
Term
«abstract»
Binder
DefinitionAbstraction
«constructor»
type
:
_Option<A>
boundName
:
EString
boundType
:
_Option<A>
body
:
Term<A>
«constructor»
boundName
:
EString
boundType
:
_Option<D>
term
:
Term<D>
U
T
DA
DA
Figure 6: Metamodel excerpt after the percolate steps.
der. For instance, typ es
Binder
and
Term
shall be in
the sam e group, since they refer each other. Th is
group is put before
Definition
, which refers to
Term
.
Step
10
introdu ces Vernacular commands (like
Inductive
) a nd builds Gallina te rms for each type
to build a correct script. Step
11
generates the text
file. For our running example, the result is equivalent
to the desired on e s given at Section 3:
Definition
ecore EString:
Type
:= string.
Definition
ecore EInt:
Type
:= Z.
Definition
ecore EEList: (
Type
→
Type
) := list.
Inductive
lambda Term: (
Type
→
Type
) :=
|
lambda Term lambda Abstraction : (∀ (A:
Type
),
(∀ (body: ( lambda Te rm A)),
(
∀ (boundName: ecore EString),
(∀ (boundType: ( Optio n A)),
(
∀ (type: ( Option A)), (lambda Term A))) )))
| lambda Term lambda Application: ( ∀ (B:
Type
),
(∀ (fu nction: (lambda Term B)),
(
∀ (parameter: (lambda Term B)),
(∀ (type: ( Option B)), (lambda Ter m B))) ))
|
lambda Term lambda Variable: (∀ (V:
Type
),
(∀ (binder: ( URI (lambda B inder V))),
MODELSWARD 2018 - 6th International Conference on Model-Driven Engineering and Software Development
492
«constructor»
Abstraction
(
A
=
A
)
type
:
_Option<A>
boundName
:
EString
boundType
:
_Option<A>
body
:
Term<A>
«constructor»
Definition
(
D
=
D
)
boundName
:
EString
boundType
:
_Option<D>
term
:
Term<D>
«constructor»
Abstraction
(
T
=
A
)
type
:
_Option<A>
boundName
:
EString
boundType
:
_Option<A>
body
:
Term<A>
«constructor»
Abstraction
(
B
=
A
)
type
:
_Option<A>
boundName
:
EString
boundType
:
_Option<A>
body
:
Term<A>
«constructor»
Definition
(
B
=
D
)
boundName
:
EString
boundType
:
_Option<D>
term
:
Term<D>
«constructor»
Application
(
T
=
A
)
...
«constructor»
Variable
(
T
=
V
)
...
Abstraction
Term
Binder
Definition
D
A
D
D
A
A
A
A
V
T
B
Figure 7: Metamodel excerpt after the flatten steps.
«abstract»
A
x
:
EInt
«abstract»
A
B
B
x
:
EInt
Figure 8: Different metamodels but identical Coq scripts.
(
∀ (type: ( Option V)), ( lambda Term V))))
with
lambda Binder: (
Type
→
Type
) :=
(* a nd so on *)
5 DISCUSSION
Except for the limitations listed in Sec tion 6, Ecore
is f ully supported. For this re ason, the transformation
cannot be bijective. Figure 8 shows a trivial exam-
ple of two different metamodels th at result in iden-
tical Coq scrip ts. Indeed , at step
6
, all the structu-
ral features are pulled from classes to constructors,
without tracking the class they originate from. We
motivate th is choice by two argu ments. First, any in-
stance of one of these metamodels is also an instance
of the other one. Indeed, in both cases, models con-
tain only instan ces of
B
, whic h contain one member
x
that is an integer. Second, our transformation is in-
tended at allowing the language designer providing
formal specifications, proving properties of these spe-
cifications, and setting up an infrastructure for pr oof-
carrying code. As long as co de and proofs written in
the formal world need not be extracted back to Java
and EMF, having a bijective transformation superflu-
ously restricts the set of eligible metamodels.
Steps
1
,
5
,
8
,
10
and
11
are bijective. No
fundamental issue prevents step
4
from making this
step bijective: more accurate typ es can easily be ge-
nerated for collections, such that exact multiplicity
and flags can be fully recovered. All the other steps
are intrisically surjective: step
2
because ther e is no
uniqueness of Ecore’s representation of types, espe-
cially f or non-gener ic types; step
9
because Ecore
does not take into account declaration ord er; step
3
because it erases behavioral e le ments of the m etamo-
del; steps
6
and
7
because th ey discard information
about inheritance.
Only the first steps
1
to
4
of the transformation
are specific to Ecore. We conjecture that subsequent
steps can be reused to build a pipeline for a nother me-
tametamodel. For instance, to switch to M O F, step
1
has to deal with nested classes similarly to the way
packages are me rged; step
4
has to deal with MOF’s
richer reified associations; and data type mapping has
to be updated, since MOF is not based on Java ty-
pes. The ba ck end intuitively starts at step
9
. Swit-
ching to, say, Isabelle/HOL would require c hanging
steps
10
and
11
in order to take into account the dif-
ferent ab stract and concrete syntax.
6 IMPLEMENTATION
The transformation supp orts all the syntactical con-
structs of Ecore (Steinberg et al., 2009), but it assumes
that the source metamodel validates correctly against
all the Ecore constraints implemented in EMF, inclu-
ding the constraints at the warning level. Some of
the pattern s that are interpreted by Ecore’s supp orting
tool such as the Java code generator are not recogni-
zed: hash maps are treated like lists o f pairs; sets and
bags are mapped to lists. Step
4
can easily be ex-
tended to specialize the generated type in these spe-
cific cases. Featu re maps, that is, groups made of a
n..∗ attribute
f
and of derived volatile transient featu-
res
s
that subset
f
by key
s
, are ignored. Any featur e
map
f
is transformed into a list of items; and subset
features
s
are eliminated at step
3
. Our im plemen-
Automatic Transformation from Ecore Metamodels towards Gallina Inductive Types
493

tation decodes the Java type that may appear in the
instanceTypeName
field o f data type d efinitions, but
EMF-generated c la sses are not c onverted to classifier-
based types. It also handles generic types described
by the extended metadata annotations. Restriction ty-
pes are mapped to their base type. These extensions
are handled in step
1
.
Because of the decomposition of the transfor-
mation, we used 11 d ifferent (meta)m etamodels.
Even if Ecore and Gallina share a lmost nothing, the
differences between consecutive (meta)metamodels
in the pipeline are small. During development,
the management of such 11 different but related
(meta)metamodels shows to be challenging, desp ite
they are rather small
2
. Following our implementa-
tion work, we observe that: interactive Ecore editors
lack macro- like systems; transformation tools provide
automation but lack interactivity; and XMI-level text
editors (e.g., Vim or Emacs) provides useful tools like
macros and regexp-search-and-replace, but they are
unaware of Ecor e. We think that there is a need at the
cross-line of these tools.
We favor industrial-strength freely-available
technologies: Eclipse’s mature EMF-and-Java
ecosystem. Step
10
involves many changes in
the structure of the transformed model, while its
algorithm is trivial. QVT-Op e rational seems a good
choice for th is step: it avoids most of the notation
burden; disjunct mappings provide an experience
similar to pattern-matching; and collection operations
like
iterate
reminds usual higher-order functions.
Steps
1
to
9
perform loc alized m odifications in
the transformed metamodel. At each step, m ost of
the metamodel is unchanged except few subtrees.
To implement these steps, we design an ad-hoc
Java-based transfo rmation framework that duplicates
an EMF (meta)model up to class names, similarly to
ATL’s refining mode (without requiring the source
and target (meta)metamod e ls be identical) and to
Rascal’s
visit
operation (w ithout making data
forcibly immutable). The deep copying mechanism
can be customized in two ways: every time an object
is copied, a h ook allows customizing the class o f the
resulting object depending on the class of the source
object; and fo r every feature in the target class, a
hook allows customiz ing how the value is obtained.
By default, the value of a feature having the same
name in the source object is copied.
The Java code for steps
1
to
9
contains
1300 SLOC. The QVT-Operational script for step
10
is made of 185 SLOC. The Acceleo template for
2
Ecore contains 20 classes, 48 references, 33 attributes,
and 33 data types. The other (meta)metamodels in the pi-
peline have similar size.
T
U
A
«bind A»
U
Inductive
T:
Type
→
Type
:= (* ... *).
Inductive
T’ (A:
Type
):
Type
:= (* ... *).
Inductive
U:
Type
:= | U U: ∀ (x: T U), U.
Figure 9: Anti- pattern leading to Coq error.
step
11
contains 40 SLOC. The code is available at
https://bitbucket.org/jbuisson/ecore2coq.
7 VALIDATION
First we ensure the transformation produce s correct
types, i. e., that the produced scripts compile. We
fetch (meta)metamodels from four third-party open -
source projects: EMF, Eclipse’s OCL, Xtext ex-
tras, and Dresden OCL. Then we c onsider all the
151 (meta)metamodels that pass Ecore’s validator.
This test su ite co ntains synthetic c ases, as well a s real-
world (meta)metamodels such as Ecor e, UML and
OCL, containing up to 24 7 classes, each having up to
8 super types and up to 11 levels of inheritance. The
suite covers all the sync tactical constructs of Ecore.
Of the resulting Coq scripts, 147 scripts compile cor-
rectly; Coq runs out of memory for 2 of them; it issues
a “non strictly positive oc currence” error for 2 scripts.
Examination of the erroneous scripts highlights the
anti-pattern of Figure 9. Coq’s error can be avoided
by using the definition
T’ instead of T, but Coq has
restrictions on this form for mutually-recursive defi-
nitions. This anti-pattern needs further investigation.
Second we e nsure that the generated types are
actually usable in the context of proof-carry ing
code ( N e cula, 1997), following the approach depicted
in Figure 1 in the context of SosADL (Oquendo et al.,
2016). Given a concrete gr ammar, Xtext (Bettini,
2013) gener a te s an Ecore metamodel that contains
85 classes, and which is in turn transformed to Coq
types. We use these Coq type s to mechanize the type
system. Then we design an ad-hoc tran sf ormation
that transforms instance s of the metamodel (SosADL
architecture descriptions) to Gallina terms, whose ty-
pes are the generated Coq types. We instrument So-
sADL’s type checker to produce a Gallina term that
witnesses the architecture description is well typed.
The fact that Coq successfully compiles the genera-
ted proof term shows that the transformation produces
correct and u sable typ es.
MODELSWARD 2018 - 6th International Conference on Model-Driven Engineering and Software Development
494

8 CONCLUSION
In this paper, we propose a transformation fro m Ecore
metamode ls to induc tive types. This transformation
allows to set u p a mode l-driven language engineering
chain, e.g., involving Xtext and, at the same time, to
specify the language using a proof assistant, such as
Coq, and then prove properties of this specifica tion.
In comparison to previous work (Djeddai et al., 201 2;
Klint and van der Storm, 2016), our transformation
has fewer co nstraints on the source Ecore metamodel
and ensures stronger typing in the generated inductive
types, but it is not bijective.
To validate our pr oposal, we implement the
transformation using QVT-Operation al, Acceleo, and
EMF-and- Java. Then we f etch 151 (meta )meta-
models, whic h contains both synthetic and r eal-world
(meta)metamodels com ing from public repositories.
147 of the genera ted Coq scripts compile success-
fully; 2 make Coq ru n out of memory; the last 2 ones
need further study in order to handle the correspon-
ding specific pattern. To our knowledge, no previous
work discusses nor deals with this pa ttern.
In future work, we will study how additional parts
of such infrastructure can be automatically derived
from the Ecore metamodel, such that model-driven
engineer ing better integrates with proof assistants.
REFERENCES
Barbier, F. and Cariou, E. (2012). Inductive UML. In Pro-
ceedings of the 2nd International Conference on Mo-
del and Data Engineering, MEDI’12, pages 153–161,
Poitiers, France. Springer.
Bertot, Y. and Castran, P. (2010). Interactive Theorem Pro-
ving and Program Development: Coq’Art The Calcu-
lus of Inductive Constructions. Springer Publishing
Company, Incorporated, 1st edition.
Bettini, L. (2013). Implementing Domain-Specific Langua-
ges with Xtext and Xtend. Packt Publishing.
Borras, P., Clement, D., Despeyroux, T., Incerpi, J., Kahn,
G., Lang, B., and Pascual, V. (1988). Centaur: The
system. I n Proceedings of the Third ACM SIGS-
OFT/SIGPLAN Software Engineering Symposium on
Practical Software Development Environments, SDE
3, pages 14–24, Boston, Massachusetts, USA . ACM.
Cabot, J., Clarisó, R., and Riera, D. (2014). On the verifi-
cation of uml/ocl class diagrams using constraint pro-
gramming. Journal of Systems and Software, 93:1–23.
Djeddai, S., Strecker, M., and Mezghiche, M. (2012). In-
tegrating a formal development for DSLs into meta-
modeling. In Proceedings of the 2nd Internatio-
nal Conference on Model and Data Engineering,
MEDI’12, pages 55–66, Poitiers, France. Springer.
Klint, P. (1993). A meta-environment for generating pro-
gramming environments. ACM Trans. Softw. Eng.
Methodol., 2(2):176–201.
Klint, P. and van der Storm, T. (2016). Model Transfor-
mation with Immutable Data, pages 19–35. Springer
International P ublishing, Cham.
Lano, K., Clark, D., and Androutsopoulos, K. (2004). UML
to B: Formal Verification of Object-Oriented Models,
pages 187–206. Springer, B erlin, Heidelberg.
Meyer, E. and S ouquières, J. (1999). A systematic appro-
ach to tr ansform omt diagrams to a b specification. In
Proceedings of the Wold Congress on Formal Methods
in the Development of Computing Systems-Volume I
- Volume I, FM ’99, pages 875–895, London, UK.
Springer-Verlag.
Mulligan, D. P., Owens, S., Gray, K. E., Ridge, T., and
Sewell, P. (2014). Lem: Reusable engineering of
real-world semantics. In Proceedings of the 19th
ACM SIGPLAN International Conference on Functio-
nal Programming, I CFP ’14, pages 175–188, Gothen-
burg, Sweden. ACM.
Necula, G. C. (1997). Proof-carrying code. In Procee-
dings of the 24th ACM SIGPLAN-SIGACT Symposium
on Principles of Programming Languages, POPL ’97,
pages 106–119, Paris, France. ACM.
Nipkow, T., Wenzel, M., and Paulson, L. C. (2002). Isa-
belle/HOL: A Proof Assistant for Higher-order Logic.
Springer-Verlag, Berlin, Heidelberg.
Oquendo, F., Buisson, J., Leroux, E., Moguérou, G., and
Quilbeuf, J. ( 2016). The SoS Architect Studio: Tool-
chain for the Formal Architecture Description and
Analysis of Software-intensive S ystems-of-Systems
with SosADL. In Proceedings of the ECSA Interna-
tional Colloquium on Software-intensive Systems-of-
Systems (SiSoS), Copenhagen, Denmark.
Ro¸su, G. and ¸Serb
˘
anu¸t
˘
a, T. F. (2014). K overview and sim-
ple case study. Electronic Notes in Theoretical Com-
puter Science, 304:3–56. Proceedings of the Second
International Workshop on the K Framework and its
Applications (K 2011).
Sewell, P., Nardelli, F. z., Owens, S., Peskine, G., Ridge,
T., Sarkar, S., and StrniŠa, R. (2010). O tt: Effective
tool support for the working semanticist. J. Funct.
Program., 20(1):71–122.
Steinberg, D., Budinsky, F., Paternostro, M., and Merks,
E. (2009). EMF: Eclipse Modeling Framework 2.0.
Addison-Wesley P r ofessional, 2nd edition.
Voelter, M. (2013). Language and IDE Modularization
and Composition with MPS, pages 383–430. Sprin-
ger, Berlin, Heidelberg.
Automatic Transformation from Ecore Metamodels towards Gallina Inductive Types
495
