Towards an Optimal Template Reduction
for Securing Embedded Fingerprint Devices
Beno
ˆ
ıt Vibert, Christophe Charrier, Jean-Marie Le Bars and Christophe Rosenberger
Normandie Univ., UNICAEN, ENSICAEN, CNRS, GREYC, 14000 Caen, France
Keywords:
Fingerprint Template, Template Reduction, Genetic Algorithm.
Abstract:
Template protection is an important issue in biometrics for security and privacy reasons. One solution for
securing fingerprint data is to store it on a Secure Element (a microcircuit chipset such as a smartcard). An
embedded On-Card-Comparison (OCC) module permits to compare two biometric templates and generates a
similarity score. The biometric template is usually composed of minutiae extracted from the fingerprint image
because a Secure element is limited in terms of memory and computation capabilities. For these reasons,
a template reduction is necessary to quickly process fingerprint comparison. In this paper, we propose a
new fingerprint template reduction scheme by approximating the optimal choice of minutiae with a genetic
algorithm. We compared the proposed method with approaches from the literature using a fingerprint dataset
and three matching algorithms. The experimental results show the benefit of the proposed method especially in
order to estimate the optimal performance when reducing the fingerprint template given a number of minutiae
to use.
1 INTRODUCTION
Nowadays, electronic transactions are part of our
daily life (e-commerce, smartphones, physical access
control . . . ). In order to guarantee the security of user
authentication, biometrics is often used. Many real
applications benefit from this technology such as for
user access control or e-payment. According to (IHS,
2016), in 2020, the market of smartphones with a fin-
gerprint sensor will reach 1.6 billions units. Never-
theless, a biometric data is very sensitive and can-
not be revoked in general (like a password). In or-
der to ensure its security and privacy, a biometric data
is usually stored in a Secure Element (SE). The Se-
cure Element could be a SmartCard, with an embed-
ded On-Card-Comparison (OCC) algorithm for com-
paring two biometric templates.
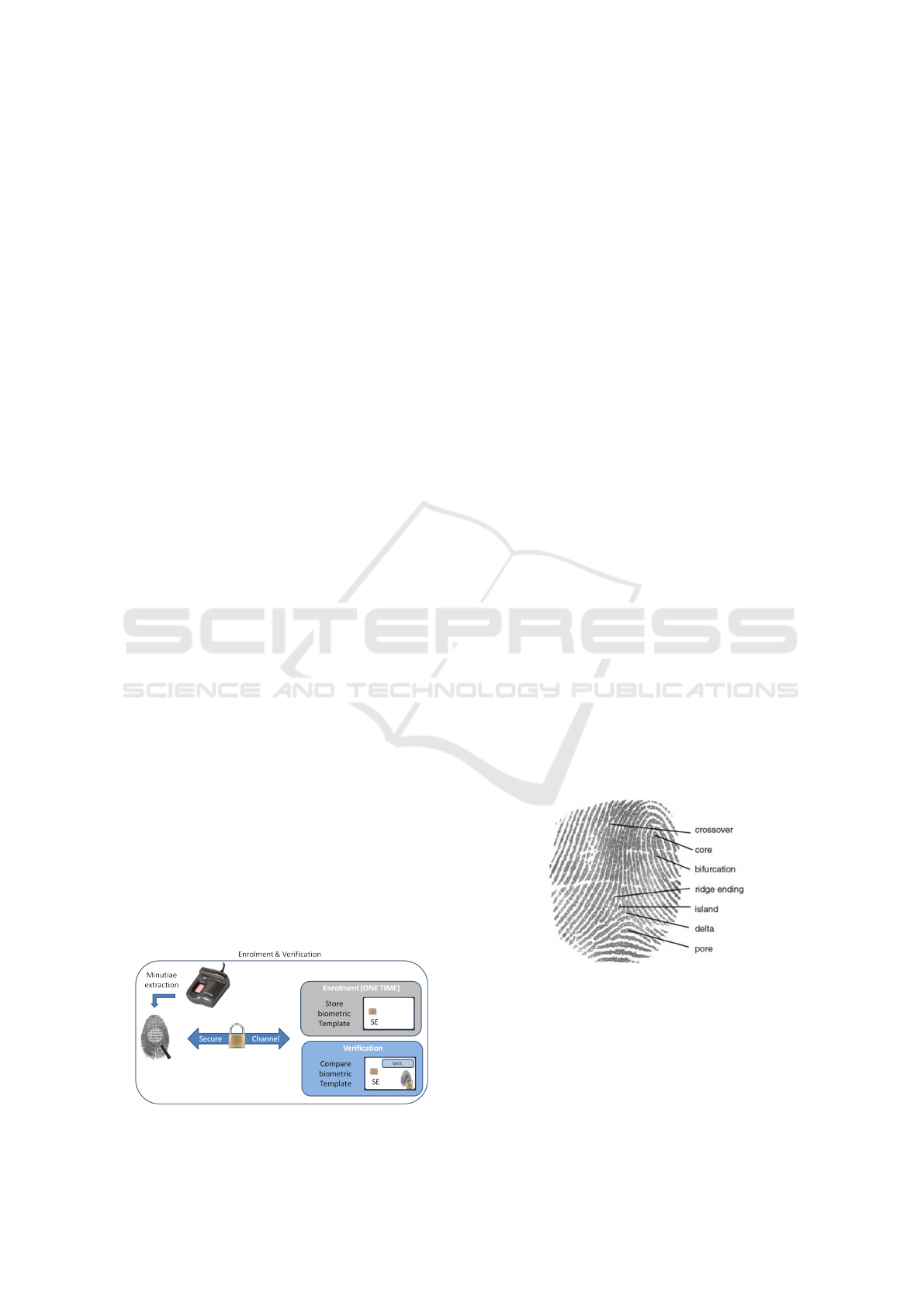
Figure 1: Enrollment and Verification step.
Two steps are necessary when using a biomet-
ric system: 1) the enrollment and 2) the verification
as described in Figure 1. The OCC algorithm com-
putes a comparison score between a captured biomet-
ric template and the reference one. The common fin-
gerprint template is composed of a set of minutiae
corresponding to specific points as described in Fig-
ure 2. The number of minutiae varies considering the
used sensor but it is lower 80 in general.
Figure 2: Fingerprint minutiae.
As common practice, the biometric template
stored in the SE follows the ISO Compact Card stan-
dard (ISO, b) to ensure the interoperability between
biometric sensors and systems. This template is com-
posed of a set of minutiae represented by 3 octets
and 4 values (x
i
, y
i
, T
i
, θ
i
), i = 1 : N
j
where the coor-
dinates (x
i
, y
i
) correspond to the location of the minu-
Vibert, B., Charrier, C., bars, J-M. and Rosenberger, C.
Towards an Optimal Template Reduction for Securing Embedded Fingerprint Devices.
DOI: 10.5220/0006608903290336
In Proceedings of the 4th International Conference on Information Systems Security and Privacy (ICISSP 2018), pages 329-336
ISBN: 978-989-758-282-0
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
329

tiae in the image, T
i
corresponds to the minutiae type
(bifurcation, ridge ending . . . ), θ
i
to the minutiae ori-
entation (related to the ridge) and N
j
the number of
minutiae for the sample j of the user.
A SE has hardware and software constraints such
as the size of memory, the number of data we can send
with an APDU command (ISO, c) (ISO 7816 stan-
dard for the communication with a SE). These lim-
itations have an impact on the embedded algorithm
and the size of the fingerprint template. The ISO/IEC
19794-2 standard recommends the maximal number
of minutiae for enrollment and verification of the ISO-
CC template is 60 (ISO, a). However, in an opera-
tional OCC application, a fingerprint template is usu-
ally limited to a specific number of minutiae which is
lower or equal to 50 to satisfy the memory space, the
APDU specifications and also the verification time (in
general lower than 500 ms). In this case, it is neces-
sary to reduce the template size when the extractor
detected more minutiae.
Some automatic methods have been proposed in
the literature such as the INCITS (Grother and Sala-
mon, 2007) standard (called ”Barycenter” on this
study) which keeps only the minutiae closest to the
CORE point. However, existing template standards
are diverse, and mostly provide minutiae type instead
of the quality of minutia point to assist the matching
algorithm. Therefore, techniques for reducing the size
of minutiae template without the quality information
of a minutia point should be considered. Few works
in the existing studies paid attention to this issue. The
ISO organization (ISO, b) proposed a method based
on peeling off minutiae (we call it ”Truncation” in
this study). Three other methods have been proposed
by Vibert et al. (Vibert et al., 2015). The ”evolu-
tive Barycenter” is based on the method proposed by
the NIST. A loop is used to re-compute the centroid
when one minutiae is peeled off, until the number of
minutiae expected is reached. The ”Truncation Ran-
dom Permutation” is based on the ISO organization
method. With this method, the template of minutiae
is shuffled, only the number of minutiae expected is
kept on the final reduced template. ”K-Means” is used
as another approach where only minutiae closest than
each cluster is kept on the final reduced template.
Yet, the main drawback of all of the above men-
tioned methods is that there is no guarantee to reach
the optimal reduced template. For us, an optimal re-
duced template maximizes the similarity score with
the original template for a selected OCC matching al-
gorithm. In other words, all the obtained templates
approximated more or less the optimal template with-
out actually reaching it. The objective of this paper
is to approximate as close as possible the optimal re-
duction of a minutiae template. This approximation
provides a landmark to determine whether it is worth
to look for better practical reduction methods. To our
knowledge, this is an original contribution of this pa-
per.
The proposed approach is presented in section 2.
Section 3 provides the experimental protocol. Evalua-
tion results are discussed in Section 4. Section 5 con-
cludes this study and gives the associated perspective.
2 PROPOSED METHOD
The general framework of this study is a two-step
work: 1) minutiae acquisition and 2) performance
evaluation. The acquisition involves two tasks which
are illustrated in Figure 3. We first use an extractor to
generate full-size minutiae template and then perform
selection operations considering the desired minutiae
number to obtain the reduced template. The quality of
the reduction is linked to security and usability since
it has an impact on performance, especially on FAR
(False Acceptance Rate) and FRR (False Rejection
Rate).
In this paper, we propose a Minutiae Reduction
with Genetic Algorithms scheme (namely MRGA) to
estimate the optimal reduction of any minutiae tem-
plate. Given a template containing N minutiae, we
want to determine the optimal reduced template con-
taining N
max
minutiae (under the constraint N
max
<
N), i.e., providing the best performance. To be sure
to determine this optimal template, we should test
N
N
max
possibilities (number of combinations of N
max
elements among N) that is not possible. To achieve
this goal, the proposed method is based on the use of
genetic algorithm (GA).
A genetic algorithm is a method for stochastic
search introduced in the 70s by John Holland (Hol-
land, 1975) and by Ingo Rechenberg (Rechenberg,
). Genetic algorithms allow to determine the optimal
value of a criterion by simulating the evolution of a
population until the survival of the best individuals
(Wall, 1996). The survivors are obtained by selection,
transformation or crossing of the previous generation.
We estimate that the optimal search function is a non-
linear multidimensional function, usually character-
ize by several minima. Therefore, the search strategy
should find the global minimum, and avoid remaining
trapped in local minima. The objective is to obtain
a reduced minutiae template having the best perfor-
mance compared to the original template applying an
OCC algorithm. A genetic algorithm is defined by
five essential elements:
1. Genotype: This is a set of characteristics rep-
ICISSP 2018 - 4th International Conference on Information Systems Security and Privacy
330

Figure 3: Two tasks involved in template reduction.
resenting each individual in the population. In
our case, the initial population consists of 500
individuals composed of N elements, N being the
desired number of minutiae within the reduced
biometric template. As we want to get a template
with minutiae existing in the initial template, the
population will be constituted by random draws
of N minutiae in the initial template containing M
minutiae.
2. Initial Population: This is a set of individuals
randomly drawn from the original template. Each
individual consists of N elements. Each element
corresponds to a unique minutiae present in the
original template.
3. Evaluation Function: It measures the quality
of an individual. If we consider individual I
1
to
evaluate, we compare it with the original template
using an OCC and we get an S(I
1
) score. The
evaluation function is based on the OCC compu-
tation, since it is fast to compare two biometric
templates and it has good performances. This
algorithm returns us a similarity score between
the two templates. The higher is the similarity
score is, better is the tested individual i.e., the
reduced template.
4. Operations on Genotypes: the genes of the indi-
viduals are modified by the use of three function-
alities:
• Selection: Individuals that do not match
the environment (insufficient score) are not
selected. To do this, we apply the elite mode
(the 5 individuals with the highest score are
kept in the next generation).
• Crossing: the genes resulting from the crossing
of two individuals is a combination of the
genes of its parents. To obtain the individual
resulting from individuals I
1
and I
2
, we look
at the elements present in the two individuals
without the duplicated ones and randomly
select the first N elements. We thus obtain an
individual (son) mixing the genes of the two
individuals (parents). As a result, the resulting
minutia template contains minutia from both
parents.
• Mutation: Random genes are modified in order
to adapt to the environment. We randomly
draw an individual, then we cross this indi-
vidual with an elite individual. The resulting
individual I
r
= mutation (I
1
) = cross(I
1
, I
a
) with
the random individual. It makes it possible to
obtain an individual having genes from an elite
individual crossed with genes of a random one.
5. Termination: This is the end-of-evolution crite-
rion depending on the score of individuals or the
number of generations. If an individual keeps the
same score for 10 generations or 500 generations
have been made, the algorithm ends.
We summarize here the work-flow of the execu-
tion of a genetic algorithm:
1. Definition of initial population of 500 individuals,
2. Evaluation of Individuals,
3. Generation of the population at current genera-
tion:
• Selection of 5 elite individuals;
• 30 % of the population (here 150 individuals)
is obtained by mutating elite individuals with
random ones;
Towards an Optimal Template Reduction for Securing Embedded Fingerprint Devices
331

• 30 % of the population (here 150 individuals)
is obtained by crossing elite individuals;
• Selection of random individuals to complete the
population.
4. Return to step 2 if the stopping criterion is not sat-
isfied.
The next section presents the results obtained with
MRGA method in comparison with some state-of-
the-art methods.
3 EXPERIMENTAL PROTOCOL
To evaluate the performance of the MRGA method,
we need to make some choices about biometric
database, minutiae extractor, comparison algorithms
and performance metrics. We detail these aspects in
the following sub-sections.
3.1 Database
In this study, the FVC2004DB1 fingerprint database
from the Fingerprint Verification Competition (FVC)
(www, ) is used. This database is composed of 800
images from 100 individuals with 8 samples from
each user. The image resolution is 640 × 480 pix-
els acquired with an optical sensor ”V300” by Cross-
Match. Figure 4 shows some examples of fingerprints
in this database.
3.2 Minutiae Extractor
The minutiae templates used in the experiment have
been extracted using the NBIS tool, and more specifi-
cally MINDTCT (Watson et al., 2007) from the NIST.
We used this extractor because it is widely used in
academic research.
3.3 Matching Algorithms
In this study, we used three matching algorithms:
1. Bozorth3 (Watson et al., 2007). This comparison
algorithm uses only the locations and orientation
of the minutiae to match the fingerprints. We get
a similarity score as output of the algorithm.
2. Minutia Cylinder-Code (MCC) Algorithm
(Cappelli et al., 2010). The representation of
MCC associates a local structure with each minu-
tia. This structure contains the spatial and di-
rectional relationships between minutia and its
neighborhood (fixed radius). Each structure is
Figure 4: Example of fingerprint images in the
FVC2004DB1 database.
invariant in translation, rotation, distortions and
small errors of extraction of characteristics. A
double measure of similarity is computed and
consolidated to provide an overall score for com-
parison.
3. Commercial OCC. We do not have information
on how this algorithm works since it is a commer-
cial one. As output of the algorithm, we do not
have a score but simply a decision result of type
”Accepted” or ”Declined”.
3.4 Evaluation Metrics
In order to assess the performance of a biometric sys-
tem, we can use the Receiver Operating characteristic
Curve (ROC). This curve plots the False Match Rate
(FMR) (i.e., accepted impostor attempts) on the x-
axis against the corresponding False Non-Match Rate
(FNMR) (i.e., rejected genuine attempts) on the y-
axis. This curve is parametrically plotted as a func-
tion of the decision threshold. An example of a ROC
ICISSP 2018 - 4th International Conference on Information Systems Security and Privacy
332
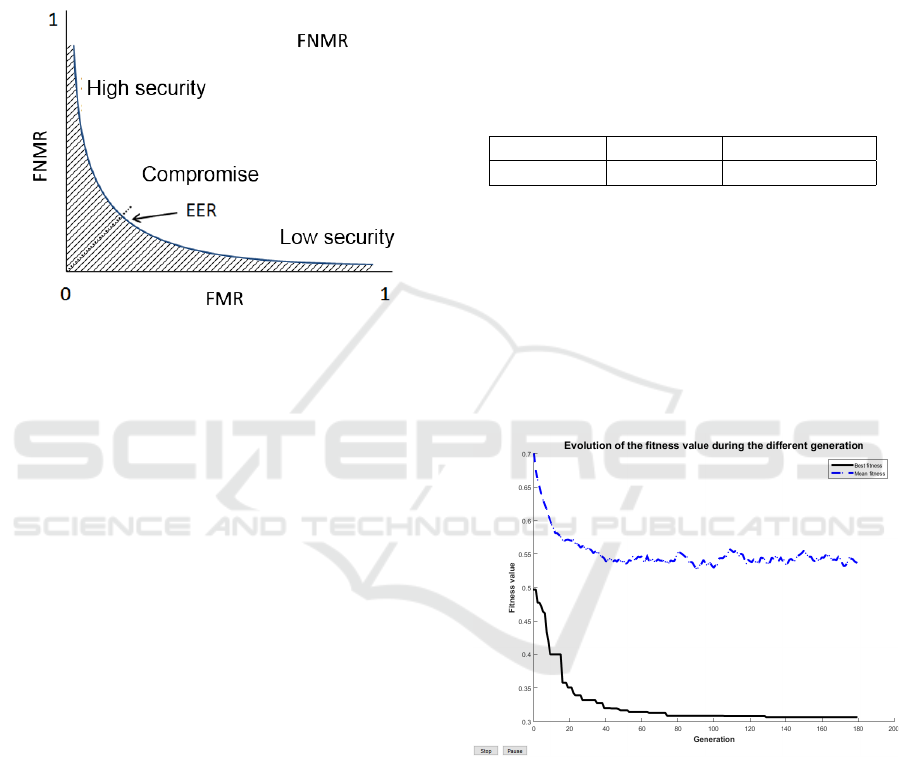
curve is presented in Figure 5. The area under the
curve (hatched zone) should be as low as possible to
minimize recognition errors. The associated measure
is called AUC (Area Under the Curve) and is often
considered as a global performance criterion. We use
this value in this paper to quantify the efficiency of all
trial minutiae selection methods.
Figure 5: Definition of the ROC curve: evolution of the
False Match Rate face to the False Non Match Rate.
The first sample from each individual is chosen
as reference template while other seven samples are
used for tests. With a matcher, we generate a group
of intra-class matching scores (GMS) and a group of
inter-class matching scores (IMS) for each dataset.
The evaluation result is indicated by the global AUC
value computed from the two groups of matching
scores. This computation is done for every group of
reduced templates. A curve of AUC values obtained
for different sizes of the reduced template is plotted
to compare one reduction algorithm with others. For
each of the AUC value, we calculated the associated
confidence interval (CI), which allows us to have an
additional precision for our results. Since we use a
small number of data for the evaluation, the confi-
dence interval gives us additional information on the
accuracy of the results. Another important criterion
in our study is the computation time needed for the
reduction of a biometric template.
4 EXPERIMENTAL RESULTS
First of all, we have to build the baseline performance
by using the original template.
4.1 Performance Evaluation of MRGA
Table 1 shows the AUC value for the original template
that will serve as baseline performance to compare
the performance of other methods with. We notice a
much better performance of the commercial OCC. We
then compute the AUC value and its associated con-
fidence interval for each reduction method with N
max
varying from 30 to 50 in steps of 4. We observe that
the NIST comparison algorithm as well as the MCC
scheme have much worse performance than the com-
mercial OCC. This is not so many surprising since
commercial algorithms are supposed to have high per-
formance level.
Table 1: AUC values for FVC2004DB1 database with Bo-
zorth, MCC and the commercial OCC.
Bozorth MCC commercial OCC
11.1% ± .18 18.4% ± .17 3.77% ± .09
Figure 6 presents the evolution of the fitness score
until the stopping criterion is reached. After 70 gener-
ations, the reduction of the template scheme provides
a solution close to the optimal reduced template. The
blue line represents the average fitness score obtained
during the generations. The black line is the best fit-
ness score obtained for each generation. We can ob-
serve that the optimal reduced template is obtained
after few generations.
Figure 6: Evolution of the Fitness score.
Obtained performances using the trial matching
algorithms are summarized in Table 2. We display the
obtained results using the MCC algorithm too, even if
it has been used in the evaluation function of the ge-
netic algorithm. This allows us to observe if we have
a performance close to the initial template. We ob-
serve that the proposed MRGA method provides per-
formance almost similar to the initial template, as it
could expected. We can conclude that the reduced
templates obtained with the MRGA method obtain a
performance very close to the original templates for
all the matching algorithms.
Towards an Optimal Template Reduction for Securing Embedded Fingerprint Devices
333

Table 2: Difference between AUC values for the initial template and MRGA method for different values N
max
of minutiae on
FVC2004DB1 for all OCC algorithm.
OCC Initial Template 30 34 38 42 46 50
Bozorth3 11.1% ±.18 +2.9%±.46 +2.71%±.32 +2.1%±.28 +0.9%±.28 +0.2%±.26 +0.1%±.24
MCC 18.4% ±.17 +0.8%±.17 +0.6%±.16 +0.4%±.15 +0.3%±.12 0%±.12 +0.1%±.09
Commercial 3.77% ±.09 +1.73%±.25 +1.13%±.24 +0.55%±.21 +0.03%±.20 0%±.18 0%±.14
(a) Bozorth
(b) MCC
(c) commercial OCC
Figure 7: Comparison of the MRGA method with the best reduction methods applied on FVC2004DB1 database for the three
fingerprint comparison algorithms.
Table 3 presents the average time needed to re-
duce a biometric template when the MRGA method
is used. This reduction has been made on Matlab run-
ning on a computer (PC) with a Intel Core I7, quad-
core with a frequency at 2.8Ghz and 16GO of RAM.
These times have to be considered for a relative com-
parison. These computation times could be easily re-
duced if the computation is made on server in C++,
that could be least 10× more efficient.
Table 3: Average time to perform the reduction for different
values N
max
of minutiae when MRGA method is used.
N
max
30 34 38 42 46 50
Time 38 min 35 min 28 min 20 min 18 min 13 min
ICISSP 2018 - 4th International Conference on Information Systems Security and Privacy
334

Considering computation times, this method can-
not be used in an operational framework but only for
validation purposes. Nevertheless, we could imagine
to use it if the computations are done on a server. Dur-
ing enrollment, the reduced biometric could be com-
puted online and sent in a secure way to the secure
element.
4.2 Comparison with State-of-the-art
Methods
We want to evaluate in which way some state-of-
the-art methods, Truncation, Barycenter, Evolutive
Barycenter, Truncation Random Permutation and K-
Means, are close to the ”optimal” reduced template.
Figure 7(a) for the Bozorth3 algorithm, figure 7(b)
for the MCC algorithm and figure 7(c) for the com-
mercial OCC show the comparison results.
We could note that the trial methods are more or
less close to the MRGA method especially for large
number of minutiae. This allows us to better un-
derstand whether a change in methods is possible to
achieve the best possible reduction. We can observe
from Figure 7(b) with MCC matching algorithm, that
K-means method provides the best reduced template
when the number of minutiae ranges from 38 to 50.
For Bozorth3 matching algorithm (Figure7(a)), K-
means is the best method but, we could improve it
to reduce the gap with the MRGA method. Consid-
ering the commercial OCC, the three state-of-the-art
methods are very close to the performance of the ini-
tial template showing the benefit of MRGA.
Figure 8 shows the initial template, in blue on each
figure, and the associated selected minutiae (red dot)
when we applies: Truncation, Barycenter, Troncation
Random Permutation, Evolutive barycenter, K-Means
and the MRGA method. We observe that, the best
method for reducing the minutiae template, K-Means
and MRGA, have a good minutiae spatial distribution
on the fingerprint image. If we analyze with more
details the MRGA reduction template we could ob-
serve, it is a combination of Barycenter approach and
K-Means.
5 CONCLUSION
When we want to have secure device to store your bio-
metric data, you use a SE. When we want to increase
the security of the matching algorithm, we have to
store very efficient biometric data on it. SE are lim-
ited in term of memory size, this is why we need to
have methods which permit to reduce the size of the
biometric template.
(a) Truncation (b) Troncation Random
Permutation
(c) Barycenter (d) Evolutive barycenter
(e) K-Means (f) MRGA
Figure 8: Illustration of a reduced fingerprint template for
each method of the state-of-the-art and the MRGA method
on the initial template (in blue on each figure).
Few methods have been proposed on the state-of-
the-art and we want to estimate in what way we are
close to the best reduction. The purpose of this pa-
per is to find a solution for estimating the best re-
duced minutiae template for different templates size.
Thus, we could increase the security of embedded fin-
gerprint systems. On the state-of-the-art, no method
which permit to estimate this ”optimal” template that
is why we proposed the MRGA approach. We have
used one database FVC2004DB1 and three matching
algorithms to test the performance of this method. We
have shown that the MRGA is for all matching algo-
rithms the best method and is close to the initial tem-
plate in term of performance. We could consider we
obtain the upper value performance and template in
Towards an Optimal Template Reduction for Securing Embedded Fingerprint Devices
335

comparison with the initial template. We observe than
some methods are closer to the MRGA method when
we have a high number of minutiae on the reduced
template. In opposition, when we have a small num-
ber of minutiae, we have many ways to improve the
reduction and obtain better performance and security.
With this study, we proposed an approach to evalu-
ate the upper performance for peeling off the minutiae
template. This method could be used on server when
enrollment part is done, to increase the efficiency of
the matching algorithm.
As perspectives, we want to analyze and proposed
new methods to reduce the initial template to be closer
to the ”optimal” reduced template provided by the
MRGA method.
REFERENCES
Fvc2004db1. http://bias.csr.unibo.it/fvc2004/databases.asp.
ISO/IEC 19794-2. information technology - biometric data
interchange format format - part 2 : Finger minutiae
data, 2011.
ISO/IEC 19795-2. information technology - biometric per-
formance testing and reporting - part 2 : Testing
methodologies for technology and scenario evalua-
tion, 2007.
Cappelli, R., Ferrara, M., and Maltoni, D. (2010). Minu-
tia cylinder-code: A new representation and matching
technique for fingerprint recognition. IEEE Transac-
tions on Pattern Analysis and Machine Intelligence,
32(12):2128–2141.
Grother, P. and Salamon, W. (2007). Interoperability of the
iso/iec 19794-2 compact card and 10 iso/iec 7816-11
match-on-card specifications 11.
Holland, J. H. (1975). Adaptation in natural and artificial
systems: an introductory analysis with applications to
biology, control, and artificial intelligence. U Michi-
gan Press.
IHS (2016). Fingerprint sensor market growth continues up-
ward trajectory, ihs says. https://technology.ihs.com/
571358/fingerprint-sensor-market-growth-continues-
upward-trajectory-ihs-says.
ISO. ISO/IEC 7816-1 to 15: Identification cards - Inte-
grated circuit(s) cards with contacts(Parts 1 to 15).
ISO/IEC, http://www.iso.org.
Rechenberg, I. Evolutionsstrategie94. frommann-holzboog-
verlag, stuttgart (germany), 1994. German; includes
also, 1581.
Vibert, B., Charrier, C., Le Bars, J.-M., and Rosenberger, C.
(2015). Comparative study of minutiae selection al-
gorithms for iso fingerprint templates. In SPIE/IS&T
Electronic Imaging, pages 94090C–94090C. Interna-
tional Society for Optics and Photonics.
Wall, M. B. (1996). A genetic algorithm for resource-
constrained scheduling. PhD thesis, Massachusetts
Institute of Technology.
Watson, C. I., Garris, M. D., Tabassi, E., Wilson, C. L., Mc-
cabe, R. M., Janet, S., and Ko, K. (2007). User’s guide
to nist biometric image software (nbis). Technical re-
port, NIST.
ICISSP 2018 - 4th International Conference on Information Systems Security and Privacy
336
