
A Security Analysis, and a Fix,
of a Code-Corrupted Honeywords System
Ziya Alper Genc¸, Gabriele Lenzini, Peter Y. A. Ryan and Itzel Vazquez Sandoval
Interdisciplinary Centre for Security, Reliability and Trust (SnT), University of Luxembourg, Luxembourg
Keywords:
Honeywords, Password-based Authentication, Secure Protocols Design, Formal Analysis, ProVerif.
Abstract:
In 2013 Juels and Rivest introduced the Honeywords System, a password-based authentication system desig-
ned to detect when a password file has been stolen. A Honeywords System stores passwords together with
indistinguishable decoy words so when an intruder steals the file, retrieves the words, and tries to log-in, he
does not know which one is the password. By guessing one from the decoy words, he may not be lucky and
reveal the leak. Juels and Rivest left a problem open: how to make the system secure even when the intruder
corrupted the login server’s code. In this paper we study and solve the problem. However, since “code cor-
ruption” is a powerful attack, we first define rigorously the threat and set a few assumptions under which the
problem is still solvable, before showing meaningful attacks against the original Honeywords System. Then
we elicit a fundamental security requirement, implementing which, we are able to restore the Honeywords
System’s security despite a corrupted login service. We verify the new protocol’s security formally, using
ProVerif for this task. We also implement the protocol and test its performance. Finally, at the light of our
findings, we discuss whether it is still worth using a fixed honeywords-based system against such a power-
ful threat, or whether it is better, in order to be resilient against code corruption attacks, to design afresh a
completely different password-based authentication solution.
1 INTRODUCTION
Password-based authentication is the most used met-
hod to validate users (Furnell et al., 2000). For users
is very simple: they type username and password
and submit the pair by pressing the return key or a
mouse’s button. For servers, it is easy as well: they
check the credentials against a database of legitimate
user-password pairs and grant access if the search
succeeds.
The authentication process is trustworthy only if
passwords remain secret. Users are expected to keep
them safe, they are supposedly transmitted over en-
crypted channels, and servers are expected not to store
them in cleartext but rather to keep them hashed (usu-
ally with some “salt”) in a file called the password
file.
Keeping passwords safe never works perfectly.
Users can (or can be lured to) reveal their creden-
tials, and servers can be hacked and have the pass-
word file stolen, exposing the hashed passwords to
offline dictionary attacks. In both cases, intruders
will gain, illegitimately, an authorized access. Re-
cent news reports on the extent of the problem. In
2016, the NY Times wrote: “Yahoo!, already reeling
from its September disclosure that 500 million user
accounts had been hacked in 2014, disclosed Wednes-
day that a different attack in 2013 compromised more
than 1 billion accounts” (Goel and Perlroth, 2016). In
the month in which we wrote this paper, Oct. 2017,
Yahoo admitted that indeed the number of accounts
affected by the data breach in 2013 is above 3 bil-
lion (Newman, 2017). As well in 2016, Mashable re-
ported: “MySpace and Tumblr have recently joined
LinkedIn on the list of websites that had millions of
login credentials stolen and put up for sale later. More
than 64 million Tumblr accounts and more than 360
million MySpace accounts were affected by the data
breaches.” (Beck, 2016). The theft was discovered in
2016 when someone tried to sell the credentials in the
black market. In these examples, what hits as drama-
tic as the number of passwords lost is the large delay
that has passed between an attack and its detection.
Failing to detect a password breakage on time wor-
sens the problem. It delays the application of coun-
termeasures to limit the damage.
To improve the awareness of password(s) theft,
computer security research has proposed solutions.
Genç, Z., Lenzini, G., Ryan, P. and Sandoval, I.
A Security Analysis, and a Fix, of a Code-Corrupted Honeywords System.
DOI: 10.5220/0006609100830095
In Proceedings of the 4th International Conference on Information Systems Security and Privacy (ICISSP 2018), pages 83-95
ISBN: 978-989-758-282-0
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
83
For instance, Google monitors suspicious activities
and invites users to review from what device and from
which location they have accessed their account. But
of course, more critical is to ensure that a service be-
come aware of the theft of a password file because,
from it, a great deal of passwords is exposed at once.
This is what we discuss next.
2 RESEARCH CONTEXT
In 2013, Juels and Rivest proposed to modify the
classical password-based authentication scheme (Ju-
els and Rivest, 2013). They called the new system,
the Honeywords System.
A Honeywords System hides and stores a user
(hashed) password in a list of decoy words, called ho-
neywords. Honeywords are to mimic the password,
so that the password cannot be distinguished from
them. So, “redsun3” is a good honeyword for “whi-
temoon5”. A sweetword should have the same pro-
bability to be guessed e.g., by dictionary search as
the original password, enjoying a property called flat-
ness (Juels and Rivest, 2013; Erguler, 2016). Several
algorithms to generate (flat) honeyword’s are extensi-
vely discussed in (Juels and Rivest, 2013). The rele-
vant point is that, since it is very unlikely that a user
types a honeyword purely by chance, any attempt to
log in with a honeyword instead of the password in-
dicates that the password file has been leaked. In that
case, the system flags the event and contingency acti-
ons are taken (e.g., system administrators are alerted,
monitors are activated, user’s execution rights are re-
duced, user’s actions are run in a sandbox, and so on).
The Honeywords System’s architecture is logi-
cally organized in two modules: (1) a “computer sy-
stem” which, according to Juels and Rivest, is “any
system that allows a user to ‘log in’ after she has pro-
vided a username and a password” (ibid) and which
we call the Login Server (LS); (2) an auxiliary har-
dened secure server that assists with the use of hone-
ywords, which Juels and Rivest call the Honeychec-
ker (HC).
For each registered user u, LS keeps (in the pas-
sword file) the ordered list of u’s sweetwords (so are
called collectively honeywords and passwords), deno-
ted here by [h(w
x
)]
u
, for x ∈ [1,k] where k is the fixed
number of sweetwords. In turn, HC stores c
u
, the in-
dex of u’s password in the list.
At authentication, the system runs a simple proto-
col: LS receives (u,w); then, it searches the hashed
version of w, in the list of (hashed) sweetwords of u.
If no match is found, login is denied. Otherwise the
LS sends to the HC the message (u, j), where j is
u,w
U
[h(w
x
)]
u
LS
c
u
HC
u,w
j ← IndexOf
h(w),[h(w
x
)]
u
u, j
resp ← ( j = c
u
?)
resp
If ( j 6= ⊥)If ( j 6= ⊥)
resp
Figure 1: Honeywords System Protocol.
the found position. This communication occurs over
dedicated and/or encrypted and authenticated chan-
nels. The HC checks whether j = c
u
. In case the
test succeeds, access is granted. In case the test fails,
it is up to the HC to decide what to do. Juels and
Rivest say: “Depending on the policy chosen, the ho-
neychecker may or may not reply to the computer sy-
stem when a login is attempted. When it detects that
something is amiss with the login attempt, it could
signal to the computer system that login should be de-
nied. On the other hand it may merely signal a ‘silent
alarm’ to an administrator, and let the login on the
computer system proceed. In the latter case, we could
perhaps call the honeychecker a ‘login monitor’ rat-
her than a ‘honeychecker’.”(ibid). Figure 1 illustrates
the protocol considering a responsive honeychecker.
The Honeywords System does not impede that a
password file is stolen nor it avoids impersonation:
an intruder who has retrieved by an offline dictionary
attack the sweetwords can still succeed in guessing
the correct password of a user by random choice.
Contribution. Juels and Rivest have left open se-
veral problems. One of them reads as follows (the
italics is ours):
“How can a Honeywords System best be de-
signed to withstand active attacks e.g., malici-
ous messages issued by a compromised com-
puter system or code modification of the com-
puter system?’ (ibid).
Here we take on the task to discuss the part of the
problem regarding “to withstand code modification of
the computer system”, which we remind is the module
that we call the LS. The corruption of this compo-
nent poses indeed the interesting case: it is discussed
in (Juels and Rivest, 2013) where the authors state:
ICISSP 2018 - 4th International Conference on Information Systems Security and Privacy
84

“compromising only the honeychecker at worst redu-
ces security to the level it was before the introduction
of honeywords and the honeychecker”. Instead, the
situation worsens if HC and LS were both corrupted.
In this case we are inclined to believe that there is no
way to detect the leakage of password file whereas the
intruder has a way to gain access unnoticed, but only a
rigorous analysis, out of scope but suitable for future
work, can provide evidence to this claim.
Thus, we study security of the Honeywords Sy-
stem against an adversary that has succeeded in “code
modifying the LS” and we propose a solution for
it. However, since the notion of “code modification”
was left informal in Juels and Rivest’s work and it is
not clear enough to understand the real nature of the
threat, we first need to critically discuss it.
In §3 we give a rigorous definition for the threat
“code modification”, which we rename “code cor-
ruption” to stress its maliciousness. We also state a
few foundational assumptions before thoroughly gi-
ving the analysis of security of the original Honey-
words System under the threat.
In §4 we prove the Honeywords System insecure,
illustrating an attack that works when the LS’s code
has been corrupted according to our model and under
our assumptions. The attack reveals that when con-
fronted against the threat, the original Honeywords
System has a core weakness. From studying the root
cause of the attack we elicit a security requirement
and by fulfilling it we are able to provide a solution to
the problem.
In §5 we describe a new cryptographic protocol
which we argue that removes the weakness and so re-
stores security. We sustain this statement formally in
§7. We model in ProVerif the protocol together with
the code-corrupting adversary and we run an automa-
tic analysis. The results of the verification confirm
that the previous attack is no more possible. Actually,
we prove that there are no more attacks against the
new protocol, in the given model.
Our solution is meant to be primarily of theoreti-
cal interest, but because its cryptographic primitives
rely on a generous use of exponentiation, we thought
useful to implement the protocol and benchmark its
performance with respect to the original Honeywords
System. The results of the tests are reported in §8:
they show that although slower than the original Ho-
neywords System, the loss in performance is linear
in k, the number of sweetwords. Roughly speaking,
our scheme can handle a few hundred authentication
requests per second on a laptop with the service run-
ning on a virtual machine. It is reasonable to expect
better results on more performing servers.
At the end, in §9, we discuss our solution in a wi-
der perspective. We look at it from distance to con-
clude that, although it solves the open problem and
works against the code-corruption threat that we have
defined, it actually suggests a completely innova-
tive design for password-based authentication stron-
ger than that of the fixed Honeywords System.
3 ADVERSARY MODELS
What is a reasonable goal for an adversary that in-
tends to code corrupt the system? What is code cor-
ruption? What levels of corruption are interesting to
study?
We have to answer these questions to fully under-
stand the threat. And understanding code corruption
requires also introducing assumptions that limit the
extension of the threat. Code corruption can be very
disruptive and not all its instances are interesting, in
the sense that they do not bring to insights that help
up understanding fundamental weaknesses of the sy-
stem design. What understanding do we gain from a
code corruption that, for instance, causes a shut-down
of the entire systems? In short, we have to define ri-
gorously our adversary model.
We start with an obvious assumption that follows
from the original Juels and Rivest’s paper:
Assumption 1. The adversary, before code-
corrupting the LS, knows the sweetwords but not the
passwords.
Assumption 1 says that the adversary has stolen
the password file and has reverse-engineered all the k
sweetwords of, say, user u: yet, he does not know
which one among u’s sweetwords is the password.
The adversary can try to guess it and log in with that
guess, which means that his probability to log in wit-
hout the HC’s raising an alarm is 1/k in the worst
case, when the intruder na
¨
ıvely picks at random a
sweetword. Additional factors, such as knowing so-
cial information about a specific user, might be used
to increase the probability of guessing the password.
Let us call this event a “successful log-in”.
Let us now start answering the first question:
“what is a reasonable goal for an adversary that in-
tends to code corrupt the system?”. We will consider
as the answer that a reasonable goal is to increase the
intruder’s probability of a successful log-in to a value
higher than that the intruder would have by guessing
the password and with an honest LS.
Definition 1. The goal of a code corruption attack is
to increase the adversary’s probability to successfully
log in with respect to the probability of guessing the
password among the sweetwords retrieved from the
passwords file.
A Security Analysis, and a Fix, of a Code-Corrupted Honeywords System
85

We answer the second question “what is code cor-
ruption?” gradually. We start with a very general
and powerful definition, but we will later constrain
it while answering the last question “what levels of
corruption are reasonable to consider”?
Definition 2. Let ls.exe be the code that defines the
protocol executed by the LS. Code corruption of LS
means changing ls.exe.
With its code corrupted, the LS’s working can
change completely. An intruder can reprogram it to
do whatever, e.g., to play chess.
1
However, we are
not interested in attacks that change the functionality
of the LS, for the reason that they do not help the ad-
versary to increase its probability of successful log-
ging in. For a similar reason, we are not interested in
attacks that shut-down the systems or cause Denial-
of-Service. These are important attacks from which
to seek defense, but out-of-scope in this study.
We also exclude attacks such as those consisting
in changing ls.exe to always grant access. Actually,
there is a technical reason for this choice. The origi-
nal paper does not give full detail of the architecture
of the “computer system”, our LS, but it seems reaso-
nable to assume that Honeywords System implements
a separation of duties (Botha and Eloff, 2001). And
the duty of LS is only to search the proffered pass-
word in the password file, to consult the HC, and pos-
sibly to report the decision to the user, but not to grant
or deny accesses.
So, what is a reasonable code corruption? We con-
sider here a particular type of corruption, as much as
possible “undetectable”, that is working without rai-
sing suspect of LS’s misbehaving into the other modu-
les. This can be achieved by changing ls.exe in such
a way that LS’s behaviour remains the same from the
point of view of the modules it interacts with, mainly
from the viewpoint of who can raise alarms, primarily
the HC and, secondarily, the system administrators.
Assumption 2. A code corruption against LS does
not change the LS’s observable behaviour.
The rationale of this assumption is that, if the ad-
versary changes the observable behaviour of LS, this
would result in an anomaly that can be detected, trig-
gering an alert in response to which a safe version of
the ls.exe can be restored. Since the adversary may
have a once-in-lifetime opportunity to corrupt LS’s
code, he may not want to see his efforts vanishing in
this way. Of course not all attackers will be so concer-
ned about being undetected. They can be satisfied by
managing to log in and say ex-filtrate sensitive data
1
This is what R. Gonggrijp did when, in 2006, proved
insecure a Dutch electronic voting machine.
might be fine, even if this leaves a trail. But we de-
cided to scope our analysis only within the context of
Assumption 2.
However, even under Assumption 2 there are sub-
tleties that need to be addressed. Interpreted strictly it
does not allow the creation of any back door between
the adversary and the LS that this last can use at any-
time to leak information. This is because, interpre-
ting strictly the term “undetectability”, an exchange
of messages from the LS towards the adversary and
outside the protocol’s message flow can be eventu-
ally detected (e.g., by monitoring the net traffic), lea-
ding to have a safe version of the ls.exe re-installed.
Thus according to this interpretation, Assumption 2
says that if the intruder wants to communicate with
the corrupted LS, it must use the same channels from
which legitimate users log in, and must respect the
message flow of the honest protocol. This does not
exclude that, when re-coding ls.exe, the adversary
can use the knowledge he has gained from having hac-
ked the password file in the first place. It can use the
user’s IDs and sweetwords, and it can hard-code this
information in the corrupted ls.exe.
Still, if we take Assumption 2 less strictly, it ad-
mits that some information can flow back to the ad-
versary, for example, in message resp. And, as we
will discuss in detail in §4, letting LS to communicate
back to the adversary leads to a powerful attack that
breaks the original Honeywords System. In short, the
attack works because LS can learn u’s password (or
the hash of it). This is a feature more than a vulnera-
bility but a feature that a collusive adversary able to
invert the hash can exploit to know the password. So,
an incentive for code corrupting the LS is exactly to
create this retroactive communication and we cannot
exclude this possibility in our analysis. We propose
thus the following methodology. By default we inter-
pret Assumption 2 strictly but, separately, we always
discuss what happens if we relax this constraint and
let LS leak information to the intruder.
Notably, the new protocol that we describe in §5,
although designed to secure the Honeywords System
under an Assumption 2 interpreted strictly turns out to
be efficient also when we relax it. The new protocol
will not impede the leak nor stop the adversary from
learning u’s password, but will make that information
useless for the adversary because it will not be able
log in with it into the system. Somehow our solution
reduces considerably the role of the password as the
only authentication token.
ICISSP 2018 - 4th International Conference on Information Systems Security and Privacy
86

4 ATTACKS
As future reference, we write down how ls.exe looks
like. Algorithm 1 shows it in pseudo-code, using a
notation whose commands are self-explanatory. Here,
passwd is the password file, passwd
u
is the row of
user u, and H is a hash function (e.g., SHA-3 (NIST,
2015)). We also assume that u is a legitimate user’s
name.
Algorithm 1: Login Server Authentication.
1: procedure ls.exe(passwd)
2: while true do;
3: ReceiveFrom(U;(u,w));
4: j ← IndexOf(H(w),passwd
u
);
5: SendTo(HC;(u, j));
6: ReceiveFrom(HC;resp);
7: SendTo(U;resp);
Algorithm 2: Code Corrupted LS.
1: procedure ls
0
.exe(passwd)
2: (u
0
,w
0
) ← (⊥,⊥) init good (u,w)
3: while true do;
4: ReceiveFrom(U;(u,w));
5: if (u
0
6= ⊥) ∧ (u = Mallory) then
6: (u,w) ← (u
0
,w
0
)
7: j ← IndexOf(H(w),passwd
u
);
8: SendTo(HC;(u, j));
9: ReceiveFrom(HC;resp);
10: if (resp = granted) then
11: (u
0
,w
0
) ← (u,w) good (u,w)
12: SendTo(U;resp);
If the adversary can corrupt ls.exe, even under our
Assumption 2 taken strictly, there is an obvious at-
tack. The corrupted ls
0
.exe is reported in Algorithm 2.
It stores a good user’s password when LS sees it, and
then it reuses that knowledge to let the adversary gain
access, when the adversary reveals itself at the log-in
with a specific user name (e.g., “Mallory”).
Actually, LS could remember only the valid j
(in step 11) and, in a next round, skip searching the
passwd
u
(step 7), and send that j to the HC (step 8).
But the corrupted ls.exe outlined above mimics the
behaviour of LS more faithfully and shows also that
LS gets knowledge of a user’s valid password. This,
we will see, is the root of serious vulnerability.
Algorithm 2 represents an ideal attack. Not al-
ways, in instruction 10, the LS learns u’s password
with certainty. This may happen, for instance, when
the HC follows a contingency policy that dictate to re-
spond by granting access even when he sees a sweet-
word, as suggested in the original work (see also our
quote of it in §2). However, the following strategy
gives the LS at least a good chance to guess the pass-
word, especially when the strategy is coordinated with
the adversary: since the adversary is the only one that
can submit honeywords, it refrains itself from trying
to access for a certain time. During this interval, the
only requests that arrive to the LS pretending to be
from user u are actually from the legitimate u; all the
w that come with the requests then must be the u’s
legitimate password. Surely, the user can sometimes
misspell the password, but that will never collide with
a honeyword (because honeywords are flat, see §2).
It is therefore possible for the LS, purely by statisti-
cal analysis and by cross comparison between what
u submits, to infer the u’s real password and at that
moment the LS can so help the adversary as we illus-
trated in our ideal version of the attack. The adversary
has raised its probability to gain a successful access to
values higher than 1/k.
This attack is already serious but under a relaxed
Assumption 2, LS can further send the password back
to the adversary, who now can use the u’s credentials
at any time.
Discussion. The root cause of the attack seems the-
refore to lie in the fact that LS knows u’s password.
Only hashing the password will not help, since the LS
can search the position in the password file or, under
a relaxed Assumption 2, send the hash back to the ad-
versary who can reserve the hash. The main problems
seem then rooted into three concomitant facts: (a) LS
receives username and password in clear; (b) LS can
query HC as an oracle to know whether that submitted
password is the user u’s valid password (in this way it
also get to know the hash of the password); (c) LS can
retrieve the index of the password in passwd
u
. So, if
a solution exists that makes the system secure despite
a corrupted ls.exe then it would be such that it avoids
that LS could perform all these three actions (a)-(c)
together. We state this finding as a requirement:
Requirement 1. A solution for a LS resilient to code
corruption should not (1) let the LS receive userna-
mes and (tentative) passwords in clear, (2) let it know
when the typed input refers to a valid password, and
(3) allow it to reuse that pair to retrieve a valid index
at any moment that is not when a legitimate user logs
in.
5 TOWARDS A SOLUTION
In searching for a solution we are not interested in
pragmatic fixes like checking regularly the integrity
A Security Analysis, and a Fix, of a Code-Corrupted Honeywords System
87

of ls.exe and reinstalling a safe copy. Our lack of
interest is not because solutions like that are not fully
effective (e.g., the intruder can still execute its attack
before any integrity check is performed) but because
such pragmatic fixes do not give any insights about
the real weakness of the system. The same argument
holds for best practices like forcing users changing the
password frequently. Thus, if a solution exists then it
must be searched in a strategy that satisfies our requi-
rement’s items (1)-(3).
One way to comply with them is by implementing
the following countermeasures: (i) passwd
u
is shuf-
fled each time LS queries HC: this avoids that LS can
reuse an index j that it has learned to be the index
of u’s password; (ii) passwd
u
is re-hashed each time
LS queries HC: this avoids that LS can search again
for the index of a typed password that it got to know
being a valid u’s password; (iii) let the LS know what
to search in passwd
u
only when user u is logging in:
this precaution is to avoid that LS can perform off-line
searches on passwd
u
.
The countermeasures (i)-(ii), and so requirements
(1)-(2), can be implemented leaving HC in charge of
shuffling and re-hashing the password file each time
that a user logs in and that the LS questions the HC
about index j.
The shuffling does not require particular explana-
tion. It must be randomized but is a standard step: gi-
ven a row [w
1
,. ..,w
k
], and a permutation π, it returns
[w
π(1)
,. ..,w
π(k)
].
The re-hashing, instead, needs to be explained. It
is implemented by cryptographic exponentiation. For
each user, HC possesses g, a generator of a multipli-
cative subgroup G of order q (so, actually, g should
be written g
u
, but to lighten the notation we omit the
index u). When first the list of sweetwords is genera-
ted, the file is initially hashed using g
r
0
, where r
0
∈
{1,· ·· ,q − 1} is a random number. The u’s row of
the file is therefore [g
r
0
·w
1
,. ..,g
r
0
·w
k
], which we write
[h
r
0
(w
1
)
,. ..,h
r
0
(w
k
)
] to stress that this is a hashing.
More synthetically we also write it as h
r
0
(w).
To rehash the row and obtain h
r
1
(w), HC choses a
new random number r
1
∈ {1,··· ,q− 1} and, for each
element w
i
of the row, it calculates
h
r
0
(w
i
)
r
1
r
0
= (g
r
0
·w
i
)
r
1
r
0
= g
r
0
·
r
1
r
0
·w
i
= g
r
1
·w
i
.
The process can be iterated: to re-hash token h
r
n
(w),
HC selects another number r
n+1
∈ {1,· ·· ,q − 1} and
computes (h
r
n
(w))
r
n+1
/r
n
which is the re-hashed token
h
r
n+1
(w).
In fact, HC reshuffles and re-hashes passwd
u
in
one single step as shown in Figure 2.
So far, we are envisioning a message flow as fol-
lows: when HC receives from LS a check query, it
HC
h
r
n
(w
π(1)
)
.
.
.
h
r
n
(w
π(k)
)
c
h
r
n+1
(w
π
0
(1)
)
.
.
.
h
r
n+1
(w
π
0
(k)
)
π
0
(c)
Figure 2: Shuffling/re-hashing w’s and updating c.
also receives passwd
r
n
u
, which it shuffles using a new
ordering π
0
, and re-hashes using a freshly generated
r
n+1
. The re-hashed, re-shuffled row of u, passwd
u
, is
therefore [h
r
n
(w
u,π
0
(i)
)]
i∈{1,...,k}
, which we write com-
pactly as passwd
r
n+1
u
. HC performs these three steps
indivisibly: the passwd
r
n
u
should not be accessed by
concurrent versions of the HC before it has been shuf-
fled and re-hashed.
What explained so far implements countermeasu-
res (i) and (ii). However, each n
th
time that a user u
logs in and submits the password w, LS needs first to
calculate h
r
n
(w) = g
r
n
·w
before being able to search
for w’s index in passwd
r
n
u
.
Letting LS to do this while avoiding that it gets to
know u’s password (i.e., by taking advantage of kno-
wing the re-hashed password file passwd
r
n
u
and the re-
hashed h
r
n
(w), so anticipating the search and using
HC as an oracle) is not obvious. We need to imple-
ment countermeasure (iii) and prevent LS from sear-
ching the file at any time that is not when a legitimate
user u logs in.
Our final solution is explained in §6 and its work-
flow is illustrated in Figure 3. Its core idea is to inform
the HC when a user is logging in, but without passing
through the LS which may otherwise interfere with
the communication. Because of the risk of man-in-
the-middle attacks, this communication should not be
over the Internet either. Instead, it must happen on a
secure second channel between the user and the HC,
which we suggest to be the ether and implement by
letting them use a One-Time-Password (OTP) device.
We are aware that, introduced without an adequate ex-
planation, the need of a second channel and our sug-
gestion to use an OTP may appear arbitrary and un-
justified. They are not. Thus, in the next section we
briefly explain our reasons, but the reader interested
only in the new protocol can skip it, and restart the
reading from §6.
Why a Second Channel? Before concluding that
we need a second channel between the user and the
HC we tried to comply with countermeasure (iii) by
other ways. One attempt was to add a module, called
ICISSP 2018 - 4th International Conference on Information Systems Security and Privacy
88

Keys Register (KR), to keep r
n
. Abstractly, this sug-
gests to outsource the calculation of the hash of the
submitted password out from the LS. In particular,
we let KR receive (u, w) and calculate the h
r
n
(w). The
token is thus forwarded to the LS, who also receives
the username u. Notably, KR’s role cannot be played
by LS itself. This would lead it to know the hash of
the password and so its valid index, consequently ena-
bling an attack as we have described previously. KR’s
role apart, the authentication process is not different
from what we described before, with the HC that also
shuffles, re-hashes, and returns the password file to
the LS, but at the end the HC sends the new r
n+1
only
to the KR, which is ready for a new session.
This solution works i.e., it is secure, but only if KR
cannot be code-corrupted. This is not an assumption
that we intend to take easily. According to Juels and
Rivest, the only component that is hardened secure is
the HC. Thus, KR should be considered corruptible.
And if it is so, the intermediate solution has a flaw. An
adversary can compromise both kr.exe and ls.exe and,
even under a strict Assumption2 with no back doors,
manage to successfully log in. The attack is imple-
mented by the following corrupted code, where we
assume h
0
and passwd
0
u
be updates of h and passwd
u
.
The corrupted instructions are in red:
Algorithm 3: Code Corrupted KR.
1: procedure kr
0
.exe(r
n
)
2: while true do;
3: ReceiveFrom(U;(u,w);
4: SendTo(LS;h
r
n
(w));
5: ReceiveFrom(HC;r
n+1
);
6: SendTo(LS;h
r
n+1
(w));
KR resends the last w, re-hashed using the new
r
n+1
received from HC. KR does not know whether
w is a valid password, but a corrupted LS does. The
attack works because LS gets pieces of information
beforehand, using which, he can anticipate querying
the new password file and get a valid j that can be
used to let the adversary in.
Alternative ways to implement (iii), such as
using timestamps from the user’s side as a proof of
freshness do not work either since LS stands in the
middle and can compromise those messages. For all
this follows our conclusion that if there must be a “sy-
nchronization” between users and the HC, it must be
happening over a channel that is not under the control
on any module of the Honeywords System nor of the
adversary.
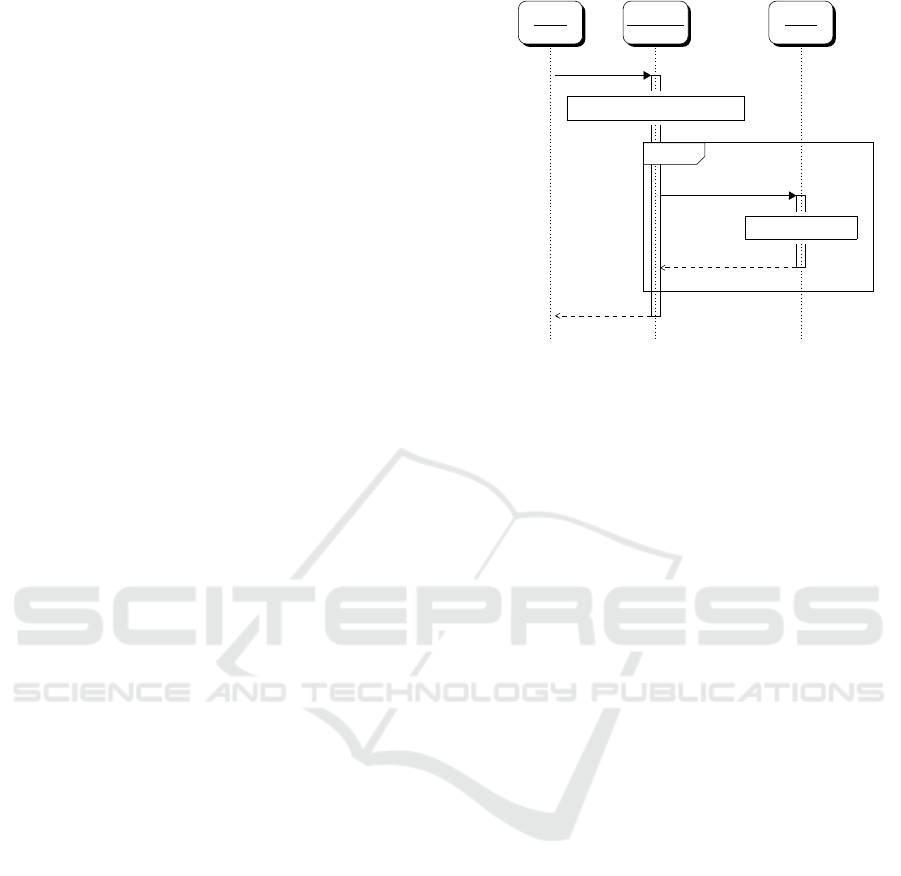
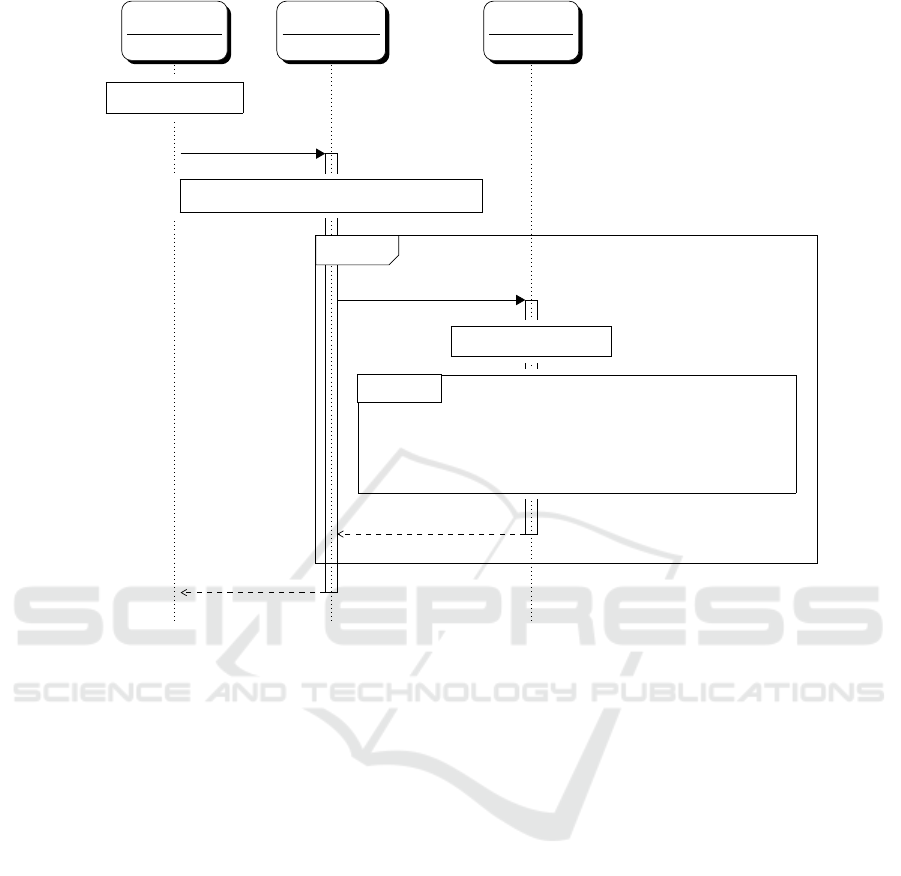
6 THE NEW PROTOCOL
One way to realize requirement’s items (i)-(iii) in
agreement with the Honeywords System solution, is
to empower the user (i.e., the user’s browser) with the
ability to hash his password w with g
r
n
using the same
r
n
that is generated by the HC. It is (almost) equiva-
lent to let the user play the role of KR.
However, letting HC send r directly to the user
over the Internet leaves the channel exposed to man-
in-the-middle attacks and introduces other issues such
as that of ensuring authentication of the user. The
channel through which the HC “communicates” with
the user must be a second channel and not in the In-
ternet. We already justified this choice in the previous
section.
The solution that we are about to discuss now and
prove secure in the next section requires that the HC
and the user share an OTP device. This is employed to
generate a new seed r each time that the OTP is used,
a seed which is also the same for the user and the HC.
The protocol message sequence diagram is detailed in
Figure 3.
The OTP serves as pseudo-random generator but
also as proof of freshness, since what it generates is
synchronized with what the OTP generates by the HC.
Here we talk of an OTP that generates a new seed each
time that it is pressed.
In Figure 3, we have indicated with OTP(n) the
action of using the OTP for the n
th
time (step 1). The
user sends to the LS, the username u and the hashed
version of its password, h
r
n
(w), where the hashing
takes the n
th
OTP-generated number r
n
as parameter
(step 2).
Then, the protocol follows as expected: the LS
searches for an index in the password file (step 3); the
file has been reshuffled and re-hashed in a previous
session by the HC, which has used in anticipation the
same OTP number that the user has now used to hash
the password (we will discuss in §6 how to handle
when a user “burns” a generated number by pressing
the OTP accidentally outside the login). The found
index j is submitted together with the username and
the row of the password file that LS has just used in
the search (step 4).
The HC checks first j against c
u
(i.e., the index
of the user’s password) to determine whether to grant
access or not (step 5), then shuffles and re-hashes the
password file’s row. It also updates the c
u
considering
the index’s re-ordering (steps 6). The shuffled and
re-hashed file is returned to the LS (step 7) and LS
notifies the user (step 8).
A Security Analysis, and a Fix, of a Code-Corrupted Honeywords System
89

Informal Security Analysis. We argue that there is
no corruption of the LS that under our assumptions
can lead to a successful attack. In particular, even if
the LS learns that a particular h
r
n
(w) is a valid pas-
sword, LS cannot make any use of it to anticipate
the index that w will have in the new reshuffled and
re-hashed password file. LS could retain an old file,
but the index retrieved from it is not the new c
0
u
that
the HC now holds. It could send to the HC the user-
name and sweetwords file’s row of another user and
so have this later reshuffled and re-hashed. The only
gain is that LS will likely have the request rejected
without never get to know whether that hashed hone-
yword (and consequently the j calculated) were good
for access. Note that even if two users use the same
password, it is very unlikely that the hashes are the
same if we assume that each user has its own OTP.
LS can send the username u and password file’s row
of another user to know the answer about the correct-
ness of j without having the file’s row of u reshuffled
and re-hashed. But then, HC changes c
u
and so the
LS will not be able to take advantage of what he has
learned; besides, the effect seems to be disastrous in
terms of compromising the integrity of a future check,
when u logs in again. This counts as a Denial-of-
Service (DoS) but not as an attack according to De-
finition 1 since it does not increase the probability of
the adversary to gain access, which remains 1/k.
Finally, our protocol is secure even under a re-
laxed Assumption 2. Even if the LS, learned that a
particular h
r
n
(w) is a valid password, sends it back to
the adversary which in turn retrieves the w, the adver-
sary cannot use either w or the token h
r
n
(w) to gain
access. He needs the token h
r
n+1
(w) which he cannot
generate without holding also the OTP.
Before concluding, we comment on what to do if
the user accidentally burns some of the valid OTPs. A
classic solution is that the HC anticipates new versi-
ons of the password file using a certain number, say
m, of the next OTPs. The file’s row for user u beco-
mes a matrix where each row is ordered with the same
π
0
:
h
r
n
(w
u,π
0
(1)
), ·· · , h
r
n
(w
u,π
0
(k)
)
.
.
.
h
r
n+m
(w
u,π
0
(1)
), · ·· , h
r
n+m
(w
u,π
0
(k)
)
The HC stores one c
u
as before, but when shuffling
and re-hashing the matrix for the new run, it discards
all the rows that correspond to the OTP numbers that
the user has accidentally burned, including the one
used in the current submission (which HC receives
from LS).
7 FORMAL ANALYSIS
We modeled the original protocol and our proposal
(Fig. 3) in the applied-π calculus and used ProVe-
rif (Blanchet, 2001) to formally verify their secu-
rity. ProVerif is an automatic verifier for crypto-
graphic protocols under the Dolev-Yao model. The
code for and results of the analysis are available at
https://github.com/codeCorruption/HoneywordsM.
Analysis of the Original System. We start by ana-
lyzing the original Honeywords System. We know al-
ready that there is an attack, but our aim is to test the
proper way to model a LS that has been code corrup-
ted according to Assumption 2. Moreover, we need to
correctly interpret the results, discarding attacks ori-
ginated from stronger attackers than the one defined
in our threat model.
Our design is based in the following decisions.
There are three parties: the User (U), the LS and the
HC. The LS is an active attacker since it is able to
read and send messages from and to the HC; the chan-
nel between LS and HC is thus public. In contrast,
the channel between U and LS is private, otherwise
the attacker can learn a correct pair of user and pas-
sword from the beginning, contradicting Assumption
1. Note that this decision together with the fact that
the password is never transmitted in the public chan-
nel, prevents the attacker to know the submitted pass-
word at any time. It also rules out the simplest gues-
sing (password) attack, which is the first one that Pro-
Verif finds in the analysis, allowing the verifier to find
attacks more related to the protocol’s flow. We know
already that a guessing attack is always possible, since
Honeywords System is not designed to avoid it.
The attack described in §4 violates the security
property:
correctIndex(u, j) =⇒ injct(indexFound(u, p, j))
&& injct(usrLogged(u, p))
It expresses that, whenever the HC sends a posi-
tive answer to the LS for a submitted pair of user and
index (u, j), all of these three actions occurred: (1) a
user logged in with a pair of credentials (u, p) (2) the
index j found by the LS corresponds to (u, p) and (3)
the value stored in HC for u is equal to j. Injectivity
in the expression (injct) captures the fact of HC pro-
cessing only once each request that LS submits after
events (1) and (2), to prevent interaction between LS
and HC in the absence of a user.
Result. As expected, the verification indicates that
the property does not hold. The attack found shows
how once the attacker (in this case the LS) gets a posi-
ICISSP 2018 - 4th International Conference on Information Systems Security and Privacy
90
u,w,OTP(·)
U
[h
r
n
(w
π(i)
)]
i
LS
c
u
,OTP(·)
HC
1 : r
n
← OTP(n)
2: u,h
r
n
(w)
3 : j ← IndexOf
h
r
n
(w),[h
r
n
(w
u,π(i)
)]
i
4:
u,[h
r
n
(w
u,π(i)
)]
i
, j
5 : resp ← ( j = c
u
)
6 :
r
n
← OTP(n)
r
n+1
← OTP(n + 1)
r
0
← r
n+1
/r
n
[h
r
n+1
(w
u,π
0
(i)
)]
i
← Shuffle&Encrypt([h
r
n
(w
u,π(i)
)]
i
,r
0
)
c
0
u
← π
0
(c
u
)
If ( j = c
u
)
7: resp,[h
r
n+1
(w
u,π
0
(i)
)]
i
If ( j 6= ⊥)If ( j 6= ⊥)
8: resp
Figure 3: The new protocol.
tive answer from the HC, it is able to send a new check
request to HC with the correct user and index, gaining
access to the system and thus contradicting injectivity,
because there was not a new usrLogged(u, p) event
for that second request. These observations support
our model design for code-corruption and provide for-
mal evidence that a Honeywords System resilient to
the flaw must satisfy Requirement 1.
Analysis of our Solution. We are now ready to ap-
ply the analysis to the new protocol. In this ProVerif
model, all channels are public since the LS can send
requests at any time and can learn the inputs from U
and HC. We choose this design to discover any at-
tack using any information available. Conversely, the
LS’s function that retrieves the index of a sweetword
is private, because LS can get information from the
password’s file but cannot modify it.
Unlike in the original, in this protocol each in-
stance of U is synchronized with a HC instance by
a seed, representing that both parts generate the same
OTP at the beginning of a round; the HC knows as
well the index of the password. Then, to give LS the
opportunity to attempt an attack using the knowledge
gained during the run of the protocol, we model the
fact that HC keeps running with the updated index
after reshuffling. The LS is almost as in the origi-
nal protocol, except that this time it receives a hashed
password parametrized by the OTP, instead of a plain
password. An index is a term determined by the has-
hed word searched and the row of sweetwords where
it is searched. Our expanded representation in ProVe-
rif is
indexOfHw(hashWord(w, getOTP(n)),
shuffleNhash(u,n))
where hashWord is the hash of the plain submitted
word w calculated with the seed n; shuffleNhash is
the sweetwords’ row for user u hashed with seed n.
Our equational theory relies on the checkEqual
function in the HC, which returns true only when all
the parameters in the indexes under comparison are
equal. After a successful match, the index hold by
the HC is affected by the next seed value, becoming
indexOfHw(...getOTP(next(n)),...(u,next(n))).
Therefore, after this point the evaluation of
checkEqual will be false for any submitted in-
dex not obtained with the new seed.
A Security Analysis, and a Fix, of a Code-Corrupted Honeywords System
91

The property that we want to prove is the same as
for the original Honeywords System:
correctIndex(u, j) =⇒ injct(usrLogged(u, p)) &&
injct(indexFound( j,
hashWord(p,x),
shuffleNhash(u,y)))
It states that every time an index j is equal to the one
in the HC’s database for u, then (a) the owner u of j
logged in with password p and (b) j corresponds to
the index of the hashed value of p in the sweetwords
row for u. The conjunction ensures the execution of
every step in the protocol; the injectivity ensures that
each is executed only once.
In addition, we introduce the property
event(unreachable) to verify that LS cannot re-
trieve a sweetword’s index of a word not submitted
by a user; the event unreachable is triggered if the
HC’s check function returns true after shuffling and
rehashing, when applied to a previously submitted
hashed password.
The model also assumes, as we stated in §5, that
HC must process LS’s requests atomically, finishing a
request before starting the next. Failing to implement
HC this way, leads to an attack as we are going to
explain in the next section, which prove that atomicity
is in fact necessary.
Result. All properties were verified to be true al-
most immediately. It follows that even knowing that a
certain hashWord(p,getOTP(n)) is a valid password,
LS cannot use it to anticipate the new good index,
since it depends on the seed value possessed only by
U and HC.
The analysis also proves that event unreachable is
actually unreachable and this implies that LS cannot
get any advantage even if using HC as an oracle if
using messages obtained from previous runs with U
and HC.
We also verified that it is necessary for the HC
to process parallel requests coming from the same
user u without breaking the indivisibility of the up-
date of passwd
u
. Removing this constrain reveals an
attack. The attack is as follows: let HC
1
and HC
2
be parallel runs of the HC, then (1) After a LS re-
quest, HC
1
verifies that the submitted index is correct
and sends the answer to LS (2) LS submits again the
correct index, HC
2
processes it, finishes the protocol
and grants access (3) HC
1
continues its execution and
grants access as well.
8 COMPLEXITY AND
PERFORMANCE
The contribution of this research is mainly theoreti-
cal but we judged useful to test the performance of
what we propose. We sketch a complexity analysis
and we benchmark an implementation of our protocol
both, with respect to the original system and by using
different parameter for the elliptic curve (EC) multi-
plication which we used to execute the main operation
of our protocol: exponentiation.
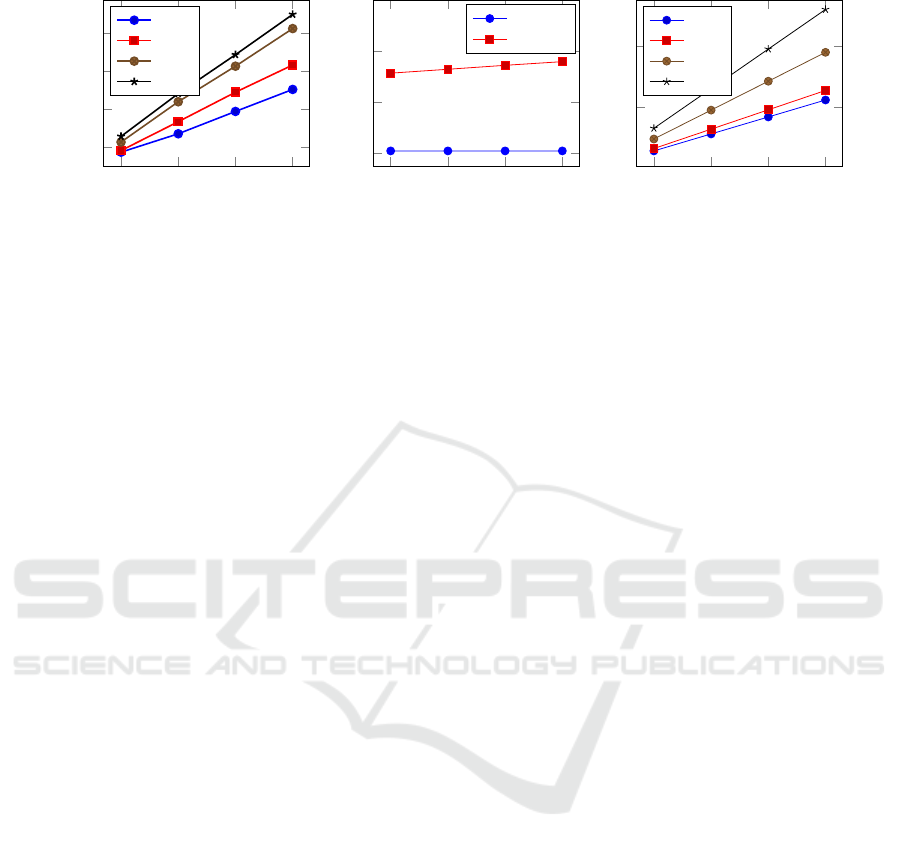
Complexity Analysis. The analysis assumes that an
elliptic curve multiplication takes constant time t
CURVE
(which depends on the employed CURVE): this pro-
tects implementations against remote timing attacks
(Brumley and Tuveri, 2011).
Let us now consider the operations that affect the
performance. Once received the password, LS calls
IndexOf to search the index of the submitted pass-
word among the sweetwords. Given that the sweet-
words are not ordered and also are constantly reshuf-
fled, this is a linear search. In the worst case it can be
done in O(k) time, where k is the number of sweet-
words per user. In case of a match, the HC checks the
validity of the index in O(1) time. Next, the HC calls
Shuffle&Hash; this function shuffles the sweetwords
in O (k) time and performs k times an EC multiplica-
tion in k · t
CURVE
time. The last equation is linear in k
for a fixed CURVE. Since each of the previous opera-
tions takes at most O (k) time, the time complexity of
the new protocol is O(k). As well, for a fixed k, the
execution time increases linearly as t
CURVE
grows. Mo-
reover, EC multiplication is CPU intensive and domi-
nates the total execution time. This is also confirmed
by our empirical results (see Fig. 4(a)).
Communication Cost. In the original Honeywords
system, the communication cost per login comes from
messages (u, j) and resp. We denote the number of
bytes required to encode (u, j) and resp by |(u, j)| and
|resp| accordingly, and obtain the data transfer rate per
login as
C = |(u, j)| + |resp|
While the data flow remains the same, our protocol
brings the following communication overhead to the
original Honeywords system: LS sends the sweet-
word hashes [h
r
n+1
(w
u,π
0
(i)
)]
k
i=1
and receives the up-
dated ones. The number of bytes required to encode a
password hash depends on the employed curve and is
denoted by H
CURVE
. Thus, LS sends |(u, j)| + kH
CURVE
bytes and receives |resp|+ kH
CURVE
bytes per login. As
a result, the total data transfer rate per login between
LS and HC is computed as C + 2kH
CURVE
bytes.
ICISSP 2018 - 4th International Conference on Information Systems Security and Privacy
92

Since k, the number of sweetwords, is a constant
defined by the system, and H
CURVE
is constant too, the
overload in communication is bounded. We have not
simulated nor evaluated how much this may affect a
server’s ability to process a great number of log-in at-
tempts per unit of time, but we are inclined to believe
that this loss in performance is not so dramatic. Of
course one may will to discuss whether the solution
that emerges from our analysis by fitting our require-
ments is not actually an overkill in itself. This is a
legitimate question which we discuss in § 9.
Implementation. We implemented our solution in
C# atop the Microsoft .NET framework.
2
Elliptic
curve operations are performed using Bouncy Castle
Cryptographic Library, although a faster version may
be obtained by native language implementations or li-
braries.
In our implementation, u, j and resp are imple-
mented as integers, hence C equals 12 bytes and
H
CURVE
takes 57, 65, 97, and 133 bytes for P-224,
P-256, P-384 and P-521 accordingly. Fig. 4(c) com-
pares data transfer rates with different settings.
Performance Analysis. We measured the effi-
ciency of our proposed protocol with two questions in
mind: How does number of verifications per second
correlates with the number of honeywords? What is
the impact of the selected curve on verification speed?
The results presented have been performed on note-
books with Intel Core i7 CPU and 8GB of RAM over
an idle network. We measured the total execution
time on server side computations and communication
over the network separately. Roughly speaking, our
prototype reaches a decision for each login request
below 9 ms. Table 1 summarizes the overall perfor-
mance with different settings.
Another performance consideration is the cost of
avoiding login failures due to out-of-synchronization
of OTPs. System policies may follow the strategy dis-
cussed in Section 6. The computational overhead of
both, Login Server and Honeychecker, increases line-
arly on the number of copies in the password file.
It is reasonable to expect that the time required for
re-encryption directly depend on the number of hone-
ywords for a user. Fig. 4 illustrates the time measure-
ments. It can be seen that the time required for veri-
fying a single user increases linearly with the number
of honeywords per user. The Honeychecker performs
one EC multiplication for each honeyword, which is
the most expensive part of its function, and the result
2
Source code is available under GPLv3 at https:// git-
hub.com/codeCorruption/HoneywordsM.
Table 1: Performance results of our implementation. Lo-
gin Server and Honeychecker columns display the time in
milliseconds for a single authentication on LS and HC, re-
spectively. Throughput column shows the maximum num-
ber of verifications per second. Round-Trip Time (RTT) is
the network delay during the experiments.
k Curve
Login Server
(ms)
Honeychecker
(ms)
Throughput
(login/s)
RTT
(ms)
5 P-224 0.011 1.709 581 24.446
5 P-256 0.009 1.796 554 28.917
5 P-384 0.009 2.242 444 31.502
5 P-521 0.010 2.541 392 30.812
10 P-224 0.009 2.680 372 24.534
10 P-256 0.009 3.317 301 29.885
10 P-384 0.010 4.365 229 34.918
10 P-521 0.010 4.793 208 29.414
15 P-224 0.009 3.856 259 27.063
15 P-256 0.010 4.868 205 30.896
15 P-384 0.009 6.240 160 36.253
15 P-521 0.010 6.842 146 31.445
20 P-224 0.009 5.016 199 26.867
20 P-256 0.010 6.301 158 29.355
20 P-384 0.010 8.220 122 32.724
20 P-521 0.011 8.965 111 31.944
is aligned with our theoretical expectations. Our so-
lution preserves the computational characteristics of
the original honeywords protocol: performance is li-
nearly dependent on the number of honeywords. On
the other hand, we can see from Fig. 4 (and from Ta-
ble 1) that the time to run the employed curves incre-
ases with the number of honeywords.
Figure 4(b) compares our protocol with the re-
ference implementation. The client side latency of
both, original and improved protocols stays almost
constant. Considering the delays caused by the net-
work, the computational overhead of our protocol is
relatively small. It might not be even noticed by the
clients.
9 DISCUSSION
This paper takes inspiration from a challenge left open
in (Juels and Rivest, 2013). There, Juels and Ri-
vest propose a password-based authentication system,
called Honeywords System, meant to detect when a
password file has been stolen. User passwords are
hidden among a list of honeywords and an attacker
that knows all of them cannot do better than guessing
which one is the rightful password. This reduces its
probability of success while revealing the leak when
the attacker types one of the supposed secret honey-
words instead. The open problem is how to make this
concept work even when a key component of the Ho-
neywords System, the Login Server (LS), has its code
corrupted by an adversary.
We defined rigorously the notion of code-
corruption, which is too powerful if taken literally.
Constrained to become tractable, the adversary mo-
del results to be a less powerful version than a Dolev-
A Security Analysis, and a Fix, of a Code-Corrupted Honeywords System
93
5
10
15
20
2
4
6
8
Number of honeywords
Time (ms)
Server Side Execution Time
P-224
P-256
P-384
P-521
(a)
5
10
15
20
0
20
40
60
Number of honeywords
Time (ms)
Client Side Latency
Original
Improved
(b)
5
10
15
20
2
4
Number of honeywords
Amount of Data (kbyte)
Data Transferred
P-224
P-256
P-384
P-521
(c)
Figure 4: (a) CPU time required to verify a user depending on the number of honeywords and employed curve. (b) Client
side latency comparison between original protocol and our proposal with NIST Curve P-256. (c) The amount of the data (in
kilobytes) transferred between the Login Server and the Honeychecker.
Yao, but such that gives the attacker a better proba-
bility of success than guessing the password from the
set of honeywords. The root cause of such attacks
lays in the LS knowing eventually a user’s valid (has-
hed) password. The solution that we propose avoids
that, but at a price that seems unavoidable. It pre-
vents the LS to make, off-session, any good use of
what he knows, but the new protocol, according to
the requirements that we elicited from studying at-
tacks on the original Honeywords System, consists
in shuffling and rehashing the password (plus hone-
ywords) after any user’s attempt to log in. The new
solution also avoids that the LS can receive a token
with which it can search in the password file at any
moment distinct from when a legitimate user is log-
ging in, but this last requirement implies that the user
and the Honeychecker (HC) somehow get synchroni-
zed by using a second channel that is not controlled
by the LS or by a man-in-the-middle. We propose
One-Time-Passwords (OTPs) for this purpose. The
solution is secure as we proved formally in ProVerif.
Although our result has meaning mainly for its
theoretical insights, it performs reasonably well as we
show in a benchmark analysis we did on a prototype
that we have implemented in C#.
Our protocol works in the original Juels and Ri-
vest’s intention to let an attacker steal a password file,
run an off-line dictionary attack on it, and have some
chance to get into the system by guessing the rightful
password. However, our solution seems making this
attack useless. The intruder does not gain anything
from knowing a user’s password because however he
does not possess the OTP with which to create the
authentication token (i.e., the hash of the password).
This is the credential that let the system grant access.
At the light of this last observation we further com-
ment that even if the adversary communicates with
the LS and gets to know the user password, (as we
explained in §3), the adversary cannot manage to log
in. Our fix, at least for the new Honeywords System,
nullifies the adversary’s possibility to exploit the pas-
sword usefully to log in, although of course leaking
a password is still a serious weakness because users
may reuse the same password across different sites.
Still the strategy that we proposed for our new pro-
tocol suggests a completely new direction for pass-
word authentication, a procedure that is resilient even
if a password is lost. Thus, at this point, one may
want to go one step ahead and rethink a new system
afresh where an intruder could not take any advan-
tage after knowing the right password. This is an
interesting question that goes beyond what we think
was the proposal of Juels and Rivest, since it would
render a Honeywords System approach completely
superfluous. Instead, it suggests a wholly reviewed
password-based authentication process where users
still type their passwords but where the token that the
LS checks in the password file is one-time-valid. If a
solution exists, still it differs from current OTP-based
solutions that are used today e.g., in home-banking,
because of the assumption that it must work even
when the LS has been code-corrupted. This is for
us an interesting future work and an open problem in
password-base authentication.
ACKNOWLEDGEMENTS
This research has been supported by pEp Security
S.A./SnT PPP, within the project “Security Protocols
for Private Communications”.
REFERENCES
Beck, K. (2016). Hackers are selling account credentials
for 400 million Tumblr and MySpace users. Ma-
ICISSP 2018 - 4th International Conference on Information Systems Security and Privacy
94

chable. http://mashable.com/2016/05/31/myspace-
tumblr-hack (last access: 4th September 2017).
Blanchet, B. (2001). An efficient cryptographic protocol
verifier based on prolog rules. In 14th IEEE Computer
Security Foundations Workshop, pages 82–96. IEEE.
Botha, R. A. and Eloff, J. H. P. (2001). Separation of duties
for access control enforcement in workflow environ-
ments. IBM Systems Journal, 40(3):666–682.
Brumley, B. B. and Tuveri, N. (2011). Remote timing
attacks are still practical. In European Symposium
on Research in Computer Security, pages 355–371.
Springer.
Erguler, I. (2016). Achieving flatness: Selecting the honey-
words from existing user passwords. IEEE Transact.
on Dependable and Secure Computing, 13(2):284–
295.
Furnell, S. M., Dowland, P., Illingworth, H., and Rey-
nolds, P. L. (2000). Authentication and supervision:
A survey of user attitudes. Computers & Security,
19(6):529–539.
Goel, V. and Perlroth, N. (2016). Yahoo Says 1 Billion
User Accounts Were Hacked. NT Times Online.
https://www.nytimes.com/2016/12/14/technology/
yahoo-hack.html (last access: 4th September 2017).
Juels, A. and Rivest, R. L. (2013). Honeywords: Making
password-cracking detectable. In Proceedings of the
2013 ACM SIGSAC conference on Computer & com-
munications security, pages 145–160. ACM.
Newman, L. H. (2017). Yahoo’s 2013 email hack ac-
tually compromised three billion accounts. Wi-
red. https://www.wired.com/story/yahoo-breach-
three-billion-accounts/.
NIST (2015). SHA-3 Standard: Permutation-Based Hash
and Extendable-Output Functions.
A Security Analysis, and a Fix, of a Code-Corrupted Honeywords System
95
