Test Generation for Performance Evaluation of Mobile Multimedia

Streaming Applications

Mustafa Al-tekreeti

, Kshirasagar Naik

, Atef Abdrabou

, Marzia Zaman

and Pradeep Srivastava

University of Waterloo, Ontario, Canada

UAE University, Al-Ain, U.A.E.

Technologie Sanstream, Quebec, Canada

Keywords:

Multimedia Mobile Streaming, Performance Testing, Coverage Criteria.

Abstract:

In this paper, we propose a model based test generation methodology to evaluate the impact of the interaction

of the wireless network and the application (app) conﬁgurations on the performance of a mobile multimedia

streaming app. The methodology requires four artefacts as inputs, namely, a behaviour model of the software

under test (SUT), a network model, a test coverage criterion, and desired performance levels. The methodology

consists of three steps. First, two performance models are developed: mathematical and simulation. Second,

to evaluate the end-user quality of experience (QOE), test generation is formulated as an inversion problem.

To account for different types of performance models, the inversion problem is solved as an optimization

problem. Third, the necessary information to execute test cases is inferred using the simulation model. Two

test coverage criteria are proposed: user-experience (UE) and user-experience-and-input-interaction (UEII).

The mathematical performance model for a streaming app is developed using Markov chain. To account for

realistic network behaviours, the Markov chain is solved using the supplementary variable technique (SVT).

A reusable network model is developed for a mobile device that has a network access through a WiFi LAN.

Finally, the effectiveness of the methodology is evaluated in comparison with random testing.

1 INTRODUCTION

Performance is an important property of software sys-

tems, having a vital impact on user’s experience. In

the mobile systems domain, the main theme is being

context sensitive (Liu et al., 2015), imposing extra re-

quirements on mobile software development. Being

able to communicate with many network types ne-

cessitates testing whether the app will perform as re-

quired under different environmental and contextual

scenarios (Diaz et al., 2010). However, testing mobile

apps for network behaviour is challenging since it re-

quires multidisciplinary expertise. Another important

aspect of mobile apps is the emphasis on the user ex-

perience. Therefore, there is a need for performance

testing methodologies that take into account both the

network behaviour and the end-user’s QOE.

In this paper, we consider an important category

of networked apps, which are mobile multimedia

streaming apps. Figure 1(a) depicts the main elements

of the system model. We aim to evaluate the interac-

tion of network operating parameters (NOPs) and app

conﬁguration parameters (ACPs) on the performance

(a)

dĞƐƚ

ĞŶĞƌĂƚŝŽŶ

ƉƉĐŽŶĨŝŐƵƌĂƚŝŽŶƉĂƌĂŵĞƚĞƌƐ;WƐͿ

ĞƚǁŽƌŬŽƉĞƌĂƚŝŶŐƉĂƌĂŵĞƚĞƌƐ;EKWƐͿ

ĞƐŝƌĞĚƉĞƌĨŽƌŵĂŶĐĞ

EĞƚǁŽƌŬŵŽĚĞů



ĞŚĂǀŝŽƌŵŽĚĞůŽĨ^hd

(b)

Figure 1: System model and test generation scheme.

of a mobile streaming app. We assume the app to be

functionally correct. NOPs are a set of controllable

parameters that model the network condition, such as

data rate. NOPs are network technology dependent.

ACPs represent a set of app conﬁguration settings that

have an impact on the performance metric under con-

sideration, such as the size of the receiving buffer.

The main idea in generating tests is shown in Fig-

ure 1(b). Determining test inputs that lead to cer-

tain performance behaviour is akin to solving the in-

version problem (Kumar et al., 2015). The inver-

Al-tekreeti, M., Naik, K., Abdrabou, A., Zaman, M. and Srivastava, P.

Test Generation for Performance Evaluation of Mobile Multimedia Streaming Applications.

DOI: 10.5220/0006609302250236

In Proceedings of the 6th International Conference on Model-Driven Engineering and Software Development (MODELSWARD 2018), pages 225-236

ISBN: 978-989-758-283-7

225

sion problem is the problem of inferring the causes

by observing the effects. This problem is solved in

three main steps: system parametrization, forward

modelling, and inverse modelling (Tarantola, 2005).

In this work, system parametrization corresponds to

identifying both ACPs and NOPs. Forward modelling

corresponds to the performance model development.

Inverse modelling is the optimization problem formu-

lation that when solved test input is generated.

The desired performance level is a quantitative

measure of the performance metric under consider-

ation. Generally, performance metrics are evaluated

using statistical measures such as mean, percentage,

and probability. The network model captures how

the quality of network service quantiﬁed in terms of

NOPs impacts the performance behaviour of the SUT.

Different metrics are used to model network quality of

service. In streaming apps, user experience is mainly

inﬂuenced by the frame inter-arrival time delay. The

behaviour model of SUT is an abstraction of the app

dynamics that capture the performance metric under

consideration. In this work, we use activity diagrams

to describe this model.

Since performance metrics are statistical mea-

sures, extra information is required to execute the

generated test cases. Test execution parameters

(TEPs) encompass all the necessary information to

execute test cases. From a statistical point of view,

each test case is an experiment. Therefore, we need

to know how many times the experiment should be

repeated, or for how long it should be executed, so

that the output is statistically reliable. Thus, we aim

to design a set of test cases where each test case is

basically a set of ACPs, NOPs, TEPs and the ex-

pected performance level. In other words, given the

SUT is executed with the determined parameters of

ACPs, NOPs, and TEPs, the observed performance

level is statistically equivalent to the expected perfor-

mance level if the SUT is correctly implemented from

the performance point of view. Because performance

metrics are mainly continuous, inﬁnite number of per-

formance levels and test cases are anticipated. There-

fore, test selection strategies are needed to generate

an effective set of performance test cases.

In this paper, we propose a methodology to gener-

ate test cases to evaluate a mobile multimedia stream-

ing app. We adopt a black-box model-based testing

approach (Siavashi and Truscan, 2015). The method-

ology is realized by a procedure of three steps. First,

two performance models (mathematical and simula-

tion) to capture the interactions between the SUT and

the network are developed using Markov chains. Sec-

ond, generating tests to evaluate the end-user experi-

ence is formulated as an inversion problem and solved

as an optimization problem. Third, TEPs are inferred

using the simulation model. To enhance the quality of

the generated test cases, two test coverage criteria are

proposed: i) user experience (UE) and ii) user experi-

ence and input interaction (UEII). In the UE criterion,

test cases are generated to fully cover the identiﬁed

categories of end-user experience. In the UEII crite-

rion, test cases are generated to cover end-user expe-

rience and interactions of the input parameters simul-

taneously. We develop a reusable network model for

a mobile app that downloads data via a WiFi inter-

face and over the User Datagram Protocol (UDP). In

summary, we make the following contributions:

• we propose a test generation methodology to eval-

uate the impact of the interaction of network and

app conﬁgurations on the performance of a mobile

streaming app;

• we propose two testing coverage criteria to enhance

the quality of the generated test cases; and

• we show by means of a procedure how TEPs are

inferred using the performance simulation model.

The paper is organized as follows. In Section 2,

the related works are reviewed. In Section 3, the

proposed methodology is introduced. In Section 4,

we use an app example to illustrate the steps of the

methodology. In Section 5, the efﬁcacy of the pro-

posed methodology is evaluated. In Section 6, the

work is concluded and key challenges in applying the

proposed methodology are discussed.

2 RELATED WORKS

In literature, considerable efforts have been made to

integrate performance analysis with the software de-

velopment life cycle. A comprehensive summary can

be found in (Koziolek, 2010; Balsamo et al., 2004).

The main objective in this research is to conduct

performance analysis to evaluate design alternatives

while the software is still in the development process,

whereas our objective is to generate test cases and de-

velop test selection strategies for performance testing.

Our approach is orthogonal to theirs, but complemen-

tary to the early-stage performance testing phase.

Frequently, performance testing is viewed as load

testing. Load testing is used to test large-scale multi-

user transaction based software systems, such as web

sites and database systems (Jiang and Hassan, 2015).

In contrast, we target software apps that are devel-

oped for mobile devices, where network access is ac-

complished via wireless technologies. This differ-

ence in scope leads to a core distinction between our

MODELSWARD 2018 - 6th International Conference on Model-Driven Engineering and Software Development

226

ĞǀĞůŽƉƉĞƌĨŽƌŵĂŶĐĞŵŽĚĞůƐ

'ĞŶĞƌĂƚĞƚĞƐƚĐĂƐĞƐ

DĂƚŚŵŽĚĞů

^ŝŵƵůĂƚŝŽŶŵŽĚĞů

EĞƚǁŽƌŬ

ŵŽĚĞů

ĞŚĂǀŝŽƌ

ŵŽĚĞůŽĨ^hd

dĞƐƚƐĞůĞĐƚŝŽŶ

ƐƚƌĂƚĞŐǇ

ĞƐŝƌĞĚ

ƉĞƌĨŽƌŵĂŶĐĞ

ůĞǀĞůƐ

EKWƐ͕WƐ͕

dWƐ

ǀĂůƵĂƚĞƚĞƐƚĞǆĞĐƵƚŝŽŶƉĂƌĂŵĞƚĞƌƐ

^ŝŵƵůĂƚŝŽŶŵŽĚĞů

EKWƐ͕WƐ

Figure 2: The main steps of the methodology.

work and the model-based load testing. The devel-

oped models in load testing is network-technology in-

dependent, while our approach models explicitly the

network technology.

In spite of the much research efforts going into

performance testing, test generation to evaluate the

network impact on the performance of mobile apps

has not received much attention (Liu et al., 2015;

Joorabchi et al., 2013). The main focus is on test-

ing networked apps for functional requirements (Se-

bih et al., 2014; Walls et al., 2015), designing soft-

ware proﬁlers to debug communication errors (Diaz

et al., 2010), or providing test execution beds to eval-

uate the impact of the environment on wireless mobile

apps (Satoh, 2004).

In software engineering, simulation models have

been widely used in different software development

activities. However, the emphasis is on using simu-

lation models to evaluate alternative design choices

(Kim et al., 2013), or to design test cases to verify

software systems represented as simulation models

(Matinnejad et al., 2016). In our work, we provide a

procedure based on two statistical procedures to infer

test execution parameters from simulation models.

3 THE METHODOLOGY

In this section, our test generation methodology is in-

troduced. Figure 2 shows the main steps, the inputs,

and the expected output of the methodology. We start

by discussing the methodology input requirements.

Then, we explain the methodology steps.

3.1 Inputs to the Methodology

The methodology requires four different artefacts as

inputs. In this section, we describe them brieﬂy:

3.1.1 Behaviour Model of the SUT

This model should describe how the app-network in-

teractions impact the performance metric under con-

sideration. According to Figure 1(a), the app-network

interactions in streaming apps are well modelled by

capturing the buffering behaviour of the app. The out-

comes of this task are the behaviour model of the SUT

and the set of app conﬁguration parameters (ACPs)

that affect the considered performance metric. We use

activity diagrams to describe this model.

3.1.2 Network Model

This model should capture how the wireless network

affects the considered performance metric. In general,

network models are determined by the technology

(WiFi or cellular) and the transport protocol (TCP or

UDP). As shown in Figure 1(a), the app interacts with

the network through a basic request-response (REQ-

RES) mechanism. In multimedia streaming, the net-

work’s impact can be captured by modelling the RES

inter-arrival time delay, which is a random variable.

The expected outcomes of network modelling are the

probability distribution of this random variable and

the NOPs. To obtain the distribution, we employ dis-

tribution ﬁtting using the ﬁrst two moments: the mean

and variance. Assuming the UDP protocol, we de-

velop in Appendix A mathematical expressions for

the mean and variance of packet (RES) inter-arrival

time delay for a mobile user in a WiFi network.

3.1.3 Desired Performance Levels

The methodology requires a set of levels of the perfor-

mance metric under consideration. In this work, we

are interested in application level performance met-

rics that directly relate to the end-user’s quality of

experience (QOE). For example, the user experience

of ﬁle transfer apps is assessed using two metrics:

goodput and transfer time performance (Ivanovici and

Beuran, 2010). Both are ratio metrics on a scale

from 0 to 1, where 1 represents the best performance.

Therefore, desired performance levels are merely nu-

merical values sampled from the interval [0,1]. How

many of those levels are needed and how they are cho-

sen are addressed in the test selection strategies.

3.1.4 Test Selection Strategies

In general, a test selection strategy encodes the main

objectives of the testing process. Satisfaction of test-

ing objectives is measured using coverage criteria. In

this methodology, we propose two coverage criteria

(UE and UEII). Initially, we need to introduce some

Test Generation for Performance Evaluation of Mobile Multimedia Streaming Applications

227

notations. The sets of NOPs and ACPs are denoted

as S

NOP

and S

ACP

with cardinalities n and m, respec-

tively. Therefore, we have n + m input parameters

, p

,..., p

n+m

. To generate a test case, we assign a

speciﬁc value vp

to each parameter p

∈ S

NOP

∪S

ACP

where vp

∈ V p

, the set of permissible values of the

parameter p

, 1 ≤ i ≤ n + m. Thus, a test case t

basically a tuple of the form (vp

, vp

, ..., vp

n+m

, l

where l

is the expected performance level.

i) User Experience (UE) Coverage Criterion

Herein, the objective is to generate test cases to cover

the whole spectrum of the considered performance

metric. However, since the performance spectrum

is most likely to be continuous, an inﬁnite number

of test cases are needed. To generate a minimal set

of test cases, partition testing (Grindal et al., 2005)

is applied. The idea is to partition the parameter

space into multiple regions where all the points of the

same region are equivalent from the testing point of

view. In our work, we apply partition testing to per-

formance metrics, utilizing the fact that the end-user

perception of the performance behaviour is discontin-

uous and can be characterized in terms of a few spe-

ciﬁc categories (QOE categories). Given R categories,

we divide the performance spectrum W into R non-

overlapped regions r

,...,r

such that W =

The number of QOE categories is app type dependent.

Next, a performance level l

is selected for each re-

gion such that l

∈ r

, 1 ≤ i ≤ R. Last, the correspond-

ing test input vp

, vp

, ..., vp

n+m

for l

is determined.

Procedure 1 summarizes the steps needed to generate

test cases that satisfy this criterion:

• Procedure 1: Test selection strategy to achieve the

UE coverage criterion

• Inputs: The number of QOE categories R

• Outputs: A test suite T of at least R test cases

S1: Partition W into R regions r

,...,r

;

S2: Select the set S

={l

: l

∈ r

, 1 ≤ j ≤ R};

S3: ∀ l

∈ S

, generate test inputs vp

,vp

,...,vp

n+m

ii) User Experience and Input Interaction (UEII)

Coverage Criterion

It may be noted that the UE coverage criterion is an

output based criterion. However, satisfying this cri-

terion is not enough to assure the quality of the app,

because the designed test suite does not adequately

cover the input space of the SUT. In combinatorial

testing, it is emphasized that the effectiveness of the

generated test cases increases as the coverage of the

interactions of the input parameters increases (Yılmaz

et al., 2014). Therefore, we are interested in generat-

ing test cases that satisfy both aspects of the SUT: the

input space and the performance behaviour. For this

purpose, we extend Procedure 1 as follows. First, we

generate the set T

of R seed test cases using Proce-

dure 1. This set does cover the performance spec-

trum. Then, to enhance input space coverage, we use

the seed tests to generate follow-up test cases so that

a combinatorial metric is satisﬁed. The combinato-

rial metric is applied on subsets g

, g

, ..., g

of the

NOP

∪S

ACP

set, where G ≥ 1. These subsets are con-

structed such that the parameters in which their inter-

actions are important to cover are grouped together

into a subset. A set of follow-up test cases T

i j

is gen-

erated for every subset g

and seed test s

∈ T

. The

parameters’ values vp

, vp

, ..., vp

n+m

of the follow-

up test cases are determined as follows. The values of

the parameters of the g

subset are determined using

the combinatorial metric. The remaining parameters

{p : p ∈ S

INP

− g

} are assigned the same values of

the seed test case s

The input space is constrained by conditions im-

posed by the network, the SUT, and by the condition

that the expected performance levels for the follow-

up test cases should remain within the same perfor-

mance region of the test seed. That is, given the sets

, S

= {g

,...,g

}, C (the set of constraints),

and a combinatorial metric b, T

i j

= Pert(g

,C,b),

1 ≤ j ≤ G, 1 ≤ i ≤ R, where Pert realizes the follow-

up test generation using the combinatorial coverage

metric b. Therefore, test generation to satisfy UEII

criterion is basically a combinatorial test generation

with constrained parameters. The generated test suite

T is the union of the follow-up test sets T

i j

and the

seed tests T

. The following procedure summarizes

the steps explained before:

• Procedure 2: Test selection strategy to achieve the

UEII coverage criterion

• Inputs: R, G, C, and b

• Outputs: A test suite T =

i, j

i j

S1: Generate the set T

using “Procedure 1”;

S2: Create the set S

={g

: g

⊂ S

INP

, 1 ≤ j ≤ G};

S3: ∀ j, i, T

i j

= Pert(g

,C,b).

Hence, the UEII criterion subsumes the UE criterion.

3.2 The Procedure of the Methodology

As shown in Figure 2, the methodology’s steps are:

3.2.1 Develop Performance Models

By the performance model we mean any mathemati-

cal representation that quantitatively captures the im-

MODELSWARD 2018 - 6th International Conference on Model-Driven Engineering and Software Development

228

pact of the interaction of NOPs and ACPs on the

performance of the SUT. In this work, we employ

the Markovian framework to develop the performance

models. This framework is appropriate when the sys-

tem state is deﬁned by the buffering behaviour of the

SUT. We use supplementary variable technique (Cox

and Miller, 1977) to solve the model. This technique

is used if the stochastic process is not Markovian,

allowing for more practical interactions between the

SUT and the network to be modelled. In this method-

ology, two performance models are developed: math-

ematical and simulation. The simulation model is

used to verify the mathematical model and in the test

generation process as well. In Appendix B, the perfor-

mance model (Equations (23-30)) of the considered

app example is developed. This step requires the net-

work model and behaviour model of the SUT.

3.2.2 Generate Test Cases

NOPs and ACPs are found by formulating test gener-

ation as an inversion problem. In order to determine

the input that leads to a certain output, an inverse re-

lationship should be derived. For most mathemati-

cal models, deducing a closed form for the inverse

relationship may not be feasible. Furthermore, the

structure of some models is unknown as in simulation

models. Therefore, we cast the inversion problem as a

root ﬁnding problem. Given the desired performance

level l

∈ S

, the test input is basically the root that

satisﬁes the relationship:

Perf model(p

,...,p

n+m

) − l

= 0 (1)

where Perf model(...) represents the performance

model. The roots (NOPs and ACPs values) can be

found by reformulating Equation (1) as a minimiza-

tion problem:

Minimize |Perf

model(p

,...,p

n+m

) − l

| (2)

where | ·| is the absolute value operator. We minimize

the absolute of the difference to force the solver that

the required minimum is zero. In this work, we use

the mathematical performance model as the objective

function, although the simulation model can also be

used. The minimization problem is constrained by

the conditions imposed by the network model and the

semantics of the SUT behaviour.

3.2.3 Evaluate Test Execution Parameters

We employ the simulation model to determine the

TEPs. We determine the parameters in two stages.

First, using a univariate sequential procedure called

Law and Carson (abbreviated as L&C) (Law, 2015),

we estimate the mean run length for the simulation

model to reach steady-state and use this value as an

estimate of the mean execution time of the test case.

We build a point estimator

and a conﬁdence inter-

val CI(

) so that the estimated value for the consid-

ered performance metric is within a pre-speciﬁed er-

ror from the true value. Second, the rest of TEPs are

inferred simultaneously by utilizing the Bonferroni

inequality (Charnes, 1995). This inequality provides

a lower bound for the overall conﬁdence level (1 − ζ)

given that the overall signiﬁcant level ζ is equal to the

sum of the individual signiﬁcant levels. We construct

individual conﬁdence intervals using the Independent

Replication Sequential (IRS) procedure (Law, 2015).

The precision of estimation is controlled by the rel-

ative error in estimation γ. Procedure 3 summarizes

how to infer TEPs using the simulation model:

• Procedure 3: Determine TEPs using the simula-

tion model

• Inputs: The test case (vp

, vp

, ..., vp

n+m

, l

), γ, ζ,

and the number of replications

• Outputs: The corresponding TEPs values

S1: Invoke the L&C procedure to obtain

and

CI(

);

S2: Choose ζ

, ζ

, ..., ζ

so that

∑

i=1

= ζ;

S3: Invoke IRS procedure to obtain the estimated

mean and the conﬁdence interval for the remain-

ing TEPs.

4 USING THE METHODOLOGY

In this section, we apply the proposed methodology

on an example of a mobile multimedia streaming app.

The considered performance quality is the smooth-

ness of the streaming as perceived by the end user. We

assume that the app utilizes the UDP protocol and the

last hop to the end user is through a wireless connec-

tion using a WiFi hotspot that implements the IEEE

802.11 protocol. We start this section by deﬁning the

behaviour model of the SUT and the network model.

Then, we apply the proposed methodology to gener-

ate test cases using both test selection strategies.

4.1 Behaviour Model of the SUT

We assume that the SUT implements a progressive

streaming in which both frame downloading and de-

coding are interleaved. The app behaviour is mod-

elled by two main components: downloader and

player. Both components interact with each other

through a playback buffer. Figure 3 shows the de-

sired behaviour of the SUT. At the beginning, the app

Test Generation for Performance Evaluation of Mobile Multimedia Streaming Applications

229

is in the Buffering phase. In this phase, the down-

loader starts fetching media frames from the network

and queues them in the buffer, while the player is still

off. The app remains in this phase until the data level

in the playback buffer reaches a certain limit usually

known as a high watermark level (M). This level de-

termines the length of the buffering phase and thereby

the length of the time period the user has to wait be-

fore the player starts playing. Also, this level deter-

mines when the app stops asking for new frames. The

downloader resumes fetching media frames whenever

data level drops below a certain limit, known as a low

watermark level (L). This level represents the mini-

mum amount of data in the buffer to ensure smooth

playback. To capture end user experience, we con-

sider the frequency of rebuffering events as the per-

formance metric (Mok et al., 2011). This metric has

a direct relationship with the frequency of visiting

the Empty Buffer state. The SUT behaviour is char-

acterised by three conﬁguration parameters (ACPs):

playback buffer size (B), M, and L.

ƵĨĨĞƌсD ƵĨĨĞƌс>

ƵĨĨĞƌсD

ƵĨĨĞƌсϬ

ƵĨĨĞƌхϬ

ŵƉƚǇ

ƵĨĨĞƌ

ƵĨĨĞƌŝŶŐ

ΘWůĂǇŝŶŐ

WůĂǇŝŶŐ

ƵĨĨĞƌŝŶŐ

Figure 3: The behaviour model of the app example.

4.2 Wireless Network Model

The streaming is through a WiFi AP. We assume all

the ﬂuctuations in the wireless channel and in the

wired network manifest as a time delay. Thus, packet

loss is negligible. The probability distribution (CDF)

of the frame inter-arrival time delay is matched with

Hyper-Erlang distribution using the mean and vari-

ance that are given by Equations (11) and (13) in Ap-

pendix A, respectively. The network impact is cap-

tured by three operating parameters (NOPs): data rate

D, the mean rate of frame arrival at the AP per user λ,

and the number of end users N connected to the AP.

To validate the matched CDF, we conduct simulation

experiments using the Network Simulator NS2. Fig-

ure 4 shows both the empirical and analytical CDFs.

4.3 The Procedure

Given the network model and the behaviour model of

the SUT, now we apply the methodology procedure:

4.3.1 Performance Models

We develop two performance models: mathematical

and simulation. The performance metric under con-

sideration correlates with the fraction of time of be-

Figure 4: The empirical and analytical CDFs.

ing in the Empty Buffer state out of the total time of

streaming. Since the performance metric is a steady-

state metric, the Buffering phase is not included in the

models. To evaluate the performance metric, the sta-

tionary distribution of the playback buffer length is

required. We are only interested in the probability of

having zero frames in the playback buffer π

To facilitate the modelling process, we assume

that the frame decoding rate is exponentially dis-

tributed. Nevertheless, the stochastic process is still

not Markovian, as the frame arrivals are not exponen-

tially distributed. Therefore, we develop the model

using the supplementary variable technique as shown

in Appendix B. The performance model is pictorially

shown by the Markov chain in Figure 7 and mathe-

matically described by the set of Equations (23-30).

To verify the performance model, Figure 5 shows

the performance metric π

with different buffer sizes

and for both simulation and mathematical models,

where µ represents the mean rate of frame decoding,

f is a tuning parameter to control the relation between

the frame arrival rate and µ; p and k are Hyper-Erlang

distribution parameters. In the simulation model, we

simulate a streaming session of 30 minutes. Each sim-

ulation experiment is repeated 50 times.

Figure 5: The considered performance metric (π

) versus

buffer size for both performance models.

4.3.2 Test Generation

Before solving the optimization problem, the con-

straints and bounds of the input parameters have to

MODELSWARD 2018 - 6th International Conference on Model-Driven Engineering and Software Development

230

be deﬁned. The ACPs (B, M, and L) are deﬁned as

integer number of multimedia frames. The semantics

of the SUT introduce the following two constraints:

M ≤ B and L ≤ M − 1.

(3)

The high watermark cannot be higher than the buffer

size, and the low watermark cannot be equal or higher

than the high watermark. For the NOPs, accord-

ing to the IEEE 802.11 a/g standard data rate D can

take either of the following values: 6, 9, 12, 18, 24,

32, 48, or 54 Mbps. It mainly relates to the qual-

ity of the wireless connection between the AP and

the end user. Regarding the number of users N, the

network model is validated with the number of users

that ranges from 4 to 30. λ is the only continuous

parameter. Using the upper and lower bounds of N

and D and the constraints imposed by the network,

we bound λ between 10 and 416 packets/sec, and we

represent this parameter by the following 42 discrete

values [10,20,30,...,410,416].

In multimedia streaming, the mean encoding rate

at the server is set according to the end-user device

characteristics. Thus, we assume that the mean arrival

rate to the end user 1/E

(Equation 11) is equal to the

mean decoding rate (µ) (Li et al., 2009), i.e.:

µ =

(4)

Solving Equation (4) in terms of NOPs (λ, N, and

D), a non-linear equality constraint is obtained. Since

most optimization solvers do not easily accommodate

non-linear equality constraints, we assume that the

mean of the packet inter-arrival time delay falls in a

closed interval around 1/µ. Thus:

≤ E

≤

(5)

where k1 and k2 are tunable parameters introduced

to control the width of the closed interval. By doing

so, we relax the non-linear equality constraint to two

non-linear inequalities that are easier to deal with.

Another constraint that should be taken into con-

sideration is that the trafﬁc intensity (ρ) at the AP

should be less than 1:

ρ < 1 (6)

Otherwise, the buffer at the AP will build up in-

ﬁnitely. Therefore, the optimization problem has ﬁve

constraints (inequalities 3, 5, and 6).

i) Test Generation using UE Coverage Criterion

In Procedure 1.S1, the performance spectrum is par-

titioned according to the end-user QOE categories.

In multimedia streaming and using the probability

of empty buffer state π

as a performance met-

ric, three different end-user experiences are reported

(Mok et al., 2011). If π

is less than 2%, the video

quality is high; between 2% and 15%, the quality is

medium; and above 15%, the quality is poor. Hence,

we divide the performance spectrum into the reported

three regions (R=3). Then, we select a performance

level for each region {π

= 0.01,π

= 0.05,π

= 0.2}.

Solving the minimization problem for each of them,

the corresponding network and SUT parameters’ val-

ues are determined as shown in part (a) of Table 1

(the left most seven columns). The buffer size B is

bounded between 10 and 40 frames, the mean of the

decoding rate µ is 30 f rames/sec, and the parameters

k1 and k2 are 0.75 and 1.25, respectively.

ii) Test Generation using UEII Criterion

We consider the three generated test cases that are

listed in part (a) of Table 1 as test seeds T

(Procedure

2.S1). We utilize the combinatorial coverage metric

each-choice (Grindal et al., 2005) to enhance the input

space coverage. We choose to cover the interaction of

ACP

and S

NOP

independently (Procedure 2.S2)(i.e.,

G=2, g

ACP

, g

NOP

). For g

subset, we apply

each-choice criterion for high watermark (M) and low

watermark (L) only, since the playback buffer size (B)

does not directly affect the system output. The param-

eters B, D, λ, and N are kept ﬁxed on seed’ values.

The same procedure is applied for g

subset.

To generate the follow-up test cases (Procedure

2.S3), we use the combinatorial tool ACTS v3 (ACT,

2016). Because the input parameters are constrained

by non-linear constraints, we ﬁrst identify the param-

eter values that satisfy the constraints and then we ap-

ply the combinatorial testing criterion. Applying Pro-

cedure 2.S3 for g

subset, we get 33 (T

), 40 (T

and 9 (T

) follow-up test cases for the performance

regions [0,0.02], (0.02,0.15], and (0.15,1], respec-

tively. As an example, we show the set T

below:

= {(10,5),(11,1),(12,1), (13,1), (8,7), (6,4),

(5,3),(9,6),(7,2)}

The ﬁrst element of each tuple is M and the second

is L. For g

subset, we get 5 (T

), 3 (T

), and

3 (T

) follow-up test cases for the regions [0,0.02],

(0.02,0.15], and (0.15,1], respectively. As an exam-

ple, we show the set T

below:

= {(54M,110,15),(54M,150,11),(54M,330, 5)}

The ﬁrst element of each tuple is D, the second is λ,

and the third is N. The remaining parameters’ (B, M,

and L) values are ﬁxed on test seed values. Hence, the

designed test suite T using the UEII criterion is the

union of the sets T

, T

, and T

Test Generation for Performance Evaluation of Mobile Multimedia Streaming Applications

231

4.3.3 Determining TEPs

For the app example, each test case is a streaming ses-

sion with certain conﬁguration parameters. To exe-

cute each test case, the length of the streaming session

and the size of the multimedia ﬁle need to be deter-

mined. Since we have two TEPs parameters only, we

do the estimations without the need to use Bonferroni

inequality (Procedure 3.S2). The used values for γ, ζ,

and the number of replications are 0.075, 0.1, and 10,

respectively. We build a point estimator and a con-

ﬁdence interval independently for the mean test case

execution time

(Procedure 3.S1) and the mean ﬁle

size

(Procedure 3.S3) so that the estimated proba-

bility of the empty playback buffer state (

) is within

a pre-speciﬁed error from the true value. We estimate

and

for the three test cases as shown in part (b)

of Table 1. We gauge the adequacy of the estimated

simulation time by controlling the width of the con-

ﬁdence interval CI(

) through the parameter γ. As

expected, test case execution time is test case depen-

dent. Moreover, as π

increases, the required time to

reach steady-state decreases.

5 EVALUATION OF THE

APPROACH

We use random testing as a baseline to evaluate the

effectiveness of the proposed methodology. Herein,

we use the phrases test conﬁgurations and test cases

interchangeably. As the implementation of the SUT

is not available, we generate test cases randomly us-

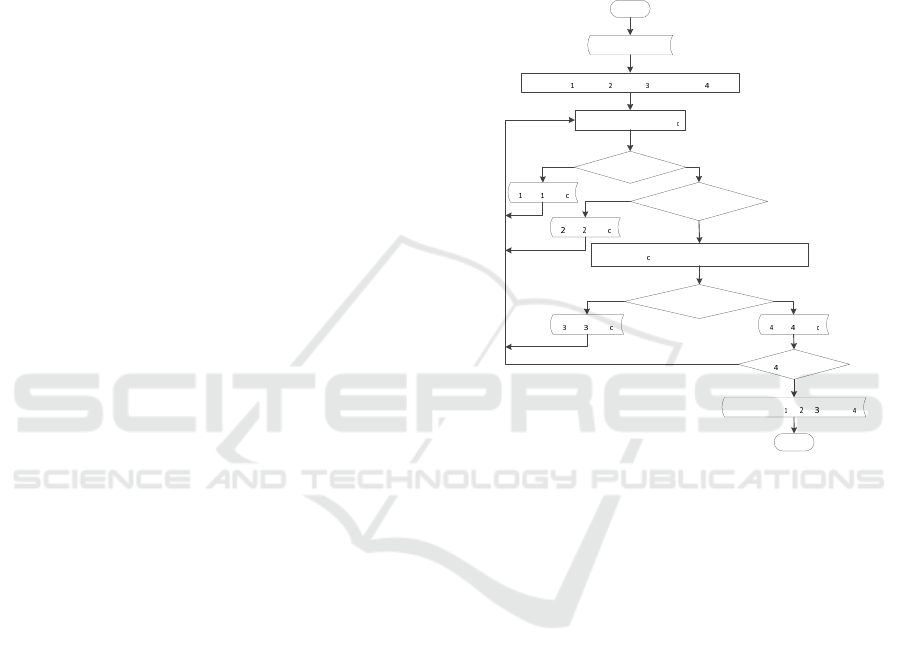
ing the procedure shown in Figure 6, where R is the

number of performance regions, Q is the number test

cases per region, and C is the coverage criterion. We

ﬁrst use the UE coverage criterion. We use the devel-

oped performance model to evaluate the performance

behaviour l

(π

) of the conﬁguration t

. To antici-

pate the incurred cost of the random test generation,

we keep track of four types of test conﬁgurations: In-

valid executable test conﬁgurations (IETCs), Invalid

non-executable test conﬁgurations (INTCs), Valid-

and-useful test conﬁgurations (VTCs), and Valid-but-

not-useful test conﬁgurations (VNTCs).

A test conﬁguration t

is invalid if the chosen pa-

rameters’ values do not satisfy the constraints im-

posed by the network model, SUT, or both. If t

does not satisfy the network requirements only (in-

valid NOPs), the SUT can still execute, while if t

does not satisfy the constraints imposed by the SUT

(invalid ACPs), it is not executable. We assume that

the SUT implements the necessary logic to catch out

inconsistent ACPs. Therefore, we have two types of

invalid test conﬁgurations: executable (IETCs) and

non-executable (INTCs). It is important to differen-

tiate between them as IETCs are more expensive than

INTCs from the time cost point of view. If t

satis-

ﬁes all the imposed constraints, it is a valid conﬁgura-

tion. Moreover, if this valid conﬁguration increases

the coverage of the designed test suite so far, it is

considered as a valid-and-useful conﬁguration. Oth-

erwise, it is a valid-but-not-useful test conﬁguration.

start

Randomly choose t

Inputs: R, Q, C

SUT constraints ?

Network constraints ?

S = S U {t }

YES

S = S U {t }

Evaluate l using the performance model

YES

Coverage criterion C ?

S = S U {t }

YES

|S | = R×Q ?

end

YES

Define S ={φ}, S ={φ}, S ={φ}, and S ={φ}

Outputs: S , S , S , and S

Figure 6: The implemented ﬂowchart of test generation us-

ing random testing. The sets S

, S

, and S

are the sets

of INTCs, IETCs, VNTCs, and VTCs, respectively.

To estimate the incurred cost of generating a test

suite of size R × Q, we design an experiment with

R and Q as controllable factors. The obtained re-

sults are shown in Table 2. The results are basically

the median of 10 repetitions. For example, to ran-

domly generate a test suite with one test case (R = 1,

Q = 1), the incurred cost is approximately the sum of

the time cost of running 566 IETCs and one VTCs,

while in our framework, we need to execute the SUT

with one VTC only. Since performance metrics are

mostly statistical, the time needed to observe the per-

formance behaviour l

of the real system is not triv-

ial. As we employ a heuristics based optimization

formulation which solely depends on function (per-

formance model) evaluations to ﬁnd the optimal point

(test case), random testing can be better than ours if

the performance model evaluation is more expensive

than running the real SUT and/or if the employed op-

timizer needs more model evaluations than random

testing. For the ﬁrst condition, even if the perfor-

mance is modelled using a simulation model, many

techniques have been proposed to speed up simulation

MODELSWARD 2018 - 6th International Conference on Model-Driven Engineering and Software Development

232

Table 1: The augmented set of test cases.

is measured in minutes, D is measured in Mbps and

is measured in MB.

(a) test cases (b) test execution parameters (TEPs)

B M L D λ N

CI(

)

CI(

)

0.01 34 34 4 18 131.965 7 159.288 [145.385,173.2] 425.8 [425.32,426.28]

0.05 38 31 7 32 162.8702 8 109.226 [74.161,144.291] 280.2018 [279.77,280.63]

0.2 24 7 2 6 98.9693 4 6.4 [4.651,8.148] 13.8505 [13.780,13.921]

Table 2: The cost of random testing in terms of the number of test conﬁgurations that need to be executed for different cases.

R Q Suite size IETCs INTCs VNTCs VTCs

1 1 1 566 1795.5 0 1

1 2 2 1471 5016 0 2

1 3 3 1849.5 6149 0 3

2 1 2 3193 10317 3 2

2 2 4 4817 15966 6.5 4

2 3 6 11472 38262 14.5 6

3 1 3 18290 60399 29.5 3

3 2 6 40018 1.3266 × 10

66.5 6

3 3 9 1.0785 × 10

3.5653 × 10

178.5 9

executions, while real system executions cannot be

accelerated. For the second condition, many heuris-

tics based optimization algorithms are available in lit-

erature that can perform better than our optimization

solver. Indeed, within the used solver, many strategies

can be used to ﬁne tune its performance. In conclu-

sion, there is still much room to enhance the perfor-

mance of our framework compared to random testing.

In addition, as R increases, the incurred time cost

increases and reaches astronomical values as the case

with R = 3 and Q = 3. In this scenario, the time

cost is approximately the sum of the time cost of run-

ning 1.0785×10

IETCs, 178.5 VNTCs, and 9 VTCs.

In theory, as the number of performance regions (R)

increases, the width of each region decreases and

thereby the probability of getting a valid test case us-

ing random testing decreases. In contrast, the time

cost of generating a test case by solving the inversion

problem does not depend on the width of the region.

Compared to random search, our optimization based

approach employs a guided search to ﬁgure out valid

test conﬁgurations. This conclusion also applies to

UEII coverage criterion, as UEII metric builds upon

UE and combinatorial metrics.

6 DISCUSSION AND

CONCLUSION

In this paper, a model based test generation method-

ology was proposed to evaluate the impact of the in-

teraction of the app conﬁguration parameters and the

network operating parameters on the performance of

mobile multimedia apps. The methodology required

four different artefacts as inputs: a behaviour model

of the SUT, a network model, desired performance

levels, and coverage criteria. The methodology com-

prised three steps: performance models development,

test inputs generation, and estimation of TEPs. Test

generation was formulated as an inversion problem

and solved as a minimization problem. To generate

effective test cases, two coverage criteria were pro-

posed: i) user experience (UE) and ii) user experi-

ence and input interaction (UEII). We applied the pro-

posed methodology on a mobile multimedia stream-

ing app example. The effectiveness of the method-

ology was empirically evaluated in comparison with

random testing. The incurred time cost to generate

a test suite using random testing was estimated to be

much more than the cost of our framework.

In model-based testing, model development is the

most critical operation that is difﬁcult to automate. In

this work, constraints derivation is another intensive

operation that is fortunately amenable to automation

especially with the promising advances that have been

made in symbolic computing. Moreover, solving the

inversion problem as a black box optimization prob-

lem has enabled test generation regardless of the inter-

nal structure of the performance model and the used

stochastic notation.

In the app example, the main observation was the

high computing cost of evaluating the mathematical

Test Generation for Performance Evaluation of Mobile Multimedia Streaming Applications

233

model compared to the simulation model when the

buffer size was beyond a certain value. To mitigate

this issue, we can employ the simulation model in

solving the inversion problem. In literature, there

is an increasing interest in using simulation models

in optimization problems (Gosavi, 2014). To en-

hance the quality of the generated test cases, we pro-

posed the UEII coverage criterion. However, the net-

work model has constrained NOPs by non-linear con-

straints, making test generation using combinatorial

metrics very complicated. To overcome this issue,

we exhaustively checked all combinations for the im-

posed constraints. However, this approach might be

very expensive in terms of execution time, especially

for systems with a large number of parameters and/or

parameter values, which indicates the need for more

powerful mechanisms to address such scenarios.

REFERENCES

(2016). Advanced combinatorial testing system (acts).

Balsamo, S. et al. (2004). Model-based performance predic-

tion in software development: A survey. IEEE Trans.

on Soft. Eng., 30(5):295–310.

Bianchi, G. (2000). Performance analysis of the ieee 802.11

distributed coordination function. IEEE Journal on

Selected Areas in Communications, 18(3):535–547.

Charnes, J. M. (1995). Analyzing multivariate output. In

Proc. of the 27th conf. on Winter simulation, pages

201–208. IEEE Computer Society.

Cox, D. R. and Miller, H. D. (1977). The theory of stochas-

tic processes, volume 134. CRC Press.

Diaz, A., Merino, P., and Rivas, F. J. (2010). Mobile appli-

cation proﬁling for connected mobile devices. IEEE

Pervasive Computing, 9(1):54–61.

German, R. (2000). Performance analysis of communica-

tion systems with non-Markovian stochastic Petri nets.

John Wiley & Sons, Inc.

Gosavi, A. (2014). Simulation-based optimization: para-

metric optimization techniques and reinforcement

learning, volume 55. Springer.

Grindal, M., Offutt, J., and Andler, S. F. (2005). Combi-

nation testing strategies: a survey. Software Testing,

Veriﬁcation and Reliability, 15(3):167–199.

Ivanovici, M. and Beuran, R. (2010). Correlating quality of

experience and quality of service for network applica-

tions. In Adibi, S., editor, Quality of service architec-

tures for wireless networks: performance metrics and

management, chapter 15, pages 326–351. IGI Global,

Pennsylvania, USA.

Jain, R. (1991). The art of computer systems performance

analysis: techniques for experimental design, mea-

surement, simulation, and modeling. John Wiley &

Sons.

Jiang, Z. and Hassan, A. (2015). A survey on load testing

of large-scale software systems. IEEE Trans. on Soft.

Eng., 41(11):1091–1118.

Joorabchi, M. E., Mesbah, A., and Kruchten, P. (2013). Real

challenges in mobile app development. In Int. Symp.

on Emp. Soft. Eng. and Meas., pages 15–24. IEEE.

Kim, Y. et al. (2013). Validating software reliability early

through statistical model checking. IEEE software,

30(3):35–41.

Koziolek, H. (2010). Performance evaluation of

component-based software systems: A survey. Per-

formance Evaluation, 67(8):634–658.

Kumar, R. et al. (2015). Inverting a steady-state. In Proc.

of the 8th Int. Conf. on Web Search and Data Mining,

pages 359–368. ACM.

Law, A. M. (2015). Simulation modeling and analysis.

McGraw-Hill, NY, ﬁfth edition.

Li, M., Claypool, M., and Kinicki, R. (2009). Playout buffer

and rate optimization for streaming over ieee 802.11

wireless networks. ACM Trans. on Multimedia Com-

puting, Communications, and Applications, 5(3):26.

Liu, Y., Xu, C., and Cheung, S.-C. (2015). Diagnosing en-

ergy efﬁciency and performance for mobile internet-

ware applications. Software, IEEE, 32(1):67–75.

Matinnejad, R. et al. (2016). Automated test suite genera-

tion for time-continuous simulink models. In 38th Int.

Conf. on Soft. Eng., pages 595–606. ACM.

Mok, R. K., Chan, E. W., and Chang, R. K. (2011). Measur-

ing the quality of experience of http video streaming.

In 12th IFIP/IEEE Int. Symp. on Integrated Network

Management and Workshops, pages 485–492. IEEE.

Satoh, I. (2004). Software testing for wireless mobile com-

puting. IEEE Wireless Communications, 11(5):58–64.

Sebih, N. et al. (2014). Software model checking of udp-

based distributed applications. In 2nd Int. Symp. on

Comp. and Net., pages 96–105. IEEE.

Siavashi, F. and Truscan, D. (2015). Environment modeling

in model-based testing: concepts, prospects and re-

search challenges: a systematic literature review. In

19th Int. Conf. on Eval. and Assess. in Soft. Eng.,

page 30. ACM.

Tarantola, A. (2005). Inverse problem theory and methods

for model parameter estimation. siam.

Walls, R. J. et al. (2015). Discovering speciﬁcation vio-

lations in networked software systems. In 26th Int.

Symp. on Soft. Reliab. Eng., pages 496–506. IEEE.

Yılmaz, C. et al. (2014). Moving forward with combinato-

rial interaction testing. Computer, 47(2):37–45.

A PACKET DELAY STATISTICS

IN A WIFI NETWORK

In this part, we derive analytical expressions for the

mean and variance of the packet (or frame) inter-

arrival time delay for streaming over a UDP protocol

and via a WiFi network. We assume that the WiFi

AP operates in the Distributed Coordination Function

MODELSWARD 2018 - 6th International Conference on Model-Driven Engineering and Software Development

234

(DCF) mode. In this mode, a station (mobile device

or AP) can only send a MAC frame if the channel is

sensed idle for a DIFS (distributed inter-frame space)

interval of time. If the sender transmits and does not

receive an ACK within a certain amount of time, a

collision is detected and the frame has to be resched-

uled for transmission. In this case, the sender has to

wait for extra random amount of time after a com-

plete DIFS interval of being sensed idle to send the

frame. This random amount of time is called the

back-off interval. We assume data exchange between

stations are achieved using the four-way handshaking

scheme. Therefore, the time needed to successfully

send a packet T

is given by (Bianchi, 2000):

= T

RT S

CT S

+3 ×T

SIFS

DIFS

ACK

+T (7)

where T

RT S

, T

CT S

, T

ACK

, and T

SIFS

are the trans-

mission times of ready-to-send packet, clear-to-send

packet, ACK packet, and short inter-frame space time

interval, respectively. The packet transmission time T

depends on the packet size P and on the data rate D of

the wireless connection:

T = T

PHY

MAC

+ H

UDP

+ P × 8

(8)

where T

PHY

, H

MAC

, and H

UDP

represent the PHY

layer overhead, MAC layer header size, and UDP

header size (20 Bytes), respectively. We assume that

the WiFi AP has inﬁnite buffer size, so the probability

of packet loss due to AP buffer overﬂow is negligible.

When a packet reaches the head of the AP buffer, the

time duration seen by this packet from this instant to

the instant at which it is successfully delivered to the

end user corresponds to the service time of the packet

and it’s mean is given by:

E[S

] = T

+ σ ×

(9)

where σ is the slot time interval. The back-off counter

is a uniform random variable in [0,W ].

Since the variance in packet service time is neg-

ligible, we assume that the AP as an M/D/1 queue-

ing system. Therefore, the mean of the packet inter-

arrival time delay E

at the end user is basically the

mean of the packet response time at the AP, which is

the sum of the mean of queueing time delay and the

packet service time (Jain, 1991):

= E[S

] +

ρ × E[S

]

2 × (1 − ρ)

(10)

where ρ is the trafﬁc intensity at the access point.

Therefore, with few simpliﬁcations, the mean packet

inter-arrival time delay is given by:

(2 − ρ)

2 × α × (1 − ρ)

(11)

Figure 7: The state diagram of the application.

where α is the packet service rate at the AP. Conse-

quently, the variance in packet inter-arrival time delay

Vard is mainly due to the variance in the AP queueing

waiting time and it is given by (Jain, 1991):

ard

NλE[S

]

3(1 − ρ)

(NλE[S

])

4(1 − ρ)

(12)

where N and λ are the number of users and the packet

mean arrival rate for each user at the AP. With few ma-

nipulations, the variance in packet inter-arrival time

delay settles down to the following equation:

ard

ρ × (4 − ρ)

12 × α

× (1 − ρ)

(13)

B PROBABILITY DISTRIBUTION

OF THE PLAYBACK BUFFER

LENGTH

In multimedia streaming, the end-user quality of ex-

perience correlates with the probability of empty

buffer state π

. Therefore, the stationary distribu-

tion of the playback buffer length should be evaluated.

Since the buffer dynamics’ process is not Markovian,

the model is solved using SVT. In this technique,

the state of the Markov chain should be redeﬁned so

that all the necessary information to determine the

next state is available in the current state. Thus, the

stochastic process is deﬁned as follows:

{B(t),V (t),t ≥ 0} (14)

where B(t) is a discrete random variable that repre-

sents the playback buffer length at time t, and V (t)

is a continuous random variable that represents the

elapsed time from the last frame arrival till time t.

Figure 7 shows the Markov chain of the SUT. All

states that are expected to receive frames are aug-

mented with the supplementary variable v to account

for the elapsed time since the last arrival. Our ob-

jective is to ﬁnd the steady state probability distribu-

tion of B(t). The derivation depends on examining

the short-term behaviour of the chain. For each state,

a difference equation is derived using the basic law

Test Generation for Performance Evaluation of Mobile Multimedia Streaming Applications

235

of total probability of two mutually exclusive events.

For state 0, it is:

(t + ∆t,v + ∆t) =π

(t, v)(1 − λ(v)∆t)

+ π

(t, v)µ∆t + o(∆t)

where o(∆t) is the probability of having more than

one event in a short interval ∆t. For states 1,2,..., and

M − 2, it is:

(t + ∆t,v + ∆t) = π

(t, v)(1 − λ(v)∆t − µ∆t)

+ π

n+1

(t, v)µ∆t + o(∆t), 1 ≤ n ≤ M − 2

For the states M − 1 and M, they are:

M−1

(t + ∆t,v +∆t) =π

M−1

(t, v)(1 − λ(v)∆t − µ∆t)

+ o(∆t)

(t + ∆t) =π

(t)(1 −µ∆t)

∞

M−1

(t, v)λ(v)∆tdv +o(∆t)

For the last M − L − 1 states, It is:

(t + ∆t) =π

(t)(1 −µ∆t) +π

n−1

(t)µ∆t

+ o(∆t), M + 1 ≤ n ≤ 2M − L − 1

The corresponding differential and partial differential

equations are:

∂π

(t, v)

∂t

∂π

(t, v)

∂v

= −π

(t, v)λ(v) + π

(t, v)µ

(15)

∂π

(t, v)

∂t

∂π

(t, v)

∂v

= −π

(t, v)(λ(v) + µ)

+ π

n+1

(t, v)µ, 1 ≤ n ≤ M − 2

(16)

∂π

M−1

(t, v)

∂t

∂π

M−1

(t, v)

∂v

= −π

M−1

(t, v)(λ(v) + µ)

(17)

dπ

(t)

= −π

(t)µ +

∞

M−1

(t, v)λ(v)dv (18)

dπ

(t)

= − π

(t)µ +π

n−1

(t)µ,

M + 1 ≤ n ≤ 2M − L − 1

(19)

subject to the following boundary conditions:

(t, 0) = 0 (20)

(t, 0) =

∞

n−1

(t, v)λ(v)dv, 1 ≤ n ≤ M − 1\{L}

(21)

(t, 0) =

∞

L−1

(t, v)λ(v)dv + π

2M−L−1

(t)µ (22)

For steady-state analysis, there is no need to spec-

ify initial conditions. To simplify solving the above

equations, there is a tactic to remove λ(v) from the

equations reported in (German, 2000). Applying this

tactic on Equations (15-18, 20-22), yields:

∂p

(t, v)

∂t

∂p

(t, v)

∂v

= p

(t, v)µ

∂p

(t, v)

∂t

∂p

(t, v)

∂v

= − p

(t, v)µ + p

n+1

(t, v)µ,

1 ≤ n ≤ M − 2

∂p

M−1

(t, v)

∂t

∂p

M−1

(t, v)

∂v

= −p

M−1

(t, v)µ

dπ

(t)

= −π

(t)µ +

∞

M−1

(t, v) f (v)dv

subject to the following boundary conditions:

(t, 0) = 0

(t, 0) =

∞

n−1

(t, v) f (v)dv, 1 ≤ n ≤ M −1\{L}

(t, 0) =

∞

L−1

(t, v) f (v)dv + π

2M−L−1

(t)µ

where p

(t, v) is the instantaneous rate function of

(t, v), the corresponding cumulative distribution of

(t, v), and f (v) is the probability density function

of the inter-arrival time delay v. As t → ∞, the sys-

tem reaches steady-state and the behaviour does not

depend any more on the time. Hence, the state equa-

tions become as follows:

(v)

= p

(v)µ (23)

(v)

= −p

(v)µ + p

n+1

(v)µ, 1 ≤ n ≤ M − 2

(24)

M−1

(v)

= −p

M−1

(v)µ (25)

0 = −π

µ +

∞

M−1

(v) f (v)dv (26)

0 = −π

µ + π

n−1

µ, M + 1 ≤ n ≤ 2M −L − 1 (27)

subject to the following boundary conditions:

(0) = 0 (28)

(0) =

∞

n−1

(v) f (v)dv, 1 ≤ n ≤ M − 1\{N}

(29)

(0) =

∞

L−1

(v) f (v)dv + π

2M−L−1

µ. (30)

The Equations (23-30) describes the dynamics of the

SUT. The probability distribution of the states are:

∞

(v)

F(v)dv, 0 ≤ n ≤ M − 1 (31)

where

F(v) is the complementary cumulative distri-

bution function of v. The solution of Equations (23-

31) with the normalization equation,

∑

2M−L−1

n=0

= 1,

gives the stationary distribution of the playback buffer

length. We are only interested in π

MODELSWARD 2018 - 6th International Conference on Model-Driven Engineering and Software Development

236