
Eco-Gresilient: Coalescing Ingredient of Economic, Green and
Resilience in Supply Chain Network Design
Ahmed Mohammed
1,2
, Irina Harris
1
and Reda Nujoom
2
1
Cardiff Business School, Cardiff University, Aberconway Building, Colum Dr, CF10 3EU, Cardiff, U.K.
2
School of Engineering, University of Portsmouth, PO1 3DJ, Portsmouth, U.K.
Keywords: Supply Chain Resilience, Go Green, RALF, Fuzzy AHP, Multi-criteria Decision Making, Multi-objective
Optimization.
Abstract: This research presents a new approach that considers green and resilience dimensions in addition to economic
(eco-gresilient, henceforth) aspects to design an eco-gresilient supply chain network. Thus, fuzzy AHP
(analytical hierarchy process) is used to determine the relative weight of evaluation criteria for each resilience
pillars (robustness, agility, leanness and flexibility (RALF)), and then it is used for assigning the importance
weight for each potential facility with respect to RALF. The determined weights revealed via fuzzy AHP are
then integrated into a multi-objective optimization model to identify the number of facilities that should be
established in the meat supply chain. Three objective functions were formulated and include minimization of
total cost and environmental impact and maximization of value of resilience (V-RALF). The ε-constraint
approach is used to obtain a set of Pareto solutions. The effectiveness of the developed eco-gresilient multi-
objective model is presented on a case study in the meat sector.
1 INTRODUCTION
The economic aspect represents the traditional
concerns in the supply chain design. Nevertheless,
environmental concerns have been increasingly
discussed in the supply chain management literature
where decision makers are required to address
increasing regulations related to green development.
Recently, there has been an increasing interest in
private and public sector and academia in improving
supply chain resilience to act against disruptions that
occur due unexpected events such as natural disasters,
earthquake, floods, and potential catastrophic failures
(Levalle and Nof, 2015). Despite various definitions
presented in the literature, the required resilience
pillars are not well identified from practical or
theoretical perspectives. Recently, Purvis et al.,
(2016) proposed a supply chain framework
highlighting the necessary ‘ingredients’ to achieve
resilience and it includes specific management
paradigms: robustness, agility, leanness and
flexibility (RALF).
In the context of supply chain network design, it
should consider economic, environmental and
resilience (Perrings, 2006). Thus, there is a need for a
survival plan through an integrated approach that
simultaneously considers resilience to efficiently
cope with unexpected disruptions and green
dimension to manage increasing global requirements
to reduce the environmental impact (Govindan et al.,
2017).
Multi-objective optimization in the supply chain
design has been widely applied in academia
(Mohammed et al., 2017a, b, c; Mohammed and
Wang, 2017 and 2015). Most recently, Govindan et
al., (2017) reviewed researches in the field of green
supply chains network design under uncertainty.
Mohammed and Wang (2017b) developed a
mathematical programming model for optimizing
location-allocation problem towards a green meat
supply chain using LP-metrics, ε-constraint and goal
programming.
Research of resilient supply chain design has been
increasing steadily in recent times. Nooraie et al.,
(2015) formulated a multi-objective model includes
minimization of investment costs, minimization of
the variance of the total cost and minimization of the
financial risk aiming to obtain a trade-off among them
using a relaxation heuristic method. Dixit et al.,
(2016) proposed a multi-objective model to maximize
supply chain resilience in minimizing unfulfilled
demand and transportation cost post-disaster. NSGA-
Mohammed, A., Harris, I. and Nujoom, R.
Eco-Gresilient: Coalescing Ingredient of Economic, Green and Resilience in Supply Chain Network Design.
DOI: 10.5220/0006614702010208
In Proceedings of the 7th International Conference on Operations Research and Enterprise Systems (ICORES 2018), pages 201-208
ISBN: 978-989-758-285-1
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
201
II and Co-Kriging approaches were adopted to solve
the model. However, the literature review revealed
that there is no research that integrates supply chain
resilience (for example with respect to RALF) and the
environmental impact.
This research paper presents a new multi-
objective optimization model for an eco-gresilient
meat supply chain network design in identifying the
optimal number of facilities that should be
established. The model considers the optimization of
three objectives: minimizing the total costs and CO
2
emissions throughout the supply chain and
maximizing the value of resilience (V-RALF) as a
third objective. Initially, the weight for each
resilience pillar and corresponding weight for each
potential facility are determined using fuzzy AHP
based on decision makers’ experts. Then, the weights
obtained by the fuzzy AHP are integrated in the
objective function that considers the four resilience
pillars. Based on the developed model, the ε-
constraint method is used to solve multi-objective
optimisation model.
2 DEVELOPING THE
ECO-GRESILIENT APPROACH
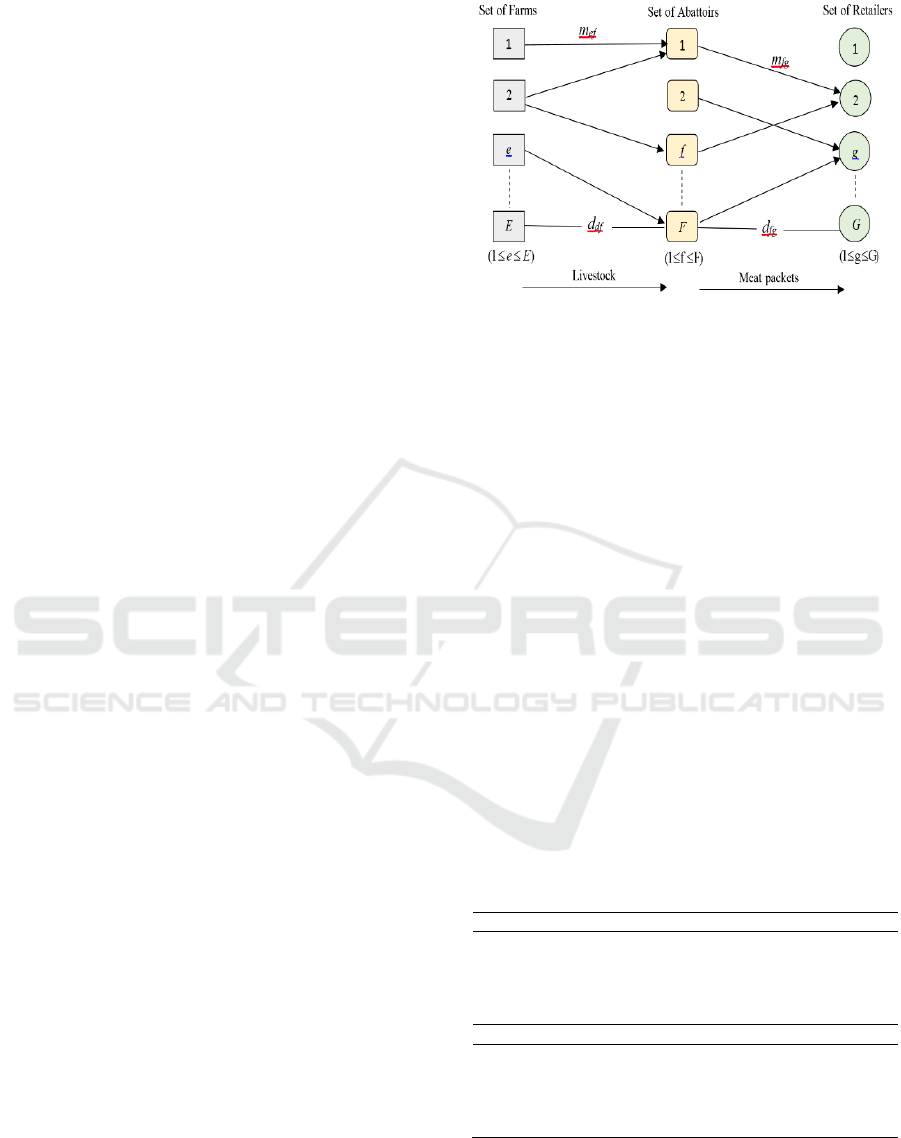
We Figure 1 illustrates the meat supply chain that is
used in the study which encompasses of multi-tier
network: farms, abattoirs and retailers. This research
aims to obtain an eco-gresilient meat supply chain
network design in identifying the optimal number of
farms and abattoirs that should be established
according to emerging economic, green and resilience
responsibilities.
The eco-gresilient approach is developed as
follows:
1. The fuzzy AHP technique is utilized to determine
relative weights for resilience pillars (i.e.,
robustness, agility, leanness and flexibility).
2. A fuzzy technique is used to determine the weight
for each potential farm and abattoir according to
their resilience performance.
3. A multi-objective optimization model is
developed towards the optimization of minimum
total cost and environmental impact and
maximum V-RALF. The latter is developed by
integrating the weights obtained from the fuzzy
techniques.
4. ε-constraint is used to generate Pareto solutions
for multi-objective optimization model.
Figure 1: Structure of the meat supply chain network under
study.
2.1 Weighting RALF and Facilities
In this research, fuzzy AHP is used to determine the
importance weight for each resilience pillar. Fuzzy
AHP is a decision-making algorithm presented by
incorporating the crisp AHP with the fuzzy set theory
(Saaty, 2000). In this algorithm, fuzzy numbers are
presented by a membership function that is a real
number between 0 and 1. Table 1 presents the
linguistic variables used for evaluating the four
resilience pillars. Decision makers need to evaluate
the importance of each pillar using the given
linguistic variables. The Fuzzy AHP is applied as
described in Srichetta and Thurachon, 2012.
Afterward, the steps were subsequently used to
determine the weight of each potential facility with
respect to resilience pillar. Table 1 presents the
linguistic variables used for evaluating farms and
abattoirs with respect to each resilience pillar based
on decision makers ’experts.
Table 1: Linguistic variables used for weighting resilience
pillars and potential facilities.
Evaluating pillars Fuzzy number (a,n,m)
Equally important (EI) (0.1, 0.1, 0.3)
Weakly important (WI) (0.1, 0.3, 0.5)
Strongly more important (SMI) (0.3, 0.5, 0.7)
Very strongly important (VSI) (0.5, 0.7, 0.9)
Extremely important (EI) (0.7, 0.9, 0.10)
Evaluating facilities Fuzzy number (a,n,m)
Very Low (VL) (1, 1, 3)
Low (L) (1, 3, 5)
Medium (M) (3, 5, 7)
High (H) (5, 7, 9)
Very High (VH) (7, 9, 9)
2.2 Model Formulation
The multi-objective optimization model supports
strategic decision in determining the optimal number
ICORES 2018 - 7th International Conference on Operations Research and Enterprise Systems
202

of farms and abattoirs that should be established with
respect to eco-gresilient performance. Three
objective functions are formulated which include
minimization of the total cost (TC), environmental
impacts (EI), and maximization of value of
robustness, agility, leanness and flexibility (V-
RALF).
Sets
E
set of farms
(1... ... )eE
F
set of abattoirs
(1... f ... F)
G
set of retailers
(1... g... G)
Input parameters
p
e
C
purchasing cost per unit of livestock ordered
from farm e
p
f
C
purchasing cost per unit of meat packets (units)
ordered from abattoir f
t
ef
C
unit transportation cost per mile from farm e to
abattoir f
t
f
g
C
unit transportation cost per mile from abattoir
f to retailer g
o
e
C
operating cost per hour required at farms e
o
f
C
operating cost per hour required at abattoir f
a
e
C
administration cost per order from fame e
a
f
C
administration cost per order from abattoir f
e
R
working rate per labourer at farm e
f
R
working rate per labourer at abattoir f
e
N
minimum required number of working hours
for labourer at farm e
f
N
minimum required number of working hours
for labourer at abattoir f
d
ef
transportation distance (mile) of livestock from
farm e t abattoir f
d
fg
transportation distance (mile) of processed meats
from abattoir f to retailer g
l
C
transportation capacity (units) per lorry
e
C
maximum supply capacity (units) of farm e
f
C
maximum supply capacity (units) of abattoir f
D
f
minimum demand (in units) of abattoir f
D
g
minimum demand (units) of retailer g
CO
2e
CO
2
emission in grams for opening farm e
CO
2f
CO
2
emission in grams for opening abattoir f
CO
2ef
CO
2
emission in grams per mile for each lorry
travelling from farm e to abattoir f
CO
2fg
CO
2
emission in grams per mile for lorry
travelling from abattoir f to retailer g
R
e
W
Weight of robustness obtained from fuzzy AHP
from the perspective of decision makers at abattoirs
R
f
W
Weight of robustness obtained from fuzzy AHP
from the perspective of decision makers at retailers
A
e
W
Weight of agility obtained from fuzzy AHP from
the perspective of decision makers at abattoirs
A
f
W
Weight of agility obtained from fuzzy AHP from
the perspective of decision makers at retailers
L
e
W
Weight of leanness obtained from fuzzy AHP
from the perspective of decision makers at abattoirs
L
f
W
Weight of leanness obtained from fuzzy AHP
from the perspective of decision makers at retailers
F
e
W
Weight of flexibility obtained from fuzzy AHP
from the perspective of decision makers at abattoirs
F
f
W
Weight of flexibility obtained from fuzzy AHP
from the perspective of decision makers at retailers
R
e
w
weight of farm e with respect to redundancy
obtained from fuzzy AHP
R
f
w
weight of abattoir f with respect to redundancy
obtained from fuzzy AHP
A
e
w
weight of farm e with respect to agility obtained
from fuzzy AHP
A
f
w
weight of abattoir f with respect to agility obtained
from fuzzy AHP
L
e
w
weight of farm e with respect to leanness obtained
from fuzzy AHP
L
f
w
weight of abattoir f with respect to leanness
obtained from fuzzy AHP
F
e
w
weight of farm e with respect to flexibility
obtained from fuzzy AHP
F
f
w
weight of abattoir f with respect to flexibility
obtained from fuzzy AHP
Output Decision variables
ef
m
quantity of livestock transported from farm e to
abattoir f
Eco-Gresilient: Coalescing Ingredient of Economic, Green and Resilience in Supply Chain Network Design
203

f
g
m
quantity of meat packets (units) transported from
abattoir f to retailer g
e
x
number of required labourers at farm e
f
x
number of required labourers at abattoir f
Binary decision variables:
e
y
1: if farm e is open
0: otherwise
f
y
1: if abattoir f is open
0: otherwise
2.2.1 Model Formulation
(1)
22
22
ee f f
eE f F
ef fg
ef ef fg fg
eEfF fFgG
Min EI CO y CO y
mm
CO CO
W
dd
W
(2)
RR R R
eeef ff
eE f F
AA A A
eeef ff
eE f F
LL L L
eeef ff
eE f F
FF FF
eeeeee
eE eE
M
ax V RALF W w y W w y
WwyWwy
WwyWwy
WwyWwy
(3)
Subject to:
ef
e
e
E
e
ymC
f
F
(4)
g
f
fg
F
ff
ymC G
(5)
D
e
E
f
f
e
m
f
F
(6)
D
f
F
gg
f
m
g G
(7)
D
gG
f
fg
m
f
F
(8)
R
ef e e
fF
mx
e E
(9)
f R
fg f f
gG
mx F
(10)
,0,,
ef fg
mm efg
(11)
,{1,0},,
ef
yy ef
(12)
Eq. 1 refers to objective function to minimize the total
transportation costs, which includes purchasing cost,
operating cost, administration cost and transportation
cost. Eq. 2 refers to the second objective function that
minimises the environmental impact, in particular
CO
2
emissions from opening network facilities and
transportation. Eq. 3 refers to the third objective
function that aims to maximize the value of supply
chain resilience in term of maximizing resilience
pillars i.e. RALF. The weights for each pillar and
each farm and abattoirs (with respect to RALF)
revealed from the fuzzy AHP are used to formalize
the maximization of V-RALF. Eq. 4 restricts the
quantity of livestock transported from farms to
abattoirs so that it cannot exceed the capacity of
farms. Eq. 5 ensures the quantity flow of meat packets
from abattoirs to retailer does not overcome the
capacity of abattoirs. Eqs. 6-8 ensure that the
demands of abattoir
f and retailer g are fulfilled from
farms e and abattoirs f, respectively. Eqs. 9 and 10
indicate the required number of labourers at farms
and abattoirs. Eqs. 11 and 12 limit the non-binary and
non-negativity restrictions on decision variables.
2.3 Revealing Pareto Solutions
In this research, the ε-constraint method is employed
towards the optimization of the three objectives. This
method transforms the multi-objective model to a
mono-objective model by keeping one of the function
as an objective function, and treating other functions
as constraints limited to ε values (Ehrgott, 2005). In
this work, minimization of total cost is used as an
objective function while minimization of
environmental impact and maximization of V-RALF
are moved to be ε-based constraints. The equivalent
solution formula (S) is given by:
TCMin S Min
(13)
Subject to:
1
EI
(14)
eEf F f FgG
eEfF fFgG
eEfF fFg
pp
eef ffg
aa
ef ef fg fg
oo
ef e e fg f f
ef fg
tt
ef ef
G
eEf F gG
fg fg
fF
Min TC m m
mCm
xN C xN
mm
C
CC
C
C
ddC
WW
ICORES 2018 - 7th International Conference on Operations Research and Enterprise Systems
204

1
min max
EI EI
(15)
2
VRALF
(16)
2
min max
V RALF V RALF
(17)
In addition to Eqs. 4-12.
3 APPLICATION AND
EVALUATION OF THE
ECO-GRESILIENT APPROACH
In this section, a case study is utilized to validate the
effectiveness of the developed eco-gresilient
approach to determine (1) the optimal number of
farms and abattoirs that should be established with
respect to economic, green and resilient
responsibilities, and (2) trade-off solutions among
three objectives: minimising total cost, environmental
impact and maximising the value of supply chain
resilience. The example includes 3 farms, 4 abattoirs
to supply 7 retailers. Table 2 presents values for input
parameters used in the model formulation discussed
in Section 3. The supply capacity of farm
e (
e
C
) is
generated in a range 1,500 – 1,800 livestock. The data
is collected from the meat committee in the UK
(HMC, 2010). The travel distances between farms
and abattoirs and between abattoirs and retailers are
estimated using the Google map. Also, the demand
values presented in Table 2, is the total demand over
a one year period. LINGO
11
software was used to
solve presented problem on a personal computer with
a Corei5 3.2GHz processor, 8GB RAM.
Table 2: Input parameters.
E = 3
t
e
C
= 1-1.5
f
g
d
= 110-205
F = 4
t
f
g
C
= 1-1.5
l
C
= 50
G = 7
a
e
C
= 3-4.5
e
C
= 1500-1800
p
e
C
= 130– 150
a
f
C
= 3-4.5
f
C
= 1600-2000
p
f
C
= 160– 190
ef
d
= 43-250
N
e
= 9
o
e
C
= 8-9.5
o
f
C
= 10-11
N
f
= 9
D
f
= 1250-1450 D
g
= 1100-1300 CO
2ef
= 271-294
CO
2fg
= 271-294
CO
2e
= 82000-
85000
CO
2f
= 220000-
250000
R
e
= 60 R
f
= 15
A decision maker (ADM) from an abattoir was
asked to evaluate the importance of resilience pillars
and the potential three farms (f1, f2 and f3) with
respect to each pillar, and two decision makers
(RDM
1
and RDM
2
) from two retailers in the UK were
asked to evaluate the importance of resilience pillars
and the potential four abattoirs (a1, a2, a3 and a4)
with respect to each resilience pillar.
Next, fuzzy AHP is applied for allocating the
importance weight for each resilience pillar
(robustness, agility, leanness and flexibility) based on
decision makers’ experts obtained in the previous
step. Table 3 shows the obtained weight for each
pillar. As can be seen in Table 3, the importance
weight order is
Agility>Robustness>flexibility>Leanness based on
ADM’s experts, and Agility> flexibility>
Robustness>Leanness based on RDMs’ experts.
Fuzzy AHP steps is then applied to determine the
importance weights of the potential three farms and
four abattoirs using the input parameters obtained
from the previous step. Table 4 shows the results
corresponding to the relevant facilities. Based on the
obtained results, farm 2 and abattoir 3 revealed the
highest resilience performance with respect to RALF
compared to farm 3 and abattoir 2 which revealed the
worst resilience performance.
The developed multi-objective optimization
model that integrates the obtained weights is
optimized using the ε-constraint method as follows:
1. Table 5 lists the minimum and maximum values
for each objective. These values are determined
by applying Eqs. 18-23, respectively. For
instance, the minimum and maximum values of
the total cost are 344,703 and 501,868,
respectively. These values are used for assigning
ε values.
Table 3: Weights of RALF.
Pilla
r
RA L F
DM ADM
Weigh
t
0.196 0.585 0.042 0.175
DM RDM1/RDM2
Weigh
t
0.123 0.438 0.036 0.400
Table 4: Weights of facilities with respect to RALF.
R A L F Global
f1 0.654 0.210 0.141 0.053 0.343
f2 0.841 0.211 0.198 0.068 0.383
f3 0.467 0.164 0.084 0.053 0.272
a1 0.397 0.131 0.101 0.087 0.269
a2 0.221 0.073 0.061 0.112 0.214
a3 0.397 0.131 0.142 0.112 0.298
a4 0.221 0.102 0.061 0.087 0.218
Eco-Gresilient: Coalescing Ingredient of Economic, Green and Resilience in Supply Chain Network Design
205

eEfF fFgG
eEfF fFgG
eEfF fFg
pp
eef ffg
aa
ef ef fg fg
oo
ef e e fg f f
ef fg
tt
ef ef
G
eEf F gG
fg fg
fF
Min TC m m
mCm
xN C xN
mm
C
CC
C
C
ddC
WW
(18)
22
22
ee f f
eE f F
ef fg
ef ef fg fg
eEfF fFgG
Mi n EI CO y CO y
mm
CO CO
W
dd
W
(19)
RR R R
eeef ff
eE f F
AA A A
eeef ff
eE f F
LL L L
eeef ff
eE f F
FF FF
eeeeee
eE eE
M
in V RALF W w y W w y
WwyWwy
WwyWwy
WwyWwy
(20)
eEfF fFgG
eEfF fFgG
eEfF fFg
pp
eef ffg
aa
ef ef fg fg
oo
ef e e fg f f
ef fg
tt
ef ef
G
eEf F gG
f
gfg
fF
Max TC m m
mCm
xN C xN
mm
C
CC
C
C
ddC
WW
(21)
22
22
ee f f
eE f F
ef fg
ef ef fg fg
eEfF fFgG
Max EI CO y CO y
mm
CO CO
W
dd
W
(22)
RR R R
eeef ff
eE f F
AA A A
eeef ff
eE f F
LL L L
eeef ff
eE f F
FF FF
eeeeee
eE eE
M
ax V RALF W w y W w y
WwyWwy
WwyWwy
WwyWwy
(23)
2. Minimizing the total cost is used as an objective
function where the environmental impact and V-
RALF aspects are considered as constraints as
previously presented in Eqs. 20-24. The range
between the maximum and minimum values for
objective functions two (environmental impact)
and three (V-RALF) are segmented into ten
segments, the points in between are assigned as ε
values in Eq. (21 and 23). However, it can be
segmented in more or less number of segments to
get more or less number of Pareto solutions.
3. Table 6 lists Pareto solutions obtained by solving
the problem formulation using ε-constraint (Eqs.
13-17). These solutions represent trade-offs
among minimizing the total cost and
environmental impact and maximization of V-
RALF. As shown in Table 6, these solutions are
also associated with the correspondence number
of farms and abattoirs that should be established.
For instance, solution#1 leads to a total cost of
361,348, a CO
2
emission of 211,000 and a value
of resilient (V-RALF) of 2. This solution requires
an establishment of farm two (0 1 0) to supply
livestock to abattoirs two and four (0 1 0 1). This
solution is obtained via an allocation of
ε1=211,075 and ε2 = 2. Pareto fronts among the
TC, EI and V-RALF are illustrated in Figure 2.
Finally, decision makers need to select the final
Pareto solution to design their supply chain
network based on their preferences. In this
research, solution#5 is selected as a final trade-off
solution among the values of the three objectives
to design the eco-gresilient meat supply chain
network.
Table 5: Maximum and minimum values related to TC, EI
and V-RALF.
Objective functions Max
Min
TC 501868 344703
EI 517847.785 180075.077
V-RALF 2.7901 1.93109
This solution leads to a minimum total cost of
427,626, a minimum CO2 emission of 335,262 and a
maximum value of resilience pillars (V-RALF) of
2.390. With respect to the allocation of facilities, this
solution requires an establishment of two farms to
supply livestock to three abattoirs. This solution is
obtained via an allocation of ε1= 337,075 and ε2 =
2.38.
4 CONCLUSIONS
Economic, green and resilient supply chain network
design has become a new challenge for supply chain
managers aiming to design a robust supply chain
network that not merely consider economic and green
objectives, but also be resilient to sustain its
operations under any disruption.
ICORES 2018 - 7th International Conference on Operations Research and Enterprise Systems
206
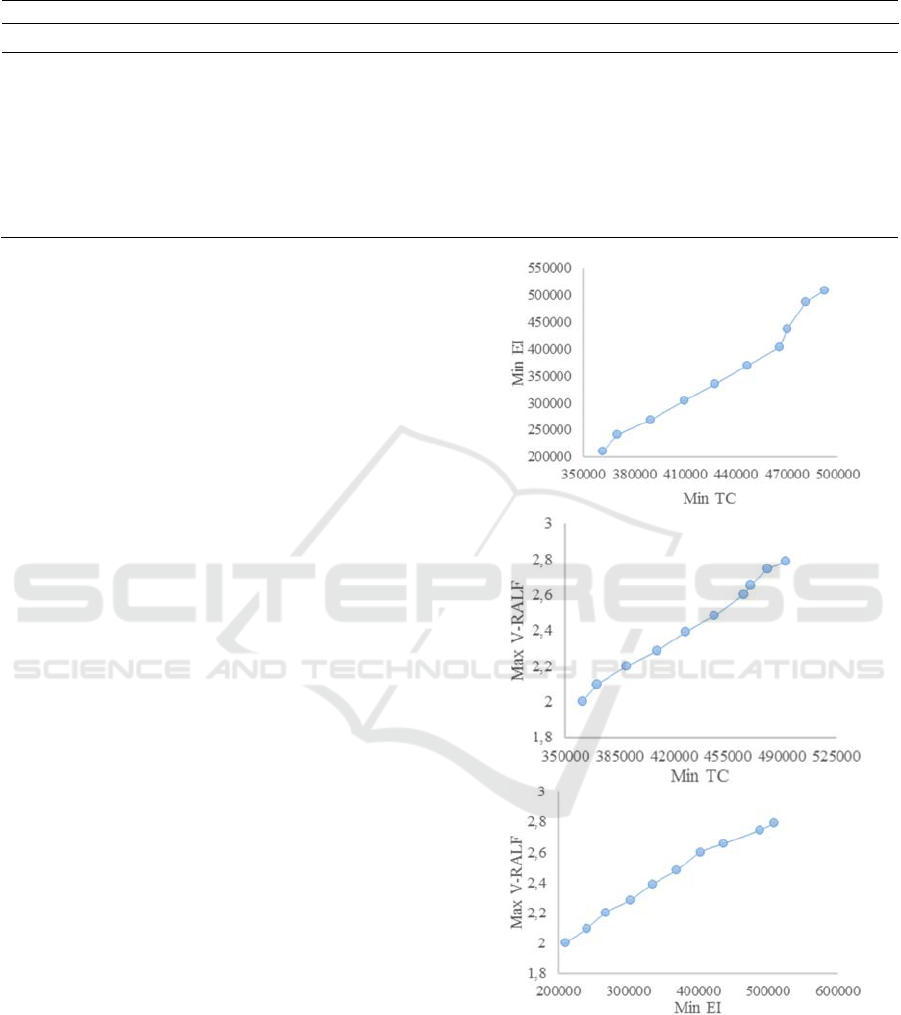
Table 6: Pareto solutions.
values
Objective function solutions Opened Facilities
#
1
2
Min TC Min EI Max V-RALF Farms Abattoirs
1 211075 2 361348 211000 2 0 1 0 1 0 1 0
2 241075 2.095 370350 241075 2.095 0 1 0 1 0 1 0
3 271075 2.190 389550 268223 2.200 1 1 0 1 0 1 0
4 304075 2.285 409515 304000 2.285 1 1 0 1 0 1 1
5 337075 2.380 427626 335262 2.390 0 1 1 1 0 1 1
6 370075 2.475 446631 369998 2.482 1 1 0 1 0 1 1
7 404075 2.570 465843 404000 2.600 1 1 1 1 1 1 0
8 437075 2.655 470052 437005 2.655 1 1 0 1 1 1 1
9 490075 2.732 481118 488200 2.744 1 1 1 1 1 1 1
10 517847 2.790 492512 509121 2.790 1 1 1 1 1 1 1
This study has motivated by this challenge in
emerging economic, green and resilience
responsibilities in the design and optimization of a
supply chain network. A hybrid MCDM-multi-
objective optimization model is developed to design
an eco-gresilient supply chain network. Fuzzy AHP
is used to determine the weight for resilience pillars
which include robustness, agility, leanness and
flexibility (RALF) based on decision makers ‘experts.
Next, fuzzy AHP is also used to determine the
importance weight for the potential facilities with
respect to their resilience performance. The obtained
weights are then integrated into a developed multi-
objective optimization model used for allocating the
optimal number of facilities that should be
established.
The model includes a formulation of three
objectives including minimization of the total cost
and environmental impact in particular the CO
2
emissions and maximization the value of supply chain
resilience in terms of maximizing resilience pillars
(Maximization of V-RALF) as a third objective.
Finally, the ε-constraint method is used to obtain
trade-offs among the three objectives via optimizing
the developed multi-objective model. The
applicability of the developed model is validated
through a case study. The results demonstrate that the
model can be used as an aid for enterprises to design
an eco-gresilient supply chain network. Furthermore,
it can be used by supply chain managers of related
facilities to improve their resilience performance.
The current work avenue includes the re-
development of the current model incorporating the
social aspect and uncertainties in the input data such
as demands, supply capacities of related facilities and
CO
2
emissions. Finally, the rank reversal approach
can be applied to help the decision makers in selecting
the final Pareto solution.
Figure 2: Pareto fronts among TC, EI and V-RALF.
REFERENCES
Bing Bing, X., Bloemhof-Ruwaard, J., Chaabane, A., van
der Vorst, J., 2015. Global reverse supply chain
Eco-Gresilient: Coalescing Ingredient of Economic, Green and Resilience in Supply Chain Network Design
207

redesign for household plastic waste under the emission
trading scheme. J. Clean. Prod. 103, 28-39.
Dixit, V., Seshadrinath, N., Tiwari, M.K. 2016.
Performance measures based optimization of supply
chain network resilience: A NSGA-II + Co-Kriging
approach. Computers & Industrial Engineering 93,
205–214.
Ehrgott, M., 2005. Multicriteria Optimization. 2
nd
ed.,
Springer, New York.
Govindan, K., Fattahi, M., Keyvanshokooh, E. 2017.
Supply chain network design under uncertainty: A
comprehensive review and future research directions,
European Journal of Operational Research, doi:
10.1016/j.ejor.2017.04.009.
Harris, I., Mumford, C.L. and Naim, M.M. 2014. A hybrid
multi-objective approach to capacitated facility location
with flexible store allocation for green logistics
modeling. Transportation Research Part E: Logistics
and Transportation Review 66, 1-22.
HMC, UK. 2010. http://www.halalhmc.org/, Available:
http://www.halalhmc.org/test-demo.htm. (Accessed
Jan 19, 2017).
IBM, 2008. Supply Chain Risk Management: A Delicate
Balancing Act. IBM Global Business Services, New
York, NY.
Levalle, R.R., Nof, S.Y. 2015. A resilience by teaming
framework for collaborative supply networks.
Computers & Industrial Engineering, 90, 67–85.
Miranda-Ackerman, M.A., Azzaro-Pantel, C., Aguilar-
Lasserre, A.A. 2017. A green supply chain network
design framework for the processed food. Computers &
Industrial Engineering, 109, 369–389.
Mohammed A. and Wang Q. 2015. Integrity of an RFID-
enabled HMSC Network. Proceedings of the Third
International Conference on Digital Enterprise and
Information Systems, Shenzhen, China, 2015a, 79-86.
Mohammed A. and Wang Q. 2017. Multi-criteria
optimization for a cost-effective design of an RFID-
based meat supply chain. British Food Journal, 119, 3,
676-689.
Mohammed A. and Wang Q. and Li X. 2017a. Developing
a meat supply chain network design using a multi-
objective possibilistic programming approach. British
Food Journal, 119, 3, 690-706.
Mohammed, A. and Wang, Q., 2017b. The fuzzy multi-
objective distribution planner for a green meat supply
chain. International J. Pro Eco., 184, 47–58.
Mohammed, A., Wang, Q., Alyahya, S. and Binnette, N.
2017c. Design and optimization of an RFID-enabled
automated warehousing system under uncertainties: A
multi-criterion fuzzy programming approach. The
International Journal of Advanced Manufacturing
Technology. 91 (5), 1661-1670.
Nooraie, S.V., Parast, M.M. 2015. A multi-objective
approach to supply chain risk management: Integrating
visibility with supply and demand risk. Int. J.
Production Economics 161 (2015) 192–200.
Srichetta, P. and Thurachon, W. 2012. Applying Fuzzy
Analytic Hierarchy Process to Evaluate and Select
Product of Notebook Computers. International Journal
of Modeling and Optimization, 2 (2), 168-173.
Pereira, C.R., Silva, A.L., 2015. Key Organisational Factors
For Building Supply Chain Resilience: A Multiple Case
Study Of Buyers And Suppliers. J. Oper. Supply Chain
Manag. 8, 77–95.
Perrings, C. Resilience and sustainable development.
Environ. Dev. Econ. 2006, 11, 417–427.
Purvis, L., Spall, S., Naim, M. and Spiegler, V. 2016.
Developing a resilient supply chain strategy during
‘boom’ and ‘bust’,
Production Planning & Control,
27:7-8, 579-590, DOI: 10.1080/09537287.2016.
1165306.
Saaty, T.L., 2000. Fundamentals of decision making and
priority theory with the analytic hierarchy process, vol.
6. Rws Publications.
Soni, U., Jain, V., Kumar, S. 2014. Measuring supply chain
resilience using a deterministic modeling approach.
Computers & Industrial Engineering. 74, 11–25.
Tiwari, A., Chang, P.C., Tiwari, M.K., Kandhway, R. 2016.
A Hybrid Territory Defined evolutionary algorithm
approach for closed. Computers & Industrial
Engineering, 99, 432–447.
ICORES 2018 - 7th International Conference on Operations Research and Enterprise Systems
208
