
Diluted Chemical Identification by Total Internal
Reflection Photonic Sensing
Biomedical Optics
Eduardo Valero, Sergio L. Carrasco-Ortiz, Maria Morant and Roberto Llorente
Nanophotonics Technology Center, Universitat Politècnica de València, Camino de Vera s/n, Valencia, Spain
Keywords: Photonic Sensor, Bio-chemical Sensing, Image Processing.
Abstract: A novel optical sensor architecture for the rapid identification of liquid samples is proposed and evaluated
experimentally. The proposed architecture is based on total internal reflection transmission of a laser beam.
A CMOS sensor is used to acquire the reflection produced by a narrow laser beam when interacting with the
liquid sample on the surface of an equilateral prism. Using digital image processing techniques, the critical
angle of the transmission is calculated and the identification of the refractive index of the liquid sample is
obtained. In the present work, distinct liquid substances were evaluated experimentally using a red He-Ne
laser at 632.8 nm wavelength obtaining the refractive index with a deviation of less than 0.0014 from the
value. Sensing by refractive index changes are of great importance in biomedical (e.g. optical diagnosis and
laser treatments) and chemical applications.
1 INTRODUCTION
In the last decades, the design of sensors has evolved
combining the fundamental biological, chemical, and
physical sciences with engineering and computer
science to fulfil concrete needs in a wide range of
application areas (Adl et al., 2017). In both medical
and industrial applications, optical biosensors have
gained attention in the last years due to their
simplicity and high sensitivity (Adl et al., 2017).
Optical biosensors can be applied to detect early
diseases (Haes et al., 2005) measure biomolecular
assays (Meglinski, 2015) or industrial applications
like process monitoring in plant factories (Chiu et al.,
2016).
In this work, we propose and demonstrate
experimentally a prism-based optical sensor for the
detection and identification of the refractive index of
liquid samples. The refractive index of a material is a
characteristic optical parameter that describes the
speed of light ratio of the material in respect of its
propagation speed in vacuum. Albeit there are some
techniques that have been proposed for measuring the
refractive index (Lai et al., 2005), the majority are
based on the measurement of light intensity
fluctuations by a photodetector (Li and Xie, 1996).
Furthermore, there have been proposed several
techniques based on the total internal reflection (TIR)
(Sainov, 1994) which demands the use of a precise
goniometer and its calibration (Onofri et al., 2007).
The proposed sensor is based on TIR propagation,
which permits detection of changes in the beam
position or refractive index variations caused by the
biological sample interacting in the sensor surface
(Watad et al., 2015). The sensor is intended to be
integrated close to the optics in conventional CCD
camera, as found in today’s cellphones, targeting a
cost-effective implementation of a complete bio-
chemical identification system.
The proposed prism-based sensor concept is
described in Figure 1, where a laser beam propagates
through a medium with high refraction index (i.e. the
prism with refractive index
) and encounters a
planar interface with a medium of lower refraction
index (water or other liquid sample with
<
). Total internal reflection occurs for
incidence angles greater than the critical angle
(
>
) (Uddin and Talukder, 2016).
Following this approach, in this work we measure
experimentally different liquid samples, searching
TIR transmission in a prism to obtain the critical
angle for each substance. In these experiments, the
critical angle is measured by means of the acquisition
of frames with a high-speed camera located
Valero, E., Carrasco-Ortiz, S., Morant, M. and Llorente, R.
Diluted Chemical Identification by Total Internal Reflection Photonic Sensing - Biomedical Optics.
DOI: 10.5220/0006616501970204
In Proceedings of the 6th International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS 2018), pages 197-204
ISBN: 978-989-758-286-8
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
197
orthogonally to the plane of propagation using proper
digital image processing techniques as described in
this paper which avoids the need of calibrating the
system with a precise goniometer. The accurate
determination of critical angle on different substances
may result on more reliable tissue characterization for
diagnostics purposes (Knüttel and Boehlau-Godau,
2000).
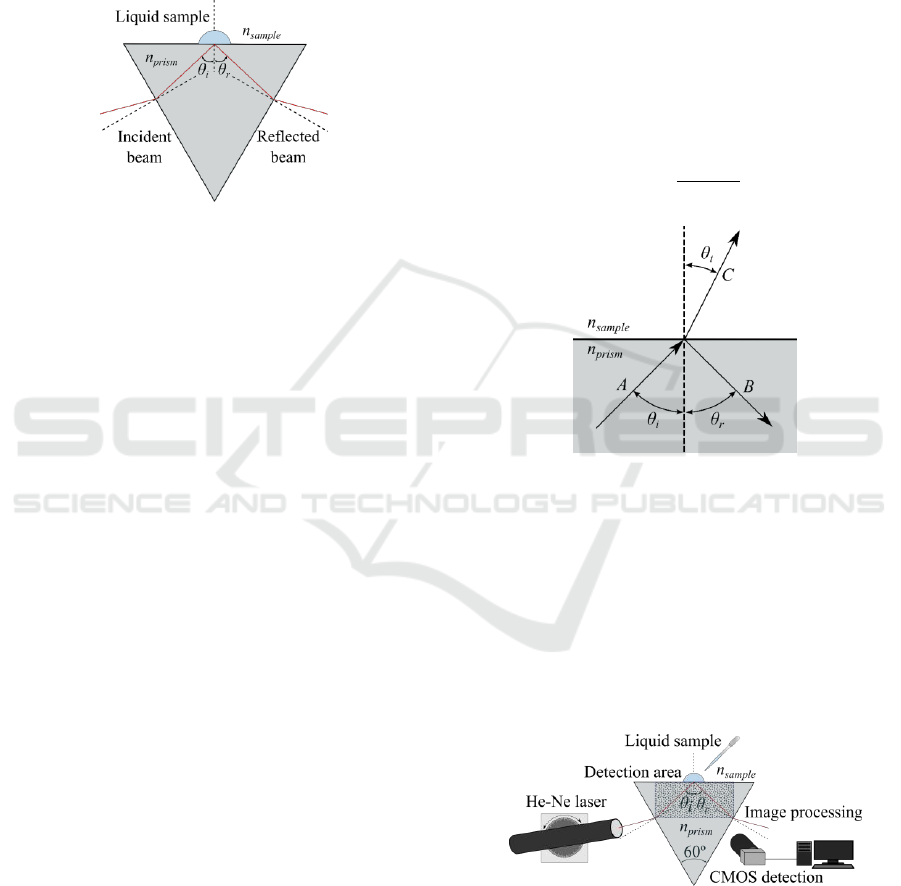
Figure 1: Proposed microprism-based sensor (refractive
index
) for the critical angle calculation of a laser
beam transmission interacting with liquid samples
(refractive index
).
This paper is structured as follows: In Section 2,
the theoretical principles of critical angle in TIR
transmission are summarized. Next, in Section 3,
simulations solving the Fresnel equations and the
Stokes parameters were carried out in order to
compare with the experimental results performed in
the laboratory depicted in Section 4. In Section 4, the
digital processing algorithms developed for the
calculation of the critical angle (
) and the
experimental results obtained for identifying the
refractive index of the sample (
) are reported.
Finally, Section 5 highlights the main conclusions.
2 PRISM-BASED OPTICAL
SENSOR FOR REFRACTIVE
INDEX IDENTIFICATION
2.1 Total Internal Reflection
Refraction is a physical phenomenon by which an
electromagnetic wave changes its direction a certain
angle as a consequence of a change in the velocity
of its medium of propagation (Hecht, 2002). Figure 2
describes the principles of reflection and refraction at
the interface of two materials with different refractive
indexes (
and
) defined by the Snell’s
Law. Considering that
and
the incident and
reflected angles respectively, then, according to the
Snell’s law of reflection the angles of reflection and
incidence are equal (Wang et al., 2016).
(1)
Moreover, the Snell’s law of refraction defines the
relationship between the angle of incidence
and the
transmitted angle
:
(2)
If the light is coming from a denser to a lighter
material, the transmission angle can take its
maximum value –also known as the critical angle of
incidence
– and, instead of passing through to the
second medium, the transmitted beam is reflected at
the interface to stay in the first medium. This critical
angle
can be calculated as:
(3)
Figure 2: Snell’s law for light reflection and refraction at
the interface of two materials.
2.2 Principle of Operation
In the proposed architecture, an equilateral prism is
used to find the critical angle and calculate the
refractive indexes of the substances on its sample
interface on top. The beam angle of incidence (
) is
adjusted in order to reach the critical angle (
)
achieving TIR transmission inside the prism.
Figure 3: Experimental setup for the calculation of the
refractive index of liquid samples (
) by means of
TIR and CMOS detection of the incident (
) and reflected
angles (
) with image processing.
Figure 3 shows the experimental setup for the
evaluation of the proposed architecture employing an
PHOTOPTICS 2018 - 6th International Conference on Photonics, Optics and Laser Technology
198
equilateral prism (60º between faces). A goniometer
with a He-Ne laser with linear polarization in the
visible red spectrum (λ = 632.8 nm) is employed to
modify the incident angle
. This incident laser beam
interferes with the sample solution (
) at the
prism top surface. When the incident angle is
adequate, the beam is TIR reflected back to the prism
with a reflected angle
. These angles (
and
) are
detected by a complementary metal-oxide-
semiconductor (CMOS) sensor array comprising
1280×1024 pixel cells. Applying equations (2) and
(3) to the prism-based sensor depicted in Figure 3,
knowing the refractive index of the prism (
)
and the propagation angles (
and
) we obtain the
refractive index of the sample (
) as:
(4)
Moreover, then TIR is achieved, there is also a change
in the polarization of the wave. This change is
produced because the component waves experience
different phase shifts
and
for the waves of
incident light linearly polarized parallel (p) and
perpendicular (s) (Azzam, 2004). Therefore, a
linearly polarized wave becomes elliptically
polarized when is reflected with an angle of incidence
greater than the critical angle (Haus, 2016).
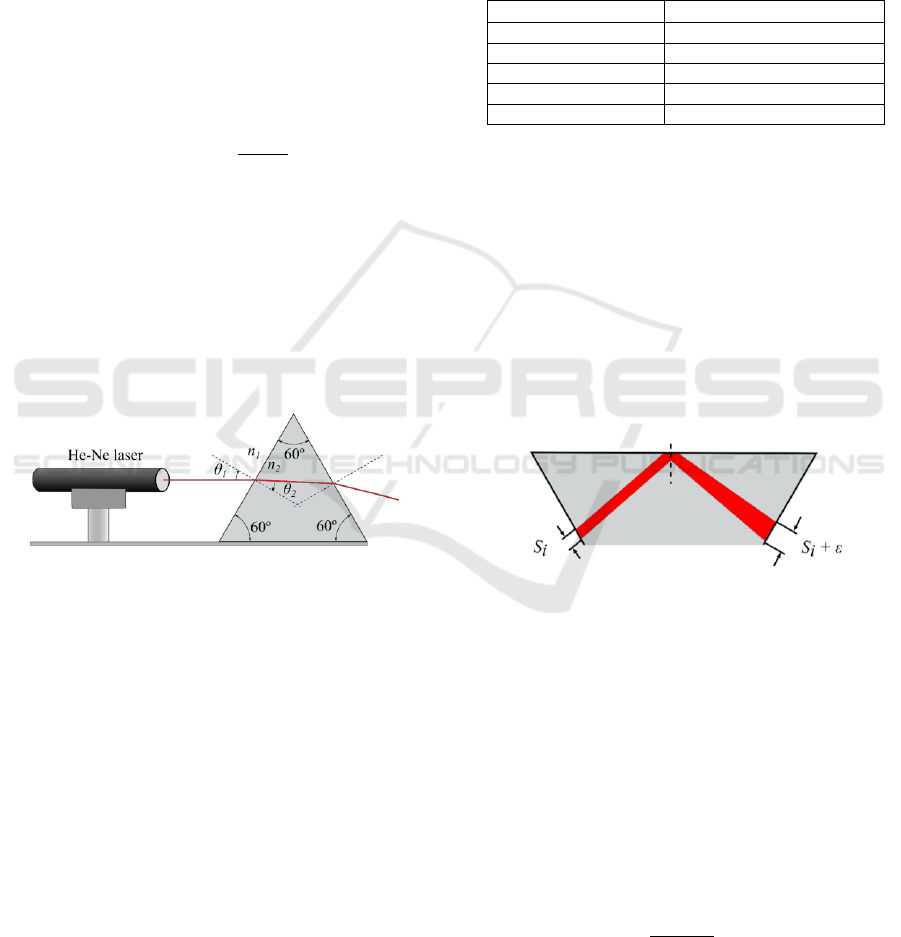
Figure 4: Schematic diagram for the calculation of the
refractive index of the prism.
Since the refractive index of the prism was not
provided by the manufacturer, we measured it
experimentally using the setup described in Figure 4.
The He-Ne laser (JDSU 1135P) is oriented into the
equilateral prism (Eisco Labs PH0554GG) with an
90º angle to the normal vector of the optical table.
Applying Snell’s law and knowing the refractive
index of air (Ciddor, 1996) and the incident angle, we
measure the transmission angle to be
=19.5174º.
Thus, the value obtained for the refractive index of
the prism was
which corresponds to
Phosphate Crown PK SCHOTT glass N-PK52A
(SCHOTT North America, Inc, 2015).
In this experimental demonstration, several liquid
substances were employed to assess the performance
of the proposed sensing method: water (H
2
O),
2-propanol (CH
3
CHOHCH
3
), absolute ethanol
(CH
3
CH
2
OH), hydrogen peroxide (H
2
O
2
) and olive
oil. The values of the refractive index of these
substances are summarized in Table 1 according to
the literature for water (Hale and Querry, 1973),
2-propanol (Sani and Dell'Oro, 2016), ethanol (Sani
and Dell'Oro, 2016), hydrogen peroxide (Phibbs and
Giguère, 1951) and olive oil (Yunus et al., 2009).
Table 1: Refractive index of the substances under study for
25 ºC room temperature.
Substance
Refractive index (
)
Water
1.3317
2-propanol
1.3763
Ethanol
1.3598
Hydrogen peroxide
1.4067
Olive oil
1.4650
2.3 Beam Digitization
The incident and the reflected beams are detected
with the CMOS sensor with a dynamic range of
62.1 dB, a dark temporal noise lower than 9 e and a
Signal to Noise Ratio of 40 dB (On-Semi Python
1300) with an optical lens with a focal length of
= 25 mm (KOWA LM25JC1MS). The pixel size of
the sensor CMOS is of 4.8 µm, hence the width of the
laser beam detected (being its size of 0.68 mm and its
divergence of 1.2 mrad) is digitized with a width of
= 21 pixels as depicted in Figure 5.
Figure 5: Schematic diagram of the divergence of the laser
beam travelling inside the prism.
The angle of incidence of the beam is estimated
using image processing techniques with MATLAB.
In order to obtain a correct estimation is important
that the width of the laser digitized is maintained, and
is not superior to the initial value
. This should be
noted because the laser beam diameter increases with
distance propagated from the optical source; this
effect is known as divergence (Sliney and Wolbarsht,
1980). We can obtain the divergence () of a laser
beam, knowing the beam diameter at two points (
and
) separated a distance () as:
(5)
With the proposed optical sensing technique to
calculate the incident and reflected angles, an could
Diluted Chemical Identification by Total Internal Reflection Photonic Sensing - Biomedical Optics
199
be originated when the original size of the laser beam
(
increases one pixel (). Each pixel of the image
acquired in these experiments is equivalent to a length
of 0.04 mm. Applying equation (5), the distance to
obtain this increment in the diameter of 0.04 mm
would be of 33.33 mm, resulting in the increment of
one pixel when digitized.
This increment can cause an error in the
estimation of the concentration of the liquid sample.
The relative error in the estimation of the angle of
incidence with MATLAB for a beam with
divergence, with regard to the same beam without
divergence, was calculated to be as small as 0.018%.
In this case, the prism used for the experimental
validation has a dimension of 25×25×22 mm, and it
is designed to be able to measure the refractive
indexes in the range from 1.3317 to 1.4741.
For example, for the refractive index of
= 1.3317, the beam travels a distance of
21.70 mm which entails an increment of 0.65 pixels.
While for the refractive index of
= 1.4741,
the beam travels a distance of 23.04 mm, resulting in
an increment of 0.69 pixels. Thus, the increment is
always less than one pixel and no error is induced by
the beam digitization in the processing of the images.
3 SIMULATION RESULTS
In-depth simulation studies have been performed
using COMSOL Multiphysics framework to analyse
the behaviour of the angle of incidence to achieve TIR
for different substances in the sensor surface. The
intensity of the optical rays was computed by the
Stokes parameters and the transmission and reflection
coefficients at the boundary of the mediums were
calculated applying the aforementioned Fresnel
equations.
3.1 TIR Propagation in the Prism
Following the experimental setup depicted in Figure
3, an equilateral prism is considered in the simulation
studies with a refractive index of
=1.4970,
according to the results reported in Section 2.2 of this
paper. The simulation studies were carried out using
an optical laser at 633 nm in the red visible spectrum.
The angle of the laser beam was iteratively modified
to ascertain the critical angle.
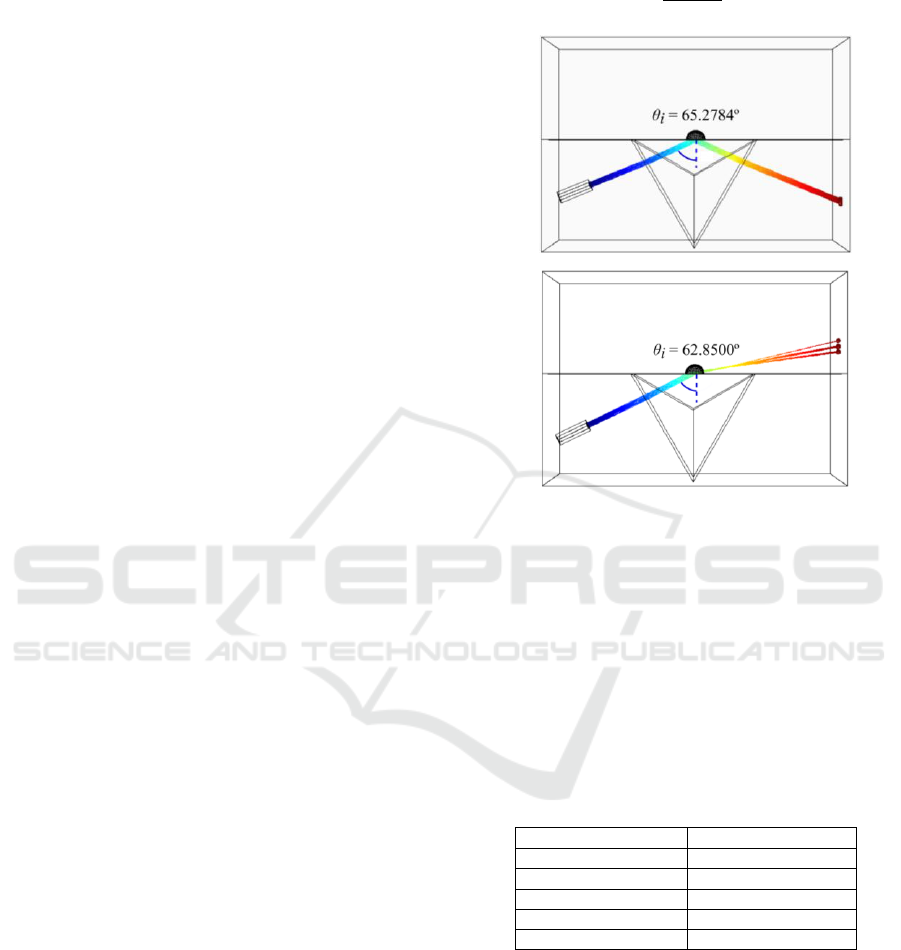
Figure 6 shows the simulation results obtained for
a semi-spherical bubble of ethanol with refractive
index
=1.3598 present in air environment.
For ethanol, the theoretical critical angle according to
equation (3) is calculated as:
65.2783º
(6)
(a)
(b)
Figure 6: Incident angle simulation results obtained for an
ethanol bubble when the incident laser beam angle is:
(a) superior to the critical angle
=65.2784º and (b) smaller
than the critical angle
=62.8500º.
As depicted in the simulation results represented
in Figure 6(a), when the angle of incidence is higher
to the critical angle (
>
), the optical beam
is reflected back to the prism by TIR propagation.
Table 2 includes the simulated results obtained for the
different liquid substances under study.
Table 2: Simulated results for critical angle calculation for
each substance under study.
Substance
Critical angle (
)
Water
62.8204º
2-propanol
66.8345º
Ethanol
65.2783º
Hydrogen peroxide
69.9978º
Olive oil
78.1320º
When the angle of incidence is close, but smaller
than the critical angle (
<
), the laser beam
is not totally reflected and secondary rays are
transmitted through the interface or to the second
medium as represented in Figure 6(b).
3.2 Evaluation of Micro-prism Size
Moreover, simulations were carried out to estimate
the theoretical minimum size of the prism. The beam
PHOTOPTICS 2018 - 6th International Conference on Photonics, Optics and Laser Technology
200
diameter of the laser is reduced from 480 µm to
45 µm with a beam reducer in order to minimize the
dimensions of the prism. The size of the side of the
prism depends on the spot size of the laser when the
total internal reflection is produced. The spot size
corresponding to the critical angle (
) of a substance
with a refractive index of
= 1.4741
(maximum value of refractive indexes to cover with
the proposed biosensor) was evaluated. The resulting
spot size of 290.8 µm restricts the minimum size of
the side of the prism in contact with the substance.
Therefore, for these range of refractive indexes, the
minimum dimensions of the prism are calculated to
be 290.8×290.8×45 µm.
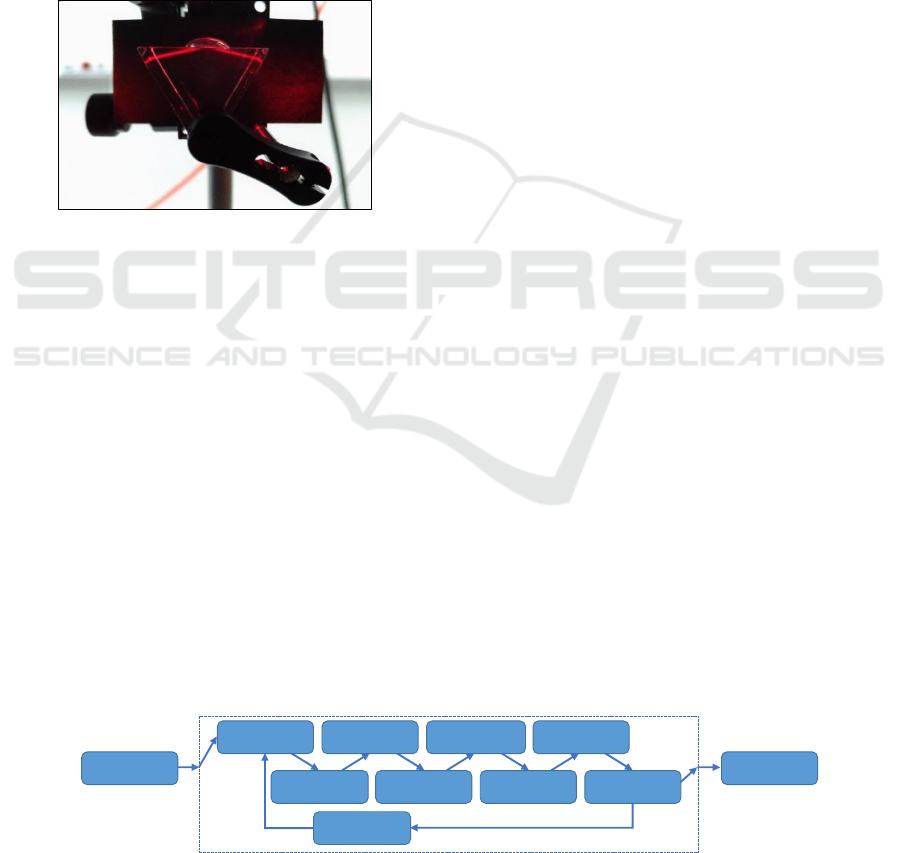
Figure 7: Laboratory caption of the experimental setup of
the biosensor for the refractive index calculation of a liquid
bubble by critical angle measurement.
A study of the effect of the beam divergence when
digitized was carried out. For the refractive index of
= 1.4741, that corresponds with the value
more affected by divergence, the beam travels a
distance of 252.41 µm, resulting in an increment of
0.11 pixels, therefore, no error is produced.
4 EXPERIMENTAL
DEMONSTRATION
4.1 Laboratory Setup and Digital
Image Processing
Figure 7 shows a photograph of the experimental
setup developed at the laboratory for the calculation
of the refractive indexes of different liquid samples
using the proposed biosensor. A He-Ne laser with a
wavelength of =632.8 nm and linear polarization
(JDSU 1135P) is employed with an equilateral prism
(Eisco Labs PH0554GG). To ensure that the room
temperature was constant an air conditioning system
was used to set it at 25 ºC and it was monitored using
a thermometer to confirm that the temperature was
not altered. A drop sample of the liquid substance
under evaluation is located on the upper side of the
prism. Images of the reflection produced by the
substance were gathered with a high-speed camera
with a resolution of 1280×1024 pixel and a sample
rate of 80 fps employing a 25 mm lens.
Figure 8 illustrates the block diagram of the algorithm
used for the calculation of the refractive index of the
substances under study. In the measurement procedure, we
first capture an image frame with the laser switched off to
detect the exact position of the prism applying a
morphological opening comprising a structuring element
with the shape of a line with the same inclination as the
prism. In order to optimize the detection conditions,
the measurements were taken without extra
illumination in the laboratory, so that the laser beam
is detected with more intensity compared to the rest
of the image. With this condition, the time exposure
was increased to use a long-duration shutter speed of
15000 , hence absorbing more light from the laser
beam.
In the next step, the laser is switched on and
several frames are captured with the CMOS sensor
while searching the critical angle by rotating the
goniometer.
In order to detect the laser beams travelling
through the prism, digital image processing has been
programmed with MATLAB including Image
Acquisition and Processing toolboxes. The main steps
of the image processing consist in:
1. Foreground detection by background
subtraction of the frame of the prism captured
with the laser switched off.
2. Crop of the detection area in the prism where
the incident and reflected beams are located.
Figure 8: Process flow diagram of the developed algorithms for the calculation of the critical angle with CMOS sensing and
digital image processing.
Morphological
opening
Image processing
False
True
Binarization
Segmentation
Background
subtraction
Image
acquisition
Angle
calculation
Image crop
Median filter
Noise
removal
Beam
detection
Consider next
frame
Diluted Chemical Identification by Total Internal Reflection Photonic Sensing - Biomedical Optics
201

3. Binarization of the frame with an adaptive
method. The pixels of the captured monochrome
frame are binarized to 0 or 1 values, being the
calculation of the threshold based on the first-
order image statistics around each pixel. More
information on adaptive image filtering can be
found in (Gonzalez and Woods, 2011)
4. Coarse noise reduction by median filtering.
5. Fine noise reduction applying a morphological
opening using a structuring element with the
shape of a disk.
6. Filtering of objects with a small area.
7. Segmentation of the objects of the image.
8. Laser beam angle calculation on the frame after
the last step in the segmentation process.
Following the aforementioned procedure, the
calculation of the angle depends on the laser beams
detected on the frame after the last step in the
segmentation process. If the incident and reflected
beams are not detected, or if there are more rays
detected besides both of them, the current frame is
discarded and the next frame is analysed following
the same procedure.
4.2 Performance Validation
Figure 9 shows the experimental results obtained after
digital image processing for a drop of water
interacting with the laser beam at the surface of the
prism. According to Table 1 and Table 2, the
refractive index of the water is
= 1.3317 (Hale
and Querry, 1973) which gives a critical angle of
= 62.8204º.
As it can be observed in Figure 9(a), when total
internal reflection is achieved (
>
), only two
laser beams are detected. Thus, we are able to
measure the angle of incidence (
) and the angle of
reflection (
) and calculate the refractive index of the
sample using equation (4). This method was applied
four times to each of the liquid substances under study
and the standard deviation of the results is calculated
for all the measures reported in Table 3.
In the case of sensing water with the proposed
biosensor, the experimental angle was measured to be
62.4636º ± 0.0236º, as represented in Figure 9(a).
In the second case, when the angle of incidence is
below the value of the critical angle (
<
), we can
observe in Figure 9(b) that a third beam appears in the
image as a result of the energy transmitted to the
second media returned to the prism. In this case, no
TIR transmission is achieved and the goniometer has
to be modified till obtaining the critical angle (
).
Figure 10 shows the experimental results taken for
2-propanol and hydrogen peroxide with measured
incident angle of
= 64.4335º and
= 69.3342º respectively.
(a)
(b)
Figure 9: Examples of the detected laser beam after
applying image processing when interacting with a drop of
water when: (a) TIR is achieved (
= 62.4528º) and
(b) TIR is not achieved in this case (
= 62.3294º).
(a)
(b)
Figure 10: Experimental results and measured incident
angle for: (a) 2-propanol (
= 64.4335º) and (b) hydrogen
peroxide (
= 69.3342º).
The experimental results of mean and standard
deviation for the four iterations of this sensing
method are included in Table 3.
Comparing the results obtained for the refractive
indexes of each substance with the values reported
before in Table 1, we observe that the most accurate
measurement was obtained sensing olive oil with an
error of only 0.16%.
Evaluating the experimental results in Table 3, the
biggest error is obtained for Hydrogen peroxide with
a 0.44%. A possible reason of this calculation error
can reside in the width of the beam spot of the laser.
Future work on this topic will evaluate more
collimated laser beams in order to reduce this error.
Another reason could reside in the shape of the prism.
Usually, fabrication of prisms have an angular
tolerance and are not perfectly equilateral. This factor
could lead to an error in the calculation of the
refractive index of the prism measured previously in
Section 2.2 of this paper. For this reason, we further
studied this aspect to reduce the error in the detection.
This and other manufacturing defects can be
compensated by a calibration process.
PHOTOPTICS 2018 - 6th International Conference on Photonics, Optics and Laser Technology
202

Table 3: Experimental measurements of the angle of
incidence and calculations of the refractive index of the
liquid substances under study (25 ºC) considering a prism
with
=1.4970.
Substance
Measured angle
(º)
Refractive index
Error
Water
62.4636 ± 0.0236
1.3274 ± 0.0003
0.0032
2-propanol
66.4762 ± 0.1184
1.3726 ± 0.0014
0.0027
Ethanol
64.9659 ± 0.0871
1.3564 ± 0.0011
0.0025
Hydrogen
peroxide
69.3100 ± 0.1151
1.4005 ± 0.0012
0.0044
Olive oil
77.7154 ± 0.1418
1.4627 ± 0.0009
0.0016
4.3 Sensor Performance with
Calibration
The calibration process targets to correct face angle
deviations and prism refraction index manufacturing
deviations. Considering a perfect calibration, we have
calculated the refractive index that minimize the error
to be
= 1.5015. The new calculations of the
refractive indexes of the liquid samples considering
and the measured incident angles are reported
in Table 4 as a best-case performance scenario for the
sensor. Observing the results of Table 4 we can see
that the refractive indexes of water, 2-propanol and
ethanol substances are detected with only 0.02%,
0.03% and 0.05% error respectively. Considering
the maximum error is reduced to 0.14% and is
given for hydrogen peroxide and olive oil samples.
Table 4: Refractive index calculation of the liquid
substances under study (25 ºC) to reduce the error
considering a prism with
=1.5015.
Substance
Measured angle (º)
Refractive index
Error
Water
62.4636 ± 0.0236
1.3314 ± 0.0003
0.0002
2-propanol
66.4762 ± 0.1184
1.3767 ± 0.0014
0.0003
Ethanol
64.9659 ± 0.0871
1.3604 ± 0.0011
0.0005
Hydrogen
peroxide
69.3100 ± 0.1151
1.4047 ± 0.0012
0.0014
Olive oil
77.7154 ± 0.1418
1.4671 ± 0.0009
0.0014
This confirms that the accuracy of the calculation
of the refractive of the prism media is essential for the
correct detection of liquid samples using the proposed
sensing technique.
5 CONCLUSIONS
This work presents and evaluates experimentally a
prism-based biosensor capable of identifying the
refractive indexes of liquid samples. This sensor is
based on TIR transmission of an optical beam
interacting with liquid drops on the surface of an
equilateral prism. This sensing method is based on
total internal reflection of the laser beam due to the
change of the refractive indexes of the two media
(prism and liquid sample). TIR transmission is
achieved for incident angles higher than the critical
angle (
>
).
A laser source in the visible spectrum range (in
this case a red He-Ne laser operating at 632.8 nm) is
transmitted through a transparent equilateral prism in
order to be able to see the incident and reflected
beams after interacting with the liquid sample located
on the upper side of the prism. The incident angle is
modified until achieving TIR transmission. The see-
through face of prism is captured with the CMOS
sensor of a camera and digital image processing is
performed with MATLAB to obtain the incident
angle values. In this work, the image processing
process is described to measure the incident and
reflected angles (
and
). From these angle values,
the refractive index of the liquid sample is calculated.
The proposed sensing method based on a single
prism and a CMOS sensor of a commercial camera
are accurate and simple, since there is no need of a
calibration with a precise goniometer as in
conventional systems. This sensor is capable of
identify refractive indexes in the range from 1.3317
to 1.4741. Depending on the resolution of the camera
employed, the size of the prism could be reduced to
micro-prism scale. The experimental results point out
that the sensing accuracy of this method rely on the
collimation of the laser source (beam width) and also
on the material of the prims used for TIR propagation.
With proper values of the material of the prism,
we were able to detect different liquid substances
with an error lower than 0.14%, being capable of
detecting water bubbles present in air with an error of
only 0.02% and 2-propanol and ethanol samples with
an error of 0.03% and 0.05%, respectively.
Knowledge of the refractive index is essential for
biomedical applications for optical diagnosis.
ACKNOWLEDGEMENTS
This research work was supported in part by Spain
National Plan MINECO/FEDER UE RTC-2014-
Diluted Chemical Identification by Total Internal Reflection Photonic Sensing - Biomedical Optics
203

2232-3 HIDRASENSE and TEC2015-70858-C2-1-R
XCORE projects. BIOFRACTIVE project with IIS
La Fe is also acknowledged. M. Morant work was
partly supported by UPV postdoc PAID-10-16
program.
REFERENCES
Adl, H. P. et al., 2017. A Defective 1-D Photonic Crystal-
Based Chemical Sensor in Total Internal Reflection
Geometry. IEEE Sensors Journal, 17(13), pp. 4046-
4051.
Azzam, R. M. A., 2004. Phase shifts that accompany total
internal reflection at a dielectric–dielectric interface.
Journal of the Optical Society of America A, 21(8), pp.
1559-1563.
Chiu, J.-S. et al., 2016. Application of Total Internal
Reflection and Heterodyne Interferometry in Electrical
Conductivity Measurements. IEEE Sensors Journal,
16(2), pp. 336-342.
Ciddor, P. E., 1996. Refractive index of air: new equations
for the visible and near infrared. Applied Optics, 35(9),
pp. 1566-1573.
Gonzalez, R. C. and Woods, R. E., 2011. Digital Image
Processing. 3rd ed. s.l.:Pearson Education.
Haes, A. J. et al., 2005. Detection of a Biomarker for
Alzheimer's Disease from Synthetic and Clinical
Samples Using a Nanoscale Optical Biosensor. Journal
of the American Chemical Society, 127(7), pp. 2264-
2271.
Hale, G. M. and Querry, M. R., 1973. Optical Constants of
Water in the 200-nm to 200-μm Wavelength Region.
Applied Optics, 12(3), pp. 55-563.
Haus, J. W., 2016. Fundamentals and Applications of
Nanophotonics. s.l.:Woodhead Publishing.
Hecht, E., 2002. Optics, 4th. International edition. 3 ed. San
Francisco: Addison-Wesley.
Knüttel, A. and Boehlau-Godau, M., 2000. Spatially
confined and temporally resolved refractive index and
scattering evaluation in human skin performed with
optical coherence tomography. Journal of Biomedical
Optics, 5(1), pp. 83-92.
Lai, J. et al., 2005. Experimental measurement of the
refractive index of biological tissues by total internal
reflection. Applied Optics, 44(10), pp. 1845-1849.
Li, H. and Xie, S., 1996. Measurement method of the
refractive index of biotissue by total internal reflection.
Applied Optics, 35(10), pp. 1793-1795.
Meglinski, I., 2015. Biophotonics for Medical Applications.
s.l.:Elsevier.
Onofri, F. et al., 2007. Critical angle refractometry and
sizing of bubble clouds. Optics Letters, 32(14), pp.
2070-2072.
Phibbs, M. K. and Giguère, P. A., 1951. Hydrogen Peroxide
and its Analogues: I. Density, Refractive Index,
Viscosity, and Surface Tension of Deuterium Peroxide
- Deuterium Oxide Solutions. Canadian Journal of
Chemistry, 29(2), pp. 173-181.
Sainov, S., 1994. Optical sensor based on total internal
reflection diffraction grating. Sensors and Actuators A:
Physical, 42(1), pp. 1-6.
Sani, E. and Dell'Oro, A., 2016. Spectral optical constants
of ethanol and isopropanol from ultraviolet to far
infrared. Optical Materials, Volumen 60, pp. 137-141.
SCHOTT North America, Inc, 2015. Optical Glass Data
Sheets. s.l.:s.n.
Sliney, D. and Wolbarsht, M., 1980. Safety with Lasers and
Other Optical Sources: A comprehensive Handbook. 1
ed. s.l.:Springer Science & Bussiness Media.
Uddin, S. Z. and Talukder, M. A., 2016. Reduction of
Detection Volume in Total Internal Reflection
Fluorescence Microscopy Using Graphene. 2016 9th
International Conference on Electrical and Computer
Engineering (ICECE).
Wang, X. et al., 2016. Progress in Planar Optical
Waveguides. Shangai: Springer.
Watad, I. et al., 2015. Critical-angle-based sensor with
improved figure of merit using dip detection. Optics
Letters, 40(19), pp. 4388-4391.
Yunus, W. M. M. et al., 2009. Refractive Index and Fourier
Transform Infrared Spectra of Virgin Coconut Oil and
Virgin Olive Oil. American Journal of Applied
Sciences, 6(2), pp. 328-331.
PHOTOPTICS 2018 - 6th International Conference on Photonics, Optics and Laser Technology
204
