
Reengineering of the Emergency Service System under Generalized
Disutility
Marek Kvet and Jaroslav Janacek
Faculty of Management Science and Informatics, University of Žilina, Univerzitná 8215/1, 010 26 Žilina, Slovakia
Keywords: Emergency Medical Service, System Reengineering, Generalized Disutility, Radial Formulation.
Abstract: Emergency medical service system structure is defined by deployment of service providing centers, number
of which is usually limited. The objective of the designer is to minimize the total discomfort of all system
users. Thus, the problem often takes the form of a weighted p-median problem. Since population and
demands for service change in time and space, current service center deployment may not meet the
requirements of the users and service providers neither. In this paper, we introduce a mathematical model
for system reengineering under the generalized disutility, which follows from the idea that the individual
user’s disutility comes from more than one located service center. At the moment of current demand
occurrence, the nearest service center may be unavailable due to satisfying another arisen demand.
Presented approach constitutes an extension of previously developed methods, where only the nearest center
was taken as a source of individual user’s demand satisfaction.
1 INTRODUCTION
The emergency service systems as the medical
emergency system, system of fire brigades and
police stations are designed for given geographical
area to satisfy the demand of population living in the
area for more secure life. The associate service is
provided from a given number of service centers and
the overwhelming objective used for the design
evaluation is the average time necessary to deliver
service from a service center to the user location, at
which a demand for service has occurred.
Host of models consider that serviced population
is concentrated to a finite number of dwelling places
of the considered area. Frequency of the demand
occurrence is proportional to the number of
inhabitants of the given town or village. A finite set
of possible service center locations is assumed and
also, the assumption is made that a user demand is
serviced from the nearest located service center.
This way, the weighted p-median problem
formulation is used to the emergency service system
design and solving the underlying problem to
optimality (Current et al., 2002, Doerner et al., 2005,
Ingolfsson et al., 2008, Jánošíková, 2007). The
original model was based on the location-allocation
decision variables and constraints (Current et al.,
2002), where an occurring demand is assigned to
exactly one possible center location. As concerns
usage of a general IP-solver, the size of the solved
integer programming problem must be taken into
account. In the real problems, the number of
serviced users takes the value of several thousands,
and the number of possible service center locations
can take this value as well (Avella et al., 2007). The
number of possible service center locations seriously
impacts the computational time and the memory of
computer due to used branch-and-bound method,
which stores the unfathomed nodes of the inspected
searching tree for the further processing. That is why
the direct attempt at solving the problem described
by a location-allocation model often fails, when
larger instances are solved by a commercial IP-
solver. Then another approach using so-called radial
formulation was developed to avoid the particular
assignment of user’s locations to the located service
centers. The radial approach successfulness is based
on the fact that there is only finite set of radii, which
must be taken into account (Elloumi et al., 2004,
García et al., 2011, Janáček, 2008). To accelerate the
p-median problem solving process, an approximate
approach has been developed (Janáček and Kvet,
2013). This approach uses an approximation of a
common time distance between a service center
location and a user by some pre-determined time
Kvet, M. and Janacek, J.
Reengineering of the Emergency Service System under Generalized Disutility.
DOI: 10.5220/0006621400850093
In Proceedings of the 7th International Conference on Operations Research and Enterprise Systems (ICORES 2018), pages 85-93
ISBN: 978-989-758-285-1
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
85

distances and gives near to optimal results in the
case of integer time distances.
A bit different situation occurres, when
reengineering of a current emergency service system
is performed. The necessity of system updating
ussualy follows from the fact that distribution of
demands for service has been developping in time
and space and thus, the originally determined center
locations do not suit both serviced population and
providers operating the service centers. Contrary to
the original system design, the current service
providers suggest changes in the center deployment
and their suggestion may be in a conflict with public
interests. That is why the system administrator
permits system reengineering only subject to some
formal rules, which are intented to prevent
worsening the service accessibility. The considered
formal rules are quantified by a maximal number of
provider’s centers, which are allowed to change their
locations and by the maximal distance between a
current center location and a possible new location.
Generally, addition of constraints may considerably
spoil the computational time necessary to obtain the
optimal solution of the problem. The study (Kvet
and Janáček, 2016) showed, that they do not impact
the computational time, when a user demand is
serviced from the nearest located center.
In this paper, we deal with more general model
of the emergency medical system design under
reengineering. We assume that service of a user
demand is provided from the nearest center only if
the center is not occupied by servicing a former
demand. Otherwise, the user’s demand is serviced
from the nearest unoccupied center. Initial
emergency system design considering the failing
centers was studied by (Snyder and Daskin, 2005)
and the associated radial formulation was presented
in (Kvet, 2014). Nevertheless, the reengineering of
service system with failing centers has not been
studied yet. Therefore, we focus on the influence of
the formal rule constraints on best possible service
availability in the service system and on the
associated computational process convergency.
In this paper, we provide a reader with a radial
model of emergency service system reengineering
with failing centers under rules imposed by the
system administrator. We perform a computational
study to find whether real-sized instances of the
problem are solvable using a common IP-solver.
The remainder of the paper is organized as
follows. The next section is devoted to the radial
model formulation, in which temporarily failing
centers are considered. In Section 3, the
administrator auxiliary rules are introduced. Section
4 contains a description of experiments. The
conclusion summarizes obtained findings and
contains possible directions of a further research.
2 REENGINEERING OF A
SERVICE SYSTEM WITH
FAILING CENTERS
To describe the problem of the users’ disutility
minimization by changing the deployment of centers
belonging to one considered provider, we introduce
J as a finite set of all users (dwelling places), where
b
j
denotes a volume of expected demand of user jJ.
Let I be a finite set of possible center locations.
Symbol d
ij
denotes the integer network time distance
between locations i and j, where i, j I
J. The
maximal relevant distance is denoted by m. The
current emergency service center deployment is
described by two disjoint sets of located centers I
L
I
and I
F
I, where I
L
contains p centers of the
considered provider, which performs updating of his
part of the system and I
F
is the set of centers
belonging to the other providers. Locations from I
F
stay unchanged. The center locations from I
L
can be
relocated within the set I
R
= I- I
F
.
In this paper, the generalized disutility perceived
by a user is modelled by a sum of weighted time
distances from the r nearest located centers. The
probabilities q
k
for k=1..r are positive real values,
which meet the following inequalities q
1
≥ q
2
≥ …
≥ q
r
and depend only on the order of distances from
the user to the r nearest centers. The k-th value can
be proportional to the probability of the case that the
k-1 nearest centers are occupied and the k-th nearest
center is available (Jankovič, 2016, Snyder and
Daskin, 2005).
We introduce coefficients a
s
ij
for each pair i, j
iI and jJ, where a
s
ij
= 1 if and only if d
ij
s and
a
s
ij
= 0 otherwise for s= 0, 1, …, m-1.
To describe decisions on new center deployment,
we introduce series of decision variables, where
binary variable y
i
defined for each iI
R
takes the
value of one, if a service center is to be located at i
and it takes the value of zero otherwise. To express
the total distance necessary for user demand
satisfaction, we introduce auxiliary zero-one
variables x
jsk
for jJ, s0, ..., m-1, k1, ..., r to
model the disutility contribution value of the k-th
nearest service center to the user j. The variable x
jsk
takes the value of 1 if the k-th smallest disutility
contribution for the customer jJ is greater than s
and it takes the value of 0 otherwise. Then the
ICORES 2018 - 7th International Conference on Operations Research and Enterprise Systems
86

expression x
j0k
+ x
j1k
+ … + x
jm-1k
constitutes the k-th
smallest distance from the user j to a located center.
If this k-th smallest distance is denoted by d
ik(j)
, then
the expression of d
ik(j)
by the auxiliary 0-1 variables
x
jsk
is clearly reported on the following figure.
Figure 1: Expression of the k-th smallest distance from the
user j to a located center by the auxiliary 0-1 variables x
jsk
for s0, ..., m-1.
Using the above introduced structures and
decision variables, we suggest the following model.
Jj
m
s
r
k
jskkj
xqbMinimize
1
0 1
(1)
pytoSubject
R
Ii
i
(2)
1...,,0,
1
msJjfor
rayax
FR
Ii
s
ij
Ii
i
s
ijjsk
r
k
(3)
Ri
Iifory }1,0{
(4)
rkmsJjfor
x
jsk
...,,1,1...,,0,
}1,0{
(5)
The objective function (1) expresses the expected
volume of transportation performance denoted by
generalized disutility in this paper. Constraint (2)
preserves constant number of centers belonging to
the considered part of the emergency service system
under reengineering. For given pair of user j and a
distance value s, constraints (3) assure relation
between the set of location variables y
i
, i I
R
and the
sum of auxiliary variables x
jsk
over range 1, …, r of
subscript k. If no center is located in the radius s,
then the sum of auxiliary variables x
jsk
equals to r. If
exactly k ≤ r centers is located in the radius s, then
the sum of variables equals to r-k due to
minimization process, which presses down the
values of the variables x
jsk
. If the sum of variables
x
jsk
equals to k<r, then the variables x
js1
, …, x
jsr-k
,
equal to zero and remaining variables equal to one
due to the used optimization process and decreasing
values of the coefficients q
1
, …, q
r
.
The objective function value of the optimal
solution of the problem (1)-(5) gives expected total
length or time of trips from the service centers to the
demand locations necessary for satisfaction of all
demands for service. This objective function value
explanation holds subject to assumption that the
coefficients q
1
, …, q
r
correspond to the probability
values expressing that the k-th nearest center is the
first available (unoccupied) service center. The next
assumption is that demand volume b
j
is proportional
to the number of trips necessary for the demand
satisfaction. The model (1)-(5) is much more
realistic than the original approach based on the
simple weighted p-median problem, which
corresponds to the case of r=1. The bigger accuracy
of the model (1)-(5) is paid for by higher complexity
of the solved problem, which may issue to enormous
increase of computational time. A question emerges
here, which limit of accuracy presented by the value
of r pays off regarding the increase of computational
time. As a solution of the problem (1)-(5) is discrete
and the values of probabilities q
k
sharply decrease,
influence of increasing value of r may appear
negligible behind some limiting value r*.
3 REENGINEERING UNDER
AUXILIARY CONSTRAINTS
As mentioned in Section 1, the administrator of the
system sets up parameters of rules to prevent a
designer of new center deployment from increasing
provider’s benefit at the expense of the system users.
The rules are easy to evaluate and check. That is
why the studied rules have a simple form. The first
rule limits the total number w of the provider’s
centers, which can be moved. The second rule limits
the distance between original and new location of a
service center.
To be able to formulate the rules in a concise
way, we derive several auxiliary structures using
Figure 2. We assume that all points 1-11 represent
system users and the black points 2, 3, 9 and 11
represent current service center locations.
Figure 2: Simple example of reengineering restrictions.
Let N
t
={iI
R
: d
ti
D} denote the set of all
possible center locations, to which the center tI
L
can be moved. If we consider the example depicted
on Figure 2, we can observe that the center located
Reengineering of the Emergency Service System under Generalized Disutility
87

at the point 9 can be moved to 6, 8, 10 and 13 or stay
unchanged. Thus, the set N
9
= {6, 8, 9, 10, 13}.
Similarly, N
3
= {3, 4, 6}. Additionally, let S
i
={tI
L
:
iN
t
} denote a set of all centers of the considered
provider, which can be moved to iI
R
. Here S
6
= {3,
9}. Realize that tN
t
and iS
i
for tI
L
and iI
R
and
thus I
L
I
R
.
Now, we introduce series of decision reallocation
variables. The variable u
ti
{0, 1} for tI
L
and iN
t
takes the value of one, if the service center at t is to
be moved to i and it takes the value of zero
otherwise. Using the above introduced structures and
variables we suggest the following model extension.
wpy
L
Ii
i
(6)
L
Ni
ti
Itforu
t
1
(7)
Ri
St
ti
Iiforyu
i
(8)
tLti
NiItforu ,}1,0{
(9)
Constraint (6) limits the number of changed
center locations by the constant w. Constraints (7)
allow moving the center from the current location t
to at most one other possible location in the radius
D. Constraints (8) enable to bring at most one center
to a location i subject to condition that the original
location of the brought center lies in the radius D.
These constraints also assure consistency among the
decisions on move and decisions on center location.
Based on our experience, we have to raise the
question of technical solvability of the formulated
problem (1)-(9). We ask whether a commercial
solver based on the branch-and-bound technique is
able to find the exact solution of a real-sized
problem in acceptable time. Consequence of
structural constraint addition to some model is
always matter of question from the point of
computational process convergence. Furthermore,
we have to realize that even if the administrator’s
rules are established to defend users’ interests, they
represent further restriction of the set of feasible
solutions. This phenomenon may lead to a less
possible benefit (higher disutility) for the average
user. That is why, the dependence of the optimal
objective function value on setting of parameters w
and D is worth to study.
4 NUMERICAL EXPERIMENTS
This section is devoted to the results of numerical
experiments performed in the optimization software
FICO Xpress 8.0, 64-bit. The experiments were run
on a PC equipped with the Intel® Core™ i7 5500U
2.4 GHz processor and 16 GB RAM.
Used benchmarks were derived from real
emergency health care system, which was originally
implemented in eight regions of Slovak Republic.
For each self-governing region, i.e. Bratislava (BA),
Banská Bystrica (BB), Košice (KE), Nitra (NR),
Prešov (PO), Trenčín (TN), Trnava (TT) and Žilina
(ZA), all cities and villages with corresponding
number of inhabitants b
j
were taken into account.
The coefficients b
j
were rounded to hundreds. The
set of communities represents both the set J of users’
locations and the set I of possible center locations as
well. The cardinalities of these sets vary from 87 to
664 locations. In all solved instances, the network
distance from a user to the located center was taken
as the user´s disutility.
An individual experiment was organized so that
the optimal solution of the reengineering problem
(1)-(5) was obtained first. The value of r was set to 7
and the associated coefficients q
k
for k=1, …, r were
set in percentage in the following way: q
1
= 77.063,
q
2
= 16.476, q
3
= 4.254, q
4
= 1.593, q
5
= 0.47, q
6
=
0.126, and q
7
= 0.018. These values follow from a
simulation model of existing emergency medical
service system in Slovakia (Jankovič, 2016). To
enrich the pool of benchmarks, for each self-
governing region ten instances were created in such
a way that they differ in the list of located service
centers operated by the considered provider. The
average results are summarized in Table 1. The left
part of this table contains the basic benchmark
characteristics. The total number of possible service
center locations regardless the service providers is
reported in the column denoted by |I|. The value of
TNC represents the total number of located centers.
The average percentage rate of the provider’s centers
is reported in the column denoted by “Prov. [%]”.
The right part of the table contains the results of the
model (1)-(5). The average computational time in
seconds of ten instances solved for each region is
reported in the column denoted by “CT [s]”. The last
column “ObjF” contains the average values of the
objective function (1).
ICORES 2018 - 7th International Conference on Operations Research and Enterprise Systems
88

Table 1: Average results of numerical experiments for
each self-governing region. The value of r was set to 7.
Reg.
|I|
TNC
Prov. [%]
CT [s]
ObjF
BA
87
14
55.1
0.5
28087.8
BB
515
36
44.9
43.6
47706.5
KE
460
32
46.0
30.4
48490.9
NR
350
27
50.7
10.8
52024.6
PO
664
32
44.3
50.5
61070.2
TN
276
21
52.9
5.1
36800.9
TT
249
18
49.6
6.1
43986.1
ZA
315
29
46.8
6.1
45341.2
The results indicate that the reengineering of the
emergency service system under generalized
disutility for r=7 from the point of service provider
does not represent a hard solvable problem. It can be
observed that the radial formulation enables to get
the optimal solution within 1 minute. In spite of this
useful feature, the second portion of experiments
was performed to find out, whether a lower value of
r will have significant influence on the resulting
solution from the point of the objective function
value. As we have mentioned in Section 2, we
assume that the influence of increasing value of r
may appear negligible behind some limiting value
r*. To verify this hypothesis and to find a suitable
value of r*, we have solved all instances with
different values of r. If r<7, then the coefficient q
r
was computed according to (10) as a complement of
the coefficients q
k
for k=1, …, r-1 to the value of
100, i.e. the sum of q
k
for k=1, …, r must equal 100.
1
1
100
r
rk
k
qq
(10)
The dependency of average computational time
on the value of r was studied first. We assume that
the computational time grows with increasing value
of r, because it affects the number of variables and
the model size as well. Our expectation has been
confirmed by the results summarized in Table 2.
Each row represents the average results of ten
instances for each region and the columns are used
for different setting of parameter r. The last row
contains the average values of all instances. The
dependency of average computational time on the
value of r is shown also on Figure 3.
Table 2: Average computational time in seconds of the
solving process depending on r for each region.
Reg.
r = 1
r = 2
r = 3
r = 4
r = 5
r = 6
BA
0.1
0.1
0.2
0.2
0.3
0.3
BB
6.5
8.3
11.5
19.3
27.1
33.7
KE
6.0
7.0
8.9
11.6
15.7
18.3
NR
2.1
2.6
3.6
6.7
6.8
8.4
PO
20.6
22.8
26.1
31.8
38.8
47.0
TN
1.4
1.8
3.2
2.8
3.4
4.3
TT
1.2
1.7
2.3
3.1
4.2
5.2
ZA
1.7
2.0
2.6
3.3
4.4
5.2
AVG
4.96
5.79
7.29
9.87
12.58
15.29
Figure 3: Dependency of average computational time in
seconds on the number r.
When studying the impact of r on the resulting
system design, we have evaluated Hamming
distance of the vectors of resulting location variables
obtained for various values of parameter r.
Generally, Hamming distance of two 0-1 vectors y
and z is defined by the expression (11). The average
results are reported in Table 3.
2
( , )
ii
iI
HD y z
yz
(11)
Table 3: Average Hamming distance from the optimal
solution obtained for r=7 computed for each region.
Reg.
r = 1
r = 2
r = 3
r = 4
r = 5
r = 6
BA
5.2
2.0
0.6
0.4
0.0
0.0
BB
12.6
11.0
3.6
0.6
0.4
0.0
KE
11.8
6.0
3.4
1.4
0.6
0.6
NR
10.2
6.6
2.0
0.4
0.0
0.0
PO
11.8
7.4
4.0
0.0
0.6
0.0
TN
8.0
2.6
0.6
0.2
0.0
0.0
TT
8.4
3.8
0.4
1.4
0.0
0.0
ZA
12.4
4.0
3.2
1.0
0.2
0.0
AVG
10.05
5.43
2.23
0.68
0.23
0.08
The dependency of average Hamming distance
from the optimal solution obtained for r=7 on the
number r of service providing centers for each
system user is shown also on Figure 4.
Reengineering of the Emergency Service System under Generalized Disutility
89
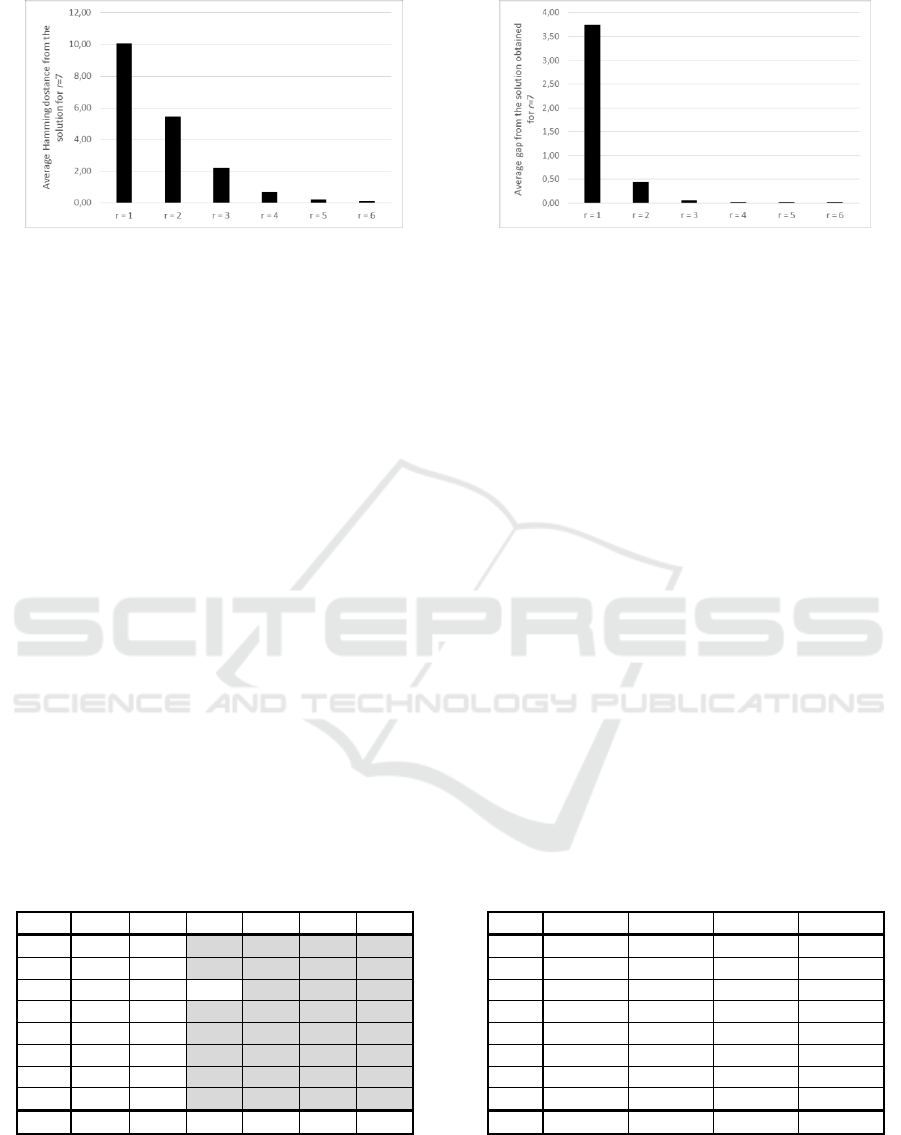
Figure 4: Dependency of Hamming distance from the
optimal solution obtained for r=7 on the number r of
service providing centers for each system user.
The reported results show that the suitable value
of r* is 3. Thus, 3 nearest located service centers are
enough to be taken into account when emergency
system reengineering under generalized disutility.
As shown, the service center deployment for r=3
differs from the service center deployment obtained
for r=7 only in one center on the average.
The last characteristics studied in this portion of
experiments consists in the objective function value.
For each system design obtained for particular value
of r=1, 2, …, 6, the objective function (1) with r=7
and the full set of coefficients q
k
was computed. This
value was compared to the objective function value
obtained for r=7 and the gap was evaluated. Here,
the gap is defined as a percentage difference of two
objective function values, where the objective
function value for r=7 was taken as the base. The
average values of gaps of ten instances computed for
each self-governing region are reported in Table 4,
which follows the structure of previous tables. To
find a suitable value of r*, the gaps lower than 0.1
percent are marked.
Table 4: Average gap from the optimal solution obtained
for r=7.
Reg.
r = 1
r = 2
r = 3
r = 4
r = 5
r = 6
BA
2.52
0.23
0.02
0.01
0.00
0.00
BB
6.19
0.43
0.07
0.00
0.00
0.00
KE
2.88
0.21
0.11
0.01
0.00
0.00
NR
2.31
0.55
0.06
0.00
0.00
0.00
PO
5.19
0.62
0.04
0.00
0.00
0.00
TN
2.81
0.24
0.04
0.01
0.00
0.00
TT
2.60
0.32
0.01
0.02
0.00
0.00
ZA
4.33
0.69
0.05
0.00
0.00
0.00
AVG
3.73
0.43
0.05
0.01
0.00
0.00
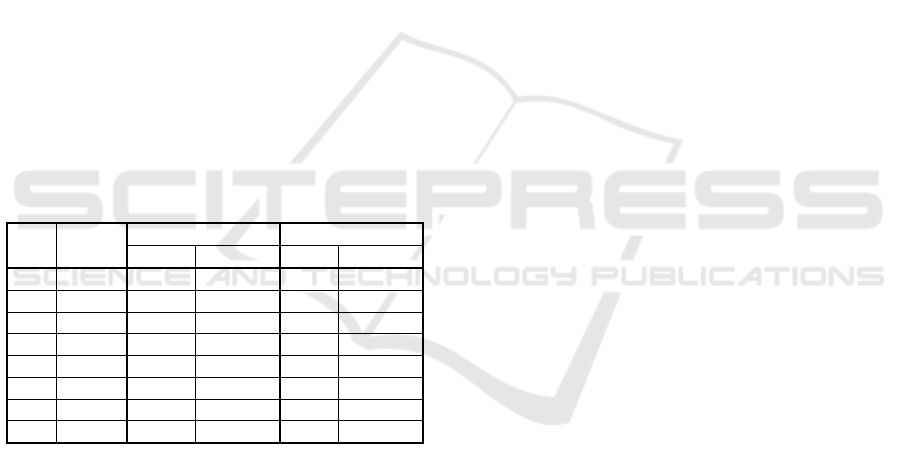
The dependency of average gap from the optimal
solution obtained for r=7 on the number r of service
providing centers for each system user is shown also
on Figure 5.
Figure 5: Dependency of average gap from the optimal
solution obtained for r=7 on the number r of service
providing centers for each system user.
The detailed analysis of presented results shows
that if we use three nearest service providing centers
for each system user instead of seven, we can obtain
very similar results and save more than one half of
computational time. That is why, the next portion of
experiments was performed with r=3. This new
portion of experiments was aimed at the additional
constraints (6)-(9) and their impact on the solving
process characteristics, mainly computational time.
This new set of experiments was organized so
that the maximal radius D, in which a center can be
moved, was fixed at the value of 15 and the maximal
number w of centers allowed to change their
locations was set to p/4, p/2, 3p/4, and p
respectively. It must be realized, that the parameter p
represents the total number of centers operated by
considered provider, who performs reengineering.
Dependency of average computational time in
seconds computed for 10 instances of each region is
reported in Table 5. Each row of the table represents
one region and the columns are devoted to different
settings of w.
Table 5: Average computational time in seconds for each
region and different values of w. Parameter D was 15.
Reg.
w = p/4
w = p/2
w = 3p/4
w = p
BA
0.11
0.11
0.11
0.12
BB
4.36
6.40
5.36
5.32
KE
4.44
5.95
5.77
5.09
NR
2.02
2.20
2.75
2.78
PO
9.78
9.76
9.79
9.83
TN
1.55
1.64
1.68
1.73
TT
1.30
2.30
1.47
1.52
ZA
1.74
1.65
1.63
1.66
AVG
3.16
3.75
3.57
3.50
The reported results show that different settings
of w do not significantly affect the computational
process, because the value of w limits only the
number of possible service center location changes
ICORES 2018 - 7th International Conference on Operations Research and Enterprise Systems
90

and thus, the number of variables and constraints is
independent on w.
The objective function values can be compared
in Table 6. Even if parameter r was set to 3 in all
solved models, the objective function values were
computed for r=7 based on the resulting service
center deployment.
Table 6: Average objective function values for each region
and different values of w. Parameter D was 15. The
objective function value was recomputed for r=7 and the
whole set of probability coefficients q
k
.
Reg.
w = p/4
w = p/2
w = 3p/4
w = p
BA
28607.0
28334.8
28334.8
28334.8
BB
50676.2
50433.7
50430.4
50430.4
KE
51141.3
50916.9
50913.4
50913.4
NR
53995.8
53482.7
53471.5
53471.5
PO
63791.3
63532.1
63526.0
63526.0
TN
37286.6
37225.5
37225.5
37225.5
TT
45670.3
44915.7
44733.6
44733.6
ZA
47278.1
46673.0
46634.3
46634.3
The last portion of experiments was aimed at
exploration of the impact of parameter D on the
solving process complexity. Here, the parameter w
was set to its maximal value p, i.e. all centers
operated by the provider could change their current
locations. The average computational times in
seconds computed for each self-governing region
and given values of D are reported in Table 7, which
has the same structure as previous tables.
Table 7: Average computational time in seconds for each
region and different values of D. Parameter w was set to
its maximal value, i.e. w=p.
Reg.
D = 5
D = 10
D = 15
D = 20
D = 25
BA
0.04
0.08
0.12
0.16
0.17
BB
0.90
3.13
5.32
10.54
15.38
KE
1.02
2.61
5.09
7.41
8.81
NR
0.42
1.11
2.78
6.91
5.31
PO
1.91
4.93
9.83
15.85
19.06
TN
0.40
1.05
1.73
2.16
2.96
TT
0.28
0.79
1.52
1.99
2.44
ZA
0.45
0.97
1.66
2.14
2.81
AVG
0.68
1.83
3.50
5.89
7.12
The results reported in Table 7 have confirmed
our expectation that the parameter D has a direct
impact on the computational process. As it can be
observed, the average computational time grows
with increasing value of D, i.e. with increasing
radius, in which current center can be removed. This
phenomenon has a simple explanation. The bigger is
the radius for center location change, the higher is
the number of its possible new locations. As we can
see in constraints (6)-(9), this parameter defines the
number of decision variables and it directly affects
the model size. Therefore, the solving process for
higher distance D takes longer time. Finally, the
dependency of objective function value on the
parameter D is shown in Table 8.
Table 8: Average objective function values for each region
and different values of D. Parameter w=p. The objective
function value was recomputed for r=7 and the whole set
of probability coefficients q
k
.
Reg.
D = 5
D = 10
D = 15
D = 20
D = 25
BA
29563.0
28798.3
28334.8
28255.0
28136.1
BB
52115.0
50635.4
50430.4
49429.6
49130.0
KE
52111.9
51398.4
50913.4
50412.6
49959.5
NR
56153.7
54360.2
53471.5
52674.5
52422.9
PO
66115.8
65081.5
63526.0
63070.1
62444.1
TN
37714.0
37320.5
37225.5
37148.4
37009.5
TT
46162.7
45395.9
44733.6
44114.7
44078.5
ZA
48712.7
47763.3
46634.3
46230.4
46115.0
As far as the objective function value expressed
by generalized disutility is concerned, the achieved
results indicate that the higher is the value of D, the
better solution can be obtained. The radius D defines
the set of all new possible locations of a center and
thus, it affects the possibility for obtaining better
results. More elements in the set N
t
for each tI
L
mean more candidates for new center locations and
bigger possible change of current center deployment,
which can bring better service accessibility for
system users.
All the experiments presented above were aimed
primarily at studying the model solvability and the
sensitivity of the associated computational process
on different model parameters. Besides some
interesting findings and suitable settings of
parameters, we also present the emergency system
characteristics in the next paragraphs. The following
table contains the comparison of current service
center deployment to the results of suggested
reengineering model, which was configured as
follows. Based on the above presented results, the
parameter r was set to 1 (simple disutility) and 3
(generalized disutility). In the experiments with the
generalized disutility, the associated probability
coefficients q
1
= 77.063, q
2
= 16.476 and q
3
= 6.461
were used. It must be noted that the objective
function reported in the table was recomputed for
r=7 and the whole set of probability values reported
at the beginning of this section. The maximal
number w of centers operated by the considered
service provider, which are allowed to change their
current location, was set to the cardinality of the set
I
L
, i.e. all considered provider’s centers could be
Reengineering of the Emergency Service System under Generalized Disutility
91
moved. The value 15 limited the radius D, in which
a center could be relocated. This initial value of D
corresponds to the rule applied in the emergency
health care system of the Slovak Republic (Kvet and
Janáček, 2016). Table 9 contains the average results
of 10 instances solved for each self-governing
region. The objective function value corresponding
to the current service center deployment is reported
in the column denoted by “Current ObjF”. The right
part of the table is dedicated to the results of
suggested reengineering problems. The abbreviation
“ObjF” denotes the objective function value of the
emergency system design obtained by solving the
reengineering model. Finally, the value of Imp was
computed to show possible improvement of the
objective function value expressed by the
generalized disutility, which can be achieved by
relocating of some service centers. Its value was
computed as a percentage difference between
objective function values of the current service
center deployment and the new system design
resulting from the model. The objective function
value of current deployment was taken as the base.
Table 9: Comparison of current service center deployment
to the results of reengineering model for r=1 (simple
disutility) and r=3 (generalized disutility). The
reengineering parameters were set at w = p and D = 15.
Reg.
Current
ObjF
r=1
r=3
ObjF
Imp. [%]
ObjF
Imp. [%]
BA
29792
28810
3.30
28335
4.89
BB
52510
51094
2.70
50430
3.96
KE
52786
51894
1.69
50913
3.55
NR
56759
54440
4.09
53472
5.79
PO
67037
65807
1.83
63526
5.24
TN
38625
38091
1.38
37226
3.62
TT
472163
45569
3.48
44734
5.25
ZA
49324
47566
3.56
46634
5.45
The reported results show that the emergency
system reengineering may bring a considerable
improvement of service accessibility for system
users expressed by general disutility. The average
values of Imp indicate that the objective function
value corresponding to the system design can be
reduced up to 6 percent. The achieved results also
confirm the usefulness of suggested reengineering
model, because it enables us to obtain better system
design from the point of service accessibility. It is
obvious from the comparison of the case r=1 to r=3
that the usage of generalized disutility leads to such
solutions, which are approximately by 2 percent
better than those, which can be obtained by usage of
simple disutility model.
5 CONCLUSIONS
This paper was focused on emergency medical
system reengineering under generalized disutility,
which follows the idea that the associated service
can be provided from more than one nearest located
centers. Presented generalized disutility makes the
model more realistic by taking into account possible
temporarily unavailability of service centers. In our
computational study we have found, that three
nearest located centers are enough to be considered
in the objective function value, because the accuracy
of the result is satisfactory. The second part of
experiments was aimed at additional constraints,
which define some new restrictions to service center
location changes. Based on reported results we can
conclude that we have constructed a very useful tool
for emergency medical system reengineering under
generalized disutility from the point of service
provider. Presented model is easy to be implemented
and solved in common optimization environment
equipped with the branch-and-bound method or
other technique to integer programming problems.
Future research in this field may be aimed at
using of the suggested modelling technique in such
situations, where the time distances are influenced
by randomly occurring failures in the underlying
transportation network.
ACKNOWLEDGEMENTS
This work was supported by the research grants
VEGA 1/0518/15 “Resilient rescue systems with
uncertain accessibility of service”, VEGA 1/0463/16
“Economically efficient charging infrastructure
deployment for electric vehicles in smart cities and
communities”, and APVV-15-0179 “Reliability of
emergency systems on infrastructure with uncertain
functionality of critical elements”.
REFERENCES
Avella, P., Sassano, A., Vasil’ev, I., 2007. Computational
study of large scale p-median problems. In
Mathematical Programming, Vol. 109, No 1, pp. 89-
114.
Current, J., Daskin, M., Schilling, D., 2002. Discrete
network location models. In Drezner Z. (ed) et al.
Facility location. Applications and theory, Berlin,
Springer, pp 81-118.
Doerner, K. F. et al., 2005. Heuristic solution of an
extended double-coverage ambulance location
ICORES 2018 - 7th International Conference on Operations Research and Enterprise Systems
92

problem for Austria. In Central European Journal of
Operations Research, Vol. 13, No 4, pp. 325-340.
Elloumi, S., Labbé, M., Pochet, Y., 2004. A new
formulation and resolution method for the p-center
problem. INFORMS Journal on Computing 16, pp. 84-
94.
García, S., Labbé, M., Marín, A., 2011. Solving large p-
median problems with a radius formulation.
INFORMS Journal on Computing, Vol. 23, No 4, pp.
546-556.
Ingolfsson, A., Budge, S., Erkut, E., 2008. Optimal
ambulance location with random delays and travel
times, In Health Care Management Science, Vol. 11,
No 3, pp. 262-274.
Janáček, J., 2008. Approximate Covering Models of
Location Problems. In Lecture Notes in Management
Science: Proceedings of the 1st International
Conference ICAOR, Yerevan, Armenia, pp. 53-61.
Janáček, J., Kvet, M., 2013. Public service system design
with disutility relevance estimation. In Mathematical
Methods in Economics 2013, Jihlava, Czech Republic,
pp. 332-337.
Jankovič P., 2016. Calculating Reduction Coefficients for
Optimization of Emergency Service System Using
Microscopic Simulation Model. In 17th International
Symposium on Computational Intelligence and
Informatics, Budapest, Hungary, pp. 163-167.
Jánošíková, Ľ., 2007. Emergency Medical Service
Planning. In Communications Scientific Letters of the
University of Žilina, Vol. 9, No 2, pp. 64-68.
Kvet, M., 2014. Computational Study of Radial Approach
to Public Service System Design with Generalized
Utility. In Digital Technologies 2014: Proceedings of
the 10th International IEEE Conference, pp. 198-208.
Kvet, M., Janáček, J., 2016. Radiálny prístup na zlepšenie
existujúceho záchranného systému. In Optimalizační
úlohy v dopravních a logistických systémech a SW
podpora rozhodování v inteligentních dopravních
systémech, Praha, Czech Republic, pp. 11-25.
Snyder, L. V., Daskin, M. S., 2005. Reliability models for
facility location; The expected failure cost case. In
Transport Science, Vol. 39, No 3, pp. 400-416.
Reengineering of the Emergency Service System under Generalized Disutility
93
