Reengineering of the Emergency Service System from the Point of

Service Provider

Jaroslav Janacek and Marek Kvet

Faculty of Management Science and Informatics, University of Žilina, Univerzitná 8215/1, 010 26 Žilina, Slovakia

Keywords: Location, Emergency Medical Service, System Reengineering, Service Providers, Transportation

Performance, Profit Sharing.

Abstract: An emergency service system design is usually worked up by a system administrator, who acts on behalf of

the public. Applied objective is either minimal disutility perceived by an average user or disutility perceived

by the worst situated user. This paper deals with a completely different case, when partial reengineering is

suggested by one of the private service providers running a considerable portion of the current service

centers. The provider tries to maximize his profit subject to the system administrator’s rules, which should

protect public from worsening of their access to the service. We model the provider’s behavior and study

efficiency of the administrator’s rules.

1 INTRODUCTION

When a brand new emergency system under limited

number of service centers is designed, the used

objective is usually to minimize the average or total

disutility perceived by the users (Brotcorne et al.,

2003, Doerner et al., 2005, Jánošíková and Žarnay,

2014). The optimal deployment of service centers

for such type of system can be obtained by exact or

approximate solving of the weighted p-median

problem modelled either by the location-allocation

or radial formulations (García et al., 2011, Janáček

and Kvet, 2013, Elloumi et al., 2004, Sayah and

Irnich, 2016). The initial emergency system design

is mostly suggested by so-called system

administrator, who represents interests of public.

The interests may have various forms, e.g. minimal

average response time or minimal response time of

the worst situated user etc. The administrator usually

supervises dispatching of emergency vehicles to

individual users’ demands in the way that each user

demand is served from the nearest available service

center. The service provision by emergency vehicles

is performed by private providers, who own and run

several service centers equipped with emergency

vehicles.

As distribution of demands for service develops

in time and space, the originally determined center

locations will cease to suit both serviced population

and providers. These discrepance can be mitigated in

different ways. In some national or local emergency

systems (Reuter-Oppermann et al, 2017, Guerriero

et al, 2016), the system administrator is responsible

for the reengineering. In other national systems, e.g.

the emergency health care system of the Slovak

Republic, the system administrator only defines

some rules, under which a service provider is

allowed to relocate his service centers (Kvet and

Janáček, 2016). In the mentioned emergency health

care system the profit of a provider is proportional to

transportation performance necessary for the

demand satisfaction.

In this paper, we study the recent case, when the

considered provider’s objective of reengineering is

to maximize his profit submit to the administrator

rules.

As the users’ and providers’objectives are in a

conflict, the user protecting rules comprise usual

condition that the average or total value of disutility

must not exceed a given limit and also disutility

perceived by the worst situated user cannot be

worsen. Additionally, some further rules can be

imposed on the process of reengineering, e.g. at

most a given number of center location can be

changed, or each center location can be moved only

in a given radius from its original possition.

Following these rules, a considered provider,

who performs reengineering, will change locations

of his centers so that he maximizes the profit by

224

Janacek, J. and Kvet, M.

Reengineering of the Emergency Service System from the Point of Service Provider.

DOI: 10.5220/0006621502240231

In Proceedings of the 7th International Conference on Operations Research and Enterprise Systems (ICORES 2018), pages 224-231

ISBN: 978-989-758-285-1

capturing much demand under assumption that each

demand is serviced from the nearest service center.

In this paper, we provide a reader with linear

programming model of provider’s reengineering of

his part of emergency service system to maximize

his profit under rules imposed by the system

administrator. As the maximization of the

considered provider’s profit must not be performed

by servicing a demand from the more distant

providers’center than necessary, a special constraints

must be implemented in the model. That is why, we

perform a computational study, to find whether real-

sized instances of the problem are solvable using a

common IP-solver. We also compare the variants of

the approach to reengineering, when the volume of

transportation performance represents the provider’s

profit.

2 MODEL OF PROVIDERS’

REENGINEERING

Coming from a conventional denotation of the

weighted p-median problem, we introduce J as a

finite set of all system users, where b

denotes a

volume of expected demand of user j



J. Let I be a

finite set of possible center locations. Symbol d

denotes the integer distance between locations i and

j, where i, j





J. The maximal relevant distance is

denoted by m. The current emergency service center

deployment is described by two disjoint sets of

located centers I



I and I



I, where I

contains p

centers of the considered provider, who performs

reengineering and I

is the set of the centers

belonging to the other providers.

The system administrator’s rules are quantified

by the following constants. The value F gives upper

limit of the total transportation performance

necessary for satisfaction of all users’ demands (the

total disutility perceived by system users). The value

H is the maximal feasible distance between a user’s

location and the nearest service center. The symbol

D denotes the maximal distance between a current

center location and the possible new location of the

center. The integer w gives the maximal number of

centers from I

, which are allowed to change

locations.

To be able to formulate the model in a concise

way, we derive several auxiliary structures. Let

={iI-I

: d

 D} denote the set of all possible

center locations, to which the center tI

can be

moved. Similarly, let S

={tI

: iN

} denote a set of

all centers of the considered provider, which can be

moved to iI

. The subset I

 I-I

is defined by the

formula













. Realize that tN

and iS

for

tI

and iI

and thus I

 I

We introduce coefficients a

for each pair i, j

iI



and jJ, where a

= 1 if and only if d



and a

= 0 otherwise for s = 0, 1, …, m-1.

We define cost coefficients for iI

and jJ so

that c

= 0 if d

≥ min{d

: tI

} and c

= b

otherwise.

The last two auxiliary structures are denoted as

} and {R

}, where jJ. The first of them is a

system of ordered lists, where list P

consisting of

iI

is ordered so that the following inequalities

hold:















 













   















. An element

of the second structure is an ordered list of

subscripts from range 1, …, I

, where R

(r) gives

the minimal subscript, for which 

































holds. Obviously r+1 R

(r).

Now, we introduce series of decision variables,

where binary variable y

defined for each iI

takes

the value of one, if a service center is to be located at

i and it takes the value of zero otherwise.

The reallocation variable u

{0, 1} for tI

and

iN

takes the value of one, if the service center at t

is to be moved to i and it takes the value of zero

otherwise.

To be able to express the total transportation

performance value, we introduce zero-one auxiliary

variables x

for jJ and s = 0, 1, …, m-1, where x

1 if there is no located service center in the radius s

from the user location j.

Finally, we introduce series of allocation

variables z

{0, 1} for iI



and jJ, where z

1 if user demand located to j is serviced from center

location i.

Using the above introduced structures and

decision variables, we suggest the following model.



 Jj Ii

ijij

zcMaximize

(1)

pytoSubject







(2)

wpy







(3)

Itforu







(4)

Iiforyu







(5)

Jjforaya







(6)

Reengineering of the Emergency Service System from the Point of Service Provider

225

1...,,0,









msJjfor

ayax

ijjs

(7)

Fxb

jsj



 







(8)

Jjforz

IIi







(9)

Riij

IiJjforyz  ,

(10)

1...,,1,

)(









jrP

kRr

IkJjfor

(11)

Iifory  }1,0{

(12)

tLti

NiItforu  ,}1,0{

(13)

1...,,0,}1,0{  msJjforx

(14)

JjIIiforz

FRij

 ,}1,0{

(15)

The objective function (1) expresses the volume

of transportation performance allocated to the

considered provider (provider’s profit). If a user is

nearer to a center of other providers, the contribution

to the considered provider is zero. The misallocation

of a user to a more distant center of the considered

provider is prevented by constraints (11).

Constraint (2) preserves constant number of

centers belonging to the considered provider under

reengineering.

Constraint (3) limits the number of changed

center locations by the constant w.

Constraints (4) allow moving the center from the

current location t to at most one other possible

location in the radius D.

Constraints (5) enable to bring at most one center

to a location i subject to condition that the original

location of the brought center lies in the radius D.

These constraints also assure consistency among the

decisions on move and decisions on center location.

Constraints (6) ensure that any user j lies in the

radius H from a located center, i.e. maximal distance

between a user and the nearest center is less than or

equal to the value H.

Constraints (7) give relation between located

variables y

and auxiliary variables x

so that x

equals to one, if no center is located in the radius s

from the user’s location j. Then, the expression x

+…+ x

jm-1

gives the distance from the user j to the

nearest service center regardless of its owner.

Constraint (8) makes use of the variables x

and

assures that the total transportation performance

does not exceed the given value F.

Constraints (9) are commonly used allocation

constraints, which assure that each user demand is

allocated to exactly one center belonging either to

the considered provider or to other providers.

Link-up constraints (10) give relation between

allocation variables z

and the location variables y

which model the decisions on locating service

centers operated by considered provider.

Constraints (11) were developed to prevent the

maximization process from allocating a demand to a

more distant service center than the nearest one. The

constraint formulated for location P

(k) and user j

forbids allocation of user’s j demand to every

service center P

(r), which is more distant from the

location j than the center location P

(k).

3 COMPUTATIONAL ASPECTS

OF THE APROACH

The original approach to the public service system

design (Current et al., 2002, Marianov and Serra,

2002) is based on solving the weighted p-median

problem. The scheme of the former approaches

consists in problem formulation by means of integer

linear programming and subsequent submission of

the problem to some solver equipped with a

universal branch-and-bound method. To overcome

the computational complexity emerging, when real-

sized instances of the problem were solved, the

radial formulation (García et al., 2011, Janáček,

2008) was developed. Then, the emergency service

system can be successively designed by solving the

problem (16), (2), (7), (12) and (14).

j js

j J s

Minimize b x







(16)

The proper function of the model is based on the

fact that the optimization process minimizing (16)

presses down values of the individual variables x

Then the value of expression x

+ x

+…+ x

jm-1

corresponds to the shortest integer distance from the

user j to the nearest located center. If some other

constraints are appended to the model (16), (2), (7),

(12) and (14), it may or need not lead to

considerable elongation of computational time

necessary for reaching the exact solution.

Whereas, addition of the constraints (4) and (5)

almost do not impact the computational time (Kvet

and Janáček, 2016), subjoining capacitated

ICORES 2018 - 7th International Conference on Operations Research and Enterprise Systems

226

constraints may considerably spoil the

computational process convergence (Janáček and

Gábrišová, 2009). Other types of constraints

deteriorating the computational process are min-max

link-up constraints used, when a robust service

system is designed employing detrimental scenarios

(Janáček and Kvet, 2017).

In comparison with the classical models of the

emergency system design problem, we have to face

the difficulty caused by maximization of the

objective function modelling the transportation

performance (provider’s profit). Whereas the

classical objective minimizes the transportation

performance and thus a user is associated with the

nearest located center (see Figure 1), the

maximization considered in our paper may lead to

the assignment depicted in Figure 2.

Figure 1: In the chart, the black circles represent locations

of user demands and the black squares depict locations of

service centers. The arcs correspond to the assignment of

the demands to the centers, which minimizes the total

travel distance.

The assignment in Figure 1 fully fulfils the

assumption that each user must be serviced from the

nearest service center, but the assignment in Figure 2

completely breaks the assumption.

Figure 2: In the chart, the black circles represent locations

of user demands and the black squares depict locations of

service centers. The arcs correspond to the assignment of

the demands to the centers, which maximizes the total

travel distance.

To avoid the misassignment, we developed a

series of constraints, which prevent user’s demand

from assignment to a more distant located service

center than the nearest one. The series of constraints

for a given user j hasI

-1 members, where I



denotes the number of possible center locations, to

which the user demand can be assigned. The

constraint construction comes from the idea that if

there is a location i

equipped with a service center

distant d

i*j

from the user j, then the demand of user j

must not be assigned to any location i, which meets

> d

i*j

. To formalize the constraint, we order all

possible center locations from I

increasingly

according to their distance from j so that the list

(1), P

(2), …, P

(I

) gives the ordered sequence of

the center locations. Thus















 













holds

for each r =1, …, I

-1. The case of tie, i.e.































, is handled by mapping R

, where R

(r)

gives the minimal subscript from the range 1, …, I



such that 













 

















holds. If no such

subscript exists, the R

(r) is set at the value I

+1.

Having defined P

(r) and R

(r) for r = 1, 2, …, I

,

we can construct the constraint in the way that if a

center is located at the location P

(r), then any

assignment of the demand of user j to any of center

locations of P

(r)), P

(r)+1), …, P

(I

) must be

forbidden. In the constraint formulation (11), we

make use of the convention that sum over the empty

range, i.e. the range, which starts with higher

subscript than the ending one, is defined as zero

value.

For given j, I

-1 constraints must be formulated.

This way, the model has to be enlarged by J*(I

-1)

constraints ensuring the proper demand assignment.

Based on the above-mentioned experience, we

have to raise the question of technical solvability of

the formulated problem (1)-(15). We ask whether a

commercial solver based on the branch-and-bound

technique is able to find the exact solution of a real-

sized problem in acceptable time.

4 EMERGENCY SERVICE

POLICY ISSUES OF THE

APPROACH

The presented approach deals with the special case

of emergency system reengineering, when a

considered service provider is allowed to change the

deployment of his service centers submit to rules,

which are determined by the system administrator.

Respecting the rules, the considered provider

naturally aims to increase his profit, which is

proportional to the traveled distance. It is obvious

that the provider’s objective is in conflict with the

system user objective.

Thus, the upcoming changes of the service center

deployment are matter of negotiation between the

two mentioned players. The administrator can set up

the general rules of the system adjustment and the

Reengineering of the Emergency Service System from the Point of Service Provider

227

considered provider suggests the location changes of

operated centers.

The suggested model together with a suitable IP-

solver represent such a tool, which can enable the

negotiation under knowledge of consequences both

rules and provider’s behavior. As the considered

rules are quantified by the values of F, H, w and D,

the provider can find, what is the optimal profit

under the values and thus, he can conclude whether

the changes pay off.

As concerns the system administrator, the tool,

which models the provider’s behavior, enables to

investigate the provider’s profit under given values

F and H. Starting with some default values, e.g. the

transportation performance and the worst distance

between a user and the nearest center obtained for

the original center deployment, the administrator can

repeat the solving algorithm with step by step

decreased values and he can suggest such values,

which improve service accessibility for users and

also let the considered provider increase the profit.

Another issue of the tool for the administrator is

represented by a possibility to test effectiveness of

the auxiliary and formal rules w and D from the

point of users’ benefit.

5 COMPUTATIONAL STUDY

To study presented approach to reengineering of the

emergency service system, we performed series of

numerical experiments, in which the optimization

software FICO Xpress 8.0 (64-bit, release 2016) was

used and the experiments were run on a PC equipped

with the Intel® Core™ i7 5500U processor with the

parameters: 2.4 GHz and 16 GB RAM.

Used benchmarks were derived from real

emergency health care system, which was originally

implemented in eight regions of Slovak Republic.

For each self-governing region, i.e. Bratislava (BA),

Banská Bystrica (BB), Košice (KE), Nitra (NR),

Prešov (PO), Trenčín (TN), Trnava (TT) and Žilina

(ZA), all cities and villages with corresponding

number b

of inhabitants were taken into account.

The coefficients b

were rounded to hundreds. The

set of communities represents both the set J of users’

locations and the set I of possible center locations as

well. The cardinalities of these sets are reported in

Table 1, where the associated column is denoted by

|I|. The total number of located centers is given in

the column denoted as TNC. The network distance

from a user to the nearest located center was taken

as the user´s disutility.

Table 1: Size of used benchmarks.

Region

|I|

TNC

515

460

350

664

276

249

315

An individual experiment was organized so that

the current deployment of service centers for each

self-governing region was studied first. The obtained

results are summarized in Table 2. The total

transportation performance was computed as a sum

of weighted distances between system users and the

nearest located service centers. The weights were set

to the number of users sharing the same location.

The values of the total transportation performance

are reported in column denoted by “Total TP”. For

each self-governing region, ten different instances

were generated randomly. These instances differ in

the list of located service centers operated by the

considered provider. The average percentage ratio of

the provider’s centers to all centers is reported in the

column denoted by “Prov. [%]”. The right part of

Table 2 denoted by “Max TP decrease” contains the

results of analysis aimed at computing the maximal

possible decrease of the total transportation

performance, which can be achieved by relocating

some of the provider’s service centers. To determine

these values, the model (1)-(15) was simplified. The

objective function value (1) was replaced by

minimization of the left part of the constraint (8),

whereas constraint (8) was completely excluded

from the model. The constraints containing variables



{0, 1} for i





and j



J were not taken into

account, because they were not needed. Other

constraints stayed unchanged. The value of

parameter w was set to the cardinality of the

provider’s service center list. It means that all

centers operated by the considered provider could

change their location. The value of D was set to 15

according to the rule applied in the emergency

health care system of the Slovak Republic (Kvet and

Janáček, 2016). The value of H was set to the

maximal value of distance between a user and the

nearest located service center in the current design.

By solving the adjusted model, we obtained the

minimal value of transportation performance, which

can be obtained by reengineering. The average

computational time in seconds necessary for

problem solving is denoted by “Time [s]”.The last

ICORES 2018 - 7th International Conference on Operations Research and Enterprise Systems

228

column of the table denoted by “Dec. [%]” contains

the maximal possible percentage decrease of the

total transportation performance, where the current

value reported in the column “Total TP” was taken

as the base.

Table 2: Analysis of current centers deployment and

possible improvement of total transportation performance.

Region

Current state

Max TP decrease

Total TP

Prov. [%]

Time [s]

Dec. [%]

21842

55.1

0.02

6.34

32476

44.9

0.21

2.40

36363

46.0

0.36

3.21

38831

50.7

0.48

3.94

42740

44.3

0.28

1.59

26683

52.9

0.12

2.50

31582

49.6

0.13

4.92

31955

46.8

0.11

3.49

The obtained results summarized in Table 2

indicate that the reengineering of the emergency

service system may bring considerable benefit for

the system users. The model for maximal possible

improvement of the total transportation performance

is easily solvable and the computational process

does not take more than 0.5 second.

The next portion of numerical experiments was

aimed at studying the characteristics of suggested

model (1)-(15) described in the previous sections.

Since the previous experiments enabled us to get the

range, in which the total transportation performance

may vary, the following case study was suggested to

answer the question, how the constraint (8)

influences the computational process of solving the

model (1)-(15). The experiments were organized in

the following way. For each solved instance, 6

problems were solved. The models differed in the

value of F used in the constraint (8). The parameter

F was set in such a way, that the total transportation

performance was reduced by 0, 20, 40, 60, 80 and

100 percent of its possible range. The upper bound

of mentioned range is represented by the

transportation performance computed for current

deployment of service centers (see column “Total

TP” in Table 2) and the lower bound can be obtained

as the result of mathematical model searching for the

maximal possible decrease of the total transportation

performance using the simplified model described

above.

The characteristic of the reengineering model

studied in this contribution consists in the considered

provider’s profit, which is to be maximized under

the condition that the total transportation

performance is limited by the value of F. The

obtained results are reported in Table 3, which

follows the structure of previous tables. The

provider’s profit is expressed in percentage of

current provider’s transportation performance. The

negative values indicate such solution, in which the

reengineering process brings worse situation for the

considered provider, i.e. the resulting provider’s

profit is less than his current profit.

Table 3: Average percentage profit of the provider's

transportation performance for individual regions and

given percentage reduction of transportation performance.

Reg\Red

100

19.6

14.3

10.5

5.4

0.6

-9.4

10.5

8.5

6.3

3.8

1.0

-2.3

20.8

17.7

14.4

11.2

7.3

-3.1

23.6

21.1

18.3

15.3

11.5

4.3

10.8

9.2

7.0

3.8

1.7

-1.0

13.8

11.6

9.0

6.0

1.8

-3.4

23.4

20.2

17.1

13.5

8.1

1.3

16.3

14.2

10.8

8.3

4.7

-1.5

AVG

17.5

14.8

11.9

8.7

4.9

-1.4

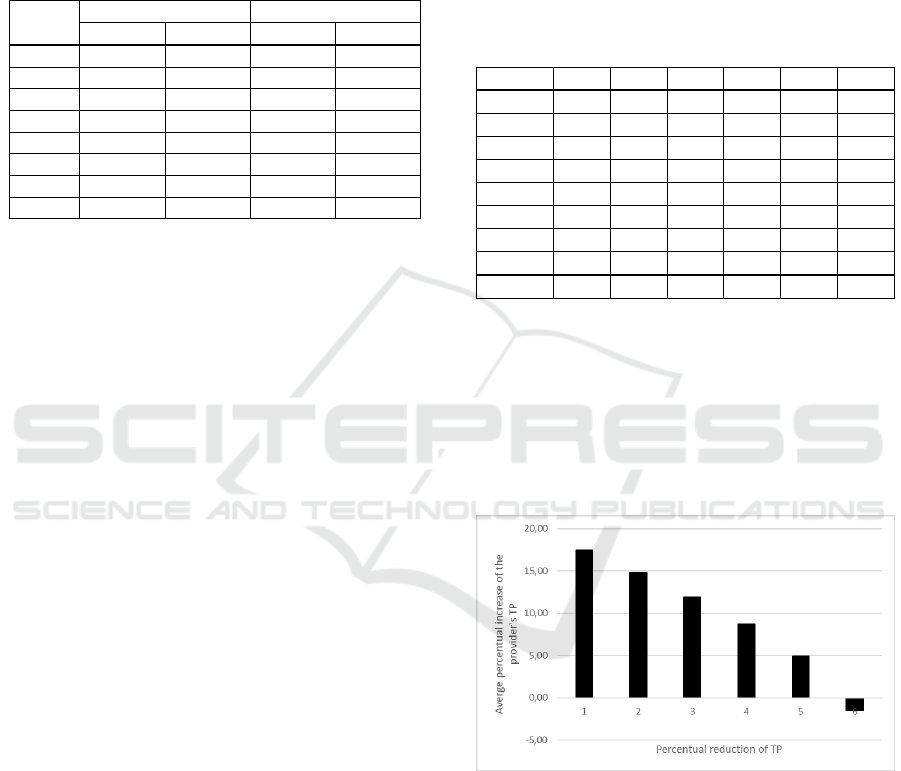
The dependency of average percentage profit of

the considered provider on percentage reduction of

the total transportation performance is shown in

Figure 3. These results confirm our expectations that

the provider's profit decreases with increasing

reduction of transportation performance. Negative

values indicate that the provider may worsen the

current provider’s profit.

Figure 3: Dependency of average percentage profit of the

considered provider on percentage reduction of the total

transportation performance.

Finally, the reengineering process may have a

secondary impact. Even if the main goal of changing

the provider’s center locations is to maximize the

provider’s profit, the obtained solution may bring

improvement also for the system users. As we have

shown, the total transportation performance can get

lower and thus, the average user distance to the

nearest located service center decreases. Table 4

Reengineering of the Emergency Service System from the Point of Service Provider

229

summarizes the average user distances for different

percentage reduction of transportation performance.

Table 4: Average user's distance for individual regions and

given percentage reduction of transportation performance.

Reg\Red

100

3.60

3.55

3.50

3.46

3.41

3.38

4.91

4.89

4.87

4.84

4.82

4.80

4.59

4.56

4.53

4.50

4.47

4.44

5.63

5.58

5.54

5.49

5.45

5.41

5.22

5.21

5.19

5.17

5.16

5.14

4.49

4.47

4.44

4.42

4.40

4.38

5.67

5.62

5.56

5.50

5.45

5.40

4.62

4.59

4.56

4.53

4.49

4.46

AVG

4.84

4.81

4.77

4.74

4.70

4.67

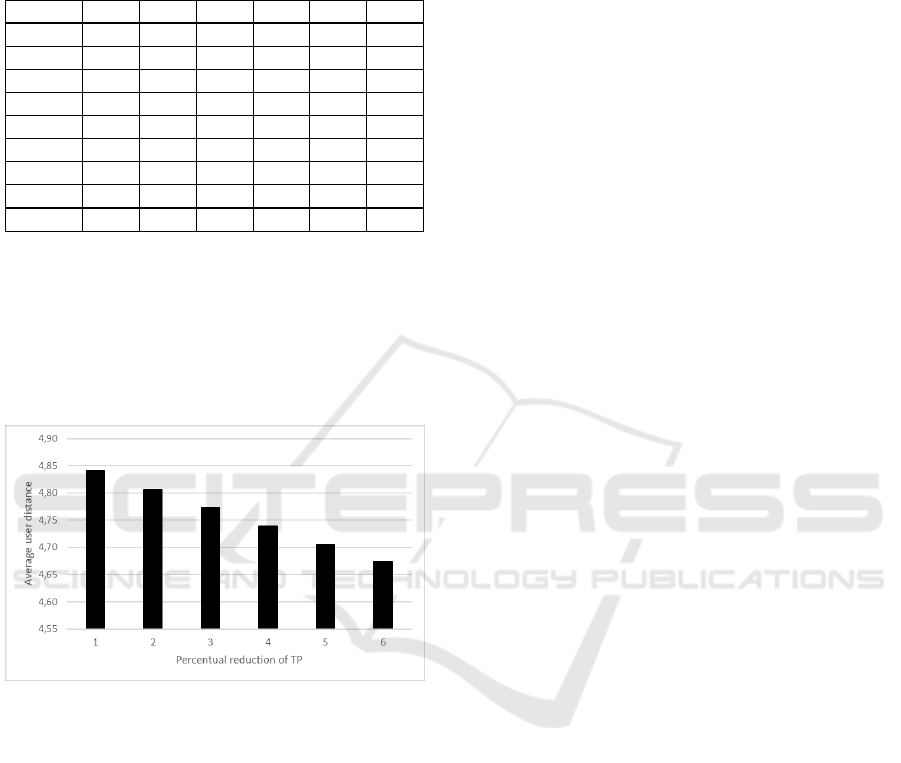
The results confirm that even if the improvement

of average user distance is not significantly high, the

reengineering process may bring some benefit also

for the system users. The dependency of average

user distance on percentage reduction of total

transportation performance computed for all solved

instances is shown in the Figure 4.

Figure 4: Dependency of average user distance on

percentage reduction of total transportation performance.

As concerns computational time, we have

observed that the time necessary for solution of the

problem (1)-(15) was in orders higher than that one

of the simplified version reported in Table 2.

Nevertheless, we have found that the time has never

exceeded the limit of three minutes.

6 CONCLUSIONS

The paper deals with an approach to emergency

service system reengineering, where change of the

service center deployment is performed by one of

the providers with the goal to maximize his profit.

The system administrator, who imposes some

constraints on the provider’s decisions, protects

users’ interests. The approach is based on the

suggested model, which includes new form of

restricted assignment constraints. We showed that

the complex problem described by the model is

solvable in acceptable computational time even if

real-world instances of the problem are solved.

Performing numerical experiments with benchmarks

derived from current state of service centers

deployment, we obtained and presented information

about possible users’ disutility improvement and the

associated provider’s profit. The presented approach

may serve as a very useful tool for possible

negotiation of the system administrator with the

service provider concerning system reengineering

and sharing the resulting benefit among system users

and the service provider.

Future research may be aimed at usage of the

suggested modelling technique in game modelling,

in which different groups of providers compete for

the profit under system administrator supervision.

ACKNOWLEDGEMENTS

This work was supported by the research grants

VEGA 1/0518/15 “Resilient rescue systems with

uncertain accessibility of service”, VEGA 1/0463/16

“Economically efficient charging infrastructure

deployment for electric vehicles in smart cities and

communities”, and APVV-15-0179 “Reliability of

emergency systems on infrastructure with uncertain

functionality of critical elements”.

REFERENCES

Brotcorne, L., Laporte, G., Semet, F. 2003. Ambulance

location and relocation models. European Journal of

Operational Research 147, pp. 451–463.

Current, J., Daskin, M., Schilling, D. 2002. Discrete

network location models. In Drezner Z. (ed) et al.

Facility location. Applications and theory, Berlin,

Springer, pp 81-118.

Doerner, K.F., et al. 2005. Heuristic Solution of an

Extended Double-Coverage Ambulance Location

Problem for Austria. Central European Journal of

operations research, Vol. 13, No 4, pp. 325-340.

Elloumi, S., Labbé, M., Pochet, Y. 2004. A new

formulation and resolution method for the p-center

problem. INFORMS Journal on Computing 16, pp. 84-

94.

García, S., Labbé, M., Marín, A. 2011. Solving large p-

median problems with a radius formulation.

ICORES 2018 - 7th International Conference on Operations Research and Enterprise Systems

230

INFORMS Journal on Computing, Vol. 23, No 4, pp.

546-556.

Guerriero, F., Miglionico, G., Olivito, F. 2016. Location

and reorganization problems: The Calabrian health

care system case. European Journal of Operational

Research 250, pp. 939-954.

Janáček, J. 2008. Approximate Covering Models of

Location Problems. In Lecture Notes in Management

Science: Proceedings of the 1st International

Conference ICAOR, Yerevan, Armenia, pp. 53-61.

Janáček, J., Gábrišová, L. 2009. A two-phase method for

the capacitated facility problem of compact customer

sub-sets. Transport: Journal of Vilnius Gediminas

Technical University and Lithuanian Academy of

Sciences, Vol. 24, No 4, pp. 274-282.

Janáček, J., Kvet, M. 2013. Public service system design

with disutility relevance estimation. In Mathematical

Methods in Economics 2013, Jihlava, Czech Republic,

pp. 332-337.

Janáček, J., Kvet, M. 2017. An approach to uncertainty in

emergency service systems via scenarios and fuzzy

values. In Croatian Operational Research Review,

Vol. 8, No 1, pp. 237-248.

Jánošíková, Ľ., Žarnay, M. 2014. Location of emergency

stations as the capacitated p-median problem. In

International scientific conference: Quantitative

Methods in Economics-Multiple Criteria Decision

Making XVII, Virt, Slovakia.

Kvet, M., Janáček, J. 2016. Radiálny prístup na zlepšenie

existujúceho záchranného systému. In Optimalizační

úlohy v dopravních a logistických systémech a SW

podpora rozhodování v inteligentních dopravních

systémech, Praha, Czech Republic, pp. 11-25.

Marianov, V., Serra, D. 2002. Location problems in the

public sector. In Drezner, Z. (Ed.). Facility location -

Applications and theory, Berlin: Springer, pp. 119-

150.

Reuter-Oppermann, M., van den Berg, P. L., Vile, J. L.

2017. Logistics for Emergency Medical Service

systems. Health Systems, Vol. 6, No 3, pp 187-208.

Sayah, D., Irnich, S. 2016. A new compact formulation for

the discrete p-dispersion problem. European Journal

of Operational Research, Vol. 256, No 1, pp. 62-67.

Reengineering of the Emergency Service System from the Point of Service Provider

231