Impact of Inter-core Crosstalk on the Performance of Multi-core

Fibers-based SDM Systems with Coherent Detection

Bruno R. P. Pinheiro, Jo

ao L. Rebola and Adolfo V. T. Cartaxo

Optical Communications and Photonics Group, Instituto de Telecomunicac¸

oes, Lisboa, Portugal

Instituto Universit

ario de Lisboa (ISCTE-IUL), Lisboa, Portugal

Keywords:

Inter-core Crosstalk, Monte-Carlo Simulation, Multi-core Fibers, Optical Coherent Detection, Space-division

Multiplexing.

Abstract:

Inter-core crosstalk (ICXT) can limit the multi-core ﬁber (MCF) systems performance and transmission reach.

Over the last years, the impact of the ICXT on the performance of MCF optical communication systems with

coherent detection has been investigated in several works. However, the inﬂuence of the MCF parameters

and transmitted signal characteristics on the ICXT mechanism and the degradation induced by it on the per-

formance of coherent detection MCF systems are still to be completely assessed. In this work, the impact

of the ICXT on the performance of coherent detection MCF-based transmission systems is assessed through

numerical simulation considering ﬁber linear propagation. The metrics used to assess the MCF system per-

formance are the bit error rate (BER) and the optical signal-to-noise ratio (OSNR) penalty due to the ICXT.

Our results show that the BER and the OSNR penalty due to the detected ICXT, in MCF-based systems with

coherent detection, are inﬂuenced by the skew, time misalignment between the transmitted signals and the

roll-off factor of the transmitted signals. In the range of skew and roll-off factors analyzed, the maximum

reduction of maximum ICXT level for a 1 dB OSNR penalty by appropriate choice of skew and roll-off factor

does not exceed 1.7 dB.

1 INTRODUCTION

Current long-haul optical networks based on stand-

ard single-mode single-core ﬁbers (SMFs) can no

longer respond efﬁciently to the exponential rapid

trafﬁc growth. Thereby, in order to respond to the

ever-growing trafﬁc demand, new technologies are re-

quired to reach higher capacities on the optical com-

munication systems (Klaus et al., 2017). Space divi-

sion multiplexing (SDM) has been proposed as a solu-

tion to achieve higher capacity in future long-haul op-

tical networks (Klaus et al., 2017). The implementa-

tion of SDM is based on two main approaches, which

consist basically on using two different types of ﬁber

(Saitoh and Matsuo, 2016). The ﬁrst type of ﬁber is

known as few-mode ﬁber (FMF) and makes use of

several propagation modes in the ﬁber as transmis-

sion channels. The main drawback of FMFs is the re-

quirement of a multi-input multi-output (MIMO) di-

gital signal processing (DSP) receiver to minimize the

group delay spread between the different modes. Fur-

thermore, the FMF limits the exploitation of the space

domain, except for enhanced capacity-transmission

reach, since all modes must be received as a single

entity (Klaus et al., 2017). The second ﬁber type

is the multi-core ﬁber (MCF), in which, independent

channels are transmitted in different cores inside the

ﬁber. Thereby, the signals transmitted in each core

of the MCF can have different symbol rates, differ-

ent modulation formats and different temporal mis-

alignments between them. In homogeneous MCFs,

the relative uniformity of the cores supports multi-

dimensional spatial channels that enable shared trans-

mitter and receiver hardware, simpliﬁed DSP and

switching (Cartaxo et al., 2016). The use of MCFs

has been proposed for several optical communication

networks such as access, long-haul, intra-data centers

and radio-over-ﬁber based networks (Puttnam et al.,

2017), and so, in this work, we restrain our studies

only to MCF-based optical communication system.

As optical coherent detection with polarization-

division multiplexing (PDM) is the selected detec-

tion technology of actual backbone optical networks

(Xia and Wellbrock, 2013), the majority of the MCF-

based SDM systems tested so far, consider coherent

detection (Puttnam et al., 2017): in 2011, a high-

capacity transmission experiment reached 112 Tbps

capacity using a MCF with 7 cores and transmitting

Pinheiro, B., Rebola, J. and Cartaxo, A.

Impact of Inter-core Crosstalk on the Performance of Multi-core Fibers-based SDM Systems with Coherent Detection.

DOI: 10.5220/0006623400740081

In Proceedings of the 6th International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS 2018), pages 74-81

ISBN: 978-989-758-286-8

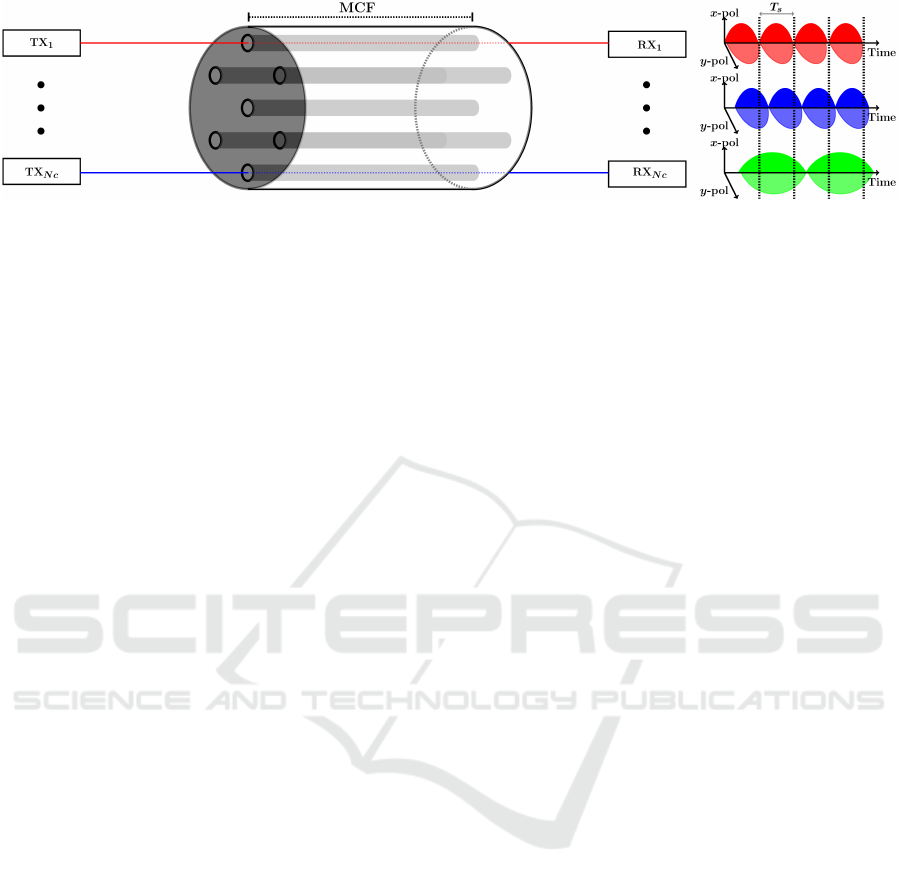
Figure 1: Schematic of the MCF-based SDM system with Nc transmitters (TX

to TX

) and the respective receivers (RX

to RX

). The signals transmitted in each core are multiplexed on the polarization.

PDM-QPSK signals (Zhu et al., 2011). By the end

of 2012, a 12 core MCF experiment exceeded 1 Pbps

capacity (Takara et al., 2012). In 2015, it was repor-

ted that a 22-core homogeneous MCF demonstration

exceeded 2 Pbps (Puttnam et al., 2015). It is ex-

pected that MCFs can attain a transmission capacity

beyond 10 Pbps (Morioka, 2017). MCF transmission

with coherent detection is deﬁnitely the most prom-

ising transmission technology that will allow to in-

crease substantially the transmission capacities of the

actual long-haul optical networks and to implement

SDM optical networks with low complexity.

However, an important limitation of the perform-

ance of the weakly-guided MCFs is the inter-core

crosstalk (ICXT) (Fini et al., 2010; Rademacher et al.,

2017a; Hayashi et al., 2014; Rademacher et al.,

2017b). ICXT arises in homogeneous MCFs which

have cores with similar properties. ICXT can be

reduced by increasing the distance between cores.

However, maintaining the same cladding diameter,

this method can lead to the reduction of the number

of cores, thus, reducing the overall transmission ca-

pacity (Hayashi et al., 2013; Hayashi et al., 2011).

Over the last years, the ICXT has been researched

and some relevant conclusions have been drawn con-

cerning the mechanism of the ICXT and its inﬂuence

on the performance of the MCF-based SDM systems

(Hayashi et al., 2014; Cartaxo et al., 2016). In (Hay-

ashi et al., 2014), a theoretical model of ICXT is pro-

posed and the impact of the ICXT on the performance

of the MCF transmission systems is assessed theor-

etically. In (Cartaxo et al., 2016), the ICXT model

presented in (Hayashi et al., 2014) is extended, by

considering the ICXT dependence on the group ve-

locity dispersion and the skew between cores. In ad-

dition, the transfer function of the ICXT ﬁeld is de-

rived for homogeneous MCF. This transfer function

helps to study the inﬂuence of the ICXT on the per-

formance degradation of MCF-based optical systems

with walk-off between ﬁber cores (skew), slightly dif-

ferent group velocities between cores, and by consid-

ering different modulation formats (as the typically

ones used for coherent detection) at the MCF input.

In this work, we assess numerically through

Monte-Carlo (MC) simulation, the inﬂuence of the

ICXT on the bit error rate (BER) and the optical

signal-to-noise (OSNR) penalty of the MCF-based

optical communication system with coherent detec-

tion, considering 4-Quadrature Amplitude Modula-

tion (QAM) signals, with different roll-off factors,

different skews and different signal time misalign-

ments between MCF cores.

This work is organized as follows. Section 2 de-

scribes the equivalent simulation model used to char-

acterize the MCF-based optical communication sys-

tem with coherent detection and the ICXT impact on

its performance. The validation of the transfer func-

tion used in this work to emulate the ICXT behavior

on the MCF-based SDM system is performed in sec-

tion 3. In section 4, the performance of the MCF-

based SDM system with coherent detection impaired

by ICXT estimated through MC simulation is ana-

lyzed. The conclusions are outlined in section 5.

2 MCF-BASED SDM SYSTEM

MODEL

Figure 1 depicts schematically a MCF-based optical

communication system, with dedicated transmitter

and receiver hardware for each core. On the transmit-

ter side, several different signals are launched in the

MCF by Nc different transmitters, TX

to TX

, with

Nc corresponding to the number of cores used. Re-

mark that it is assumed that these transmitters gener-

ate independent SDM PDM-M-QAM signals, where

M is the modulation format order. The PDM-M-QAM

signals are propagated through the MCF and are de-

tected individually by Nc optical coherent receivers,

to RX

. Core-coded modulation or polariza-

tion core-coded modulation is not considered, since

the characterization of the ICXT impact on the per-

formance of MCFs with independent transmission of

PDM-M-QAM signals in each core is not fully un-

derstood (Rademacher et al., 2017a). On the right

Impact of Inter-core Crosstalk on the Performance of Multi-core Fibers-based SDM Systems with Coherent Detection

MCF

ASE noise

Coherent

Receiver

Decision

Circuit

BER

(t)

(t) E

(t)

F (ω)

(ω)

′

(t)

Figure 2: Equivalent simulation model for the MCF-based SDM system, considering single polarization transmission.

hand side of Figure 1, some of the detected PDM-

M-QAM signals in each core are depicted illustrat-

ively. Since, each core works as a transmission chan-

nel independent of the other cores, each transmitted

signal can have different symbol rates, different mod-

ulation formats and different temporal misalignments

between them.

Figure 2 depicts the equivalent simulation model

of MCF-based SDM with coherent detection consid-

ering single polarization transmission and only two

cores. The interfered core is the core n and the in-

terfering core is the core m. The performance of a

PDM system with optical coherent detection can be

assessed by evaluating only one signal polarization

as long as ideal PDM is assumed (Essiambre et al.,

2010). Moreover, we assume ideal compensation of

the chromatic dispersion at the coherent receiver out-

put. The detected signals have a raised-cosine (RC)

pulse shape in order to eliminate the inter-symbol in-

terference at the decision circuit. The RC signals

can be generated by making use of the RC ﬁlter,

which transfer function, H

( f ), is (Carlson and Cri-

lly, 2009)

( f ) =











0 ≤ |f |≤

1−β

cos

πT

2β



|f |−

1−β

i

1−β

≤ |f |≤

1+β

0 |f |>

1+β

(1)

where T

is the symbol period and β is the roll-

off factor. Alternatively, the RC signals can be ob-

tained by having root raised-cosine (RRC) ﬁlters at

the transmitter and at the receiver, in such a way that

RRC

(t)∗h

RRC

(t) = h

(t), where * is the convolution

operator (Carlson and Crilly, 2009). Hence, the trans-

fer function of the RRC ﬁlter is H

RRC

( f ) =

( f ).

The transmitter output signal of the core n, E

(t),

with RRC pulse shape, can be expressed by

(t) =

√

+∞

∑

i=−∞

I,i

+ ja

Q,i

RRC

(t −iT

) (2)

where a

I,i

and a

Q,i

are the amplitude of the in-phase

(I) and quadrature (Q) components of the i-th M-

QAM transmitted symbol, respectively, and P

is the

average power of the transmitted signal at core n. The

transmitted signal at core m, E

(t) is expressed as

(t) =

√

+∞

∑

i=−∞

(m)

I,i

+ ja

(m)

Q,i

RRC

(t −iT

−τ

)

(3)

where P

is the average power of the transmitted sig-

nal at core m, a

(m)

I,i

and a

(m)

Q,i

are the I and Q com-

ponents of the i-th M-QAM transmitted symbol of

(t), respectively. The amplitude levels, a

b,i

and

(m)

b,i

, ∀b ∈ {I,Q} are random variables that take on

equally likely the following values:

b,i

∈ {±1,±3, ...,±

√

M −1}A (4a)

(m)

b,i

∈ {±1,±3, ...,±

√

M −1}A

(m)

(4b)

where A and A

(m)

are amplitudes that are deﬁned in

order that the powers corresponding to the ﬁelds E

(t)

and E

(t) are P

and P

, respectively. τ

is the

temporal misalignment between E

(t) and E

(t), that

takes values between 0 and T

. The temporal mis-

alignment is the difference between the signal trans-

mission time instants of the each transmitter with ref-

erence to the interfered core, i.e., the core in which

the receiver performance is assessed.

The propagation in core n is characterized by the

transfer function H

(ω) = e

−jβ

(ω)L

, where β

is the

propagation constant of core n and L is the length of

the MCF. The resulting signal after propagation in

the n-th core, E

(t), is described by E

(t) = E

(t) ∗

−1

(ω)] (Agrawal, 2010), where F

−1

[ ] is the in-

verse Fourier transform operator.

The equivalent simulation model of the MCF to

characterize the ICXT between cores m and n is

deﬁned by the ICXT ﬁeld transfer function F(ω)

given by (Cartaxo et al., 2016)

F(ω) = −jK

−jβ

(ω)L

∑

k=1

−j∆β

(ω)z

−jφ

(5)

where K

is the discrete coupling coefﬁcient

between cores m and n, N is the number of phase-

matching points (PMPs), and φ

is the random phase

PHOTOPTICS 2018 - 6th International Conference on Photonics, Optics and Laser Technology

shift, introduced at the k-th center point (with longit-

udinal coordinate z

) between consecutive PMPs, that

is distributed uniformly between 0 and 2π (Cartaxo

and Alves, 2017). In Equation (5), ∆β

is the differ-

ence between the propagation constants of core m and

n, given by

∆β

(ω) = ∆β

0,mn

+ d

ω −

∆D

2πc

(6)

In Equation (6), c is the speed of light in vacuum,

λ is the wavelength, ∆β

0,mn

is the difference of the

propagation constants at zero frequency, ∆D

is the

difference between the dispersion parameters of core

m and n, and d

is the walkoff between cores m and

n, deﬁned by d

= ν

−1

−ν

−1

, with ν

and ν

being

the group velocities in cores m and n, respectively. In

this work, we assume that ∆β

0,mn

and ∆D

are 0.

Hence, Equation (5) is rewritten as

F(ω) = −jK

−jβ

(ω)L

∑

k=1

−jωS

−jφ

(7)

where S

denotes the skew between the cores m and

n and is given by d

The ICXT signal at the output of core n due to the

signal in core m, E

(t), is given by

(t) = −jK

√



∑

k=1

[cosφ

− j sin φ

]·

+∞

∑

i=−∞

(m)

I,i

+ ja

(m)

Q,i

RRC

(t −iT

−S

/L −τ

)



∗F

−1

(ω)]

(8)

After the MCF, the ampliﬁed spontaneous emis-

sion (ASE) noise is added to the interfered and the

ICXT signals. The ASE noise is generated from the

optical ampliﬁcation and is an additive white Gaus-

sian noise with a singlesided power spectral density in

each polarization, N

, deﬁned as 2 P

/(OSNR B

sim

where 2 P

is the total average signal power summed

over the two states of polarization and B

sim

is the

bandwidth used in the MC simulation (Jeruchim et al.,

2000). From this deﬁnition, the optical signal-to-

noise ratio (OSNR) is deﬁned as the ratio between the

total signal power and the total ASE noise power and

it is estimated at the coherent receiver input.

Figure 3 depicts the model of a coherent receiver

with a 2x4 90

◦

hybrid for a single-polarization trans-

mission (Essiambre et al., 2010). The main goal of

the 2x4 90

◦

hybrid is to combine the local oscillator

signal, E

(t), with the incoming signal, E

(t). The

optical ﬁelds at the output of the 2x4 90

◦

hybrid are

given by (Essiambre et al., 2010)







(t)













1 −1

j j

j −1

−1 j









(t)



(9)

where E

(t) = E

(t) + E

ASE

(t). In this work,

we assume an ideal synchronization (in time, carrier

frequency, phase and polarization) between the LO

and the received signals. We also assume that the sig-

nal, ICXT and the ASE noise are perfectly aligned in

the polarization.

The coherent receiver detects the I and Q com-

ponents of the incoming signal and then, each IQ

component is ﬁltered by H

( f ), which impulse re-

sponse is h

RRC

(t) ∗h

cdc

(t). This block has two main

goals: perform RRC ﬁltering and ideally compensate

chromatic dispersion using the ﬁlter with impulse re-

sponse h

cdc

(t). The ideal balanced photodetectors,

placed at the 2x4 90

◦

hybrid output, are modeled as

square-law devices. Hence, following the conﬁgura-

tion of the coherent receiver depicted in Figure 3, I

(t)

and I

(t) are expressed by

(t) = ℜ{E

(t)E

∗

(t) + E

(t)E

∗

(t)+

ASE

(t)E

∗

(t)}∗h

(t)

(10a)

(t) = ℑ{E

(t)E

∗

(t) + E

(t)E

∗

(t)+

ASE

(t)E

∗

(t)}∗h

(t)

(10b)

where ℜ{Z} and ℑ{Z} are, respectively, the real and

the imaginary parts of a complex number Z, with the

complex conjugate represented by Z

∗

By examining Equations (10), we identify

three terms: the desired received electrical signal

(t)E

∗

(t), the ICXT-LO beating term E

(t)E

∗

(t)

and the ASE-LO beating term E

ASE

(t)E

∗

(t).

The performance of the SDM optical system rep-

resented in Figure 2 is assessed by evaluating the BER

of the detected currents I

(t) and I

(t) at the optimum

sampling time instants and the OSNR penalty due to

the presence of ICXT. The OSNR penalty quantiﬁes

the impact of the ICXT on the performance of the

coherent receiver and is deﬁned as the ratio between

the required OSNR with ICXT that leads to a BER

Figure 3: Model of a coherent receiver with electrical RRC

ﬁltering and ideal dispersion compensation.

Impact of Inter-core Crosstalk on the Performance of Multi-core Fibers-based SDM Systems with Coherent Detection

of 10

−3

and the required OSNR without ICXT for the

same BER. The ICXT level that leads to a 1 dB OSNR

penalty is a typical reference to evaluate the tolerance

to ICXT.

3 VALIDATION OF THE ICXT

TRANSFER FUNCTION

The validation of the transfer function F(ω) is per-

formed through the comparison between the empir-

ical estimations of the mean and variance of the

amplitude of the ICXT transfer function, XTTF(ω),

deﬁned in (Cartaxo et al., 2016), and the mean and

variance obtained by simulation.

The XTTF(ω) is obtained from the ﬂuctuations

after the photodetection of the crosstalk ﬁeld at the

output of core n, and is given by (Cartaxo et al., 2016)

XTTF(ω) =

∗

(0)F(ω) +F(0)F

∗

(−ω)]

(11)

Since E[|XTTF(0)|] = N|K

, with E[ ] denoting the

expected operator value. the normalized XTTF, X(ω),

is deﬁned by X(ω) =XTTF(ω)/



N|K



The empirical expressions of the mean of the

|X(ω)| is given by (Cartaxo et al., 2016)

E[|X(ω)|] =



∞

+ sinc



ωS

2π





−x

∞

cos



2πc



(12)

where x

∞

≈ 0.5549 (Cartaxo et al., 2016) and sinc(x)

is the sinc function, deﬁned by sin(πx)/(πx) (Carlson

and Crilly, 2009). The variance of |X(ω)| is obtained

from (Cartaxo et al., 2016)

Var

{

|X(ω)|

}

−x

∞

+ sinc



ωS

2π





∞

cos



2πc



(13)

Figure 4 shows the comparison of the numer-

ical simulation results for the mean and variance of

the normalized XTTF amplitude with those estimated

from the empirical model. The numerical simulations

consider 10

samples of ICXT signals with N = 1000

PMPs, which are randomly distributed along the MCF

following a uniform distribution. The parameters for

the MCF are: L=25 km, λ= 1550 nm , ∆D

= 0,

= {25, 125} ps and D

= {0, 17} ps/nm/km. The

empirical estimations of the mean and variance of

X(ω) are marked with solid lines, while the mean

and variance of X(ω) obtained through simulation are

0 5 10 15 20 25 30 35 40

0.2

0.4

0.6

0.8

1.2

1.4

1.6

Modulation Frequency [GHz]

Mean of normalized XTTF amplitude

=1 ps/km D

=0 (12)

=1 ps/km D

=17 ps/nm/km (12)

=5 ps/km D

=17 ps/nm/km (12)

=1 ps/km D

=0 (S)

=1 ps/km D

=17 ps/nm/km (S)

=5 ps/km D

=17 ps/nm/km (S)

(a)

0 5 10 15 20 25 30 35 40

0.2

0.4

0.6

0.8

1.2

1.4

Modulation Frequency [GHz]

Variance of normalized XTTF amplitude

=1 ps/km D

=0 (13)

=1 ps/km D

=17 ps/nm/km (13)

=5 ps/km D

=17 ps/nm/km(13)

=1 ps/km D

=0 (S)

=1 ps/km D

=17 ps/nm/km (S)

=5 ps/km D

=17 ps/nm/km (S)

(b)

Figure 4: Comparison between the theoretical mean (Equa-

tion (12)) and variance (Equation (13)) and simulations (S)

results of the (a) mean and (b) variance of the normalized

XTTF as a function of the modulation frequency.

shown with dashed lines. Figure 4 shows an excellent

agreement between the theoretical and the simulation

results for the mean and the variance of X(ω), hence,

showing that the simulation model is properly imple-

mented.

4 PERFORMANCE ANALYSIS

In this section, we assess the performance of the

MCF-based SDM system with optical coherent detec-

tion using MC simulation. The performance metrics

used in this work are the BER and the OSNR pen-

alty due to the ICXT. The BER is estimated using

direct error counting (DEC) and the BER is given by

/(N

), where N

is the number of counted er-

rors at the decision circuit input, N

is the number of

bits per symbol given by log

(M), N

is the number

of simulated QAM symbols and N

is the number of

iterations of the MC simulation.

Table 1 presents the parameters used in MC simu-

lation in order to assess the performance of the MCF-

PHOTOPTICS 2018 - 6th International Conference on Photonics, Optics and Laser Technology

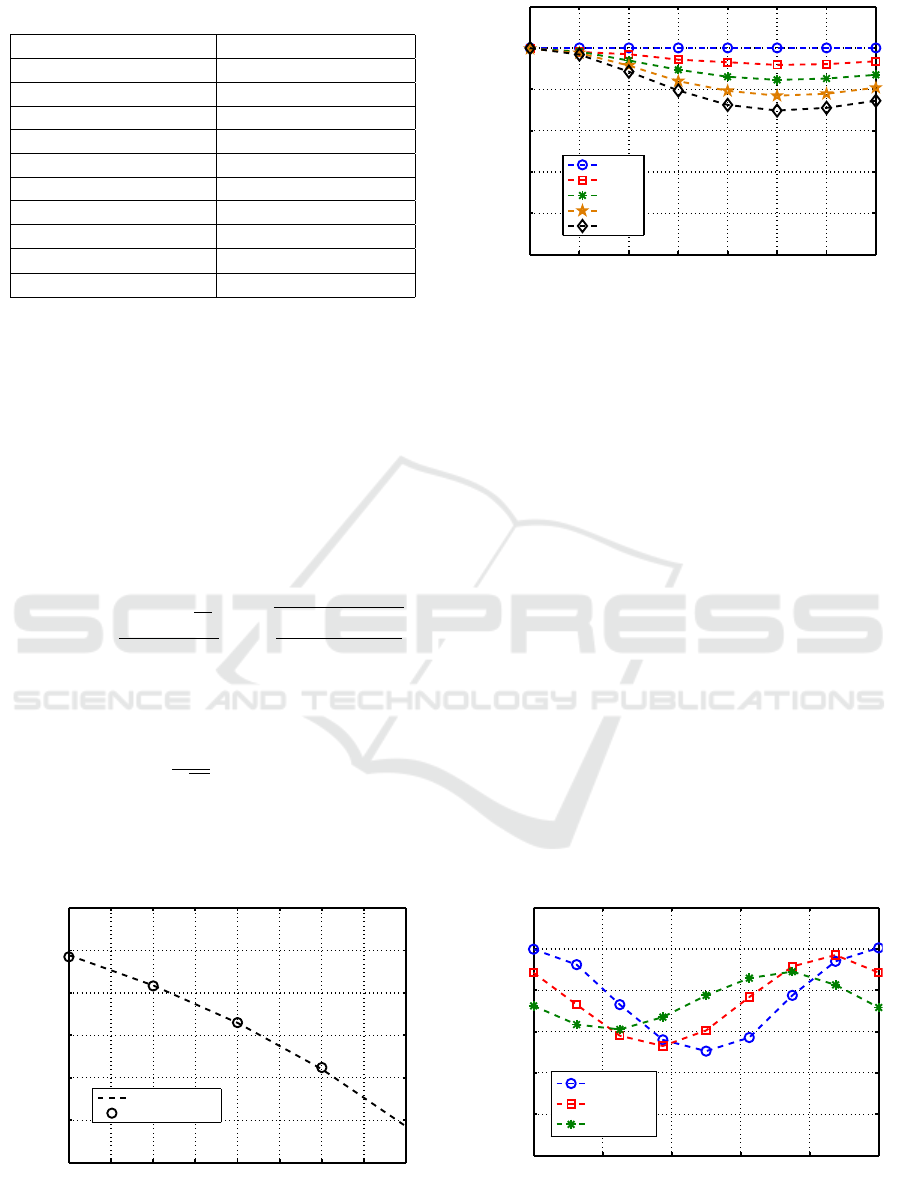
Table 1: Parameters of the MCF-based SDM system.

Parameter Value

[Gbps] 56

β {0, 0.25, 0.5, 0.75, 1}

[0, 1]

[ps] [0, 35]

Modulation format 4-QAM

[ps] 35.7

Number of PMPs 1000

OSNR

[dB] 10.3

Number of symbols N

Counted errors N

based SDM system with optical coherent detection in

presence of ASE noise and ICXT. OSNR

is the re-

quired OSNR for a BER of 10

−3

in absence of ICXT,

i.e. this parameter is the reference OSNR to quantify

the OSNR penalty due to the ICXT.

The validation of the simulation model of the co-

herent receiver presented in Figure 3 must be per-

formed previously without ICXT. Figure 5 depicts

the BER as a function of the OSNR estimated using

DEC (circles) and the theoretical BER (dashed line),

BER

QAM

, as a function of the OSNR obtained using

(Essiambre et al., 2010)

BER

QAM

= 4

(1 −1/

√

log

6 ·OSNR ·B

OSA

(M −1)R

(14)

where Q(x) is the Q function, which is given by

(Carlson and Crilly, 2009)

Q(x) =

√

2π

+∞

−t

dt (15)

OSA

is the optical spectrum analyzer bandwidth,

deﬁned as 12.5 GHz (Hui and O’Sullivan, 2008) in

which the OSNR is estimated, and R

is the symbol

8 8.5 9 9.5 10 10.5 11 11.5 12

−4.5

−4

−3.5

−3

−2.5

−2

−1.5

OSNR [dB]

log

(BER)

Without ICXT (T)

Without ICXT (S)

Figure 5: log

(BER) as a function of the OSNR obtained

through simulation (circles) and theoretically (dashed line)

for the 4-QAM modulation format without ICXT.

0 5 10 15 20 25 30 35

0.2

0.4

0.6

0.8

1.2

[ps]

Normalized Variance of the Detected ICXT

β = 0

β = 0.25

β = 0 5

β = 0.75

β = 1

Figure 6: Normalized variance of the detected ICXT as a

function of the skew, considering β = {0,0.25, 0.5,0.75,1}

and τ

= 0.

rate. From Figure 5, a perfect agreement between

the DEC estimation and the theoretical BER is no-

ticed, which validates the coherent receiver simula-

tion model in a back-to-back conﬁguration in pres-

ence of ASE noise and without ICXT.

In the following, we analyze the variance of the

current due to the ICXT at the decision circuit input.

Hence, we estimate the variance of the detected ICXT

using the MC simulation, for different skews, time

misalignments between the interfered and interfering

core signals, and roll-off factors.

Figure 6 depicts the variance of the detected

ICXT, normalized to N|K

, as a function of the

skew and the roll-off factors of 0, 0.25, 0.5, 0.75 and

1 estimated through MC simulation.

Firstly, we consider a perfect alignment between

the interfered and the interfering signals, i.e. τ

= 0,

in order to analyze solely the inﬂuence of the skew

on the ICXT variance. Figure 6 shows that the vari-

ance of the detected ICXT as a function of the skew is

constant when β is 0. For higher roll-off factors, and

considering 0 ≤ S

≤ 35 ps, the lowest ICXT vari-

0 0.2 0.4 0.6 0.8 1

0.2

0.4

0.6

0.8

1.2

Normalized Variance of the Detected ICXT

= 0 ps

= 10 ps

= 20 ps

Figure 7: Normalized variance of the detected ICXT as a

function of the temporal misalignment considering β = 1

and S

of 0, 10 and 20 ps.

Impact of Inter-core Crosstalk on the Performance of Multi-core Fibers-based SDM Systems with Coherent Detection

ance is reached when the skew is 25 ps. Figure 6 also

allows to conclude that the increase of the roll-factor

and skew leads to a reduced ICXT variance and, con-

sequently, lower degradation of the coherent receiver

performance due to the ICXT.

Figure 7 depicts the normalized variance estim-

ated through MC simulation as a function of the tem-

poral misalignment between the interfered and inter-

fering signals considering a roll-off factor of 1.

Figure 7 shows that the minimum and the max-

imum value of the ICXT variance are spaced by 0.5T

Figure 7 also shows that the change of the skew leads

to a temporal shift of the time instants that lead to the

minimum and the maximum ICXT variances and also

to a reduction of the difference between the maximum

and minimum ICXT variances.

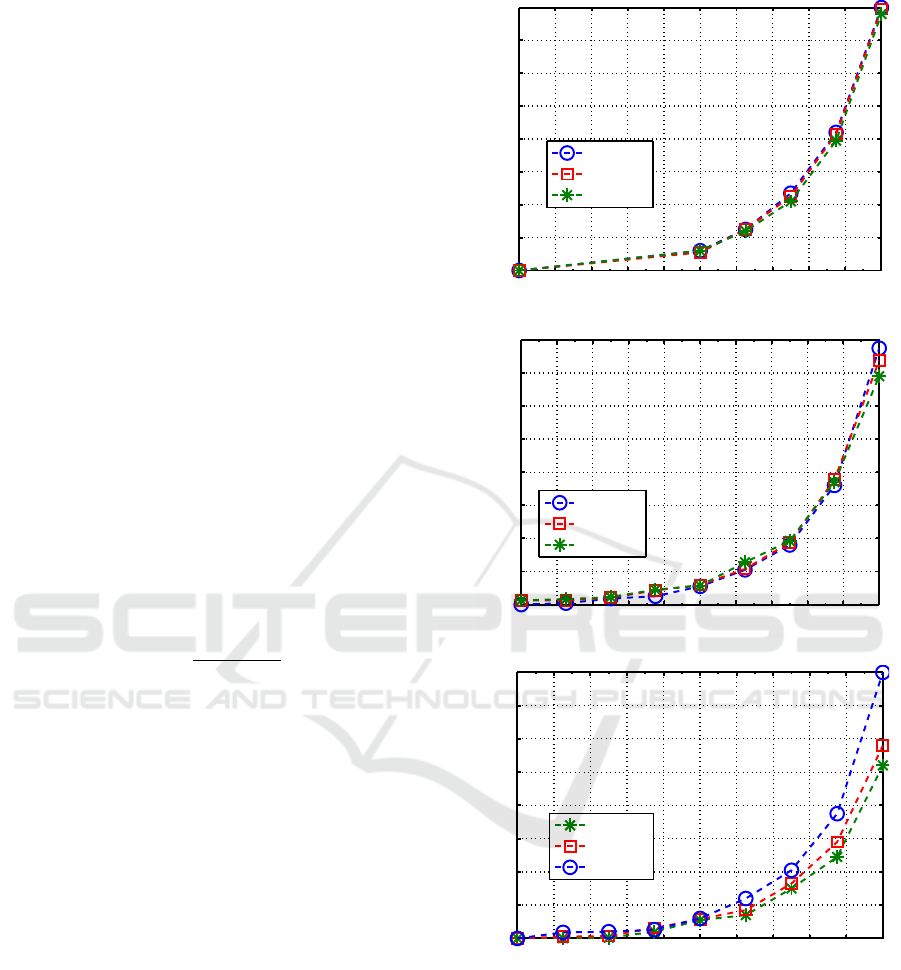
Next, we evaluate the penalty on the required

OSNR that leads to a BER of 10

−3

due to the ICXT.

Figure 8 depicts the OSNR penalty due to the ICXT

as a function of the ICXT level for the 4-QAM modu-

lation format, considering τ

= 0 and a roll-off factor

of (a) 0, (b) 0.5 and (c) 1 for different values of skew.

The chosen values of skew are based on the results

obtained in Figure 6. The ICXT level, X

, is deﬁned

as the ratio between the ICXT signal power and the

interfered core signal power at the coherent receiver

input and is given by

N|K

(16)

Figure 8(a) shows that, when the roll-off factor is

0, the variation of the skew has no inﬂuence on the

OSNR penalty. This conclusion is in agreement with

the results of Figure 6, since when the roll-factor is

0, the variance of the detected ICXT is independent

of the skew. Moreover, Figure 8 allows to conclude

that, when the interfering signal is aligned with the

interfered signal, i.e. τ

= 0, the OSNR penalty for

a given ICXT level decreases for higher skew. For

instance, in Figure 8(c), considering an ICXT level

of −17 dB and β = 1, the OSNR penalty is 0.9, 0.7

and 0.6 dB for a skew of 0, 15 and 25 ps, respect-

ively. These results are in agreement with the conclu-

sions drawn from the analysis of Figure 6, where it

is observed that the variance of the detected ICXT is

lower when S

is increased. Figure 8(c) also allows

to conclude that a roll-off factor of 1 and a skew of

25 ps leads to a tolerance gain to the ICXT of 1.7 dB,

as the ICXT level for a 1 dB OSNR penalty with a

null skew is −16.7 dB, while, for a skew of 25 ps, the

ICXT level for the same OSNR penalty is −15 dB.

−35 −33 −31 −29 −27 −25 −23 −21 −19 −17 −15

0.2

0.4

0.6

0.8

1.2

1.4

1.6

ICXT level [dB]

OSNR penalty [dB]

= 0

= 15 ps

= 25 ps

(a) β = 0.

−35 −33 −31 −29 −27 −25 −23 −21 −19 −17 −15

0.2

0.4

0.6

0.8

1.2

1.4

1.6

ICXT level [dB]

OSNR penalty [dB]

= 0

= 15 ps

= 25 ps

(b) β = 0.5.

−35 −33 −31 −29 −27 −25 −23 −21 −19 −17 −15

0.2

0.4

0.6

0.8

1.2

1.4

1.6

ICXT level [dB]

OSNR penalty [dB]

= 25 ps

= 15 ps

= 0

Figure 8: OSNR penalty due to the ICXT as a function of

the ICXT level considering the 4-QAM modulation format,

= 0 and (a) β = 0, (b) β = 0.5 and (c) β = 1, and for

= 0, S

= 15 ps and S

= 25 ps.

5 CONCLUSION

In this work, we assess the impact of ICXT on the

BER and OSNR penalty of a MCF communication

system with optical coherent detection for signals

PHOTOPTICS 2018 - 6th International Conference on Photonics, Optics and Laser Technology

with 4-QAM modulation. The impact is assessed for

different skew between the signals transmitted in the

interfered and interfering cores, different time mis-

alignments and by varying the signals roll-off factors.

To complement our results, the variance of the detec-

ted ICXT is also studied.

Our results show that the roll-off factor of the RC

pulse shape and the skew has a signiﬁcant inﬂuence

on the variance of the detected ICXT. Considering a

null roll-off factor, the variance of the detected ICXT

is constant as a function of the skew. In presence

of skew and with a roll-off factor higher than 0, the

variance of the detected ICXT signal decreases with

the increase of the roll-off factor. For a roll-off factor

higher than 0 and a skew of 25 ps, the variance of the

ICXT reaches its lowest value.

The temporal misalignment has also inﬂuence on

the variance of the ICXT signal at the coherent re-

ceiver. Our results reveal that for a given skew, the

variation of the temporal misalignment leads to a ”si-

nusoidal” behavior of the detected ICXT variance.

When the skew is reduced, the difference between

the highest and the lowest variance becomes smal-

ler. Without skew, our results reveal that the OSNR

penalty is independent of the roll-off factor and the 1

dB OSNR penalty is reached with a −16.7 dB ICXT

level. With skew between the cores, the ICXT level

that leads to a 1 dB OSNR penalty is higher for skew

of 25 ps: for β = 0, the ICXT level is −16.7 dB; for

β = 1, the ICXT level for the same OSNR penalty is

−15 dB, due to the reduction of the ICXT variance.

ACKNOWLEDGEMENTS

This work was supported in part by Fundac¸

ao para

a Ci

encia e a Tecnologia (FCT) from Portugal un-

der the project of Instituto de Telecomunicac¸

oes

AMEN-UID/EEA/50008/2013 and the ISCTE-IUL

Merit Scholarship BM-ISCTE-2016.

REFERENCES

Agrawal, G. (2010). Fiber-Optic Communication Systems.

John Wiley & Sons, 4 edition.

Carlson, A. and Crilly, P. (2009). Communication Systems.

McGraw-Hill, Boston, 5. ed edition.

Cartaxo, A. and Alves, T. (2017). Discrete Changes Model

of Inter-core Crosstalk of Real Homogeneous Multi-

core Fibers. J. Lightwave Technol., 35(12):2398–

2408.

Cartaxo, A. et al. (2016). Dispersion Impact on

the Crosstalk Amplitude Response of Homogeneous

Multi-Core Fibers. IEEE Photon. Technol. Lett.,

28(17):1858–1861.

Essiambre, R. et al. (2010). Capacity limits of optical ﬁber

networks. J. Lightwave Technol., 28(4):662–701.

Fini, J. M. et al. (2010). Statistics of Crosstalk in Bent Mul-

ticore Fibers. Opt. Express, 18(14):15122–15129.

Hayashi, T. et al. (2011). Design and Fabrication of Ultra-

Low Crosstalk and Low-Loss Multi-core Fiber. Opt.

Express, 19(17):16576–16592.

Hayashi, T. et al. (2013). Physical Interpretation of Inter-

core Crosstalk in Multicore Fiber: Effects of Mac-

robend, Structure Fluctuation, and Microbend. Opt.

Express, 21(5):5401.

Hayashi, T., Sasaki, T., and Sasaoka, E. (2014). Behavior

of Inter-Core Crosstalk as a Noise and Its Effect on Q

-Factor in Multi-Core Fiber. IEICE Trans. Commun,

(5):936–944.

Hui, R. and O’Sullivan, M. (2008). Fiber Optic Measure-

ment Techniques. Elsevier Academic Press.

Jeruchim, M., Balaban, P., and Shanmugan, K. (2000). Sim-

ulation of communication systems: modeling, method-

ology and techniques. Kluwer Academic Publishers,

Norwell, MA, 2nd edition.

Klaus, W. et al. (2017). Advanced Space Division Multi-

plexing Technologies for Optical Networks. J. Opt.

Commun. Netw., 9(4):C1–C11.

Morioka, T. (2017). High-Capacity Transmission Using

High-Density Multicore Fiber. In Optical Fiber Com-

munication Conference, page Th1C.3.

Puttnam, B. J. et al. (2015). 2.15 Pb/s Transmission Us-

ing a 22 Core Homogeneous Single-Mode Multi-Core

Fiber and Wideband Optical Comb. In European Con-

ference on Optical Communication (ECOC), pages 1–

Puttnam, B. J. et al. (2017). High Capacity Transmission

Systems Using Homogeneous Multi-Core Fibers. J.

Lightwave Technol., 35(6):1157–1167.

Rademacher, G. et al. (2017a). Crosstalk Dynamics in

Multi-Core Fibers. In Opt. Express, pages 12020–

12028.

Rademacher, G. et al. (2017b). Time-Dependent Crosstalk

from Multiple Cores in a Homogeneous Multi-Core

Fiber. In Optical Fiber Communications Conference

and Exhibition (OFC), pages 1–3.

Saitoh, K. and Matsuo, S. (2016). Multicore Fiber Techno-

logy. J. Lightwave Technol., 34(1):55–66.

Takara, H. et al. (2012). 1.01-Pb/s (12 SDM/222 WDM/456

Gb/s) Crosstalk-managed Transmission with 91.4-

b/s/Hz Aggregate Spectral Efﬁciency. In European

Conference and Exhibition on Optical Communica-

tion (ECOC), page Th.3.C.1.

Xia, T. and Wellbrock, G. (2013). Commercial 100-Gbit/s

Coherent Transmission Systems. In Optical Fiber

Telecommunications, chapter 2, pages 45 – 82. Aca-

demic Press, Boston, 6 edition.

Zhu, B. et al. (2011). 112-Tb/s Space-Division Multiplexed

DWDM transmission with 14-b/s/Hz Aggregate Spec-

tral Efﬁciency over a 76.8-km Seven-Core Fiber. Opt.

Express, 19(17):16665–16671.

Impact of Inter-core Crosstalk on the Performance of Multi-core Fibers-based SDM Systems with Coherent Detection