
Reducing Disruptive Effects of Service Interruptions in Appointment
Scheduling
Matthias Deceuninck
1
, Stijn De Vuyst
1
and Dieter Fiems
2
1
Department of Industrial Systems Engineering and Product Design, Ghent University,
Technologiepark 903, Zwijnaarde, Belgium
2
Department of Telecommunication and Information Processing, Ghent University, Gent, Belgium
Keywords:
OR in Health Services, Appointment Scheduling, Stochastic Programming.
Abstract:
This paper considers appointment scheduling for outpatient services when the service of scheduled patients
can be interrupted by emergency arrivals. We consider a single doctor who consults K patients during a
fixed-length session. Each patient has been given an appointment time during the session in advance. Our
evaluation approach aims at obtaining accurate predictions at a very low computational cost for the waiting
times of the patients and the idle time of the doctor. To this end, we investigate a modified Lindley recursion
in a discrete-time framework. We assume general, possibly distinct, distributions for the patient’s consultation
times and allow for individual no-show probabilities. This fast evaluation method is then used in a local search
algorithm to provide insights into scheduling with service interruptions. Numerical examples show that this
method outperforms simulation optimization and naive approaches in terms of cost and running time.
1 INTRODUCTION
Due to the demographic development and increasing
need of health care services, health care providers are
faced with certain operational challenges. In order to
give timely medical access to all patients while still
maintaining a high level of service, hospitals need to
improve the efficiency of their processes. One of the
tools to achieve this is the design of the appointment
system. A good and effective appointment schedul-
ing system tries to balance two important factors: the
waiting times experienced by the patients and the idle-
ness experienced by the service provider. Scheduling
appointments closely together leads to longer waiting
times but less risk of idleness for the doctor. On the
other hand, spacing appointments far apart reduces
the waiting times at the expense of increased idleness
of the doctor. This dilemma becomes even more com-
plex when we also consider emergency arrivals which
have to be served as soon as possible.
In this paper, we investigate the optimization of
appointment schedules with heterogeneous patients
in the presence of no-shows and service interrup-
tions. We primarily focus on service interruptions that
are caused by emergency arrivals and require non-
preemptive priority. This contribution builds upon
the fast procedures to evaluate patient schedules un-
der uncertainty introduced in Lau and Lau (2000) and
De Vuyst et al. (2014). We then include this fast
evaluation method in a local search algorithm and
compare our results with simulation optimization and
naive methods.
The outline of this paper is as follows. In the next
section, we review the relevant literature. In Section
3 we introduce our mathematical model. The calcu-
lations of the performance measures are presented in
Section 4. Section 5 demonstrates our approach and
presents some numerical results. Section 6 concludes
and suggests ideas for future work.
2 LITERATURE REVIEW
An overview of the literature on appointment schedul-
ing can be found in the survey papers Cayirli and Ve-
ral (2003) and Gupta and Denton (2008). While being
prevalent in many service systems, limited attention
has been given to service interruptions. In what fol-
lows we discuss contributions on service interruptions
and emergency arrivals.
Fiems et al. (2007) developed a discrete-time
queueing model with preemptive service of emer-
Deceuninck, M., Vuyst, S. and Fiems, D.
Reducing Disruptive Effects of Service Interruptions in Appointment Scheduling.
DOI: 10.5220/0006624802390246
In Proceedings of the 7th International Conference on Operations Research and Enterprise Systems (ICORES 2018), pages 239-246
ISBN: 978-989-758-285-1
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
239

gency patients and loss of work. Service times are
assumed to be deterministic and steady-state analysis
is carried out to investigate the impact on the wait-
ing time of regularly scheduled patients in a radiology
department. In Begen and Queyranne (2011), a non-
preemptive approach is discussed in which emergency
jobs may arrive during the processing of another job.
The approach considered in the paper falls short in
taking into account emergency jobs that arrive during
idle time. This can be a restriction if the service times
of emergency patients are longer than those of sched-
uled patients. In addition, there are also limitations on
the number of emergency jobs that can arrive during
the processing of a job.
Luo et al. (2012) proposed a model where ser-
vice interruptions have an exponentially distributed
duration and occur according to a, possibly non-
homogeneous, Poisson process. Additionally, the
service times of scheduled patients are assumed to
be identically distributed according to an exponen-
tial distribution. Their results indicate that signifi-
cant savings can be made by including interruptions
in the evaluation and optimization model. They also
report that when the interruption rate is high the op-
timal policy has a monotone structure rather than
a “dome-shape”. Klassen and Yoogalingam (2013)
used a simulation optimization approach to study the
effects of service interruptions on outpatient appoint-
ment scheduling. They report that a “plateau-dome”
scheduling rule is robust for low interruption rates.
The present study most closely relates to Koeleman
and Koole (2012), where the scheduling problem is
studied for homogeneous patients.
Furthermore, the problem of service failures and
service vacations is also studied in the traditional
queueing literature. The vast majority of these papers
however conduct a steady-state analysis, which does
not really fit for the appointment scheduling prob-
lem where only a limited number of services are per-
formed. For example, Fiems et al. (2004) considers
a discrete-time queueing model in which the service
process is subject to interruptions which are modelled
as an on–off-process with geometrically distributed
on-times and generally distributed off-times.
Finally, mixed arrival processes are also studied
in Kolisch and Sickinger (2008) and Sickinger and
Kolisch (2009). Besides regularly scheduled patients
and emergency patients, these studies also consider
unscheduled inpatients who are available for treat-
ment at any time during the day. Kortbeek et al.
(2014) considers a non-stationary stream of unsched-
uled patients without priority (walk-ins). Their goal is
to balance the access time of scheduled patients and
the waiting time on the day of service.
3 MODEL DESCRIPTION
In this section we briefly describe the methodology
used in this paper. We adopt the notation of De Vuyst
et al. (2014), which provides an evaluation method
for the appointment scheduling problem under the im-
plicit assumption that there are no interruptions.
3.1 Mathematical Model
We consider a consultation session of a single doctor,
which is divided into T slots of equal length ∆. The
session spans a time period of [0,t
max
]. Prior to this
session, a practitioner has to choose K, the number
of patients to be scheduled in this session and subse-
quently needs to allocate appointment times to each
of these K patients. Let τ
k
denote the slot that is as-
signed to the appointment of the kth patient. A sched-
ule is then fully defined by the vector τ = (τ
1
, τ
2
, . . . ,
τ
K
). We assume that all patients either arrive punc-
tually at their appointed time or do not arrive at all
(no-show). Let p
k
denote the probability that the kth
patient does not show up. We assume that the consul-
tation times form a sequence of independent random
variables. Let s
k
(n) = Pr[S
k
= n] denote the proba-
bility mass function of the consultation time S
k
of the
kth patient.
Emergency arrivals are modelled by a sequence
of independent Bernoulli random variables {N
t
}, t =
0,. .. ,T − 1 with constant event probability α, N
t
= 0
if no emergency arrived at slot t. Here, we assume
that whenever an emergency patient arrives, he gets
non-preemptive priority over the regularly scheduled
patients. That is, once started, the service of a pa-
tient needs to be carried out till completion. If there
are multiple emergencies, they are served in order.
The inter-arrival times of emergencies thus consti-
tute a series of geometrically distributed random vari-
ables. Finally, the consultation times of emergen-
cies are modelled as a series of i.i.d. positive ran-
dom variables with common probability mass func-
tion s
e
(n) = Pr[S
e
= n].
The fact that each patient can have an individual
service time distribution and no-show probability al-
lows us to take prior knowledge about the patients into
account. For example, for each appointment request,
the scheduler can estimate the service time distribu-
tion based on the patient’s characteristics like age and
medical record. Similarly, no-show probabilities can
be estimated based on the type of service, appoint-
ment lead time and past no-show record.
Effective Service Times. When emergencies occur
during the service time of a patient, the waiting time
ICORES 2018 - 7th International Conference on Operations Research and Enterprise Systems
240

t
1
t
2
S
1
S
(1)
e
S
(2)
e
B
1
Figure 1: Illustration of the effective service time approach
when there are two emergency arrivals, one at time t
1
and
one at time t
2
.
of the next patient can be calculated by means of an
effective service times approach. Such an approach
replaces the service time of a patient by an effec-
tive service time which not only includes the patient’s
own service time, but also all time dedicated to emer-
gency patients that arrived while the patient was be-
ing treated, as well as all service of emergency pa-
tients that arrived while an emergency patient was be-
ing treated, etc. Formally, the effective service time
B
k
starts when the patient’s service time starts, and
ends when the doctor becomes available for the next
scheduled patient.
Let S
k
(z) be the probability generating function of
the (discretised) service time S
k
of the kth patient and
S
e
(z) that of the consultation time S
e
of an emergency
patient, then the generating function of the effective
service time B
k
of the kth patient is
B
k
(z) = S
k
((αB(z) + 1 − α)z)
with B(z) the probability generating function of the
time to process a single emergency as well as all
emergencies that arrived while processing this emer-
gency, etc.
Because in every slot of the service time of the
emergency there is a probability α to have a new
emergency which needs to be processed, we have the
following functional equation for the generating func-
tion B(z),
B(z) = S
e
((αB(z) + 1 − α)z) (1)
We provide the derivation of (1) in Appendix. We
thus have,
E[B] =
E[S
e
]
1 − α E[S
e
]
, (2)
E[B
2
] =
E[S
2
e
](1 − α
2
E[S
e
])
(1 − αE[S
e
])
3
(3)
and
E[B
k
] = E[S
k
](1 + αE[B]), (4)
E[B
2
k
] = E[S
2
k
](1 + αE[B])
2
− E[S
k
](α
2
E
2
[B] − αE[B
2
])
(5)
We need the probabilities b
k
(n) corresponding to
the generating function B
k
(z) as well as the corre-
sponding moments. To obtain these, we first have to
solve for the probabilities b(n) corresponding to gen-
erating function B(z). Since emergencies are indepen-
dent of each other, the probabilities can be found by
applying the property of composite generating func-
tions:
B(z) = S
e
((αB(z) + 1 − α)z)
=
∞
∑
m=0
s
e
(m) ((αB(z) + 1 − α)z)
m
The nth coefficient in the series expansion of B(z) is
the probability b(n) equal to
b(n) =
n
∑
m=0
s
e
(m) Pr[
m
∑
k=0
B
k
A
k
= n − m]
=
n
∑
m=0
s
e
(m) x
∗
m
(n − m)
with x
∗
m
(n) recursively defined by
x
∗
m
(n) =
(
1
{n=0}
if m = 0,
∑
n
`=0
x(n − `) x
∗
m−1
(`) otherwise.
x(n) =
(
(1 − α) + αs
e
(0) if n = 0,
b(n) α otherwise.
Analogously, for the nth probability of the effective
consultation time we find
b
k
(n) =
n
∑
m=0
x
∗
m
(n − m) s
k
(m)
Note that we need the emergencies to be independent
of the scheduled patients as well as independent of
each other.
Now, consider the situation where the doctor has
finished the consultation of patient k and that there
are no patients left in the waiting room. Without the
possibility of emergencies arriving to the system, we
know that the next scheduled patient, patient k + 1,
will experience zero waiting time. This is no longer
true with emergencies since an emergency may arrive
prior to the arrival of patient k+1. Since the idle times
are bounded by the inter-arrival time, we can calculate
the distribution of the waiting time of patient k + 1.
Let g(n|i) denote this distribution, given that the idle
time has length i, then
g(n|i) = α b(n + i − 1) + α
i−1
∑
`=0
b(`) g(n|i − ` − 1)
+ (1 − α) g(n|i − 1)
where the first term corresponds to the case an emer-
gency period starts and ends after the idle time, the
Reducing Disruptive Effects of Service Interruptions in Appointment Scheduling
241

second to the case where an emergency period starts
and ends before the end of the idle time and the last
term corresponds to the case where no emergency ar-
rives during the idle period. We are able to do the
same for the moments of the waiting time, after an
idle time. Let E[G
q
i
] be the qth moment of the waiting
experienced after an idle time of length i, then
E[G
q
i
] = αE[B
q
1
{B>i}
] + α
i−1
∑
`=0
b(`)E[G
q
i−`−1
]
+ (1 − α) E[G
q
i−1
],
where the first expectation can easily be rewritten in
terms of E[B] and the probabilities b(n).
4 PERFORMANCE MEASURES
In this section we show how to evaluate the perfor-
mance of a given schedule, i.e. assuming the appoint-
ment times τ are fixed. We consider the following
measures: the patient waiting times, the doctor’s idle
time and the session overtime.
First of all, we introduce a virtual arrival instant
τ
K+1
at the end of the session. This will enable us
to calculate the overtime of the service provider (see
Section 4.3). Furthermore, we introduce a notation
for the time between consecutive appointment times:
a
k
= τ
k+1
− τ
k
, k = 1,.. . , K with a
0
= τ
1
. Note that,
in accordance with this definition, a
K
denotes the time
between the appointment time of the last patient and
the end of the session.
4.1 Waiting Times
Let the waiting time W
k
of the kth patient be the num-
ber of slots between the arrival of this patient and the
start of his consultation. Consecutive waiting times
then relate as
E[W
q
k+1
] = −`
(q)
k
+
q
∑
r=0
q−r
∑
m=0
q
r
q − r
m
E[B
m
k
]
× (−a
k
)
q−r−m
E[W
(r)
k
] +
a
k
∑
i=1
d
k
(i)E[G
q
i
],
with
`
(q)
k
=
a
k
−1
∑
r=0
r
∑
m=0
b
k
(r − m) w
k
(m) (r − a
k
)
q
,
and with d
k
(i), the probability of an idle time of length
i,
d
k+1
(i) =
a
k
−i
∑
r=0
b
k
(a
k
− i − r) w
k
(r) .
The probabilities of the waiting times are denoted
by w
k
(n) = Pr[W
k
= n] and relate as
w
k+1
(n) =
n+a
k
∑
m=0
b
k
(n + a
k
− m) w
k
(m)
+
a
k
∑
m=0
a
k
−m
∑
`=0
b
k
(`) w
k
(m) g(n|a
k
− ` − m) ,
if n > 0 and
w
k+1
(0) =
a
k
∑
m=0
a
k
−m
∑
`=0
b
k
(`) w
k
(m) g(0|a
k
− ` − m) .
The moments and probabilities of the first patients are
treated separately. Note that it is possible that be-
tween the start of the session and the service of the
first scheduled patient, emergency patients arrive and
thus extend the waiting time of the first patient
E[W
q
1
] = E[G
q
τ
1
],
w
1
(n) = g(n|τ
1
).
Note that the calculations are also valid for a pre-
emptive interruption if we assume that the waiting
time is defined as the time the patient has to wait un-
til the treatment starts and if there is no loss of work.
That is, if we exclude any intermediate waiting time
of a preemptive treatment of emergency patients.
4.2 Effective Idle Times
We define the idle time I
k
of the kth patient as the time
the doctor has to wait between the end of the service
of the kth patient and the start of the service of the
(k +1)th patient excluding any service of emergencies
during this period of time. The qth moment of this
effective idle time is then equal to
E[I
q
k
] =
a
k
−1
∑
r=0
r
∑
m=0
b
k
(r − m) w
k
(m) Z
q
k
(a
k
− r),
with Z
k
(i) denoting the expected effective idle time
given an idle time of length i,
Z
q
k
(i) =
i
∑
n=1
z
k
(n,i)n
q
and,
z
k
(n,i) = (1 − α) z
k
(n − 1, i − 1)
+ α
i−1
∑
m=1
z
k
(n,i − m) b(m)
+ α z
k
(n − 1, 0)
1 −
l−1
∑
m=1
b(m)
.
ICORES 2018 - 7th International Conference on Operations Research and Enterprise Systems
242

4.3 Overtime
The overtime O, which is the amount of time that the
service provider works beyond the previsioned ses-
sion length, can be calculated as the waiting time of
the virtual patient. Indeed, if a patient were to be
scheduled at the end of the session, this patient must
wait till the overtime is completed. Hence, we find,
E[O
q
] = E[W
q
K+1
].
4.4 Local Search Algorithm
Because of the sheer number of possible schedules,
a heuristic method is required to find a good solu-
tion in a reasonable amount of time. Other studies in
the literature have shown that local search procedures
perform well for this type of problem (Kaandorp and
Koole, 2007; Koeleman and Koole, 2012). The main
idea of local search algorithms is to perform an itera-
tive search throughout the solution space, by contin-
uously evaluating and making small adjustments to a
solution. The local search algorithm used in this study
uses tabu search as a secondary heuristic and uses the
search neighborhood N which is defined as,
N (τ ) = {τ
0
: (∃!k : τ
0
k
= τ
k
± 1 , τ
0
`
= τ
`
,` 6= k)}.
The algorithm is initialized with the best candidate
solution from a reference set containing diverse so-
lutions. The goal of the local search algorithm is to
determine the vector of appointment times τ which
minimizes a certain objective function. For simplicity,
we choose an objective function which only includes
the first moments of the performance measures:
TC(τ ) = c
W
E[
∑
k
W
k
] + c
I
E[
∑
k
I
k
] + c
O
E[O], (6)
where c
W
, c
I
and c
O
respectively denote the wait-
ing, idle and overtime cost per time unit (e.g. dol-
lars per time unit). Note that the relative importance
of each term greatly depends on the type of service
and organisation. The overtime cost c
O
for example
depends on the equipment and the number of assis-
tants that are needed. In most environments, a greater
weight will be assigned to idle time and overtime
since the doctor’s time is typically valued higher than
the patient’s time.
5 NUMERICAL RESULTS
In this section, we report the results of our numerical
study. In particular, we focus on studying the effects
of service interruptions and emergency arrivals on pa-
tient scheduling and the performance of our heuristic
compared to simulation optimization.
5.1 Base Case Scenario
The parameters for our base case scenario are based
on empirical results and assumptions made in prior
studies. The parameters are given in Table 1. We
use a time granularity of ∆ = 1 minute to make a rea-
sonable trade-off between precision and computation
time. In practice, data about service distributions will
often be available as discrete data (a histogram). If
this is not the case, discrete approximations can be
obtained from the corresponding continuous distribu-
tion
ˆ
S as
s(n) = Pr[
ˆ
S < (n +
1
2
)∆] − Pr[
ˆ
S < (n −
1
2
)∆], n ∈ N.
Table 1: Parameters base case scenario.
K = 10 (number of patients)
t
max
= 240 min (session length)
c
I
= 2 (idle time cost per time slot)
c
O
= 3 (overtime cost per time slot)
p
k
= 20% ∀k (no-show probability)
α = 0.5% (probability emergency arrival at slot)
ˆ
S
k
∼ LogN(µ = 25,σ=15) ∀k
ˆ
S
e
∼ Exp(µ=40)
∆ = 1 min (slot length)
5.2 Comparison to Simulation
First of all, to illustrate the usefulness of our ex-
act evaluation algorithm, we compare its performance
with simulation in terms of precision and running
times. Most studies in the literature rely entirely
on brute-force simulation to evaluate and optimize
schedules. For example, Klassen and Yoogalingam
(2014) applied a simulation optimization approach,
in which they replicated each solution 10 000 times.
Table 2 compares the computed values with the cor-
responding confidence intervals for their estimation
by simulation for two sample sizes, i.e. 10 000 and
100 000 replications. It can be seen that the width
of the 95% confidence intervals of the total cost TC
is about 6% and 2% of the exact solution for respec-
tively SS=10 000 and SS=100 000. The experiment is
executed in Java Eclipse 2.0 on a Dell laptop with an
i7-4900MQ 2.8 GHz processor and we find that the
simulation run with sample size SS=10 000 (or 100
000) requires 1.3 (or 11) times more CPU time than
our exact evaluation procedure which took less than
0.1s when we omit the preprocessing calculations of
E[B] and E[G].
Next, we included our evaluation method in a lo-
cal search algorithm as described in Section 4.4 to
compare its performance with a simulation optimiza-
Reducing Disruptive Effects of Service Interruptions in Appointment Scheduling
243

Table 2: Comparison of computed values with the 95%
confidence intervals of their estimates by simulation, for
some performance measures of the base case scenario with
a
k
=a=24. (SS = sample size, number of replications).
Measure Values
Simulated values
SS=10 000 SS=100 000
E[W
2
] 8.93 8.43-9.62 8.88-9.24
E[I
2
] 8.17 8.00-8.36 8.13-8.25
E[W ] 272 259-279 270-277
E[I] 40.5 39.6-42.2 40.0-40.8
E[O] 63.8 62.0-65.3 63.5-64.5
TC 544 524-559 540-552
tion method. Numerous test instances were devel-
oped to capture a diverse set of environments. For
each instance, we run the local search algorithm five
times using simulation to estimate a schedule’s per-
formance. We then compared the average cost TC
sim
over these five runs with the cost obtained by using
our exact evaluation method TC
∗
. The gap between
these costs is defined as,
gap =
TC
sim
− TC
∗
TC
∗
100%
The following parameters were represented in the
experiment:
• The number of patients K in the schedule is equal
to 6, 8, 10 or 12 patients.
• Service interruptions occur with a probability of
α= 0.005 for each time slot, and are exponentially
distributed with mean 30 minutes.
• The service times follow, before discretisation,
a lognormal distribution with a mean equal to
200
K(1−p
k
)
, resulting in an average of 200 minutes of
work. The standard deviations σ
k
are calculated in
order to get coefficients of variation equal to one
of the following values: {0.2, 0.4, 0.6}.
• The no-show probability p
k
of a patient was se-
lected from the set {0, 0.1, 0.2}.
This represents a total of 36 different environments.
From a practitioners point of view, the choice of cost
function is of great importance as well. To this end,
we consider four different cost functions for which
the c
I
/c
O
ratio is fixed at 1.5. The c
I
level was then
selected from the set {1, 2, 5, 10}. This adds up to
a total of 144 test instances. These values reflect en-
vironments where patients’ waiting times are highly
valued as well as environments with high fixed costs
for the service provider.
From Table 3 we can see that the exact evalua-
tion method outperforms the simulation heuristics and
1 2 5 10
0
10
20
c
I
Average gap (%)
Bailey
SS=10 000
SS=100 000
Figure 2: Effect of the cost structure on the performance
of Bailey’s rule and the heuristic solutions obtained with
simulation. The gaps are averaged over all scenarios.
significant cost reductions are obtained in about 10
seconds. Clearly, the variance on the simulated val-
ues has a big impact on the performance of the lo-
cal search algorithm. The heuristic is often stuck in a
suboptimal point after it underestimated the cost of a
certain schedule.
Table 3: Comparison between our approach and simulation
optimization: the running time and gap between TC
∗
and
TC
sim
for sample sizes 10 000 and 100 000. The values in
the table are the averages over the different scenarios for the
given number of patients K.
K
SS=10 000 SS=100 000 Exact
Gap Time Gap Time Time
(%) (s) (%) (s) (s)
6 3.7 2.6 0.8 40.9 6.6
8 5.6 3.8 1.1 70.0 8.8
10 7.8 4.8 1.8 104.0 11.0
12 10.2 5.9 2.8 139.1 12.4
Finally, we look at the performance of Bailey’s
rule in these environments. In Sickinger and Kolisch
(2009), it is shown that Bailey’s rule performs very
well over a wide range of problem parameters if the
cost of waiting is relatively low. Bailey’s rule sched-
ules two patients in the first slot, i.e. τ
1
= τ
2
= 0, while
for the other patients the appointment time τ
k
is equal
to τ
k−1
+ E[S
k−1
].
Figure 2 compares the heuristic solutions with
Bailey’s rule for the four different cost structures. It
can be seen that the cost structure has a big impact on
Bailey’s performance.
5.3 Service Time Distribution
Emergency
In this section we look at the impact of the service
time distribution of the emergencies S
e
. We consider
ICORES 2018 - 7th International Conference on Operations Research and Enterprise Systems
244
1 2 3 4 5 6
7
8 9
0
10
20
30
k
a
k
E[S
e
]=5
E[S
e
]=10
E[S
e
]=30
E[S
e
]=60
Figure 3: Heuristic solutions of inter-appointment times for
Scenario 1.
three different scenarios for the scheduled patients.
For Scenario 1, we assume deterministic service times
of 20 minutes and set p = 0. For Scenario 2, we as-
sume S
k
∼ logN(20,4) with p
k
= 0 while for Scenario
3 we set p
k
= 0.2 and
ˆ
S
k
∼ logN(25,12). For each
scenario, we set K=10, t
max
= 240, c
I
= 2 and c
O
= 3.
For each scenario, we assume that the service time
of the emergency is exponentially distributed and vary
its mean E[S
e
], namely 5, 10, 30 and 60 minutes. The
arrival rate of the emergencies, α, is chosen so that
the expected effective service time is the same for
each scenario (E[B
k
]=22.22). For each instance of the
problem, we first determine the local search solution
by taking emergency arrivals into account. We de-
note the total cost of this heuristic solution as TC
∗
.
In addition, we also determine the performance of
the following policies: the policy that ignores emer-
gencies and the policy that considers emergencies ap-
proximately by assuming that service times follow the
corresponding distribution where the mean and vari-
ance are adjusted to its respective values of the ef-
fective service time given in equations 4 and ??. In
the following, we use TC
nointer
and TC
approx
to denote
the value of the total cost under these policies respec-
tively.
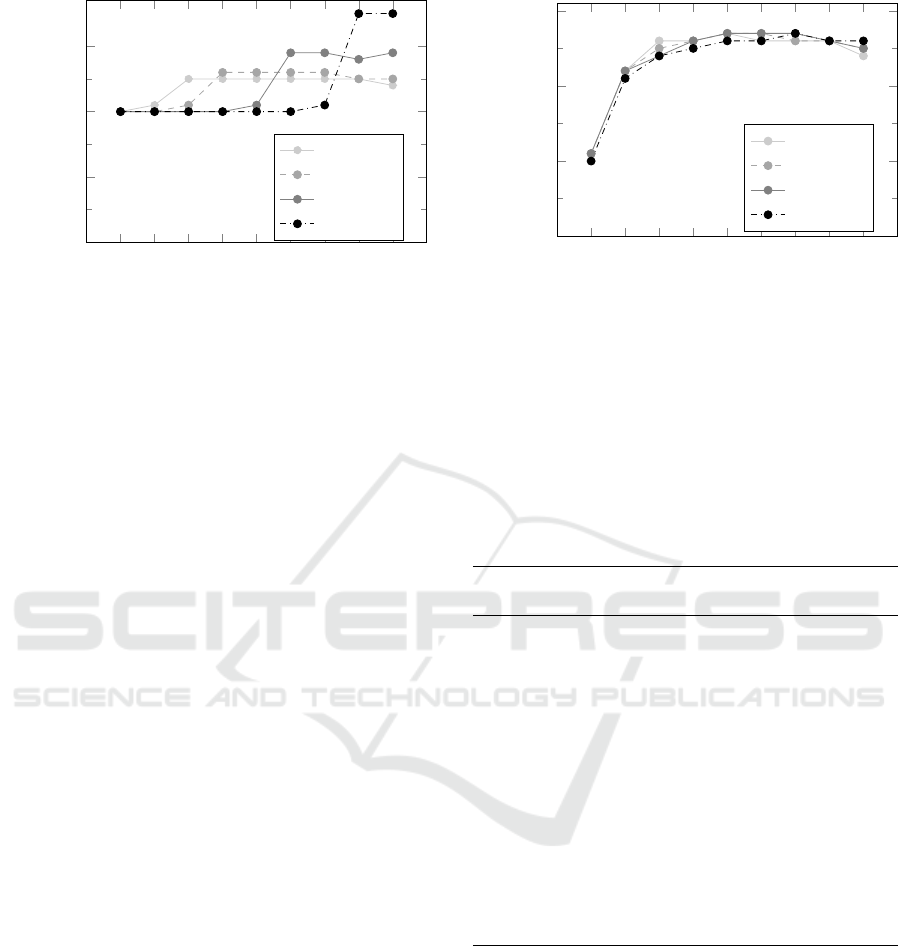
Figure 3 depicts the heuristic solutions for Sce-
nario 1 for different values of E[S
e
]. Clearly, for
this scenario, the best found inter-appointment times
greatly depend on S
e
and the interruption rate α.
When the expected length of a service interruption is
small and α is high, we find a dome-shaped pattern
for the inter-appointment times.
Figure 4 depicts the heuristic solutions for Scenario 3.
It can be seen that in a more stochastic environment,
the service time distribution of the emergencies S
e
has
a much smaller impact on the solution.
From Table 4, we can see that capturing the inter-
ruptions approximately by adjusting the service time
1 2 3 4 5 6
7
8 9
0
10
20
30
k
a
k
E[S
e
]=5
E[S
e
]=10
E[S
e
]=30
E[S
e
]=60
Figure 4: Heuristic solutions of inter-appointment times for
Scenario 3.
distribution seems to work reasonably well for short
and common service interruptions (low E[S
e
], high
α). However, when there are few other sources of
variability (Scenario 1 and 2), the difference between
TC
∗
and TC
approx
is significantly greater for long and
uncommon interruptions.
Table 4: Numerical results.
E[S
e
] TC
∗
TC
nointer
TC
approx
5 121.2 190.8 122.4
Scenario 1 10 161.8 208.8 166.2
30 234.9 248.9 248.4
60 276.3 279.1 298.4
5 152.9 157.6 153.2
Scenario 2 10 188.3 194.1 189.0
30 259.0 265.8 263.9
60 301.4 308.2 313.4
5 360.4 362.0 360.5
Scenario 3 10 373.5 375.4 373.6
30 416.5 418.3 416.7
60 449.3 451.1 450.1
6 CONCLUSIONS
This paper presents a method to assess the moments
of the waiting times of patients as well as the idle
times and overtime of the doctor in a setting with
emergency arrivals. The method allows patients to
have general, distinct service time distributions and
can handle no-shows. The algorithmic approach ad-
vocated here is fast in comparison with simulation and
was included in a local search algorithm. Some nu-
Reducing Disruptive Effects of Service Interruptions in Appointment Scheduling
245

merical examples are presented in which we focus on
the effects of emergency arrivals and service interrup-
tions on patient scheduling. A possible direction for
future research could be to investigate non-stationary
arrival processes for the emergencies.
REFERENCES
Begen, M. A. and Queyranne, M. (2011). Appointment
scheduling with discrete random durations. Mathe-
matics of Operations Research, 36(2):240–257.
Cayirli, T. and Veral, E. (2003). Outpatient scheduling in
health care: a review of literature. Production and
operations management, 12(4):519–549.
De Vuyst, S., Bruneel, H., and Fiems, D. (2014). Computa-
tionally efficient evaluation of appointment schedules
in health care. European Journal of Operational Re-
search, 237(3):1142–1154.
Fiems, D., Koole, G., and Nain, P. (2007). Waiting times
of scheduled patients in the presence of emergency
requests. Technisch rapport. URL http://www. math.
vu. nl/koole/articles/report05a/art. pdf,(Accessed on
18/12/2012), pages 1–19.
Fiems, D., Steyaert, B., and Bruneel, H. (2004). Discrete-
time queues with generally distributed service times
and renewal-type server interruptions. Performance
Evaluation, 55(3):277–298.
Gupta, D. and Denton, B. (2008). Appointment schedul-
ing in health care: Challenges and opportunities. IIE
transactions, 40(9):800–819.
Kaandorp, G. C. and Koole, G. (2007). Optimal outpatient
appointment scheduling. Health Care Management
Science, 10(3):217–229.
Klassen, K. J. and Yoogalingam, R. (2013). Appointment
system design with interruptions and physician late-
ness. International Journal of Operations & Produc-
tion Management, 33(4):394–414.
Klassen, K. J. and Yoogalingam, R. (2014). Strategies for
appointment policy design with patient unpunctuality.
Decision Sciences, 45(5):881–911.
Koeleman, P. M. and Koole, G. M. (2012). Optimal out-
patient appointment scheduling with emergency ar-
rivals and general service times. IIE Transactions on
Healthcare Systems Engineering, 2(1):14–30.
Kolisch, R. and Sickinger, S. (2008). Providing radiology
health care services to stochastic demand of different
customer classes. OR spectrum, 30(2):375–395.
Kortbeek, N., Zonderland, M. E., Braaksma, A., Vliegen,
I. M., Boucherie, R. J., Litvak, N., and Hans, E. W.
(2014). Designing cyclic appointment schedules for
outpatient clinics with scheduled and unscheduled pa-
tient arrivals. Performance Evaluation, 80:5–26.
Lau, H.-S. and Lau, A. H.-L. (2000). A fast procedure
for computing the total system cost of an appointment
schedule for medical and kindred facilities. Iie Trans-
actions, 32(9):833–839.
Luo, J., Kulkarni, V. G., and Ziya, S. (2012). Appointment
scheduling under patient no-shows and service inter-
ruptions. Manufacturing & Service Operations Man-
agement, 14(4):670–684.
Sickinger, S. and Kolisch, R. (2009). The performance of a
generalized bailey–welch rule for outpatient appoint-
ment scheduling under inpatient and emergency de-
mand. Health care management science, 12(4):408.
APPENDIX
Functional Relation for the Generating
Function of the Unavailability Time due
to an Emergency
Let B denote the time that the service provider is un-
available for scheduled patients due to the service
of an emergency. This time equals the time that is
needed to serve this initiating emergency as well as
all other emergencies that arrived while serving these
emergencies (Fiems et al., 2007):
B = S
e
+
G
S
∑
j=1
B
( j)
where G
S
denotes the number of emergency arrivals
during the service of the initiating emergency and
where B
( j)
denotes the unavailable period correspond-
ing to the jth emergency arrival during the service
of the initiating emergency. In contrast to Fiems et
al. (2007), service times are stochastic now. Due to
the Bernoulli nature of the emergency arrival process,
one easily verifies that the random variables B
( j)
are
mutually independent and have the same distribution
as B. This expression then translates into the follow-
ing functional equation for the probability generating
function B(z) of the unavailable periods
B(z) = E[z
S
e
+
∑
G
S
j=1
B
( j)
] = E
S
[E[z
n+
∑
G
n
j=1
B
( j)
|S
e
= n]]
=
∑
n≥1
s
e
(n) z
n
E[z
∑
G
s
j=1
B
( j)
]
=
∑
n≥1
s
e
(n) z
n
(1 − α + αB(z))
n
=
∑
n≥1
s
e
(n) [z(1 − α + αB(z))]
n
= S
e
((αB(z) + 1 − α)z) .
ICORES 2018 - 7th International Conference on Operations Research and Enterprise Systems
246
