
Dynamic Linear Assignment for Pairing Two Parts in Production
A Case Study in Aeronautics Industry
Clémence Bisot
Safran Aircraft Engines, Rond Point René Ravaud, 77550 Moissy Cramayel, France
Keywords: Dynamic Linear Assignment, Linear Optimization, Pairing, Myopic Assignment, Dynamic Assignment,
Aeronautics Industry.
Abstract: In some manufacturing industries, the task of assembling two parts is a time-consuming step in production.
Bonding can be more or less easy depending on the parts relative geometry. In this case, it becomes interesting
to carefully choose the two pieces to be paired among available parts. As one does not know exactly the
geometrical characteristics of the items that will be produced in the future, the problem of wisely choosing,
over the long haul, the pairs to be bonded is dynamic. Minimizing the cost of pairing operation can be
formulated as a dynamic linear assignment problem. This paper presents different heuristics used to solve the
dynamic linear assignment problem in the framework of a specific application in the aeronautics industry.
The article highlights how strong characteristics of the case study are used to choose adapted heuristics.
1 INTRODUCTION
In a plant, the task of assembling two parts can be
more or less easy depending on the parts relative
geometry. In the Aeronautics Industry, the problem of
slotting two parts is encountered during the
production of Composite Fan Blades. The two parts
to be paired are: the Composite Fan Blade and its
Metallic Leading Edge (MLE). These two parts are
illustrated on Figure 1.
Figure 1: Engine Fan Blade and Metallic Leading Edge: the
two parts to be paired.
If the two parts fit well, the pairing can be easy.
On the other hand, if the two parts do not fit, it can be
necessary to make some adjustment by benching the
blade before pairing. Benching is a time-consuming
step one wants to avoid. Thus, the following question
is raised every day : given the sets of blades and
MLEs available in the stock which
pairs should be
bonded so has to minimize, over the long haul, the
cost of this production step? In our case, the static
problem of choosing the best
pairs for an optimal
cost at date , is easy: the sets of available blades and
MLEs is small and there is no need for a quick online
computation (choice of pair is done only once a day).
On the contrary, optimizing in the long term is hard:
we do not know the characteristic of the items which
will be produced in the future and choices made at
date have an impact on available choices at date
.
The static version of our problem, is in fact an
extension of the Linear Sum Assignment Problem
(LSAP): how to assign a number of tasks to a number
of resources so as to minimize the total cost of the
assignment where the global cost of the assignment
corresponds to the sum of each individual
assignment’s cost. The small difference with the
classical LSAP is that, here, the number of tasks and
resources is higher than the number of pairs to be
done (cf. part 3.1.1). Linear Assignment Problem and
its extensions are linear optimization problems which
254
Bisot, C.
Dynamic Linear Assignment for Pairing Two Parts in Production - A Case Study in Aeronautics Industry.
DOI: 10.5220/0006627402540263
In Proceedings of the 7th International Conference on Operations Research and Enterprise Systems (ICORES 2018), pages 254-263
ISBN: 978-989-758-285-1
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

have numerous applications in various fields: pairing
weapons with targets (Ahuja et al., 2007), machine
scheduling (Pinto and Grossmann, 1998), vehicle
routing (Dantzig and Ramser, 1959) etc. It has been
extensively studied and many algorithms have been
proposed to solve it, among which the Hungarian
algorithm (Kuhn, 1955) efficiently implemented in
(Jonker and Volgenant, 1987). In our case, the
dimension of the problem is small and computation
time constraints are low, the static linear assignment
is thus easily solved.
The problem of wisely choosing pairs in a long
run is referred to as the Dynamic Assignment
Problem: choosing the best assignment at date
without knowing which resources and tasks will enter
the system in the future. The mathematical
framework of a general class of dynamic assignment
problems is established in (Spivey and Powell, 2004).
This paper explains how the framework of
Dynamic Linear Assignment is applied to the specific
case of pairing blades with MLE in a plant. We will
highlight how some strong characteristics of the case
study are taken advantage of to find satisfying
heuristics for the optimization.
In a first part, the characteristics of the case study
are described in details: cost, constraints, parts’ flows
in the plant and final cost function to be minimized.
In a second part, different heuristics to solve the
problem are proposed. In the last part the heuristics
are tested on a set of real data coming from a plant so
as to evaluate performances and compare strategies.
2 PROBLEM FORMULATION
In this part, the different costs and constraints of the
case study are presented. Then the dynamic of the
system is described. Finally, the total cost function
function to be minimized is written. In a last parts, the
specificities of our case study are highlighted.
2.1 Pairing Cost
The cost of pairing a MLE with a blade depends
on two elements:
- How much material has to be benched to make the
pair. The contribution of benching to the total cost
is thus a function of and geometrical
characteristic that we will note:
. If the pair can
be done without benching,
.
- The relative position of the bonded blade and
MLE compared to nominal position. The relative
position of blade and MLE is characterized by a
few geometrical measures on the bonded blade
noted
. We are aiming at having pairs with
relative position as close as possible to the
nominal
. The distance to nominal is measured
by a well-chosen norm (not detailed here):
.
Thus, if a MLE and a blade are pairable, the cost
of the pair is defined as:
(1)
For now, we suppose that given the geometrical
characteristics of two parts and , we are able to
predict both how much material will have to be
removed and the relative position of the two parts on
the bonded blade. Predicting cost is a challenge by
itself which can be done using different technics.
Here we can mention in particular S. Flöry’s work on
point clouds and surfaces matching (Flöry, 2010). In
reality, cost prediction is imperfect and is
known with uncertainties: is a random
variable, we know only its expectation. This will limit
the performance of any heuristics used to optimize
pairs’ choices.
2.2 Constraints on Production Flows
2.2.1 Production Rate
Most important constraint on production flow is the
number of pairs which have to be done every day. Let
be the number of pairs to be done at date . If the
pairs cannot be done at date , the production is
delayed. The cost of not being able to make a pair
when we are asked to (there is not enough pairable
parts available in the batch) is noted . For example,
on date if only
pairs can be done, this will
cost : .
If MLE, , and blade, , are not pairable, as an
artefact in the computation, we can say that the cost
of the pair is:
(2)
Let
be a Boolean giving the pairability of MLE
with blade . For any pair nature (pairable or not
pairable), the pair cost is:
(3)
2.2.2 MLE Limited Life
Because of a surface treatment performed on MLEs
to improve bonding quality, MLE cannot wait for too
long in the batch at pairing post. If it stays more than
Dynamic Linear Assignment for Pairing Two Parts in Production - A Case Study in Aeronautics Industry
255
, it will be scraped (i.e removed
from the system).
The cost of scraping a MLE is noted
.
2.2.3 Ordering of Blades Flow
For production engineers, it is better if blades
production order is not shuffled too much. This is an
important constraint because, among others things, it
helps detecting production crisis.
This constraint was modeled as follows: if a blade
stays more than
at the pairing post,
we get a delay penalty of
. Unlike MLEs, when a
blade stays more than
at pairing post, it is not
scraped and thus stays in the system.
Note that we can get a penalty only once in a blade
life: for it doesn’t cost more if a blades stays more
than 7 days in the batch than if it spends exactly 7
days. It is also important to notice that in our
application
.
2.3 System Dynamic
The production and parts flows at the plant are
modelled as follows:
- Each working day (5 days a week), pairs have
to be done.
- Every day, the pairs are chosen among the sets of
MLEs and blades available at the pairing post. We
call those parts “actionable parts”. There is
constant buffers of MLEs and blades
actionable in the batch. A larger buffer of MLEs
is needed since MLEs present more geometrical
variability than blades.
- Every week, a batch of MLEs enters the
plant. The 3D geometry of these MLEs is known
immediately when it enters the plant. However,
the MLEs are not instantly actionable because
MLEs have to be inspected before entering the
pairing post. These MLEs are progressively
inspected during the week and become actionable
little by little. A batch of known but not actionable
MLE is always available. The number of MLEs in
this batch varies from , at the beginning of
the week, to at the beginning of the week.
Following notation will be used later:
- is the set of actionable MLEs at date .
-
is the set of known but not actionable MLEs
at date .
- is the set of actionable blades at date .
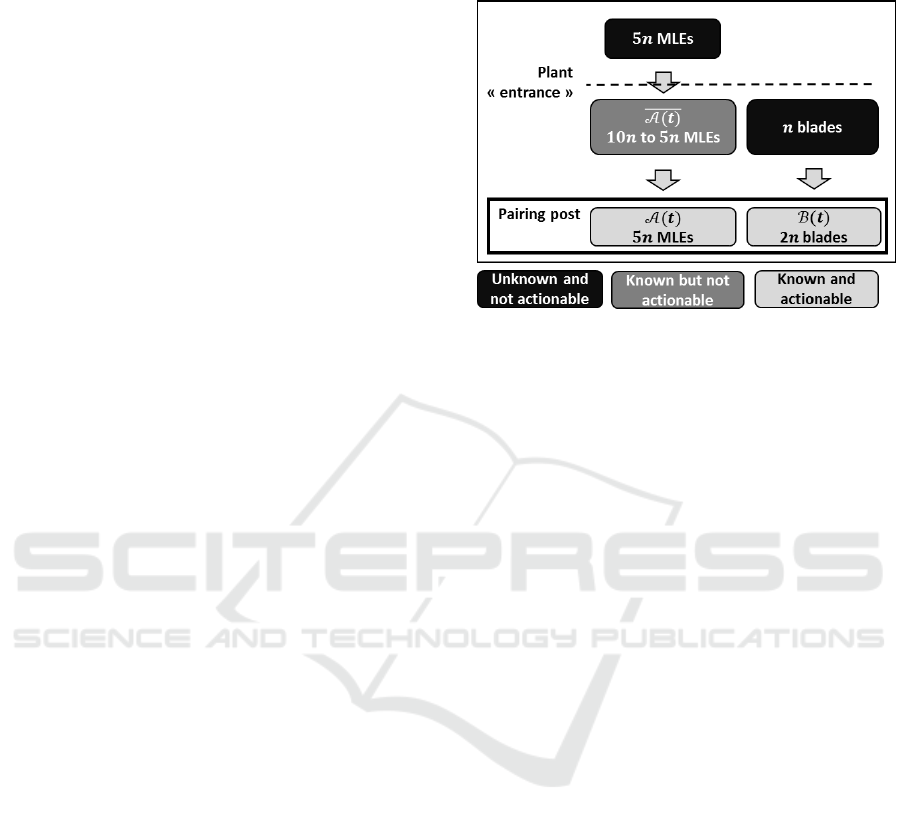
Figure 2 gives an overview of the production flows
described above. What is important to remember here
is that MLEs are known before being actionable
(from one to two weeks beforehand). This is a rich
information to be used for long term optimization.
Figure 2: Blades and MLE flows at the plant. is the
number of pairs to be done at each working day .
and are the different sets of available parts.
2.4 Total Cost Function
2.4.1 Total Cost of Pairing Operation
The total cost of pairing operation between dates
and ( is typically a value big in comparison
with Δ
, the limit time a MLE can stay in the
batch before being scraped), , can now be written as
follows:
(4)
With:
-
, the number of assignments to be done at date
.
-
, the
pair chosen at date . MLE
and blade
are chosen among the actionable
parts at date .
-
, the cost of the pair
as
defined in equation (3).
-
, the number of MLE which had to be scraped
(spent more than
days in the stock) between
and .
-
, the number of blades which were delayed
(spent more than
days in the stock) between
and .
is the total cost to be minimized. Our problem is to
find heuristics to choose the pairs
so as to
minimize this total cost . The pairs
are
ICORES 2018 - 7th International Conference on Operations Research and Enterprise Systems
256

chosen in the sets and . Choice are made
at date given the information on the system
available at date , i.e. only knowing
and
for any date before .
2.4.2 Costs Hierarchy
The orders of magnitude of the different sources of
cost in are the following:
- , the cost of a delay in production, and
, the
cost of scraping a MLE, are of the same order of
magnitude.
-
, the cost of having a blade delayed, is about
.
-
, the cost of benching varies between
and (except for pairs feasible without
benching for which
).
-
the cost of being away from nominal
position varies between and .
Costs are strongly hierarchical: it is much more
important to avoid production delay or MLE scraping
than to avoid benching which is also much more
important than minimizing bonded blade distance to
nominal. This hierarchical structure of costs will help
a lot for choosing an adapted heuristic for long term
optimization.
2.5 Case Study Important Properties
The constraints and costs of pairing for this specific
problem has four strong characteristics which will
help finding a satisfying heuristic to solve the
problem:
- The
pairs to be done at date are chosen once
all together at the beginning of the day. There is
no computation time constraints.
- Blades and MLEs play very asymmetrical roles:
production flow properties and constraints are
very different for the two parts.
- The total costs of the pairing step is made up of
different components (cost of not being able to
keep production speed, cost of benching, cost of
scraps etc.). The cost structure is very hierarchical
so that it is easy to know which events should
absolutely be avoided without taking any risk and
which events are acceptable.
- The MLEs entering the system are known in
advance (before the MLEs become available for
pairing). This helps taking decision at date which
will not badly impact the choices available at date
.
3 HEURISTICS
In this part, we first present some of the basic blocks
composing the different strategies proposed to solve
the problem. Then, we present in details five different
heuristics: one simple myopic strategy serving as a
reference, three other more sophisticated myopic
strategies and one non-myopic strategy. We call
myopic strategies those in which decisions are made
without using information given by the set of known
but not actionable MLEs,
.
3.1 Basic Blocks
In this part, we first present three basic bricks which
are part of the heuristics presented later. Then, in part
3.1.4, the general structure of the heuristics described
later is presented.
3.1.1 A Static Linear Assignment
The static linear assignment in our case, can be
formulated as a generalization of the classical Linear
Sum Assignment Problem. Given a set of
resources (MLE), a set of
tasks (blades) and a
number of pairs to be done , the goal is to find the
set of pairs which minimize total cost of the
assignment.
This problem can be written in the form of a linear
optimization problem:
(5.1)
With
-
the cost of pairing resource with task .
-
the decision variables with
if
resource (MLE) is assigned with task (blade) ,
0 otherwise.
Under the constraints:
- The decision variables
are Booleans:
(5.2)
- Each resource is assigned at most once:
(5.3)
- Each task is assigned at most once:
(5.4)
- assignments have to be done:
Dynamic Linear Assignment for Pairing Two Parts in Production - A Case Study in Aeronautics Industry
257

(5.5)
This linear optimization problem can be solved using
any standard linear programing algorithms.
3.1.2 Correction of Cost Matrix
One other important block of our heuristics is the
computation of a corrected cost matrix
. The
basic idea is to artificially reduce the cost of pairs
containing old MLE or old blades. A static linear
assignment (cf. part 3.1.1) will then be performed on
the corrected cost matrix and oldest blades or MLEs
will be favored. The goal is to anticipate MLEs’
scraps and blades’ delays.
We can correct cost matrix in a simple way that
we will call a myopic correction.
At each time step :
- The cost of any pair realized with a “too old” (i.e
close from being scraped) MLE is artificially
reduced to favor this pair.
Let
be the age of MLE at date and
be an age limit close to
. Cost is corrected
as follows:
,
(6)
This accounts for the risk that, if MLE is older than
and not paired at time , this will cost
because
the MLE will be scraped in the following days.
- Similarly, for each blade which is too old, i.e
close from
limit (older than an age limit
),
the cost of feasible pairs is reduced (so as to favor
these pairs):
,
(7)
This accounts for the risk that, if this blade older
than
and not paired at time , this will cost
because the blade will be considered as delayed in
the following days.
The values of
and
are tuned based on the
problem characteristics:
,
, global
proportion of not pairable pairs, sizes of blades and
MLEs buffers etc. These parameters can be optimized
by simulations similar to those presented in part 4.
For the non-myopic strategy, the cost matrix is
corrected in a more sophisticated way which will be
described in part 3.2.5 but basic idea stays the same:
favor oldest blades and MLEs by reducing the cost of
their pairs.
3.1.3 Maximum Cardinality Bipartite
Matching
In our strategies, it is often useful to answer following
question: given a set of MLEs and a set of blades,
what is the maximal number of feasible pairs?
This can be done using a maximum bipartite
matching algorithm like Ford-Fulkerson algorithm
for example (Ford and Fulkerson, 1962). The sets of
MLEs and blades are represented as a binary bipartite
graph linking the set of MLEs with the set of blades.
If the pair is feasible, edge exist. If the pair
is not feasible, the edge does not exist.
3.1.4 Structure of the Strategies
The different strategies described in the following
sections all have in common a four steps structure. At
each time step :
- First a cost matrix is calculated using all
actionable blades and MLEs.
- Then we select a subset of blades and MLEs
among all actionable ones so as to favor oldest
blades and oldest MLEs (avoid MLE’s scrap and
blade’s delay). We obtain a paring cost submatrix.
In this part maximum cardinality bipartite
matching algorithm plays an important role.
- The paring cost submatrix is then corrected so as
to favor again old blades and old MLEs. For
myopic strategies, cost correction is done as
described in part 3.1.2. For the non-myopic
strategy, cost correction is performed in a more
subtle way described in part 3.2.5
- Finally a static linear assignment optimization
(3.1.1) is performed on the corrected cost
submatrix
to choose the
assignments
which minimize total cost of the assignment.
3.2 Detailed Heuristics
In this part, the different heuristics imagined to help
choosing which
pairs should be done at each time
are described in details. Each strategy is later
evaluated on real data coming from the plant. Myopic
strategies are strategies where no more future
prediction than cost correction described in 3.1.2 is
used.
3.2.1 Myopic Linear Assignment (MLA)
This strategy is the simplest strategy one can think of
and will serve as a reference to evaluate efficiency of
the others. Pairs are suggested in batch at each date .
ICORES 2018 - 7th International Conference on Operations Research and Enterprise Systems
258

Among all actionable blades and MLEs at time ,
we chose the
pairs so as to minimize the total cost
of pairing (optimization is done solving a static linear
assignment as described in 3.1.1). The cost matrix
used for the assignment, is the corrected cost matrix
as described in 3.1.2 (i.e. anticipating the cost of
scraped MLE and delayed blades).
3.2.2 MLA with FIFO on Blades
At each time step, we select a subset of all actionable
blades. The subset is the smallest and oldest set of
blades so that it is possible to make
pairs between
those blades and all actionable MLEs. This set is
chosen so as to take oldest blades first and it is noted
. The selection of is done solving a
succession of maximum cardinality bipartite
matching (cf. part 3.1.3). In the set and the set
of all actionable MLEs , we choose the
pairs
minimizing the total cost of pairing (using corrected
cost matrix as described in 3.1.2).
This algorithm combine advantages of assigning
pairs by batch and keeping FIFO (First In First Out)
lines on blades so as to avoid blades delays. However,
this strategy doesn’t favor oldest MLEs so that we do
not avoid MLEs scrap (except through basic cost
correction).
3.2.3 Myopic Linear Assignment with FIFO
on Blades and MLE
A each time step, we first select , smallest and
oldest set of blades so that it is possible to make
pairs with the set of all actionable MLE . Then,
we select the smallest set of MLEs so that it is
possible to make
pairs with the set . is
chosen so as to take oldest MLEs first. Then, amongst
and , we choose the
pairs so as to
minimize the total cost of pairing.
This algorithm combines the advantages of
assigning pairs by batch, assigning oldest blades and
oldest MLEs first. An advantage is given to oldest
blades over oldest MLEs since the time before delay
of a blade is a lot shorter than time before the scrap of
a MLE. The drawback of this strategy, is that the
static linear assignment is performed on narrowed
sets of MLEs and blades (see Figure 3) with reduced
choices for the pairs.
3.2.4 MLA with FIFO on Blades and Partial
FIFO on MLEs
We select the set . With this set and the set
of all actionable MLE , it is possible to make a
maximum of pairs without benching the blades.
We want to perform pairing on oldest MLEs without
degrading the number of pairs which can be done
without benching.
We select the smallest set of MLEs so that
it is possible to make
pairs and pairs without
benching with the sets . is chosen so as to
take oldest MLEs first. Then, among and
, we choose the
pairs so as to minimize the
total cost of pairing.
This algorithm is a compromise between
algorithms 3.2.2 and 3.2.3. It combines the
advantages of assigning pairs by batch, assigning
oldest blades first and giving advantage to oldest
MLEs. With this strategy, we perform an optimal
linear assignment on a larger sets of MLEs than with
strategy 3.2.3 so that this gives more chance for
optimization. However, more risk of MLE scrap is
taken. This strategy takes advantage of the cost
hierarchy to choose the set : the number of
pairs done without benching is the same as the one for
strategy 3.2.2, this implies that cost of the assignment
is not degraded too much by the reduction of MLE
set.
3.2.5 Non-myopic Strategy
In this non-myopic strategies, the goal is to correct
cost matrix in a more subtle way than what was
described in part 3.1.2. The goal is to favor pairing of
MLEs and blades which are hard to pair over those
which are easy. Most important contributors to final
total price are MLE’s scraps and blade’s delays. Thus,
we focused on anticipating those costs and avoiding
it. This is why we try to pair blades and MLEs which
are hardly pairable first (they have a higher risk to be
delayed or scraped).
In this strategy, no sub-matrix is selected, a static
linear assignment is performed on all actionable
MLEs and blades using a cost corrected matrix. At
each date , the goal is to subtract from the initial cost
of a pair,
, an estimation of how much it could
cost if MLE and blade were not paired at and
were thus kept in the system. The expectation of the
cost of keeping MLE (blade ) in the system is
estimated through the risk that the MLE (blade )
will be scraped (delayed). Cost correction is done for
blade and MLE separately as described below.
Cost Correction for MLE Scrap Anticipation
For each actionable MLE of age
at time , we
denote:
-
the number of blades which will become
actionable before this MLE gets scraped. In other
Dynamic Linear Assignment for Pairing Two Parts in Production - A Case Study in Aeronautics Industry
259

words, this is the number of blades entering the
system in the next
days.
-
the probability that this MLE is pairable with a
blade.
is estimated based on MLE’s pairability
with blades which previously entered the system.
It is re-estimated at each time step as new blades
enter the system.
The probability that none of the
incoming blades
will be pairable with MLE is:
(8)
The cost of keeping MLE in the system, is mainly
driven by the increase of the risk for the MLE to be
scraped (because scrap is the most expensive source
of cost). Then, the cost of each pairable sets of MLE
and blade is corrected as follows:
(9)
Cost Correction for Blade Delay Anticipation
For each blade , of age
, actionable at time ,
we know which MLEs will enter the system before it
gets too old. In other words, we know which MLEs
will become actionable in the next
days. This is thanks to the important batch of MLEs
known but not actionable described in part 2.3. The
set of MLEs which will become actionable in the next
is called
. It is a subset of
.
The cost of keeping blade in the system, is
mainly driven by the increase of the risk for the blade
to be delayed (because delay is the most expensive
source of cost generated by the blade).
If there is no MLE in set
with which blade
is pairable we perform a cost correction. Otherwise
no cost correction is done.
(10)
Remarks on Flows Anticipation
Here it is important to highlight that practically, flows
are not perfectly known:
- In reality,
will have to be estimated.
- In reality, we do not know precisely the order and
when MLEs will become actionable:
is not
perfectly known.
3.3 Summary of the Different
Heuristics
The different myopic strategies presented above are
all very similar: assignment is performed by batch
using static linear assignment. The difference
between those strategies is only the sets of MLEs and
blades on which the static linear assignment problem
(3.1.1) is solved. Figure 3 presents a schematic view
of the sets on which linear assignment algorithm is
applied for the different strategies. The best strategy
will depend on the proportion of non-pairable pairs,
the proportion of pairable pairs without benching and
the balance between the different costs. Moreover,
Table 1 gives an overview of the different strategies
pro and cons.
Figure 3: Graphical representation of the different
strategies. The rectangles represent the sets of blades and
MLEs on which static linear assignment is performed.
Table 1: Summary of the different heuristics properties. This table highlights the pros and cons of the heuristics proposed.
MLA,
3.2.1
MLA + FIFO on
blades, 3.2.2
MLA + FIFO on
blades and MLE,
3.2.3
MLA + FIFO blades and
partial FIFO MLA, 3.2.4
Non-Myopic, 3.2.5
FIFO blades
No
Yes
Yes
Yes
No
FIFO MLE
No
No
Yes
Partial
No
Favor pairing without
benching
Yes
Yes
No
Yes
Yes
Improved prediction
of MLE scrap
No
No
No
No
Yes
Improved prediction
of Blades delay
No
No
No
No
Yes
ICORES 2018 - 7th International Conference on Operations Research and Enterprise Systems
260

4 HEURISTICS COMPARISONS
In this part, heuristics efficiencies are compared in
two different cases:
- The case where the algorithm to estimate the cost
of a pair is supposed to be perfect:
• We know if a pair is feasible or not.
• If the pair is feasible, we know if it can be done
without benching.
• The cost of the pair is exactly known.
- The case where algorithm to estimate the cost of a
pair has uncertainties:
• We know if the pair is feasible or not.
• If the pair is feasible, we only know the
probability that the pair is feasible with
benching,
, or feasible without benching,
.
Let
be the expected cost of the pair knowing
that it is feasible with benching and
be the
cost of the pair knowing that it feasible
without benching. The expected pair’s cost is:
(11)
• In this part simulated uncertainties are
representative of uncertainties encountered in
practice.
4.1 Simulation Description
Simulations are based on data from a three week
production at the plant: we know the geometrical
characteristics and, thus, the expected cost matrix and
the real cost matrix for a large set of blades and MLE.
Strategies efficiencies are estimated by simulating
400 weeks of production for each strategy (enough
for the operation average cost to converge). The
production is simulated as follows:
- Ingoing and outgoing flows are simulated
according to the flows described in part 2.3.
- Ingoing MLEs (blades) are simulated with a
random sampling (with replacement) among the
input MLEs set (blades set) with known
geometrical characteristics issued from
production. This means that we make the
hypothesis that the shape of MLEs (blades)
entering the system at date is completely
independent from the shape of MLEs (blades)
entering the system at date . This hypothesis
was roughly verified on the 3 weeks production
dataset which was studied.
- Outgoing flows are the result of tested strategy.
4.2 Results with Perfect Cost
Predictions
In this part, strategies efficiency are compared with
the hypothesis that real cost (and real pair nature: non-
feasible, feasible with benching or feasible without
benching) is known.
The results are summarized in the Table 2. For
each strategy, we have:
- The proportion of blades delayed: the ratio of the
number of blades which stayed in the system more
than
over the number of pairs which were
asked to be done (
.
- The proportion of inactivity: the ratio of the
number of pairs which couldn’t be done over the
number of pairs which were asked to be done
(
.
- The proportion of scraped MLEs: the ratio of the
number scraped MLEs over the number of pairs
which were asked to be done.
- The proportion of benched pairs: the ratio of the
number of pairs which were benched over the
number of pairs which were asked to be done.
- The average cost of a week of production.
We see that every strategy enables to reach 0% of
scraped MLEs and 0% of “inactivity”. This is,
amongst other things, related to the fact that
proportion of non-feasible pairs are rather rare in our
dataset (5% of the pairs). We also see that the best
strategy is the non-myopic one which enables to
avoid all sources of high costs: inactivity, scraping,
delay and benching. However, given the fact that
proportion of non-feasible pairs in our data set is low,
the performances of the non-myopic strategy are not
much higher than those of the myopic strategies.
4.3 Results with Uncertainties on Cost
Predictions
In this part the difference is that decision are made
based on expected cost matrix instead of real cost
matrix.
Results are summarized in Table 3. We see that
average cost of a week of production is much higher
than when cost are known without uncertainty. With
a perfect cost estimation, we can expect to bench 0%
of the pairs whereas with uncertainties on cost
estimation representative of real cost uncertainties,
best strategy leads to 25% of benched pairs. This
shows how important quality of cost prediction
algorithm is. We also see that with cost uncertainties,
the differences between strategies efficiencies are
much smaller.
Dynamic Linear Assignment for Pairing Two Parts in Production - A Case Study in Aeronautics Industry
261

Table 2: Strategies comparison with exact cost predictions. This table summarises the results of the simulations used to
compare the efficiency of the different heuristics. The simulation are done, in the theoretical case where we suppose that we
are able to perfectly predict the cost of the pair before doing it.
MLA,
3.2.1
MLA +
FIFO on
blades,
3.2.2
MLA + FIFO
on blades and
MLE, 3.2.3
MLA + FIFO
blades and partial
FIFO MLA, 3.2.4
Non-
Myopic,
3.2.5
Algorithm
parameters
Correction horizon MLE,
7 days
7 days
7 days
7 days
NA
Correction horizon blades,
1 day
1 day
1 day
1 day
NA
Results
Proportion of blades delayed
0,00475
0
0
0
0
Proportion of inactivity
0
0
0
0
0
Proportion of scraped MLEs
0
0
0
0
0
Proportion of pairs benched
0
0,00181
0,0463
0
0,00012
Average cost of a week of
production
10,5
6,15
24,4
5,88
5,47
Table 3: Strategies comparison with uncertainties on cost predictions. This table shows the results of the simulations used to
compare heuristics efficiency. The simulation are done in the case where algorithm to predict pairs’ cost is not perfect: real
cost of a pair can be different from what was predicted before pairing.
MLA, 3.2.1
MLA +
FIFO on
blades,
3.2.2
MLA + FIFO
on blades and
MLE, 3.2.3
MLA + FIFO blades
and partial FIFO
MLA, 3.2.4
Non-Myopic,
3.2.5
Proportion of blades delayed
0,00881
0
0
0
0
Proportion of inactivity
0
0
0
0
0
Proportion of scraped MLEs
0
0
0
0
0
Proportion of pairs benched
0,26
0,256
0,256
0,254
0,262
Average cost of a week of production
120
110
110
109
111
5 CONCLUSIONS
This article shows how the framework of dynamic
linear assignment was applied to the specific problem
of pairing blades with MLEs in a plant. The strong
characteristics of the studied system were taken
advantage of so as to design a few adapted pairing
strategies. Among the strategies, one was a simple
myopic strategy serving as a reference, three were
adapted myopic strategies and one was a non-myopic
heuristic.
The different strategies were tested on a set of real
data in the case where exact pairs costs are known
before pairing and in the case where there is
uncertainties on cost prediction. We highlighted the
fact that strategies efficiency is strongly related to the
quality of cost estimation. We also showed that the
fours strategies proposed (three myopic, one non-
myopic) enable to significantly reduce the cost of
pairing operation. If costs are perfectly known, the
non-myopic heuristic is the best one. However, this
strategy is harder to implement in reality since more
inputs (about the incoming flows of blades and
MLEs) are needed.
Future work on the subject will include, influence
studies to see how system reacts to changes on some
key inputs of the model: buffer size for MLE and
blade stocks, proportion of non-feasible pairs in the
simulation, proportion of pairs feasible without
benching in the simulation etc.
Some work should also be done to analyze the
effect on the system to have time dependency
between geometrical attributes of blades (MLEs)
entering the system a and those entering at .
The fact that time series of blades (MLEs) attributes
are not completely random makes a lot of sense since
two blades (MLEs) entering the system roughly at the
same date will tend to come from the same batch of
production and thus to share more similarities than
two blades (MLEs) coming from different batches.
REFERENCES
Ahuja, R., Kumar, A., Jha, K. C. and Orlin, J. B., 2007.
Exact and Heuristic Algorithms for the Weapon-Target
Assignment Problem. Operations Research, 55(6), p.
1136–1146.
Dantzig, G. and Ramser, J., 1959. The Truck Dispatching
Problem. Management Science, 6(1), pp. 80-91.
ICORES 2018 - 7th International Conference on Operations Research and Enterprise Systems
262

Flöry, S., 2010. Constrained Matching of Point Clouds and
Surfaces, TU Wien: PhD Thesis.
Ford, L. R. and Fulkerson, D. R., 1962. Flows in Networks.
Princeton University Press.
Jonker, R. and Volgenant, A., 1987. A shortest augmenting
path algorithm for dense and sparse linear assignment
problems. Computing, Volume 38, p. 325.
Kuhn, H., 1955. The Hungarian Method for the Assignment
Problem. Naval Research Logistics Quaterly 2, pp. 83-
97.
Pinto, J. M. and Grossmann, I. E., 1998. Assignment and
sequencing models for the scheduling of process
systems. Annals of Operations Reasearch, Volume 81,
pp. 433-466.
Spivey, M. Z. and Powell, W. B., 2004. The Dynamic
Assignment Problem. Transportation Science, 38(4),
pp. 399-419.
Dynamic Linear Assignment for Pairing Two Parts in Production - A Case Study in Aeronautics Industry
263
