
A Framework Supporting Literacy in Mathematics and Software
Programming
Addressing Some Challenges in STEM Education
Georg Peters
1,2
, Tom Rueckert
1
and Jan Seruga
2
1
Department of Computer Science and Mathematics, Munich University of Applied Sciences,
Lothstr. 34, 8033 Munich, Germany
2
Faculty of Education and Arts, Australian Catholic University, 25A Barker Rd, Strathfield NSW 2135, Australia
Keywords: e-Learning, STEM Subjects, Mathematics Education, Software Programming, R-Project Software
Environment.
Abstract: The second half of the last century was characterised by a shift from manufacturing to services, particularly
in mature economies. This transformation has accelerated in the past decade, due to rapid progress in
information technology. Excellence in the so-called STEM subjects (science, technology, engineering and
mathematics) is crucial if countries are to remain competitive. Mathematics as a universally applicable method
is of special significance, as is IT, which impacts on virtually all industries and can dramatically change
economies. Literacy in mathematics and computers, therefore, is more important than ever for individuals,
companies and countries. We propose a framework based on R to support the training of students in these
crucial areas. We discuss its features, including platform neutrality, costs and specialization flexibility in our
paper.
1 INTRODUCTION
We are experiencing a rapid change towards a data
driven economy. Companies like the big social media
firms or the large global online retailers that collect
data on their customers enjoy strategic advantages
over so-called old economy firms that lack such direct
access to customer data. Buzz words like big data,
business analytics, business intelligence and data
science are used to describe this trend. Recently,
artificial intelligence has been rediscovered; it finally
seems to have reached a stage of development where
it can have a significant impact on real life.
Mathematics and computer skills are of crucial
importance when it comes to analyzing this data.
Knowledge in these fields is relevant not only to
professionals working in the area but also to ordinary
people who should understand, to a certain degree,
one of the major driving forces that may impact their
lives. From an economic point of view, and from
sociological and demographic perspectives,
mathematics and computer skills are essential to
maintain a functioning society.
Embedded into STEM subjects (science,
technology, engineering and mathematics), skills in
mathematics and software programming are already
fostered in schools and universities, while
corresponding apps for smartphones have gained
attention. The use of information technology to
support mathematics education has already been
successful in various studies (Ruthven & Hennessy,
2005; Niess, 2005).
What is needed now is a tool that seamlessly
covers basic as well as advanced mathematics and
also addresses statistical analysis and data mining
techniques. Furthermore, it would be desirable that
the tool provides access through a well-designed web-
based interface for beginners with an option for
programming in a more technically-oriented console
for advanced users.
The objective of our paper is to present a
framework which is intended to support literacy in
mathematics and software programming, addressing
some vital needs in education today. In the further
course of the paper, we give the framework the
working title M*TH-F
RAMEWORK.
The remainder of the paper is organized as
follows. In the next section, we briefly review the
Peters, G., Rueckert, T. and Seruga, J.
A Framework Supporting Literacy in Mathematics and Software Programming.
DOI: 10.5220/0006629304970506
In Proceedings of the 20th International Conference on Enterprise Information Systems (ICEIS 2018), pages 497-506
ISBN: 978-989-758-298-1
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
497
need for mathematics literacy and programming skills
and the respective performances of students in
selected countries. In Section 3, we analyze the major
requirements for the framework, followed by the
selection of an appropriate technological platform for
our framework. We briefly review important features
of the selected platform in Section 4 and, in Section
5, we introduce our framework to support literacy in
mathematics and programming and discuss its
properties. The paper concludes with a summary in
Section 6.
2 STUDENTS’ PERFORMANCE
IN MATHEMATICS IN
SELECTED COUNTRIES
In this section, we concentrate on mathematics,
stressing the need to remain competitive in a
globalized economy. We summarize the performance
of school students in mathematics according to the
international PISA study of the OECD and also
briefly address the need for programming skills.
2.1 Need for Mathematics and
Software Programming
The vital importance of mathematics has been
recognized by governments and industry around the
world.
Leading German engineering companies are
aware of the crucial importance of mathematics and
actively promote it. The former chairman of Siemens,
Peter Löscher, expressed it thus (cited at Neunzert &
Prätzel-Wolters, 2015): “Mathematics – this is the
language of science and technology. This makes it a
driving force behind all high technologies and, thus,
a key discipline for industrial nations. Without
mathematics, there is no progress and technical
innovation.” Dieter Zetscher, current chairman of the
automotive company Daimler, said (cited at Neunzert
& Prätzel-Wolters, 2015): “As does no other science,
mathematics helps us in our branch to solve the most
varied sorts of problems – and it is exactly this
universal applicability that makes it the royal
discipline.”
Moreover, related fields like data mining and
artificial intelligence that are based on mathematics
are becoming increasingly important. A good
understanding of these fields is not only of crucial
importance for professionals working in IT-related
jobs like computer science and information systems
but for an economy as a whole to remain competitive
in a globalized world.
Regarding the importance of teaching software
programming in schools, for example, the German
chancellor Angela Merkel remarked recently
(translated from Merkel (2017): "I am convinced [..].
that the ability to program, the easy ways of
programming, that children should learn to do this.
Because they will then have a basic understanding of
how a robot works, how certain things work, how an
app is created."
2.2 Performance in Mathematics and
Software Programming
Nevertheless, despite excellent job prospects, it is still
a challenge to motivate a sufficient number of
students to step into these fields and secure a sound
education in mathematics, computer science and
information systems at schools and universities.
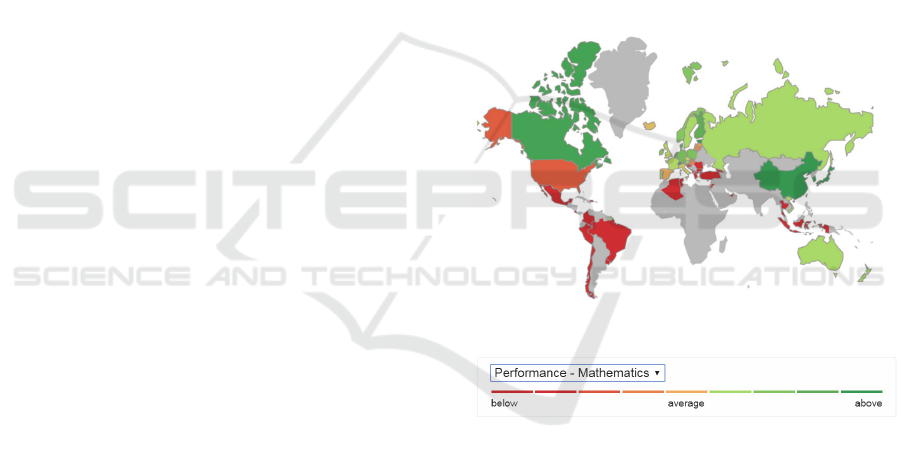
Figure 1: PISA - Performance in Mathematics in Selected
Countries in 2015 (OECD, 2016b).
Germany, for instance, is poor in natural resources
but has a large engineering sector, so a strong
performance in mathematics at school and university
is important to its economy. However, according to a
recent PISA study, German school students are not
amongst the top performers in mathematics. They
perform only slightly above average (OECD, 2016a).
Meanwhile, in the U.S.A., interest in STEM
subjects improved, but not in mathematics, according
to a recent study (Neuhauser & Cook, 2016): “The
2016 U.S. News/Raytheon STEM Index recorded a
slight rise in hiring, education and general interest in
technology and engineering over last year, while
math education and general interest in science
ICEIS 2018 - 20th International Conference on Enterprise Information Systems
498

declined.”
Performance in mathematics of the countries
covered by the PISA is depicted in Figure 1. The
study shows that eastern Asian countries like China,
South Korea and Singapore are top performers with
respect to education in mathematics. The countries on
the American continents, except Canada, are
performing under average while most countries in
Europe are ranked above average.
We are not aware of any similar study that
evaluates and compares programming skills of school
students in an international context. A possible reason
is that computer science software programming is not
a widely established subject in schools in many
countries. Due to its importance this makes the need
to support it even more pressing.
3 REQUIREMENTS FOR AND
SELECTION OF A PLATFORM
3.1 Requirements for the Framework
In this section, we present the results of our
requirements analysis for the platform that we use for
the framework to support literacy in mathematics and
programming.
In our analysis, we identified the following
criteria as essential to a framework’s success:
Cost efficiency
Platform independence
Size of the platform network
Comprehensiveness of the mathematical
implementations
Support for possible levels of user experience.
We address these criteria in more detail in the
following paragraphs.
Cost Efficiency. Most educational sectors around
the world suffer from budget constraints even though
education is regarded as possibly the most crucial
factor to address significant issues such as
overcoming inequality and poverty, and
strengthening the competiveness of firms and
economies in a globalized world. Financing a
framework, therefore, might be a considerable
challenge for many educational institutions. Hence, a
cost efficient, ideally free, approach is of crucial
importance for the success of the framework.
Platform independence. With respect to platform
independence we distinguish two factors, namely (1)
independency from hardware platforms and (2)
independency from software. The first is related to the
possible use of the framework on smartphones,
tablets and personal computers. The second
corresponds to the independence from any particular
operating system. Note that these two factors are
beginning to overlap, for example, see the first
attempts to use the Android operating system on
personal laptops and computers (and, of course, the
initially failed strategy of Microsoft to launch a
virtually identical Windows system for all platforms,
including smartphones, tablets and personal
computers).
Size of the platform network. The underlying
platform should be well accepted, i.e., the network of
users of the platform should be large. This criterion is
motivated by classic arguments well known from the
theory of network externalities (Katz & Shapiro,
1985). For example, a large network has positive
effects on learning since support is generally
available, ranging from (online) textbooks to
discussion group and forums. A large network also
makes it more likely that the platform will be
available for the foreseeable future. This would
secure the developers’ and users’ investment in the
framework.
Comprehensiveness of the mathematical
implementations. The platform should already
provide a large range of mathematical concepts and
predefined solutions that can be used immediately.
This avoids the cost and time of starting from scratch.
Possible Levels of User Experience. Here we refer
to the different needs of a diverse range of users,
including absolute beginners and experts. The
advantages of a diverse range of users are twofold.
First, the different groups can learn from each other:
the beginners learn from the advice of the experts and
the experts benefit from explaining and answering
questions from the beginners. Second, when a
beginner improves her/his knowledge she/he can
continue to use the same platform by gradually
increasing her/his level of expertise within the
framework.
3.2 Selection of a Platform for the
Framework
In our analysis, we distinguish between three
categories of possible platforms for the framework:
General purpose programming languages
Mathematics solution apps, webpages and
software
Numerical computing environments.
Note that in general some applications do not fit
into one single category but offer functionalities
across these categories.
A Framework Supporting Literacy in Mathematics and Software Programming
499

General purpose programming languages.
General purpose programming languages like C/C++
or Java provide excellent frameworks for virtually
any kind of task. In particular, due to its efficiency,
C/C++ has been a leading platform for the
implementation of mathematical/numerical problems
in industry and academia over the past decades. Take-
up by a wide range of respected libraries is an
impressive indicator of its success.
However, we wish to establish a framework that
suits beginners as well as advanced learners.
Programming languages like C/C++ are already too
“sophisticated” for beginners and will possibly lead
to frustration. On the other hand, implementing a
framework including the mathematical algorithms
from scratch would possibly exceed our resources,
even considering the advanced apps and websites
tools that are available.
Thus, general purpose programming languages do
not satisfactorily address the levels of user experience
that will be covered and also violate our cost
efficiency criteria.
Mathematics solution apps, software or
webpages. Examples of mathematics solution apps
are Mathway (mathway.com), MATH 42 (math-
42.com), MalMath (malmath.com) and Wolfram
Alpha (wolframalpha.com). All run on Android, and
Mathway, MATH 42 and Wolfram Alpha are also
available for further operating systems. Mathway and
Wolfram Alpha offer websites for mathematical
problem solving. Wolfram Alpha’s website even goes
beyond mathematics towards a structured general
purpose search engine.
While the apps and webpages are excellent for
addressing mathematical problems, they lack a
programming environment for advanced learners
who are wanting individually designed software that
perfectly fits their needs. Therefore, as with general
purpose programming languages, mathematics
solution apps, software or webpages do not
satisfactorily address our criterion about levels of user
experience.
Numerical computing environments. Leading
numerical computing environments include
Mathematica (wolfram.com/mathematica) and
MATLAB (mathworks.com/products/matlab.html).
While MATLAB has had a leading role in
engineering with many corresponding libraries,
Mathematica has a strong position in the education
sector and is also frequently used as a problem
solving tool in industry. Its particular strength is that
it integrates mathematical symbolic computation
functionality; it can, for example, symbolically
integrate or differentiate (note the same applies to the
related website Wolfram Alpha).
While Mathematica and MATLAB are
commercial products there are free alternatives
available, in particular to MATLAB. For example,
the numerical computing environment GNU Octave
(gnu.org/software/octave) claims to be compatible
with MATLAB; another popular environment, Scilab
(scilab.org/), is similar/partly compatible with
MATLAB.
R-Project (r-project.org) has gained increasing
popularity in the past decade. R started as a free
alternative to S as an environment for statistical
computing. Since then, its range of applications has
gone beyond statistics and now covers wide parts of
numerical analysis, data mining and mathematics.
According to the TIOBE Index (tiobe.com/tiobe-
index/), which ranks the popularity of programming
languages, it is leading the field of special purpose
languages for numerical computing, slightly ahead of
MATLAB: in August 2017, R is ranked #15 and
MATLAB #17 among all programming languages.
The core features of these numerical computing
environments include integrated development
environments (IDEs), purpose-built programming
languages, graphing utilities and respective
substantial libraries. Numerical computing
environments, therefore, generally address our
criterion about possible levels of user experience. All
these environments are excellent bases for the
framework.
Mathematica, with its mathematical symbolic
computation power, is an outstanding product and
leads the field in the educational sector. However, one
of our essential criteria in the framework selection
process was that the framework can be accessed for
free (cost efficiency criterion). Firstly, schools and
universities are under budget restraints that may make
it difficult or even impossible to obtain commercial
software and, secondly, students should be able to get
the framework for free and independent of their
enrolment status (for example whether they are a
current or former student). The cost efficiency
criterion also leads to the exclusion of MATLAB.
All remaining free numerical computing
environments run on all major operating systems for
personal computers. So, in terms of our platform
independence criterion they are equally suitable for
our framework. We would also consider the criterion
about comprehensiveness of the mathematical
implementations as fulfilled. However, a detailed
comparison is practically impossible: virtually
everyone can upload improved and new packages to
the R repository anytime. This has led to a puzzlingly
high number of packages, which is one of the biggest
ICEIS 2018 - 20th International Conference on Enterprise Information Systems
500

advantages - and disadvantages - of R.
Our final decision between GNU Octave, R and
Scilab, therefore, is based on network aspects (size of
the network of the platform criterion) and the
possibility of integrating different levels of user
experience (possible levels of user experience
criterion).
In relation to the size of the network, we have the
impression that R has a strong momentum which puts
it significantly ahead of GNU Octave and Scilab. R
and MATLAB family (in particular GNU Octave,
Scilab and MATLAB itself) are similarly popular
according to the TIOBE Index (see above). With
respect to the possibility of integrating different levels
of user experience, we found that R provides
excellent packages, particularly Shiny
(https://shiny.rstudio.com, see further down for
examples), that support the development of
interactive webpages to suit the needs of beginners.
The evaluation is summarised in Table 1. Note
that platforms with a minus (–) are excluded
(essential criteria) and the remaining criteria are not
further investigated. Therefore, general purpose
programming languages and mathematics solution
apps, software or webpages are excluded from any
further evaluation. The same applies to the
commercial numerical computing environments
Mathematica and MATLAB. Among the rest, we
consider R stronger with respect to its network size
and the possible levels of user experience that can be
addressed in comparison to GNU Octave and Scilab.
Hence R was selected as the platform for the M*TH-
F
RAMEWORK as it addresses most of the criteria well.
Its only considerable weakness is that it does not offer
symbolic computation functionalities like
Mathematica.
4 THE R-PROJECT
ENVIRONMENT
In this section, we briefly review the major features
of R-Project. Firstly, we describe its origin; then we
give a very brief impression about its power to deal
with mathematics and statistics. Lastly, we discuss
the package Shiny which supports the generation of
dynamic websites.
Table 1: Summary of the Evaluation of the Platforms.
Cost Efficiency Platform
Independency
Size of Network Comprehensivene
ss of Math.
Implementation
Possible Levels of
User Experience
General purpose programming language
C/C++,
Java etc.
–
not suitable for
beginners
Mathematics solution apps, software or webpages
MATH 42,
MalMath
etc.
–
limited flexibility
for experts
Numerical computing environments
Mathe-
matica
–
commercial tool
MATLAB
–
commercial tool
GNU
Octave
+
runs on all major
platforms
=
good
=
sufficient, no
symbolic comp.
=
R-Project +
runs on all major
platforms
+
excellent
=
sufficient, no
symbolic comp.
+
console+packages
for webpages
Scilab +
runs on all major
platforms
=
good
=
sufficient, no
symbolic comp.
=
Legend: + fine, = acceptable, – essential criterion, leads to exclusion.
A Framework Supporting Literacy in Mathematics and Software Programming
501

4.1 Fundamentals about R-Project
R-Project (r-project.org) was founded as an
alternative to S at the University of Auckland, New
Zealand, in 1993 (Ihaka, 1993). Initially its focus was
on statistical computing, but it has since become a
universal platform for mathematics, with a particular
strength in data analysis. In the past decade, it has
rapidly gained attention and is now used by both
academics and company professionals.
A core team organizes and maintains R-Project. In
addition to its core functions the user can write
packages and upload them to R repository. This
means there is a large community contributing
packages to virtually any area of mathematical
analysis.
4.2 R’s Programming Environment
The R software is console-based and can be accessed
by R’s standard console or by third party IDEs, with
RStudio (rstudio.org) probably the most popular (see
Figure 2 for a simple mathematics example using
RStudio IDE). R’s programming language is
optimized for statistical analysis and therefore
provides convenient commands to manipulate data
structures like vectors and matrices as well as more
complex structures like R’s data frames.
For example, the command for addressing the 5th
column of matrix a is:
a[,5]
or the multiplication of matrixes a and b is just one
command:
a %*% b
R not only provides virtually all standard
statistical functions, for example mean() or standard
deviation sd(), but also provides advanced
statistical methods in corresponding packages.
Besides statistics, several other areas of mathematics
are covered by R packages, for example operations
research with classic algorithms for linear
programming, or linear algebra, with linear equation
systems packages. Moreover, R has sophisticated
graphics and plotting functionalities (Murrell, 2011)
such as 2D and 3D plots, pie chart, histograms and
contour lines. R provides the possibility of writing
one’s own programs in R. The inclusion of code
writing in, e.g., C/C++ is also possible.
Figure 2: Mathematics Example in RStudio IDE (rstudio.com).
ICEIS 2018 - 20th International Conference on Enterprise Information Systems
502

Global companies also integrate R in their
products. Microsoft, for example, recently took over
Revolution Analytics, a company which specialises in
R. It maintains Microsoft R Open, an enhanced R
distribution (https://mran.microsoft.com/), and also
supports R in its cloud computing service Azure
(Olavsrud, 2015). Another example of the
commitment of major companies to R is Oracle,
which provides Oracle R Enterprise to support R
(Oracle, 2017). Hence, R is not only used in academia
but is also employed in and supported by companies
throughout the world as a professional statistical and
numerical computing environment (Heller, 2017;
Vance, 2009).
This popularity has generated comprehensive
literature about R. There are several text books on R,
for example Matloff (2011) and Teetor (2011), many
online resources, the most notable being
“Introduction to R” (Venables, Smith, R Core Team,
2017) by some of the main drivers of R, and a range
of discussion groups and blogs.
In our context so far, R is an excellent platform
for advanced learners in mathematics and data
analysis who can develop their mathematical skills as
well as their programming experience. However, this
console-driven programming environment would
probably overwhelm most beginners in mathematics.
For this user group app- or web-based interfaces
like MATH 42, MalMath and others would provide a
better starting point. However, as we discuss in the
next section, R has also excellent packages that
support the development of user-friendly interactive
interfaces.
4.3 Interfaces of R
Besides the console, R has strong export facilities
including several packages that help the user report
the results of an analysis. These include Sweave
(Leisch, 2016) that generates LaTeX documents from
R code.
Another package that supports the reporting is
Markdown (rmarkdown.rstudio.com/). It can
generate Word, HMTL or LaTeX/PDF files. The
basic workflow of the generation of such documents
is shown in Figure 3.
For the M*TH-F
RAMEWORK, we use R’s Shiny
package which is a web application framework
(Chang, 2017) that generates interactive and dynamic
webpages from R. Due to limited space we refrain
from a detailed technical discussion of the Shiny web
application framework and refer the reader to the
respective webpages and documents for further
information. The homepage of the Shiny framework
at https://shiny.rstudio.com/ is an especially rich
resource, providing impressive examples for websites
generated by Shiny and detailed documentations on
the framework.
An example for a webpage generated by the
framework is depicted in Figure 4. In the next section,
we discuss the concept and the layout of these
webpages.
5 A COMPUTER-BASED
FRAMEWORK FOR
MATHEMATICAL EDUCATION
In this section, we present a computer-based
framework for mathematical education based on the
R-Project.
5.1 Layout of the Web-based Interface
As already mentioned, an example for the M*TH-
F
RAMEWORK is depicted in Figure 4. In this case, the
screenshot was taken from the framework running in
web browser on a personal computer. However, on
smartphones and tablets the layouts are virtually
identical, allowing the user to switch seamlessly
between her/his devices. Therefore, it is sufficient to
discuss the layout as shown in Figure 4.
Figure 3: Workflow of R Markdown to Generate Reports (RStudio, 2014).
A Framework Supporting Literacy in Mathematics and Software Programming
503
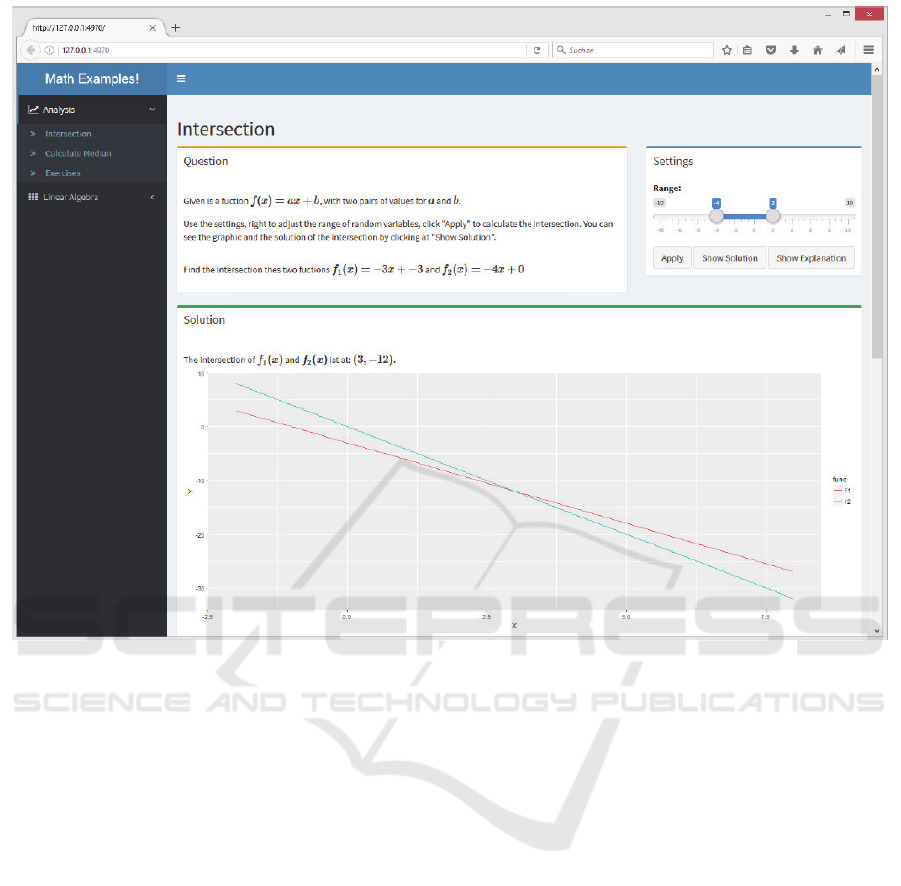
Figure 4: Mathematics Example for a Webpage of the Framework.
On the left side of the browser a navigation bar
shows the tasks that are available. On the right side
the selected task is presented. In the example, the task
is to determine the intersection point of two linear
functions. The frame of the task has an orange bar at
the top. To the right there is another frame, with a blue
bar at the top. In this frame settings can be chosen,
such as the range of the parameters of the two linear
functions. Within this range the parameters are set
randomly to provide new tasks every time.
Furthermore, the command buttons are located in this
frame. The standard ones are “Apply”, “Show
Solution” and “Show Explanation”. While the latter
two are self-explanatory, “Apply” means that a new
task is generated based on the range of the parameters
as defined in the frame. In a future release of the
framework, we are considering implementing a fourth
standard button (“Show Code”) that bridges the gap
between the interface and the underlying R code.
In Figure 4, the solution is shown in a separate
frame with a green bar at the top. Besides the
numerical values of the intersection, a graph is also
shown to illustrate the solution. The mathematical
background of the solution can be found when the
user scrolls further down in the window; it is not
presented here due to space restrictions.
The presentation of the M*TH-F
RAMEWORK on a
smartphone is virtually the same since it is a website-
based framework with no separate app for mobiles.
This has the advantage that the framework runs on
personal computers/laptops and smartphones
independently of an operating system. This means
that the development and maintenance costs are
minimal in comparison to a solution where the
software needs to be adapted to PC and smartphone
operating systems. In particular, for smartphones
there is no need to develop and maintain different
apps for different mobile environments.
Finally, besides the core application involving
mathematics tasks, it is intended that the framework
will also support functions that let students interact
with each other and communicate with their
instructors (see Figure 5a). It should have a memo
board (see Figure 5b) where messages are displayed,
for example new students joining a course or the
proportion of exercises completed. It will also
provide basic tools to manage and monitor the
progress of a student from both the student and the
ICEIS 2018 - 20th International Conference on Enterprise Information Systems
504

Figure 5: Dashboard and Messaging Functionality of the Framework.
tutor’s perspective (see Figure 5c).
A feasibility study confirmed that these
functionalities can be implemented in R. They have
not been implemented yet as our current focus is on
extending and completing the portfolio of
mathematics tasks and developing tasks in the area of
data mining. They are scheduled for future versions
of the framework.
5.2 Discussion
The project so far has confirmed that R is an excellent
platform for the development of the framework.
Its specialized programming language makes it a
perfect environment to develop respective code very
quickly. Furthermore, CRAN (Comprehensive R
Archive Network at https://cran.r-project.org/), with
its large number of packages, is a rich repository for
“off the shelf” applications. These packages not only
support solutions for mathematical algorithms but
also support exporting functions and frameworks for
interactive dynamic websites.
R’s large network, which embraces both academia
and major international companies, has led to an
active community that provides support, including
IDE and special purpose packages. Many blogs and
tutorials can be found free of charge on the web.
Therefore, the framework is not only a tutorial in
mathematics but it also introduces beginners to R, one
of the leading platforms for statistical analysis and
data mining. In this context, it is a very suitable
environment to gain and enhance programming
experience. Furthermore, as many applications in
academia and industry show, it can be used to address
real life problems. Last but not least, there are
practically no entry barriers as it runs on virtually any
operating system and is free.
6 CONCLUSIONS
In this paper, we presented a framework for
mathematics education using R-Project. The
framework also supports the acquisition of
knowledge in computer science and information
systems, in particular in programming.
Crucial advantages of R are that it is free and runs
on virtually any platform, so it can be used regardless
of budget constraints or a given computer
infrastructure. Another important advantage is that it
A Framework Supporting Literacy in Mathematics and Software Programming
505

provides facilities that support beginners (for
example, through its interactive Shiny web
framework) as well as experts (by its programming
facilities in the console).
Finally, R already offers a portfolio of sound
mathematical functions. Many packages, often
written by senior experts in their field or even by the
people who proposed the algorithms, offer a wide
range of mathematical tools. Although R’s main
strength is in the field of statistics and data mining,
several other fields of mathematics are also covered.
Therefore, R is an ideal platform for the
framework to support mathematics and computer
literacy. Presently, we are extending the portfolio of
mathematical tasks within the Shiny web framework
and working on pathways to bridge the gap between
web- and console-based access to mathematics.
Dashboards, messaging and monitoring tools are
planned for a future version.
We are also intending to form a group of
educators who use and contribute to the framework to
further advance its coverage of important fields of
mathematics.
In the long run, a portfolio of applications in data
mining would be desirable to address one of the
hottest areas in computer science and information
systems today.
REFERENCES
Chang, W., 2017. Package ‘shiny’. (https://cran.r-
project.org/web/packages/shiny/shiny.pdf, accessed
18.08.2017).
Heller, M., 2017. 10 Hot Data Analytics Trends - and 5
Going Cold. CIO (http://www.cio.com/
article/3213189/analytics/10-hot-data-analytics-trends-
and-5-going-cold.html, accessed 18.08.2017).
Ihaka, R., 1998. R: Past and Future History. Report
Statistics Department, University of Auckland
(https://www.stat.auckland.ac.nz/~ihaka/downloads/In
terface98.pdf, accessed 18.08.2017).
Katz, M. L., Shapiro, C., 1985. Network Externalities,
Competition, and Compatibility. The American
Economic Review 75(3), 424-440.
Leisch, F., R Core Team, 2016. Sweave User Manual.
Technical Report ETH Zuerich (https://stat.ethz.ch/R-
manual/R-devel/library/utils/doc/Sweave.pdf, accessed
18.08.2017).
Matloff, N., 2011. The Art of R Programming: A Tour of
Statistical Software Design. No Starch Press, San
Francisco.
Merkel, A., 2017. StZ im Gespräch / treffpunkt foyer - Dr.
Angela Merkel. Stuttgarter Zeitung & Stuttgarter
Nachrichten. (Youtube https://youtu.be/h2ifRKQqTus,
accessed 11.09.2018).
Murrell, P., 2011. R Graphics. CRC Press, Taylor &
Francis Group, Boca Raton, FL, 2
nd
edition.
Neuhauser, A., Cook, L., 2016. 2016 U.S. News/Raytheon
STEM Index Shows Uptick in Hiring, Education. U.S.
News & World Report (https://www.usnews.com/
news/articles/2016-05-17/the-new-stem-index-2016,
accessed 18.08.2017).
Neunzert, H., Prätzel-Wolters, D., 2015. Problems Trump
Method: A Somewhat Different Mathematics for a
Somewhat Different Institute. In Currents in Industrial
Mathematics. Springer-Verlag, Berlin, Heidelberg, p.
3-30.
Niess, M. J., 2005. Preparing teachers to teach science and
mathematics with technology: Developing a technology
pedagogical content knowledge. Teaching and Teacher
Education 21(5), 509-523.
OECD, 2016a. Germany: Country Note – Results from
PISA 2015 (https://www.oecd.org/pisa/PISA-2015-
Germany.pdf, accessed 18.08.2017).
OECD, 2016b. PISA: Programme for International Student
Assessment (https://www.oecd.org/pisa, accessed
18.08.2017).
Olavsrud, T., 2015. Microsoft closes acquisition of R
software and services provider. CIO
(http://www.cio.com/article/2906456/data-
analytics/microsoft-closes-acquisition-of-r-software-
and-services-provider.html, accessed 18.08.2017).
Oracle Inc., 2017. Oracle R Enterprise
(http://www.oracle.com/technetwork/database/databas
e-technologies/r/r-enterprise/overview/index.html,
accessed 18.08.2017).
Ruthven, K and Hennessy, S., 2002. A practitioner model
of the use of computer-based tools and resources to
support mathematics teaching and learning.
Educational Studies in Mathematics 49(1), 47-88.
RStudio Inc., 2014. R Markdown Cheat Sheet.
(https://www.rstudio.com/wp-
content/uploads/2015/02/rmarkdown-cheatsheet.pdf,
accessed 18.08.2017).
Teetor, P., 2011. R Cookbook. O'Reilly Media, Sebastopol
CA.
Vance, A., 2009. Data Analysts Captivated by R’s Power.
New York Times (http://www.nytimes.com/
2009/01/07/technology/business-
computing/07program.html, accessed 18.08.2017).
Venables, W. N., Smith, D. M., R Core Team, 2017. An
Introduction to R, version 3.4.1 (https://cran.r-
project.org/doc/manuals/R-intro.pdf, accessed
18.08.2017).
TRADEMARKS
RStudio and Shiny are trademarks of RStudio Inc.
Mathematica is a trademark of Wolfram Research, Inc.,
MATLAB is a trademark of MathWorks, Inc. Microsoft
and Windows are trademarks of Microsoft Inc. and Oracle
is a trademark of Oracle Inc. All other trademarks are
property of their respective owners.
ICEIS 2018 - 20th International Conference on Enterprise Information Systems
506
