Bayesian Network and Structured Random Forest Cooperative Deep

Learning for Automatic Multi-label Brain Tumor Segmentation

Samya Amiri

1,2

, Mohamed Ali Mahjoub

and Islem Rekik

Isitcom - Higher Institute of Computer Science and Communication Techniques of Hammam Sousse,

University of Sousse, Tunisia

LATIS Eniso - National Engineering School of Sousse, University of Sousse, Tunisia

BASIRA Lab, CVIP Group School of Science and Engineering, Computing, University of Dundee, U.K.

Keywords: Structured Random Forest, Bayesian Network, Deep Cooperative Network, Autocontext Model, Brain

Tumor Segmentation, MRIs.

Abstract: Brain cancer phenotyping and treatment is highly informed by radiomic analyses of medical images.

Specifically, the reliability of radiomics, which refers to extracting features from the tumor image intensity,

shape and texture, depends on the accuracy of the tumor boundary segmentation. Hence, developing fully-

automated brain tumor segmentation methods is highly desired for processing large imaging datasets. In this

work, we propose a cooperative learning framework for multi-label brain tumor segmentation, which

leverages on Structured Random Forest (SRF) and Bayesian Networks (BN). Basically, we embed both

strong SRF and BN classifiers into a multi-layer deep architecture, where they cooperate to better learn

tumor features for our multi-label classification task. The proposed SRF-BN cooperative learning integrates

two complementary merits of both classifiers. While, SRF exploits structural and contextual image

information to perform classification at the pixel-level, BN represents the statistical dependencies between

image components at the superpixel-level. To further improve this SRF-BN cooperative learning, we

‘deepen’ this cooperation through proposing a multi-layer framework, wherein each layer, BN inputs the

original multi-modal MR images along with the probability maps generated by SRF. Through transfer

learning from SRF to BN, the performance of BN improves. In turn, in the next layer, SRF will also benefit

from the learning of BN through inputting the BN segmentation maps along with the original multimodal

images. With the exception of the first layer, both classifiers use the output segmentation maps resulting

from the previous layer, in the spirit of auto-context models. We evaluated our framework on 50 subjects

with multimodal MR images (FLAIR, T1, T1-c) to segment the whole tumor, its core and enhanced tumor.

Our segmentation results outperformed those of several comparison methods, including the independent

(non-cooperative) learning of SRF and BN.

1 INTRODUCTION

The emergence of the new field of radiomics, which

addresses the conversion of medical images into

mineable data through the extraction of large

amounts of quantitative features (Aerts et al.,2014),

has led to major advances in tumor diagnosis,

phenotyping, and patient treatment planning.

Notably, the reliability of radiomics fundamentally

depends on the accuracy of the tumor boundary

segmentation, as radiomic features are generally

extracted from within and around the tumor lesion.

Hence, fully automated brain tumor segmentation

methods are highly desired. This will in part

alleviate the burden of manually segmenting tumor

lesions on brain images, as well as facilitate the task

of statistically analyzing big brain tumor image

datasets for clinical studies. The large variation in

tumor characteristics (shape, position, texture)

makes the segmentation task very challenging.

To solve this problem, several previous works

considered tumor segmentation as a classification

problem at the pixel, voxel, patch or region level

(Havaei et al., 2017; Koley et al.,2016; Lefkovits et

al.,2016; Christ at al., 2017; Folgoc et al., 2016). In

particular, Random Forest (RF) was previously used

for tumor segmentation, where basically each input

intensity image patch is mapped to a class label at

Amiri, S., Mahjoub, M. and Rekik, I.

Bayesian Network and Structured Random Forest Cooperative Deep Learning for Automatic Multi-label Brain Tumor Segmentation.

DOI: 10.5220/0006629901830190

In Proceedings of the 10th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2018) - Volume 2, pages 183-190

ISBN: 978-989-758-275-2

183

Figure 1: Proposed deep SRF-BN cooperative learning for multi-label tumor lesion segmentation. In each layer, the SRF

inputs different features extracted at the 2D patch-level and generates an intermediate segmentation result, while the BN

inputs different features extracted at the superpixel-level. In the next layer, SRF has two inputs: the original patch features

and the output segmentation result from the previous layer; while BN has three inputs: the original patch features, the output

segmentation result from the previous layer and the output SRF segmentation map in the same layer. This deep multi-layer

cooperative-learning architecture provides contextual information for both classifiers through the intermediate segmentation

maps to gradually improve their learning.

at the center pixel of the patch, thereby performing

patch-to-pixel mapping (Breiman, 2001). As a

variant of RF, Structured Random Forest (SRF) was

used to take into account the image structure when

producing the final segmentation maps, through

estimating a patch-to-patch mapping. This allows

integrating more spatial information through

averaging neighboring output label patches. SRF

demonstrated high-performance in different

challenging classification tasks such as in (Zhang et

al., 2016; Kontschieder et al., 2011; Zhang et al.,

2017).

On one hand, the increasingly popular

convolutional neural networks were used for tumor

segmentation (Havaei et al., 2017). However, fine-

tuning of an entire deep network still requires a lot

of efforts and resources, and SVM-based methods

also involve time consuming grid search and cross

validation to identify good regularization

parameters. In addition, when multiple pre-trained

deep CNN models are available, it is unclear which

pre-trained models are appropriate for target tasks

and which classifiers would maximize accuracy and

efficiency. On the other hand, among all the

graphical models as Neural Networks and decision

trees, Bayesian Networks (BNs) nicely overcome

these limitations. Indeed, they are powerful tools in

first representing probabilistic dependencies and

uncertainty between different image features (Zhang

and Ji, 2008), second modeling and fusing complex

relationships between image features of different

natures (e.g., multimodal features), and third

handling noisy as well as missing signals in images.

Together, these facts made

BNs well suited for multimodal image

classification since they are easily adaptable for

multi-label problems compared to other classifiers

such as SVM, moreover they encode dependencies

between the learned features of different class labels.

While different object segmentation and action

recognition problems in computer vision were

solved based on Bayesian graphical representations

(Panagiotakis et al., 2011; Zhang and Ji, 2011; Yang

at al., 2015), the use of BN remains absent in tumor

segmentation literature.

Although regarded as strong classifiers, both

SRF and BN might suffer from a few limitations

when used separately. For instance, SRF does not

perform well when classifying transitions between

label classes, while BN parameter learning such as

prior probabilities is challenging and

computationally expensive. Combining them

together, may help iron out the weaknesses of each

when used separately as well as leverage on their

strengths (i.e., preserving the learned structural

information for SRF and the integration of

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

184

multimodal features for BN). Hence, we propose to

combine both SRF and BN classifiers into a multi-

layer deep architecture, where they can cooperate to

perform joint multi-label brain tumor segmentation.

Our framework incorporates different features

derived from different image components

(superpixel and patch) such as intensity features. We

further integrate contextual features, which capture

semantic relations (i.e., label relations) between

neighboring patches and enforce spatial consistency

between patches within and around the tumor lesion.

The proposed SRF-BN cooperative learning strategy

ensures the transfer of the probability maps

outputted from SRF to BN of the same layer, which

enables the integration of both patch and superpixel

level knowledge in a unified framework.

Additionally, in the spirit of auto-context model, the

output segmentation map of each layer is further

aggregated with the original input features, thereby

augmenting the inputs to subsequent layers. This

allows boosting the classification performance of

both classifiers and improving feature learning,

which progressively refines the segmentation result

from layer to layer.

2 DEEP COOPERATIVE

LEARNING FOR

MULTI-LABEL

CLASSIFICATION

PREPARATION

In the following, we present the main steps of our

multi-label cooperative-learning based segmentation

framework. Fig.1 illustrates the proposed multi-layer

architecture composed of cascaded SRF-BN blocks,

where each block ultimately outputs the BN

posterior probability map fed as semantic context to

the next SRF-BN block of the subsequent layer.

Specifically, in each block excluding the first one,

SRF inputs the intensity patch features of the

original MR scans with the segmentation result (i.e.,

semantic context) of the previous layer. In turn, the

prior probabilities required for BN learning are

statistically computed using (1) the probability

segmentation maps generated by SRF of the same

layer and (2) the BN posterior probability of the

previous layer. In the following sections, we will

present the design of the two components (SRF and

BN) making each block in our deep auto-context

multi-label segmentation architecture.

2.1 Structured Random Forest

SRF is a variant of the traditional Random Forest

classifier, which is able to handle and preserve the

structure of different labels in the image

(Kontschieder et al., 2011). While, standard RF

maps an intensity feature vector extracted from a 2D

patch centered at pixel x to the label of its center

pixel x (i.e., patch-to-pixel mapping), SRF maps the

intensity feature vector to a 2D label patch centered

at x (patch-to-patch mapping). This is achieved at

each node in the SRF tree, where the function that

splits patch features between right and left children

nodes depends on the joint distribution of two labels:

a first label at the patch center x and a second label

selected at a random position within the training

patch (Kontschieder et al.,2011). We also note that

in SRF, both feature space and label space nest

patches that may have different dimensions. Despite

its elegant and solid mathematical foundation as well

as its improved performance in image segmentation

compared with RF, SRF might perform poorly at

irregular boundaries separating different label

classes since it is trained using regularly structured

patches (Kontschieder et al., 2011). Besides, it does

not include contextual information to enforce spatial

consistency between neighboring label patches.

To address these limitations, we propose to

embed SRF into a deep autocontext framework,

where the contextual information is provided by a

Bayesian network which learns to segment the

image at the superpixel level, allowing to better

capture irregular boundaries in the image.

2.2 Bayesian Network

Various BN-based models have been proposed for

image segmentation (Zhang and Ji, 2008;

Panagiotakis et al., 2011; Zhang and Ji, 2011; Guo et

al., 2017). In our work, we adopt the BN architecture

proposed in (Zhang and Ji, 2011). As a

preprocessing step, we first generate the edge maps

from the input MR image modalities (Fig. 1). The

edge map consists of a set of superpixels {Sp

},i=1,..,N (or regional blobs) and edge segments

},j=1,..,L.

We define our BN as a four-layer network,

where each node in the first layer stores a

superpixel. The second layer is composed of nodes

each storing a single edge from the edge map. The

two remaining layers store the extracted superpixel

features and edge features, respectively. During the

training stage, for BN parameters, we define the

prior probability of p(Sp

) as a uniform distribution

Bayesian Network and Structured Random Forest Cooperative Deep Learning for Automatic Multi-label Brain Tumor Segmentation

185

and then learn the conditional probability p(MS

│Sp

) representing the relationship between the

superpixel features and their corresponding labels

using a mixture of Gaussians model. In addition, we

empirically define the conditional probability

modeling the relationships between each superpixel

label and each edge state (i.e., true or false edge)

p(E

│Pa (E

) ), where Pa (E

) denotes the parent

superpixel nodes of E

During the testing stage, we learn the BN

structure encoding the contextual relationships

between superpixels and edge segments.

Specifically, each edge node has for parent nodes the

two superpixel nodes that are separated by this edge.

In other words, each superpixel provides contextual

information to judge whether the edge is on the

object boundary or not. If two superpixels have

different labels, it is more likely that there is a true

object boundary between them, i.e. E

=1, otherwise

=0. Although automatic segmentation methods

based on BN have shown great results in the state-

of-the-art, they may perform poorly in segmenting

low-contrast image regions and different regions

with similar features (Zhang and Ji, 2011). To

further improve the segmentation accuracy of BN,

we propose to include additional information

through cooperative learning using SRF.

2.3 SRF-BN Cooperative Learning

(One Layer)

To take advantage of the strengths of both classifiers

and overcome their limitations, we first propose a

one-layer cooperative learning strategy, where BN

benefits from the learned patch-to-patch mapping by

SRF. First, the trained SRF generates the

segmentation result, using the feature patches

extracted from the different MRI modalities of the

testing subject. Then, BN uses the SRF segmentation

result to define the prior probabilities p(Sp

) for each

superpixel region Sp

. Hence, with this cooperative

learning, the BN prior probabilities are estimated

based on the input SRF segmentation probability

maps. Such one-layer cooperative learning strategy

only boosts the BN performance since it is

performed in one way (from SRF to BN), while SRF

does not benefit from BN learning.

2.4 Deep SRF-BN Cooperative

Learning (Two Layers)

To address the aforementioned limitation of the one-

layer SRF-BN architecture, we further propose to

deepen the cooperative learning between SRF and

BN in the spirit of auto-context model (Tu and Bai,

2010). Basically, in the proposed deep auto-context

SRF-BN cooperative learning architecture, each

layer inputs the segmentation result of the previous

layer to boost the per formance of both SRF and BN

classifiers. In each layer, excluding the first one,

SRF classifier inputs the segmentation result of the

previous layer along with the original input

multimodal feature patches (Fig. 1). This allows the

integration of contextual features learned at both the

patch level (from SRF in the previous layer) and

superpixel level (from BN in the previous layer).

Similarly, BN inputs the segmentation result of the

previous layer along with the original input

multimodal superpixel features, while adding the

probability segmentation map output of the SRF in

the same layer. In this way, BN prior probabilities

are updated in each layer based on the posterior

probability of the previous layer and the SRF

probability map in the same layer.

2.5 Preprocessing and Features

To improve the performance of our segmentation

framework, we perform a few preprocessing steps.

Hence, we apply the N4 filter for inhomogeneity

correction, and use the histogram linear

transformation for intensity normalization. To train

the previous models, we use conventional features

(e.g., patch intensity) and we also propose a rich

feature set as follows:

▪ Statistical Features: First order operators

(mean, standard deviation, max, min, median,

Sobel, gradient); higher order operators

(laplacian, difference of gaussian, entropy,

curvatures, kurtosis, skewness); texture features

(Gabor filter); spatial context features

(symmetry, projection, neighborhoods)

(Prastawa et al., 2004).

▪ Symmetric Features: This is originally used to

describe and to exploit the symmetrical

properties of the brain structure. Thus, we define

the symmetry descriptor characterizing the

differences between symmetric pixels with

respect to the mid-sagittal plane. The adopted

symmetry measure is the intensity variance.

3 RESULTS AND DISCUSSION

In this section, we display the evaluation results of

our proposed brain tumor segmentation framework

on the Brain Tumor Image Segmentation Challenge

(BRATS, 2015) dataset. It contains brain MRI scans

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

186

Table 1: Segmentation results of the proposed framework and comparison methods averaged across 50 patients.(HT: whole

Tumor; CT: CoreTumor; ET: Enhanced Tumor; L=i, i=1,_,3 denotes the number of layers; * indicates outperformed

methods with p-values<0.05.

Results

Dice score

Features

Intensity

Intensity+symmetry

descriptor

Intensity + statistical

features

Intensity + statisical

features+symmetry

descriptor

Methods

Deep-AC

SRF-BN(L=3)

86,8

75,9

73,8

87,2

76,3

89,09

78,4

78,9

89,1

80,92

79,2

Deep-AC

SRF-BN (L=2)*

73,65

70,6

85,4

74,87

73,3

88,79

77,8

78,1

88,9

78,2

78,9

SRF-BN (L=1)*

79,2

70,15

70,85

82,5

72,6

83,6

72,88

70,05

AC-SRF*

75,29

58,69

32,5

70,05

37,12

80,23

37,5

SRF*

72,9

75,8

35,2

BN*

62,96

30,8

70,8

71,3

for more than 200 patients with high-grade gliomas.

For each patient, the four MRI modalities along with

the corresponding manually labeled glioma's

segmentation are available; they are rigidly

coregistered and resampled to a common resolution.

To generate the oversegmented MR image

modalities we extract the edge-map from the FLAIR

MRI using SLIC oversegmentation algorithm

(Achanta et al., 2010) then we apply it for the

corresponding T1.c and T2 MRIs. We fix the

number of superpixels to 1000 and the compactness

to 10.

For the BN model, the conditional probabilities

modeling the relationships between the superpixel

labeling and the edge state are fixed as follows:

p(E

│Pa (E

) ) = 0.8 if the parent region nodes have

different labels and 0.2 otherwise. For the SRF, we

use a 10x10 feature patches and a 7x7 label patches

to train 15 trees using 500 iterations for the node

tests.

In our experiments we show a comparison to

several baseline methods: SRF and BN used solely,

the auto-context SRF (AC-SRF) and SRF-BN

cooperative learning approach (SRF-BN (L=1)).

Besides, we test the influence of the layer's number

on our deep auto-context SRF-BN framework. The

classifiers were trained using leave-one-patient

cross-validation experiments. The quality of the

obtained segmentation was evaluated on the basis of

the manually annotated ground truth using the well-

known Dice index. In Fig. 2, we show some

qualitative segmentation results and in Table. 1 and

Fig. 3 we provide the mean Dice index over 50

testing subject randomly taken from the Brats

dataset.

According to the qualitative and quantitative

results, the proposed segmentation approach clearly

outperforms the baseline methods, independently of

the number of layers, with highly statistical

significance (p_value <0.05). This proves that (1)

leveraging the two classifiers does alleviate their

limitations (2) the integration of the superpixel

features and patch features in a deep manner boosts

the performance of the segmentation framework (3)

the information fusion of multiple image modalities.

The feature set highly influences the

classification results of our framework as well as the

baseline methods. In this respect, the weak effect of

the symmetry descriptor can be explained by the

miss-detection of the mid-sagittal plane for some

subjects.

In addition, we have performed 5-cross

validation on the whole dataset (220 subjects) to

benchmark our results against (Zhao et al., 2016)

which integrated a Fully Convolutional Neural

Network and Conditional Random Fields for

BRATS 2015 segmentation. Our deep SRF-BN

cooperative learning still outperformed all

comparison methods (p-value <0.05) and in

particular the proposed method in (Zhao et al.,

2016): 0.88 vs 0.8 for whole, 0.78 vs 0.68 for core,

and 0.68 vs 0.65 for enhanced tumor. Although our

results slightly dropped using using 5-fold cross-

validation, they still achieve the best performance.

Bayesian Network and Structured Random Forest Cooperative Deep Learning for Automatic Multi-label Brain Tumor Segmentation

187

Figure 2: Qualitative segmentation results for four representative subjects using different segmentation methods: (a) the BN

segmentation result; (b) the SRF segmentation result, (c) the auto-context SRF; (d) SRF+BN segmentation result; (e) our

method (2 layers); (f) our method (3 layers); (g) the ground truth segmentation map.

Also, all proposed and comparison methods

significantly improved when using 3 modalities

compared with 1 by 8-9%. The training time took

about 5 hours and testing on one image took about 4

minutes.

We would like to note that the use of the term

learning ‘transfer’ and ‘deep’ learning was meant in

the broad sense of both words: (1) mutual

autocontext information (semantic map) transfer

between BN and SRF classifiers for progressively

improving their performances, and (2) ‘deepening’

our SRF-BN architecture to gradually improve their

cooperative learning differs from deep neural

networks, although both architectures can go deeper.

However, unlike deep one-step CNN architectures,

our method is able to consider appearance and

spatial consistency between neighboring superpixels

and patches via the gradual autocontext feed

between SRF and BN. We also stopped at layer

(L=3) in depth since the improvement became

negligible at L>3.

Although the proposed framework showed good

segmentation results thanks to the deep cooperation

between the two classifiers (BN and SRF); a few

limitations can be pointed out for further

improvements:

(1) Edge-map estimation. The considered edge-map

is estimated from a single modality (i.e.,

FLAIR), which limits the learned Bayesian

mapping to one type of imaging data.

Estimating edge-maps from different modalities

(e.g., T1.c and T2 MRIs) will help capture

different radiomic properties of the tumor lesion

especially around its boundary.

(2) Unidirectional flow between classifiers. The

learning transfer between the classifiers of the

same block as well as through the pipeline is

unidirectional, which means it can only go from

one classifier to the next one. Hence there is no

mutual benefit between the classifiers of the

same block.

(3) Hemispheric brain symmetry detection. The

brain symmetry method that we used (Loy and

Eklundh, 2006) fails in detecting the mid-sagittal

plane in a few cases. This might produce

unreliable symmetric features.

We anticipate that addressing these limitations will

further boost up the performance of our proposed

framework. We plan to investigate these in our

future work on a larger dataset.

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

188

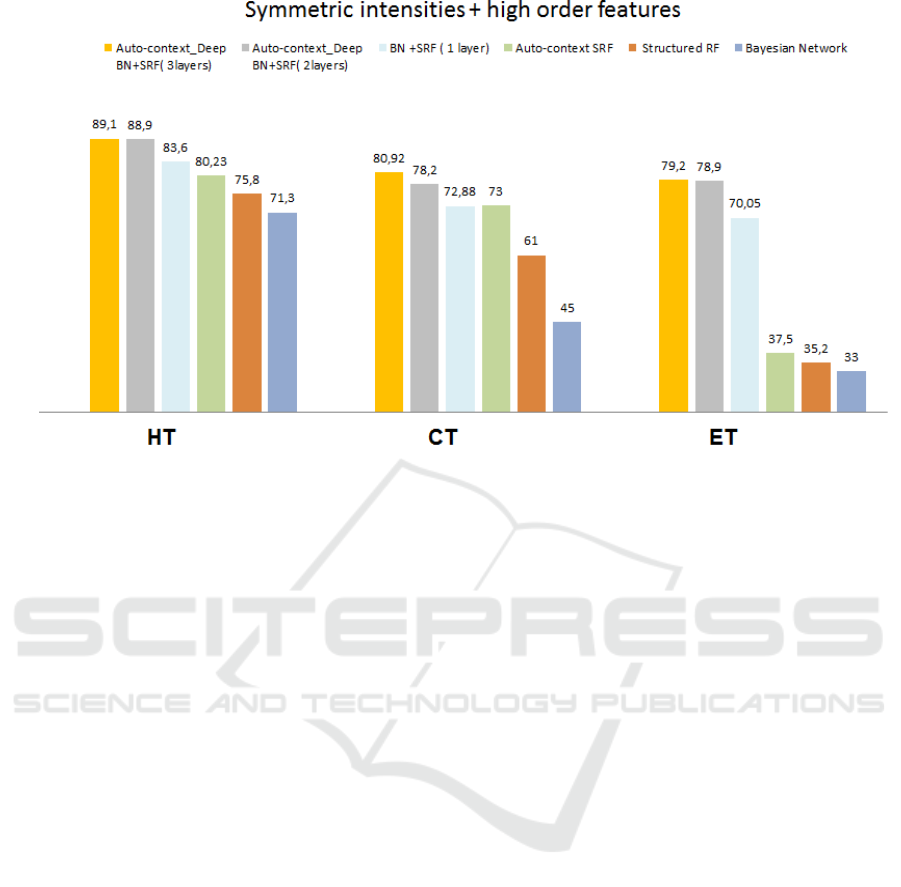
Figure 3: Average Dice index across 50 subjects using our proposed framework and all comparison methods for the three

tumor tissue classes (whole:HT, core:CT, and enhanced:ET).

4 CONCLUSIONS

In this paper, we proposed an automatic brain tumor

segmentation method based on a cooperative

learning between two classifiers, Structured RF and

BN, embedded within a deep auto-context

architecture. The experimental results prove the

efficiency of our proposed concept. Thus, SRF-BN

cooperative learning method outperforms the two

classifiers used solely, which proves that their

combination alleviates their limitations. Moreover,

the application of the deep auto-context architecture

has shown better performances for both the

quantitative and the qualitative results demonstrating

its effectiveness to boost the two classifiers and to

improve the feature learning.

Since the obtained results showed the

effectiveness of stacking SRF and BN within a

multi-label segmentation framework, we intend to

explore other architectures composed of these two

classifiers while addressing the limitations of our

proposed framework. Besides we will compare our

method with deep learning methods using multiple

BRATS testing datasets, including BRATS 2013.

REFERENCES

Aerts, H. J., Velazquez, E. R., Leijenaar, R. T., Parmar,

C., Grossmann, P., Cavalho, S., ... & Hoebers, F.

(2014). Decoding tumour phenotype by noninvasive

imaging using a quantitative radiomics approach.

Nature communications, 5.

Havaei, M., Davy, A., Warde-Farley, D., Biard, A.,

Courville, A., Bengio, Y., ... & Larochelle, H. (2017).

Brain tumor segmentation with deep neural

networks. Medical image analysis, 35, 18-31.

Koley, S., Sadhu, A. K., Mitra, P., Chakraborty, B., &

Chakraborty, C. (2016). Delineation and diagnosis of

brain tumors from post contrast T1-weighted MR

images using rough granular computing and random

forest. Applied Soft Computing, 41, 453-465.

Lefkovits, L., Lefkovits, S., & Szilágyi, L. (2016,

October). Brain Tumor Segmentation with Optimized

Random Forest. In International Workshop on

Brainlesion: Glioma, Multiple Sclerosis, Stroke and

Traumatic Brain Injuries (pp. 88-99). Springer, Cham.

Zhang, J., Gao, Y., Park, S. H., Zong, X., Lin, W., &

Shen, D. (2016, October). Segmentation of

perivascular spaces using vascular features and

structured random forest from 7T MR image.

In International Workshop on Machine Learning in

Medical Imaging (pp. 61-68). Springer International

Publishing.

Kontschieder, P., Bulo, S. R., Bischof, H., & Pelillo, M.

(2011, November). Structured class-labels in random

forests for semantic image labelling. In Computer

Vision (ICCV), 2011 IEEE International Conference

on (pp. 2190-2197). IEEE.

Zhang, L., & Ji, Q. (2008, June). Integration of multiple

contextual information for image segmentation using a

bayesian network. In Computer Vision and Pattern

Recognition Workshops, 2008. CVPRW'08. IEEE

Computer Society Conference on (pp. 1-6). IEEE.

Bayesian Network and Structured Random Forest Cooperative Deep Learning for Automatic Multi-label Brain Tumor Segmentation

189

Panagiotakis, C., Grinias, I., & Tziritas, G. (2011). Natural

image segmentation based on tree equipartition,

bayesian flooding and region merging. IEEE

Transactions on Image Processing, 20(8), 2276-2287.

Zhang, L., & Ji, Q. (2011). A Bayesian network model for

automatic and interactive image segmentation. IEEE

Transactions on Image Processing, 20(9), 2582-2593.

Yang, S., Yuan, C., Wu, B., Hu, W., & Wang, F. (2015).

Multi-feature max-margin hierarchical Bayesian

model for action recognition. In Proceedings of the

IEEE Conference on Computer Vision and Pattern

Recognition (pp. 1610-1618).

Tu, Z., & Bai, X. (2010). Auto-context and its application

to high-level vision tasks and 3d brain image

segmentation. IEEE Transactions on Pattern Analysis

and Machine Intelligence, 32(10), 1744-1757.

Prastawa, M., Bullitt, E., Ho, S., & Gerig, G. (2004). A

brain tumor segmentation framework based on outlier

detection. Medical image analysis, 8(3), 275-283.

Achanta, R., Shaji, A., Smith, K., Lucchi, A., Fua, P., &

Süsstrunk, S. (2010). Slic superpixels (No. EPFL-

REPORT-149300).

Zhao, X., Wu, Y., Song, G., Li, Z., Fan, Y., & Zhang, Y.

(2016, October). Brain Tumor Segmentation Using a

Fully Convolutional Neural Network with Conditional

Random Fields. In International Workshop on

Brainlesion: Glioma, Multiple Sclerosis, Stroke and

Traumatic Brain Injuries (pp. 75-87). Springer, Cham.

Loy, G., & Eklundh, J. O. (2006, May). Detecting

symmetry and symmetric constellations of features.

In European Conference on Computer Vision (pp.

508-521). Springer, Berlin, Heidelberg.

Breiman, L. (2001). Random forests. Machine learning,

45(1), 5-32.

Christ, P. F., Ettlinger, F., Grün, F., Elshaera, M. E. A.,

Lipkova, J., Schlecht, S., ... & Rempfler, M. (2017).

Automatic Liver and Tumor Segmentation of CT and

MRI Volumes using Cascaded Fully Convolutional

Neural Networks. arXiv preprint arXiv:1702.05970.

Folgoc, L. L., Nori, A. V., Alvarez-Valle, J., Lowe, R., &

Criminisi, A. (2016). Segmentation of brain tumors

via cascades of lifted decision forests. In Proceedings

MICCAI-BRATS Workshop (pp. 26-30).

Zhang, L., Wang, Q., Gao, Y., Li, H., Wu, G., & Shen, D.

(2017). Concatenated spatially-localized random

forests for hippocampus labeling in adult and infant

MR brain images. Neurocomputing, 229, 3-12.

Guo, H., Hu, H., & Fan, G. (2017). A novel segmentation

method of medical CBCT image in liver organ based

on Bayesian network. Biomedical Research, 1-1.

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

190