
Behaviour of a Hybrid ILS Heuristic on the Capacitated Profitable Tour
Problem
Hayet Chentli
1
, Rachid Ouafi
1
and Wahiba Ramdane Cherif-Khettaf
2
1
Department of Operations Research, USTHB, P. O. Box 32 El Alia, 16111, Bab Ezzouar, Algiers, Algeria
2
LORIA, UMR 7503, Lorraine University, Mines Nancy, France
Keywords:
Heuristics, Iterative Local Search, Vehicle Routing Problem.
Abstract:
In the present paper, we study the behaviour of a hybrid Iterative Local Search heuristic (ILS). A Large Neigh-
borhood Search heuristic (LNS) and a Variable Neighborhood Descent with Random neighborhood ordering
(RVND) are used in the local search phase of the proposed ILS. The approach is evaluated on a well-known
variant of the Vehicle Routing Problem (VRP) called Capacitated Profitable Tour Problem (CPTP). In this
variant, the vehicles are no longer required to visit all the customers. However, a specific profit is obtained
each time a customer is visited. The goal of the CPTP is to design routes with maximum difference between
collected profits and routing costs, which satisfy the capacity constraint of the vehicles. The experimental
study consists in comparing different combinations of ILS, LNS and RVND. The computational results show
that the hybridization of the three heuristics leads to better solutions. Furthermore, comparisons with a Vari-
able Neighborhood Search and two Tabu Searches from the literature indicates that our hybrid approach is
competitive.
1 INTRODUCTION
The Capacitated Profitable Tour Problem (CPTP) can
be defined as a variant of the Vehicle Routing Problem
(VRP) in which the visit of all customers is no longer
mandatory. In particular, a specific profit is collected
each time a customer is visited. In addition, each cus-
tomer is visited at most once by one of the available
capacitated and identical vehicles. The goal is to de-
sign feasible vehicle routes that maximize the differ-
ence between collected profits and routing costs.
Archetti et al. (Archetti et al., 2009) have im-
plemented three methodologies to solve the CPTP
namely Variable Neighborhood Search (VNS), Tabu
Feasible (TF) and Tabu Admissible (TA). The TF
algorithm accepts only feasible solutions, while TA
allows the visit of infeasible solutions by favouring
those with small infeasibilities. In both tabu searches,
the employed movements are inter-routes movements.
The first movement is the 1-move. It consists in the
relocation of a given customer in another route (a
deletion of the customer is also considered). The sec-
ond movement is the swap-move. Swap-move aims
at exchanging the positions of two given customers.
For deleting or at least decreasing a solution’s infea-
sibility, Archetti et al. have proposed a repair heuris-
tic based on series of 1-move. To evaluate the solu-
tions, several functions are used. Those functions deal
with difference between total profit and total distance,
route duration, number of routes and maximum con-
straint violation. In the diversification phase, series
of 1-move are executed between “good” and “bad”
routes. On the other hand, the VNS algorithm uses
the Tabu Feasible method with a small number of it-
erations. This allows the VNS to visit a larger number
of regions within the search space.
Some researchers attempted the resolution of the
CPTP using exact methods. Among these works one
can find the branch and price algorithm of Archetti
et al. (Archetti et al., 2009). More recently, Archetti
et al. (Archetti et al., 2013) proposed a branch and
price algorithm for both the CPTP and another vari-
ant of the Vehicle Routing Problem with Profits called
the Capacitated Team Orienteering Problem. Finally,
Jepsen et al. (Jepsen et al., 2014) presented a branch
and cut algorithm to solve the CPTP. For more details
on Vehicle Routing Problems with Profits, we refer
the reader to (Archetti et al., 2014).
In the present paper, we propose a hybrid Iterative
Local Search heuristic (ILS) for the CPTP. The pro-
Chentli, H., Ouafi, R. and Cherif-Khettaf, W.
Behaviour of a Hybrid ILS Heuristic on the Capacitated Profitable Tour Problem.
DOI: 10.5220/0006630401150123
In Proceedings of the 7th International Conference on Operations Research and Enterprise Systems (ICORES 2018), pages 115-123
ISBN: 978-989-758-285-1
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
115

posed approach makes use of both a Large Neighbor-
hood Search heuristic (LNS) and a Variable Neigh-
borhood Descent with Random neighborhood order-
ing (RVND) in the intensification phase. The diversi-
fication is ensured by the perturbation mechanism of
the ILS heuristic. To the best of our knowledge, it is
the first time that ILS, RVND and LNS are combined
to solve a VRP variant. The approach is evaluated on
CPTP benchmark instances from the literature.
In the following, we describe the proposed ap-
proach (Section 2). After that, we evaluate the per-
formance of the hybrid ILS (Section 3): First we pro-
vide a comparison between different combinations of
the components. Then, we contrast our results with
those presented in the literature of the CPTP. Finally,
we give some concluding remarks (Section 4).
2 THE PROPOSED
METHODOLOGY
In the present section, we briefly describe the Iterative
Local Search heuristic (ILS), the Variable Neighbor-
hood Descent with Random neighborhood ordering
(RVND) and the Large Neighborhood Search (LNS),
which are the main components of our approach.
Combinations of ILS and RVND were success-
fully applied to a variant of the VRP called Vehicle
Routing Problem with Simultaneous Pick-up and De-
livery services (see (Subramanian et al., 2010), (Sub-
ramanian et al., 2013)) and are still competitive with
other new approaches proposed for the same prob-
lem. The ILS and the Variable Neighborhood Descent
(VND) heuristics also provide good quality solutions
for other variants of VRPs see (Subramanian and
Battarra, 2013), (Erdo
˘
gan et al., 2009), (Hern
´
andez-
P
´
erez et al., 2009), (Rodr
´
ıguez-Mart
´
ın and Salazar-
Gonz
´
alez, 2012) and (Todosijevi
´
c et al., 2017). In
addition, the two heuristics perform well on some Ve-
hicle Routing Problems with Profits (see (Assis et al.,
2013) and (Gansterer et al., 2017)). Furthermore,
several versions of VND are used to solve different
variants of transportation problems (see (Sifaleras and
Konstantaras, 2017), (Sam
`
a et al., 2017) and (Hassan-
nayebi and Zegordi, 2017)).
To the best of our knowledge, no paper from the
literature proposes a combination of ILS with LNS
to solve a VRP variant. However, the two heuristics
have been successfully applied independently to sev-
eral variants of VRPs as well as to some transporta-
tion problems (see for instance (Cuervo et al., 2014),
(Silva et al., 2015), (Morais et al., 2014) and (Li et al.,
2015) for ILS, and (Franc¸ois et al., 2016), (Grang-
ier et al., 2017), (Akpinar, 2016), (Dominguez et al.,
2016) and (Canca et al., 2017) for LNS).
The ILS heuristic aims at improving solutions of
basic local searches. Indeed, after a local search is
performed, a local optimum is found, then ILS per-
turbs the so obtained local optimum and recall the lo-
cal search to improve it. This process iterates until
stopping criteria are met.
In a RVND heuristic, a list of neighbourhood
structures is used in such a way that, at each iteration,
a neighbourhood structure is chosen at random and is
applied to the current solution. The new solution is
accepted or not according to given criteria. After that,
the chosen neighbourhood structure is removed from
the list and the process continues with the remaining
structures. RVND stops when the list of neighbour-
hood structures is empty.
In comparison to other local search heuristics,
LNS allows the visit of larger areas in the search space
by changing the structure of the studied solution. In-
deed, LNS removes a relatively large number of cus-
tomers from a current solution, and re-inserts these
deleted customers in different positions. This leads to
a completely different solution, that helps the heuris-
tic to escape local optima. If the number of deleted
customers is set to a small value, LNS can be consid-
ered as a simple local search heuristic.
Our approach combines ILS, LNS and RVND in
a multi-start heuristic denoted ILS LNS RVND. First,
a sequential insertion heuristic is used to generate a
different initial solution at each iteration. Then, for
each initial solution, an ILS heuristic is executed un-
til reaching a given number of iterations without im-
provement. In ILS, a hybrid LNS RVND heuristic
plays the role of the local search procedure. The
perturbation mechanism of ILS is ensured by a dele-
tion/reinsertion procedure that randomly deletes cus-
tomers and reinserts other ones. In the local search
phase, ILS LNS RVND accepts only improved solu-
tions (better than the current solution). However, in
the perturbation phase, all solutions are accepted. The
pseudo-code of ILS RVND LNS is given below.
Algorithm ILS_LNS_RVND.
Inputs: A CPTP instance.
Outputs: The best solution found.
Begin
While (stopping criteria are not met)
do
Generate an initial solution;
While (ILS stopping criteria are not met)
do
LNS_RVND();
Update the best solution;
Perturb();
End While
End While
End.
ICORES 2018 - 7th International Conference on Operations Research and Enterprise Systems
116

In the following subsections, we give more de-
tails about ILS LNS RVND. We start by describing
the sequential insertion heuristic. Then, we present
the LNS, the RVND and the LNS RVND heuristics.
Finally, we describe the perturbation mechanism.
2.1 Sequential Insertion Heuristic
To generate an initial solution for the CPTP, we im-
plement a multi-start sequential heuristic based on
the I1 heuristic (see (Solomon, 1987)). Initially the
I1 heuristic was implemented for the Vehicle Routing
Problem with Time Window constraints (VRPTW).
First, I1 fills an empty route with a so-called seed
customer. Second, I1 evaluates all the possible inser-
tions of the remaining customers into the route. Third,
I1 selects the best position for each customer under
some criteria. Finally, I1 retains the insertion that op-
timizes the studied criteria. To adapt I1 to the CPTP,
we slightly change its selection criteria. The new cri-
teria deal with profits and distances and are described
using Expressions ( (1)– (4)). These criteria aim at
evaluating the insertion of a customer u between cus-
tomers i and j. In Expressions ( (1)– (4)), c
xy
stands
for the distance between customers x and y, pr
u
is the
profit of customer u, i
0
and i
l
refer to the depot (the
first and the last points of a studied route), α
1
+α
2
= 1
with α
1
≥ 0 and α
2
≥ 0.
cr
1
(i(u),u, j(u)) = min
ρ=1,..,l
cr
1
(i
ρ−1
,u, i
ρ
); (1)
cr
1
(i,u, j) = α
1
cr
11
(i,u, j)
−α
2
cr
12
(i,u, j); (2)
cr
11
(i,u, j) = pr
u
; (3)
cr
12
(i,u, j) = c
iu
+ c
u j
− c
i j
; (4)
The second criterion of I1, that sets the importance
of the distance between customer and depot, is not
used in our heuristic. In addition, the seed customer
is randomly selected in our heuristic.
2.2 Local Search Phase
2.2.1 Large Neighborhood Search
The LNS heuristic proposed in the present paper uses
one removal and one insertion operator. To select the
best couple of operators for the CPTP, we implement
all those presented by (Pisinger and Ropke, 2007) us-
ing the objective function and the constraints of the
CPTP. After that, we test all the possible combina-
tions of removal/insertion couples and retain the re-
lated removal and the regret-4 heuristic. We recall
that the related removal aims at deleting customers
that are somehow similar in order to interchange them
easily. The similarity s
i j
between customers i and j is
defined by Formula (5), where c
i j
is the distance be-
tween i and j, pr
i
and pr
j
are the profits of i and j
respectively. On the other hand, the regret-4 heuristic
aims at inserting a given customer in its 4th best po-
sition. The goal is to avoid postponing the placement
of difficult customers to the last iterations which may
produce local optima. LNS stops when a given num-
ber of iterations without improvement is reached.
s
i j
=
pr
i
− pr
j
+ c
i j
(5)
2.2.2 Variable Neighborhood Descent with
Random Neighborhood Ordering
The RVND heuristic uses four intra- and three inter-
route(s) operators. The latter are randomly chosen at
each iteration in such a way that, each operator is ex-
ecuted only once.
The neighbourhood operators used in our RVND
heuristic are described below. Examples of neigh-
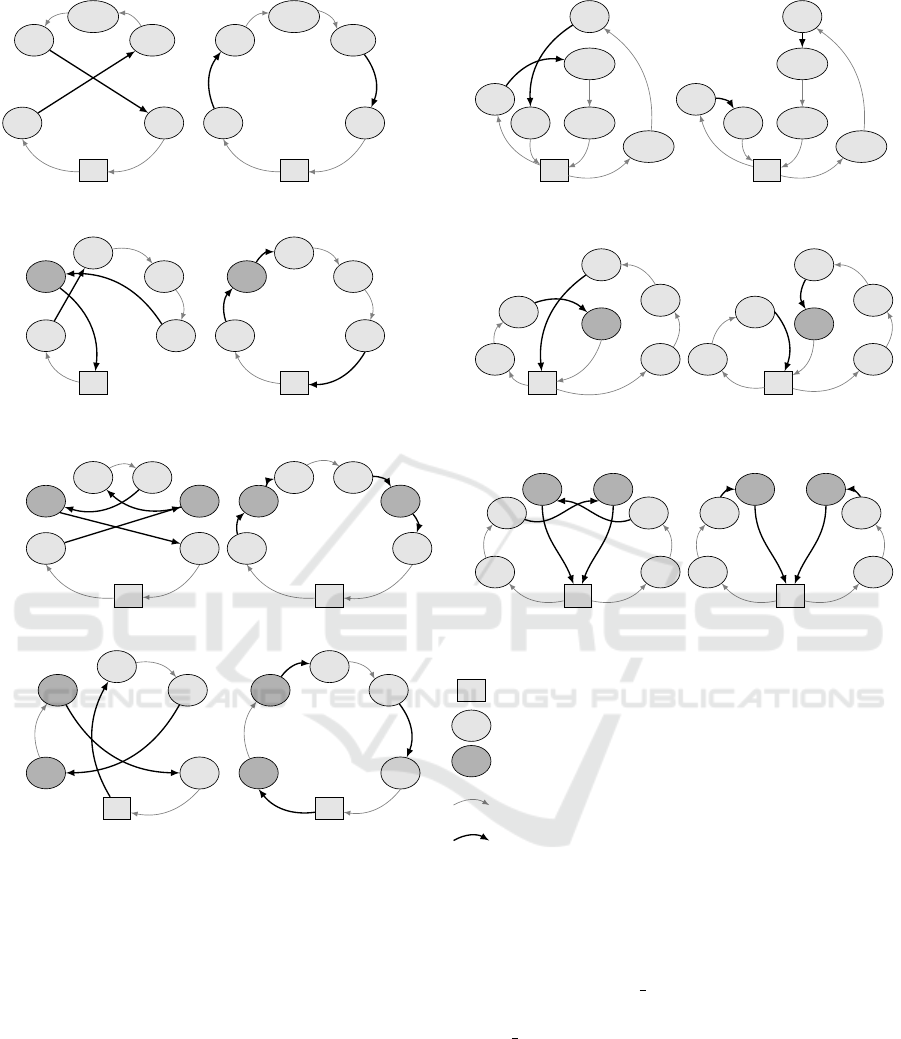
bourhood movements are given in Figure 1.
2-Opt. This operator connects two customers k and
l within a same route by reversing the path between k
and l. In Figure 1, customer 1 stands for k, while cus-
tomer 2 stands for l. Customers 1 and 2 are connected
and the path between them is reversed. To maintain
the connectivity of the route, customer 4 is connected
to customer 5.
2-Opt*. This operator first divides two routes into
four sections. Then, the first section of the first route
is connected with the second section of the second
route and the first section of the second route is con-
nected with the second section of the first route. In
Figure 1, the first route is divided by disconnecting
customers 1 and 2, and the second route is divided
by disconnecting customers 5 and 6. After that, cus-
tomers 1 and 6 and customers 5 and 2 are connected
to create the new routes.
Intra-route 1-0 Exchange. This operator moves
customer l to position k + 1 within a same route. In
Figure 1, customer 2 stands for l and position k is the
position of customer 1, which is position 1. Hence,
customer 2 is moved to position k + 1, i.e. position 2.
Inter-routes 1-0 Exchange. This operator moves
customer l to position k + 1 in a different route. In
Figure 1, l is customer 3 and position k is the position
of customer 6, which is position 3. Hence, customer
3 is moved to position k + 1 = 4 within the second
route.
Behaviour of a Hybrid ILS Heuristic on the Capacitated Profitable Tour Problem
117
0
1
2
3
4
5
Initial configuration
0
1
2
3
4
5
2-Opt
0
1
2
3
4
5
6
2-Opt*
0
1
2
3
4
5
6
Initial configuration
0
1
2
3
4
5
6
1-0 Exchange inter
0
1
2
3
4
5
6
Initial configuration
0
1
2
3
4
5
Initial configuration
0
1
2
3
4
5
1-0 Exchange intra
0
1
2
3
4
5
6
Initial configuration
0
1
2
3
4
5
6
1-1 Exchange intra
0
1
2
3
4
5
6
1-1 Exchange inter
0
1
2
3
4
5
6
Initial configuration
0
1
2
3
4
5
Initial configuration
0
1
2
3
4
5
Or-Opt
0
depot
X
customer X
X
customer X involved in the movement
arc: direction of visit
arc involved in the movement
Figure 1: Illustration of neighbourhood movements in the RVDN heuristic.
Intra-route 1-1 Exchange. This operator swaps the
positions of two customers k and l within a same
route. In Figure 1, customer 2 stands for k and cus-
tomer 5 stands for l.
Inter-routes 1-1 Exchange. This operator swaps
the positions of two customers k and l in two differ-
ent routes. In Figure 1, customer 3 stands for k and
customer 6 stands for l.
Or-Opt. This operator moves two consecutive cus-
tomers k and k + 1 between two other consecutive
customers (or a customer and the depot) l and l + 1.
This results in a sequence (l, k,k + 1,l + 1). In Figure
1, customer 1, customer 2, the depot and customer 3
stand for k, k + 1, l and l + 1 respectively.
2.2.3 Hybrid LNS RVND
LNS RVND first executes the LNS heuristic until a
given number of iterations without improvement are
reached. The best solution found so far is then im-
proved using RVND. This process is repeated for a
given number of iterations.
2.3 Perturbation Mechanism
The perturbation procedure is also based on the LNS
principle. However, to maintain the diversification
ICORES 2018 - 7th International Conference on Operations Research and Enterprise Systems
118

aspect of the perturbation, the random removal de-
scribed by (Pisinger and Ropke, 2007) is used. Cus-
tomer insertions are done using the basic greedy
heuristic (see (Pisinger and Ropke, 2007)).
3 COMPUTATIONAL RESULTS
In the present section, we assess the performance
of ILS LNS RVND: we run different versions of the
heuristic to evaluate the impact of each component
(ILS, LNS and RVND) and to study different combi-
nations of these components. Then, we compare our
approach with some heuristics from the literature. A
brief description of CPTP instances is given in the first
subsection.
All the heuristics are implemented in C and run on
a laptop with an Intel(R) Core (TM) i7-4600U CPU
@ 2.10GHz 2.70GHz with 8.00 Gb RAM and 64-bit
operating system. Due to the random aspect, the ap-
proaches are run 3 times for each instance. The best
encountered solutions are reported.
3.1 CPTP Instances
The studied CPTP instances are proposed by (Archetti
et al., 2009). They are derived from the Capaci-
tated Vehicle Routing Problem instances proposed by
(Christofides et al., 1979). Archetti et al. generate
these instances by modifying the capacity bounds and
the number of vehicles of the original instances. The
number of customers varies between 50 and 199.
3.2 Study of the LNS Heuristic
We implement all the removal/insertion operators pre-
sented by (Pisinger and Ropke, 2007) using CPTP
objective function. In order to select the best cou-
ple of removal/insertion operators to use in the lo-
cal search phase of ILS LNS RVND, we run 30 LNS
basic versions
{
V 1,.. .,V 30
}
that use different pairs
of removal/insertion operators. Each version starts
from an initial solution generated by our construction
heuristic using random values of parameters α
1
and
α
2
. The studied LNS versions delete 1 to 3 customers
at each iteration. The insertion heuristics try to insert
profitable customers. The best LNS version so ob-
tained is used in the ILS LNS RVND heuristic. LNS
stops when 50000 iterations without improvement are
reached.
Table 1 gives the pair of removal/insertion opera-
tors used in each version. In this Table, ind refers to
the indices of removal/insertion couples. The symbol
“X” indicates whether an operator is used or not.
Figure 2 compares the average deviation (gap)
from the solutions of the literature and the average
computing time (in seconds) of the 30 versions. All
versions are tested on all CPTP instances and they
are run until 50000 iterations without improvement
are reached. From Figure 2, we remark that the ver-
sion using the related removal combined to the regret
heuristic with a regret number of 4 is the best version
in terms of solution quality. It also provides reason-
able computing time. Hence, this version is retained
for the local search phase of the ILS LNS RVND
heuristic.
3.3 Hybrid ILS LNS Heuristic
The hybrid ILS LNS heuristic is a multi-start heuris-
tic that executes, at each iteration, an ILS heuristic
with LNS in the local search phase.
The LNS heuristic implemented here uses the best
couple of removal/insertion operators found in Sub-
section 3.2. We test four configurations of the num-
ber of customers to delete at each iteration. We re-
tain the following configuration: the number r of cus-
tomers to delete is randomly chosen from the interval
[1,0.4 ∗ n], where n is the number of customers in the
current solution. LNS stops when 50 iterations with-
out improvement are reached.
The perturbation procedure of ILS LNS is de-
scribed in Subsection 2.3. Each time, the perturba-
tion procedure is executed, r
0
customers are deleted,
where r
0
∈ [0.1, 0.4] ∗ n and n is the number of cus-
tomers that belong to the current solution. After that,
the basic greedy heuristic tries to insert profitable cus-
tomers. Note that, a random insertion of customers
was also developed but the latter leads to low quality
solutions.
ILS LNS stops when 50 iterations without im-
provement are reached.
Table 2 compares the results of LNS using the
best couple of removal/insertion and two versions
of ILS LNS. In the first version, the number r of
customers to delete is randomly chosen from [1,3].
While, in the second version, r is randomly cho-
sen from [1,0.4 ∗ n]. We remark that the first ver-
sion of ILS LNS provides better results and needs
less computing time than LNS. When r is chosen
from [1, 0.4 ∗ n], the heuristic provides better solu-
tions. However, it is more time consuming. As the
computing time of all these heuristics is reasonable,
we chose to continue the study using the ILS LNS
heuristic with r ∈ [1, 0.4 ∗ n].
Behaviour of a Hybrid ILS Heuristic on the Capacitated Profitable Tour Problem
119

Table 1: Removal/insertion couples.
ind random
re-
moval
worst
re-
moval
related
re-
moval
historical
node-pair
removal
historical
request-
pair
removal
cluster
re-
moval
basic
greedy
regret-2 regret-3 regret-4 regret-m
1 X X
2 X X
3 X X
4 X X
5 X X
6 X X
7 X X
8 X X
9 X X
10 X X
11 X X
12 X X
13 X X
14 X X
15 X X
16 X X
17 X X
18 X X
19 X X
20 X X
21 X X
22 X X
23 X X
24 X X
25 X X
26 X X
27 X X
28 X X
29 X X
30 X X
Table 2: Comparison between LNS with the best couple of
removal/insertion and two versions of ILS LNS.
LNS ILS LNS ILS LNS
r ∈ [1, 3] r ∈ [1, 0.4 ∗ n]
gap 12,16 5,61 5,07
CPU 23,78 14,75 36,35
3.4 Hybrid ILS RVND Heuristic
Instead of using LNS in the local search of ILS,
ILS RVND uses RVND with the same perturbation
procedure presented in Subsection 3.3.
As the heuristic is very fast, we increase the num-
ber of iterations without improvement of ILS. We re-
mark that ILS RVND with 50 iterations without im-
provement converges in only 1.26 seconds. However,
the gap of this heuristic with respect to the bench-
mark solutions equals 7.59%, which is larger than the
gap of ILS
LNS. When we fix the number of iter-
ations without improvement of ILS to 500, the gap
of ILS RVND reaches 4.95% in only 10.57 seconds.
This shows that ILS RVND outperforms ILS LNS in
both solution quality and computing time. These re-
sults are summarized in Table 3.
Table 3: Comparison between ILS LNS and ILS RVND.
ILS LNS ILS RVND ILS RVND
r ∈ [1,0.4 ∗ n] 50 iterations 500 iterations
gap 5,07 7,59 4,95
CPU 36,35 1,26 10,57
3.5 Hybrid LNS RVND Heuristic
LNS RVND is a heuristic that combines the best ver-
sion of LNS found in Subsection 3.2 with the RVND
heuristic. LNS RVND is not a multi-start heuristic.
Indeed, it starts from an initial solution generated by
our construction heuristic using random values of pa-
rameters α
1
and α
2
. LNS is then executed, and each
time i iterations are reached, the current solution is
improved by RVND using a given probability P. We
have studied the configurations (i = 100, P = 1/10),
(i = 1000, P = 1/10) and (i = 1000, P = 1/100). We
remark that the second configuration provides the best
ICORES 2018 - 7th International Conference on Operations Research and Enterprise Systems
120
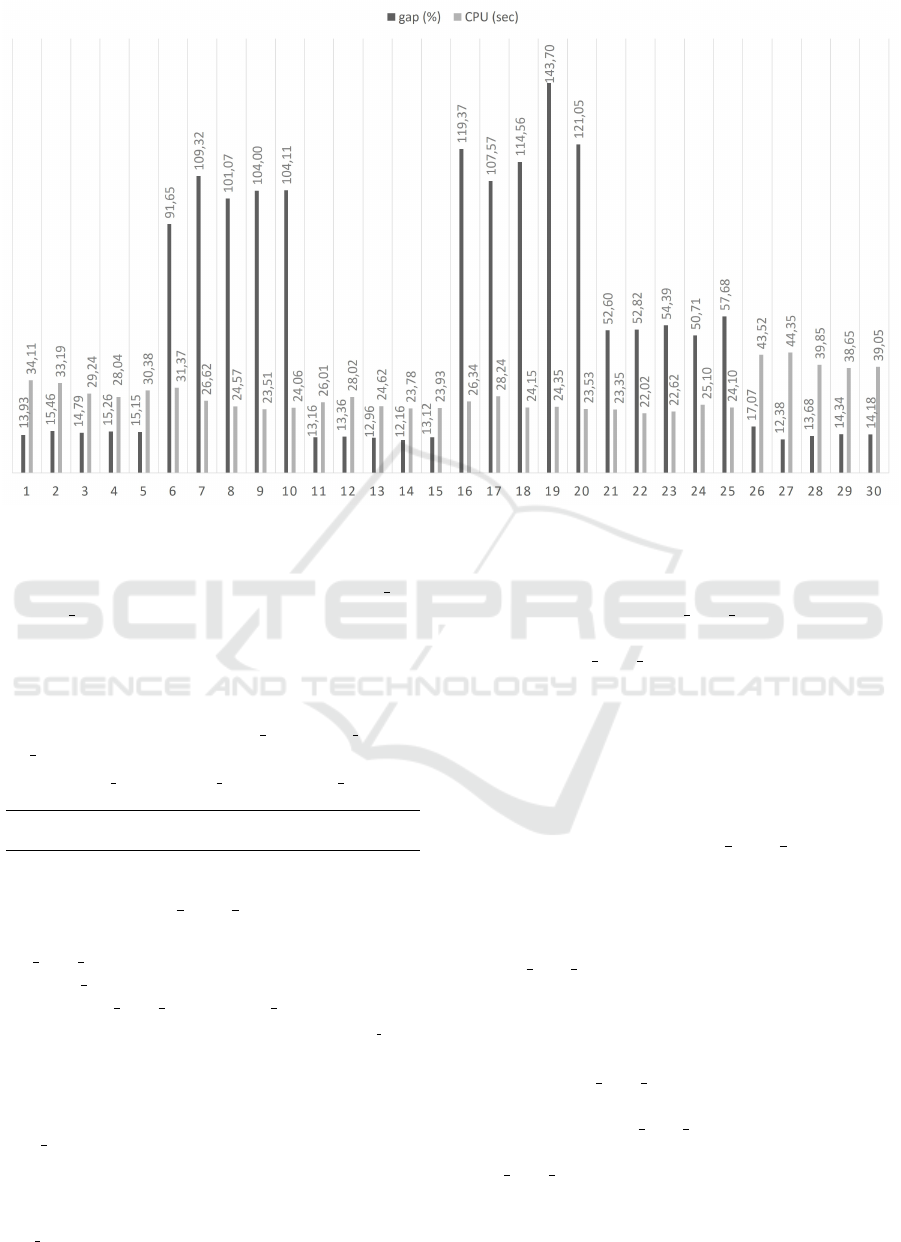
Figure 2: Comparison between LNS versions.
gap and computing time. However, these results are
not promising in comparison with those of ILS LNS
and ILS RVND as shown in Table 4. We conclude
that the multi-start ILS heuristic plays a key role in
the achievement of good quality solutions in reason-
able computing time.
Table 4: Comparison between LNS RVND, ILS LNS, and
ILS RVND.
LNS RVND ILS LNS ILS RVND
r ∈ [1,0.4 ∗ n] 500 iterations
gap 11,94 5,07 4,95
CPU 67,10 36,35 10,57
3.6 Hybrid ILS LNS RVND Heuristic
ILS LNS RVND is a multi-start ILS that uses the hy-
brid LNS RVND heuristic described in 2.2.3. Ac-
tually, in ILS LNS RVND, LNS RVND is repeated
until reaching a given number of iterations i
LNS RV ND
.
Then, the perturbation mechanism described in Sub-
section 2.3 is executed. This process is repeated
until reaching a fixed number of iterations without
improvement denoted maxOcc. We choose to stop
LNS RVND when a given number of iterations is
reached instead of a given number of iterations with-
out improvement because this led to better results.
The parameters of the approach are set as follow:
i
LNS RV ND
equals 7, maxOcc is set to 200, the max-
imum number of iterations without improvement in
LNS maxOcc
LNS
is set to 20.
Table 5 compares ILS LNS RVND with the pre-
viously studied heuristics. From this table, we re-
mark that ILS LNS RVND obtains the best results
with reasonable computing time. We also remark that
the more a heuristic is hybridized, the better are the
results. However, this may cause additional comput-
ing time. This is because, if we do not hybridize a
heuristic, it will be trapped in a local optimum very
quickly.
3.7 Comparison of ILS LNS RVND
with Heuristics from the Literature
We compare our approach with other approaches
from the literature. Table 6 compares the results
of ILS LNS RVND with the Variable Neighborhood
Search (VNS), the Tabu Feasible (TF) and the Tabu
Admissible (TA) heuristics of (Archetti et al., 2009).
In this table, gap refers to the average deviation of
each heuristic with respect to the best solutions (so-
lutions of ILS LNS RVND included). CPU(min)
is the computing time of each heuristic in minutes.
We remark that ILS LNS RVND provides competi-
tive results in reasonable computing time. Note that
ILS LNS RVND provides better solutions in compar-
ison to the other heuristics in 6 cases.
Behaviour of a Hybrid ILS Heuristic on the Capacitated Profitable Tour Problem
121

Table 5: Comparison between ILS LNS RVND and the other heuristics.
LNS LNS RVND ILS LNS ILS RVND ILS RVND LNS
r ∈ [1, 0.4 ∗ n] 500 iterations
gap 12,16 11,94 5,07 4,95 1,57
CPU 23,78 67,1 36,35 10,57 28,39
Table 6: Comparison between ILS LNS RVND and other
heuristics from the literature.
ILS LNS RVND VNS TF TA
gap 0,66 0,18 0,78 0,73
CPU(min) 9,94 10,3 2,83 8,54
4 CONCLUSION
In this paper, we present a hybrid ILS heuristic that
makes use of LNS and RVND in the local search
phase. We compare several versions of ILS using
different levels of hybridization of the components.
The proposed heuristic is evaluated on a well known
variant of the Vehicle Routing Problem called Capac-
itated Profitable Tour Problem. The results show that
the more we hybridize ILS, the better are the results.
Finally, we contrast our results with those obtained
in the literature. This shows that our hybrid ILS is
competitive in terms of solution quality and comput-
ing time. A future work may consist in applying the
hybrid ILS heuristic to other variants of Vehicle Rout-
ing Problems with Profit.
REFERENCES
Akpinar, S. (2016). Hybrid large neighbourhood search al-
gorithm for capacitated vehicle routing problem. Ex-
pert Systems with Applications, 61:28–38.
Archetti, C., Bianchessi, N., and Speranza, M. G. (2013).
Optimal solutions for routing problems with profits.
Discrete Applied Mathematics, 161(4):547–557.
Archetti, C., Feillet, D., Hertz, A., and Speranza, M. G.
(2009). The capacitated team orienteering and prof-
itable tour problems. Journal of the Operational Re-
search Society, 60(6):831–842.
Archetti, C., Speranza, M. G., and Vigo, D. (2014). Ve-
hicle routing problems with profits. Vehicle Routing:
Problems, Methods, and Applications, 18:273.
Assis, L. P., Maravilha, A. L., Vivas, A., Campelo, F., and
Ram
´
ırez, J. A. (2013). Multiobjective vehicle routing
problem with fixed delivery and optional collections.
Optimization Letters, 7(7):1419–1431.
Canca, D., De-Los-Santos, A., Laporte, G., and Mesa, J. A.
(2017). An adaptive neighborhood search metaheuris-
tic for the integrated railway rapid transit network de-
sign and line planning problem. Computers & Opera-
tions Research, 78:1–14.
Christofides, N., Mingozzi, A., and Toth, P. (1979). The ve-
hicle routing problem. In Christofides, N., Mingozzi,
A., Toth, P., and Sandi, C., editors, Combinatorial Op-
timization, pages 315–338. Wiley, Chichester.
Cuervo, D. P., Goos, P., S
¨
orensen, K., and Arr
´
aiz, E. (2014).
An iterated local search algorithm for the vehicle rout-
ing problem with backhauls. European Journal of Op-
erational Research, 237(2):454–464.
Dominguez, O., Guimarans, D., Juan, A. A., and de la
Nuez, I. (2016). A biased-randomised large neigh-
bourhood search for the two-dimensional vehicle rout-
ing problem with backhauls. European Journal of Op-
erational Research, 255(2):442–462.
Erdo
˘
gan, G., Cordeau, J.-F., and Laporte, G. (2009). The
pickup and delivery traveling salesman problem with
first-in-first-out loading. Computers & Operations Re-
search, 36(6):1800–1808.
Franc¸ois, V., Arda, Y., Crama, Y., and Laporte, G. (2016).
Large neighborhood search for multi-trip vehicle rout-
ing. European Journal of Operational Research,
255(2):422–441.
Gansterer, M., K
¨
uc¸
¨
uktepe, M., and Hartl, R. F. (2017). The
multi-vehicle profitable pickup and delivery problem.
OR Spectrum, 39(1):303–319.
Grangier, P., Gendreau, M., Lehu
´
ed
´
e, F., and Rousseau,
L.-M. (2017). A matheuristic based on large neigh-
borhood search for the vehicle routing problem with
cross-docking. Computers & Operations Research,
84:116–126.
Hassannayebi, E. and Zegordi, S. H. (2017). Variable
and adaptive neighbourhood search algorithms for rail
rapid transit timetabling problem. Computers & Op-
erations Research, 78:439–453.
Hern
´
andez-P
´
erez, H., Rodr
´
ıguez-Mart
´
ın, I., and Salazar-
Gonz
´
alez, J. J. (2009). A hybrid grasp/vnd heuris-
tic for the one-commodity pickup-and-delivery travel-
ing salesman problem. Computers & Operations Re-
search, 36(5):1639–1645.
Jepsen, M. K., Petersen, B., Spoorendonk, S., and Pisinger,
D. (2014). A branch-and-cut algorithm for the capac-
itated profitable tour problem. Discrete Optimization,
14:78–96.
Li, J., Pardalos, P. M., Sun, H., Pei, J., and Zhang, Y.
(2015). Iterated local search embedded adaptive
neighborhood selection approach for the multi-depot
vehicle routing problem with simultaneous deliver-
ies and pickups. Expert Systems with Applications,
42(7):3551–3561.
Morais, V. W., Mateus, G. R., and Noronha, T. F. (2014).
Iterated local search heuristics for the vehicle routing
problem with cross-docking. Expert Systems with Ap-
plications, 41(16):7495–7506.
ICORES 2018 - 7th International Conference on Operations Research and Enterprise Systems
122

Pisinger, D. and Ropke, S. (2007). A general heuristic for
vehicle routing problems. Computers and operations
research, 34(8):2403–2435.
Rodr
´
ıguez-Mart
´
ın, I. and Salazar-Gonz
´
alez, J. J. (2012).
A hybrid heuristic approach for the multi-commodity
one-to-one pickup-and-delivery traveling salesman
problem. Journal of Heuristics, 18(6):849–867.
Sam
`
a, M., Corman, F., Pacciarelli, D., et al. (2017). A vari-
able neighbourhood search for fast train scheduling
and routing during disturbed railway traffic situations.
Computers & Operations Research, 78:480–499.
Sifaleras, A. and Konstantaras, I. (2017). Variable neigh-
borhood descent heuristic for solving reverse logistics
multi-item dynamic lot-sizing problems. Computers
& Operations Research, 78:385–392.
Silva, M. M., Subramanian, A., and Ochi, L. S. (2015). An
iterated local search heuristic for the split delivery ve-
hicle routing problem. Computers & Operations Re-
search, 53:234–249.
Solomon, M. M. (1987). Algorithms for the vehicle rout-
ing and scheduling problems with time window con-
straints. Operations research, 35(2):254–265.
Subramanian, A. and Battarra, M. (2013). An iterated local
search algorithm for the travelling salesman problem
with pickups and deliveries. Journal of the Opera-
tional Research Society, 64(3):402–409.
Subramanian, A., Drummond, L. M. d. A., Bentes, C., Ochi,
L. S., and Farias, R. (2010). A parallel heuristic for
the vehicle routing problem with simultaneous pickup
and delivery. Computers and Operations Research,
37(11):1899–1911.
Subramanian, A., Uchoa, E., and Ochi, L. S. (2013). A hy-
brid algorithm for a class of vehicle routing problems.
Computers & Operations Research, 40(10):2519–
2531.
Todosijevi
´
c, R., Hanafi, S., Uro
ˇ
sevi
´
c, D., Jarboui, B., and
Gendron, B. (2017). A general variable neighbor-
hood search for the swap-body vehicle routing prob-
lem. Computers & Operations Research, 78:468–479.
Behaviour of a Hybrid ILS Heuristic on the Capacitated Profitable Tour Problem
123
