
Evolutionary Clustering Techniques for Expertise Mining Scenarios
Veselka Boeva
1
, Milena Angelova
2
, Niklas Lavesson
1
, Oliver Rosander
1
and Elena Tsiporkova
3
1
Computer Science and Engineering Department, Blekinge Institute of Technology, Karlskrona, Sweden
2
Computer Systems and Technologies Department, Technical University of Sofia Plovdiv Branch, Plovdiv, Bulgaria
3
The Collective Center for the Belgian Technological Industry, Brussels, Belgium
Keywords:
Data Mining, Expert Finding, Health Science, Knowledge Management, Natural Language Processing.
Abstract:
The problem addressed in this article concerns the development of evolutionary clustering techniques that can
be applied to adapt the existing clustering solution to a clustering of newly collected data elements. We are
interested in clustering approaches that are specially suited for adapting clustering solutions in the expertise
retrieval domain. This interest is inspired by practical applications such as expertise retrieval systems where
the information available in the system database is periodically updated by extracting new data. The experts
available in the system database are usually partitioned into a number of disjoint subject categories. It is
becoming impractical to re-cluster this large volume of available information. Therefore, the objective is
to update the existing expert partitioning by the clustering produced on the newly extracted experts. Three
different evolutionary clustering techniques are considered to be suitable for this scenario. The proposed
techniques are initially evaluated by applying the algorithms on data extracted from the PubMed repository.
1 INTRODUCTION
Currently, organizations search for new employees
not only relying on their internal information sour-
ces, but they also use data available on the Inter-
net to locate the required experts. Thus the need
for services that enable finding experts grows es-
pecially with the expansion of virtual organizati-
ons. People are more often working together by
forming task-specific teams across geographic boun-
daries. The formation and sustainability of such
virtual organizations greatly depends on their abi-
lity to quickly trace those people who have the re-
quired expertise. In response to this, research on
identifying experts from online data sources (Abra-
mowicz et al., 2011),(Balog and Rijke, 2007),(Boz-
zon et al., 2013),(Hristoskova et al., 2013),(Jung
et al., 2007),(Stankovic et al., 2011),(Harpreet et al.,
2013),(Tsiporkova and Tourw
´
e, 2011),(Zhang et al.,
2007) has been gradually gaining interest in the re-
cent years. For instance, a Web-based biomedical
expert finding system, proposed in (Harpreet et al.,
2013), can be applied to identify subject experts and
subjects associated with an expert. The system builds
and maintains a big repository of biomedical experts
by extracting the information about experts’ peer-
reviewed articles that are published and indexed in
PubMed. The experts stored in such big data reposi-
tories are usually partitioned into a number of subject
categories in order to facilitate the further search and
identification of experts with the appropriate skills
and knowledge.
The problem addressed in this article concerns
with the development of evolutionary clustering
techniques that can be used to adjust the existing clus-
tering solution to newly arrived data. This is mo-
tivated by practical applications such as, expertise
retrieval systems discussed above, where the infor-
mation available in the system database is periodi-
cally updated by collecting new data. The available
data elements are usually partitioned into a number of
disjoint subject categories. It is becoming impractical
to re-cluster this large volume of available informa-
tion. Therefore, we propose and study three different
evolutionary clustering algorithms that are suited for
the considered problem: Partitioning-based, PivotBi-
Cluster (PBC) and Merge-Split PBC.
2 RELATED WORK
The model of incremental algorithms for data cluste-
ring is motivated by practical applications where the
demand sequence is unknown in advance and a hier-
Boeva, V., Angelova, M., Lavesson, N., Rosander, O. and Tsiporkova, E.
Evolutionary Clustering Techniques for Expertise Mining Scenarios.
DOI: 10.5220/0006630605230530
In Proceedings of the 10th International Conference on Agents and Artificial Intelligence (ICAART 2018) - Volume 2, pages 523-530
ISBN: 978-989-758-275-2
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
523

archical clustering is required. Incremental clustering
methods process one data element at a time and main-
tain a good solution by either adding each new ele-
ment to an existing cluster or placing it in a new sing-
leton cluster while two existing clusters are merged
into one (Charikar et al., 1997).
To qualify the type of cluster structure present in
data, Balcan et al. introduced the notion of cluste-
rability (Balcan et al., 2008). It requires that every
element be closer to data in its own cluster than to ot-
her points. In addition, Balcan et al. showed that the
clusterings that adhere to this requirement are readily
detected offline by classical batch algorithms. On the
other hand, it was proven by Ackerman et al. (Acker-
man and Dasgupta, 2014) that no incremental method
can discover these partitions. Thus, batch algorithms
are significantly stronger than incremental methods in
their ability to detect cluster structure.
Incremental algorithms also bear a resemblance to
one-pass clustering algorithms for data stream pro-
blems (O’Callaghan et al., 2002). For example, the
algorithm in (O’Callaghan et al., 2002) is implemen-
ted as a continuous version of k-means algorithm
which continues to maintain a number of cluster cen-
ters which change or merge as necessary throughout
the execution of the algorithm. Although, one-pass
stream clustering methods address the scalability is-
sues of the clustering problem, they are not sensitive
to the evolution of the data.
The clustering scenario discussed herein is diffe-
rent from the one treated by incremental clustering
methods. Namely, the evolutionary clustering techni-
ques considered in this work are supposed to provide
the flexibility to compute clusters on a new portion of
data collected over a defined time period and to up-
date the existing clustering solution by the computed
new one. Such an updating clustering should better
reflect the current characteristics of the data by being
able to examine clusters occurring in the considered
time period and eventually capture interesting trends
in the area.
Gionis et al. proposed an approach to clustering
that is based on the concept of aggregation (Aristides
et al., 2007). Clustering aggregation provides a fra-
mework for dealing with a variety of clustering pro-
blems. For instance, it can handle categorical or he-
terogeneous data by producing a clustering on each
available attribute and then aggregating the produced
clusterings into a single result. Consensus clustering
algorithms deal with similar problems to those tre-
ated by clustering aggregation techniques. Namely,
such algorithms try to reconcile clustering informa-
tion about the same data set coming from different
sources or from different runs of the same algorithm
(Goder and Filkov, 2008). The both clustering techni-
ques are not suited for our expert mining scenario,
since they are used to integrate a number of cluste-
ring results generated on one and the same data set.
3 EXPERTISE RETRIEVAL
3.1 Partitioning of Experts
In the context of expertise retrieval, two interesting
research tasks can be considered: how to cluster ex-
perts into groups according to the degree of their ex-
pertise (topic) similarity and how to partition topics
according to their semantic relatedness.
Accurate measurement of semantic similarity be-
tween words is essential for the both tasks, since the
expert expertise profiles are usually presented by lists
of subject terms (keywords) extracted from the avai-
lable information about the experts. Semantically re-
lated words of a particular word are listed in manu-
ally created general-purpose lexical ontologies such
as WordNet (Fellbaum, 1998; Miller, 1995).
In the context of expertise retrieval the cluster
hypothesis states that similar people tend to be experts
on the same topics. Traditional clustering approaches
assume that data objects to be clustered are indepen-
dent and of identical class, and are often modelled by
a fixed-length vector of feature/attribute values. The
similarities among objects are assessed based on the
attribute values of involved objects. However, the cal-
culation of expertise similarity is a complicated task,
since the expert expertise profiles usually consist of
domain-specific keywords that describe their area of
competence without any information for the best cor-
respondence between the different keywords of two
compared profiles. In addition, the degree of hetero-
geneity among the experts in terms of expertise could
have an impact on the scalability of the applied algo-
rithms. Consequently, the sparse and high dimensio-
nal representation of the different experts necessitate
the design of specific algorithms for expert represen-
tation and processing. One such approach for cluste-
ring of experts has already been introduced in (Boeva
et al., 2014b). A further refinement of the model has
been proposed in (Boeva et al., 2016).
3.2 Profiling of Expertise
An expertise profiling is the task of describing of sub-
ject areas that an individual is proven to have a com-
petence, i.e. constructing of person’s expertise pro-
file. The data needed for constructing the expert profi-
les could be extracted from various Web sources, e.g.,
ICAART 2018 - 10th International Conference on Agents and Artificial Intelligence
524

LinkedIn, the DBLP library, Microsoft Academic Se-
arch, Google Scholar Citation, PubMed etc.
A conceptual model of the domain of interest,
such as a thesaurus, a taxonomy etc., can be availa-
ble and used to attain accurate and topic relevant ex-
pert profiles. When a conceptual model is missing
then, e.g., the Stanford part-of-speech tagger (Touta-
nova and Manning, 2000) can be used to annotate the
different words in the text collected for each expert
with their specific part of speech. However, an expert
profile may be quite complex and can, for example,
be associated with information that includes: e-mail
address, affiliation, a list of publications, co-authors,
but it may also include or be associated with: educati-
onal and (or) employment history, the list of LinkedIn
contacts etc. All this information could be separated
into two parts: expert’s personal data and information
that describes the competence area of expert.
The expert’s personal data can be used to resolve
the problem with ambiguity. This problem refers to
the fact that multiple profiles may represent one and
the same person and therefore must be merged into a
single generalized expert profile, e.g., the clustering
algorithm discussed in (Buelens and Putman, 2012)
can be applied for this purpose. A different appro-
ach to the ambiguity problem has been proposed in
(Boeva et al., 2012). Namely, the similarity between
the personal data (profiles) of experts is used to re-
solve the problem with ambiguity.
In view of the above, an expert profile can be defi-
ned as a list of keywords, extracted from the available
information about the expert in question, describing
her/his subjects of expertise.
3.3 Expertise Similarity
As it was discussed above, an important task in the
considered context is to establish a way to estimate
the expertise similarity between experts. This task can
be additionally complicated in case when weights are
introduced in order to optimize expert representation.
In (Boeva et al., 2012) the similarity between two
expertise profiles is measured as the strength of the re-
lations between the semantic concepts associated with
the keywords of the two compared profiles. Anot-
her possibility to measure the expertise similarity bet-
ween two expert profiles is by taking into account the
semantic similarities between any pair of keywords
that contain in the profiles. Thus in (Boeva et al.,
2017) the expertise similarity between two expert pro-
files is defined as the weighted mean of semantic si-
milarities between the corresponding keywords. Wit-
hout loss of generality we assume that in the conside-
red context each expert is described by only a list of
the domain-specific topics in which he/she is an ex-
pert. Assume that each expert profile i is represented
by a list of p
i
keywords. Then let s be a similarity me-
asure that is suitable to estimate the semantic related-
ness between any two keywords used to describe the
expert profiles in the domain. Then the expertise si-
milarity S
i j
between two expert profiles i and j (i 6= j),
can be defined by the arithmetic mean of semantic si-
milarities between the corresponding keywords, i.e.
S
i j
=
1
p
i
·p
j
∑
p
i
l=1
∑
p
j
m=1
s(k
il
,k
jm
), where s(k
il
,k
jm
) is
the semantic similarity between keywords k
il
and k
jm
.
4 THE PROPOSED SOLUTIONS
4.1 Description of the Framework
Let us formalize the cluster updating problem we are
interested in. We assume that X is the available set
of experts and each expert is represented by a non-
fixed length vector of domain-specific keywords des-
cribing her/his expertise. In addition, the experts are
partitioned into k groups with respect to given sub-
ject categories describing the domain of interest, i.e.
C = {C
1
,C
2
,... ,C
k
} is an existing clustering solution
of X and each C
i
(i = 1, 2,. .. ,k) can be considered as
a distinctive expert area. In addition, a new set X
0
of
recently extracted experts is created, i.e. X ∩ X
0
is an
empty set. Each expert in X
0
is again modeled by a
list of keywords and C
0
= {C
0
1
,C
0
2
,. .. ,C
0
k
0
} is a clus-
tering solution of X
0
w.r.t. the same or different dom-
ain description. The objective is to produce a single
clustering of X ∪ X
0
by combining C and C
0
in such a
way that the obtained clustering realistically reflects
the current expertise distribution in the domain.
4.2 Cluster Centers Partitioning based
Algorithm
A MapReduce approach for clustering of datasets ge-
nerated in multiple-experiment settings has been in-
troduced in (Boeva et al., 2014a). It consists of two
distinctive phases. Initially, the selected clustering al-
gorithm is applied to each experiment separately. This
produces a list of different clustering solutions, one
per experiment. These are further transformed by por-
tioning the cluster centers into a single clustering so-
lution. The second phase of the MapReduce appro-
ach can be applied to the cluster integration problem,
we are interested in this paper. Namely, in order to
integrate the two clusterings C and C
0
into a single
clustering solution, we can use the following merge
schema. The cluster centers of the available clusters
Evolutionary Clustering Techniques for Expertise Mining Scenarios
525

represented by their expert expertise profiles are con-
sidered. Subsequently, these expert profiles can be
divided into groups according to the degree of their
expertise similarity by applying some clustering al-
gorithm. Subsequently, the clusters whose centers be-
long to the same group are merged in order to obtain
the single clustering.
4.3 Correlation Bi-clustering Algorithm
A different approach to the above problem can also be
applied. For example, instead of considering the clus-
ter centers of the clusters we can present each cluster
by an expert area profile, i.e. analogously to the ex-
perts’ expertise profiles. Consequently, each cluster
will be modelled by a list of domain-specific topics
that describes the corresponding expert area. Then
the clusters can be divided into groups according to
the degree of their expert area similarity. Two clus-
tering techniques are suitable for the considered con-
text: correlation clustering (Bansal et al., 2004) and
bipartite correlation clustering (Ailon et al., 2011).
The latter algorithm seems to be better aligned to our
expert clustering scenario. In Bipartite Correlation
Clustering (BCC) a bipartite graph is given as input,
and a set of disjoint clusters covering the graph no-
des is output. Clusters may contain nodes from either
side of the graph, but they may possibly contain nodes
from only one side. A cluster is thought as a bi-clique
connecting all the objects from its left and right coun-
terparts. Consequently, a final clustering is a union of
bi-cliques covering the input node set. We compare
our evolutionary correlation clustering algorithm des-
cribed in the following section with PivotBiCluster
realization of the BCC algorithm (Ailon et al., 2011).
Notice that in the clustering scenario discussed he-
rein the input graph nodes are clusters of experts and
in the final clustering some clusters are obtained by
merging clusters (nodes) from both side of the graph,
i.e. some of existing clusters will be updated by some
of the computed new ones. However, existing clus-
ters cannot be split by the BCC algorithm even the
corresponding correlations with clusters from the ne-
wly extracted experts reveal that these clusters are not
homogeneous.
4.4 Evolutionary Bipartite Clustering
Algorithm
We propose herein an evolutionary clustering algo-
rithm that overcomes the above mentioned disadvan-
tage of BCC algorithm. Namely, our algorithm is able
to analyze the correlations between two clustering so-
lutions C and C
0
and based on the discovered patterns
it treats the existing clusters (C) in different ways.
Thus some clusters will be updated by merging with
ones from newly constructed clustering (C
0
) while ot-
hers will be transformed by splitting their elements
among several new clusters. One can find some simi-
larity between our idea and an interactive clustering
model proposed in (Awasthi et al., 2017). In this mo-
del the algorithm starts with some initial clustering of
the data and the user may request a certain cluster to
be split if it is overclustered (intersects two or more
clusters in the target clustering). The user may also
request to merge two given clusters if they are under-
clustered (both intersect the same target cluster).
Our evolutionary clustering algorithm is based on
the PivotBiCluster algorithm defined in (Ailon et al.,
2011). Suppose that each cluster from the clustering
solutions C and C
0
is presented by a list of domain-
specific topics that describes its expert area. Next our
input graph is G = (C,C
0
,E), where C and C
0
are the
sets of left and right nodes and E is subset of C × C
0
that presents correlations between the nodes of two
sets. A detail explanation of the proposed Merge-Split
PivotBiCluster is given in Algorithm 1.
Algorithm 1 : Merge-Split PivotBiCluster.
1: function MERGE-SPLIT PBC(G = (C,C
0
,E))
2: for all nodes c ∈ C ∪C
0
do
3: if c is an unreachable node then
4: Turn c into a singleton and remove it from G
5: end if
6: end for
7: while C 6=
/
0 do
8: Choose c
1
uniformly at random from C
9: if c
1
takes part in a bi-clique connecting it with several
nodes from C
0
then
10: Split c
1
among the corresponding nodes from C
0
11: else
12: Form a new cluster by merging c
1
with its neig-
hbors from C
0
The neighbors of c
1
is denoted by
N(c
1
).
13: for all nodes c
2
∈ C \ {c
1
} do
14: Consider the sets: R
1
= N(c
1
) \ N(c
2
), R
2
=
N(c
2
) \ N(c
1
) and R
1,2
= N(c
1
) ∩ N(c
2
)
15: Calculate probability p = min
{|
R
1,2
|
/
|
R
2
|
,1
}
16: if
|
R
1,2
|
≥
|
R
1
|
then
17: with probability p append c
2
to the above
cluster
18: end if
19: end for
20: end if
21: Remove all clustered nodes from G
22: end while
23: return all connected components (bi-cliques) as clusters
of C ∪C
0
24: end function
Initially, the proposed algorithm finds all unrea-
chable nodes from either side of G (steps 2 to 6).
These are singelton clusters in our final clustering so-
lution. We remove these nodes from the graph. Then
any other node from the the left side of G is conside-
red in order to decide how it will be updated by the ne-
ICAART 2018 - 10th International Conference on Agents and Artificial Intelligence
526

wly arrived information. Thus if the considered node
takes part in a bi-clique connecting it with several no-
des from C
0
its elements have to be split among the
corresponding nodes from C
0
(steps 9 and 10). Other-
wise (from steps 12 to 18) our algorithm follows the
original PivotBiCluster algorithm and identifies those
nodes from the right side of G that have to be merged
with the considered node. Notice that in contrast to
PivotBiCluster algorithm when the condition in step
16 is not true we decide nothing about c
2
.
At the 10th step of the above algorithm it is neces-
sary to split the elements belonging to cluster c
1
∈ C
among several clusters from C
0
. This can be imple-
mented in several different ways. For example, each
expert from C can be classified into one of the pos-
sible clusters of experts from C
0
by determining the
set of experts who have similar expertise to his/hers
with respect to any of the considered clusters. Na-
mely, for each possible cluster from C
0
it is necessary
to identify experts with similar area of competence,
i.e. ones who have at least minimum (preliminary de-
fined) expertise similarity with the considered expert.
Then the expert in question is assigned to that cluster
of experts for which the corresponding set has the lar-
gest cardinality. Another possibility is to calculate the
expertise similarity between each expert belonging to
c ∈ C and each of the possible clusters from C
0
and
then the expert in question is assigned to the closest
cluster.
5 EXPERIMENT DESIGN
5.1 Test Data
We need test data that is tied to our specific task, na-
mely the expert clustering. For this task, we use the
test collection from a scientific conference devoted to
integrative biology
1
. For each topic, participants (102
in total) of the corresponding conference session are
regarded as experts on that topic. This is an easy way
of obtaining topics and relevance judgements. A to-
tal of 8 topics (sessions) are created by the conference
science committee. A list of researchers for these to-
pics are also supplied, i.e., names that are listed in the
conference program on the sessions (topics) informa-
tion. These researchers are considered as relevant ex-
perts, thus, used as the ground truth to benchmark the
results of the proposed clustering methods.
The data needed for constructing the expert pro-
files of the above 102 researchers are extracted from
1
Integrative Biology 2017: 5th International Conference
on Integrative Biology (London, UK, June 19-21, 2017).
PubMed, which is one of the largest repositories of
peer-reviewed biomedical articles published world-
wide. Medical Subject Headings (MeSH) is a con-
trolled vocabulary developed by the US National Li-
brary of Medicine for indexing research publications,
articles and books. Using the MeSH terms associa-
ted with peer-reviewed articles published by the above
considered researchers and indexed in the PubMed,
we extract all such authors and construct their expert
profiles. An expert profile is defined by a list of MeSH
terms used in the PubMed articles of the author in
question to describe her/his expertise areas.
In addition to the above set of 102 biomedical re-
searchers we have extracted a set of 4343 Bulgarian
authors from the PubMed repository. After resolving
the problem with ambiguity the set is reduced to one
containing only 3753 different researchers. Then each
author is also represented by a list of all different
MeSH headings used to describe the major topics of
her/his PubMed articles.
5.2 Metrics
One of the most important issues in cluster analysis
is the validation of clustering results. The data mi-
ning literature provides a range of different cluster va-
lidation measures, which are broadly divided into two
major categories: external and internal (Jain et al.,
1988). External validation measures have the bene-
fit of providing an independent assessment of cluste-
ring quality, since they validate a clustering result by
comparing it to a given external standard. However,
an external standard is rarely available. Internal vali-
dation techniques, on the other hand, avoid the need
for using such additional knowledge, but have the al-
ternative problem to base their validation on the same
information used to derive the clusters themselves.
In this work, we have implemented two diffe-
rent validation measures for estimating the quality of
clusters, produced by the proposed clustering algo-
rithms. Since we have a benchmark clustering of the
set of 102 biomedical researchers, described in the fo-
regoing section, we have used the F-measure as an
external validation measure to evaluate the accuracy
of the generated clustering solutions (Larsen et al.,
1999). The F-measure is the harmonic mean of the
precision and recall values for each cluster. For a per-
fect clustering the maximum value of the F-measure
is 1. In addition, Silhouette Index has been applied
as an internal measure to assess compactness and se-
paration properties of the clustering solutions (Rous-
seeuw, 1987). The values of Silhouette Index vary
from -1 to 1.
Evolutionary Clustering Techniques for Expertise Mining Scenarios
527
5.3 Implementation and Availability
We used the Entrez Programming Utilities (E-
utilities) to download all the publications associa-
ted with authors from the considered conference and
those originating from Bulgarian authors (Sayers,
2010). The E-utilities are the public API to the NCBI
Entrez system and allow access to all Entrez databases
including PubMed, PMC, Gene, Nuccore and Protein.
For calculation of semantic similarities between
MeSH headings, we use MeSHSim which is an R
package. It also supports querying the hierarchy in-
formation of a MeSH heading and information of a gi-
ven document including title, abstraction and MeSH
headings (Zhou and Shui, 2015). The three cluster
updating algorithms used in our experiments are im-
plemented in Python.
Supplementary information is available at
GitLab (https://gitlab.com/machine learning vm/
clustering techniques).
5.4 Experiments
Initially, a benchmark set of 102 different expert profi-
les is formed as it was explained in Section 5.1. Then
this set is used to generated 10 test data set couples by
randomly separating the experts (researchers) in two
sets. The one set (containing 70 experts) of each cou-
ple presents the available set of experts and the other
one (32 experts) is the set of newly extracted experts.
In that way 10 test clustering couples are created.
We have studied two different experiment scena-
rios. In the first scenario the experts in each test set are
grouped into clusters of experts with similar expertise
based on the conference session information, i.e. each
set is partitioned into 8 clusters. In the second scena-
rio for each data set the optimal number of clusters is
determined by clustering the set applying k-means for
different k and evaluating the obtained solutions by
SI. In this way two different experiments have been
conducted on 10 test data set couples. In both experi-
ments in order to be able to calculate the correlation
between any pair of clusters we describe each clus-
ter by a vector of those MeSH terms that have a high
degree of frequency in its expert profiles.
In both experiments the three evolutionary cluste-
ring algorithms considered in Section 4 are executed
10 time on each test couple (i.e., 300 executions in
total for each experiment) to integrate the correspon-
ding clusterings. The cluster centers partitioning ba-
sed algorithm (shortly called Partitioning-based) has
been implemented by using k-means. It has been exe-
cuted on each test couple for k = 8, since we know
that this is the number of clusters in the benchmark
set, i.e. the optimal one. The number of clusters in
the clustering solutions generated by the two BCC al-
gorithms however, varies from 5 to 8. The number
of clusters for these algorithms depends on the cor-
relations between the currently integrated clustering
solutions, i.e. it flexibly adapts to the integrated data.
The F-measure is used to assess the accuracy of
the generated clustering solutions. We have also eva-
luated the compactness and separation properties of
the obtained clustering solutions by applying SI.
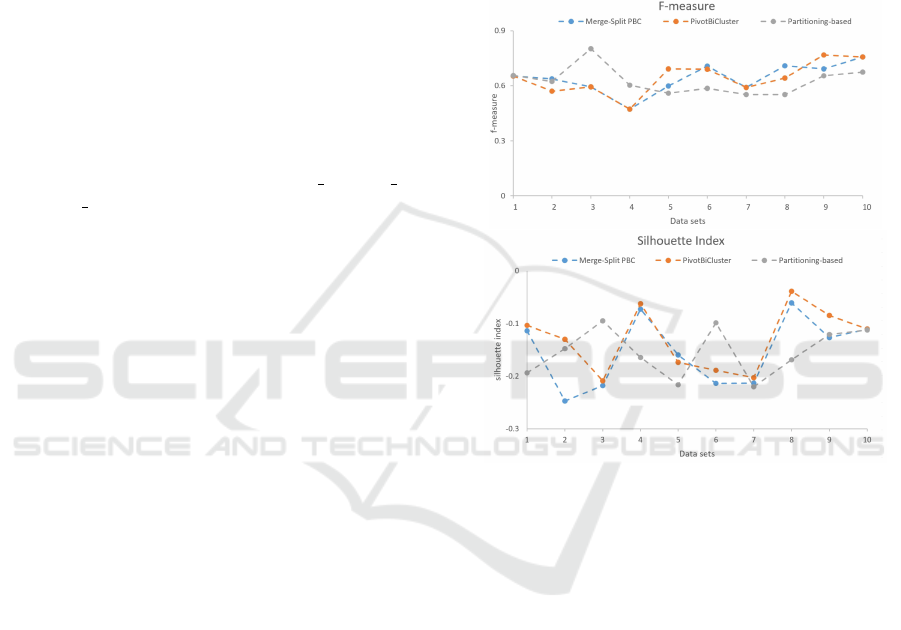
Figure 1: Experiment 1: F-measure and SI values genera-
ted on the clustering solutions produced by the three cluster
updating algorithms on 10 test data set couples.
6 RESULTS AND ANALYSIS
The results are depicted in Fig. 1 and Fig. 2. We
can notice the three clustering algorithms have simi-
lar performance with respect to both validation me-
asures. This is not surprising since the benchmark
data set is very well separable into 8 clusters. The
two BCC algorithms have produced higher F-measure
and SI scores than the Partitioning-based (PB) algo-
rithm on two-thirds of the test data sets in the first
experiment and on the half of data sets in the second
experiment. The corresponding average values can
be seen in Table 1 and Table 2. The two BCC algo-
rithms outperform the Partitioning-based on average
w.r.t. both cluster validation measures in the first ex-
periment (see Fig. 1). In addition, the PivotBiCluster
(PBC) and Merge-Split PBC perform almost equally
well, because the former one has not found many
ICAART 2018 - 10th International Conference on Agents and Artificial Intelligence
528
overclustered nodes, i.e. it has not executed many
cluster splitting for the considered 10 test data sets.
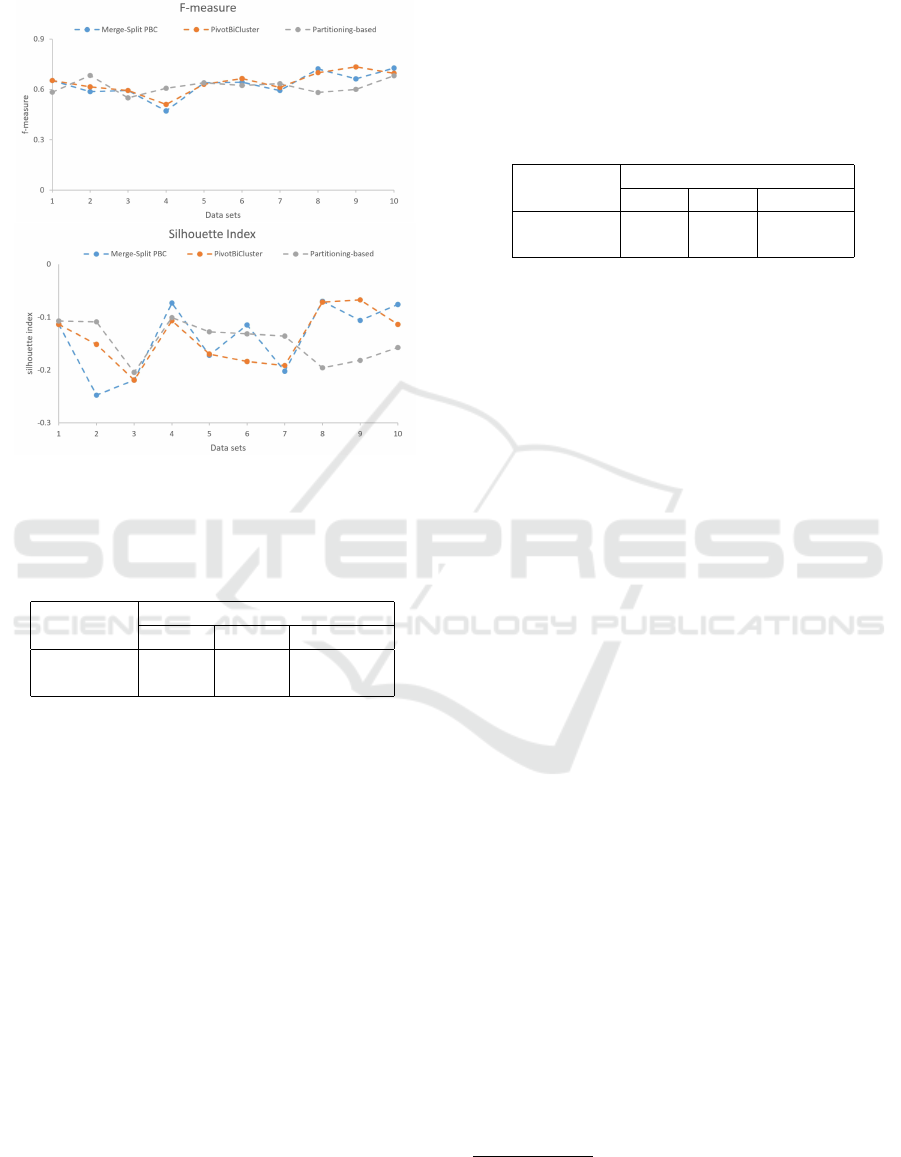
Figure 2: Experiment 2: F-measure and SI values genera-
ted on the clustering solutions produced by the three cluster
updating algorithms on 10 test data set couples.
Table 1: Average F-measure and SI values generated on the
clustering solutions of the 10 data set couples.
Experiment 1
Metrics PB PBC MS PBC
2
F-measure 0.618 0.640 0.628
SI -0.145 -0.139 -0.139
In the second experiment (see Fig. 2) the SI scores
are not only higher in comparison to the ones genera-
ted in the first experiment, but they are also positive.
Evidently, using the optimal number of clusters sig-
nificantly improves the quality of the generated clus-
tering solutions with respect to compactness and se-
paration properties. However, the corresponding F-
measure scores are lower than the ones generated in
the first experiment. This is mainly due to the fact that
the number of clusters in the clustering solutions pro-
duced in the second experiment can be different from
the benchmark one.
We have also executed k-means clustering algo-
rithm 10 time on the whole benchmark set of 102 ex-
perts for k = 8. This experiment has been conducted
in order to obtain an idea of the performance of the
proposed evolutionary clustering algorithms compa-
red to a non-evolutionary one. The computed average
values for F-measure and SI are 0.09 and 0.287, re-
spectively. It is interesting to notice that the three evo-
lutionary clustering algorithms significantly outper-
form k-means in all run experiments w.r.t. F-measure,
but k-means performs better w.r.t. SI. The former
might be due to the fact that the three evolutionary
clustering algorithms are able to produce clustering
solutions that are closer to ”natural” partitions really
present in the underlying data.
Table 2: Average F-measure and SI values generated on the
clustering solutions of the 10 data set couples.
Experiment 2
Metrics PB PBC MS PBC
F-measure 0.321 0.308 0.302
SI 0.137 0.164 0.159
Next we use the second built set that contains 3753
PubMed expert profiles of Bulgarian researchers. The
researchers of this set are randomly separated in two
sets. The one set contains 2407 experts grouped into
122 clusters by using k-means and the other one has
1346 experts separated into 112 clusters again by ap-
plying k-means. The three evolutionary clustering
algorithms are then executed twice to integrate the
clustering solutions of these two data sets. The ge-
nerated clustering solutions are evaluated by SI and
the average scores are -0.094 (PB), -0.158 (PBC) and
-0.067 (MS PBC). The MS PBC algorithm outper-
forms the other two algorithms on this data set. We
believe this is due to the fact that it adjusts better
to data by being able not only to merge those clus-
ters that are undersclustered but also to split those
that are overclustered. Notice that Partitioning-based
demonstrates close performance to MS PBC. This is
because it has been executed for the optimal number
of clusters. We have preliminarily found this num-
ber (k = 72) by applying k-means for different k and
evaluating the obtained clustering solutions by SI.
However, the latter could become difficult if the
data set is very large or is multi-dimensional. Usually
in order to find a reasonable number of clusters, clus-
tering methods must be run repeatedly with different
parameters, i.e. this is impractical for real-world data
sets that are often quite large.
7 CONCLUSION
This paper has compared three different evolutio-
nary clustering approaches specially suited for ex-
pertise retrieval scenarios: a Partitioning-based and
two graph-based (bipartite correlation) clustering al-
gorithms (PivotBiCluster and Merge-Split PBC). The
2
Merge-Split PBC
Evolutionary Clustering Techniques for Expertise Mining Scenarios
529

considered approaches have initially been evaluated
by applying the algorithms on data extracted from Pu-
bMed repository. The produced clustering solutions
have been validated on two different datasets by two
different cluster validation measures: F-measure and
Silhouette Index (SI). The two Bipartite Correlation
Clustering (BCC) algorithms have slightly outperfor-
med the Partitioning-based on average with respect to
SI on the first data set. The Merge-Split PBC algo-
rithm has also demonstrated better performance than
the other two algorithms on the second data set. This
algorithm is able to analyze the correlations between
two clustering solutions and based on the discovered
patterns it treats the clusters in different ways. In ad-
dition, in comparison to the Partitioning-based clus-
tering algorithm the two BCC algorithms do not need
prior knowledge about the optimal number of clusters
in order to produce a good clustering solution. The
BCC algorithms are also more suitable for the consi-
dered expertise retrieval context, because each cluster
is modelled by a list of domain-specific topics, i.e.
analogously to the experts’ expertise profiles.
For future work, we aim to pursue further compa-
rison and evaluation of the three proposed clustering
approaches on richer data extracted from different on-
line sources.
REFERENCES
Abramowicz, W. et al. (2011). Semantically enabled experts
finding system - ontologies, reasoning approach and
web interface design. In ADBIS, volume 2, pages 157–
166.
Ackerman, M. and Dasgupta, S. (2014). Incremental cluste-
ring: The case for extra clusters. In Proc. of Advances
in Neural Inf. Proc. Sys. 27, pages 307–315.
Ailon, N. et al. (2011). Improved Approximation Algo-
rithms for Bipartite Correlation Clustering, pages 25–
36. ESA.
Aristides, G. et al. (2007). Clustering aggregation. TKDD,
1:4.
Awasthi, P. et al. (2017). Local algorithms for interactive
clustering. J. Mach. Learn. Res., 18:75–109.
Balcan, M.-F. et al. (2008). A discriminative framework for
clustering via similarity functions. In Proceedings of
the 40th annual ACM symposium on Theory of Com-
puting, pages 671–680. ACM.
Balog, K. and Rijke, M. d. (2007). Finding similar experts.
In ACM SIGIR’07, pages 821–822.
Bansal, N. et al. (2004). Correlation clustering. Machine
Learning, 56:89–113.
Boeva, V. et al. (2012). Measuring expertise similarity in
expert networks. In Proceedings of 6th IEEE Int.
Conf. on Intelligent Systems, pages 53–57. IEEE.
Boeva, V. et al. (2014a). Analysis of multiple DNA microar-
ray datasets, pages 223–234. Springer DE.
Boeva, V. et al. (2014b). Semantic-Aware Expert Partitio-
ning, pages 13–24. LNAI Springer.
Boeva, V. et al. (2016). Identifying a group of subject ex-
perts using formal concept analysis. In IEEE Conf. on
Intelligent Systems, pages 464–469. IEEE.
Boeva, V. et al. (2017). Data-driven techniques for expert
finding. In Proc. 9th Int. Conference on Agents and
AI, pages 535–542.
Bozzon, A. et al. (2013). Choosing the right crowd: expert
finding in social networks. In EDBT, pages 637–648.
Buelens, S. and Putman, M. (2012). Identifying experts
through a framework for knowledge extraction from
public online sources. Ghent University.
Charikar, M. et al. (1997). Incremental clustering and dyna-
mic information retrieval. In Proc. 29th Annual ACM
Symposium on Theory of Computing, pages 626–635.
ACM.
Fellbaum, C. (1998). WordNet: an electronic lexical data-
base. MIT Press.
Goder, A. and Filkov, V. (2008). Consensus clustering al-
gorithms: Comparison and refinement. In Algorithm
Engineering and Experimentation - ALENEX, pages
109–117. SIAM.
Harpreet, S. et al. (2013). Developing a biomedical expert
finding system unsing medical subject headings. HIR,
4:243–249.
Hristoskova, A. et al. (2013). A graph-based disambigua-
tion approach for construction of an expert repository
from public online sources. In ICAART, pages 24–33.
Jain, A. K. et al. (1988). Algorithms for Clustering Data.
Prentice-Hall, Inc.
Jung, H. et al. (2007). Finding topic-centric identified ex-
perts based on full text analysis. In FEWS’07, pages
56–63.
Larsen, B. et al. (1999). Fast and effective text mining using
linear-time document clustering. In Proceedings of
KDD-99, pages 16–22. ACM.
Miller, G. A. (1995). Wordnet: A lexical database for eng-
lish. Commun. ACM, 38:39–41.
O’Callaghan, L. et al. (2002). Streaming-data algorithms
for high-quality clustering. In Proceedings of ICDE
Conference, pages 685–694. IEEE Computer Society.
Rousseeuw, P. (1987). Silhouettes: A graphical aid to the in-
terpretation and validation of cluster analysis. J. Com-
put. Appl. Math., 20:53–65.
Sayers, E. (2010). A general introduction
to the e-utilities. Available from:
https://www.ncbi.nlm.nih.gov/books/NBK25497/.
Stankovic, M. et al. (2011). Linked data metrics for flexible
expert search on the open web. In ESWC (1), volume
6643, pages 108–123.
Toutanova, K. and Manning, C. D. (2000). Enriching the
knowledge sources used in a maximum entropy part-
of-speech tagger. In Proceeding of the Joint SIGDAT
Conference on Empirical Methods in NLP and Very
Large Corpora, pages 63–70.
Tsiporkova, E.and Tourw
´
e, T. (2011). Tool support for
technology scouting using online sources. volume
6999, pages 371376. LNCS Springer.
Zhang, J. et al. (2007). Expert Finding in a Social Network,
pages 1066–1069. LNCS Springer.
Zhou, J. and Shui, Y. (2015). The meshsim package.
ICAART 2018 - 10th International Conference on Agents and Artificial Intelligence
530
