
Multi-Concerns Engineering for Safety-Critical Systems
Philipp Lohm
¨
uller, Andrea Fendt and Bernhard Bauer
Institute of Computer Science, University of Augsburg, Universit
¨
atsstr. 6a, 86159 Augsburg, Germany
Keywords:
Safety-Critical Systems, Dependability, Tradeoff Analysis, Multi-Criteria Decision Analysis, Multi-Concerns.
Abstract:
Modern cars are equipped with a large number of electronic assistance systems such as Adaptive Cruise Con-
trol (ACC) to improve road safety and driving comfort. These systems require a complex cross-linking, both
inside and outside the vehicle, e.g., by means of bus systems or wireless interfaces like Bluetooth. Thus, safety
of road users can endangered if the communication between these systems failed. Communication failures can
be affected by hacking attacks, e.g., delayed decelerating of an ACC system, thereby presenting a security and
timing vulnerability endangering safety of road users. Hence, in this paper safety is considered as primary
goal. Goals that contribute to achieve the primary goal can be in contradiction to each other under certain
circumstances. Therefore, an approach is proposed to model Safety, Security and Timing (SST) constraints to
guarantee maximum safety. Furthermore, a preventative risk assessment of the individual concerns including
a tradeoff analysis is performed to enable the development of Safety-Critical Systems (SCS).
1 INTRODUCTION
The development of safety critical embedded systems
involves the consideration of certain requirements and
objectives. Objectives include essential safety, secu-
rity and real-time demands, which do not only vary in
their importance, but usually are even partially con-
flicting. Consequently, amendments made on behalf
of a safety or security target possibly introduce or in-
tensify other threats. Thus, fixing a safety or security
vulnerability might introduce significant safety prob-
lems. For instance, modern vehicles are equipped
with various wired and wireless interfaces. According
to the automotive industry, wireless communication
of vehicles will increase tremendously in the future by
introducing car-to-car and car-to-infrastructure com-
munication. By broadcasting most current and very
important information to neighboring vehicles, e.g.,
hazard warnings, weather conditions or traffic news,
road safety can be increased significantly. Wireless
communication comes at the cost of a massive risk of
hacking attacks, representing a severe issue for secu-
rity as well as safety, since the majority of car func-
tionalities are highly safety critical. Even a minor
interference can result in serious consequences, due
to strong functional interdependencies [Nilsson et al.,
2008]. Although wireless car-to-x communication
can provide a significant safety improvement it also
introduces new security and safety issues by increas-
ing the vulnerability for hacking attacks. Amend-
ing the problem by using a secure encryption for the
wireless communication might jeopardize timing con-
strains, since encryption comes at the cost of addi-
tional processing load. When confronted with such
conflicting SST objectives, it is most important to an-
alyze proposed solutions comprehensively and to take
all potential side effects of a particular design into
account. This might reveal unresolvable contradic-
tions, affording a transparent and traceable tradeoff
analysis. In the course of this paper an approach is
presented to analyze SST issues systematically, struc-
turing them hierarchically and performing a tradeoff
analysis on them.
2 APPROACH
The Multi-Concerns Engineering (MCE) process is
relevant in the design phase of SCS, when important
design decisions regarding unresolvable contradicting
SST issues have to be evaluated. In this paper we pro-
pose a comprehensive process of trading off conflict-
ing SST requirements:
1. Devise potential alternative system designs
2. Identify and structure SST objectives
3. Perform a Failure Mode and Effects Analysis
(FMEA)
4. Apply an MCDA to find the safest solution
504
Lohmüller, P., Fendt, A. and Bauer, B.
Multi-Concerns Engineering for Safety-Critical Systems.
DOI: 10.5220/0006631705040510
In Proceedings of the 6th International Conference on Model-Driven Engineering and Software Development (MODELSWARD 2018), pages 504-510
ISBN: 978-989-758-283-7
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

When confronted with contradicting SSTs in the
design phase of an SCS, several competing system
models are developed. This approach helps to evalu-
ate the alternative solutions regarding potentially con-
flicting SST issues, to identify the best tradeoff and
to reveal individual vulnerabilities of a solution. For
instance, when trying to find the best solution for
a vehicle’s ACC, one might consider several sensor
types, data encryption mechanism or maximum al-
lowed cruising speeds.
Subsequently, these insights are transferred into
a standardized Safety Goal Hierarchy (SGH), which
builds the basis for the actual FMEA risk assessment.
For a clear graphical representation, the SGH makes
use of the Goal Structuring Notation (GSN) as pro-
posed by Tim Kelly and Rob Weaver in [Kelly et al.,
2004]. The strength of GSN is to present the goals
while preventing various possible failures in a stan-
dardized, structured and understandable manner, em-
phasizing their relationships and revealing potential
goal conflicts.
A promising approach for resolving goal conflicts
in the design of safety critical systems is to rate safety
as primary goal and considering security and tim-
ing objectives as subordinated goals that might affect
safety concerns. Therefor an SGH is always initiated
with a top-level goal: Assuring that the system is ac-
ceptably safe which has to be decomposed into more
concrete subgoals regarding the system under devel-
opment, usually including security requirements and
real-time constraints.
Based on the definition of different solutions the
potential risks of failure for each alternative have to
be identified by means of the FMEA. The FMEA is
a well accepted method for identifying and prevent-
ing or reducing potential risks of failure associated
with an arbitrary system or process preemptively. [Liu
et al., 2016] It’s first step is to answer the following
questions: ”What can go wrong?”, ”Why did this fail-
ure occur?” and ”What would be the impact of the
identified failure?” After having identified potential
failure modes and their causes, they are integrated
into the SGH already prepared. Possibly the SGH
designed in advance has to be extended to include
aspects that have not been considered so far. That
means, refining the SGH until each potential failure
mode is represented by a goal on the lowest level (1).
Note that the goal structure can be arbitrarily complex
and nested, while always ending at the Single Point of
Failures (SPOFs).
Afterwards the risk associated with each SPOF
has to be evaluated. The FMEA measures this risk by
three factors, denoted as OSD in the following: the
Occurrence (O) is the likelihood of a failure to oc-
System is
acc. safe
Prevent
SPOF 1
Prevent
SPOF 2
Subgoal 1 Subgoal 2 Subgoal 3
Subgoal 2.1
Subgoal 2.2
Prevent
SPOF 3
Prevent
SPOF 4
Prevent
SPOF 5
Prevent
SPOF 6
Prevent
SPOF 7
Prevent
SPOF 8
Prevent
SPOF 9
Figure 1: Exemplary SGH.
cur, the Severity (S) the impact a failure can have and
the Detection (D) denotes the probability that a fail-
ure will be detected. Each of these criteria is assigned
an integer value between 1 and 10, whereas 1 stands
for the lowest probability of occurrence, the lowest
impact or the highest probability of detecting the fail-
ure (vice versa for 10). The detailed ratings and their
interpretations can be looked up at [Bundesminis-
terium des Inneren, 2017]. Then the risk evaluation of
OSD is aggregated to a Risk Priority Number (RPN)
by multiplying the ratings: RPN = O × S × D. Al-
though this simple aggregation has been reasonably
criticized, e.g., in [Bowles, 2003], the RPN evalua-
tion is a compulsory requirement of software devel-
opment for the automotive industry. A more sophisti-
cated aggregation mechanism will be presented in 3.1.
According to the RPN potential failures are classified
into risk levels. For RPNs of 50 or more, actions on
behalf of risk mitigation or risk reduction are manda-
tory, this usually means to change the system design
or exclude potentially dangerous use cases. These
changes might introduce new threats or intensify ex-
isting ones. Therefore the whole FMEA has to be
repeated to assure that the amended system accom-
plishes an acceptable risk level. [Bundesministerium
des Inneren, 2017]
In order to identify the safest, realizable imple-
mentation, an adapted version Saaty’s Analytic Hier-
archy Process (AHP) [Saaty, 1990] is applied to the
SGH. The AHP is a Multi-Criteria Decision Analy-
sis (MCDA) method, that calculates the best compro-
mise based on a structured goal hierarchy and com-
parison matrices, that asses the relative importance of
the goals for their common super-ordinated objective.
Creating a comparison matrix (also called pairwise ra-
tio matrix) means to rate the relative importance for
every pair of subgoals, when they are directly com-
pared to each other. The AHP proposes to set ratings
between 1 and 9, where 1 means that the two com-
pared subgoals are equally important and 9 means that
the objective rated with 9 is extremely more important
for it’s super-ordinated goal than the other one [Saaty,
1990]. Inconsistent ratings can be introduced eas-
Multi-Concerns Engineering for Safety-Critical Systems
505

ily, for example by setting non-transitive comparison
judgments. However, the ratings are not required to
result in a fully transitive judgment, since this can
hardly be achieved for more than three subgoals by
human decision making and usually is impossible for
the whole number of ratings. Therefor, only a certain
degree of consistency is required, the so called Con-
sistency Ratio [Saaty, 1990]. In literature several al-
gorithms for identification of inconsistent ratings can
be found, e.g. [Harker, 1987].
Based on the pairwise comparison matrix, local
priorities, i.e., the importance of subgoals contribut-
ing to their super-ordinated objective, can be calcu-
lated using the eigenvector of the matrix AHP. These
local priorities are used to calculate the global priori-
ties of the single points of failure, meaning the abso-
lute importance of the objectives on the lowest level
for reaching the top-level safety goal. In the next step
we have to determine how well the alternative solu-
tions fulfill the objectives of preventing SPOFs. Since
this has already been evaluated with the FMEA, hav-
ing ratings between 1 and 10 for failure OSD, FMEA
judgments only have to be transfered into suitable
AHP pairwise comparison ratios which can be done
automatically. Two suitable transformation meth-
ods, namely RPN Comparison Method (RCM) and
Pairwise Comparison Method (PCM), will be pre-
sented. Thereby RCM directly uses the RPN calcu-
lation. Therefor, the FMEA ratings of alternative so-
lutions are compared by normalizing their inverse ra-
tios. The resulting local priorities in form of percent-
ages of importance, can be used directly by the AHP
to calculate global priorities for proposed alternative
solutions. The result is a weighted prioritization of the
alternative solutions, identifying the one which best
fulfills the SST objectives.
O S D RPN
S
1
o
1
s
1
d
1
r
1
S
2
o
2
s
2
d
2
r
2
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
S
n
o
n
s
n
d
n
r
n
For RCM, a vector of RPNs a = (r
1
, r
2
, ..., r
n
) is ex-
tracted from the matrix above. Subsequently, the in-
verse vector of a is created: a
−1
= (r
−1
1
, r
−1
2
, ..., r
−1
n
).
Then, a
−1
is normalized by the formula: α =
1
∑
i=n
i=1
r
−1
i
.
Finally, the local priorities π(S
i
) for every alternative
solution S
i
are derived by: π(S
i
) = r
−1
i
· α.
The RCM directly reflects the RPN values in the
tradeoff analysis and its calculation is quite simple,
whereas PCM is much more related to AHP. More-
over, it does not depend on the flawed RPN calcula-
tion, as it is directly based on OSD ratings, whereas
PCM allows a much more flexible and accurate con-
sideration of FMEA judgments. For the PCM, first of
all the FMEA ratings for OSD of the potential fail-
ure modes have to be judged in their relative impor-
tance for the criticality of a failure. Therefor we de-
fine a so called OSD-Matrix, that is kept constant for
all SPOFs. It is a simple judgment matrix comparing
the importance of OSD on behalf of safety. By de-
fault it is an all-one matrix, which would imply that
OSD are considered equally important. In a second
step, the FMEA ratings for the alternative solutions
have to be transformed into judgment matrices. Since
the values of OSD are multiplied with each other to
determine the RPN, higher ratings result in exponen-
tially higher RPNs. To reflect this characteristic in the
matrices of pairwise ratios a cubic function is used to
transform OSD ratings: Let X be one of the ratings
X ∈ {O, S, D} and x
i
∈ {o
i
, s
i
, d
i
} for i ∈ {1, 2, . . . , n},
then each rating is transformed by x
0
i
= x
3
i
for all x
i
.
By raising the rating to the third power, the multipli-
cation that would have been made when calculating
the RPN is approximated. Again the inverse ratios
of the transformed judgments have to be used, since
higher OSD ratings represent a higher risk of failure
and though a worse, i.e., a lower, AHP judgment. The
three pairwise ratio matrices are calculated as follows:
S
1
S
2
·· · S
n
S
1
1
x
0
2
x
0
1
·· ·
x
0
n
x
0
1
S
2
x
0
1
x
0
2
1 ·· ·
x
0
n
x
0
2
.
.
.
.
.
.
.
.
.
.
.
.
S
n
x
0
1
x
0
n
x
0
2
x
0
n
·· · 1
Prevent SPOF
Occurrence Severity Detection
Solu-
tion 1
Solu-
tion p
Solu-
tion 2
. . .
Figure 2: PCM: Goal Hierarchy Extension.
Obviously, this is a consistent reciprocal matrix. To
determine the local and global priorities with the
AHP, the goal hierarchy has been extended at every
SPOF (2). The regular AHP algorithm can be ap-
plied on this extended goal hierarchy to find the safest
tradeoff between evaluated alternative solutions.
3 EVALUATION
In this section the position paper brings a real ap-
plication example that includes the whole approach
MODELSWARD 2018 - 6th International Conference on Model-Driven Engineering and Software Development
506

of the tradeoff analysis more closer. Furthermore,
a szenario based evaluation is performed that cov-
ers three szenarios applying the approach presented
in this paper.
3.1 Application Example
The tradeoff analysis is operated by means of a self-
developed Eclipse plugin enabling automated calcu-
lations and graphical visualizations. The work flow
presented in 2 thereby serves as a basis. It is analyzed
which kind of ACC system, the ACC with a maxi-
mum permissible speed of 210 km/h or 160 km/h,
complies the safety requirements more. With com-
mon sense it can be concluded that the ACC with a
maximum permissible speed of 160 km/h is safer than
the other one. Thus, the alternative solutions are ex-
tended to an ACC (210 km/h) with Radar + Camera
and 256 bit Encryption as well as an ACC (160 km/h)
with Radar and 128 bit Encryption. The next step in-
cludes designing (sub-)goals and SPOFs for an ACC
being acceptably safe. For that purpose subgoals are
designed aiming at correctly working sensors, actua-
tors, software and the communication between them.
All these subgoals are split in two or more SPOFs.
For instance, in case of subgoal ACC Actuators are
working correctly there are two SPOFs: Brake fail-
ure is sufficiently mitigated as well as Engine failure
is sufficiently mitigated. The complete goals as well
as all associated SPOFs (marked with the individual
concerns) are illustrated in a GSN hierarchy (3) where
each of the SPOFs is connected with the two afore-
mentioned alternative solutions.
For each SPOF, it is mandatory to perform FMEA
risk assessments, i.e., RPN values must be calculated
based on OSD probabilities. The exemplary assess-
ment of the SPOF Missing an obstacle can be ruled
out with sufficient certainty is listed in 1. All deter-
mined RPN values can be found in 3 assigned to the
respective SPOF. Since there are SPOFs with associ-
ated RPNs values that will endanger safety risk sig-
nificantly, improvements according RPN calculations
have to be performed.
Table 1: FMEA risk assessment of the SPOF.
O S D RPN
ACC 210 km/h 1 9 6 54
ACC 160 km/h 2 8 6 96
With the completion of the risk assessments it is
necessary to rate (sub-)goals and SPOFs by their im-
portance according to the AHP algorithm in [Saaty,
1990]. The AHP rating of the top goal can be seen
in 2. It can be observed here that ACC communica-
tion is acceptably reliable is more important than all
the other goals. Hence the local priority for the com-
munication (Comm. in 2) is better than for the sen-
sors, actuators (Act.) and software (SW). Since the
resulting maximum consistency ratio has not been ex-
ceeded, no further improvements are required.
Table 2: AHP rating of the goal ACC is acceptably safe.
Act. SW Sensor Comm.
Act. 1 1 1
1
2
SW 1 1 1
1
2
Sensor 1 1 1
1
2
Comm. 2 2 2 1
Local Prio. 20% 20% 20% 40%
Consis. Rat.: 0%
Finally, the tradeoff analysis can be done compar-
ing local priorities of the RCM and PCM method (4).
By applying the PCM the judgments of OSD were
changed according to 3.
Table 3: OSD Matrix of the PCM.
O S D Local Priority
O 1 2 5 58,2%
S
1
2
1 3 30,9%
D
1
5
1
3
1 10,9%
The results show that the ACC (210 km/h) with
Radar + Camera and 256 bit Encryption is safer than
the ACC (160 km/h) with Radar and 128 bit Encryp-
tion. As can be seen there is no significant difference
between the two methods.
Table 4: Global priorities of the alternative solutions.
Alternative Solution RCM PCM
ACC 210 km/h 54,4% 56,2%
ACC 160 km/h 45,6% 43,8%
3.2 Szenario based Evaluation
Three additional scenarios are evaluated:
1. The approach is also compatible with other risk
assessment methods than FMEA. Therefore,
Fault Tree Analysis (FTA) has been analyzed.
2. Changes on the system model effect changes on
the approach. Therefore, the ACC system is com-
plemented by a Lane Assist (LA) system. It is
evaluated which parts are concerned and how to
solve upcoming problems.
Multi-Concerns Engineering for Safety-Critical Systems
507
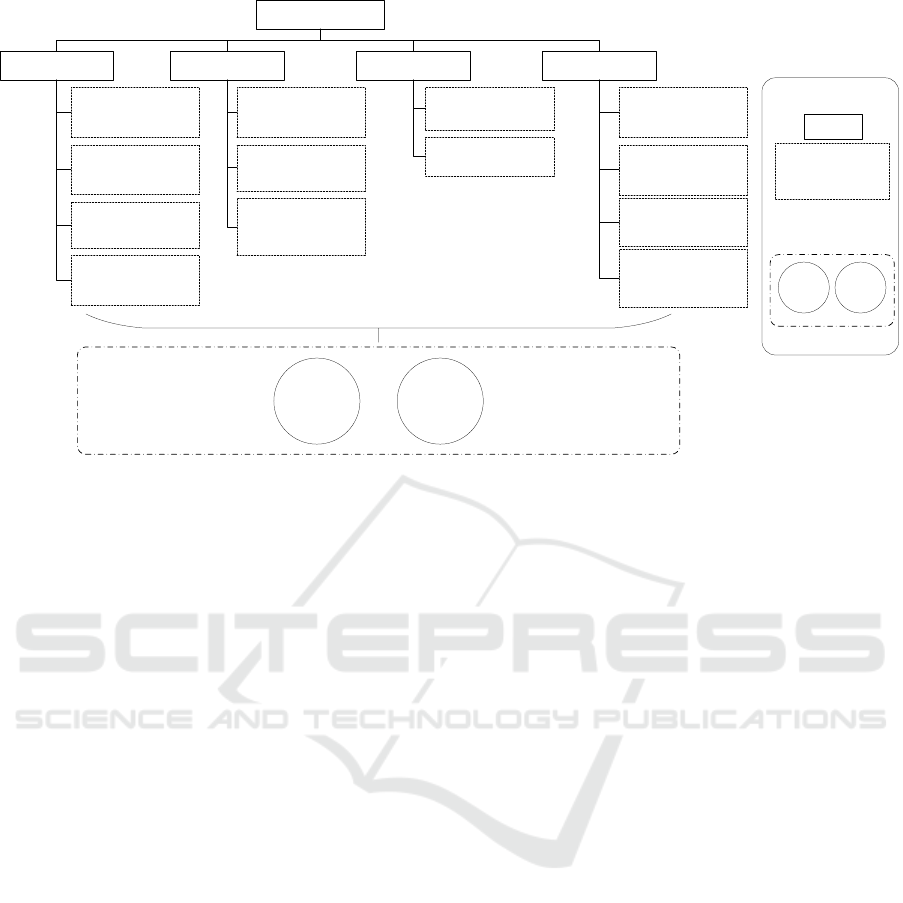
ACC is acceptably safe
ACC Sensors are working
correctly
ACC Software is working
correctly
ACC Actuators are
working correctly
ACC communication is
acceptably reliable
Brake failure is sufficiently
mitigated (SA)
27 27 88,9%
Engine failure is sufficiently
mitigated (SA)
21 21 11,1%
Results are correct. Errors
are sufficiently mitigated.
(SA)
90 90 40,0%
Results are calculated in
time. Delays are sufficiently
mitigated. (TI)
100 100 40,0%
Software acceptably secure
against manipulation and
hacking attacks (SE)
162 81 20,0%
Missing an obstacle can be
ruled out with sufficient
certainty (SA)
54 96 38,8%
Distance to the obstacle is
acceptably accurate (not too
short) (SA)
48 90 8,0%
The probability of detecting
an obstacle in time is
acceptable. (TI)
80 70 38,5%
Detecting a non existing
obstacle can be ruled out
with sufficient certainty (SA)
45 45 14,7%
Communication is
acceptably secured against
data theft (SE)
180 90 10,0%
Communication is
acceptably secured against
manipulation (SE)
72 144 30,0%
Messages arrive in time with
acceptable reliability (TI)
48 48 30,0%
Messages are transferred
correctly with acceptable
reliability (SA)
48 48 30,0%
ACC (210 km/h)
with Radar +
Camera, 256 Bit
Encryption
ACC (160 km/h)
with Radar, 128
Bit Encryption
any Goal
any SPOF
RPN ACC 160 km/h
RPN ACC 210 km/h
Local Priority
Legend
Note: Solutions relate to
all SPOFs
any
Solution
any
Solution
2
(SA) Safety
(SE) Security
(TI) Timing
Figure 3: Abstract goal hierarchy of the application example.
3. The approach is scalable as required, i.e., the SGH
and alternative solutions are expandable. For eval-
uation alternative solutions will be modified.
The fundamental difference between FMEA and FTA
is that FMEA lists the probability of OSD based on
a SPOF whereas FTA lists all events that lead to a
SPOF. This means that FMEA calculates the risk
top-down whereas FTA calculates the corresponding
risk bottom-up. Another difference is, that FTA deter-
mines the percentage probability that the correspond-
ing SPOF applies whereas FMEA determines the re-
sulting RPN. As stated in 2 there are two methods for
calculating the tradeoff: RCM and PCM. If the RCM
method is applied with FMEA the tradeoff is calcu-
lated based on the ratio between the current RPN and
the maximal possible RPN whereas for FTA this is
done based on the ratio between the current proba-
bility and the maximal possible probability that the
SPOF occurs. Even though the PCM algorithm is ap-
plied the tradeoff can be calculated using FTA risk
assessment. In contrast to FMEA, FTA does not need
any priorities for calculating the tradeoff, i.e., a classic
AHP can be performed for calculation. It is therefore
possible to apply any other risk assessment method if
probabilities are assigned to the SPOFs.
The second scenario proves stability if some
changes on the system model are made, i.e., im-
pact analyses must be performed [Langermeier et al.,
2015]. Due to the rapid development in the auto-
motive industry, new assistance systems occur from
time to time and hence, new hardware and software
must be installed in the car. This involves changes
ton the system model and thus also the safety risk
which makes it necessary to update the SGH. Assum-
ing there is an additional LA system, a new subtree
LA is acceptably safe with all its subgoals and SPOFs
must be created. In the same way as the ACC the LA
considers goals and SPOFs with respect to sensors,
actuators, software as well as the communication be-
tween them. Pairwise comparisons as well as the risk
assessments must be performed in accordance with 2.
Finally, a new top goal ACC and LA are acceptably
safe must be created that combines the two subtrees,
including a pairwise comparison between the ACC-
and the LA subtree.
In practice, there are some regulations regarding
software and hardware that are given by certification
authority, impacting the SGH or alternative solutions
[Langermeier et al., 2015]. Scenario 2 already cov-
ered scalability of the SGH indirectly, hence, objec-
tive of this scenario is to change alternative solutions
and to evaluate it. Assuming there is an SGH cov-
ering an LA system, the certification authority stipu-
lates the minimal resolution of the installed cameras.
Thus, alternative solutions have to be adapted with
the new resolution and risk assessments between all
SPOFs and the updated alternative solutions must be
set again before calculating the updated tradeoffs.
4 RELATED WORK
In this section, related publications and projects will
be presented and compared with the approach of a
tradeoff analysis on SCS.
MODELSWARD 2018 - 6th International Conference on Model-Driven Engineering and Software Development
508

4.1 Safety Assessment with the AHP
and the FMEA
The AHP by Thomas L. Saaty [Saaty, 1990] is used
for making decisions regarding safety in various do-
mains, e.g., in [Jianbin et al., 2009], [Wang et al.,
2011] and [Cheng et al., 2011]. However, the AHP
is also used for making decisions based on security
concerns, e.g., in [Ji et al., 2010] and [Taha et al.,
2014]. A tradeoff analysis on behalf of safety, con-
sidering security and timing concerns as well as func-
tional demands does not seem to have been evaluated
scientifically before and is therefore unique in liter-
ature. Although the AHP is also used for making
decisions on security concerns, e.g., [Jianbin et al.,
2009] and [Taha et al., 2014] a tradeoff analysis on
behalf of safety, taking security and timing issues
as well as functional demands into account doesn’t
seem to have been evaluated scientifically before and
is therefore unique in literature. A fairly similar ap-
proach, performing a tradeoff analysis on behalf of
safety that combines the FMEA with the AHP, is the
work of [Zhao et al., 2013]. They focus on analyzing
the reliability of manufactoring processes by means of
the Process Failure Mode Effect and Critically Anal-
ysis (PFMECA), enhanced by the AHP. This method
has solely been designed for analyzing safety in man-
ufacturing processes. The method proposed in this
paper can be applied to any SCS, product or process.
4.2 Related Projects on Safety and
Security
There is a project which is important to be consid-
ered: SESAMO (Security and Safety Modelling).
Although it pursues quite similar objectives, it fo-
cuses on safety and security requirements, aiming
”to develop a component-oriented design methodol-
ogy based upon model-driven technology, jointly ad-
dressing safety and security aspects and their inter-
relation for networked embedded systems in multi-
ple domains.” [SESAMO, 2015]. One major objec-
tive has been developing procedures for integrated
analysis of safety and security demands, focusing on
identifying hazards to facilitate an informed tradeoff
between contradicting safety and security demands.
One goal is to provide convincing evidence, justifying
”that the risks associated with the system are as low
as reasonably practicable” [Paulitsch et al., 2012].
Stating that a system cannot be safe without being se-
cure, the SESAMO project supports the position of
considering safety as the top-level goal, that can be
affected by security issues. [Paulitsch et al., 2012] In
contrast to this paper, the SESAMO project does not
provide a competitive tradeoff analysis by a system-
atic method like the modified AHP combined with the
FMEA. Moreover, the results of the tradeoff analy-
sis as proposed by SESAMO are not fully compatible
with the FMEA. However, the FMEA is a compulsory
part of the certification requirements in the automo-
tive industry [Paulitsch et al., 2012]. Moreover, there
is another project called SafeCer (Safety Certification
of Software-Intensive Systems with Reusable Com-
ponents). It aims to increase ”[...] efficiency and re-
duce(d) time-to-market by composable safety certifi-
cation of safety-relevant embedded systems.” [Safe-
Cer, 2015] The project focused on providing methods
and tools composing safety arguments for a system
by reusing already established arguments and proven
properties of the subsystems. This project share the
goal of providing means (architectures, tools, pro-
cesses or standardization) to enhance efficient safety
assurance and certification. However, this project
doesn’t explicitly aim to support a MCDA taking
safety, security and timing issues into account, as it
has been proposed in this paper. [SafeCer, 2015]
5 CONCLUSION AND OUTLOOK
In this paper an approach has been presented how to
combine SST concerns for the development of safety-
critical systems. Thereby, safety issues with a max-
imum degree of safety are of primary importance.
For that purpose, an SGH has been introduced which
is based on GSN. This SGH contains all safety-,
security- or timing goals and SPOFs within a hierar-
chical structure. Furthermore, it contains alternative
solutions, in order to calculate a tradeoff. Addition-
ally, it has been demonstrated how to perform risk as-
sessments of the SPOFs using the FMEA technique.
The tradeoff in itself is calculated by means of two
possible methods: The RCM and the PCM. The ba-
sis for the calculation is either the FMEA technique
or the AHP algorithm. Furthermore, the approach has
been evaluated based on an application example com-
paring two different ACC systems by means of three
selected scenarios with respect to stability and adapt-
ability of applied techniques. For further work, it
would be useful to cluster some goals and to perform
the tradeoff analysis in an abstract manner. Thus, it
would be possible without any effort to check if a sys-
tem component is profitable or not. Another aspect
that has not been considered in this paper concerns
product line engineering. In those days there are nu-
merous configuration options of an automotive vehi-
cle. Hence, a product line approach will be developed
contemporary.
Multi-Concerns Engineering for Safety-Critical Systems
509

REFERENCES
Bowles, J. (2003). An assessment of RPN prioritization
in a failure modes effects and criticality analysis. In
Annual Reliability and Maintainability Symposium,
2003, Columbia, USA.
Bundesministerium des Inneren (2017). Fehler-
moeglichkeits - und einflussanalyse (FMEA). In
Organisationshandbuch, Berlin, Germany.
Cheng, C. et al. (2011). An AHP method for road traf-
fic safety. In Fourth International Joint Conference
on Computational Sciences and Optimization (CSO),
Dalian, China.
Harker, P. (1987). Derivatives of the perron root of a posi-
tive reciprocal matrix: With application to the analytic
hierarchy process. In Applied Mathematics and Com-
putation, volume 22, Philadelphia, USA.
Ji, X. et al. (2010). AHP implemented security assessment
and security weight verification. In Second Interna-
tional Conference on Social Computing (SocialCom),
Leeds, UK.
Jianbin, G. et al. (2009). The safety detection research of
wind power units based on ahp method. In Interna-
tional Conference on Sustainable Power Generation
and Supply, Nanjing, China.
Kelly, T. et al. (2004). The goal structuring notation - a
safety argument notation. In Proceedings of the De-
pendable Systems and Networks 2004 Workshop on
Assurance Cases, New York, USA.
Langermeier, M. et al. (2015). Adaptive approach for im-
pact analysis in enterprise architectures. In Business
Modeling and Software Design. BMSD 2014, Cham,
Switzerland.
Liu, H. et al. (2016). Risk evaluation in failure mode and
effects analysis using fuzzy digraph and matrix ap-
proach. In Journal of Intelligent Manufacturing, vol-
ume 27, New York, USA.
Nilsson, D. et al. (2008). A roadmap for securing ve-
hicles against cyber attacks. In National Workshop
on High-Confidence Automotive Cyber-Physical Sys-
tems, Michigan, USA.
Paulitsch, M. et al. (2012). Evidence-based security in
aerospace. In ISSRE Workshops 2012.
Saaty, T. (1990). How to make a decision: The analytic hi-
erarchy process. In European Journal of Operational
Research, volume 48.
SafeCer (2015). SafeCer project homepage.
http://safecer.eu. accessed November, 13th.
SESAMO (2015). SESAMO project homepage. http://
sesamo-project.eu/. accessed November, 13th.
Taha, A. et al. (2014). Ahp-based quantitative approach for
assessing and comparing cloud security. In 13th In-
ternational Conference on Trust, Security and Privacy
in Computing and Communications, Darmstadt, Ger-
many.
Wang, H. et al. (2011). Safety assessment on railway cross-
ings based on extension ahp and set pairs analysis. In
International Conference on Management and Service
Science (MASS), Dalian, China.
Zhao, Y. et al. (2013). An improved risk priority number
method based on ahp, reliability and maintainability
symposium (rams). In 2013 Proceedings - Annual,
Beijing, China.
MODELSWARD 2018 - 6th International Conference on Model-Driven Engineering and Software Development
510
