Data Mining Applied to Transportation Mode Classification Problem

Andrea Vassilev

CEA, LETI, MINATEC Campus F-38054, Grenoble, France

Keywords: Context Awareness, Transportation Mode, Data Mining, Classification, Smartphone, Sensors, Principal

Component Analysis, Mahalanobis Distance, Linear Discriminant Analysis.

Abstract: The recent increase in processing power and in the number of sensors present in today’s mobile devices leads

to a renewed interest in context-aware applications. This paper focuses on a particular type of context, the

transportation mode used by a person or freight, and adequate methods for automatically classifying

transportation mode from smartphone embedded sensors. This classification problem is generally solved by

a searching process which, given a set of design choices relative to sensors, feature selection, classifier family

and hyper parameters, etc., find an optimal classifier. This process can be very time consuming, due to the

number of design choices, the number of training phases needed for a cross validation step and the time

necessary for one training phase. In this paper, we propose to simplify this problem by applying three data

mining tools - Principal Component Analysis, Mahalanobis distance and Linear Discriminant Analysis - in

order to clean the data, simplify the problem and finally speed up the searching process. We illustrate the

different tools on the transportation mode classification problem.

1 INTRODUCTION

The field of context recognition has gathered a lot of

attention in recent years mostly thanks to the

widespread of mobile devices (for e.g. smartphones

and wearable). With the continuous integration of

new sensors, their ever increasing computing power

and their virtual omnipresence, these devices have

become ideal tools for context recognition. More

precisely, our interest here is the recognition of the

transportation modes used by a person or freight. The

applications are numerous:

 Carbon footprint evaluation (Manzoni et al.,

2010),

 Real-time door-to-door journey smart

planning,

 Smart mobility survey (Nitsche et al., 2014),

 Driving analysis (Vlahogianni and

Barmpounakis, 2017),

 Road user analysis and collision prevention,

 Goods mobility tracking

 Traffic Management

This classification problem is generally solved by

a searching process which, given a set of design

choices find an optimal classifier.

A design choice involves 3 main aspects:

 Sensors: modern mobile devices contain

several different sensors, at least the

following eight: accelerometer (ACC),

magnetometer (MAG), gyroscope,

barometer, GPS, Wifi, GSM, audio… Each

of these sensor can be used for transportation

mode classification. Most widely used are

ACC and GPS (Wu et al., 2016), (Stenneth

et al., 2011), (Hemminki et al., 2013),

(Reddy et al., 2010), but some authors use

only GSM (Anderson and Muller, 2006) or

only barometer (Sankaran et al., 2014). The

number of different sensor combinations

(for 8 sensors) is already important

=256).

 Features: raw sensor data are rarely used

directly, but are often pre-processed leading

to features. E.g., given the accelerometer

readings over a finite time window (E.g. 5

seconds.) on can compute the mean value,

the variance, the skewness, the number of

zero crossings, the Fast Fourier Transform

(FFT) coefficients, the energy for different

frequency bands,…

Given a set of sensors there is almost an

infinite number of features that can be

computed.

Vassilev, A.

Data Mining Applied to Transportation Mode Classiﬁcation Problem.

DOI: 10.5220/0006633300360046

In Proceedings of the 4th International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS 2018), pages 36-46

ISBN: 978-989-758-293-6

 Classifier family and associated hyper

parameters: each classifier family (decision

tree (DT), neural network (NN),…) has its

own hyper parameters that need to be fixed

before training: e.g., for DT, the maximum

number of splits, for NN, the number of

hidden layers and the number of neurons by

layer,…

Testing different combinations of sensors, fea-

tures, classifiers and hyper-parameters often lead to a

rapid increase of the total number of design choices

(phenomenon known as combinatorial explosion).

Moreover, given a design choice, once a classifier

is trained, its classification performance has to be

evaluated. The most widely used technique is a

K-fold cross validation approach (Arlot and Celisse,

2010) which needs K+1 training phases, leading to a

total number ~N

.K of training phases.

Finally, the training phase duration is very

sensitive to the problem dimension, i.e. the number of

features (a.k.a. “curse of dimensionality”).

In conclusion, the searching process becomes

rapidly intractable.

The aim of this article is to propose a method to

simplify this problem. Section 2 describes the

approach. In section 3 it is applied to real data

concerning the transportation mode classification

problem. Discussion and conclusions can be found in

Section 4.

2 PROPOSED APPROACH

2.1 Overview

Instead of trying to blindly investigate various

combinations among all possible ones, the proposed

approach consists in focussing on sensors and

features, and not on classification aspects.

Using two simple data mining tools, the aim is to

 Clean the data,

 Simplify the problem.

Once it is done, a searching process involving

only classifier family and associated hyper

parameters can be conducted more easily.

To do so, we use 3 data mining tools:

 Principal Component Analysis (PCA)

 Mahalanobis distance (MD)

 Linear Discriminant Analysis (LDA)

As the first two tools are related, they will be

presented in the same Section 2.2, whereas LDA will

be explained in Section 2.3.

2.2 Principal Component Analysis

PCA is a widely used procedure (Wikipedia, 2017)

and (Martinez and Kak, 2001).

It computes an orthogonal transformation to

convert a set of observations of possibly correlated

variables into a set of values of linearly uncorrelated

variables called principal components. This

transformation is defined in such a way that each

component has the largest possible variance, under

the constraint that it is orthogonal to the preceding

components. The resulting vectors are an

uncorrelated orthogonal basis set.

Note that PCA is an unsupervised technique in the

sense that the data class is not taken into account in

the process.

In the following, we will summarize the PCA

implementation and present 3 interesting

applications:

 detecting outliers,

 checking linear dependency between

features,

 reducing dimension.

2.2.1 PCA Implementation

Let X be the data in the original space, a matrix Nxp,

with N instances and p predictors. The

implementation is the following:

 As PCA is very sensitive to outliers, remove

the outliers

 As PCA is very sensitive to the relative

scaling of the original variables, normalize

data (e.g., so each column of X has mean 0

and standard deviation 1); let X

be the

normalized matrix (same size as X).

 Let C

be the covariance matrix of X

 Apply the PCA; it outputs (P, D) the

eigenvectors and eigenvalues of C

, so we

have C

.P = P.D. The columns of the

orthogonal p*p matrix P (P.P

= I

with I

the identity p*p matrix) are the principal

components (PC), whereas the p*p diagonal

matrix D (let D

be the j

diagonal element)

represents the variance of data on each axis

of the new basis.

 Data in the new PC space are

  



  (1)

 They are uncorrelated as it can be easily

shown that the covariance of Y is matrix D.

Data Mining Applied to Transportation Mode Classiﬁcation Problem

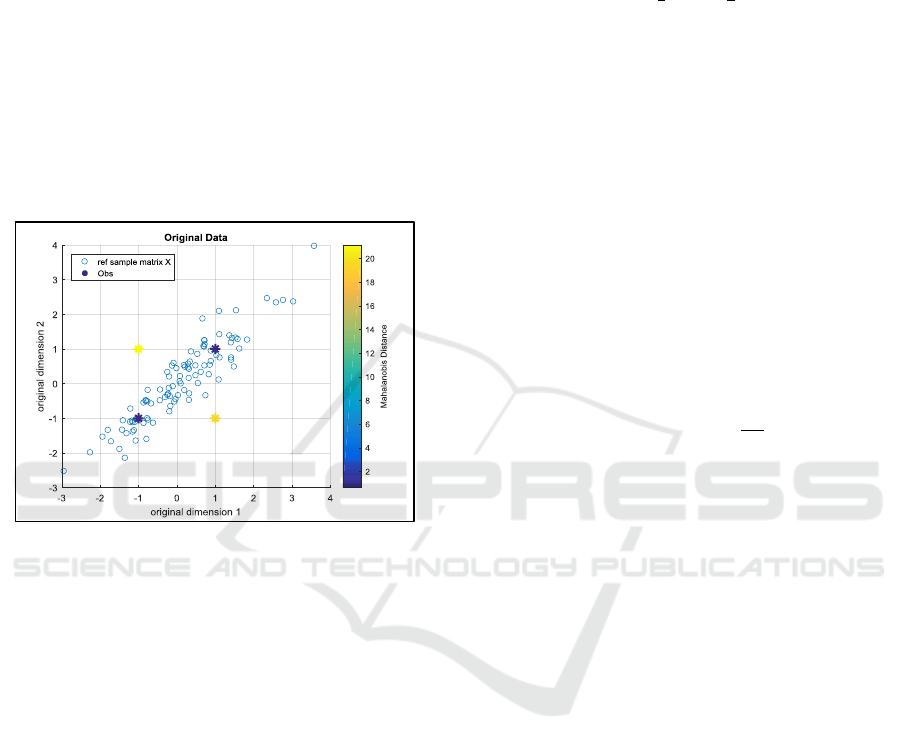
2.2.2 Detecting Outliers

In the original space, because of the correlation of the

predictors, computing a Euclidean distance (ED)

between 2 points is inappropriate. E.g., on the Figure

1, we generate synthetic centered correlated data in a

2D space (blue circles). One can see that probably the

blue stars and the data are coming from the same

distribution, whereas it is much less likely for the

yellow stars.

By using Euclidean distance, with respect to the

centre of the data (0, 0), the 4 stars would be at the

same distance (√2). Therefore ED is not appropriate

to measure distance between points and detect

outliers.

Figure 1: Synthetic data.

This is why Mahalanobis distance (MD) (De

Maesschalck et al., 2000), (Li et al., 2011) was

introduced. The idea was to de-correlate the data

before computing a Euclidean distance.

Let x

be an instance (1xp) in the original space, µ

the mean vector (1xp) of the p predictors and C the

covariance matrix of the data X. The squared

Mahalanobis distance 





is defined by:















 













 





(2)

It measures how many variances away, the

instance is from the centre of the cloud.

Now we are going to demonstrate how MD is

linked to PCA.

Let V be the diagonal p*p matrix, such as

diag(V)=diag(C) (i.e. with the variance of each

predictor in the original space on the diagonal), and

let M be the Nxp matrix with identical row equal to

µ.

The normalized matrix X

can be rewritten:









  



 



(3)

And for the particular instance i:













 



 



(4)

From the basic properties of covariance operation

(cov(X.A+a)=A

.cov(X).A) and as V is diagonal, we

have:





 









  







 



  (5)

Using (2), (3), (4) and (5), we get







 















(6)

Let y

be the particular instance i in the PC space.

From (1), we have





 



  (7)

and









 



 



    (8)

Using (6), (7), (8), it comes







 



 



 





(9)

Let y

i,j

be the j

component of y

. (9) can be

rewritten as:























(10)

The Mahalanobis distance appears to be, in the PC

space, a simple sum of squares weighted by the

inverse of variances on each PC.

Finally, in a similar way to the original space, it is

interesting to define a normalized PC space, in which

the data Y

are:





  



(11)

Using the same reasoning, it comes that the

covariance matrix of Y

is the identity matrix and that

the Mahalanobis distance is simply equal to the

Euclidean distance in the normalized PC space.







 



 





(12)

Which can be rewritten:



















(13)

In conclusion, there are 4 different spaces: the

original one (X), the normalized one (X

), the PC

space (Y) and the normalized PC space (Y

). Each

space is defined from the previous by a simple

operation (translation, stretching and rotation) – see

equations (3), (1) and (11). In each of these spaces,

the Mahalanobis distance can be expressed, see

equations (2), (6), (9) and (12). The writing is more

or less complex, depending on the covariance matrix.

The last writing, in the normalized PC space is the

simplest and is interesting because it is a simple ED.

VEHITS 2018 - 4th International Conference on Vehicle Technology and Intelligent Transport Systems

The outlier detection procedure is therefore:

 Run a PCA and get D, P and Y.

 Using (11) project the data in the normalized

PC space, and compute for each instance the

MD using the simple ED (12).

 An instance will be considered as an outlier

if its MD (or its squared MD) is above a

given threshold t: 





 .

The choice of the threshold t is not straightforward

and could be sometimes arbitrary. It may be helpful

to compute and plot the empirical cumulated

distribution function of the squared MD.

Once the outliers detected, it becomes possible to

identify which components are responsible for the

instances being classified as outliers. This can be

done by computing a normalized contribution of each

principal component (j=1..p) to the squared MD (14)

and looking if some components are more important

than the others:







 













(14)

Once some particular components have been

identified, it is sometimes possible to come back to

the original space (see the application example 3.2.1).

2.2.3 Checking Linear Dependency Between

Features

PCA helps to reveal the sometimes hidden, simplified

structures that underlie the data; an extreme case is

the linear dependency between features. In that

situation, the p

eigenvalue is very small D

≈0,

meaning that the data projected on the associated

Principal Component p

have almost no variance;

using the fact that data are centered, this implies that:





 



  (15)

represents the linear combination of the data in

normalized space. If we want to come back to the

original space, we use (3) and define a new (px1)

vector:





 







 



(16)

Such as

 



  



  (17)

Therefore, the vector q

represents the linear

combination of the data in the original space.

2.2.4 Dimension Reduction

The most popular use of the PCA is to find the dimen-

sion of the data and/or reduce the dimension without

losing too much variance. The idea is to compute the

cumulated variance v

k, k=1..p

in the PC space:













(18)

And determine when its normalized value w

(19)

exceeds a given threshold t (between 0 and 1); let q

be the number of components.















(19)

The intrinsic dimension is therefore q≤p and the

data can be represented in the PC space by only the

first q PCs.

After these three steps, outliers from the data have

been removed, linear dependency between features

has been studied and data dimension has been

reduced.

2.3 Linear Discriminant Analysis

Linear Discriminant Analysis (LDA) is also called

Fisher Linear Discriminant (FDA) (Duda et al., 2001)

or Fisher Score (Gu et al., 2012). Contrary to PCA, it

is a supervised technique, which given some data,

searches for a linear combination of original variables

that best discriminates among classes (rather than best

describe the data as with PCA).

In the following, we will summarize the LDA

implementation and present an interesting

applications: feature selection.

2.3.1 LDA Implementation

Let us define some notations:

 X: data in the original space, a matrix Nxp,

with N instances and p predictors.

 K: number of different classes

 D

: the subset of samples belonging to class

 n

: cardinal of D

 m

: the p-dimensional mean of samples of

 m: the p-dimensional mean of all samples.

The implementation is the following:

 Compute the within-class scatter matrix S

which is the sum of scatter matrices S

















(20)







 

  





  











(21)

 Compute the between-class scatter matrix

Data Mining Applied to Transportation Mode Classiﬁcation Problem



















 







 







(22)

One can show that the total scatter matrix S

defined by (23) is the sum of S

and S







 

  



  







(23)

 Solve for the eigenvalues and the

eigenvectors of S

-1

matrix; it leads to p

eigenvectors c

j, j=1..p

and p eigenvalues e

j=1..p

. It can be shown S

is of rank K-1 at

most; therefore, there are K-1 nonzero

eigenvalues at most.

 The eigenvectors, also called discriminant

axis, are linear combination of original

vectors and define a new ‘C space’ that

maximizes the class separability.

 Let define a separability criteria SC as the

sum the eigenvalues (also equal to

tr(S

-1

). It gives an idea of how well the

classes are separated in the new C space.

 







Tr















(24)

2.3.2 LDA for Feature Selection

LDA is very useful for feature selection. Given a set

of p features,

 We apply the LDA procedure and get an

initial separability criteria SC

 We remove each feature j=1..p one by one

and compute the new separability criteria

and the impact on class separability

=1- SC

/SC

 We remove features whose impact is low,

i.e. |r

| below a threshold (typ. 0.05).

3 RESULTS

In a first section, we present the data relative to the

transportation mode problem.

Then, we apply the proposed approach.

3.1 The Data

Details about data collection, data pre-processing and

feature extraction are given in (Lorintiu and Vassilev,

2016).

A smartphone application for Android based

smartphones was developed to perform the data

collection. The application stores the raw sensor data

such as GPS, accelerometer and magnetometer. The

subjects were asked to install the developed

application on a compatible smartphone and use it

during their commute to work or any other trip. They

were also asked to choose the travel mode they are

using during the recording process. The subjects

weren’t imposed any position for their smartphone.

22 subjects participated to the database setup,

using 12 different smartphones. About 400 trips were

recorded, representing 225 hours of recording.

Three sensors, ACC, MAG and GPS were taken

into account. From the raw sensor data, signals were

segmented using a 5 seconds non overlapping

window, leading to an initial number N

= 161489

instances. On each window, a pre-processing was

applied to ACC whose steps are:

 Estimate gravity, and subtract it from

acceleration measured, leading to the linear

acceleration

 Decompose the linear acceleration into a

vertical acceleration APV and a horizontal

one APH,

 Decompose the horizontal acceleration APH

into a longitudinal (or forward) H1 and a

lateral H2 acceleration.

Then, 14 a priori relevant features were computed

(see Table 1). Note that the 4 features whose name

starts with ‘ACC_V_BAND’ are defined so their sum is

equal to 1.

Table 1: The 14 features.

Seven different transportation modes were

considered: ‘bike’, ‘plane’, ‘rail’, ‘road’, ‘run’, ‘still’,

‘walk’. An additional class named ‘other’ contains

activities that are irrelevant for this study.

‘rail’ class regroups transportation modes such as

tramway, subway, train and high speed train, whereas

‘road’ assembles transportation modes such as ‘car’

and ‘bus’.

It is important to note that GPS sensor is

unavailable 42.3% of the time, representing 68316

(resp. 93173) instances unavailable (resp. available).

This quite surprising result can be explained by the

fact that as GPS is a sensor that relies on a radio wave

communication with a set of satellites, the quality of

this communication depends on

ID Name Unit Description

1 MAG_NORM_STD µT Standard deviation of magnetic field norm

2 ACC_STD_V m/s² Standard deviation of APV

3 ACC_STD_H1 m/s² Standard deviation of H1

4 ACC_STD_H2 m/s² Standard deviation of H2

5 ACC_V_BAND_EN_1 - Relative energy of APV in the band [0.7-3.5 Hz]

6 ACC_V_BAND_EN_2 - Relative energy of APV in the band [3.5-8.5 Hz]

7 ACC_V_BAND_EN_3 - Relative energy of APV in the band [8.5-18.5 Hz]

8 ACC_V_BAND_EN_4 - Relative energy of APV in the band [18.5-45 Hz]

9 ACC_SPEC_CENTROID_V Hz Spectral centroid of APV

10 MAG_SPEC_CENTROID Hz Spectral centroid of magnetic field norm

11 ACC_SPEC_SPREAD_V Hz² Spectral spread of APV

12 MAG_SPEC_SPREAD Hz² Spectral spread of magnetic field norm

13 GPS_SPD_MED m/s Median of GPS speed

14 ACC_NORM_VAR (m/s²)² Variance of accelerometer norm

VEHITS 2018 - 4th International Conference on Vehicle Technology and Intelligent Transport Systems

 the GPS receiver sensitivity (often poor for

low cost GPS chip embedded in mobile

devices),

 Radio wave attenuation due to aircraft or

train cabin or car body.

 Relative position of satellites with respect to

the GPS receiver.

3.2 Application of PCA on the Data

3.2.1 Detecting Outliers

Given the available data (93173 instances), after

removing the 6615 irrelevant annotations (e.g.,

instances corresponding to ‘other’ annotations), it

remains 86558 instances.

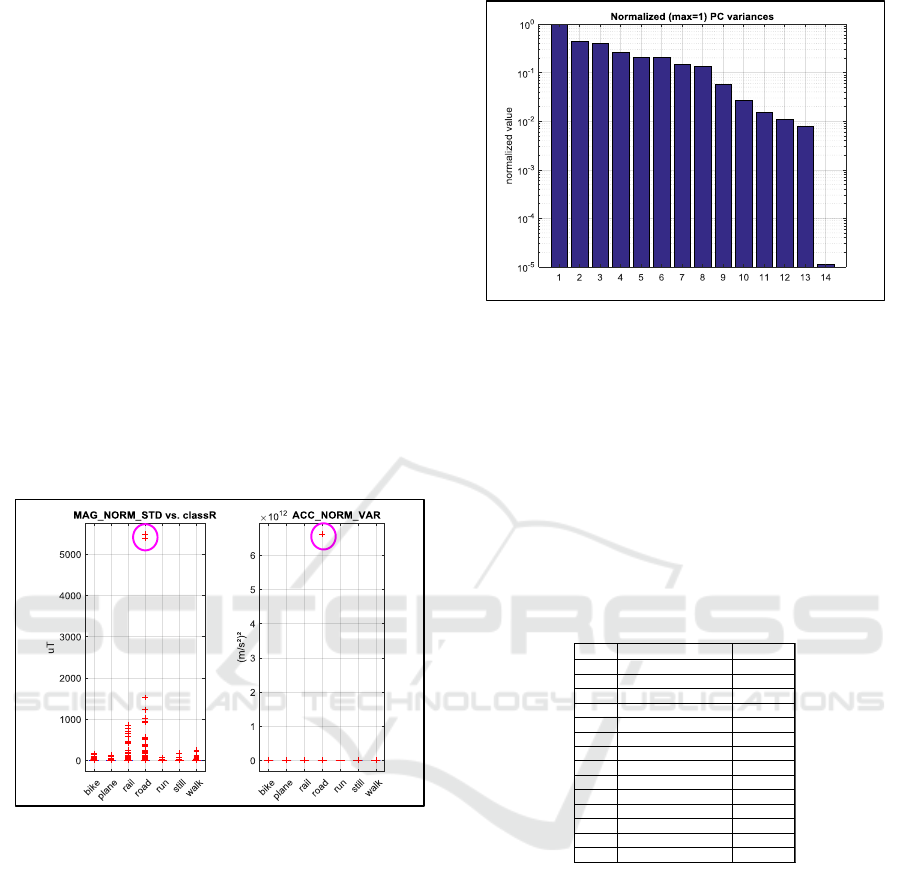
Sensor readings can be erroneous, leading to non-

physical value; below, on a 1D scatterplot (see Figure

2), it is easy to see 3 outliers, 2 relative to

MAG_NORM_STD (above 5000 µT) and one

relative to ACC_NORM_VAR (>6e12 m²/s

Figure 2: Outliers due to erroneous sensor readings.

It is very important to remove these 3 evident

outliers because, otherwise they would have distorted

the computation of mean and standard deviation when

normalizing the data for PCA computation.

Out of the 86555 remaining instances, some other

outliers are harder to discover, as each instance is

defined in a 14 dimensions feature space. To do so,

we applied the procedure presented in 0, i.e., running

a PCA and computing a MD.

The PCA computation leads to a 14

eigenvalue

~1000 times smaller than the others (see Figure 3

where the eigenvalues normalized have been plotted).

Figure 3: PCA normalized variances on the 14 features

data.

As explained in 2.2.3, this reveals a linear

dependency between features. From the linear

combination q

(see Table 2), given by the associated

principal component (see equation 16), we can

conclude that 4 features (ID between 5 and 8),

corresponding to relative energy of APV in different

frequency bands are linearly dependent. This is not

surprising given how these 4 features have been

computed (see 3.1).

Table 2: Linear combination of the 14 features.

Therefore, we remove one of the 4 features; we

arbitrary chose to remove the last one,

‘ACC_V_BAND_EN_4’. We run again a PCA in the

dimensional space. Figure 4 displays the matrix

P. Columns correspond to principal components and

rows to features (The “_N” added at the end of each

feature name reminds that the PCA is done on

normalized data). We can see, e.g., that the 2

(column 2) involves mainly the 2 features,

‘MAG_SPEC_CENTROID’ and ‘MAG_SPEC_SPREAD’

which are the relative spectral energy of the magnetic

field.

ID Name

1 MAG_NORM_STD 0.000

2 ACC_STD_V 0.000

3 ACC_STD_H1 0.000

4 ACC_STD_H2 0.000

5 ACC_V_BAND_EN_1 2.174

6 ACC_V_BAND_EN_2 2.174

7 ACC_V_BAND_EN_3 2.174

8 ACC_V_BAND_EN_4 2.174

9 ACC_SPEC_CENTROID_V 0.000

10 MAG_SPEC_CENTROID 0.004

11 ACC_SPEC_SPREAD_V 0.000

12 MAG_SPEC_SPREAD 0.000

13 GPS_SPD_MED 0.000

14 ACC_NORM_VAR 0.000

Data Mining Applied to Transportation Mode Classiﬁcation Problem

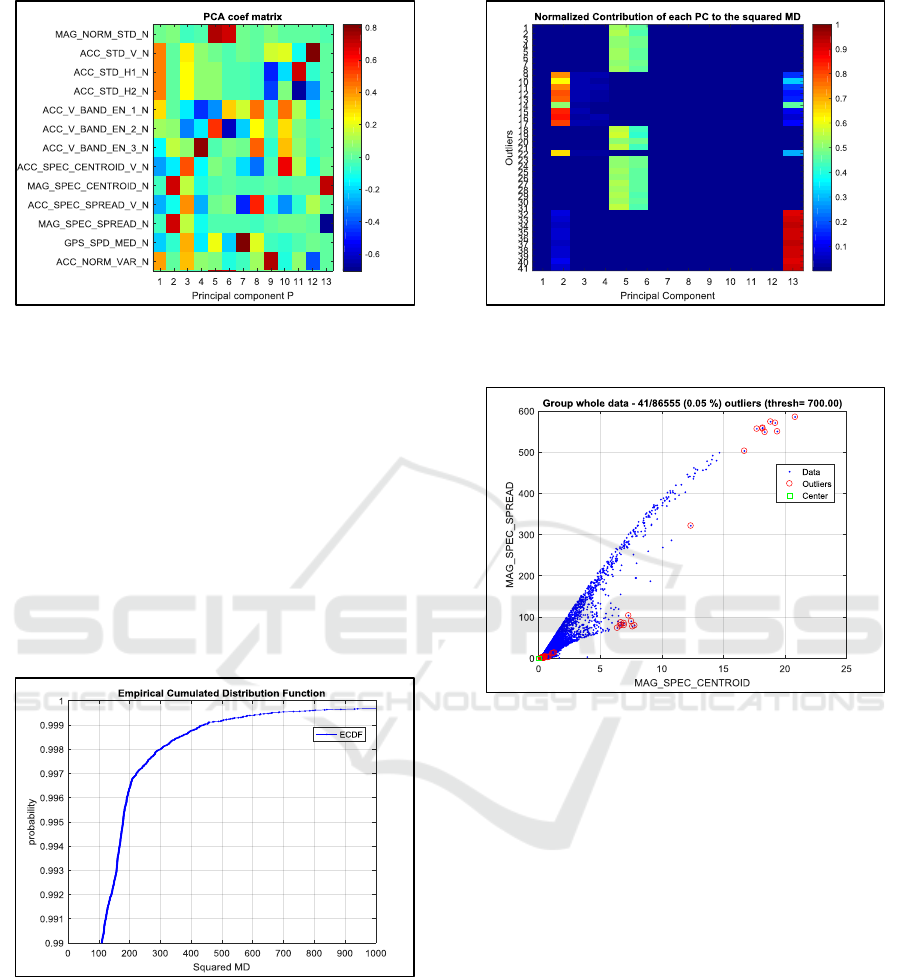
Figure 4: Principal Components on the 13 features data.

Then, for each of the 86555 instances, we

compute the squared MD according to equations 11

and 12.

Considering the empirical cumulated distribution

function of the squared MD (Figure 5), we decided to

set a relatively high threshold (equal to 700) in order

to remove a small number of outliers.

For the resulting 41 outliers, we compute the

normalized contribution of each principal component

to the squared MD (see equation 14). Figure 6 shows

2 distinct groups of outliers, the first one due to high

values on components 2 and 13, the 2

one due to

high values on components 5 and 6.

Figure 5: Empirical cumulated distribution function of

the squared MD.

Regarding the 1

group, Figure 4 shows that

principal components 2 and 13 involve mainly the

two previously mentioned features relative to spectral

energy of the magnetic field. Plotting the outliers in

this 2D space is therefore relevant as Figure 7 shows

it.

Figure 6: Normalized contribution of each PC to squared

MD for the 41 outliers.

Figure 7: 41 outliers displayed in a 2D original space.

This procedure to automatically locate the outliers

can be applied either on the global dataset, as it has

been done, or for each of the seven classes. It leads to

the removal of a total of 504 outliers.

The last source of outliers was wrong user

annotation. E.g., each time the subject was moving

and stopped for any reason (for e.g., when walking to

look to a map, or to wait for the red-light, or in a train

that stops at a station), the user annotation should be

changed to ‘still’; obviously, we could not ask the

volunteer to do so, because it would have been too

cumbersome. The consequence is that some instances

are not correctly annotated. After checking the

instances thanks to the GPS speed, we discard 3251

outliers; most are due to walking at very low speed

(<1 km/h).

Finally, after removing the different outliers

(3+504+3251), it remains 82000 instances, i.e. 89%

of the 93173 original instances.

VEHITS 2018 - 4th International Conference on Vehicle Technology and Intelligent Transport Systems

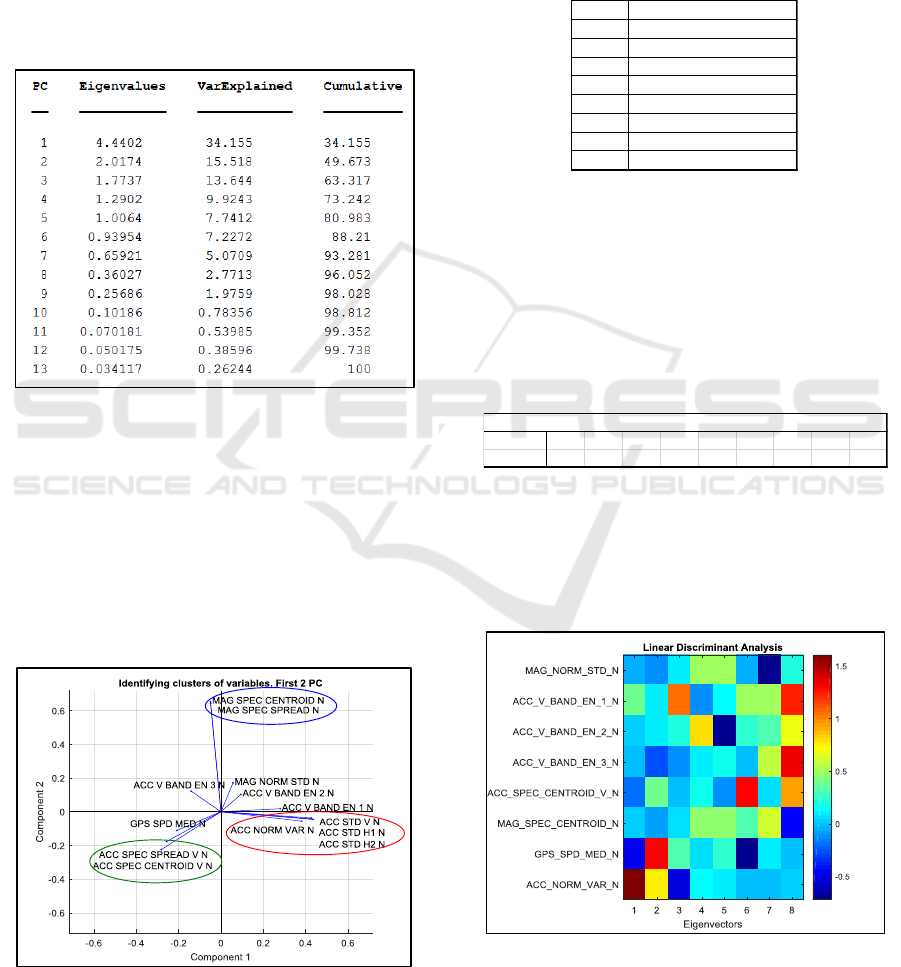
3.2.2 Dimension Reduction

After the outliers were removed, a 3

and last PCA

was performed. Eigenvalues are displayed in the 2

column of Table 3. The 3

column corresponds to the

ratio between each eigenvalue and the sum of the

eigenvalues in percentage. Finally, the last column is

the cumulated sum of the previous one. This table

shows that 8 components explains 96 % of the

variance of the data.

Table 3: Eigenvalues.

Therefore the dimension of the data can be

reduced from 13 to 8 and the next steps, such as

classifier training could be done on the 8 components

in the PC space: p

, p

, …, p

. But working with data

in the PC space is less intuitive and more complex.

This is why, it is often better practice, if possible, to

remove original variables. To do so, we focussed on

the first 2 columns of the P matrix. In Figure 8, each

of the 13

original variables was plotted with a blue

line starting from the origin, in the 2D plane formed

by the first 2 PCs.

Figure 8: Identifying clusters of original variables.

Three main clusters stick out from Figure 8 (resp.

displayed in red, blue and green), with resp. 2, 2 and

4 features.

Therefore, one feature by cluster can be kept,

removing 1+1+3=5 features. The problem could

therefore be simplified to 8 dimensions. Table 4

summarizes the 8 features finally kept.

Table 4: 8 features after dimension reduction.

3.3 Application of LDA on the Data

We apply a LDA on the database obtained after PCA

application (see 3.2), which has 82800 samples and 8

features. Among the 8 eigenvalues, 6 are non-null

(see Table 5). For this nominal configuration, the

separability criteria is 5.05.

Table 5: Eigenvalues of the LDA.

Figure 9 presents the 8 eigenvectors (in column)

which are linear combination of the 8 original

variables (in row). E.g., the first eigenvector, i.e. the

vector that best linearly separates the classes appears

to be a combination of the GPS speed and the

accelerometer variance.

Figure 9: Eigenvectors.

In this case, it is also meaningful to represent the

data in the 2D spaced formed the first two

ID Name

1 MAG_NORM_STD

2 ACC_V_BAND_EN_1

3 ACC_V_BAND_EN_2

4 ACC_V_BAND_EN_3

5 ACC_SPEC_CENTROID_V

6 MAG_SPEC_CENTROID

7 GPS_SPD_MED

8 ACC_NORM_VAR

ID 1 2 3 4 5 6 7 8 Sum

Eigenvalue 3.00 1.60 0.19 0.17 0.08 0.01 0.00 0.00 5.05

LDA - Eigenvalues

Data Mining Applied to Transportation Mode Classiﬁcation Problem

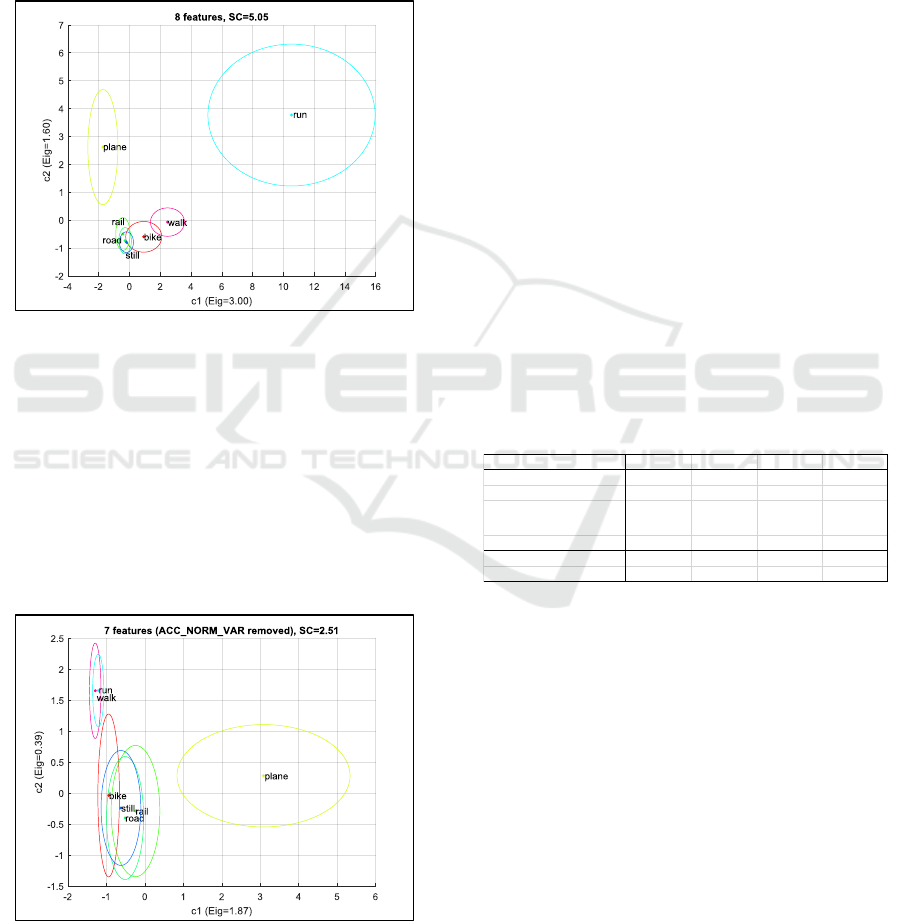
eigenvectors. As there may be confusions between

some classes, instead of plotting each sample, we

draw, for each class an ellipse representing the

dispersion. The ellipse’s centre stands for the mean,

whereas the semi axis length is equal to the standard

deviation. On Figure 10, one can see, that ‘run’ and

‘plane’ are well separated in this space, whereas there

is some confusion between ‘bike’ and ‘walk’ and

even more confusion between the 3 remaining classes

‘rail’, ‘road’ and ‘still’.

Figure 10: Class separability with 8 features.

Now, if we remove one feature, e.g.

‘ACC_NORM_VAR’, and do again a LDA, we get a new

set of eigenvectors and eigenvalue. Compared to the

previous nominal configuration, the separability

criteria highly decreases to 2.51 (-50%). Figure 11 is

a good illustration: ‘plane’ is still an isolated class

(thanks to the GPS speed), but it is no more the case

for ‘run’ which is now confused with ‘walk’. We can

conclude that ‘ACC_NORM_VAR’ is an important

feature.

Figure 11: Class separability with 7 features

(ACC_NORM_VAR removed).

On the contrary if we remove the feature

‘MAG_NORM_STD’, the separability criteria is very few

changed: 4.97, compared to 5.05.

3.4 Validation

To validate the results obtained after the previous

processing, we considered the 82000 instances

database obtained after outliers’ removal. We built 4

classification models (M1, M2, M3 and M4), the first

one M1 using the 13 features, M2 the 8 ones after

dimension reduction, M3 and M4 7 features. In M3,

with respect to M2, we removed one feature:

‘ACC_NORM_VAR’, whereas in M4 we removed

‘MAG_NORM_STD’.

These classifiers were all based on decision trees

constrained by a maximum number of splits of 32

(this figure represents a good compromise between

classifier’s performance and complexity).

Performance assessment for each model is done

via a Leave-One-Subject-Out Cross Validation

(LOSO CV) procedure (Arlot and Celisse, 2010),

which involves the partition of the database into K

folds, each fold representing a subject. The

performance metric used is the F-measure (harmonic

mean of precision and recall) averaged over the

different classes.

The results are summarized in Table 6.

Table 6: performance for the different models.

Comparing M1 and M2, it appears that reducing

the dimension using a PCA even improves the

performance: 0.714 instead of 0.689, i.e. +0.025. This

can be explained by the fact that removing 5 features

might have simplified the problem.

Comparing M3 and M4 with respect to M2 shows

that the separability criteria seems to be a good

indicator of the importance of a feature and its impact

on classification performance; so, removing

‘ACC_NORM_VAR’ reduces SC by 50% and

performance drops by ~0.1 whereas removing

‘MAG_NORM_STD’ decreases only slightly the SC

(-1.6%) and performance (-0.01).

The resulting decision trees have a number of

nodes comprised between 53 and 61, which is too

high if one wants to display the trees. Nevertheless,

comparing them shows that M2 and M4 are quite

similar (their 2 most important variables are

M1 M2 M3 M4

Number of predictors 13 8 7 7

Predictor removed w.r.t M2 ACC_NORM_VAR MAG_NORM_STD

Important variables

ACC_STD_V,

ACC_NORM_VAR,

GPS_SPD_MED

ACC_NORM_VAR,

GPS_SPD_MED

ACC_NORM_VAR,

GPS_SPD_MED

Performance (Avg. F-measure) 0.689 0.714 0.612 0.703

Separability Criteria (SC) 5.05 2.51 4.97

impact on SC -50.3% -1.6%

VEHITS 2018 - 4th International Conference on Vehicle Technology and Intelligent Transport Systems

ACC_NORM_VAR and GPS_SPD_MED), whereas the

other 2 models M1 and M3 are different: M1 differs

because it involves ACC_STD_V which brings the same

information as ACC_NORM_VAR. M3 differs because it

does not have access to ACC_NORM_VAR.

4 CONCLUSIONS

Given a classification (or regression) problem, due to

the number of different possible combinations of

sensors, features, classifiers and hyper-parameters,

finding an optimal classifier is a very time consuming

task.

This is why, simplifying the problem, using quick

data mining tools is very interesting.

In this study, we present three simple data mining

tools: Principal Component Analysis, Mahalanobis

distance and Linear Discriminant Analysis.

We apply them on real data concerning the

transportation mode classification problem and show

that we are able to

 clean the data: we remove outliers

representing 11% of the samples

 simplify the problem: we reduce data

dimension from 14 to 8 and this

simplification even improves the classifier

performance

 study the importance of each of 8 features;

it turns out that feature ‘ACC_NORM_VAR’ is

very important whereas ‘MAG_NORM_STD’ can

be removed with a small effect on

performance (-0.01).

ACKNOWLEDGEMENTS

This work is part of the BONVOYAGE project which

has received funding from the European Union’s

Horizon 2020 research and innovation programme

under grant agreement No 635867.

REFERENCES

Anderson, I., Muller, H., 2006. Exploring GSM Signal

Strength Levels in Pervasive Environments, in: 20th

International Conference on Advanced Information

Networking and Applications, 2006. AINA 2006.

Presented at the 20th International Conference on

Advanced Information Networking and Applications,

2006. AINA 2006, pp. 87–91. https://doi.org/10.1109/

AINA.2006.176

Arlot, S., Celisse, A., 2010. A survey of cross-validation

procedures for model selection. Stat. Surv. 4, 40–79.

https://doi.org/10.1214/09-SS054

De Maesschalck, R., Jouan-Rimbaud, D., Massart, D.L.,

2000. The Mahalanobis distance. Chemom. Intell. Lab.

Syst. 50, 1–18. https://doi.org/10.1016/S0169-

7439(99)00047-7

Duda, R.O., Hart, P.E., Stork, D.G., 2001. Pattern

Classification by Richard O. Duda, David G. Stork,

Peter E.Hart .pdf.

Gu, Q., Li, Z., Han, J., 2012. Generalized fisher score for

feature selection. ArXiv Prepr. ArXiv12023725.

Hemminki, S., Nurmi, P., Tarkoma, S., 2013.

Accelerometer-based Transportation Mode Detection

on Smartphones, in: Proceedings of the 11th ACM

Conference on Embedded Networked Sensor Systems.

ACM, New York, NY, USA, p. 13:1–13:14.

https://doi.org/10.1145/2517351.2517367

Li, C., Georgiopoulos, M., Anagnostopoulos, G.C., 2011.

Kernel principal subspace Mahalanobis distances for

outlier detection, in: The 2011 International Joint

Conference on Neural Networks. Presented at the The

2011 International Joint Conference on Neural

Networks, pp. 2528–2535. https://doi.org/10.1109/

IJCNN.2011.6033548

Lorintiu, O., Vassilev, A., 2016. Transportation mode

recognition based on smartphone embedded sensors for

carbon footprint estimation, in: 2016 IEEE 19th

International Conference on Intelligent Transportation

Systems (ITSC). Presented at the 2016 IEEE 19th

International Conference on Intelligent Transportation

Systems (ITSC), pp. 1976–1981. https://doi.org/

10.1109/ITSC.2016.7795875

Manzoni, V., Maniloff, D., Kloeckl, K., Ratti, C., 2010.

Transportation mode identification and real-time CO2

emission estimation using smartphones.

Martinez, A.M., Kak, A.C., 2001. PCA versus LDA. IEEE

Trans. Pattern Anal. Mach. Intell. 23, 228–233.

https://doi.org/10.1109/34.908974

Nitsche, P., Widhalm, P., Breuss, S., Brändle, N., Maurer,

P., 2014. Supporting large-scale travel surveys with

smartphones – A practical approach. Transp. Res. Part

C Emerg. Technol. 43, 212–221. https://doi.org/

10.1016/j.trc.2013.11.005

Reddy, S., Mun, M., Burke, J., Estrin, D., Hansen, M.,

Srivastava, M., 2010. Using Mobile Phones to

Determine Transportation Modes. ACM Trans Sen

Netw 6, 13:1–13:27. https://doi.org/10.1145/1689239.

1689243

Sankaran, K., Zhu, M., Guo, X.F., Ananda, A.L., Chan,

M.C., Peh, L.-S., 2014. Using Mobile Phone Barometer

for Low-power Transportation Context Detection, in:

Proceedings of the 12th ACM Conference on

Embedded Network Sensor Systems. ACM, New York,

NY, USA, pp. 191–205. https://doi.org/10.1145/

2668332.2668343

Stenneth, L., Wolfson, O., Yu, P.S., Xu, B., 2011.

Transportation Mode Detection Using Mobile Phones

and GIS Information, in: Proceedings of the 19th ACM

SIGSPATIAL International Conference on Advances

Data Mining Applied to Transportation Mode Classiﬁcation Problem

in Geographic Information Systems. ACM, New York,

NY, USA, pp. 54–63. https://doi.org/10.1145/2093973.

2093982

Vlahogianni, E.I., Barmpounakis, E.N., 2017. Driving

analytics using smartphones: Algorithms, comparisons

and challenges. Transp. Res. Part C Emerg. Technol.

79, 196–206. https://doi.org/10.1016/j.trc.2017.03.014

Wikipedia, 2017. Principal component analysis. Wikipedia.

Wu, L., Yang, B., Jing, P., 2016. Travel mode detection

based on GPS raw data collected by smartphones: A

systematic review of the existing methodologies. Inf.

Switz. 7. https://doi.org/10.3390/info7040067

VEHITS 2018 - 4th International Conference on Vehicle Technology and Intelligent Transport Systems