
Earth Mover’s Distances for Rooted Labaled Unordered Trees based on
Tai Mapping Hierarchy
Taiga Kawaguchi and Kouichi Hirata
Kyushu Institute of Technology, Kawazu 680-4, Iizuka 820-8502, Japan
Keywords:
Earth Mover’S Distance, Rooted Labeled Unordered Tree, Tai Mapping Hierarchy, Tree Edit Distance.
Abstract:
In this paper, we introduce earth mover’s distances (EMDs, for short) for rooted labeled trees based on Tai
mapping hierarchy. First, by focusing on the restricted mappings in the Tai mapping hierarchy providing the
tractable variations of the tree edit distance, we formulate the EMDs whose signatures are all of the pairs of a
complete subtree and its frequency and whose ground distances are the tractable variations. Then, we compare
the EMDs with their ground distances, which are tractable variations.
1 INTRODUCTION
Comparing tree-structured data such as HTML and
XML data for web mining or DNA and g lycan d ata
for bioinformatics is one of the important task s for
data mining. The most famous distance measure bet-
ween rooted labeled unordered trees (trees, for short)
is the edit distance (Tai, 1979). The edit distance is
formu late d as the minimum c ost of edit operations,
consisting of a substitution, a deletion and an inser-
tion, applied to transform from a tree to another tree.
Whereas the edit distance is a metric, the problem of
computing the edit distan ce is MAX SNP-hard even if
trees are binary (Hirata et al., 2011; Zhang a nd Jiang,
1994).
As constant-factor low er bounding distances of
the edit distance, several histogram distances based
on local information (Aratsu et al., 2009; Kailing
et al., 2004; Li et al., 2013) have introduced. Whe-
reas w e can co mpute them more efficiently than the
edit distance, none of them is a metric.
On the other hand, an earth mover’s distance
(EMD, for short) has originally d eveloped to com-
pare with two images in image retrieval and pattern
recogn ition (Rubner et al., 2007) and is formulated
as the solution of the transportation problem between
the distributions of fe a tures in signatures in two ima-
ges. It is known that the EMD is a metric if so is the
ground distance between single features.
Gollapudi and Panigrahy (Gollapudi and Pani-
grahy, 2008) have extended the EMD to th at between
two leaf-labeled trees with the same height, whe re a
tree is leaf-labe led if all of the labels are assigned to
just leaves. However, it is difficult for the EM D to
extend to be applica ble to standard two trees, that is,
labels are assigned to all the nodes and having possi-
ble different height as follows. In the EMD, first, by
comparing each pair of leaves (that is, the nodes with
height 1), we set the value 1 if both leaves have the
same label and 0 otherwise. Then, by using the infor-
mation between the pair of nodes in the height k − 1,
we solve the transportation problem of the pair of no-
des in the height k. Hence, in order to apply such a
recursion to tre es, the trees are ne c essary to have the
same height and have no internal nodes with labels.
Kawaguchi and Hirata (Kawaguchi and Hirata,
2017) have introdu ced another EMD based on com-
plete subtrees. The EMD is formulated by the his-
tograms consisting of either c omplete subtrees, co-
complete subtree or both and their frequencies as sig-
natures a nd the L
1
-distance between the h isto grams as
ground distances, so we can apply the EMD to rooted
labeled trees. Also the E MD is a metric and tracta-
ble. On the other hand, there exist trees that the EMD
cannot reflect intuitive similarity.
Since the edit distance betwe e n trees is corre-
sponding to a Tai mapping ( Tai, 1979 ), many vari-
ations of th e edit distan c e have developed as more
structurally sensitive distances obtained by restricting
the Tai mapping, that is, a top-down distance (Cha-
wathe, 1999; Selkow, 1977 ), an LCA- and root-
preserving distance (Yoshino and Hirata, 2017), an
LCA-preserving distance (Zhang et al., 1996), an
accordant distance (Kuboyama, 2007), an isolated-
subtree (or a constrained) distance (Zhang, 1995;
Zhang, 1996) and an alignment distance (Jiang et al.,
Kawaguchi, T. and Hirata, K.
Earth Mover’s Distances for Rooted Labaled Unordered Trees based on Tai Mapping Hierarchy.
DOI: 10.5220/0006633701590168
In Proceedings of the 7th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2018), pages 159-168
ISBN: 978-989-758-276-9
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
159

1995). Almost variations are metrics except an align-
ment distance (Jiang et al., 1995). Also, whereas the
problem of computing the edit distance or the align-
ment distance between trees is MAX SNP-hard (Hi-
rata et al., 2011; Jiang et al., 1995; Zhang and Jiang,
1994), the problem of computing the other variations
is tractable.
The reason why these variations are tractable is
that the maximum weight bipartite matching pro-
blem can be applied to computing the variations after
decomp osing trees from the root (Yamamoto et al.,
2014). In contrast, it cannot b e applied to computing
the edit distance and the alignm e nt distance, because
computing them is necessary to compare the decom-
posed trees and the remained tre es after decomposin g
trees from the root.
Since we can regard the minimum weig hted b i-
partite pro blem as a special case of the transportation
problem in EMDs, in this paper, we formulate new
EMDs based on the Tai mapping hierarchy whose sig-
natures are pairs of a complete subtree and the ratio
of frequencies oc c urring in a whole tree and whose
ground distances are the tractable variations of the
edit distance . Then, we show that the EMDs are al-
ways metrics and tractable. Finally, we give experi-
mental results to evaluate the EMDs to compare them
with their ground distanc es and investigate the pro-
perties of the E MDs.
2 PRELIMINARIES
A tree T is a connected graph (V,E) without cycles,
where V is the set of vertices and E is the set of edges.
We denote V an d E by V (T ) and E(T ). The size of
T is |V | and denoted by |T |. We sometime denote
v ∈ V (T ) by v ∈ T . We denote an empty tree (
/
0,
/
0) by
/
0. A rooted tree is a tree with one node r chosen as its
root. We d e note the root of a rooted tree T by r(T ).
For each node v in a rooted tree with the root r,
let UP
r
(v) be the unique path from v to r. The pare nt
of v(6= r), which w e denote by p ar(v), is its adjacent
node on UP
r
(v) and the a ncestors of v(6= r) are the
nodes on UP
r
(v) − {v}. We denote the set of all an-
cestors of v by anc(v). We say th at u is a child of v if
v is the parent of u and u is a descendant of v if v is
an ancestor of u. We use the ancestor orders < and ≤,
that is, u < v if v is an ancestor of u and u ≤ v if u < v
or u = v. We say that w is the least common ancestor
of u and v, denoted by u ⊔ v, if u ≤ w, v ≤ w a nd there
exists no w
′
such that w
′
≤ w, u ≤ w
′
and v ≤ w
′
. is
the numb er of children of v. The degree of a rooted
tree T , denoted by d(T ), is the maximum number of
d(v) for every v ∈ T .
For n odes u,v ∈ T , u is to the left of v if pre(u) ≤
pre(v) for the preorder number pre and post(u) ≤
post(v) for the postor der number post. We say that
a rooted tree is ordered if a lef t-to-right order among
siblings is given; unordere d oth e rwise. We say that a
rooted tree is labeled if each node is assigned a sym-
bol from a fixed finite alphabet Σ. For a node v, we
denote the labe l o f v by l(v), and sometimes identif y
v with l(v). In this paper, we call a rooted labeled
unordered tree a tree simply.
Let T be a tree (V , E) and v a node in T . A com-
plete subtree of T at v, de noted by T [v], is a tree
T
′
= (V
′
,E
′
) such that r(T
′
) = v, V
′
= {u ∈ V | u ≤ v}
and E
′
= {(u,w) ∈ E | u,w ∈ V
′
}. We denote the
(multi)set {T [v] | v ∈ T } of all the com plete subtrees
in T by cs(T ). For a complete subtree S in T , we
denote the frequency of the occurrences of S in T by
f (S,T ).
Next, we introduce an edit distance an d a Tai map-
ping.
Definition 1 (Edit operations (Tai, 1979)). The edit
operations of a tree T are defined as follows. (Fi-
gure 1).
1. Substitution: Change the label of the node v in T .
2. Deletion: Delete a node v in T with parent v
′
, ma-
king the children of v become the childr en of v
′
.
The children are inserted in the place of v as a sub-
set of the children of v
′
. In particular, if v is the
root in T , then th e result apply ing the deletion is a
forest consisting of the children of the root.
3. Insertion: The complement of deletion. Insert a
node v as a child of v
′
in T making v the parent o f
a subset of the children of v
′
.
Substitution (v 7→ w)
v
7→
w
Deletion (v 7→ ε)
v
′
v
7→
v
′
Insertion (ε 7→ v)
v
′
7→
v
′
v
Figure 1: Edit operations for trees.
Let ε 6∈ Σ denote a special blank symbol and d efine
Σ
ε
= Σ ∪ {ε}. Then, we represent each edit operation
ICPRAM 2018 - 7th International Conference on Pattern Recognition Applications and Methods
160

by (l
1
7→ l
2
), where (l
1
,l
2
) ∈ (Σ
ε
×Σ
ε
−{(ε,ε)}). The
operation is a substitution if l
1
6= ε and l
2
6= ε, a dele-
tion if l
2
= ε, and an insertion if l
1
= ε. For n odes u
and v, we also denote (l(u) 7→ l(v)) by (u 7→ v). We
define a c ost function γ : (Σ
ε
×Σ
ε
−{(ε,ε)}) 7→ R
+
on
pairs of labels. We often c onstrain a cost function γ to
be a metric, that is, γ(l
1
,l
2
) ≥ 0, γ(l
1
,l
2
) = 0 iff l
1
= l
2
,
γ(l
1
,l
2
) = γ(l
2
,l
1
) an d γ(l
1
,l
3
) ≤ γ(l
1
,l
2
)+γ(l
2
,l
3
). In
particular, we call the cost functio n that γ(l
1
,l
2
) = 1
if l
1
6= l
2
a unit cost function.
Definition 2 (Edit distance (Tai, 1979)). For a cost
function γ, the c ost of an edit operation e = l
1
7→ l
2
is given by γ(e) = γ(l
1
,l
2
). The cost of a sequence
E = e
1
,... ,e
k
of edit operations is given by γ(E) =
∑
k
i=1
γ(e
i
). Then, an edit distance τ
TA I
(T
1
,T
2
) bet-
ween trees T
1
and T
2
is defined as follows:
τ
TA I
(T
1
,T
2
)
= min
γ(E)
E is a sequence
of edit operations
transforming T
1
to T
2
.
Definition 3 (Tai mapping (Tai, 1979)). Let T
1
and
T
2
be tree s. We say that a triple (M, T
1
,T
2
) is an unor-
dered Tai mapping (a mapping, for short) from T
1
to
T
2
if M ⊆ V (T
1
) × V (T
2
) and every pair (u
1
,v
1
) and
(u
2
,v
2
) in M satisfies that (1) u
1
= u
2
iff v
1
= v
2
(one-
to-one condition) a nd (2) u
1
≤ u
2
iff v
1
≤ v
2
(ancestor
condition). We will use M instead of (M,T
1
,T
2
) when
there is no confusion denote it by M ∈ M
TA I
(T
1
,T
2
).
Let M be a mapping from T
1
to T
2
. Let I
M
and J
M
be the sets of nodes in T
1
and T
2
but not in M, that is,
I
M
= {u ∈ T
1
| (u,v) 6∈ M} and J
M
= {v ∈ T
2
| (u,v) 6∈
M}. Then, the cost γ(M) of M is given as follows.
γ(M) =
∑
(u,v)∈M
γ(u,v) +
∑
u∈I
M
γ(u,ε) +
∑
v∈J
M
γ(ε,v).
Theorem 1. The following statement holds (Tai,
1979).
τ
TA I
(T
1
,T
2
) = min{γ(M) | M ∈ M
TA I
(T
1
,T
2
)}.
Unfortu nately, the following theorem holds for
computing τ
TA I
between unordered trees.
Theorem 2. For uno rdered trees T
1
and T
2
, the
problem of computing τ
TA I
(T
1
,T
2
) is MAX SNP-
hard (Zhang and Jiang, 1994). This statement also
holds even if both T
1
and T
2
are binary (Hirata et al.,
2011).
Finally, we introduce the variations of a Tai map-
ping and an edit distance.
Definition 4 (Variations of Tai mapping). Let T
1
and
T
2
be trees and M ∈ M
TA I
(T
1
,T
2
). We denote M \
{(r(T
1
),r(T
2
))} by M
−
.
1. We say that M is an isolated-subtree map-
ping (Zhang, 1995; Zhang, 1996), denoted by
M ∈ M
ILST
(T
1
,T
2
), if M satisfies the following
condition.
∀(u
1
,v
1
)(u
2
,v
2
)(u
3
,v
3
) ∈ M
(u
3
< u
1
⊔ u
2
⇐⇒ v
3
< v
1
⊔ v
2
).
2. We say that M is a n accordant mapping (Ku-
boyama, 2007), denoted by M ∈ M
ACC
(T
1
,T
2
), if
M satisfies the following con dition.
∀(u
1
,v
1
)(u
2
,v
2
)(u
3
,v
3
) ∈ M
(u
1
⊔ u
2
= u
1
⊔ u
3
⇐⇒ v
1
⊔ v
2
= v
1
⊔ v
3
).
3. We say that M is an LCA-preserving map-
ping (Zhang et al., 1996), denoted by M ∈
M
LCA
(T
1
,T
2
), if M satisfies the following condi-
tion.
∀(u
1
,v
1
)(u
2
,v
2
) ∈ M ((u
1
⊔ u
2
,v
1
⊔ v
2
) ∈ M) .
4. We say that M is an LCA- and root-preserving
mapping (Yoshino a nd Hirata, 2017) , denoted by
M ∈ M
LCART
(T
1
,T
2
), if M ∈ M
LCA
(T
1
,T
2
) and
(r(T
1
),r(T
2
)) ∈ M.
5. We say that M is a Top-down mapping (Ch a-
wathe, 1999; Selkow, 1977), denoted by M ∈
M
TOP
(T
1
,T
2
), if M satisfies the following condi-
tion.
∀(u,v) ∈ M
−
((par(u),par (v)) ∈ M).
The above variation of Tai mapping provides the
following hierarchy (Kuboyama , 2007; Yoshino and
Hirata, 2017).
M
TOP
(T
1
,T
2
) ⊆ M
LCART
(T
1
,T
2
) ⊆ M
LCA
(T
1
,T
2
)
⊆ M
ACC
(T
1
,T
2
) ⊆ M
ILST
(T
1
,T
2
) ⊆ M
TA I
(T
1
,T
2
).
Definition 5 (Variations of e dit distance). For every
A ∈ {ILST, ACC, LCA, LCART, TOP}, we define the
distance τ
A
(T
1
,T
2
) as follows.
τ
A
(T
1
,T
2
) = min {γ(M ) | M ∈ M
A
(T
1
,T
2
)}.
Here we call τ
ILST
an isolated-subtree dis-
tance (Zhang, 1995; Zhang, 1996), τ
ACC
an accordant
distance (Kuboyam a , 2007 ), τ
LCA
an LCA-preserving
distance (Zha ng et al., 1996), τ
LCART
an LCA- and
root-preserving distance (Yoshino and Hirata, 2017),
and τ
TOP
a top-down distance (Chawathe, 1999; Sel-
kow, 1977). By the Tai mapping hierarchy, the fol-
lowing inequality for the variation of edit distanc e
holds.
τ
TA I
(T
1
,T
2
) ≤ τ
ILST
(T
1
,T
2
) ≤ τ
ACC
(T
1
,T
2
) ≤
τ
LCA
(T
1
,T
2
) ≤ τ
LCART
(T
1
,T
2
) ≤ τ
TOP
(T
1
,T
2
).
Furthermore, f or all the above variations, the follo -
wing theorem holds.
Earth Mover’s Distances for Rooted Labaled Unordered Trees based on Tai Mapping Hierarchy
161

Theorem 3 (cf., (Yamamoto et al., 2014; Yoshino and
Hirata, 2017; Zhang et al., 1996)). For every A ∈
{ILST, ACC, LCA, LCART, TOP}, we can compute
τ
A
(T
1
,T
2
) in O(n
2
d) time, where n = max (|T
1
|,|T
2
|)
and d = min{d(T
1
),d(T
2
)}.
3 EARTH MOVER ’S DISTANCE
FOR TREES
In this section , we first introduce an earth mover’s dis-
tance (Rubner et a l., 20 07) and then extend to that for
trees based on Tai mapp ing hierarc hy.
We call the set of pairs of a fe a ture p
i
and its
weight w
i
a signature and denote it by P = {(p
i
,w
i
)}.
For a feature p
i
such that (p
i
,w
i
) ∈ P, we denote
p
i
∈ P simp ly. An earth mover’s distance (EMD, for
short) between two signature s is given as the mini-
mum cost of the transportation problem fr om a signa-
ture to another signature.
Let P = {(p
i
,u
i
)} and Q = {(q
j
,v
j
)} be signatu-
res. We call a distance between p
i
and q
j
a grou nd
distance and denote it by gd(p
i
,q
i
). Also w e denote
the flow from p
i
to q
j
by f
i j
. Whe n the cost of the flow
from p
i
to q
j
is given by gd(p
i
,q
j
) f
i j
, the overall cost
of the flows from P to Q is defined as follows.
∑
p
i
∈P
∑
q
j
∈Q
gd(p
i
,q
j
) f
i j
.
Then, find the minimum cost flow f
∗
i j
subject to the
following constraints:
1. f
i j
≥ 0,
2.
∑
p
i
∈P
f
i j
≤ u
i
,
3.
∑
q
j
∈Q
f
i j
≤ v
j
,
4.
∑
p
i
∈P
∑
q
j
∈Q
f
i j
= min
∑
p
i
∈P
u
i
,
∑
q
j
∈Q
v
j
.
The constraint (1) allows moving “ supplies” from P
to Q and not vice versa. The co nstraints (2) and (3)
limit the amount of supp lies within the weight. The
constraint (4) forces to move the maximum amount
of supplies possible.
Let f
∗
i j
be the optimum flow of the transportation
problem. Then, we define the EMD between two sig-
natures P and Q as follows.
EMD
gd
(P,Q) =
∑
p
i
∈P
∑
q
j
∈Q
gd(p
i
,q
j
) f
∗
i j
∑
p
i
∈P
∑
q
j
∈Q
f
∗
i j
=
∑
p
i
∈P
∑
q
j
∈Q
gd(p
i
,q
j
) f
∗
i j
min
∑
p
i
∈P
u
i
,
∑
q
j
∈Q
v
j
.
Note that the EMD allows for partial matches
when the total weight of a signature is different from
that of another signature, which is impor ta nt for
image retrieval applications (Rubner et al., 2007). We
can realize the partial match to transpo rt from a signa-
ture whose total we ight is smaller than a part of anot-
her signature. Also the following theor em holds for
the EMD.
Theorem 4. Suppose that two signatures have the
same total weight. If a ground distance is a me-
tric, then so is the EMD. F urthermore, we can
compute the EMD in O(n
3
log n) time, where n =
max{|P|,|Q|} (Rubner et al., 2007).
Next, we formulate the E MD for trees based on
Tai ma pping hie rarchy.
It is necessary for the EMD to introduce a signa-
ture and a groun d distance between features. In order
to fo rmulate the EMD for trees, we transform from a
tree to a signature. In this p aper, we adopt the follo-
wing signature s(T ) for a tree T .
s(T ) =
(S,w)
S ∈ cs(T ), w =
f (S,T )
|T |
.
The features of s(T ) are complete subtrees of T and
the weight of s(T ) is the ratio of the occurrences of
complete subtrees. Hence, the total weight of s is 1.
Since this signature contains T itself, we can trans-
form T to s(T ) uniquely. On the other hand, as a
ground distance between trees, we adopt 5 tractable
variations of the edit distance, that is, τ
TOP
, τ
LCART
,
τ
LCA
, τ
ACC
and τ
ILST
.
Hence, by combinin g signatures and ground dis-
tances, we formalize the following 5 kinds of an
EMD for trees. In the following, we assume that
A ∈ {ILST, ACC, LCA, LCART, TOP}.
Definition 6 (EMD for trees) . We define an EMD
for trees as EMD
τ
A
(s(T
1
),s(T
2
)) betwee n signatures
s(T
1
) and s(T
2
) for a ground distance τ
A
and denote it
by EMD
A
(T
1
,T
2
).
Corollary 1. EMD
A
(T
1
,T
2
) is a metr ic .
Proof. It is straightforward since a ground distance
τ
A
is a metric and the total weight of signatures is 1
and by Theorem 4.
Theorem 5. We can compute EMD
A
(T
1
,T
2
) in
O(n
3
logn) time, where n = max{|T
1
|,|T
2
|}.
Proof. By u sing s(T
1
), s(T
2
) and {τ
A
(T
1
[u],T
2
[v]) |
(u,v) ∈ T
1
× T
2
}, we can design the following algo-
rithm to compute EMD
A
(T
1
,T
2
).
1. Co nstruct s(T
1
) and s(T
2
) from T
1
and T
2
.
2. Co mpute G = {τ
A
(T
1
[u],T
2
[v]) | (u, v) ∈ T
1
× T
2
}.
3. Co mpute EMD
A
(T
1
,T
2
) from G.
ICPRAM 2018 - 7th International Conference on Pattern Recognition Applications and Methods
162
It is obvious th at the running time of Step 1 is
O(n). For Step 2, since the algorithm of computing
τ
A
(T
1
,T
2
) can store the value of τ
A
(T
1
[u],T
2
[v]) for
every (u,v) ∈ T
1
×T
2
and by Theorem 3, w e can com-
pute G in O(n
2
d) time, where d = min {d(T
1
),d(T
2
)}.
Since |s(T
1
)| = |s(T
2
)| = O(n) and by Theo rem 4,
the running time of Step 3 is O(n
3
logn). Hence,
we can compute EMD
A
(T
1
,T
2
) in O(n) + O(n
2
d) +
O(n
3
logn) = O(n
3
logn) time.
4 EXPERIMENTAL RESU LTS
In this section, we give experimental results to evalu-
ate EMD
A
to compar e EMD
A
with τ
A
and investigates
the properties of EMD
A
. He re, we assume that a cost
function is a unit cost function.
In this section, we use two kinds of data; One is N-
glycan data provided from KEGG
1
as real data. Anot-
her is 6 data of randomly generated trees by using the
algorithm PTC (Luke and Panait, 2001). We call them
R
i
(1 ≤ i ≤ 6), where the number of nodes in R
i
is
50 × i. Furthermore, we use the computer environ-
ment that CPU is Intel Xeon E51650 v3 (3.50GHz),
RAM is 1GB and OS is Ubuntsu Linux 14. 04 (64bit).
Table 1 illustrates the details of data, that is, the
number of data (#), the average number of nodes (n),
the average degre e (d) a nd the average heig ht (h).
Table 1: The details of data.
data # n d h
N-glycan 2142 11.07 2.07 6.20
R
1
100 50.00 2.00 8.75
R
2
100 100.00 2.00 10.69
R
3
100 150.00 2.00 12.12
R
4
100 200.00 2.00 12.75
R
5
100 250.00 2.00 13.81
R
6
100 300.00 2.00 14.24
4.1 Running Time
First, we compare the running time to co mpute EMD
A
and τ
A
for N-glycan data and randomly generated
trees in Table 1. Table 2 illustrates the running time
to compute such distances.
Tables 1 and 2 show that the running time of both
EMD
A
and τ
A
is increasing when the numbe r of nodes
is increasing and the ratio of increasing for EMD
A
is
larger than that for τ
A
.
1
Kyoto Encyclopedia of Genes and Genomes.
http://www.kegg.jp/
Table 2: The running time to compute the distances (sec.).
distance N-glycan R
1
R
2
τ
ILST
1580.95 69.72 289.48
τ
ACC
1386.33 60.18 285.78
τ
LCA
1129.97 49.13 201.78
τ
LCART
1109.80 49.64 203.96
τ
TOP
485.42 20.71 83.56
EMD
ILST
1592.32 77.00 351.81
EMD
ACC
1399.14 66.23 307.31
EMD
LCA
1133.82 55.17 261.24
EMD
LCART
1128.05 55.08 261.36
EMD
TOP
509.49 26.45 138.04
distance R
3
R
4
R
5
R
6
τ
ILST
665.12 118 6.53 187 4.17 272 2.80
τ
ACC
578.79 101 3.98 159 7.39 230 8.71
τ
LCA
461.58 824.09 1298.07 1873.32
τ
LCART
467.38 834.47 1313.06 1891.92
τ
TOP
189.58 336.86 527 .42 760. 66
EMD
ILST
894.53 180 2.92 307 3.49 483 2.80
EMD
ACC
790.38 158 3.50 276 3.23 437 6.64
EMD
LCA
687.20 140 1.26 247 4.14 396 5.60
EMD
LCART
687.29 141 4.33 247 4.22 396 1.98
EMD
TOP
397.84 875.98 1637.42 2759.20
Table 3 illustrates the ratio (EMD
A
/τ
A
) of the run-
ning time of computing the EMDs (EMD
A
) for that of
computing the ground distances (τ
A
) in Table 2. Here,
we call it the ratio of EMD
A
for τ
A
simply.
Table 3: The ratio (EMD
A
/τ
A
) of the running time of com-
puting the EMDs (EMD
A
) for that of computing the ground
distances (τ
A
) in Table 2.
A N-glycan R
1
R
2
R
3
R
4
R
5
R
6
ILST 1.01 1.10 1.22 1.34 1.52 1.64 1.77
ACC 1.01 1.10 1.08 1.37 1.56 1.73 1.90
LCA 1.00 1.12 1.29 1.49 1.70 1.91 2.12
LCART 1.02 1.11 1.28 1.47 1.69 1.88 2.09
TOP 1.05 1.28 1.65 2.10 2.60 3.10 3.63
Table 3 shows that, w hereas the ratio of EMD
A
for
τ
A
is between 1.00 and 1.05 for N-glycan data, the ra-
tio of EMD
TOP
for τ
TOP
is over 3 for the data R
6
. On
the other hand, smaller distance in the inequality for
the variations (τ
ILST
≤ τ
ACC
≤ τ
LCA
≤ τ
LCART
≤ τ
TOP
)
tends to give smaller ra tio of EMD
A
for τ
A
except
LCA and LCART; The ratio of EMD
LCA
for τ
LCA
is
greater than the ratio of EMD
LCART
for τ
LCART
.
Furthermore, whereas the ratio of EMD
A
for τ
A
is
O(nlog n/d) in theoretical by Theorems 3 and 5, the
ratio is at most 4 in experimental. Then, the problems
Earth Mover’s Distances for Rooted Labaled Unordered Trees based on Tai Mapping Hierarchy
163
of computing EMDs are e fficient for trees with at least
300 nodes and small d egre e.
4.2 Comparing EMDs with Ground
Distances
Next, we investigate the relationship between the
EMD EMD
A
and its ground distance τ
A
for N-glycan
data.
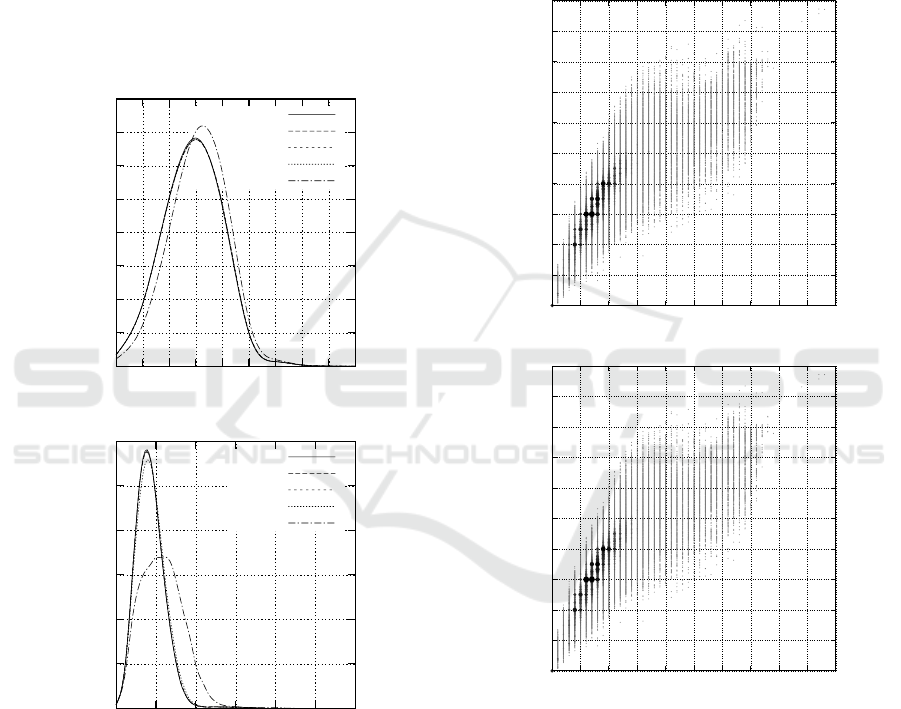
Figure 2 illustrates the distributions of E MDs (up-
per) and ground distances (lower). Here, the x-axis is
the value of the distance and the y-axis is the percen-
tage of pairs with the distance pointed by the x-axis.
0
5
10
15
20
25
30
35
40
0 1 2 3 4 5 6 7 8 9
percentage(%)
distance
EMD_Ilst
EMD_Acc
EMD_Lca
EMD_LcaRt
EMD_Top
0
2
4
6
8
10
12
0 10 20 30 40 50 60
percentage(%)
distance
Ilst
Acc
Lca
LcaRt
Top
Figure 2: The distributions of EMDs (upper) and ground
distances (lower) for N-glycan data.
Figure 2 shows that both EMDs and gr ound dis-
tances are near to normal distribution. Also the distri-
butions of EMD
TOP
and τ
TOP
are right to other EMD
A
and τ
A
(A ∈ {ILST, ACC, LCA, LCART}), respecti-
vely. Whereas the peak of the distribution of EMD
TOP
is larger than that of other distributions of EMD
A
, the
peak of the distribution of τ
TOP
is smaller than that of
other distributions of τ
A
.
Figures 3 and 4 illustrate the scatter charts bet-
ween the number of pairs of trees with τ
A
pointed
at the x-axis and that with EMD
A
pointed at the y-
axis for N-g lycan data whose number of total pairs is
2,293,011. Here, the diameter a nd th e colo r represent
the number of pairs of trees such that longer diameter
and deeper color are larger number. Also, Figures 3
and 4 represent the cases that A ∈ {ILST, ACC} and
A ∈ {LCA, LCART, TOP}, respectively.
0
1
2
3
4
5
6
7
8
9
10
0 5 10 15 20 25 30 35 40 45 50
ILST
0
1
2
3
4
5
6
7
8
9
10
0 5 10 15 20 25 30 35 40 45 50
ACC
Figure 3: The scatter charts between the number of pairs
of trees with τ
A
pointed at the x-axis and that with EMD
A
pointed at the y-axis for A ∈ {ILST, ACC}.
Figures 3 and 4 show that EMD
A
is relative to
τ
A
and almost values of τ
A
are larger tha n those of
EMD
A
. Also the plots of TOP vary more widely than
others.
4.3 Typical Cases
In the following, we point out the typical cases of
trees with different values between of τ
A
and EMD
A
.
ICPRAM 2018 - 7th International Conference on Pattern Recognition Applications and Methods
164

0
1
2
3
4
5
6
7
8
9
10
0 5 10 15 20 25 30 35 40 45 50
LCA
0
1
2
3
4
5
6
7
8
9
10
0 5 10 15 20 25 30 35 40 45 50
LCART
0
1
2
3
4
5
6
7
8
9
10
0 10 20 30 40 50 60
TOP
Figure 4: The scatter charts between the number of pairs
of trees with τ
A
pointed at the x-axis and that with EMD
A
pointed at t he y-axis for A ∈ {LCA, LCART, TOP}.
Here, let u
i
be a node in T
1
such that pre(u
i
) = i and
v
i
a node in T
2
such that pre(v
i
) = i.
Example 1. Consider trees T
1
and T
2
illustra-
ted in Figure 5, that is, one tree (T
1
) is obtai-
ned by deleting leaves to another tree (T
2
). In
this case, it holds that τ
A
(T
1
,T
2
) ≤ EMD
A
(T
1
,T
2
).
For the trees T
1
and T
2
in Figure 5, it holds that
τ
A
(T
1
,T
2
) = 1 and EMD
A
(T
1
,T
2
) = 1.357 for every
A ∈ {ILST, ACC, LCA, LCART, TOP}.
It is obvious that τ
A
(T
1
,T
2
) = 1. On the ot-
her hand, it holds that τ
A
(T
1
[u
i
],T
2
[v
i
]) = 1 and
τ
A
(T
1
[u
i
],T
2
[v
7
]) = |T
1
[u
i
]| (1 ≤ i ≤ 6). Since the
weight of T
1
[u
i
] (resp., T
2
[v
i
]) is 1/6 (resp., 1/7), the
optimum flow consists of the 6 flows from T
1
[u
i
] to
T
2
[v
i
] whose costs are 1/7 and the 6 flows from T
1
[u
i
]
to T
2
[v
7
] whose costs are 1/42. Then, the cost of the
optimum flow is 6(1/7)+(6+5+4+3+2+1)/ 42 =
57/42 = 1.357 = EMD
A
(T
1
,T
2
).
Hence, wherea s the ground distance s are not sen-
sitive to inserting leaves, the EMD is necessary to
transport th e remained weig hts for every node in one
tree to an inserted leave in an other tree.
T
1
= G01687 T
2
= G02836
Figure 5: Trees T
1
and T
2
.
Example 2. Consider trees T
1
and T
2
illustrated in
Figure 6, th at is, just a label of the root in one tree
(T
1
) is different from that in another tree (T
2
). In
this case, it holds that EMD
A
(T
1
,T
2
) ≤ τ
A
(T
1
,T
2
).
For the trees T
1
and T
2
in Figure 6, it holds that
τ
A
(T
1
,T
2
) = 1 and EMD
A
(T
1
,T
2
) = 0.083 for every
A ∈ {ILST, ACC, LCA, LCART, TOP}.
It is obvious that τ
A
(T
1
,T
2
) = 1. On the other
hand, the signature containing r(T
1
) (resp., r(T
2
)) is
just T
1
(resp., T
2
) itself. Since τ
A
(T
1
[u
i
],T
2
[v
i
]) = 0
for 2 ≤ i ≤ 12, the cost of the flow from T
1
[u
i
] to T
2
[v
i
]
is 0. Since the weight of T
1
[u
i
] and T
2
[v
i
] is 1/12 and
τ
A
(T
1
[u
1
],T
2
[v
1
]) = 1, the cost of the optimum flow is
1/12 + 11(0/12) = 0.083 = EMD
A
(T
1
,T
2
).
Hence, the difference near to the root is more sen-
sitive to the ground distances rather than the EMDs.
Furthermore, in this case, th e E MDs is much smaller
than the ground distance.
Example 3. Consider trees T
1
and T
2
illustrated in
Figure 7 and T
3
and T
4
illustrated in Figure 8, that
Earth Mover’s Distances for Rooted Labaled Unordered Trees based on Tai Mapping Hierarchy
165

T
1
= G00340 T
2
= G01413
Figure 6: Trees T
1
and T
2
.
is, one tree (T
1
or T
3
) is obtained by deleting the
root of another tree ( T
2
or T
4
). For these cases,
it holds that EMD
LCART
(T
1
,T
2
) ≤ τ
LCART
(T
1
,T
2
) and
EMD
TOP
(T
3
,T
4
) ≤ τ
TOP
(T
3
,T
4
). For the trees T
1
and
T
2
in Figure 7, τ
A
(T
1
,T
2
) and EMD
A
(T
1
,T
2
) are:
A τ
A
EMD
A
LCA 2 0.841
LCART 12 0.91 7
TOP 17 1.512
For the tre es T
3
and T
4
in Figure 8, τ
A
(T
3
,T
4
) and
EMD
A
(T
3
,T
4
) are:
A τ
A
EMD
A
LCA 2 0.810
LCART 4 0.813
TOP 34 1.092
Here, we also illustrate the minimum cost map-
ping in M
A
in Figures 7 and 8, where the correspon-
ding node is denoted by ◦ and the non-corresponding
node is denoted by •, which implies τ
A
.
The reason is that the structural difference near to
the root is much sensitive to τ
LCART
and τ
TOP
, whose
values tend to be large, but th e EMDs are not.
T
1
= G00449 T
2
= G00513
M
LCA
(T
1
,T
2
) M
LCART
(T
1
,T
2
) M
TOP
(T
1
,T
2
)
Figure 7: Trees T
1
and T
2
.
Example 4. Consider trees T
1
and T
2
illustrated in
Figure 9, that is, subtrees in one tree (T
1
) frequently
occur in another tree (T
2
). In this case, it holds
T
3
= G03673 T
4
= G04688
M
LCA
(T
3
,T
4
) M
LCART
(T
3
,T
4
) M
TOP
(T
3
,T
4
)
Figure 8: Trees T
3
and T
4
.
that EMD
A
(T
1
,T
2
) is much smaller than τ
A
(T
1
,T
2
).
For the trees T
1
and T
2
in Figure 6, it holds that
τ
A
(T
1
,T
2
) = 16 and EMD
A
(T
1
,T
2
) = 1.63 for every
A ∈ {ILST, ACC, LCA, LCART, TOP}. Since T
2
is
obtained by inserting 16 nodes to T
1
, it holds that
τ
A
(T
1
,T
2
) = 16.
The weight of T
1
[u] (resp., T
2
[v]) is 1/20 (resp.,
1/36). Then, T
1
[u
4
], T
1
[u
13
], T
2
[v
4
], T
2
[v
12
], T
2
[v
21
]
and T
2
[v
29
] are isomorphic an d T
1
[u
6
], T
1
[u
9
], T
1
[u
15
],
T
1
[u
18
], T
2
[v
6
], T
2
[v
9
], T
1
[u
14
], T
1
[u
17
], T
2
[v
23
], T
2
[v
26
],
T
1
[u
31
] and T
1
[u
34
] are isomorphic, so the we ights of
T
1
[u
4
], T
2
[v
4
], T
1
[u
6
] and T
2
[u
6
] as features are 2/20,
4/36, 4/20 and 8/36, respectively. Since these weig-
hts are preser ved in the su btrees of them, the total
weight of features consisting of T
1
[u
4
] and its sub -
trees in T
1
is 2/20 +2/20 +4/20+4/20= 16/20 and
that of T
2
[v
4
] and its subtrees in T
2
is 4/36 + 4/36 +
8/36 + 8/36 = 32/36. Hence, the cost of flows in
these isomorphic subtree s from T
1
to T
2
is 0, be-
cause τ
A
(T
1
[u
4
],T
2
[v
4
]) = 0, for example. Since these
flows move all the weight 16/ 20 of T
1
[u
4
], T
2
[v
4
] and
its subtrees can receive the weight 32/36 − 16/20 =
4/45.
For the remained featu res in T
2
, the weights of
T
2
[v
1
], T
2
[v
2
] and T
2
[v
3
] as features are 1/36, 1/36
and 2/36, respectively. Furthermore, as T
2
[v
4
] and its
subtrees receive the weights, it is necessary to con-
sider the ground distances between T
1
[u
3
] and T
2
[v
i
]
(4 ≤ i ≤ 8). The ground distances necessary to com-
pute EMD
A
(T
1
,T
2
) are given as follows.
ICPRAM 2018 - 7th International Conference on Pattern Recognition Applications and Methods
166

τ
A
(T
1
[u
1
],T
2
[v
1
]) = 16, τ
A
(T
1
[u
2
],T
2
[v
2
]) = 16,
τ
A
(T
1
[u
3
],T
2
[v
3
]) = 8, τ
A
(T
1
[u
1
],T
2
[v
3
]) = 3,
τ
A
(T
1
[u
2
],T
2
[v
3
]) = 4, τ
A
(T
1
[u
3
],T
2
[v
4
]) = 1,
τ
A
(T
1
[u
3
],T
2
[v
5
]) = 2, τ
A
(T
1
[u
3
],T
2
[v
6
]) = 6,
τ
A
(T
1
[u
3
],T
2
[v
7
]) = 7, τ
A
(T
1
[u
3
],T
2
[v
8
]) = 8.
Hence, by computing the optimum flow to re ceive
the weight 4/ 45 + 4/36 = 1/5 in T
2
, we can o btain
EMD
A
(T
1
,T
2
) as 16(1/ 36) + 16(1/36) + 8(1/90) +
3(1/45)+ 4 (1/45) + 1(1/90) +2(1/90)+ 6(1/45) +
7(1/45) + 8(1/45) = 49/30 = 1.633.
T
1
= G03824 T
2
= G04045
Figure 9: Trees T
1
and T
2
.
4.4 Properties of EMDs for Trees
Finally, we investigate the properties of the EMDs for
trees by summarizing the typical c ases in Section 4 .3.
1. Concerned with Example 1, just the case that one
tree is obtained by deleting leaves to another tree
implies th at τ
A
(T
1
,T
2
) ≤ EMD
A
(T
1
,T
2
) for N-
glycan data. Whereas the trees T
1
and T
2
in Ex-
ample 1 are paths, the statement holds when some
internal nodes have some leaves as children.
As another case concerned with Example 1, con-
sider trees T
i
(1 ≤ i ≤ 6) in Figure 10. Then, it
holds that τ
A
(T
1
,T
i
) = 1 for every i (2 ≤ i ≤ 6)
but EMD
A
(T
1
,T
2
) = 0.2, EMD
A
(T
1
,T
3
) = 0.4,
EMD
A
(T
1
,T
4
) = 0.6, EMD
A
(T
1
,T
5
) = 0.8 and
EMD
A
(T
1
,T
6
) = 1. The reason is that the farther
node with a different label from the root makes
more different signatures.
T
1
T
2
T
3
T
4
T
5
T
6
Figure 10: Trees T
i
(1 ≤ i ≤ 6).
2. Concerned with Examples 2 and 3, consider
complete binary trees T
1
and T
2
with 15 no-
des and a tree T
3
adding the root to T
1
illustra-
ted in Figure 11. Then, for A ∈ {ILST, TOP},
EMD
A
(T
1
,T
i
) and τ
A
(T
1
,T
i
) are as follows.
T
i
T
2
T
3
EMD
ILST
(T
1
,T
i
) 0.067 0.796
EMD
TOP
(T
1
,T
i
) 0.067 1.07
τ
ILST
(T
1
,T
i
) 1 1
τ
TOP
(T
1
,T
i
) 1 23
Hence, the difference of bo th labels and structu -
res near to the root is more sensitive to τ
TOP
than
EMD
TOP
. On the other hand, for the difference
of labels near to the root, EMD
A
is much smal-
ler than τ
A
. As stated in Examples 2 and 3, there
also exists a case that LCATOP is sensitive to the
difference of both labels a nd structures nea r to the
root.
T
1
T
2
T
3
Figure 11: Trees T
1
, T
2
and T
3
.
3. Co ncerned with Example 4, co nsider a tree T
1
with 10 nodes and trees T
i
(2 ≤ i ≤ 5) contai-
ning T
1
as subtrees illustrated in Figure 12. Then ,
EMD
A
(T
1
,T
i
) and τ
A
(T
1
,T
i
) are as follows.
T
i
T
2
T
3
T
4
T
5
EMD
A
(T
1
,T
i
) 0.5 0.738 0.822 0.866
τ
A
(T
1
,T
i
) 1 11 21 31
In this case, whereas the ground distances are ne-
cessary to insert new nodes, the EMDs tend to ab-
sorb the influence of isomorphic subtrees.
T
1
T
2
T
3
T
4
T
5
Figure 12: Trees T
i
(1 ≤ i ≤ 5).
Earth Mover’s Distances for Rooted Labaled Unordered Trees based on Tai Mapping Hierarchy
167

5 CONCLUSION
In this paper, for the variations of edit distance τ
A
for
A ∈ {ILST, ACC, LCA, LCART, TOP}, we have for-
mulated the earth mover’s distances EMD
A
based on
τ
A
. Then, we have given experimental results to eva-
luate EMD
A
comparing with τ
A
. As a result, we have
investigated the properties of EMD
A
.
It is a future work to give experimental results for
more large data (with large degrees) to analyze the
theoretical ratio O(n logn/d) in Section 4.1 in expe-
rimental. Also it is a future work to formulate EMDs
to other tra c ta ble variations in Tai mapping hierar-
chy (Yoshino and Hirata, 2017).
Concerned w ith Ex ample 1 in Section 4.3 and Ste-
tement 1 in Section 4. 4, we have found no trees T
1
and T
2
such that τ
A
(T
1
,T
2
) < EMD
A
(T
1
,T
2
) except
the case that T
1
is obtained by deleting leaves to T
2
.
Then, it is a fu ture work to determine whether or
not there exist other cases satisfying that τ
A
(T
1
,T
2
) <
EMD
A
(T
1
,T
2
).
It is a future work to analyze the properties of
EMDs in Section 4.4 in more detail and investigate
how data are appropriate for EMDs. In particular,
since it is possible that the number of the signature is
too small to formulate EMDs for trees, it is an impor-
tant future work to investigate appropriate signatures
for EMDs for trees.
ACKNOWLEDGEMENTS
This work is partially supported by Grant-in-
Aid for Scientific Research 17H00762, 16H02870,
16H01743 and 15K12102 fro m the Ministry of Edu-
cation, Cu lture, Sports, Science and Te chnology, Ja-
pan.
REFERENCES
Aratsu, T., Hirata, K., and Kuboyama, T. (2009). Sibling
distance for rooted labeled trees. In JSAI PAK DD ’08
Post-Workshop Proc. (LNAI 5433), pages 99–110.
Chawathe, S. S. (1999). Comparing hierarchical data in ex-
ternal memory. In Proc. VLDB’99, pages 90–101.
Gollapudi, S. and Panigrahy, R. (2008). The power of two
min-hashes for similarity search among hierarchical
data objects. In Proc. PODS’08, pages 211–219.
Hirata, K., Yamamoto, Y., and Kuboyama, T. (2011). Im-
proved MAX SNP-hard results for finding an edit dis-
tance between unordered trees. In Proc. CPM’11
(LNCS 6661), pages 402–415.
Jiang, T., Wang, L., and Z hang, K. (1995). Al ignment of
trees – an alternative to tree edit. Theoret. Comput.
Sci., 143:137–148.
Kailing, K., Kriegel, H.-P., Sch¨onaur, S., and Seidl, T.
(2004). Efficient simi larity search for hierarchical data
in large databases. In Proc. EDBT’04, pages 676–693.
Kawaguchi, T. and Hirata, K. (2017). On earth mover’s
distance based on complete subtrees for rooted labeled
trees. In Proc. SISA’17, pages 225–228.
Kuboyama, T. (2007). Matching and learning in trees. Ph.D
thesis, University of Tokyo.
Li, F., Wang, H., Li, J., and Gao, H. (2013). A survey on
tree edit distance lower bound estimation techniques
for similarity join on XML data. SIGMOD Record,
43:29–39.
Luke, S. and Panait, L. (2001). A survey and comparison
of tree generation algorithms. In Proc. GECCO’01,
pages 81–88.
Rubner, Y., Tomasi, C., and Guibas, L. J. (2007). The earth
mover’s distance as a metric for image retrieval. Int.
J. Comput. Visi on, 40:99–121.
Selkow, S. M. (1977). The tree-to-tree editing problem. In-
form. Process. Lett., 6:184–186.
Tai, K.-C. (1979). The tree-to-tree correction problem. J.
ACM, 26:422–433.
Yamamoto, Y., Hirata, K., and Kuboyama, T. (2014). Trac-
table and intractable variations of unordered tree edit
distance. Internat. J. Found. Comput. Sci., 25:307–
329.
Yoshino, T. and Hirata, K. ( 2017). Tai mapping hierarchy
for rooted labeled trees through common subforest.
Theory of Comput. Sys., 60:769–787.
Zhang, K. (1995). Algorithms for t he constrained edi-
ting distance between ordered labeled trees and related
problems. Pattern Recog., 28:463–474.
Zhang, K. (1996). A constrained edit distance between
unordered labeled trees. Algorithmica, 15:205–222.
Zhang, K. and Jiang, T. ( 1994). Some MAX SNP-hard re-
sults concerning unordered labeled trees. Inform. Pro-
cess. Lett., 49:249–254.
Zhang, K., Wang, J., and Shasha, D. (1996). On the editing
distance between undirected acyclic graphs. I nternat.
J. Found. Comput. Sci., 7:43–58.
ICPRAM 2018 - 7th International Conference on Pattern Recognition Applications and Methods
168
