Logics and Translations for Inconsistency-tolerant Model Checking

Norihiro Kamide

and Kazuki Endo

Teikyo University, Faculty of Science and Engineering, Department of Information and Electronic Engineering,

Toyosatodai 1-1, Utsunomiya-shi, Tochigi 320-8551, Japan

Teikyo University, Faculty of Science and Engineering, Department of Human Information Systems, Toyosatodai 1-1,

Utsunomiya-shi, Tochigi 320-8551, Japan

Keywords:

Model Checking, Paraconsistent Logic, Linear-time Temporal Logic, Computation-tree Logic, Embedding

Theorem.

Abstract:

In this study, we develop logics and translations for inconsistency-tolerant (or paraconsistent) model checking

that can be used to verify systems with inconsistencies. Paraconsistent linear-time temporal logic (pLTL)

and paraconsistent computation tree logic (pCTL) are introduced, and these are extensions of standard linear-

time temporal logic (LTL) and standard computation tree logic (CTL), respectively. These novel logics can

be applied when handling inconsistency-tolerant temporal reasoning. These logics are also regarded as four-

valued temporal logics that extend the four-valued logic of Belnap and Dunn. Translations from pLTL into

LTL and pCTL into CTL are deﬁned, and these are used to prove the theorems for embedding pLTL into LTL

and pCTL into CTL. These embedding theorems allow the standard LTL- and CTL-based model checking

algorithms to be used for verifying inconsistent systems that are modeled and speciﬁed by pLTL and pCTL.

A new illustrative example for inconsistency-tolerant model checking is also presented on the basis of the

proposed logics and translations.

1 INTRODUCTION

Inconsistencies are frequent and inevitable when ver-

ifying and specifying large, complex, and open sys-

tems. The goal of this study is to develop simple log-

ics and translations for inconsistency-tolerant model

checking (or paraconsistent model checking) that can

be used to verify systems with inconsistencies. Model

checking is a formal and automated technique for

verifying concurrent systems (Clarke and Emerson,

1981; Clarke et al., 1999; Holzmann, 2006). We de-

velop two novel and simple versions of paraconsistent

four-valued temporal logics such as paraconsistent

linear-time temporal logic (pLTL) and paraconsistent

computation tree logic (pCTL). These are extensions

of the standard temporal logics: linear-time tempo-

ral logic (LTL) (Pnueli, 1977) and computation-tree

logic (CTL) (Clarke and Emerson, 1981), typically

used in model checking. pLTL and pCTL may be ap-

plied when handling inconsistency-tolerant temporal

reasoning, and may also provide the base logics for

inconsistency-tolerant model checking. These four-

valued temporal logics are also regarded as exten-

sions of Belnap and Dunn’s four-valued logic (Bel-

nap, 1977b; Belnap, 1977a; Dunn, 1976). In this

paper, we deﬁne the translations of pLTL into LTL

and pCTL into CTL. These translations will be used

to prove the theorems for embedding pLTL into LTL

and pCTL into CTL. These embedding theorems al-

low us to repurpose the standard LTL- and CTL-based

model checking algorithms for verifying inconsistent

systems that are modeled and speciﬁed by pLTL and

pCTL.

LTL (Pnueli, 1977) is one of the most useful tem-

poral logics for model checking based on the linear-

time paradigm, which uses linear order to represent

the passage of time. CTL (Clarke and Emerson, 1981)

is another form of temporal logic that is widely used

for model checking. It is based on the branching-time

paradigm that uses computation trees to represent the

passage of time. Since these standard temporal logics

lack paraconsistency, they are unsuitable for speci-

fying and verifying inconsistent systems. The sat-

isfaction relation |= of a logic is considered to be

paraconsistent with respect to a negation connective

∼ if the following condition holds: ∃α,β (M,x) 6|=

(α ∧ ∼α)→β, where x is a state or position in a se-

mantic structure M of the underlying logic. This con-

Kamide, N. and Endo, K.

Logics and Translations for Inconsistency-tolerant Model Checking.

DOI: 10.5220/0006640601910200

In Proceedings of the 10th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2018) - Volume 2, pages 191-200

ISBN: 978-989-758-275-2

191

dition reﬂects that formulas of the form (α ∧ ∼α)→β

are not valid in the underlying logics.

Compared to other non-classical logics, para-

consistent logics such as pLTL and pCTL can be

appropriately used in inconsistency-tolerant reason-

ing (Priest, 2002; da Costa et al., 1995; Wansing,

1993). For example, the following scenario is unde-

sirable: (s(x) ∧ ∼s(x))→d(x) is valid for any symp-

tom s and disease d, where ∼s(x) implies that “a per-

son x does not have a symptom s” and d(x) implies

that “a person x suffers from a disease d.” The in-

consistent scenario written as melancholia( john) ∧

∼melancholia( john) will inevitably arise from the

uncertain deﬁnition of melancholia; the statement

“John has melancholia” may be judged true or

false based on the perception of different patholo-

gists. In this case, the formula (melancholia( john)∧

∼melancholia( john))→cancer( john) is valid in

classical logic (as an inconsistency that has an un-

desirable consequence), but invalid in paraconsis-

tent logics (as these logics are inconsistency-tolerant).

Typical examples of non-temporal paraconsistent log-

ics are Belnap and Dunn’s four-valued logic (Belnap,

1977b; Belnap, 1977a; Dunn, 1976) and Nelson’s

paraconsistent four-valued logic (Almukdad and Nel-

son, 1984; Nelson, 1949). The proposed logics, pLTL

and pCTL, are based on these typical paraconsistent

four-valued logics.

The idea of introducing paraconsistent versions

of LTL and CTL is not a new one. Multi-valued

computation tree logic, χCTL, was introduced by

Easterbrook and Chechik (Easterbrook and Chechik,

2001) as the base logic for multi-valued model check-

ing, which is considered to be the ﬁrst framework

for inconsistency-tolerant model checking. Quasi-

classical temporal logic, QCTL, was introduced by

Chen and Wu (Chen and Wu, 2006) to verify inconsis-

tent concurrent systems using inconsistency-tolerant

model checking. Paraconsistent full computation

tree logic, PCTL

∗

, proposed by Kamide (Kamide,

2006), applied bisimulations to inconsistency-tolerant

model checking. Another paraconsistent linear-time

temporal logic, PLTL, was introduced by Kamide

and Wansing (Kamide and Wansing, 2011) to ob-

tain a cut-free and complete Gentzen-type sequent

calculus. Another paraconsistent computation tree

logic, PCTL, was proposed by Kamide and Kaneiwa

(Kamide and Kaneiwa, 2010; Kaneiwa and Kamide,

2011), providing an alternative inconsistency-tolerant

model checking framework. Kamide (Kamide,

2015) also introduced sequence-indexed paraconsis-

tent computation tree logic, SPCTL, which extended

CTL by adding a paraconsistent negation connec-

tive and a sequence modal operator. SPCTL was

used for the representation and veriﬁcation of med-

ical reasoning with hierarchical and inconsistent in-

formation. Paraconsistent probabilistic computation

tree logic, PpCTL, was introduced by Kamide and

Koizumi (Kamide and Koizumi, 2016) for the veriﬁ-

cation of randomized and stochastic inconsistent sys-

tems.

In this study, we developed pLTL and pCTL as

novel versions of paraconsistent linear-time tempo-

ral logic and paraconsistent computation tree logic

by extending LTL and CTL, respectively. While

PLTL (Kamide and Wansing, 2011), PCTL (Kamide

and Kaneiwa, 2010; Kaneiwa and Kamide, 2011),

SPCTL (Kamide, 2015), and PpCTL (Kamide and

Koizumi, 2016) have two types of dual satisfaction

relations |=

(veriﬁcation or justiﬁcation) and |=

−

(refutation or falsiﬁcation), pLTL and pCTL are sim-

pler, having a single satisfaction relation |=

∗

that is

highly compatible with the standard single satisfac-

tion relations of LTL and CTL. These single satis-

faction relations provide simple proofs for the em-

bedding theorems of pLTL and pCTL, and the para-

consistent negation connective ∼ used in pLTL and

pCTL can be simply formalized and uniformly han-

dled. pLTL is also more expressive than PLTL, since

it lacks the standard until and release temporal op-

erators found in LTL. Furthermore, pLTL and pCTL

employ novel sets of axiom schemes for combining

the paraconsistent negation connective ∼, classical

negation connective ¬, and implication connective

→. The negated implication and negation axioms

used in pLTL and pCTL are ∼(α→β) ↔ ¬∼α ∧ ∼β

and ∼¬α ↔ ¬∼α. These recently introduced axiom

schemes by De and Omori are natural and plausible

from the point of view of many-valued semantics (De

and Omori, 2015). The logic BD+ (De and Omori,

2015) of these axiom schemes was shown to be essen-

tially equivalent to B

eziau’s four-valued modal logic

PM4N (Beziau, 2011) and Zaitsev’s paraconsistent

logic FDEP (Zaitsev, 2012).

The contents of this paper are organized as fol-

lows.

Section 2 discusses the linear-time case based on

LTL and pLTL. The new formulation pLTL is in-

troduced on the basis of the single satisfaction re-

lation |=

∗

. A function translating pLTL into LTL

is deﬁned. This is a simpliﬁcation of the transla-

tion functions used in (Kamide and Wansing, 2011;

Kamide and Kaneiwa, 2010; Kaneiwa and Kamide,

2011; Kamide, 2015; Kamide and Koizumi, 2016).

The proposed translation function is then used to

prove the theorem for embedding pLTL into LTL.

The present and previous versions of these translation

functions are regarded as modiﬁcations or extensions

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

192

of those used by Gurevich (Gurevich, 1977), Raut-

enberg (Rautenberg, 1979), and Vorob’ev (Vorob’ev,

1952) to embed Nelson’s constructive logic (Almuk-

dad and Nelson, 1984; Nelson, 1949) into intuitionis-

tic logic. Similar translations have recently been used

(Kamide, 2016; Kamide and Shramko, 2017) to em-

bed some of the paraconsistent logics into classical

logic.

Section 3 discusses the branching-time case based

on CTL and pCTL. Similar to the linear-time case,

pCTL is introduced on the basis of the single satis-

faction relation |=

∗

, a function translating pCTL to

CTL is deﬁned, and the theorem for embedding pCTL

into CTL is proved. The translation function is con-

structed in a similar manner to that of pLTL.

Section 4 presents a new illustrative example for

inconsistency-tolerant model checking on the basis of

the proposed logics and translations.

Section 5 concludes the paper. It is noted in

that two further alternative logics, pLTL

and pCTL

can be respectively obtained from pLTL and pCTL

by replacing the axiom schemes ∼(α→β) ↔ ¬∼α ∧

∼β and ∼¬α ↔ ¬∼α with the axiom schemes

∼(α→β) ↔ α ∧ ∼β and ∼¬α ↔ α by Odintsov

(Odintsov, 2005). It is further noted that, by appropri-

ate modiﬁcation of the translation functions for pLTL

and pCTL, the embedding theorems for pLTL

into

LTL and pCTL

into CTL can also be obtained.

2 LINEAR-TIME CASE

Formulas of linear-time temporal logic (LTL) are

constructed from countably many propositional vari-

ables, → (implication), ∧ (conjunction), ∨ (disjunc-

tion), ¬ (classical negation), X (next), G (globally), F

(eventually), U (until) and R (release). An expression

α ↔ β is used to denote (α→β)∧(β→α). Lower-case

letters p,q,... are used to denote propositional vari-

ables, and Greek lower-case letters α,β,... are used to

denote formulas. The symbol ω is used to represent

the set of natural numbers. Lower-case letters i, j and

k are used to denote any natural numbers. The symbol

≥ or ≤ is used to represent the linear order on ω. An

expression A ≡ B is used to indicate the syntactical

identity between A and B.

Deﬁnition 2.1. Formulas of LTL are deﬁned by the

following grammar, assuming p represents proposi-

tional variables:

α ::= p | α ∧α | α ∨ α | α→α | ¬α | Xα | Gα |

Fα | αUα | αRα.

Deﬁnition 2.2 (LTL). Let S be a non-empty set of

states, and Φ be the set of propositional variables.

A structure M := (σ,I) is a model iff

1. σ is an inﬁnite sequence s

,... of states in S,

2. I is a mapping from Φ to the power set of S.

A satisfaction relation (M,i) |= α for any formula

α, where M is a model (σ,I) and i (∈ ω) represents

some position within σ, is deﬁned inductively by:

1. for any p ∈ Φ, (M,i) |= p iff s

∈ I(p),

2. (M,i) |= α ∧ β iff (M, i) |= α and (M,i) |= β,

3. (M,i) |= α ∨ β iff (M, i) |= α or (M,i) |= β,

4. (M,i) |= α→β iff (M,i) |= α implies (M,i) |= β,

5. (M,i) |= ¬α iff (M,i) 6|= α,

6. (M,i) |= Xα iff (M,i + 1) |= α,

7. (M,i) |= Gα iff ∀ j ≥ i [(M, j) |= α],

8. (M,i) |= Fα iff ∃ j ≥ i [(M, j) |= α],

9. (M,i) |= αUβ iff ∃ j ≥ i [(M, j) |= β and ∀i ≤ k < j

(M,k) |= α],

10. (M,i) |= αRβ iff ∀ j ≥ i [(M, j) |= β or ∃i ≤ k < j

(M,k) |= α].

A formula α is valid in LTL iff (M, 0) |= α for any

model M := (σ,I).

The language of paraconsistent linear-time tem-

poral logic (pLTL) is obtained from that of LTL by

adding ∼ (paraconsistent negation).

Deﬁnition 2.3. Formulas of pLTL are deﬁned by the

following grammar, assuming p represents proposi-

tional variables:

α ::= p | α ∧ α | α ∨ α | α→α | ¬α | ∼α |

Xα | Gα | Fα | αUα | αRα.

Deﬁnition 2.4 (pLTL). Let S be a non-empty set of

states, Φ be the set of propositional variables and Φ

∼

be the set {∼p | p ∈ Φ} of negated propositional vari-

ables.

A structure M := (σ, I

∗

) is a paraconsistent model

iff

1. σ is an inﬁnite sequence s

,... of states in S,

2. I

∗

is a mapping from Φ ∪ Φ

∼

to the power set of

A paraconsistent satisfaction relation (M,i) |=

∗

for any formula α, where M is a paraconsistent model

(σ,I

∗

) and i (∈ ω) represents some position within σ,

is deﬁned inductively by:

1. for any p ∈ Φ, (M,i) |=

∗

p iff s

∈ I

∗

(p),

2. for any ∼p ∈ Φ

∼

, (M,i) |=

∗

∼p iff s

∈ I

∗

(∼p),

3. (M,i) |=

∗

α ∧ β iff (M, i) |=

∗

α and (M,i) |=

∗

β,

4. (M,i) |=

∗

α ∨ β iff (M, i) |=

∗

α or (M,i) |=

∗

β,

5. (M,i) |=

∗

α→β iff (M, i) |=

∗

α implies (M,i) |=

∗

β,

6. (M,i) |=

∗

¬α iff (M,i) 6|=

∗

α,

Logics and Translations for Inconsistency-tolerant Model Checking

193

7. (M,i) |=

∗

Xα iff (M,i + 1) |=

∗

α,

8. (M,i) |=

∗

Gα iff ∀ j ≥ i [(M, j) |=

∗

α],

9. (M,i) |=

∗

Fα iff ∃ j ≥ i [(M, j) |=

∗

α],

10. (M,i) |=

∗

αUβ iff ∃ j ≥ i [(M, j) |=

∗

β and ∀i ≤

k < j (M,k) |=

∗

α],

11. (M,i) |=

∗

αRβ iff ∀ j ≥ i [(M, j) |=

∗

β or ∃i ≤ k <

j (M,k) |=

∗

α],

12. (M,i) |=

∗

∼∼α iff (M,i) |=

∗

α,

13. (M,i) |=

∗

∼(α ∧ β) iff (M,i) |=

∗

∼α or (M,i) |=

∗

∼β,

14. (M,i) |=

∗

∼(α ∨ β) iff (M,i) |=

∗

∼α and

(M,i) |=

∗

∼β,

15. (M,i) |=

∗

∼(α→β) iff (M,i) 6|=

∗

∼α and

(M,i) |=

∗

∼β,

16. (M,i) |=

∗

∼¬α iff (M,i) 6|=

∗

∼α,

17. (M,i) |=

∗

∼Xα iff (M,i + 1) |=

∗

∼α,

18. (M,i) |=

∗

∼Gα iff ∃ j ≥ i [(M, j) |=

∗

∼α],

19. (M,i) |=

∗

∼Fα iff ∀ j ≥ i [(M, j) |=

∗

∼α],

20. (M,i) |=

∗

∼(αUβ) iff ∀ j ≥ i [(M, j) |=

∗

∼β or

∃i ≤ k < j (M,k) |=

∗

∼α],

21. (M,i) |=

∗

∼(αRβ) iff ∃ j ≥ i [(M, j) |=

∗

∼β and

∀i ≤ k < j (M,k) |=

∗

∼α].

A formula α is valid in pLTL iff (M,0) |=

∗

α for

any paraconsistent model M := (σ, I

∗

We make some remarks.

1. pLTL is paraconsistent with respect to ∼. The

reason is explained as follows. Assume a para-

consistent model M := (σ,I

∗

) such that s

∈ I

∗

(p),

∈ I

∗

(∼p) and s

/∈ I

∗

(q) for a pair of distinct

propositional variables p and q. Then, (M,i) |=

∗

(p ∧ ∼p)→q does not hold.

2. pLTL is regarded as a four-valued logic. The rea-

son is explained as follows. For each i ∈ σ and

each formula α, we can take one of the following

four cases:

(a) α is veriﬁed at i, i.e., (M,i) |=

∗

α,

(b) α is falsiﬁed at i, i.e., (M, i) |=

∗

∼α,

(d) α is neither veriﬁed nor falsiﬁed at i.

Next, we deﬁne a translation function f from

pLTL into LTL.

Deﬁnition 2.5. Let Φ be a non-empty set of propo-

sitional variables, and Φ

be the set {p

| p ∈ Φ} of

propositional variables. The language L

(the set of

formulas) of pLTL is deﬁned using Φ, ∧,∨,→,¬, X,

G, F, U, R and ∼. The language L of LTL is obtained

from L

by adding Φ

and deleting ∼.

A mapping f from L

to L is deﬁned inductively

by:

1. for any p ∈ Φ, f (p) := p and f (∼p) := p

∈ Φ

2. f (α ] β) := f (α) ] f (β)

where ] ∈ {∧,∨,→,U,R},

3. f (]α) := ] f (α) where ] ∈ {¬,X,F,G},

4. f (∼∼α) := f (α),

5. f (∼(α ∧ β)) := f (∼α) ∨ f (∼β),

6. f (∼(α ∨ β)) := f (∼α) ∧ f (∼β),

7. f (∼(α→β)) := ¬ f (∼α) ∧ f (∼β),

8. f (∼]α) := ] f (∼α) where ] ∈ {¬,X},

9. f (∼Fα) := G f (∼α),

10. f (∼Gα) := F f (∼α),

11. f (∼(αUβ)) := f (∼α)R f (∼β),

12. f (∼(αRβ)) := f (∼α)U f (∼β).

In order to obtain the theorem for embedding

pLTL into LTL, we need to show some lemmas.

Lemma 2.6. Let f be the mapping deﬁned in Deﬁ-

nition 2.5, and S be a non-empty set of states. For

any paraconsistent model M := (σ,I

∗

) of pLTL, any

paraconsistent satisfaction relation |=

∗

on M, and any

state s

in σ, we can construct a model N := (σ,I) of

LTL and a satisfaction relation |= on N such that for

any formula α in L

, (M,i) |=

∗

α iff (N,i) |= f (α).

Proof. Let Φ be a non-empty set of propositional

variables, Φ

∼

be {∼p | p ∈ Φ}, and Φ

be {p

| p ∈

Φ}. Suppose that M is a paraconsisitent model (σ,I

∗

)

where I

∗

is a mapping from Φ ∪ Φ

∼

to the power set

of S. We then deﬁne a model N := (σ, I) such that

1. I is a mapping from Φ ∪ Φ

to the power set of S,

2. for any s

in σ,

(a) s

∈ I

∗

(p) iff s

∈ I(p),

(b) s

∈ I

∗

(∼p) iff s

∈ I(p

Then, this lemma is proved by induction on the

complexity of α.

• Base step:

1. Case α ≡ p ∈ Φ: We obtain: (M,i) |=

∗

p iff s

∈

∗

(p) iff s

∈ I(p) iff (N,i) |= p iff (N,i) |= f (p)

(by the deﬁnition of f ).

2. Case α ≡ ∼p ∈ Φ

∼

: We obtain: (M,i) |=

∗

∼p iff

∈ I

∗

(∼p) iff s

∈ I(p

) iff (N,i) |= p

iff (N, i) |=

f (∼p) (by the deﬁnition of f ).

• Induction step: We show some cases.

1. Case α ≡ βUγ: We obtain:

(M,i) |=

∗

βUγ

iff ∃ j ≥ i [(M, j) |=

∗

γ and ∀i ≤ k < j (M,k) |=

∗

β]

iff ∃ j ≥ i [(N, j) |= f (γ) and ∀i ≤ k < j (N,k) |=

f (β)] (by induction hypothesis)

iff (N, i) |= f (β)U f (γ)

iff (N, i) |= f (βUγ) (by the deﬁnition of f ).

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

194

2. Case α ≡ ∼(β∧γ): We obtain: (M, i) |=

∗

∼(β∧γ)

iff (M,i) |=

∗

∼β or (M,i) |=

∗

∼γ iff (N,i) |=

f (∼β) or (N, i) |= f (∼γ) (by induction hypoth-

esis) iff (N,i) |= f (∼β) ∨ f (∼γ) iff (N,i) |=

f (∼(β ∧ γ)) (by the deﬁnition of f ).

3. Case α ≡ ∼(β→γ): We obtain: (M,i) |=

∗

∼(β→γ) iff (M, i) 6|=

∗

∼β and (M, i) |=

∗

∼γ iff

(N,i) 6|= f (∼β) and (N, i) |= f (∼γ) (by induc-

tion hypothesis) iff (N,i) |= ¬ f (∼β) ∧ f (∼γ) iff

(N,i) |= f (∼(β→γ)) (by the deﬁnition of f ).

4. Case α ≡ ∼¬β: We obtain: (M,i) |=

∗

∼¬β iff

(M,i) 6|=

∗

∼β iff (N,i) 6|= f (∼β) (by induction hy-

pothesis) iff (N,i) |= ¬ f (∼β) iff (N, i) |= f (∼¬β)

(by the deﬁnition of f ).

5. Case α ≡ ∼∼β: We obtain: (M, i) |=

∗

∼∼β iff

(M,i) |=

∗

β iff (N,i) |= f (β) (by induction hy-

pothesis) iff (N,i) |= f (∼∼β) (by the deﬁnition

of f ).

6. Case α ≡ ∼Xβ: We obtain: (M, i) |=

∗

∼Xβ iff

(M,i+1) |=

∗

∼β iff (N,i+1) |= f (∼β) (by induc-

tion hypothesis) iff (N, i) |= X f (∼β) iff (N,i) |=

f (∼Xβ) (by the deﬁnition of f ).

7. Case α ≡ ∼Gβ: We obtain: (M, i) |=

∗

∼Gβ iff

∃ j ≥ i [(M, j) |=

∗

∼β] iff ∃ j ≥ i [(N, j) |= f (∼β)]

(by induction hypothesis) iff (N,i) |= F f (∼β) iff

(N,i) |= f (∼Gβ) (by the deﬁnition of f ).

8. Case α ≡ ∼(βUγ): We obtain:

(M,i) |=

∗

∼(βUγ)

iff ∀ j ≥ i [(M, j) |=

∗

∼γ or ∃i ≤ k < j (M,k) |=

∗

∼β]

iff ∀ j ≥ i [(N, j) |= f (∼γ) or ∃i ≤ k < j (N,k) |=

f (∼β)] (by induction hypothesis)

iff (N, i) |= f (∼β)R f (∼γ)

iff (N, i) |= f (∼(βUγ)) (by the deﬁnition of f ).

9. Case α ≡ ∼(βRγ): We obtain:

(M,i) |=

∗

∼(βRγ)

iff ∃ j ≥ i [(M, j) |=

∗

∼γ and ∀i ≤ k < j (M, k) |=

∗

∼β]

iff ∃ j ≥ i [(N, j) |= f (∼γ) and ∀i ≤ k < j (N, k) |=

f (∼β)] (by induction hypothesis)

iff (N, i) |= f (∼β)U f (∼γ)

iff (N, i) |= f (∼(βRγ)) (by the deﬁnition of f ).

Q.E.D.

Lemma 2.7. Let f be the mapping deﬁned in Deﬁni-

tion 2.5, and S be a non-empty set of states. For any

model N := (σ,I) of LTL, any satisfaction relation |=

on N, and any state s

in σ, we can construct a para-

consisitent model M := (σ,I

∗

) of pLTL and a satis-

faction relation |=

∗

on M such that for any formula α

in L

, (N,i) |= f (α) iff (M, i) |=

∗

α.

Proof. Similar to the proof of Lemma 2.6. Q.E.D.

Theorem 2.8 (Embedding from pLTL into LTL). Let

f be the mapping deﬁned in Deﬁnition 2.5. For any

formula α, α is valid in pLTL iff f (α) is valid in LTL.

Proof. By Lemmas 2.6 and 2.7. Q.E.D.

3 BRANCHING-TIME CASE

Formulas of computation tree logic (CTL) are con-

structed from countably many propositional variables,

→, ∧, ∨, ¬, X, G, F, U, R, A (all computation paths),

and E (some computation path). The same notions

and notations as those in the previous sections are also

used in the following.

Deﬁnition 3.1. Formulas of CTL are deﬁned by the

following grammar, assuming p represents proposi-

tional variables:

α ::= p | α ∧ α | α ∨ α | α→α | ¬α |

AXα | EXα | AGα | EGα | AFα | EFα |

A(αUα) | E(αUα) | A(αRα) | E(αRα).

Note that pairs of symbols like AX and EU are in-

divisible, and that the symbols X,G,F,U, and R can-

not occur without being preceded by an A or an E.

Similarly, every A or E must have one of X, G, F, U,

and R to accompany it.

Deﬁnition 3.2 (CTL). A structure (S,S

,R, L) is a

model iff

1. S is the set of states,

2. S

is a set of initial states and S

⊆ S,

3. R is a binary relation on S which satisﬁes the con-

dition: ∀s ∈ S ∃s

∈ S [(s,s

) ∈ R],

4. L is a mapping from S to the power set of a

nonempty set Φ of propositional variables.

A path in a model is an inﬁnite sequence of states,

π = s

,... such that ∀i ≥ 0 [(s

i+1

) ∈ R].

A satisfaction relation (M,s) |= α for any formula

α, where M is a model (S, S

,R, L) and s represents a

state in S, is deﬁned inductively by:

1. for any p ∈ Φ, (M,s) |= p iff p ∈ L(s),

2. (M,s) |= α ∧ β iff (M,s) |= α and (M,s) |= β,

3. (M,s) |= α ∨ β iff (M,s) |= α or (M,s) |= β,

4. (M,s) |= α→β iff (M, s) |= α implies (M,s) |= β,

5. (M,s) |= ¬α iff (M,s) 6|= α,

6. (M,s) |= AXα iff ∀s

∈ S [(s, s

) ∈ R implies

(M,s

) |= α],

7. (M,s) |= EXα iff ∃s

∈ S [(s,s

) ∈ R and

(M,s

) |= α],

Logics and Translations for Inconsistency-tolerant Model Checking

195

8. (M,s) |= AGα iff for all paths π ≡ s

,...,

where s ≡ s

, and all states s

along π, we have

(M,s

) |= α,

9. (M,s) |= EGα iff there is a path π ≡ s

,...,

where s ≡ s

, and for all states s

along π, we have

(M,s

) |= α,

10. (M,s) |= AFα iff for all paths π ≡ s

,...,

where s ≡ s

, there is a state s

along π such that

(M,s

) |= α,

11. (M,s) |= EFα iff there is a path π ≡ s

,...,

where s ≡ s

, and for some state s

along π, we

have (M,s

) |= α,

12. (M,s) |= A(αUβ) iff for all paths π ≡ s

,...,

where s ≡ s

, there is a state s

along π such that

(M,s

) |= β and ∀0 ≤ k < j (M,s

) |= α,

13. (M,s) |= E(αUβ) iff there is a path π ≡

,..., where s ≡ s

, and for some state s

along π, we have (M,s

) |= β and ∀0 ≤ k < j

(M,s

) |= α,

14. (M,s) |= A(αRβ) iff for all paths π ≡ s

,...,

where s ≡ s

, and all states s

along π, we have

(M,s

) |= β or ∃0 ≤ k < j (M,s

) |= α,

15. (M,s) |= E(αRβ) iff there is a path π ≡

,..., where s ≡ s

, and for all states s

along π, we have (M,s

) |= β or ∃0 ≤ k < j

(M,s

) |= α.

A formula α is valid in CTL iff (M,s) |= α holds

for any model M := (S,S

,R, L), any s ∈ S, and any

satisfaction relation |= on M.

The language of paraconsistent computation tree

logic (pCTL) is obtained from that of CTL by adding

∼.

Deﬁnition 3.3. Formulas of pCTL are deﬁned by the

following grammar, assuming p represents proposi-

tional variables:

α ::= p | α ∧ α | α ∨ α | α→α | ¬α | ∼α |

AXα | EXα | AGα | EGα | AFα | EFα |

A(αUα) | E(αUα) | A(αRα) | E(αRα).

Deﬁnition 3.4 (pCTL). Let Φ be a non-empty set of

propositional variables, and Φ

∼

be the set {∼p | p ∈

Φ} of negated propositional variables.

A structure (S,S

,R, L

∗

) is a paraconsistent model

iff

1. S is the set of states,

2. S

is a set of initial states and S

⊆ S,

3. R is a binary relation on S which satisﬁes the con-

dition: ∀s ∈ S ∃s

∈ S [(s,s

) ∈ R],

4. L

∗

is a mapping from S to the power set of Φ∪Φ

∼

A path in a paraconsistent model is an inﬁnite se-

quence of states, π = s

,... such that ∀i ≥ 0

[(s

i+1

) ∈ R].

A paraconsistent satisfaction relation (M,s) |=

∗

for any formula α, where M is a paraconsistent model

(S,S

,R, L

∗

) and s represents a state in S, is deﬁned

inductively by:

1. for any p ∈ Φ, (M,s) |=

∗

p iff p ∈ L

∗

(s),

2. for any ∼p ∈ Φ

∼

, (M,s) |=

∗

∼p iff ∼p ∈ L

∗

(s),

3. (M,s) |=

∗

α ∧ β iff (M, s) |=

∗

α and (M,s) |=

∗

β,

4. (M,s) |=

∗

α ∨ β iff (M, s) |=

∗

α or (M,s) |=

∗

β,

5. (M,s) |=

∗

α→β iff (M,s) |=

∗

α implies (M,s) |=

∗

β,

6. (M,s) |=

∗

¬α iff (M,s) 6|=

∗

α,

7. (M,s) |=

∗

AXα iff ∀s

∈ S [(s,s

) ∈ R implies

(M,s

) |=

∗

α],

8. (M,s) |=

∗

EXα iff ∃s

∈ S [(s,s

) ∈ R and

(M,s

) |=

∗

α],

9. (M,s) |=

∗

AGα iff for all paths π ≡ s

,...,

where s ≡ s

, and all states s

along π, we have

(M,s

) |=

∗

α,

10. (M,s) |=

∗

EGα iff there is a path π ≡ s

,...,

where s ≡ s

, and for all states s

along π, we have

(M,s

) |=

∗

α,

11. (M,s) |=

∗

AFα iff for all paths π ≡ s

,...,

where s ≡ s

, there is a state s

along π such that

(M,s

) |=

∗

α,

12. (M,s) |=

∗

EFα iff there is a path π ≡ s

,...,

where s ≡ s

, and for some state s

along π, we

have (M,s

) |=

∗

α,

13. (M,s) |=

∗

A(αUβ) iff for all paths π ≡

,..., where s ≡ s

, there is a state s

along π such that (M,s

) |=

∗

β and ∀0 ≤ k < j

(M,s

) |=

∗

α,

14. (M,s) |=

∗

E(αUβ) iff there is a path π ≡

,..., where s ≡ s

, and for some state s

along π, we have (M,s

) |=

∗

β and ∀0 ≤ k < j

(M,s

) |=

∗

α,

15. (M,s) |=

∗

A(αRβ) iff for all paths π ≡

,..., where s ≡ s

, and all states s

along

π, we have (M,s

) |=

∗

β or ∃0 ≤ k < j (M,s

) |=

∗

α,

16. (M,s) |=

∗

E(αRβ) iff there is a path π ≡

,..., where s ≡ s

, and for all states s

along π, we have (M,s

) |=

∗

β or ∃0 ≤ k < j

(M,s

) |=

∗

α,

17. (M,s) |=

∗

∼∼α iff (M,s) |=

∗

α,

18. (M,s) |=

∗

∼(α∧β) iff (M, s) |=

∗

∼α or (M, s) |=

∗

∼β,

19. (M,s) |=

∗

∼(α ∨ β) iff (M,s) |=

∗

∼α and

(M,s) |=

∗

∼β,

20. (M,s) |=

∗

∼(α→β) iff (M, s) 6|=

∗

∼α and

(M,s) |=

∗

∼β,

21. (M,s) |=

∗

∼¬α iff (M,s) 6|=

∗

∼α,

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

196

22. (M,s) |=

∗

∼AXα iff ∃s

∈ S [(s,s

) ∈ R and

(M,s

) |=

∗

∼α],

23. (M,s) |=

∗

∼EXα iff ∀s

∈ S [(s, s

) ∈ R implies

(M,s

) |=

∗

∼α],

24. (M,s) |=

∗

∼AGα iff there is a path π ≡

,..., where s ≡ s

, and for some state s

along π, we have (M,s

) |=

∗

∼α,

25. (M,s) |=

∗

∼EGα iff for all paths π ≡ s

,...,

where s ≡ s

, there is a state s

along π such that

(M,s

) |=

∗

∼α,

26. (M,s) |=

∗

∼AFα iff there is a path π ≡

,..., where s ≡ s

, and for all states s

along π, we have (M,s

) |=

∗

∼α,

27. (M,s) |=

∗

∼EFα iff for all paths π ≡ s

,...,

where s ≡ s

, and all states s

along π, we have

(M,s

) |=

∗

∼α,

28. (M,s) |=

∗

∼A(αUβ) iff there is a path π ≡

,..., where s ≡ s

, and for all states s

along π, we have (M,s

) |=

∗

∼β or ∃0 ≤ k < j

(M,s

) |=

∗

∼α,

29. (M,s) |=

∗

∼E(αUβ) iff for all paths π ≡

,..., where s ≡ s

, and all states s

along π, we have (M,s

) |=

∗

∼β or ∃0 ≤ k < j

(M,s

) |=

∗

∼α,

30. (M,s) |=

∗

∼A(αRβ) iff there is a path π ≡

,..., where s ≡ s

, and for some state s

along π, we have (M,s

) |=

∗

∼β and ∀0 ≤ k < j

(M,s

) |=

∗

∼α,

31. (M,s) |=

∗

∼E(αRβ) iff for all paths π ≡

,..., where s ≡ s

, there is a state s

along π such that (M,s

) |=

∗

∼β and ∀0 ≤ k < j

(M,s

) |=

∗

∼α.

A formula α is valid in pCTL iff (M, s) |=

∗

α holds

for any paraconsistent model M := (S, S

,R, L

∗

), any

s ∈ S, and any paraconsistent satisfaction relation |=

∗

on M.

We make some remarks.

1. pCTL is paraconsistent with respect to ∼. The

reason is explained as follows. Assume a para-

consistent model M = (S,S

,R, L

∗

) such that p ∈

∗

(s), ∼p ∈ L

∗

(s) and q /∈ L

∗

(s) for a pair of

distinct propositional variables p and q. Then,

(M,s) |=

∗

(p ∧ ∼p)→q does not hold.

2. pCTL is regarded as a four-valued logic. The rea-

son is explained as follows. For each s ∈ S and

each formula α, we can take one of the following

four cases:

(a) α is veriﬁed at s, i.e., (M,s) |=

∗

α,

(b) α is falsiﬁed at s, i.e., (M, s) |=

∗

∼α,

(d) α is neither veriﬁed nor falsiﬁed at s.

Deﬁnition 3.5. Let Φ be a non-empty set of propo-

sitional variables, and Φ

be the set {p

| p ∈ Φ} of

propositional variables. The language L

(the set of

formulas) of pCTL is deﬁned using Φ, ∧, ∨, →,¬, X,

F, G, U, R, A, E and ∼. The language L of CTL is

obtained from L

by adding Φ

and deleting ∼.

A mapping f from L

to L is deﬁned inductively

by:

1. for any p ∈ Φ, f (p) := p and f (∼p) := p

∈ Φ

2. f (α ] β) := f (α) ] f (β) where ] ∈ {∧, ∨,→},

3. f (]α) := ] f (α)

where ] ∈ {¬,AX, EX, AG, EG, AF, EF},

4. f (A(αUβ))) := A( f (α)U f (β)),

5. f (E(αUβ))) := E( f (α)U f (β)),

6. f (A(αRβ))) := A( f (α)R f (β)),

7. f (E(αRβ))) := E( f (α)R f (β)),

8. f (∼∼α) := f (α),

9. f (∼(α ∧ β)) := f (∼α) ∨ f (∼β),

10. f (∼(α ∨ β)) := f (∼α) ∧ f (∼β),

11. f (∼(α→β)) := ¬ f (∼α) ∧ f (∼β),

12. f (∼¬α) := ¬ f (∼α),

13. f (∼AXα) := EX f (∼α),

14. f (∼EXα) := AX f (∼α),

15. f (∼AGα) := EF f (∼α),

16. f (∼EGα) := AF f (∼α),

17. f (∼AFα) := EG f (∼α),

18. f (∼EFα) := AG f (∼α),

19. f (∼(A(αUβ))) := E( f (∼α)R f (∼β)),

20. f (∼(E(αUβ))) := A( f (∼α)R f (∼β)),

21. f (∼(A(αRβ))) := E( f (∼α)U f (∼β)),

22. f (∼(E(αRβ))) := A( f (∼α)U f (∼β)).

Lemma 3.6. Let f be the mapping deﬁned in Def-

inition 3.5. For any paraconsistent model M :=

(S,S

,R, L

∗

) of pCTL, and any paraconsistent satis-

faction relation |=

∗

on M, we can construct a model

N := (S,S

,R, L) of CTL and a satisfaction relation

|= on N such that for any formula α in L

and any

state s in S, (M,s) |=

∗

α iff (N,s) |= f (α).

Proof. Let Φ be a nonempty set of propositional vari-

ables, Φ

∼

be {∼p | p ∈ Φ}, and Φ

be {p

| p ∈

Φ}. Suppose that M is a paraconsistent model

(S,S

,R, L

∗

) such that L

∗

is a mapping from S to the

power set of Φ ∪ Φ

∼

. We then deﬁne a model N :=

(S,S

,R, L) such that

1. L is a mapping from S to the power set of Φ∪ Φ

2. for any s ∈ S and any p ∈ Φ,

(a) p ∈ L

∗

(s) iff p ∈ L(s),

(b) ∼p ∈ L

∗

(s) iff p

∈ L(s).

Logics and Translations for Inconsistency-tolerant Model Checking

197

Then, this lemma is proved by induction on the

complexity of α.

• Base step:

1. Case α ≡ p ∈ Φ: We obtain: (M,s) |=

∗

p iff p ∈

∗

(s) iff p ∈ L(s) iff (N, s) |= p iff (N,s) |= f (p)

(by the deﬁnition of f ).

2. We obtain: (M,s) |=

∗

∼p iff ∼p ∈ L

∗

(s) iff p

∈

L(s) iff (N, s) |= p

iff (N, s) |= f (∼p) (by the def-

inition of f ).

• Induction step: We show some cases.

1. Case α ≡ ∼AXβ: We obtain: (M,s) |=

∗

∼AXβ

iff ∃s

∈ S [(s,s

) ∈ R and (M,s

) |=

∗

∼β] iff

∃s

∈ S [(s, s

) ∈ R and (N, s

) |= f (∼β)] (by

induction hypothesis) iff (N, s) |= EX f (∼β) iff

(N,s) |= f (∼AXβ) (by the deﬁnition of f ).

2. Case α ≡ ∼AGβ: We obtain:

(M,s) |=

∗

∼AGβ

iff there is a path π ≡ s

,..., where s ≡ s

, for

some state s

along π, we have (M,s

) |=

∗

∼β

iff there is a path π ≡ s

,..., where s ≡ s

, for

some state s

along π, we have (N, s

) |= f (∼β)

(by induction hypothesis)

iff (N, s) |= EF f (∼β)

iff (N, s) |= f (∼AGβ)) (by the deﬁnition of f ).

3. Case α ≡ ∼A(βUγ): We obtain:

(M,s) |=

∗

∼A(βUγ)

iff there is a path π ≡ s

,..., where s ≡ s

and for all states s

along π, we have (M, s

) |=

∗

∼γ or ∃0 ≤ k < j (M,s

) |=

∗

∼β

iff there is a path π ≡ s

,..., where s ≡ s

and for all states s

along π, we have (N,s

) |=

f (∼γ) or ∃0 ≤ k < j (N, s

) |= f (∼β) (by in-

duction hypothesis)

iff (N, s) |= E( f (∼β)R f (∼γ))

iff (N, s) |= f (∼A(βUγ)) (by the deﬁnition of f ).

4. Case α ≡ ∼A(βRγ): We obtain:

(M,s) |=

∗

∼A(βRγ)

iff there is a path π ≡ s

,..., where s ≡

, and for some state s

along π, we have

(M,s

) |=

∗

∼γ and ∀0 ≤ k < j (M,s

) |=

∗

∼β

iff there is a path π ≡ s

,..., where s ≡ s

and for some state s

along π, we have (N,s

) |=

f (∼γ) or ∀0 ≤ k < j (N, s

) |= f (∼β) (by in-

duction hypothesis)

iff (N, s) |= E( f (∼β)U f (∼γ))

iff (N, s) |= f (∼A(βRγ)) (by the deﬁnition of f ).

Q.E.D.

Lemma 3.7. Let f be the mapping deﬁned in Deﬁni-

tion 3.5. For any model N := (S,S

,R, L) of CTL, and

any satisfaction relation |= on N, we can construct a

paraconsistent model M := (S, S

,R, L

∗

) of pCTL and

a paraconsistent satisfaction relation |=

∗

on M such

that for any formula α in L

and any state s in S,

(N,s) |= f (α) iff (M, s) |=

∗

α,

Proof. Similar to the proof of Lemma 3.6. Q.E.D.

Theorem 3.8 (Embedding from pCTL into CTL). Let

f be the mapping deﬁned in Deﬁnition 3.5. For any

formula α, α is valid in pCTL iff f (α) is valid in CTL.

Proof. By Lemmas 3.6 and 3.7. Q.E.D.

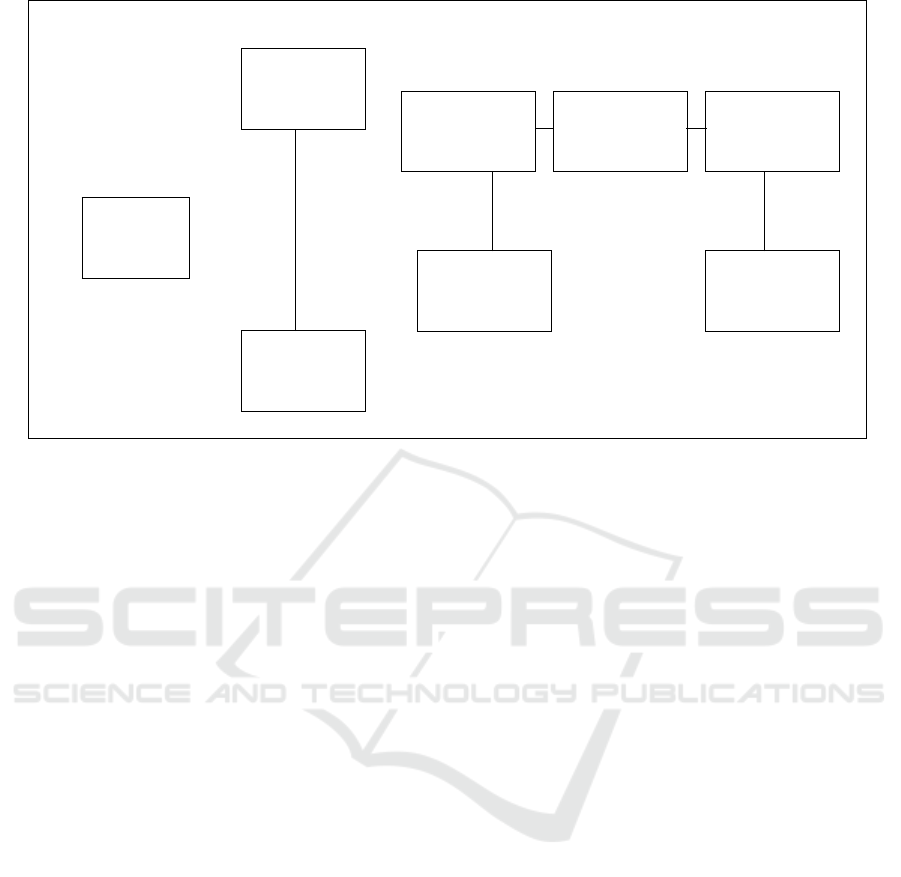
4 ILLUSTRATIVE EXAMPLE

We present a new illustrative example for

inconsistency-tolerant model checking, as shown in

Figure 1 for representing the health of a person who

has a tumor. The proposed example is regarded as a

modiﬁcation of the example presented in (Kamide

and Kaneiwa, 2010; Kaneiwa and Kamide, 2011).

In this example, a paraconsistent negation connec-

tive ∼ is used to express the negation of ambiguous

concepts. If we cannot determine whether someone

is healthy, then the ambiguous concept healthy can

be represented by asserting the inconsistent formula

healthy ∧ ∼healthy. This is well-formalized because

(healthy ∧ ∼healthy)→⊥ is not valid in pLTL and

pCTL. On the other hand, we can decide whether

someone has a tumor. The decision is represented

by hasTumor or ¬hasTumor, where (hasTumor ∧

¬hasToumor)→⊥ is valid in pLTL and pCTL.

In the model of Figure 1, the initial state implies

that a person is healthy. When a person undergoes a

medical checkup, his or her state changes to one of

the two states. If a tumor is detected in a person by

the medical checkup, he or she is both healthy and

not healthy, i.e., both healthy and ∼healthy are true,

because it is unknown if the tumor is malignant (i.e.,

cancer) or not. If cancer is detected in a person (i.e.,

the tumor is diagnosed with cancer), then ∼healthy

is true. This means that the person is not healthy,

but he or she may return to good health if the cancer

is completely removed by surgical operation. More-

over, when the cancer increases, the diagnosis reveals

worse cancer. If the cancer is cured, the person will

be healthy. Otherwise, if the cancer is not controlled,

the person will die.

We can verify the statement “Is there a state in

which a person is both healthy and not healthy?”

This statement is true and expressed as: EF(healthy ∧

∼healthy). We can also verify the statement “Is

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

198









- -

? ?





medicalCheckup

cured

curedsurgicalOperation

thoroughExamination

cancerIncrease cancerIncrease

cancerIncrease

healthy

∼healthy

hasTumor

healthy

¬hasTumor

stage1

∼healthy

hasCancer

stage2

∼healthy

hasCancer

stage3

∼healthy

hasCancer

healthy

∼healthy

¬hasCancer

died

hasCancer

Figure 1: A clinical reasoning process model.

there a state in which a dead person will not be alive

again?” This statement is true and expressed as:

EF(died ∧ ¬EF¬died).

As already pointed out in (Kamide and Kaneiwa,

2010; Kaneiwa and Kamide, 2011), two negative ex-

pressions can be differently interpreted as ¬healthy

(deﬁnitely unhealthy) and ∼healthy (not healthy).

The ﬁrst statement indicates that a person is deﬁnitely

unhealthy that is inconsistent with his or her health.

The second statement means that we can say that a

person is not healthy but he or she may be healthy.

The interpretation of the two negations leads to some

useful veriﬁcation examples. For example, the state-

ment “Is there a state in which a person is not deﬁ-

nitely unhealthy?” can be expressed as EF¬¬healthy.

Moreover, the statement “Is there a state in which it

is not true that a person is not healthy?” can be ex-

pressed as: EF¬∼healthy.

5 CONCLUDING REMARKS

In this paper, we proposed pLTL and pCTL as

novel versions of paraconsistent linear-time tempo-

ral logic and paraconsistent computation tree logic,

respectively. These provided a logical basis for

inconsistency-tolerant model checking, and were de-

veloped by extending the standard temporal logics

LTL and CTL. These are also regarded as extensions

of Belnap and Dunn’s four-valued logics. The trans-

lations from pLTL into LTL and pCTL into CTL were

deﬁned, and were used to prove the theorems for em-

bedding pLTL into LTL and pCTL into CTL. It was

thus demonstrated that the standard LTL- and CTL-

based model checking algorithms can be repurposed

for verifying inconsistent systems that are modeled

and speciﬁed using pLTL and pCTL. A new illustra-

tive example for verifying clinical reasoning process

was presented on the basis of the proposed logics and

translations.

Finally, we note that the proposed framework is

applicable to other new variants pLTL

and pCTL

pLTL and pCTL, respectively. The proposed logics

pLTL and pCTL have the axiom schemes ∼(α→β) ↔

¬∼α ∧ ∼β and ∼¬α ↔ ¬∼α by De and Omori (De

and Omori, 2015), using the paraconsistent negation

connective ∼ and the classical negation connective ¬.

These axiom schemes are known to be plausible can-

didates for combining ∼ and ¬ within a logic (De

and Omori, 2015). Our framework is equally appli-

cable to the logics pLTL

and pCTL

. These are ob-

tained from pLTL and pCTL by replacing the follow-

ing clauses for x ∈ {i,s}:

1. (M,x) |=

∗

∼(α→β)

iff (M,x) 6|=

∗

∼α and (M,x) |=

∗

∼β,

2. (M,x) |=

∗

∼¬α iff (M,x) 6|=

∗

∼α,

with the following clauses for x ∈ {i, s}, which just

correspond to the axiom schemes ∼(α→β) ↔ α ∧∼β

and ∼¬α ↔ α by Odintsov (Odintsov, 2005):

1. (M,x) |=

∗

∼(α→β)

iff (M,x) |=

∗

α and (M,x) |=

∗

∼β,

Logics and Translations for Inconsistency-tolerant Model Checking

199

2. (M,x) |=

∗

∼¬α iff (M,x) |=

∗

α.

By applying appropriate modiﬁcations to the transla-

tion functions of pLTL and pCTL, we obtain the em-

bedding theorems of pLTL

into LTL and pCTL

into

CTL, in the same way as with pLTL and pCTL.

ACKNOWLEDGEMENTS

We would like to thank the anonymous referees for

their valuable comments. We would also like to thank

Yosuke Matsuo and Ryu Yano for their assistance of

this research. This research has been supported by the

Kayamori Foundation of Informational Science Ad-

vancement. This research was partially supported by

JSPS KAKENHI Grant (C) JP26330263.

REFERENCES

Almukdad, A. and Nelson, D. (1984). Constructible falsity

and inexact predicates. Journal of Symbolic Logic,

49:231–233.

Belnap, N. (1977a). How a computer should think. Con-

temporary Aspects of Philosophy, (G. Ryle ed.), Oriel

Press, Stocksﬁeld, pages 30–56.

Belnap, N. (1977b). A useful four-valued logic. Modern

Uses of Multiple-Valued Logic, G. Epstein and J. M.

Dunn, eds. Dordrecht: Reidel, pages 5–37.

Beziau, J.-Y. (2011). A new four-valued approach to modal

logic. Logique et Analyse, 54 (213):109–121.

Chen, D. and Wu, J. (2006). Reasoning about inconsistent

concurrent systems: A non-classical temporal logic.

In Lecture Notes in Computer Science, volume 3831,

pages 207–217.

Clarke, E. and Emerson, E. (1981). Design and synthesis of

synchronization skeletons using branching time tem-

poral logic. In Lecture Notes in Computer Science,

volume 131, pages 52–71.

Clarke, E., Grumberg, O., and Peled, D. (1999). Model

checking. The MIT Press.

da Costa, N., Beziau, J., and Bueno, O. (1995). Aspects of

paraconsistent logic. Bulletin of the IGPL, 3 (4):597–

614.

De, M. and Omori, H. (2015). Classical negation and ex-

pansions of belnap-dunn logic. Studia Logica, 103

(4):825–851.

Dunn, J. (1976). Intuitive semantics for ﬁrst-degree entail-

ment and ‘coupled trees’. Philosophical Studies, 29

(3):146–168.

Easterbrook, S. and Chechik, M. (2001). A framework for

multi-valued reasoning over inconsistent viewpoints.

In Proceedings of the 23rd International Conference

on Software Engineering, pages 411–420.

Gurevich, Y. (1977). Intuitionistic logic with strong nega-

tion. Studia Logica, 36:49–59.

Holzmann, G. (2006). The SPIN model checker: Primer

and reference manual. Addison-Wesley.

Kamide, N. (2006). Extended full computation tree logics

for paraconsistent model checking. Logic and Logical

Philosophy, 15 (3):251–276.

Kamide, N. (2015). Inconsistency-tolerant temporal rea-

soning with hierarchical information. Information Sci-

ences, 320:140–155.

Kamide, N. (2016). Paraconsistent double negation that

can simulate classical negation. In Proceedings of

the 46th IEEE International Symposium on Multiple-

Valued Logic (ISMVL 2016), pages 131–136.

Kamide, N. and Kaneiwa, K. (2010). Paraconsistent nega-

tion and classical negation in computation tree logic.

In Proceedings of the 2nd International Conference

on Agents and Artiﬁcial Intelligence (ICAART 2010),

Vol.1, pages 464–469.

Kamide, N. and Koizumi, D. (2016). Method for combin-

ing paraconsistency and probability in temporal rea-

soning. Journal of Advanced Computational Intelli-

gence and Intelligent Informatics, 20:813–827.

Kamide, N. and Shramko, Y. (2017). Embedding from mul-

tilattice logic into classical logic and vice versa. Jour-

nal of Logic and Computation, 25 (5):1549–1575.

Kamide, N. and Wansing, H. (2011). A paraconsistent

linear-time temporal logic. Fundamenta Informaticae,

106 (1):1–23.

Kaneiwa, K. and Kamide, N. (2011). Paraconsistent com-

putation tree logic. New Generation Computing, 29

(4):391–408.

Nelson, D. (1949). Constructible falsity. Journal of Sym-

bolic Logic, 14:16–26.

Odintsov, S. (2005). The class of extensions of nelson para-

consistent logic. Studia Logica, 80:291–320.

Pnueli, A. (1977). The temporal logic of programs. In Pro-

ceedings of the 18th IEEE Symposium on Foundations

of Computer Science, pages 46–57.

Priest, G. (2002). Paraconsistent logic, handbook of philo-

sophical logic (second edition), d. gabbay and f. guen-

thner (eds.). Handbook of Philosophical Logic (Sec-

ond Edition), D. Gabbay and F. Guenthner (eds.),

6:287–393.

Rautenberg, W. (1979). Klassische und nicht-klassische

Aussagenlogik. Vieweg, Braunschweig.

Vorob’ev, N. (1952). A constructive propositional calculus

with strong negation (in Russian). Doklady Akademii

Nauk SSR, 85:465–468.

Wansing, H. (1993). The logic of information structures.

Springer.

Zaitsev, D. (2012). Generalized relevant logic and models

of reasoning. Moscow State Lomonosov University

(Doctoral Dissertation).

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

200