Improving Text Classification with Vectors of Reduced Precision
∗
Krzysztof Wr´obel
1,2
, Maciej Wielgosz
2,3
, Marcin Pietro´n
2,3
, Michał Karwatowski
2,3
, Jerzy Duda
2
and Aleksander Smywi´nski-Pohl
2
1
Jagiellonian University, Krak´ow, Poland
2
AGH University of Science and Technology, Krak´ow, Poland
3
Academic Computer Centre CYFRONET, Krak´ow, Poland
Keywords:
Precision Reduction, Text Classification, SVD.
Abstract:
This paper presents the analysis of the impact of a floating-point number precision reduction on the quality of
text classification. The precision reduction of the vectors representing the data (e.g. TF–IDF representation
in our case) allows for a decrease of computing time and memory footprint on dedicated hardware platforms.
The impact of precision reduction on the classification quality was performed on 5 corpora, using 4 different
classifiers. Also, dimensionality reduction was taken into account. Results indicate that the precision reduction
improves classification accuracy for most cases (up to 25% of error reduction). In general, the reduction from
64 to 4 bits gives the best scores and ensures that the results will not be worse than with the full floating-point
representation.
1 INTRODUCTION
Natural LanguageProcessing (NLP), as well as Image
Processing, is a part of Artificial Intelligence. Despite
intensive research and huge recent progress in Deep
Learning Techniques, applications of NLP have not
reached a level that would allow a construction and
a practical implementation of robots and machines
operating like humans. Such human-level solutions
would allow for seamless and smooth communica-
tion between machines and people. The future com-
munication interfaces will allow to convey informa-
tion directly to the machines processing units using
natural language (Bengio et al., 2013)(Schmidhuber,
2015)(Kumar et al., 2015). This future vision, how-
ever, requires a substantial progress in both speech
recognition and text processing domains. Applica-
tions of those two domains are in an essence very sim-
ilar and share most of the processing flow. In our re-
search (Karwatowski et al., 2015) we focus on text
processing, but the proposed modules may also be
employed in voice processing solutions.
NLP as a research and application field has been
developed in a course of last few decades (Manning
and Sch¨utze, 1999)(Collobert et al., 2011)(Hermann
∗
This research was supported in part by PLGrid Infras-
tructure.
et al., 2014)(Petrovet al., 2012). Three different mod-
els of the language representation have been estab-
lished, namely Boolean Model, Vector Space Model
(VSM) and Sparse Representation Model (Mikolov
et al., 2013a). The latter model slowly becomes a
standard for applications and systems using Natural
Language Processing (Mikolov et al., 2013b). This is
due to its superior performance, which in turn results
from the fact that it mimics the language representa-
tion within a human brain (Hawkins and Blakeslee,
2004). It is worth noting that a language as such be-
longs to a human cognition domain. It was devel-
oped by humans to enable communication and was
implemented with biological components in a neural
fashion (Mountcastle, 1997). Therefore, pure onto-
logical models of the language tend to be inferior to
the biologically–inspired ones (Hawkins and George,
2006).
Representation of knowledge within a human
brain is highly distributed, sparse and hierarchical
(Hawkins and Blakeslee, 2004)(Mountcastle, 1997).
Neural operations of cognition, which also involve
language processing, are performed using single bit
precision. Every bit of the information carries seman-
tic meaning which reflects relationships between con-
cepts acquired and stored within the brain. Inspired
by this we decided to examine to what extent it is pos-
sible to implement such a bit processing scheme on a
Wróbel, K., Wielgosz, M., Pietron, M., Karwatowski, M., Duda, J. and Smywinski-Pohl, A.
Improving Text Classification with Vectors of Reduced Precision.
DOI: 10.5220/0006641505310538
In Proceedings of the 10th International Conference on Agents and Artificial Intelligence (ICAART 2018) - Volume 2, pages 531-538
ISBN: 978-989-758-275-2
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
531

top of currently used models in NLP. We focused on
the Vector Space Model (tf-idf) as one which is pop-
ular and widely used in various applications. How-
ever, the research results may also be transferred to
the other models since all of them employ vector as a
basic representation structure. The vectors are a col-
lection of fixed or floating–point numbers which rep-
resent a certain dynamic range of a data representa-
tion. It turns out that the dynamic range, at least in
the case of floating–point numbers, is too large and
can accommodate much more information than nec-
essary. Therefore, we decided to reduce the range to
the extent that, on the one hand still preserves a re-
quired precision and on the other hand substantially
decreases the number of bits. Precision reduction of
vector representation may be perceivedas way of con-
cept generalization.
Precision reduction approach may not have sig-
nificant performance impact on standard processors,
as they typically operate on fixed data width, usu-
ally stored in IEEE–754 floating–point representa-
tion. Therefore, reduction to below standard width
or, moreover, not byte aligned width, does not intro-
duce notable speedup. The situation improves for sin-
gle instruction, multiple data (SIMD) processors, like
general–purpose computing on graphics processing
units (GPGPU), or vector CPUs however data align-
ment is still required and speedup is only achieved
through parallelism and reduction of clock cycles re-
quired to process given an amount of data. Real ben-
efits of precision reduction can be observed on fully
customizable platforms, such as field-programmable
gate arrays (FPGA) (Wielgosz et al., 2013a)(Wielgosz
et al., 2013b)(Wielgosz et al., 2012). They are not
bound to any specific bitwidth or representation. Data
may be stored in any integer bitwidth, which can also
differ between consecutive processing stages. Nar-
rower representation requires a less complicated cir-
cuit to execute calculations, which improves operat-
ing frequency. Switching to fixed point representation
further reduces circuit complexity, thus increases op-
erating frequency, which can also vary between pro-
cessing stages. Data flow architecture can also be de-
signed to process data in a parallel manner. A com-
bination of aforementioned features makes FPGA a
very interesting choice as a hardware platform. How-
ever, creating efficient design architecture and its im-
plementation are not trivial and generate interesting
research task. As authors of this paper already be-
gan work on the dedicated hardware platform and
presented their initial results in (Karwatowski et al.,
2017), we will not cover this topic. Still much ef-
fort needs to be put into FPGA implementation in or-
der to utilize its potential in NLP tasks. Additionally,
precision reduction can be perceived as an alternative
method to SVD or PCA to achieve memory footprint
reduction without drop in classification accuracy.
Consequently, the paper addressed two main ob-
jectives:
• an examination of the precision reduction impact
on the text classification results,
• proposition and practical verification of vari-
ous popular classification methods with different
grade of reduced precision,
The rest of the paper is organized as follows. Sec-
tion 2 describe a procedure of precision reduction
used in our experiments. Section 3 describes classifi-
cation parameters of the employed classifiers. Exper-
iments are presented in Section 4. Finally, we present
our conclusions in Section 5.
2 PRECISION REDUCTION
Language models are usually very large multidimen-
sional structures composed of vectors. The vectors
contain IEEE–754 floating–point numbers which can
be either stored in dense or sparse format for a sake
of a storage space utilization reduction.
We reduce precision of each vector element given
by Eq. 1:
S
single
: {±2
−126
.. .(2− 2
−23
) × 2
127
}
1×n
(1)
where S and n is a vector of IEEE–754 floating–
point numbers and its dimension, respectively.
Generated TF–IDF coefficients are in IEEE–754
double floating–point format and their values span be-
tween 0 and 1. Therefore to map these values to de-
sired fixed precision is enough to multiply them by the
maximal value possible to encode with that precision:
1. max
value = 2
bitwidth
− 1
2. for t f
id f in database :
3. norm
t f id f = ceil(t f id f ∗ max value)
after that we receive rounded values from a set:
{0,
1
2
bitwidth
.. .,1 −
1
2
bitwidth
,1}
1×n
× 2
bitwidth
− 1
(2)
Back normalization to floating–point format is
performed accordingly, only the value needs to be di-
vided by maximal value.
1. max
value = 2
bitwidth
− 1
2. for norm
value in results :
ICAART 2018 - 10th International Conference on Agents and Artificial Intelligence
532

3. value = norm value/max value
The set values after normalization are represented
by a following set:
{0,
1
2
bitwidth
.. ., 1−
1
2
bitwidth
,1}
1×n
(3)
The reduction parameter bitwidths strongly af-
fects performance results since it directly decides
about a number of bits which are left for the vector el-
ements representation. It is worth noting that it is pos-
sible to employ global dimensionality reduction tech-
niques such as SVD along with the methods proposed
in this paper. In this work, we consider the order of
these operations (precision reduction before or after
SVD) for the sake of the best final results.
3 CLASSIFICATION
In order to evaluate the influence of the precision re-
duction on the robustness of VSM model we em-
ployed them in the problem of multi-class (single-
lable) text classification. We have chosen k–nearest
neighbors algorithm (KNN), logistic regression (LR)
and support vector machines (SVM) as the tested clas-
sifiers.KNN was used with cosine similarity metric
and the number of neighbors k ∈ {1,5}. The algo-
rithm does not require training, but the testing phase
involves calculating similarity with every document.
It also needs to store all the documents from the train-
ing corpus. As such it is not well suited for large
corpora, which are much more popular in the recent
years. In LR we applied L2 regularization. SVM was
trained with hinge loss and linear kernel. Both exe-
cute iterative training and do not store documents for
testing.
For macro–averaged objective the weights associ-
ated with classes were adjusted inversely proportional
to class frequencies in the input data
w
c
=
∑
n
i
n
c
, (4)
where w
c
is a weight associated with class c and n
i
is
a number of samples in class i.
4 EXPERIMENTS AND THE
DISCUSSION
4.1 Experimental Setup
4 modules were developed in order to execute experi-
ments:
• Term frequency–inversedocument frequency was
calculated on training data without setting any
limit on the number of words.
• Precision reduction was performed on VSM rep-
resentation of documents as described in 2, where
b is the precision in bits.
• Singular value decomposition was used to reduce
the dimensionality of data, where k is the number
of components.
• 4 classifiers were used: k–nearest neighbors algo-
rithm with cosine similarity metric for k ∈ {1,5},
logistic regression and support vector machines
with linear kernel.
5 variants of experiments were performed:
• TF–IDF and Classification,
• TF–IDF, Precision reduction (b) and Classifica-
tion,
• TF–IDF, Precision reduction (b), SVD (k) and
Classification,
• TF–IDF, SVD (k) and Classification,
• TF–IDF, SVD (k), Precision reduction (b) and
Classification,
where b ∈ {16,8,7,6,5,4, 3,2, 1} and k ∈
{100, 200,300,400,500,1000}.
All results were obtained by taking an average of
5–fold cross–validation scores. Each datasets was
randomly shuffled, partitioned into 5 subsets. The
process of evaluation was repeated 5 times, with one
subset used exactly once as testing data and the rest 4
as training data.
All experiments were performed in Python us-
ing scikit–learn (Pedregosa et al., 2011) library with
default parameters. Calculations were performed
on 64–bit floating point type with 4 cores of Intel
Xeon E5–2680v3. Framework performing precision
reduction is available at:
https://github.com/
kwrobel-nlp/precision-reduction
. It deter-
mines what is the best number of bits for classifica-
tion of specified corpus. Datasets used in this work
are shared for reproducibility of results.
4.2 Datasets
Experiments were performed on multi–class (single–
label) datasets. 5 datasets are publicly available:
•
webkb - webpages collected from computer sci-
ence departments,
• r8 - Reuters articles with single label from R10
subcollection of Reuters-21578,
• r52 - Reuters articles with single label from R90
subcollection of Reuters-21578,
Improving Text Classification with Vectors of Reduced Precision
533

Table 1: Volume of datasets: number of classes, number of
documents, number of unique words, average length of doc-
uments in terms of number of words, smallest and largest
class.
Dataset webkb r8 r52 20ng cade
Classes 4 8 52 20 12
Documents 4199 7674 9100 18821 40983
Vocabulary 7770 17387 19241 70213 193997
Average number of
words in document
909 390 418 851 913
Smallest class 504 51 3 628 625
Largest class 1641 3923 3923 999 8473
Average size of
classes
1049 959 175 914 3415
Standard deviation
of sizes of classes
408 1309 613 94 2451
Relative
standard deviation
of sizes of classes
0.39 1.36 3.51 0.10 0.72
• 20ng - newsgroup messages,
• cade - webpages extracted from the CAD
ˆ
E Web
Directory.
All of them are pre–processed by (Cardoso-
Cachopo, 2007):
• all letters turned to lowercase,
• one and two letters long words removed,
• stopwords removed,
• all words stemmed.
Multi–label datasets were transformed to single–label
by removing samples with more than one class. Table
1 shows summary of corpora’s main features. Cor-
pora
webkb , r8 , r52 and 20ng are in English, cade
is in Brazilian-Portuguese. cade is the largest dataset
in terms of the number of documents, vocabulary and
average length of documents.
20ng is the most bal-
anced (0.1 relative standard deviation), others are very
skewed.
4.3 Quality Measure
The macro–averaged F1 score is used as a quality
evaluation of the experiments’ results presented in
this paper. The precision and recall for correspond-
ing classes are calculated as follows:
Precision(i) =
tp
i
tp
i
+ f p
i
, (5)
Recall(i) =
tp
i
tp
i
+ fn
i
, (6)
where tp
i
is the number of items of class i that were
classified as members of class i, f p
i
is the number of
items of class other than i that were wrongly classified
as members of class i and fn
i
is the number of items
of class i wrongly classified as members of class other
than i. The class’ F1 score is computed as harmonic
average of class precision and recall parameters.
The overall quality of the classification can be ob-
tained by taking the unweighted average F1 scores for
each class. It is given by the equation:
F1 =
1
c
∑
i
F1(i), (7)
where c is the number of all classes. The F1 score
value ranges from 0 to 1, with a higher value indicat-
ing a higher classification quality.
The error is defined as:
Error = 1− F1. (8)
The error reduction is defined as:
ErrorReduction =
(Error
ref
− Error
new
)
Error
ref
, (9)
where Error
ref
is a reference value of error and
Error
new
is the new value of error.
To compare the results with other studies, micro–
averaged accuracy is used. Micro–averaging does not
take imbalance of classes into account.
Accuracy =
∑
tp
i
n
, (10)
where n is a number of all training samples.
4.4 Results
Error values on the corpora for each classifier in func-
tion of precision bits are shown in Fig. 1. For every
dataset logistic regression and SVM obtain smaller
error than KNNs. LR and SVM are more powerful
because they model inputs (i.e. terms) in relation to
classes. Precision reduction with KNNs improves re-
sults on
webkb , r8 and 20ng datasets. KNN 5 scores
higher than KNN 1 on
webkb and cade .
Fig. 2 shows averaged error reduction among the
corpora for the classifiers. For SVM the precision
reduction is the least beneficial. It can be observed
that greater the complexity of the classifing algorithm,
the bigger the drop in accuracy. For other classifiers
macro–averaged errors decrease with the reduction of
precision down to 3 bits. However, micro–averaged
errors are the smallest for the precision of 1-3 bits.
Four times reduction of precision from 64 bits to 16
bits does not change the classification results.
Fig. 3 shows averaged error reduction measure
among the corpora for the classifiers with a precision
ICAART 2018 - 10th International Conference on Agents and Artificial Intelligence
534

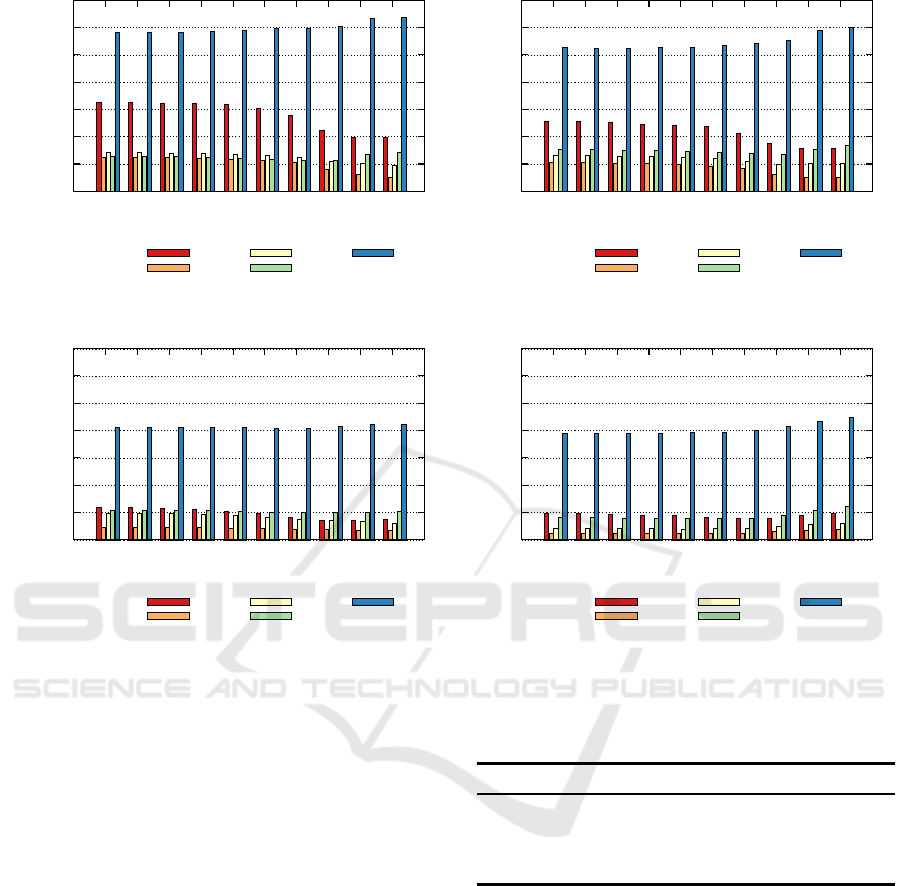
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
64 16 8 7 6 5 4 3 2 1
Error
Precision [bits]
webkb
r8
r52
20ng
cade
(a) KNN 1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
64 16 8 7 6 5 4 3 2 1
Error
Precision [bits]
webkb
r8
r52
20ng
cade
(b) KNN 5
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
64 16 8 7 6 5 4 3 2 1
Error
Precision [bits]
webkb
r8
r52
20ng
cade
(c) Logistic Regression
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
64 16 8 7 6 5 4 3 2 1
Error
Precision [bits]
webkb
r8
r52
20ng
cade
(d) SVM
Figure 1: Error values of the classifiers on the corpora in function of precision bits.
reduction after SVD. The results indicate that intro-
ducing the precision reduction after SVD generates
more errors in every case. These results prove that
sparse distributed representation of vectors is more re-
sistant for reduced precision than dense counterpart.
Fig. 4 presents F1 measure for 3 variants: TF–
IDF, TF–IDF with the best precision reduction and
TF–IDF with the best SVD. Precision reduction gives
better or similar results as applying SVD except for
KNNs on
r8 . k–nearest neighbors algorithm with
precision reduction gives similar results as raw logis-
tic regression on
r8 , r52 , and 20ng datasets. In the
raw form SVM has the best results for the English
datasets.
Fig. 5 presents comparison of F1 score on vari-
ant TF–IDF with SVD with and without precision re-
duction before SVD. Precision reduction before SVD
has always positive impact, especially seen on
webkb
dataset.
Table 2 shows overall macro–averaged F1 scores
for every classifier on each corpus. The best results
are obtained by logistic regression and SVM. Classifi-
cation of
cade is the most difficult task, the best
Table 2: Macro–averaged F1 in 5-fold cross-validation
scheme for each corpus and each classifier.
webkb r8 r52 20ng cade
KNN 1 76.54 87.47 70.76 88.56 37.17
KNN 5 80.33 86.80 66.00 86.21 42.96
Logistic Regression 92.44 93.41 81.88 90.04 55.25
Linear SVM 91.17 94.48 84.02 92.04 52.67
classifier has only 55% of F1 measure.
Table 3 shows overall micro–averaged accuracy
for every classifier on each corpus compared with
the results of SVM from (Cardoso-Cachopo, 2007)
and SVM with random search from (Puurula, 2012).
Our SVM with precision reduction is superior on 4
datasets:
webkb , r52 , 20ng and cade .
SVD is the most time consuming phase in training
in comparison to classification. However, it can re-
duce time of testing. Time of testing using KNNs is
higher than other classifiers, because it is proportional
to number of documents. Time of precision reduction
is negligible.
Improving Text Classification with Vectors of Reduced Precision
535

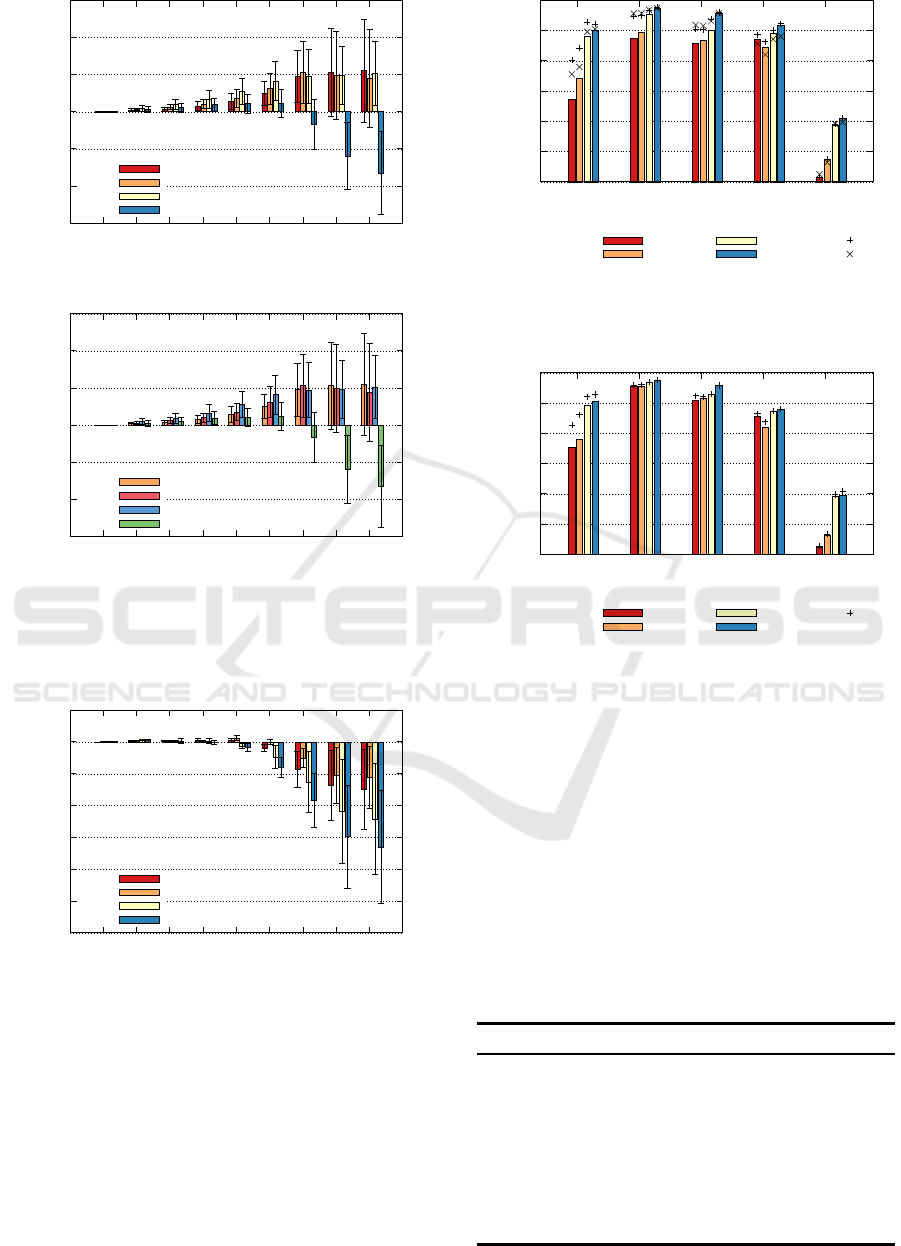
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
16 8 7 6 5 4 3 2 1
Error reduction
Precision [bits]
KNN1
KNN5
LR
SVM
(a) Macro–averaged
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
16 8 7 6 5 4 3 2 1
Error reduction
Precision [bits]
KNN1
KNN5
LR
SVM
(b) Micro–averaged
Figure 2: Average and standard deviation of error reduction
among the corpora for the classifiers in function of precision
bits.
-1.2
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
16 8 7 6 5 4 3 2 1
Error reduction
Precision [bits]
KNN1
KNN5
LR
SVM
Figure 3: Average and standard deviation of error reduction
among the corpora for the classifiers in function of precision
bits for the variant with a precision reduction after SVD.
5 CONCLUSIONS AND FUTURE
WORK
The conducted experiments show that it is benefi-
cial to the perform precision reduction on the term–
document representations. However, it is unclear
0.4
0.5
0.6
0.7
0.8
0.9
1
webkb r8 r52 ng20 cade
F1
Dataset
KNN1
KNN5
LR
SVM
Reduced
SVD
Figure 4: F1 of the classifiers on the corpora with only TF–
IDF, TF–IDF with the best precision reduction and TF–IDF
with the best SVD.
0.4
0.5
0.6
0.7
0.8
0.9
1
webkb r8 r52 ng20 cade
F1
Dataset
KNN1
KNN5
LR
SVM
Reduced
Figure 5: F1 of the classifiers on the corpora with TF–IDF
with the best precision reduction and SVD compared to TF–
IDF with SVD.
what number of bits gives the best results for the spe-
cific corpus. For some corpora, a precision reduction
to 1 bit is possible without loss of accuracy. On the
other hand it is safe to reduce the number of bits from
64 to 4, which usually improves the quality of the ob-
tained results and never leads to their degradation. As
Table 3: Micro–averaged accuracy in 5-fold cross-
validation scheme for each corpus and each classifier com-
pared to another system. SVM results are from (Cardoso-
Cachopo, 2007) and SVM with random search is from (Pu-
urula, 2012).
webkb r8 r52 20ng cade
KNN 1 80.28 94.81 90.49 88.67 41.67
KNN 5 84.30 94.99 90.28 86.36 47.47
Logistic Regression 92.78 96.57 93.89 90.04 59.07
Linear SVM 92.11 97.69 95.96 92.27 61.07
Best 92.78 97.69 95.96 92.27 61.07
SVM 86.97 97.08 95.08 91.53 53.57
SVM with
random search
92.69 97.90 95.37 84.39 60.69
ICAART 2018 - 10th International Conference on Agents and Artificial Intelligence
536

such, precision reduction seems the be very promising
result, especially combined with FPGA implemen-
tation, which should lead to significant computation
speed-up and memory footprint reduction.
The precision reduction is also a good alternative
to dimensionality reduction by SVD. It can lead to
better accuracy. This feature is specially important for
scenarios with very large vocabularies and document
data sets. If SVD is still considered, the precision re-
duction should be applied before SVD, not in oppo-
site order. It should be also observed that focusing on
micro–averaged objective allows for stronger reduc-
tion than in macro-averaged measures. It should be
noticed that reduced precision in more complex algo-
rithms leads to higher probability of drop in accuracy
because the error of data representation is propagated
through longer computational path. Therefore KNN
gives the highest gain in accuracy after precision re-
duction.
The approach developed and described in this pa-
per enables porting NLP and VSM–based solutions
to FPGA or embeded devices with reduced mem-
ory capacity or reduced precision arithmetic. This is
done through reduction of the model memory foot-
print which results from low-bit vector representation.
It is worth noting that the reduced memory occupa-
tion also affect the performance of the system, es-
pecially the response latency which is critical in em-
bedded systems. Smaller vectors mean less computa-
tions which in turn leads to lower energy consump-
tion. Further analysis will concentrate on datasets
structures and theirs impact on reduction ability and
simulations with other quantized vector space models
(e.g. log tf, boolean).
Nowadays neural networks are one of the most
popular machine learning tools used to solve NLP
problems. Our further research will be focused on
testing precision reduction on distributional represen-
tations, which are typically used as inputs to neu-
ral networks. It is not uncommon that neural net-
works have millions of parameters (e.g. Alexnet,
Resnet 152, Inception Resnet) – the reduction of pre-
cision of the vector weights is an interesting direc-
tion of research, which will be pursued in our fu-
ture work. Comparative studies on compressed deep
learning models and reduced VSM representations
with machine learning model presented in this arti-
cle can show which method need less storage and be
run in less number of cycles without significant drop
in performance.
REFERENCES
Bengio, Y., Courville, A., and Vincent, P. (2013). Repre-
sentation Learning: A Review and New Perspectives.
IEEE Transactions on Pattern Analysis and Machine
Intelligence, 35(8):1798–1828.
Bingham, E. and Mannila, H. (2001). Random projec-
tion in dimensionality reduction: Applications to im-
age and text data. In Proceedings of the Seventh
ACM SIGKDD International Conference on Knowl-
edge Discovery and Data Mining, KDD ’01, pages
245–250, New York, NY, USA. ACM.
Cardoso-Cachopo, A. (2007). Improving Methods for
Single-label Text Categorization. PdD Thesis, Insti-
tuto Superior Tecnico, Universidade Tecnica de Lis-
boa.
Collobert, R., Weston, J., Bottou, L., Karlen, M.,
Kavukcuoglu, K., and Kuksa, P. (2011). Natural lan-
guage processing (almost) from scratch. J. Mach.
Learn. Res., 12:2493–2537.
Deerwester, S., Dumais, S. T., Furnas, G. W., Landauer,
T. K., and Harshman, R. (1990a). Indexing by la-
tent semantic analysis. JOURNAL OF THE AMER-
ICAN SOCIETY FOR INFORMATION SCIENCE,
41(6):391–407.
Deerwester, S., Dumais, S. T., Furnas, G. W., Landauer,
T. K., and Harshman, R. (1990b). Indexing by latent
semantic analysis. Journal of the American society for
information science, 41(6):391.
Hawkins, J. and Blakeslee, S. (2004). On Intelligence.
Times Books.
Hawkins, J. and George, D. (2006). Hierarchical temporal
memory: Concepts, theory and terminology. Techni-
cal report, Numenta.
Hermann, K. M., Das, D., Weston, J., and Ganchev, K.
(2014). Semantic frame identification with distributed
word representations. In Proceedings of ACL. Associ-
ation for Computational Linguistics.
Karwatowski, M., Russek, P., Wielgosz, M., Koryciak, S.,
and Wiatr, K. (2015). Energy efficient calculations of
text similarity measure on FPGA-accelerated comput-
ing platforms. Lecture Notes in Computer Science,
pages 31 – 40.
Karwatowski, M., Wielgosz, M., Pietro´n, M., and Wiatr, K.
(2017). Comparison of semantic vectors with reduced
precision using the cosine similarity measure.
Kumar, A., Irsoy, O., Ondruska, P., Iyyer, M., Bradbury,
J., Gulrajani, I., Zhong, V., Paulus, R., and Socher, R.
(2015). Ask me anything: Dynamic memory networks
for natural language processing.
Manning, C. D. and Sch¨utze, H. (1999). Foundations of
Statistical Natural Language Processing. MIT Press,
Cambridge, MA, USA.
Mikolov, T., Chen, K., Corrado, G., and Dean, J. (2013a).
Efficient estimation of word representations in vector
space. CoRR, abs/1301.3781.
Mikolov, T., Yih, W., and Zweig, G. (2013b). Linguistic
regularities in continuous space word representations.
In Human Language Technologies: Conference of the
Improving Text Classification with Vectors of Reduced Precision
537

North American Chapter of the Association of Com-
putational Linguistics, Proceedings, June 9-14, 2013,
Westin Peachtree Plaza Hotel, Atlanta, Georgia, USA,
pages 746–751.
Mountcastle, V. (1997). The columnar organization of the
neocortex. Brain, 120(4):701–722.
Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V.,
Thirion, B., Grisel, O., Blondel, M., Prettenhofer,
P., Weiss, R., Dubourg, V., Vanderplas, J., Passos,
A., Cournapeau, D., Brucher, M., Perrot, M., and
Duchesnay, E. (2011). Scikit-learn: Machine learning
in Python. Journal of Machine Learning Research,
12:2825–2830.
Petrov, S., Das, D., and McDonald, R. (2012). A universal
part-of-speech tagset. In Proc. of LREC.
Puurula, A. (2012). Combining Modifications to Multino-
mial Naive Bayes for Text Classification, pages 114–
125. Springer Berlin Heidelberg, Berlin, Heidelberg.
Robertson, S. E., Walker, S., Jones, S., Hancock-Beaulieu,
M. M., Gatford, M., et al. (1995). Okapi at trec-3. Nist
Special Publication Sp, 109:109.
Salton, G., Wong, A., and Yang, C.-S. (1975). A vector
space model for automatic indexing. Communications
of the ACM, 18(11):613–620.
Schmidhuber, J. (2015). Deep learning in neural networks:
An overview. Neural Networks, 61:85–117.
Wielgosz, M., Jamro, E.,
˙
Zurek, D., and Wiatr, K. (2012).
FPGA Implementation of the Selected Parts of the Fast
Image Segmentation, pages 203–216. Springer Berlin
Heidelberg, Berlin, Heidelberg.
Wielgosz, M., Panggabean, M., and Rønningen, L. A.
(2013a). Fpga architecture for kriging image interpo-
lation. International Journal of Advanced Computer
Science and Applications (IJACSA), 4(12):193—201.
Wielgosz, M., Panggabean, M., Wang, J., and Rønningen,
L. A. (2013b). An FPGA-based platform for a net-
work architecture with delay guarantee. Journal of
Circuits, Systems and Computers, 22(6):1350045–1—
1350045–20.
ICAART 2018 - 10th International Conference on Agents and Artificial Intelligence
538