The Wrong Tool for Inference

A Critical View of Gaussian Graphical Models

Kevin R. Keane and Jason J. Corso

Computer Science and Engineering, University at Buffalo, SUNY, Buffalo, New York, U.S.A.

Electrical Engineering and Computer Science, University of Michigan, Ann Arbor, Michigan, U.S.A.

Keywords:

Multivariate Normal Distributions, Gaussian Graphical Models, Degenerate Priors.

Abstract:

Myopic reliance on a misleading ﬁrst sentence in the abstract of Covariance Selection

Dempster (1972)

spawned the computationally and mathematically dysfunctional Gaussian graphical model (GGM). In stark

contrast to the GGM approach, the actual (Dempster, 1972, § 3) algorithm facilitated elegant and powerful ap-

plications, including a “texture model” developed two decades ago involving arbitrary distributions of 1000+

dimensions Zhu (1996). The “Covariance Selection” algorithm proposes a greedy sequence of increasingly

constrained maximum entropy hypotheses Good (1963), terminating when the observed data “fails to reject”

the last proposed probability distribution. We are mathematically critical of GGM methods that address a

continuous convex domain with a discrete domain “golden hammer”. Computationally, selection of the wrong

tool morphs polynomial-time algorithms into exponential-time algorithms. GGMs concepts are at odds with

the fundamental concept of the invariant spherical multivariate Gaussian distribution. We are critical of the

Bayesian GGM approach because the model selection process derails at the start when virtually all prior mass

is attributed to comically precise multi-dimensional geometric “conﬁgurations” (Dempster, 1969, Ch. 13). We

propose two Bayesian alternatives. The ﬁrst alternative is based upon (Dempster, 1969, Ch. 15.3) and (Hoff,

2009, Ch. 7). The second alternative is based upon Bretthorst (2012), a recent paper placing maximum entropy

methods such as the “Covariance Selection” algorithm in a Bayesian framework.

1 INTRODUCTION

Gaussian graphical models (GGMs) have a nice inter-

pretation: the absence of an edge implies conditional

independence between the corresponding pair of vari-

ables (Whittaker, 1990, Ch. 6). Both the search based

GGM approach, for example Jones et al. (2005);

Moghaddam et al. (2009); Wang et al. (2011) and,

the l

regularization based GGM approach, for exam-

ple Dahl et al. (2005); Meinshausen and B

uhlmann

(2006); Banerjee et al. (2006); Yuan and Lin (2007);

Friedman et al. (2008) focus on interpretation and ex-

ploitation of the pairwise Markov property. Given an

undirected dependency graph G = (V,E) with node

set V and edge set E for a set of random variables X ,

two variables x

and x

are independent given all other

variables X

V \{ j,k}

if the edge { j,k} is not in the edge

set E,

⊥⊥ X

| X

V \{ j,k}

if { j,k} /∈ E . (1)

“The covariance structure of a multivariate normal popu-

lation can be simpliﬁed by setting elements of the inverse

of the covariance matrix to zero.”

A zero in the precision matrix elements ( j, k) and

(k, j) corresponds to { j,k} /∈ E. We are concerned

that certain fundamental Gaussian and Bayesian con-

cepts fade from consciousness with myopic focus on

these graph representations of the multivariate Gaus-

sian distribution.

2 GAUSSIAN GRAPHICAL

MODELS

The concept of a ﬁnite enumeration of graphs (Whit-

taker, 1990, Ch. 6) clouds the natural characterization

of the multivariate Gaussian as an invariant spheri-

cal distribution (Dempster, 1969, Ch. 12). A graph’s

structure corresponds to strict constraints on the an-

gles among the random variables. Adhesion to the

original coordinates of a data set is at odds with a typi-

cal approach for multivariate Gaussian analysis where

measured data x ∼ N (µ,Σ) is translated, rotated and

scaled y = Σ

−

(x − µ) to equivalent linear combina-

470

Keane, K. and Corso, J.

The Wrong Tool for Inference - A Critical View of Gaussian Graphical Models.

DOI: 10.5220/0006644604700477

In Proceedings of the 7th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2018), pages 470-477

ISBN: 978-989-758-276-9

tions which are independent and normally distributed

y ∼ N(0,I). The concept of search over a discrete

space is at odds with geometric exploitation of a con-

tinuous convex distribution.

2.1 Imposition of Graph Structure

Conditional independence corresponds to a precise

alignment of the measured variables. Even in a man-

made setting – sensors in a building – the simple logic

and attractiveness of a GGM may not prevail Gonza-

lez and Hong (2008):

We can see that adding the graphical interpre-

tation gave slightly worse predictions than us-

ing just the kernel function. One explanation

may be that the graph does not accurately re-

ﬂect the conditional independence structure of

the room. For example, all sensors near win-

dows were linked by the outside temperature

and therefore not conditionally independent

even though the ﬂoor plan does not suggest

strong spatial linkage between them.

We are somewhat sympathetic to the attractiveness of

specifying a GGM in scenarios with comparable ex-

ogenous structural information. But, we will make

two points. First, the graph in Gonzalez and Hong

(2008) was not obtained by search over 2

(p−1)p/2

can-

didate graphs, but from architectural plans. Second,

constraining inference to the graph did not yield su-

perior performance. We greatly appreciate access to

this experimental result as it effectively illustrates our

concern with GGMs: the focus on pairwise interac-

tion and desperate desire to specify models that “make

sense” risks misspeciﬁcation for subtle factors.

2.1.1 Relative Alignment of Variables

The off-diagonal elements of the variance matrix

specify the relative alignment of a pair of ran-

dom variables. Consider the case of two zero

mean, unit variance Gaussian variables. The vari-

ance σ

implies an angle γ

between the two vari-

ables since σ

= E(x

· x

) = E(|x

||x

|cos (γ

)) =

cos(γ

) = cos(γ

). When x

⊥⊥ x

, σ

cos(γ

) = 0, and the variables are independent.

When a GGM’s graph omits one or more edges from

the complete graph, a rigid alignment of the variables

is imposed. Point estimates for continuous parameters

such as γ

should raise a large red ﬂag for Bayesians;

but, we will delay that discussion to Section 3.

2.2 Adhesion to the Initial Basis

Multivariate Gaussian inference is fundamentally

based upon the concept of a spherical distribution that

is invariant under all linear transformations which

carry an origin-centered sphere into itself (Dempster,

1969, Ch. 12.2). A concept of special coordinates,

including the original coordinates of the data set, is

problematic. GGMs appear to be stuck in the original

coordinates whereas a change of basis is a fundamen-

tal technique in analysis of Gaussian data.

2.2.1 Univariate Change of Basis

The concept of the standard normal distribution is

widely understood. To display a histogram of x ∼



µ,σ



observations, the mean µ is subtracted, and

the data is scaled by its standard deviation σ to ob-

tain y ∼ N (0,1), y =

x − µ

. To sample the distribu-

tion of x, standard normal variate y is obtained, scaled,

and translated to yield x = σy + µ. This ﬂuid change

of basis — well known for univariate data — applies

equally to multivariate data.

2.2.2 (Dempster, 1969, Thrm. 12.4.1)

Suppose that X has the N(µ

µ,Σ

Σ) distribution

where X and µ

µ have dimensions 1 × p and Σ

is a p × p positive deﬁnite, or semi-deﬁnite,

symmetric matrix of rank q ≤ p. Suppose

that ∆

∆

∆ is any p × q matrix such that Σ

Σ = ∆

∆

∆∆

∆

and suppose that Γ

Γ is a pseudoinverse of ∆

∆

∆.

Then Y = (X −µ

µ)Γ

has the N(0,I) distribu-

tion where Y, 0, and I have dimensions 1 × q,

1 × q, and q ×q, respectively. Furthermore, X

may be recovered from Y with probability 1

using X = µ

µ + Y∆

∆

The GGM community appears opposed to (Demp-

ster, 1969, Thrm. 12.4.1) and stuck in arbitrary mea-

surement bases. This makes no sense for the mul-

tivariate Gaussian distribution with readily accessi-

ble, analytically attractive coordinates. All the GGM

discussions of decomposable and non-decomposable

graphs are a red herring. The conventional and sim-

ple mathematical approach to analyzing multivariate

Gaussian data is to translate, rotate, and scale the data

to a multivariate standard normal distribution which is

trivial to manipulate and interpret. Inference compu-

tations for graphs with no edges, the N(0, I) graphs,

are trivial.

The Wrong Tool for Inference - A Critical View of Gaussian Graphical Models

471

2.2.3 Discarding Information

In an experimental setting, more likely than not the

subtle factors are unknown. The problem with incom-

plete graphs in measurement coordinates is that the

sample statistics corresponding to missing edges on

the graph are discarded – an obstructive approach to

inference. Maximum entropy and Bayesian methods

begin with a simple distribution typically character-

ized by a diagonal precision matrix and incorporate

structure as justiﬁed by the data. It is an entirely dif-

ferent approach to discard sample statistics that do not

conform to an arbitrary graph.

GGM methods that set elements of the precision

matrix to zero is in direct opposition to the spirit

of the “Covariance Selection” maximum entropy al-

gorithm where constraints are introduced when the

data demands doing so as determined by a statisti-

cal test. Setting precision matrix elements to zero

risks destruction of subtle (and not so subtle) structure

in data sets. (Dempster, 1972, Introduction, second

paragraph) warns “errors of misspeciﬁcation are in-

troduced because the null values are incorrect.” (Tib-

shirani, 1996, § 11(c)) identiﬁes a similar problem for

subset selection in the presence of a “large number of

small effects”. (West and Harrison, 1997, Ch. 16.3.1)

warns (emphasis theirs) “These factors, that dominate

variations at the macro level, often have relatively lit-

tle apparent effect at the disaggregate level and so

are ignored.” Our fear is that the pairwise removal of

structure corresponds to a scenario where one “can’t

see the forest for the trees.” Starting with a diagonal

precision matrix and adding structure demonstrably

necessary seems more prudent.

2.3 Computational Considerations

A ﬁnal complaint we will raise for the search based

GGM approach is the acceptance of exponential-time

discrete search algorithms when a distribution deﬁned

by a log quadratic density function should clearly ex-

ploit more efﬁcient polynomial-time algorithms. This

appears to be an example of a discrete “golden ham-

mer” inappropriately applied to a continuous convex

domain.

3 BAYESIAN GAUSSIAN

GRAPHICAL MODELS

Bayesians typically prefer minimally informative pri-

ors and produce posterior distributions, not point es-

timates or points with probability mass. For all

GGM graphs except the complete graph, one or more

natural parameters are constrained to a point or set

of points which would be expected to reﬂect true

continuous parameter values with probability zero.

In high dimension, the concept of a uniform prior

over the graphs (Giudici and Green, 1999, § 1.2)

results in the allocation of virtually all prior mass,



(p−1)p/2

− 1



(p−1)p/2

, to point estimates for the

continuous natural parameters.

3.1 Bayesian Model Selection

Giudici and Green (1999) utilize a model selection

framework described by MacKay (1992). There are

(p−1)p/2

potential graphs for p-variables. Giudici

and Green (1999) limit consideration to d decompos-

able graphs, therefore the uniform prior for the graph

g is:

P(g) = d

−1

. (2)

In Figure 1, Giudici and Green (1999) would assign

priors for the graphs:

p(G

) = p (G

) =

(3)

The problem from a Bayesian perspective is that as-

signing probability mass to a graph assigns probabil-

ity mass to a point in the natural parameters. The pri-

ors for continuous model parameter θ given the graph

g, illustrated in Figure 2, are:

p(θ|G

) =











if θ =

π ,

if θ =

π ,

0 otherwise.

(4)

p(θ|G

) =

2π

dθ . (5)

We ﬁnd the model parameter prior p (θ|G

) ob-

jectionable. Trading technical precision for intuition,

we consider p (θ|G

) to be a degenerate prior

. To

the extent p(θ|G

) is justiﬁable, we would propose

consideration of an equally “justiﬁable” inﬁnite class

of Sure Thing hypotheses (attributed to E.T. Jaynes in

MacKay, 1992, p. 12) with unit mass at θ =

π +

φ, φ ∈ [0,2π].

A degenerate distribution places all probability mass on

one point; we mean to describe a broader concept inclu-

sive of mixtures of degenerate and non-degenerate distri-

butions characterized by probability mass greater than zero

occurring at a ﬁnite set of points.

ICPRAM 2018 - 7th International Conference on Pattern Recognition Applications and Methods

472

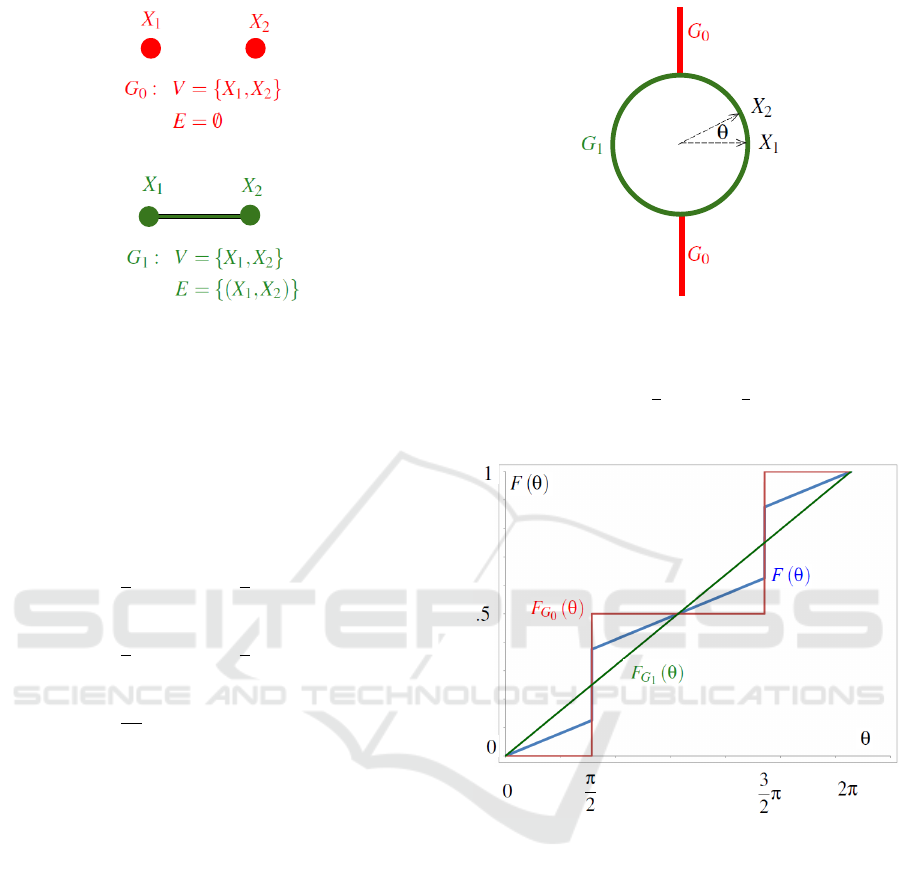
Figure 1: An enumeration of the Gaussian graphical mod-

els for the bivariate normal distribution. Graph G

corre-

sponds to independent normal variables x

and x

. Graph

corresponds to the general case where covariance struc-

ture between normal variables x

and x

is unrestricted.

Equation 3 deﬁnes the “uniform prior” for these two graphs

(Giudici and Green, 1999, § 1.2).

Figure 2: Geometric interpretation of the relative alignment

parameter θ for a bivariate standard normal distribution.

1 2

= E (x

· x

) = E(|x

||x

|cos(θ)) = cos (θ).

Equation 4 permits θ =

π and θ =

π for G

;

Equation 5 permits 0 ≤ θ ≤ 2π for G

The unconditional prior p(θ) illustrated in Fig-

ure 3 is:

p(θ) = p (θ|G

) p (G

) + p(θ|G

) p (G

) (6)











if θ =

π ,

if θ =

π ,

4π

dθ otherwise.

(7)

We ﬁnd priors assigning point mass to continuous pa-

rameters objectionable. With that caveat, the remain-

der of the Bayesian GGM model comparison frame-

work proceeds as follows. The evidence P(X |g) for

structure g is:

P(X|g) =

P(X|θ,g)P (θ|g)dθ , (8)

and the probability of graph g given the data X is:

P(g|X) ∝ P(X|g)P(g) . (9)

We like the Bayesian model selection approach in

MacKay (1992) and the more recent computational

advances in Skilling (2004). However, Bayesian

GGM approach never gives the process a fair shake.

The number of graphs is 2

(p−1)p/2

. Assuming a uni-

form prior over the graphs as proposed in Giudici and

Green (1999),



(p−1)p/2

− 1



(p−1)p/2

≈ 1 of the prior mass is as-

signed to speciﬁed points for the continuous natural

parameters. Any ﬁnite set of points should collec-

tively have zero probability with a “reasonable prior”

Figure 3: A “uniform prior” on the graphs in Figure 1 re-

sults in a “degenerate prior” for θ in Figure 2. p(θ|G

)

deﬁned in Equation 4, p(θ|G

) deﬁned in Equation 5, and

p(θ) deﬁned in Equation 7. Cumulative probability F (φ) =

p(θ)dθ.

(for continuous parameters). We view the Bayesian

GGM priors as so inequitable, only an unrealistic

number of observations n → ∞ will mitigate its effect.

4 RELATED ARGUMENTS

The beauty of Bayesian methods is the ability to gen-

erate reasonable inference from “complex” models

with limited data. Andrew Gelman’s blog provides

many insightful comments and references relevant to

The Wrong Tool for Inference - A Critical View of Gaussian Graphical Models

473

the issues we wrestle with in this paper. A number

of lively, good natured debates on the blog encour-

aged the use of “complex”

models. We view sparse

GGMs as a misguided attempt to maintain parsimony

and simplicity. The following comments encouraged

us to question the wisdom of pursuing simplicity or

parsimony with GGMs.

Gelman (2004) identiﬁes (Neal, 1996, pp. 103-

104) as a favorite quote:

Sometimes a simple model may outperform a

more complex model, at least when the train-

ing data is limited. Nevertheless, I believe

that deliberately limiting the complexity of the

model is not fruitful when the problem is evi-

dently complex. Instead, if a simple model is

found that outperforms some particular com-

plex model, the appropriate response is to de-

ﬁne a different complex model that captures

whatever aspect of the problem led to the sim-

ple model performing well.

A comment that appears speciﬁcally related to our

discomfort with uniform priors over the graphs and

point mass distributions for continuous model param-

eters appears in Gelman (2011):

The Occam applications I don’t like are the

discrete versions such as advocated by Adrian

Raftery and others, in which some version of

Bayesian calculation is used to get results say-

ing that the posterior probability is 60%, say,

that a certain coefﬁcient in a model is exactly

zero. I’d rather keep the term in the model and

just shrink it continuously toward zero.

Gelman (2013) nicely clariﬁed that over-ﬁtting is

not attributable to ﬂexibility alone (i.e. the complete

graph in GGMs):

Overﬁtting comes from a model being ﬂexible

and unregularized. Making a model inﬂexible

is a very crude form of regularization. Often

we can do better.

5 PREFERABLE METHODS

5.1 Option One

For high dimensional Gaussian inference we ﬁrst

suggest a full Bayesian implementation as outlined

in (Dempster, 1969, Ch. 15.3) and its equivalent

(Hoff, 2009, Ch. 7). Starting with a prior for the

We put “complex” in quotes because its not clear that high

dimensionality alone equates to complexity; and, a log

quadratic density certainly is not that “complex.”

mean p (µ) ∼ N (µ

,Λ

) and the variance p(Σ) ∼

inverse-Wishart



−1



, the conditional posterior

distributions are:

p(µ|x

,... , x

,Σ) ∼ N(µ

,Λ

) (10)

p(Σ|x

,... , x

,µ) ∼ inverse-Wishart



−1



(11)

where



−1

+ nΣ

−1



−1

(12)

= Λ



−1

+ nΣ

−1



(13)

= ν

+ n (14)

= S

+ S

(15)

∑

i=1

− µ)(x

− µ)

(16)

The joint posterior p (µ, Σ|x

,... , x

) is available from

a Gibbs sampler using these conditional distributions

Equation 10 and Equation 11.

5.1.1 Implementation Considerations

Transforming the sampling problem to a set of in-

dependent variables, (Dempster, 1969, Thrm. 12.4.1)

quoted in subsubsection 2.2.2 facilitates straight for-

ward parallel implementation of Equation 10 and

Equation 11 in a Gibbs sampler. Sherman-Morrison-

WoodburyBindel (2009) will be helpful in computing

−1

in Equation 11 and Λ

in Equation 12, treating

the n  p samples as low n rank updates to the p × p

diagonal matrices S

−1

and Λ

respectively.

5.2 Option Two

The second alternative where both p and n are very

large would be to use a maximum entropy algorithm.

Assuming streaming data, one would deﬁne a set of

domain speciﬁc marginals of interest – for example,

the ﬁlters in Zhu (1996) and the gene regulatory net-

work modules in Celik et al. (2014). We would then

implement a maximum entropy algorithm beginning

with the identity matrix and use the framework of

Bretthorst (2012) to determine a posterior distribu-

tion for both the number of constraints and the range

of Lagrange multiplier values deﬁning the synthe-

sized distribution. Bretthorst (2012) nicely demon-

strates Bayesian inference of the appropriate number

of marginal constraints and inference as to the distri-

bution of Lagrange multipliers enforcing a particular

constraint. A ﬁnal consideration in a dynamic envi-

ronment would be a method to gracefully forget past

observations – perhaps randomly removing one ob-

servation at each iteration to keep a recent weighted

constant size sample; or perhaps weighting the obser-

vations vectors directly for a ﬁnite horizon.

ICPRAM 2018 - 7th International Conference on Pattern Recognition Applications and Methods

474

6 CONCLUSION

The dominant discrete theme of GGM obscures

the continuous convex properties of the multivariate

Gaussian distribution. Restricting inference to a par-

ticular graphical model obstructs accumulation of in-

formation describing the underlying distribution. For

Bayesian GGMs, uniform priors over the graphs re-

sults in extremely concentrated probability mass in

the natural parameters.

We support the use of GGMs for interpretation

and communication of approximate inference results

from multivariate Gaussian distributions. We strongly

discourage the use of GGMs directly for multivariate

Gaussian inference.

REFERENCES

Banerjee, O., Ghaoui, L. E., d’Aspremont, A., and Nat-

soulis, G. (2006). Convex optimization techniques for

ﬁtting sparse gaussian graphical models. In Proceed-

ings of the 23rd international conference on Machine

learning, pages 89–96. ACM.

Bindel, D. (2009). Sherman-Morrison-Woodbury. Matrix

Computations (CS 6210), Cornell University lecture.

Bretthorst, G. (2012). The maximum entropy method of

moments and Bayesian probability theory. In 32nd

International Workshop on Bayesian Inference and

Maximum Entropy Methods in Science and Engineer-

ing, Carching, Germany, pages 3–15.

Celik, S., Logsdon, B., and Lee, S. (2014). Efﬁcient di-

mensionality reduction for high-dimensional network

estimation. In Proceedings of the 31st International

Conference on Machine Learning (ICML-14), pages

1953–1961.

Dahl, J., Roychowdhury, V., and Vandenberghe, L. (2005).

Maximum likelihood estimation of Gaussian graphi-

cal models: numerical implementation and topology

selection. Technical report, Department of Electrical

Engineering, University of California, Los Angeles.

Dempster, A. (1969). Elements of continuous multivariate

analysis. Addison-Wesley.

Dempster, A. (1972). Covariance selection. Biometrics,

pages 157–175.

Dobra, A. and West, M. (2004). Bayesian covariance selec-

tion. Duke Statistics Discussion Papers, 23.

Fan, J., Feng, Y., and Wu, Y. (2009). Network exploration

via the adaptive lasso and scad penalties. The Annals

of Applied Statistics, 3(2):521.

Friedman, J., Hastie, T., and Tibshirani, R. (2008). Sparse

inverse covariance estimation with the graphical lasso.

Biostatistics, 9(3):432–441.

Gelman, A. (2004). Against parsimony. [Online; accessed

15-April-2015].

Gelman, A. (2011). David MacKay and Occam’s Razor.

[Online; accessed 15-April-2015].

Gelman, A. (2013). Flexibility is good. [Online; accessed

20-May-2015].

Giudici, P. and Green, P. (1999). Decomposable graph-

ical Gaussian model determination. Biometrika,

86(4):785–801.

Gonzalez, J. and Hong, S. (2008). Linear-time in-

verse covariance matrix estimation in Gaussian pro-

cesses. Technical report, Computer Science Depart-

ment, Carnegie Mellon University.

Good, I. J. (1963). Maximum entropy for hypothesis

formulation, especially for multidimensional contin-

gency tables. The Annals of Mathematical Statistics,

34(3):911–934.

Hoff, P. (2009). A ﬁrst course in Bayesian statistical meth-

ods. Springer Science & Business Media.

Jalobeanu, A. and Guti

errez, J. (2007). Inverse covariance

simpliﬁcation for efﬁcient uncertainty management.

In 27th MaxEnt workshop, AIP Conference Proceed-

ings, Saratoga Springs, NY.

Jones, B., Carvalho, C., Dobra, A., Hans, C., Carter, C., and

West, M. (2005). Experiments in stochastic computa-

tion for high-dimensional graphical models. Statisti-

cal Science, 20(4):388–400.

Knuiman, M. (1978). Covariance selection. Advances in

Applied Probability, pages 123–130.

Lian, H. (2011). Shrinkage tuning parameter selection in

precision matrices estimation. Journal of Statistical

Planning and Inference, 141(8):2839–2848.

MacKay, D. (1992). Bayesian methods for adaptive models.

PhD thesis, California Institute of Technology.

Meinshausen, N. and B

uhlmann, P. (2006). High-

dimensional graphs and variable selection with the

lasso. The Annals of Statistics, pages 1436–1462.

Moghaddam, B., Marlin, B., Khan, M., and Murphy, K.

(2009). Accelerating Bayesian structural inference

for non-decomposable Gaussian graphical models. In

NIPS.

Neal, R. (1996). Bayesian Learning for Neural Networks.

Springer.

Skilling, J. (2004). Nested sampling. Bayesian Inference

and Maximum Entropy Methods in Science and Engi-

neering, 735:395–405.

Tibshirani, R. (1996). Regression shrinkage and selection

via the lasso. Journal of the Royal Statistical Society.

Series B (Methodological), pages 267–288.

Wang, H., Reeson, C., and Carvalho, C. (2011). Dynamic

ﬁnancial index models: Modeling conditional depen-

dencies via graphs. Bayesian Analysis, 6(4):639–664.

West, M. and Harrison, J. (1997). Bayesian forecasting and

dynamic models. Springer Verlag.

Whittaker, J. (1990). Graphical models in applied multi-

variate statistics. John Wiley & Sons Ltd.

Yuan, M. and Lin, Y. (2007). Model selection and esti-

mation in the Gaussian graphical model. Biometrika,

94(1):19–35.

Zhu, S. (1996). Statistical and computational theories

for image segmentation, texture modeling and object

recognition. PhD thesis, Harvard University.

The Wrong Tool for Inference - A Critical View of Gaussian Graphical Models

475

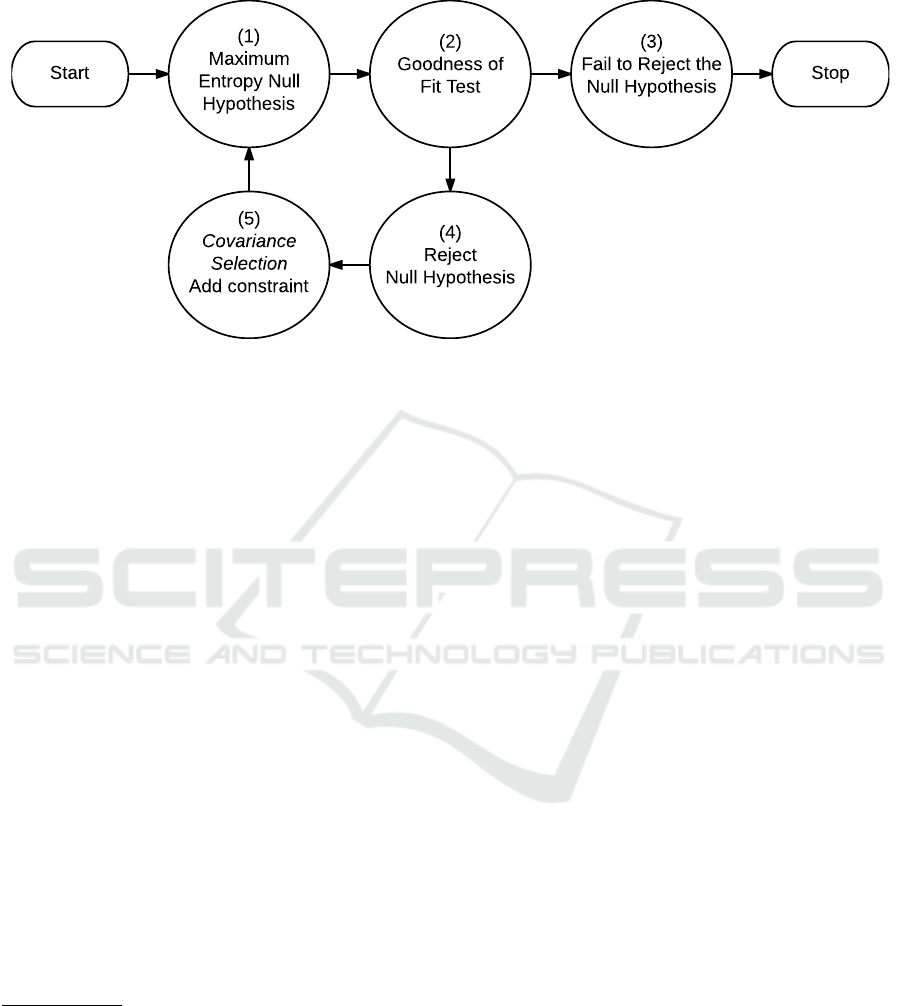
APPENDIX

Start Stop

(1)

Maximum

Entropy Null

Hypothesis

(2)

Goodness of

Fit Test

(3)

Fail to Reject the

Null Hypothesis

(4)

Reject

Null Hypothesis

(5)

Covariance

Selection

Add constraint

Figure 4: “Covariance Selection” algorithm. “The principle of maximum entropy generates much of statistical mechanics as

a null hypothesis, to be tested by experiment” (Good, 1963, p. 912). The above diagram is the algorithm demonstrated in

Dempster (1972). The diagram accurately describes the algorithm appearing in Zhu (1996).

The Covariance Selection Algorithm

The ﬁrst sentence of the abstract (Dempster, 1972,

Summary) is misleading:

The covariance structure of a multivariate nor-

mal population can be simpliﬁed by setting el-

ements of the inverse of the covariance matrix

to zero.

With respect to the demonstrated algorithm in

(Dempster, 1972, § 3), the widely repeated assertion

that “covariance selection” inserts zeros in a precision

matrix

is false. Non-zero entries are placed in a pre-

cision matrix as covariance constraints are added to

a maximum entropy distribution. The matrices gen-

erated are maximally sparse, with non-zeros corre-

sponding to statistically signiﬁcant structure in the ob-

served data.

The technique demonstrated in (Dempster, 1972,

§ 3) is not about setting elements of the precision ma-

trix (inverse of the covariance matrix) to zero. As

shown in Figure 4, the technique is as follows: 1)

propose a maximum entropy distribution for the “null

hypothesis”; 2) test the “null hypothesis” using ob-

served data; 3) if you “fail to reject the null hypothe-

For example, (“setting concentrations (elements of the in-

verse covariance matrix) to zero” Knuiman, 1978); (“spec-

iﬁes that certain elements in the inverse of the variance ma-

trix are zero” Whittaker, 1990, p. 11); (“by setting to zero

selected elements of the precision matrix” Dobra and West,

2004); (“setting to zero some of the elements of the inverse

covariance matrix” Jalobeanu and Guti

errez, 2007); (“set-

ting some elements of the precision matrix to zero” Fan

et al., 2009) (“simpliﬁed the matrix structure by setting

some entries to zero.” Lian, 2011)

sis,” STOP; otherwise, 4) “reject the null hypothesis;”

5) “Covariance Selection” – add a covariance con-

straint requiring the proposed distribution match the

observed distribution for the marginal with the worst

discrepancy, this augmented proposal is a new “null

hypothesis,” loop to step 1.

Sparsity in the Precision Matrix

Sparsity is a pervasive topic in papers citing Demp-

ster (1972). It is important to observe that the algo-

rithm directly constructs sparse precision matrices.

The maximum number of zeros in the precision ma-

trix occurs at initialization, when the precision matrix

and the variance matrix for the proposed distribution

are both diagonal. Under duress, as a sequence of

proposed models are rejected by the observed data,

“Covariance Selection” adds non-zeros to the preci-

sion matrix. In Table 1, we provide a sequence of cor-

relation matrices that match each stage of (Dempster,

1972, § 3 Tbl. 1 and system output) exactly and we

provide the corresponding sequence of inverse corre-

lation matrices to clarify the non-zero ﬁll pattern to

show that the maximum entropy algorithm in “Co-

variance Selection” deﬁnes sparse precision matrices

by construction.

Replicating the Covariance Selection Example

In Table 1, we are able to fully replicate (Dempster,

1972, § 3 Tbl. 1 and system output) using the algo-

rithm deﬁned in Figure 4 by selecting for inclusion

the pair (i, j) = arg max

(i, j)

i, j

− Σ

i, j

| in algorithm step

ﬁve “Covariance Selection”.

ICPRAM 2018 - 7th International Conference on Pattern Recognition Applications and Methods

476

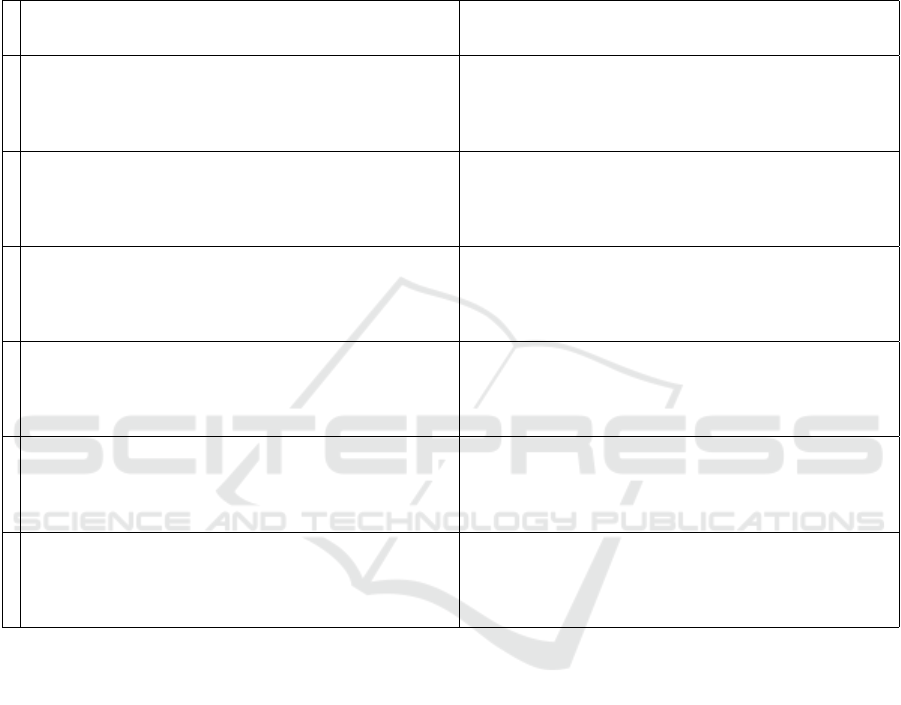
Table 1: Using the algorithm in Figure 4 and specifying at each iteration a covariance constraint for the variable pair with

the maximum absolute discrepancy between the observed covariance s

i j

and the synthesized covariance σ

i j

, the column Σ

below exactly replicates the output of (Dempster, 1972, § 3). Although more iterations are shown in Dempster (1972) and

below, Dempster suggests stopping the algorithm after stage 5 based upon a statistical signiﬁcance test. We provide for review

the precision matrices at each stage. Note in the “Covariance Selection” algorithm only one symmetric pair of non-zeros (in

bold) enters the precision matrix Σ

−1

at each iteration. The algorithm of Dempster (1972) is widely misrepresented as “setting

elements of the precision matrix to zero.” Clearly, zeros reside in the precision matrix Σ

−1

from initialization, dropping out

as constraints are imposed.

−1

1.000000

1.279033 0.597405

0.597405 1.279033

1.000000

1.000000 -0.467075

-0.467075 1.000000

1.000000

1.273150 0.589712

1.000000

1.279033 0.597405

0.589712 0.597405 1.552183

1.000000

1.000000 0.216345 -0.463192

1.000000

0.216345 1.000000 -0.467075

-0.463192 -0.467075 1.000000

1.000000

1.459781 -0.470598 0.589712

-0.470598 1.186631

1.000000

1.279033 0.597405

0.589712 0.597405 1.552183

1.000000

1.000000 0.396583 0.216345 -0.463192

0.396583 1.000000 0.085799 -0.183694

1.000000

0.216345 0.085799 1.000000 -0.467075

-0.463192 -0.183694 -0.467075 1.000000

1.000000

1.617232 -0.470598 -0.426898 0.589712

-0.470598 1.186631

-0.426898 1.157451

1.279033 0.597405

0.589712 0.597405 1.552183

1.000000

1.000000 0.396583 0.368826 0.216345 -0.463192

0.396583 1.000000 0.146270 0.085799 -0.183694

0.368826 0.146270 1.000000 0.079794 -0.170837

0.216345 0.085799 0.079794 1.000000 -0.467075

-0.463192 -0.183694 -0.170837 -0.467075 1.000000

1.000000

1.617232 -0.470598 -0.426898 0.589712

-0.470598 1.186631

-0.426898 1.157451

1.279033 0.597405

0.589712 0.597405 1.706470 0.422009

0.422009 1.154287

1.000000 0.396583 0.368826 0.216345 -0.463192 0.169344

0.396583 1.000000 0.146270 0.085799 -0.183694 0.067159

0.368826 0.146270 1.000000 0.079794 -0.170837 0.062458

0.216345 0.085799 0.079794 1.000000 -0.467075 0.170763

-0.463192 -0.183694 -0.170837 -0.467075 1.000000 -0.365602

0.169344 0.067159 0.062458 0.170763 -0.365602 1.000000

The Wrong Tool for Inference - A Critical View of Gaussian Graphical Models

477