The Role of a Discontinuous Free-Electron Density in

Harmonic Generation from Metal Surfaces

Michael Scalora

, Maria Vincenti

, Domenico de Ceglia

, Neset Akozbek

, Mark Bloemer

Jose Trull

and Crina Cojocaru

Charles M. Bowden Research Center, AMRDEC, RDECOM, Redstone Arsenal, AL 35898-5000, U.S.A.

Department of Information Engineering, University of Brescia, Via Branze 38, 25123 Brescia, Italy

National Research Council, AMRDEC, Charles M. Bowden Research Center, Redstone Arsenal, AL 35898-5000, U.S.A.

AEgis Technologies Inc., 401 Jan Davis Dr. 35806, Huntsville, AL, U.S.A.

Departament de Física i Enginyeria Nuclear, Universitat Politècnica de Catalunya,

Rambla Sant Nebridi, 08022 Terrassa, Spain

Keywords: Harmonic Generation, Nonlinear Frequency Conversion, Plasmonics, Electron Cloud, Metal Optics.

Abstract: We discuss a dynamical model of harmonic generation that arises from surfaces that demarcate regions of

discontinuous free electron densities. These circumstances can arise from a simple metal mirror, to more

complex structures such as layered structures composed of different metals or a metal and a conducting

oxide. Using a modified hydrodynamic model we examine the simple case of a metal mirror, assuming the

surface is characterized by an electron cloud that spills out into vacuum and shields the internal portions of

the remaining medium. We also assess the relative importance of additional nonlinear sources that arise

when a free electron discontinuity is present, and show that under the right circumstances both second and

third harmonic generation can be very sensitive to the nature, density and thickness of the free electron

cloud. Our findings suggest the possibility to control surface harmonic generation through surface charge

engineering.

1 INTRODUCTION

The study of second harmonic generation (SHG)

from surfaces has simultaneously captivated and

frustrated researchers since the early days of

nonlinear optics: captivated because it is an ideal

tool to study surfaces; frustrated because while

different theoretical models may yield similar

angular dependence of the generated SH signal,

there is disagreement on the magnitude of the

predicted SH signal, with results sometimes

differing by several orders of magnitude. It may be

said that this apparent, model-dependent

inconsistency is perhaps symptomatic of a

combination of incomplete knowledge of surface

composition and the relative importance of a number

of unfolding physical phenomena. When the

material in question is centrosymmetric, as for noble

metals, or if it generally lacks a bulk second order

nonlinear coefficient, SHG is particularly sensitive

to surface properties such as roughness, sample

thickness, deposition methods, dielectric constant,

and other prominent surface features that may be

accidental or otherwise. For example, the resulting

electron effective mass appears to be somewhat

sensitive to the particular deposition method

employed (Dryzek and Czapla, 1985). Through the

detection of surface plasmon modes, it has also been

shown that a simple metal layer may be denser on

the side of the substrate compared to the air side,

leading to a position dependent dielectric function

(Maaroof et al., 2009) and large discrepancies

between actual and tabulated values. At the same

time, the dielectric “constant” itself may become a

function of both frequency and wave vector via the

excitation of nonlocal effects, e.g. electron gas

pressure (Sipe et al., 1980; Sipe and Stegeman,

1982).

In addition to questions regarding deposition

processes and surface preparation, substantial issues

have been raised about the methods employed in

predicting the electrodynamics that unfolds in

nanoscale systems. Over the years, technological

progress has led to a steady miniaturization

Scalora, M., Vincenti, M., Ceglia, D., Akozbek, N., Bloemer, M., Trull, J. and Cojocaru, C.

The Role of a Discontinuous Free-Electron Density in Harmonic Generation from Metal Surfaces.

DOI: 10.5220/0006645800980104

In Proceedings of the 6th International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS 2018), pages 98-104

ISBN: 978-989-758-286-8

progression that has produced devices having near-

atomic size, in turn generating questions about the

very applicability of classical electrodynamics at

those length scales. Classical electrodynamics is

based on a process that turns the rapidly fluctuating

microscopic fields found near individual atoms into

macroscopic fields averaged over a volume of space

that may contain myriad of such atoms, or dipoles,

so much so that the medium loses its granularity and

becomes a continuum, necessitating only the mere

application of boundary conditions (Jackson, 1999).

If unaltered, this simplified picture obviously fails if

the macroscopic theory is in turn applied to systems

with features that are only a few atomic diameters in

size. This is already the case for typical nanowire

and/or nanoparticle systems that are now easily

fabricated with features so small and so closely

spaced that the electronic wave functions spilling

outside their respective surfaces may begin to

overlap. The diameter of a typical noble metal atom

is approximately 3Å (Fig. 1), while the electronic

cloud forming and shielding a flat, noble metal

surface may extend several Ås into free space.

The study of light interactions with optically

thick metal layers (mirrors) below their plasma

frequencies (long wavelengths), where the dielectric

constant is negative, is limited only to the study of

reflection due to the large negative dielectric

constant and the absence of propagation modes. At

the nanometer scale, transmission through thick

structures that may contain a large total metal

thickness (100nm or more) has been shown to be

possible by exploiting simple cavity/interference

phenomena and surface plasmon excitation (Ebbesen

et al., 1998). The typical, linear optical response of

metals is modelled almost exclusively using the

simple Drude model, which assumes the metal is

essentially a cloud of free electrons that responds

and is driven by an incident electric field. The

resulting dielectric response then depends only on

frequency.

Free electron systems like Indium Tin Oxide

(ITO) or Cadmium Oxide (CdO) are characterized

by absorption that is smaller compared to that of

noble metals, especially in the range where the real

part of the dielectric constant crosses the axis and

takes on near-zero values. The consequences of

these peculiar dispersive properties are important

because they can trigger novel, low-intensity

nonlinear optical phenomena that usually require

high local fields may be of some relevance to

surface harmonic generation and thus shed new light

on the process. The mechanism is triggered by the

requirement that the longitudinal component of the

displacement vector of a TM-polarized field be

continuous, which for homogeneous, flat structures

is exemplified by the relationship:

in in out out





()in out



is the dielectric constant inside (outside) the

medium, and

()

in out

is the corresponding

longitudinal component of the electric field

amplitude inside (outside) the material. It is easy to

see that if





, it follows that

E 

Additionally, nonlocal effects in these materials can

become more pronounced compared to noble metals,

as both field penetration inside the medium and field

derivatives are correspondingly more prominent,

leading to significant deviations from the predictions

of local electromagnetism. For subnanometer

spacing between metal objects quantum tunnelling

phenomena have to be taken into account.

As a representative example, we start our

discussion with the seemingly simple problem of a

gold film interface as seen from the atomic scale. In

Fig. 1a we depict a typical noble metal atom, which

is characterized by a nearly-free, s-shell electron that

orbits at an approximate distance r

~ 1.5Å from the

nucleus, and d-shell electrons whose orbits extend

out approximately r

~ 0.5Å from the nucleus. The

simple picture that emerges even from a cursory

look at Fig.1b, which schematically represents atoms

distributed at and just below the surface of a

hypothetical metallic medium, is one of a negatively

charged electron cloud that spills outside the ionic

surface (the dashed line in Fig. 1b) and screens the

inside portions of the metal. Upon further reflection

it becomes obvious that the interior sections of the

medium contain a combination of free and bound

charges, which are schematically shown in Fig. 1c

and are represented as Lorentz oscillators, which

present their own surface to the incoming

electromagnetic wave. Therefore, it becomes

plausible to assume that the reasons for the

discrepancies between experimental results and most

theoretical models, and between theoretical models

themselves, may to some extent reside in the failure

to accurately describe the spatial distribution of the

electron cloud that spills outside the medium’s ionic

surface, to account for all surfaces (free and bound

electrons alike) in and around the transition region

indicated by the dashed line. In addition, nonlinear

optical phenomena due to anharmonic spring

behavior is necessarily confined to the volume

below the dashed line in Fig. 1, i.e. the free electron

gas shields nonlinear third order effects arising from

bound electrons.

The Role of a Discontinuous Free-Electron Density in Harmonic Generation from Metal Surfaces

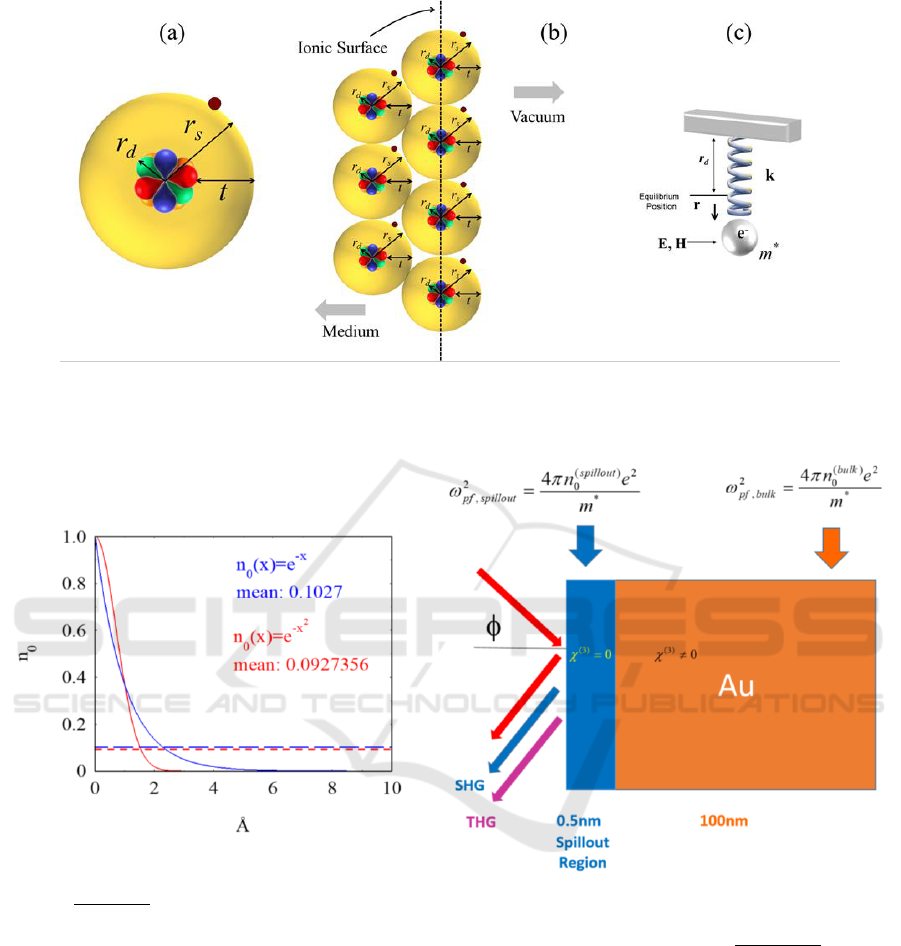
Figure 1: (a) A typical noble metal atom. The radii represent the maximum amplitude of orbital wave functions calculated

using a many-body approach. (b) The dashed line represents a perfectly aligned last row of atoms in a medium that extend

to the left. (c) Schematic representation of bound, d-shell electrons as nonlinear Lorentz oscillators.

Figure 2: Left Panel: depiction of two types of exponential decay of the electron cloud that covers the metal surface. Both

decays yield a mean density approximately 10% of the value at the hard, ionic surface, i.e. the dashed line in Fig. 1. The

main difference between the two density profiles is the spatial extension into vacuum, i.e. 2Å-5Å. Right Panel: Once the

average density and spatial extension into vacuum have been chosen, the electromagnetic problem is solved by introducing

two surfaces and an external layer that contains only free charges, and an internal medium that is now screened and contains

both free and bound charges. The bulk, third order nonlinear coefficient is assumed to originate only in bound charges,

which are described as collections of nonlinear Lorentz oscillators.

2 THE MODEL

It can be shown that for real metals the charge

density decays exponentially with distance from the

ionic surface (Lang and Kohn, 1970; Lang and Kohn

1971; Kenner et al., 1972). Therefore, we adopt a

similar model, at first assuming some type of

exponential decay of the free charge density from

the surface (Fig. 2, left panel and relative inset), and

subsequently assigning average value and thickness

to an external charge density that in our modified

vision forms a single, uniform layer composed only

of free charges (see Fig. 2, right panel). Fig. 2 shows

the modified configuration of Fig. 1.

PHOTOPTICS 2018 - 6th International Conference on Photonics, Optics and Laser Technology

100

A gold mirror may thus be thought of as a two-

layer system: a free electron layer between 0.2Å-

0.5Å thick that covers the remaining thickness of

material where one finds a mix of both free and

bound electrons. Of course, a similar free-electron

layer should be considered on the right side of the

mirror, but its effects are negligible for thick layers.

For the moment we assume the bulk, third order

nonlinear coefficient is intrinsic to bound, d-shell

electrons described as nonlinear Lorentz oscillators,

depicted in Fig. 1c, which as indicated above

shielding occurs. However, free electrons are also

capable of generating a third harmonic signal via a

cascaded process. Therefore, the classical

description that we weave together attacks the

problem as a classical boundary value problem

where the composition of individual layers and their

thicknesses are chosen according to the quantization

of atomic orbitals. The local dielectric constant of

the free electron layer is Drude-like and given by:

( ) 1



pf spillout

spillout





  

(1)

,pf spillout



is the plasma frequency and



is the

related damping coefficient. The local dielectric

constant of the interior bulk section also contains a

Drude portion that describes free electrons, and at

least two Lorentz oscillator contributions (this

allows one to model a more accurate medium

response down to approximately 200nm or so) that

take into account the contribution to the dielectric

constant by d-shell electrons, as follows:

2 2 2 2

01 01 02 02

( ) 1





   

pf bulk

bulk





  



       

(2)

1,2p



are the bound electrons’ plasma frequencies

and

01,2



the related damping coefficients. As we

will see below, in addition to bound electrons the

total linear dielectric function is

augmented/modified dynamically by an additional

term, a second order spatial derivative of the free

electron polarization that describes electron gas

pressure in the two relevant regions of space

depicted in Fig. 2. Most of what occurs at the

surface and the evolution of the harmonically

generated signals may, under the right

circumstances, be determined entirely by the density

of the thin, external layer of free charges. The full

dynamical equation of motion that describes

harmonic generation from the free electron gas only,

modified to account for a discontinuous charge

density (i.e. a spatial derivative,) nonlocal effects,

magnetic contributions and convection may be

written as follows:

 

   

 

0 0 0 0

* * 2 * 2

0 0 0





  •  







  •  • 







 •     •











f f f

f f f f

f f f

n e e e

m m c m c

n e n



  



E P E P B

P P P P

P P P

(3)

where

is the free electron polarization;

and

are the propagating electric and magnetic fields,

respectively;

is the free electron’s effective mass;

is the background charge density with no applied

field;

is the Fermi energy; c is the speed of light

in vacuum. The equation is scaled with respect to

dimensionless time, longitudinal and transverse

coordinates (2-D),

/,ct





/,z





/,yy





respectively, where

1 m





is chosen as a

convenient reference wavelength. The effect of a

discontinuous free charge density between the

external and internal free electron distributions is

described by a new term that appears inside the

bracketed expression on the right hand side, i.e.

 

nn•PP

. Eq.(3) represents a simple

Drude model when









is the only driving

term, augmented by a number of linear and

nonlinear source terms as follows: the magnetic

Lorentz force,

 

e m c



PH

; a Coulomb

term,

 

e m c



 •EP

that describes

redistribution of free charges at and near each

boundary, according to the strength of the

derivatives; convective terms,

     

f f f f f f





•  •  •











P P P P P P

where, as stated earlier, the last term is newly

derived; and a linear electron gas pressure term

proportional to

 

 • P

that leads to a k-

dependent dielectric constant. Similarly to Eq.(3),

The Role of a Discontinuous Free-Electron Density in Harmonic Generation from Metal Surfaces

101

each species of bound electrons is described by a

nonlinear oscillator equation of the following type:

 

1 01 1 01 1 1 1 1 1

01 0 0

* 2 * 2

   •

  

n e e

m c m c





P P P P P P

E P H

(4)

Bound electrons are characterized by their own

effective mass,

; resonance frequency,



;

density,

; damping,



; and third order nonlinear

spring constant

, which as the form suggests, is

generally proportional to

(3)



and leads directly to

self-phase modulation and third harmonic

generation. Ultimately, the material equations of

motion yield a polarization that is the vectorial sum

of each contribution, namely

...

Total f

   P P P P

, which is in turn inserted

into Maxwell’s equations to solve for the dynamics.

3 RESULTS: GOLD MIRROR

In Fig. 3 we show the typical behavior of SH

conversion efficiency vs. incident angle when the

internal and external electron densities are identical

(no density discontinuities), for incident pulses tuned

to three different carrier wavelengths. The

calculations are carried out by simultaneous

integration of Eqs.(3-4) together with Maxwell’s

equations. Each vector equation contains one spatial

component for each coordinate, and one for each

harmonic. We note that curve shape does not change

much for the three cases, except for slight shifts of

the maximum as field penetration changes with

incident wavelength. These shapes are similar to the

shapes predicted by other models (Sipe et al., 1980;

Sipe and Stegeman, 1982).

On the other hand, the predicted maximum

conversion efficiencies can differ dramatically

compared to other models and to experimental

results (Akhmediev et al., 1994; O’Donnell and

Torre, 2005), unless significant adjustments are

made to free and bound effective electrons masses

and densities. Alternatively, since effective masses

and densities are often known precisely and are not

usually taken as free parameters, one may look at the

subtleties of surface composition, i.e. density and

thickness of the outer patina, as discussed above, in

an attempt to reconcile predictions and observations.

In Fig. 4a we show the results of a calculation of

SH conversion efficiencies as a function of the free

electron layer density in the spillout region, for

electron cloud layer thickness of 0.5nm and angle of

incidence fixed at 68°. This angle corresponds to the

approximate location of maximum SH efficiency in

Fig. 3. We also contrast the results with and without

the new, extra convective term that includes the

spatial derivative of the free electron density

highlighted above.

Figure 3: Second Harmonic conversion efficiency vs

incident angle for 100fs pulses incident on a gold mirror,

tuned as indicated in the color-coded caption, as a function

of incident angle. Peak pump intensity is approximately

2GW/cm

Two distinct peaks appear, at

0.13

spillout bulk

nn

and

0.03

spillout bulk

nn

: these values correspond to

( ) 0





and

(2 ) 0





, respectively, resulting in

an increase in conversion efficiency between four

and six orders of magnitude compared to the case

where there is no spillout region (no density

discontinuity, which is indicated by the solid blue

line,) due to the enhancement of the local fields at

the respective





conditions. The impact of the

extra convective nonlinear term in the equations of

motion is also clear, with conversion efficiencies

that can change by as much as two orders of

magnitude. The results summarized in Figs. 4 thus

strongly suggest that variations in surface layer

charge density can have significant consequences on

the predicted outcome. In fact, it is reasonable to

assume that the disposition of surface charges will

be different for every sample fabricated, due to

different conditions that may evolve inside the

fabrication chamber, possibly due to local

temperature and pressure fluctuations that lead to

accidental roughness and thus, different effective

local parameters. The issue of THG from the gold

mirror is also as interesting and perhaps as subtle as

SHG. As mentioned earlier, the outer free electron

patina is not assumed to possess an intrinsic third

PHOTOPTICS 2018 - 6th International Conference on Photonics, Optics and Laser Technology

102

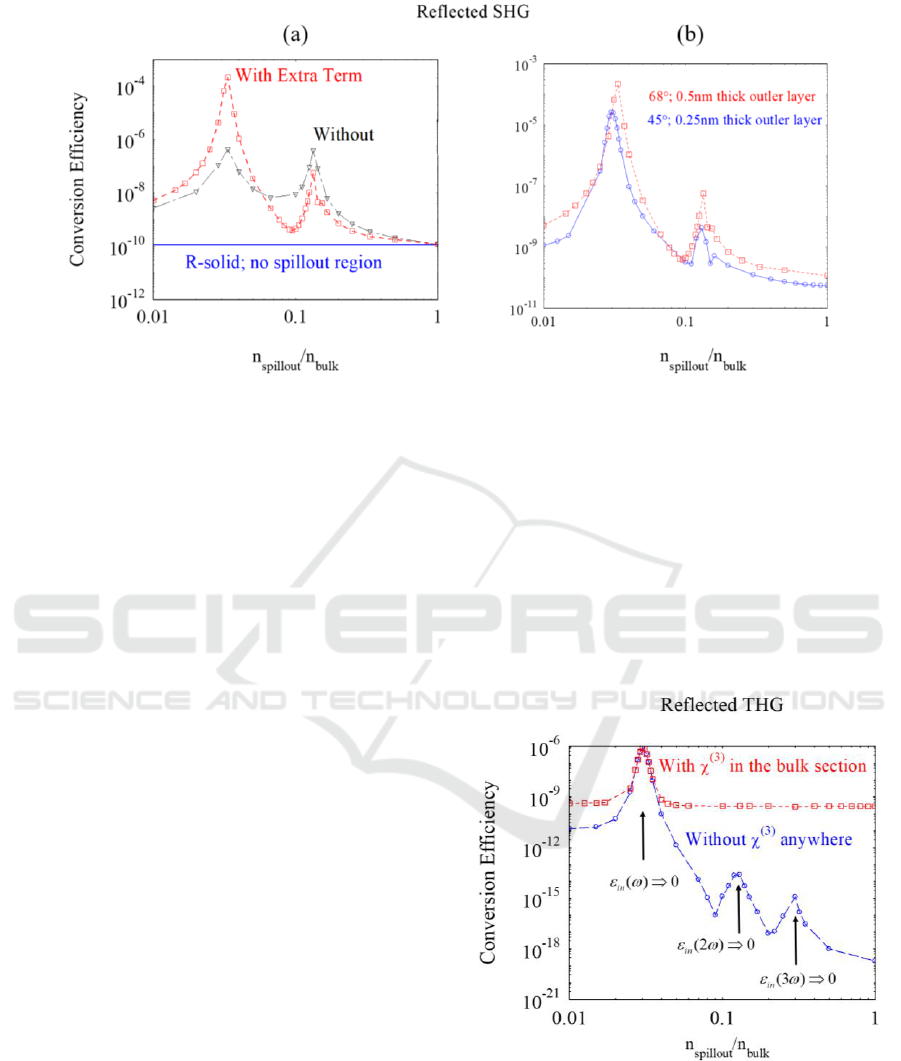
Figure 4: (a) Reflected second harmonic conversion efficiency for 50fs pulses incident at 68° on the gold mirror shown in

Fig. 2, which contains an external free-electron-only layer of variable density. (b) Comparison of the results in (a) with a

different angle of incidence and thinner outer free electron layer. The outer electron density drives the interaction, not the

thickness.

order coefficient, b (proportional to

(3)



), but it can

nevertheless trigger THG via a frequency mixing

that evolves from explicit nonlinear sources present

on the right side of Eq.(3), namely convection,

Coulomb, and magnetic Lorentz components.

Normally, however, the presence of a bulk b

anywhere inside the structure overwhelms these

contributions, so much so that surface generated (i.e.

free electron) THG can always be neglected. Here,

we report that surface generated THG can in fact

overwhelm the TH signal produced by the bulk,

provided the right conditions are met: for example, if

the density of the outer layer is such that the

condition

( ) 0





is met for the pump field. To

demonstrate this we perform calculations in both the

presence and in the absence of a bulk

(3)



, which in

our specific case means a non-zero b coefficient in

Eq. 4, as a function of outer layer density, and report

the results in Fig. 5. When the bulk nonlinearity is

present (

0b 

), the reflected TH signal is predicted

to displays a single peak, which occurs near the

( ) 0





condition. Removing the bulk nonlinearity

(

0b 

everywhere) reveals two additional, surface

generated TH peaks of much lower amplitude,

whose locations correspond to the two remaining

conditions that tend to maximize TH conversion

efficiency:

(2 ) 0





and

(3 ) 0





, which as

mentioned earlier, produce amplified local fields.

The fact that the maximum produced by the

( ) 0





condition persists even after b is set equal

to zero signifies that this particular TH peak is

independent of

, and is solely due to surface

phenomena, while the remaining two peaks are

easily overwhelmed. While satisfying the

( ) 0





at the pump field appears to yield the most efficient

conversion efficiency, designing a surface charge

having those characteristics is probably an arduous

process, given the much reduced surface charge

density required.

Figure 5: Reflected third harmonic conversion efficiency

for 50fs pulses incident at 45° on the gold mirror shown in

Fig. 2 as a function of free-electron-only layer of variable

density, with and without a bulk nonlinearity. When the

condition

( ) 0





is satisfied for the outer free electron

gas layer, THG displays a maximum in either case. This is

an indication that surface THG dominates even in the

presence of a non-zero bulk

coefficient.

The Role of a Discontinuous Free-Electron Density in Harmonic Generation from Metal Surfaces

103

4 CONCLUSIONS

We have shown that surface harmonic generation

from a simple gold mirror can be a very sensitive

function of the parameters that characterize the

external free electron cloud that spills outside the

ionic surface and screens the internal portions of the

medium. In addition our calculations suggest that a

discontinuous free electron gas density can introduce

nonlinear, convective sources that can significantly

increase/modify nonlinear conversion efficiencies.

These results demonstrate that it may well be

possible to engineer a surface charge and actively

control it through charge injection to maximize

harmonic generation for a number of technological

applications.

REFERENCES

Akhmediev, N. N., Mel’nikov, I. V. and Robur, L. J.

(1994). Second-Harmonic Generation by a Reflecting

Metal Surface", Laser Physics 4(6), p.1194; O’Donnell

K. A. and Torre, R. (2005). Characterization of the

second-harmonic response of a silver–air interface",

New Journal of Physics 7(1), p.154.

Dryzek, J. and Czapla, A. (1985). Free-electron

parameters of sputtered noble metal films. Journal of

Materials Science Letter, 4 p.154.

Ebbesen, T. W., Lezec, H. J., Ghaemi, H. F., T. Thio, T.

and Wolff P. A., (1998). Extraordinary

optical transmission through sub-wavelength hole

arrays. Nature, 391(6668), p.667.

Jackson, J. D. (1999). The Classical Electromagnetic

Field (Wiley, New York).

Lang, N. D. and Kohn, W. (1970). Theory of Metal

Surfaces: Charge Density and Surface Energy,

Physical Review B, 1(12), p. 4555; Lang, N. D. and

Kohn, W. (1971). Theory of Metal Surfaces: Work

Function. Physical review B, 3(4), p.1215; Kenner, V.

E., Allen, R. E. and Saslow, W. M. (1972). Screening

of external fields and distribution of excess charge

near a metal surface. Physics Letters A, 38(4) p.255.

Maaroof, A.I., Gentle, A., Smith, G. B. and Cortie, M. B.

(2009). Bulk and surface plasmons in highly

nanoporous gold films. Journal of physics D: Applied

Physics, 40 (18), p.5675.

Sipe, J. E., So, V. C. Y., Fukui, M. and Stegeman, G. I.

(1980). Analysis of second-harmonic generation at

metal surfaces, Physical Review B, 21(10) p 4389;

Sipe, J. E. and Stegeman, G. I. (1982). In Surface

Polaritons: Electromagnetic Waves at Surfaces and

Interfaces, edited by V. M. Agranovich and D. Mills

North-Holland, Amsterdam.

PHOTOPTICS 2018 - 6th International Conference on Photonics, Optics and Laser Technology

104