Dimensionality Reduction with Evolutionary Shephard-Kruskal

Embeddings

Oliver Kramer

Department of Computer Science, University of Oldenburg, Oldenburg, Germany

Keywords:

Dimensionality Reduction, Iterative Learning, Evolutionary Optimization, Shephard-Kruskal Measure.

Abstract:

This paper introduces an evolutionary iterative approximation of Shephard-Kruskal based dimensionality re-

duction with linear runtime. The method, which we call evolutionary Shephard-Kruskal embedding (EvoSK),

iteratively constructs a low-dimensional representation with Gaussian sampling in the environment of the la-

tent positions of the closest embedded patterns. The approach explicitly optimizes the distance preservation

in low-dimensional space, similar to the objective solved by multi-dimensional scaling. Experiments on a

small benchmark data set show that EvoSK can perform better than its famous counterparts multi-dimensional

scaling and isometric mapping and outperforms stochastic neighbor embeddings.

1 INTRODUCTION

Dimensionality reduction (DR) is the important prob-

lem class in machine learning that offers methods

for reducing the data dimensionality to a reason-

able degree, e.g., for preprocessing in classiﬁca-

tion or for data space visualization (Lee and Verley-

sen, 2007). Many DR methods compute a point-

wise embedding of high-dimensional patterns based

on different criteria. Prominent examples are princi-

pal component analysis (PCA) (Jolliffe, 1986), ker-

nel PCA (Sch

olkopf et al., 1998), multi-dimensional

scaling (MDS) (Borg and Groenen, 2005), isomet-

ric mapping (ISOMAP) (Tenenbaum et al., 2000),

and t-distributed stochastic neighbor embedding (t-

SNE) (van der Maaten and Hinton, 2008). With grow-

ing data set sizes, methods are required that scale well

with the number of patterns.

In dimensionality reduction we seek for low-

dimensional representations z

∈ R

for each high-

dimensional pattern x

∈ R

with i = 1, . . . , N and d <

q without losing essential information. This infor-

mation can be distances between patterns, or neigh-

borhoods of patterns, which should be maintained in

low-dimensional space. This paper presents an ap-

proach that iteratively constructs a low-dimensional

representation with evolutionary Gaussian sampling

for minimizing the Shepard-Kruskal measure in each

step.

The paper is structured as follows. Section 2 gives

an introduction to related work while introducing a

short taxonomy of iterative evolutionary embedding

methods. Section 3 introduces the novel EvoSK ap-

proach. It is experimentally evaluated in Section 4

and compared to MDS, ISOMAP, and t-SNE. Con-

clusions are drawn in Section 5 with an overview of

prospective future work.

2 RELATED WORK

Many DR algorithms have been introduced that pro-

cess data sets pattern by pattern. They are also known

as incremental or streaming methods. But for the

class of DR methods, only few variants have been in-

troduced in the past, e.g., a variant of PCA that is able

to process streaming data (Mitliagkas et al., 2013).

MDS computes the embeddings based on a Cholesky

or singular value decomposition resulting in eigenval-

ues, whose eigenvectors with the q-largest eigenval-

ues are the low-dimensional embeddings.

The line of research on methods that iteratively

construct a solution with stochastic sampling has

recently been established (Kramer, 2015a; Kramer,

2015b). It began as variant of unsupervised regres-

sion. Figure 1 shows a small taxonomy of this

emerging ﬁeld. All variants have in common that

they iteratively construct an embedding based on ran-

domly sampling in the environment using Gaussian

sampling. The latent positions of the closest em-

bedded patterns are the origin of this sampling pro-

478

Kramer, O.

Dimensionality Reduction with Evolutionary Shephard-Kruskal Embeddings.

DOI: 10.5220/0006645904780481

In Proceedings of the 7th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2018), pages 478-481

ISBN: 978-989-758-276-9

[e.g. Shepard-Kruskal,

co-ranking]

mapping

unsupervised regression

DR measures

supervised regression

iterative evolutionary embeddings

[e.g. UKR, UNN]

[e.g. nearest neighbors]

Figure 1: Taxonomy of iterative evolutionary embedding.

cess. Methods from the three branches differ in

the selection criterion they employ. The left part of

the taxonomy is based on the reconstruction error

of unsupservised regression. Unsupervised regres-

sion maps patterns from the low-dimensional space

to the high-dimensional space using a multi-label re-

gression method (Meinicke et al., 2005). The op-

timization problem is to optimally reconstruct the

high-dimensional patterns. Unsupervised nearest

neighbors (Kramer, 2015b) employs nearest neigh-

bor regression, while unsupervised kernel regression

(UKR) is based on the Nadaraya-Watson estimator.

The middle part of the taxonomy is based on the

optimization of embeddings using label information.

Instead of the reconstruction error, it makes use of the

regression error, i.e., the low-dimensional patterns are

optimized to achieve the same regression error as their

high-dimensional counterparts (Kramer, 2015a).

The right part of the taxonomy is new and the ﬁrst

approach in this line of research is introduced in this

paper. We propose the employment of DR measures

like the Shephard-Kruskal measure or the co-ranking

matrix (Hastie et al., 2009).

3 SHEPHARD-KRUSKAL

EMBEDDINGS

This section introduces the evolutionary Shephard-

Kruskal embedding approach, which is called EvoSK

in the following. Similar to the approaches that have

been introduced for the iterative evolutionary embed-

dings of unsupervised regression, the mechanism is

introduced inductively.

Let X = [x]

i=1

be the patterns that have to be em-

bedded. The ﬁrst pattern x

is embedded at an arbi-

trary position in latent space, e.g., at the origin z

= 0.

At this time the current latent matrix is Z = [z

] with

a corresponding pattern matrix X = [x

]. Now, let

, . . . , x

n−1

be the sequence of embedded patterns

with corresponding latent positions z

, . . . , z

n−1

. Pat-

tern x

with n ≤ N is embedded by ﬁrst searching for

the closest embedded pattern

∗

= arg min

x=x

n−k

,...,x

− xk

(1)

among the last k embedded patterns X = [x

]

n−1

j=n−k

We call parameter k window size in the following.

Based on its latent position z

∗

, µ candidate positions

∗

, . . . , z

∗

are sampled using the Gaussian distribu-

tion

∼ N (0, σ) with

∗

= z

∗

(2)

for l = 1, . . . , µ. For preservation of distances between

patterns in low-dimensional space the standard devi-

ation σ = kx

− x

∗

k is used for the sampling process,

i.e., large distances result in large σ, small distances

in sample close to z

∗

From the µ candidate latent positions, the one

leading to the lowest Shepard-Kruskal error E

is se-

lected. E

measures the maintenance of distances in

the low dimensional space (Hastie et al., 2009). Let

be the distance matrix in data space and D

be the

distance matrix in the low-dimensional space. Both

contain the pairwise Euclidean distances and are con-

sidered as normalized. The Shepard-Kruskal measure

is deﬁned as the norm of the differences of the nor-

malized distance matrixes

= kD

− D

. (3)

A low Shepard-Kruskal measure is preferable. For

example, if distances are completely preserved, the

Shepard-Kruskal measure is zero.

Figure 1 shows the pseudocode of the EvoSK ap-

proach. The search for the closest pattern in Line 4 re-

duces to a constant runtime, if window size k does not

depend on N, as the number of considered compar-

isons in high-dimensional space does not grow with

the number of embedded patterns. Further, the inner

loop of µ sampling steps obviously also require a con-

stant time.

Algorithm 1: Pseudo-code of EvoSK.

Require: X, µ

Z = [0], X = [x

]

for n = 2 to N do

choose x

select closest pattern x

∗

among X = [x

]

n−1

j=n−k

with latent position z

∗

for l = 1 to µ do

∗

∼ σ · N (z

∗

, 1) with σ = kx

− x

∗

end for

choose z

= arg min

z=z

∗

,...,z

∗

E([Z, z])

Z = [Z, z

], X = [X, x

]

end for

return Z

For k = n the approach has quadratic runtime of

O(N

). If data structures are applicable like ball-trees

Dimensionality Reduction with Evolutionary Shephard-Kruskal Embeddings

479

that allow a neighborhood search in log(N) the run-

time reduces to O(N log N). For a constant window

size of k the search can be performed in k or even

log(k) steps offering a linear runtime of O(N).

4 EXPERIMENTS

In this section, we analyze the DR pipeline evolu-

tion experimentally on a small set of benchmark prob-

lems. For this sake, we concentrate on an experimen-

tal comparison between EvoSK, MDS, ISOMAP, and

t-SNE. The control methods and data sets (with ex-

ception of the Wind data set) are based on SCIKIT-

LEARN (Pedregosa et al., 2011).

Table 1 shows the Shephard-Kruskal measure E

of EvoSK with best, mean, standard deviation, and

worst values of 100 runs and a comparison to MDS,

ISOMAP, and t-SNE. The experiments use a window

size of k = 50 and all data sets use the ﬁrst N = 200

patterns. The results show that EvoSK performs bet-

ter in mean than MDS and ISOMAP on Digits, and

on Friedman. On Image, only some runs, in partic-

ular the best one of EvoSK is better than the MDS

and the ISOMAP result. However, on Housing and

on the Wind data set, MDS and ISOMAP outper-

form EvoSK, while t-SNE is clearly outperformed by

EvoSK on all data sets.

Our further experimental analysis has shown that

the choice of k has no signiﬁcant impact on the

achieved Shephard-Kruskal measure as of 10% of N.

Obviously the orientation to the last few embedded

patterns is sufﬁcient, as the sampling process is more

important for the decision, at which position the pat-

terns should be embedded.

0 5 10

15 2520 30

EvoSK

(a) Digits

0 5 10

15 2520 30

EvoSK

(b) Image

Figure 2: Analysis of number µ of sampling steps in each

iteration on the data sets Digits and Image.

An analysis of the search effort invested into the

sampling process shows Figure 2. For the data sets

Digits and Image, E

is shown depending on the

number µ of sampling steps in each iteration. It turns

out that E

is decreasing signiﬁcantly with increasing

µ. Few more sampling steps are beneﬁcial and more

lead to less improvements. The best and worst E

de-

velopments deviate from the mean only slightly on all

data sets indicating that this dependency is signiﬁcant.

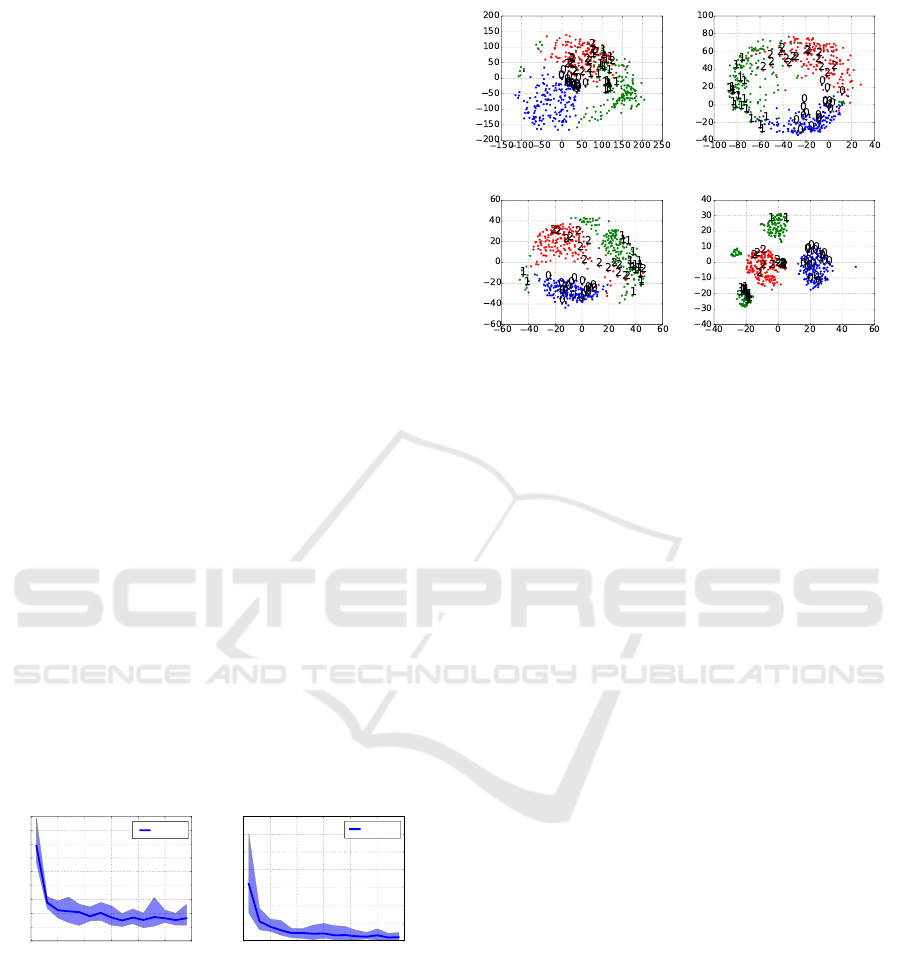
(a) EvoSK, µ = 2 (b) EvoSK, µ = 10

Figure 3: Visualization of embeddings of the Digits data set

with EvoSK employing µ = 2, 10 sampling steps in compar-

ison to MDS and t-SNE.

In Figure 3 we visualize the embeddings of

EvoSK. The plots show a comparison between the

embeddings of EvoSK with the sampling sizes µ =

2, 10 with MDS and t-SNE on the Digits data set

with three classes and N = 537 patterns to a two-

dimensional space. Colors and ﬁgures indicate the la-

bel assignment, i.e., the three digits the data contains.

The plots show that EvoSK is clearly able to separate

patterns from different classes with only few outliers.

The observation that spending more effort into the

search process is advantageous can also be conﬁrmed

by the visual inspection of the embeddings. For µ = 2,

i.e., only two alternatives in each step, the worst low-

dimensional representation is computed with overlap-

ping regions, while the embeddings with µ = 10 have

similar shapes like the MDS result. t-SNE computes

low-dimensional representations with completely dif-

ferent shapes and three small areas for digit ’1’.

EvoSK has numerous advantages in comparison

to MDS and t-SNE. With only few and uncomplicated

adaptations, it is applicable to large data sets. For

embedding a novel pattern, the search for the clos-

est embedded pattern lasts longer with growing data

sets. The search can be accelerated with efﬁcient data

structures like ball-trees. A stochastic shortcut is to

restrict the neighborhood search by sampling µ times

from the embedded patterns and choosing the closest

pattern x

∗

with counterpart z

∗

Further, EvoSK can easily be employed to incom-

plete data sets. Let x

−i

be a pattern that has to be

embedded with missing value x

. The best position

for y can still be computed ignoring the dimensions,

in which parts are missing, e.g., we deﬁne the error as

sk,−i

= kD

X,−i

− D

Z,−i

, (4)

ICPRAM 2018 - 7th International Conference on Pattern Recognition Applications and Methods

480

Table 1: Experimental analysis of EvoSK and control methods on benchmark problem set mapping to a q = 2-dimensional

space in terms of E

. The best results in each line are shown in bold numbers.

EvoSK control

problem best mean dev worst MDS ISOMAP t-SNE

Digits 44.17 45.25 0.89 46.52 48.50 46.91 100.01

Housing 0.27 0.63 0.26 1.01 0.08 0.36 33.52

Image 4.09 4.54 0.34 5.10 4.24 4.30 32.89

Friedman 82.14 83.45 1.63 86.66 92.07 91.65 140.52

Wind 22.32 26.52 3.23 30.17 16.11 14.41 84.98

where D

X,−i

and D

Z,−i

are the distance matrices with

the i-th columns and rows missing.

5 CONCLUSIONS

The iterative evolutionary variant of MDS approx-

imates a low-dimensional representation that mini-

mizes the Shepard-Kruskal measure, i.e., optimizes

the maintenance of distances of the high-dimensional

space in its low-dimensional counterpart. This op-

timization objective is inspired by MDS. EvoSK is

an approximation heuristic with random elements, in

particular based on Gaussian sampling. The outcome

of the DR result depends on the order the patterns are

embedded. But the randomness is the key property to

achieve a linear runtime.

In the line of research of iterative constructive em-

beddings, EvoSK is the ﬁrst variant that considers

only the last n embedded patterns resulting in linear

runtime and turning out to be sufﬁcient for minimiza-

tion of the Shephard-Kruskal measure. Experimen-

tal results have shown that the introduced variants can

compete with the related method MDS, ISOMAP, and

with t-SNE.

The runtime of EvoSK is linear when employing

a window size k. For a choice of k = 50, the embed-

dings turn out to show good characteristics. But the

results show that EvoSK signiﬁcantly depends on the

effort µ invested into the sampling process.

REFERENCES

Borg, I. and Groenen, P. (2005). Modern Multidimensional

Scaling: Theory and Applications. Springer.

Hastie, T., Tibshirani, R., and Friedman, J. (2009). The

Elements of Statistical Learning. Springer, Berlin.

Jolliffe, I. (1986). Principal component analysis. Springer

series in statistics. Springer, New York.

Kramer, O. (2015a). Supervised manifold learning with in-

cremental stochastic embeddings. In European Sym-

posium on Artiﬁcial Neural Networks (ESANN), pages

243–248.

Kramer, O. (2015b). Unsupervised nearest neighbor re-

gression for dimensionality reduction. Soft Comput.,

19(6):1647–1661.

Lee, J. A. and Verleysen, M. (2007). Nonlinear Dimension-

ality Reduction. Springer.

Meinicke, P., Klanke, S., Memisevic, R., and Ritter, H.

(2005). Principal surfaces from unsupervised kernel

regression. IEEE Transactions on Pattern Analysis

and Machine Intelligence, 27(9):1379–1391.

Mitliagkas, I., Caramanis, C., and Jain, P. (2013). Memory

limited, streaming PCA. In Advances in Neural Infor-

mation Processing Systems (NIPS), pages 2886–2894.

Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V.,

Thirion, B., Grisel, O., Blondel, M., Prettenhofer,

P., Weiss, R., Dubourg, V., Vanderplas, J., Passos,

A., Cournapeau, D., Brucher, M., Perrot, M., and

Duchesnay, E. (2011). Scikit-learn: Machine learning

in Python. Journal of Machine Learning Research,

12:2825–2830.

Sch

olkopf, B., Smola, A., and Mller, K.-R. (1998). Nonlin-

ear component analysis as a kernel eigenvalue prob-

lem. Neural Computation, 10(5):1299–1319.

Tenenbaum, J. B., Silva, V. D., and Langford, J. C. (2000).

A global geometric framework for nonlinear dimen-

sionality reduction. Science, 290:2319–2323.

van der Maaten, L. and Hinton, G. E. (2008). Visualiz-

ing high-dimensional data using t-sne. Journal of Ma-

chine Learning Research, 9:2579–2605.

Dimensionality Reduction with Evolutionary Shephard-Kruskal Embeddings

481