Searching and Ranking Educational Resources based on

Terms Clustering

Marina A. Hoshiba Pimentel, Israel Barreto Sant’Anna and Marcos Didonet Del Fabro

C3SL Labs, Informatics Department, Federal University of Paran

a, Curitiba, Brazil

Keywords:

Educational Resources, Terms Clustering, Ranking.

Abstract:

Open Educational Resources (OER) are important digital assets used for teaching and learning. There exists

different repositories, but searching for such items is often a difﬁcult task. On one hand, most part of the

solutions implement engines with syntactic search based on term frequency metrics, or using the only item’s

metadata. On the other hand, the utilization of terms clustering (TC) have been used in other search and

ranking contexts and they have shown to be effective. In this paper, we present an approach for searching and

ranking for Open Educational Resources within a repository of objects, deﬁning a set of tasks and an hybrid

metric that integrates different ranking metrics obtained through terms clustering with the results of existing

search engines (SE). We present an extensive implementation and experiments to validate our approach. The

results empirically showed that our approach is effective to rank relevant OERs.

1 INTRODUCTION

We are living in an era of information abundance,

available mostly through the internet. Digital reposi-

tories with their set of documents organized and avai-

lable electronically are also part of this source of in-

formation (Lagoze et al., 2006). However, the great

volume has implications in the process of organiza-

tion, representation and management of all this va-

riety of contents. The format and number of infor-

mation has a direct impact on their retrieval process.

It is not a trivial task to categorize them adequately

to enable relevant information retrieval for those who

are searching them in a digital environment (Aguiar

et al., 2014).

In the context of Education, the searching and se-

lecting relevant Open Educational Resources (OER)

in digital repositories has been an exhausting and ar-

duous task for teachers (Pontes et al., 2014). Large

repositories can contain tens of thousands of diffe-

rent learning objects, making it difﬁcult to ﬁnd rele-

vant objects. OER retrieval is usually a difﬁcult task,

mainly due to implementations of search algorithms

based on metadata or keywords, which are common

in these repositories. These techniques limit further

the syntactic search process (de Souza et al., 2008).

(Costa et al., 2013) shows how challenging is for te-

achers the search and selection of OERs available in

digital repositories. The study shows that although

search engines are heavily used, irrelevant content is

returned to teachers.

In studies carried out by (Coelho et al., 2012), it

was possible to verify that the search engines and the

existing digital repositories present difﬁculties in the

OER recovery process. The identiﬁed difﬁculties are

long result lists, few relevant and often poorly ran-

ked results, that reinforces the need to create an ap-

propriate mechanism for OER recovery using other

resources to facilitate the search process, such as the

use of tags or keywords. It is worth mentioning that

tags clustering has been exploited to improve search,

navigation and recommendation services used on the

internet (Gemmell et al., 2008)(Shepitsen et al., 2008)

(Rafailidis and Daras, 2013)(Liu and Niu, 2014).

Existing solutions ((de Souza et al., 2008)(Patro-

cinio and Ishitani, 2009)(Costa et al., 2013)) show

that the search services implemented in these repo-

sitories have limitations that return few meaningful

results. Among the limitations we can highlight pro-

blems such as strictly syntactic search and those based

only on metadata analysis (de Souza et al., 2008). In

addition, if the search result is not well ranked, the

problem is aggravated because, according to the sur-

veys, users usually analyze only the ﬁrst result page or

the ﬁrst ten results obtained (Silverstein et al., 1999).

For these reasons, the main objective of this work

is to present a search model of OER in digital reposi-

tories that will handle the restriction of the syntactic

Hoshiba Pimentel, M., Barreto Sant’Anna, I. and Didonet Del Fabro, M.

Searching and Ranking Educational Resources based on Terms Clustering.

DOI: 10.5220/0006647305070516

In Proceedings of the 20th International Conference on Enterprise Information Systems (ICEIS 2018), pages 507-516

ISBN: 978-989-758-298-1

507

search, as well as to apply a good ranking to improve

the relevance of the returned resources.

The main contributions are a search model that

combines the use of a well-known search techni-

que/engine with a search process based on terms clus-

tering, and a set of metrics adapted to OER to be in-

tegrated with search engines. We present a set of new

metrics that are improvements from existing works,

adapted to OERs. They have shown to be effective in

a set of experiments realized in a real-world setting

searching in a repository with 19,159 items, resulting

in broader, diversiﬁed OER set with more relevant and

better ranked items. The implemented components

are integrated within the MECRED Portal

This paper is organized as follows. First, we pre-

sent the background for relevance calculation, data

clustering and educational resources. Second, in

Section 3 we present our approach for integrating a

syntactic search with terms clustering, adapted for

OERs. Section 4 contains the experiments. We ﬁ-

nalize with the related work and conclusions.

2 BACKGROUND

Information retrieval (IR) is the process of ﬁnding

material (usually documents) of an unstructured na-

ture (usually text) that satisﬁes an information need

from within large collections (usually stored on com-

puters) (Manning et al., 2008).

There are several components in an IR workﬂow,

and the relevance calculation of the items is one cen-

tral aspect. In this section, we introduce the base

concepts of relevance calculation, data clustering and

educational resources, which are the objects of study

from our work.

2.1 Relevance Calculation

A search procedure for an IR system is developed

whereby the answer to a question is obtained by max-

imizing an evaluation function of the system’s out-

put in terms of the probability of relevance (Goffman,

1964). In repositories with large number of docu-

ments, the result of a search can return a number of

documents that can easily exceed the human capacity

to ﬁlter them, so it is essential that a search engine

ranks the documents properly.

A searching procedure that allows users to type

free text without using any type of operator (such as

booleans) are popular on the web, and they handle

Plataforma MEC de Recursos Educacionais Digitais:

http://portalmec.c3sl.ufpr.br/

the query as a set of words, calculating a weight of

the terms that match the search terms (Manning et al.,

2008).

Relevance can be calculated in a number of ways

as Neural Networks (Benediktsson et al., 1990), Na-

tural Language Processing (Blosseville et al., 1992),

Boolean models (Lee et al., 1994) and Support Vector

Machines (Thet et al., 2007).

One well-known and widely used weight assign-

ment scheme is the term frequency. Denoted as T F

t,d

it represents the number of occurrences of a term t in a

document d. The simplest approach is to assign to the

weight the number of occurrences of the term t in do-

cument d (Manning et al., 2008). The more frequent,

the more relevant.

T F as above deﬁned, presents a critical problem:

all terms are considered equally important. In fact,

some terms have little or no discriminatory power

to determine relevance. To mitigate this problem,

the document frequency is adopted and is denoted as

. DF

denotes the number of documents in the

collection containing the term t and N is the number

of documents in the collection. To adjust the term

weight using the measure DF, the inverse of the fre-

quency in the documents is deﬁned (IDF

) as shown

in Equation (1).

IDF

= log

. (1)

T F−IDF

t,d

= T F

t,d

× IDF

(2)

Term Frequency - Inverse Document Frequency

(TF-IDF) calculates the relative frequency of terms

in a speciﬁc document compared to the inverse pro-

portion of that term over the entire document corpus

(Ramos, 2003). This calculation determines how re-

levant a given term t is in a particular document d

given by Equation (2). The TF-IDF assigns to term

t a weight in document d that is (i) highest when t

occurs many times within a small number of docu-

ments; (ii)lower when the term occurs fewer times in

a document, or occurs in many documents and (iii) lo-

west when the term occurs in virtually all documents

(Manning et al., 2008).

The table 1 represents an example of a TF-IDF

calculation for four terms (car, auto, insurance, best)

in three documents (d1, d2 and d3) in a collection

composed of 806,791 documents. The DF column

denotes the number of documents in the collection

in which each term occurs. In this way we can cal-

culate the inverse of the frequency in the documents

(Equation (1)) represented in the IDF column. The

frequency of terms in each document is represented

in the columns TF. We can then calculate the weight

given by TF-IDF (Equation (2)) for each term in each

ICEIS 2018 - 20th International Conference on Enterprise Information Systems

508

of the documents as shown in the table. For example,

the term car has a weight equal to 44,5 for the docu-

ment d1; 6,6 for document d2 and 39,6 for document

d3.

Table 1: TF-IDF calculation example.

TF TF-IDF

Term DF IDF d1 d2 d3 d1 d2 d3

car 18,16 1.6 27 4 24 44.5 6.6 39.6

autol 6,72 2.0 3 33 0 6.2 68.6 0

insur. 19,24 1.6 0 33 29 0 53.4 46.9

best 25,23 1.5 14 0 17 21 0 25.5

2.2 Data Clustering

Clustering algorithms group a set of objects into sub-

sets or clusters, creating clusters that are coherent in-

ternally, but clearly different from each other (Man-

ning et al., 2008). In other words, objects within a

cluster should be as similar as possible (Aggarwal and

Reddy, 2013).

Networks of nodes and links are powerful repre-

sentations of datasets of interactions from a great

number of different sources (Bohlin et al., 2014). One

of the most relevant features of graphs representing

real systems is community structure, or clustering, i.e.

the organization of vertices in clusters, with many ed-

ges joining vertices of the same cluster and compara-

tively few edges joining vertices of different clusters.

Such clusters, or communities, can be considered as

fairly independent compartments of a graph (Fortu-

nato, 2010).

We live in the era of Big Data and fortunately we

have several tools for classifying data from many dif-

ferent sources. The challenge is to extract useful in-

formation. Therefore, tools for simplifying and high-

lighting important structures in networks are essential

and such tools are called community detection met-

hods and they are designed to identify strongly intra-

connected modules (Bohlin et al., 2014).

2.3 Educational Resources

Open Educational Resources describes any educatio-

nal resources that are openly available for use by edu-

cators and students, without any need to pay royalties

or licence fees (Butcher, 2015). A repository is a da-

tabase or collection of OER.

Metadata, in the context of digital repositories, is

the information about a given object. As the number

of objects grows exponentially, the lack of informa-

tion or metadata about objects places a critical and

fundamental constraint on the ability to discover, ma-

nage, and use objects (Committee et al., 2002). A

metadata instance for a learning object describes rele-

vant characteristics of the learning object to which it

applies. Such characteristics may be grouped in gene-

ral, life cycle, meta-metadata, educational, technical,

educational, rights, relation, annotation, and classiﬁ-

cation categories (Committee et al., 2002). Table 2

shows a simple example of an OER and its metada-

tas.

Table 2: Simpliﬁed example of an OER.

Metadata ﬁeld Value

dc.contributor.author Moondigger

dc.date.created 2005-11-07

dc.description

Provides a close-up view of

the constellation of Sagittarius

dc.title Milky way 2

dc.type Image

dc.rights.license

Creative Commons Attribution

ShareAlike 2.5 License

dc.subject.keyword Astronomy

dc.subject.keyword Constellation

dc.subject.keyword Sagittarius

dc.subject.keyword Space

dc.subject.keyword Star

dc.subject.keyword Universe

dc.subject.category College education

3 SEARCHING AND RANKING

OERs

This section presents our approach for searching and

ranking OERs supported by terms clustering and TF-

IDF searching. Our goal is to improve the search re-

sults of an existing search engine by increasing the

number of relevant OERs related to the search terms.

It is worth noting that in this work we are referring

simply as terms all the keywords or tags that are asso-

ciated with a given OER.

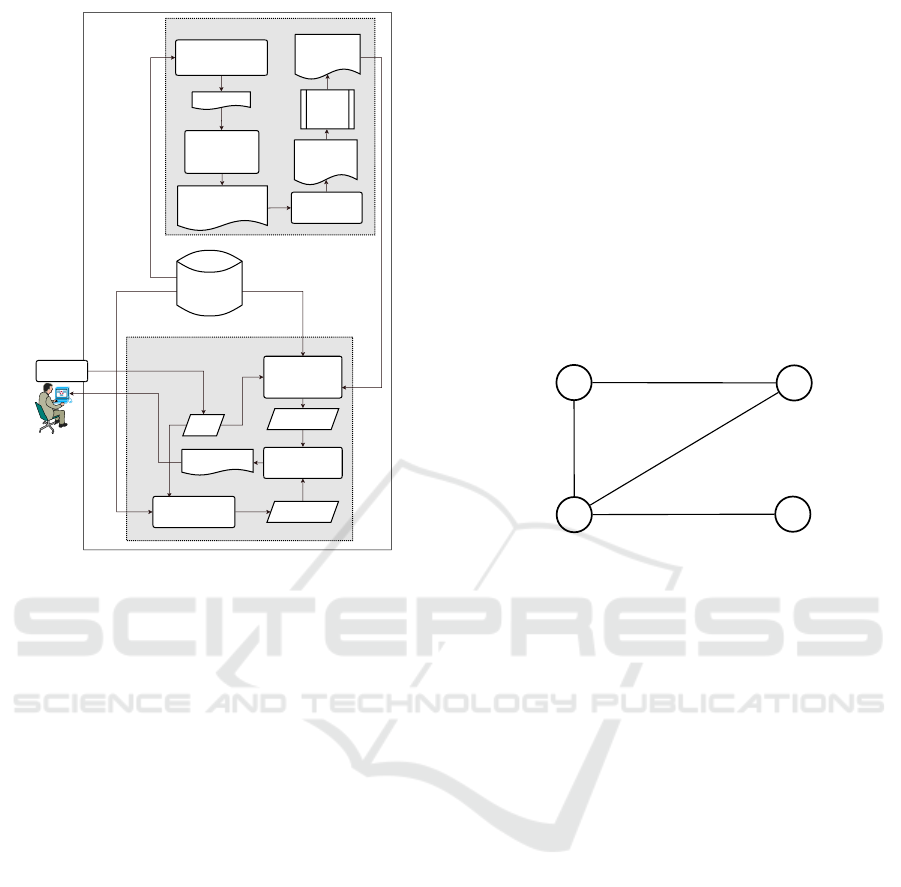
Figure 1 shows an overview of the tasks and inter-

task ﬂows required to perform an OER search and

ranking supported by terms clustering. There are two

large groups of processes, named Clustering Process

and Search and Ranking Process. The main goal of

the tasks from the ﬁrst group Clustering Process is

to form the terms clustering. And the tasks from the

second group aim to perform the OER searching and

ranking based on the cluster of terms resulted from

the ﬁrst group.

3.1 Clustering Process

The task Extracting OERs and its terms is respon-

sible for extracting the list of all OERs and its re-

spective terms. Suppose that an repository contains

the OERs and the respective terms given by S

= {r1 :

Searching and Ranking Educational Resources based on Terms Clustering

509

Searching via

search engine

Ranked OER

term

Searching via

terms clustering

Ranked OER

OER mix and

reclassiﬁcation

Searching and Ranking Process

OER

Repository

Extracting

OER and its terms

Mapping term

co-occurrence

{terms,

relationships

and weights}

Graph

generation

Terms

clustering

clusters, terms

and term

rankings

Clustering Process

Open

Educational

Resources

Social

Networking

Final ranked OER

{pair of co-occurrent

terms,

similarity coeﬃcient}

{OER, terms}

Searching

Figure 1: OER search and ranking process.

{t10, t12}, r2 : {t10, t11, t13}, r3 : {t10, t11}}. In this

simple example, OER r1 has two terms t10 and t12.

The fundamental task for our approach is the cal-

culation of terms similarity, task performed by Map-

ping term co-occurrence, and subsequent clustering.

The similarity between two terms can be calculated

with different measures and coefﬁcients. Our term

clusters are based on term co-occurrences, and we

use the common similarity measure Cosine (Manning

et al., 2008) coefﬁcient. The co-occurrent terms are

considered correlated terms as well in this work.

The input for this task is the set S

given by the

previous task Extracting OERs and its terms. The

goal here is to map all the pairs of co-occurrent terms.

Co-occurring terms are terms assigned to the same

OER. Based on S

, we illustrate a map where term

t10 co-occurs with t11, t12 and t13. Beyond that,

the number of times each pair of terms co-occurs is

also calculated. The intermediate resulting set is gi-

ven by the Map

in the following format Map

{t10 : {t11 : 2, t12 : 1, t13 : 1}, t11 : {t10 : 2}, t12 :

{t10 : 1}, t13 : {t10 : 1, t11 : 1}}. This means that term

t10 co-occurs with t11 two times, with t12 and t13

once and so on. Next, the similarity coefﬁcient for

each co-occurrent pair of terms is calculated by Co-

sine similarity measure and stored in Map

, and the

result for our example can be represented as Map

{t10 : {t11 : 0.82, t12 : 0.58, t13 : 0.58}, t11 : {t10 :

0.82}, t12 : {t10 : 0.58}, t13 : {t10 : 0.58, t11 : 0.71}},

where the similarity coefﬁcient calculated for the pair

t10 and t11 is equal 0.82. The representation of the

set Map

as a graph structure is required for the clus-

tering algorithm.

At this point the necessary information is available

to perform the task Graph generation. Then we can

compose a non-directed graph G(V, E, W ), formed by

a set of vertices V , a set of edges E and respective

weights W . Each vertex v

from V represents a term

of the set Map

and there will exist an edge e

i, j

bet-

ween v

e v

only if v

is co-occurrent with v

, and the

weight w

i, j

is the similarity coefﬁcient for the pair of

terms v

and v

. Figure 2 represents the graph struc-

ture formed from the Map

data.

t10

t13

t12

t11

0.58

0.82

0.58

0.71

Figure 2: Graph G formed from Map

The development of an clustering algorithm is not

part of this work, therefore to perform the task Terms

clustering we will use an available tool, the Map

equation/Infomap, to form our term clusters from the

graph G generated on the previous task.

Map equation/Infomap (Bohlin et al., 2014) is a

fast stochastic and recursive search algorithm, that

follows closely the method presented by (Blondel

et al., 2008), a heuristic method based on the optimi-

zation of modularity. Neighboring nodes are joined

into modules, which subsequently are joined into su-

permodules and so on. First, each node is assigned

to its own module. Then, in random sequential order,

each node is moved to the neighboring module that

results in the largest decrease of the map equation. If

no move results in a decrease of the map equation,

the node stays in its original module. This procedure

is repeated, each time in a new random sequential or-

der, until no move generates a decrease of the map

equation.

Our term clusters are based on term pair co-

occurrence and consist of undirected graph, from

which we obtain clusters of similar and ranked terms.

This way every cluster can offer additional seman-

tically similar terms which users might not have

thought at their search. With the formation of the

clusters the tasks from the Clustering Process are con-

cluded.

ICEIS 2018 - 20th International Conference on Enterprise Information Systems

510

3.2 Searching and Ranking Process

The Searching and Ranking Process begins when a

user enters a term or a set of terms to be searched.

First, the search engine is invoked in the task Sear-

ching via search engine to perform the search for the

terms the user has provided. At the end, a result set

of ranked OERs is returned. It is not the purpose

of this work to develop a search engine, so we must

use an available tool that accomplishes this functiona-

lity.

The task Searching via terms clustering per-

forms the search supported by the clusters of co-

occurrent terms provided at Subsection 3.1. The task

ﬁrst identiﬁes which cluster the term belongs to, then

the correlated terms are recovered. This way quantita-

tive and semantic expansion can be achieved. Quanti-

tative because it increases the number of search terms,

and semantic because it considers similar and correla-

ted terms. So it is possible to retrieve different OERs

from those retrieved by the search engine.

Once the clusters of terms are formed, they do not

change, but to calculate the found OER relevance and

ranking for a speciﬁc search, we consider the term

corresponding to the original search term the more re-

levant element in the cluster for this search. We de-

nominate it main term. The relevance of the other

correlated terms are normalized relatively to the main

term. Their weights will be inversely proportional to

the distance (difference) that they are in relation to the

main term in the cluster. The greater the distance, less

relevant the term.

The original terms weights in a cluster may suf-

fer wide range of magnitudes as shown in Table 3.

Simply calculating the difference between the origi-

nal weights would not allow new weights to be obtai-

ned on a practical scale (e.g. between 0 and 1). To

circumvent this problem we use the logarithmic scale.

First we obtain the measure of the distance bet-

ween the main term and the other terms of the cluster,

given by dist

= |(log

rank

)− log

rank

|, where

rank

and rank

are the values of the original weights

assigned to the terms t

and t

respectively. The lower

the resulting value dist, the closer and more similar

the terms are considered. Besides that, let max dist

be the value of the maximum distance between t

and

. The relevance (weight) of the term t

should be in-

versely proportional to the value of its distance from

the main term t

. To evenly distribute the distances

in a scale, their values are normalized with the Min-

Max Normalization, multiplying the max

dist value

by a scalar 1 + a, avoiding that the most distant term

to have relevance equals to 0, whereas it belongs to

the same cluster as the searched term. The resulting

Table 3: Co-ocurrent terms for “Sagittarius”.

Id Term

Original

weight

Normalized

weight

1 Sagittarius 2.31473e-05 1.00

2 Dwarfstar 2.42713e-05 0.99

3 Luminous star 2.42713e-05 0.98

4 Peony 3.11466e-05 0.93

5 Shine 3.11466e-05 0.93

6 W5 1.55874e-05 0.91

7 Stars movement 1.46697e-05 0.89

8 The Cartwheel Galaxy 1.18271e-05 0.84

9 Recycle 1.11963e-05 0.83

10 Protoplanetary disk 6.47752e-06 0.71

11 Hertzsprung Russell Diag. 6.13133e-06 0.70

12 Star 0.00021569 0.50

equation is given by Equation (3) (the minimum dis-

tance possible is 0, so it’s not represented in the equa-

tion).

rank

= 1 −



dist

)

max dist × (1 + a)



(3)

Table 3 shows an example of this calculation, set-

ting a up to 0.5. Consider the search term “Sagitta-

rius”. The ﬁrst column shows all co-occurring terms.

The second column shows the original weight of the

terms and the third column shows the weight norma-

lized by Equation (3).

Once the weights of the terms have been normali-

zed, we can ﬁnally perform the search for the OERs.

Based on the TF idea, for each OER found, the score

is calculated as the sum of the weights of its co-

occurring terms: Rank

OER

∑

i=1

rank

, where n is

the number of cluster terms that the OER owns and

rank

is the normalized weight of the term i.

At the end of this task, the result set RS

is retur-

ned with all OERs ranked according to the total score

of their terms. Consider the cluster which the term

“Sagittarius” belongs to as shown in Table 3. Consi-

der yet that the OER “Stars and HR Diagram” own

the co-occurrent terms “Hertzsprung Russell Diag.”,

“Satr”, “Dwarfstar” and “Luminous star”, so your

score is given by Rank

OER

= 0, 70 + 0, 50 + 0, 99 +

0, 98 = 3, 17.

We start now the last task OER mix and reclas-

siﬁcation. The input for the task are the two set RS

and RS

resulted from the tasks Searching via search

engine and Searching via terms clustering respecti-

vely. Since the weights from the two sets have diffe-

rent dispersions, a normalization of the OERs weig-

hts is made to adjust the scale of values, so enabling

to join the two sets. To do this, an equation based

on linear normalization is used. In the case of the re-

sult generated by the search engine, the normalization

of the OERs score is given by Equation (4), where

min sc and max sc are respectively the minimum and

Searching and Ranking Educational Resources based on Terms Clustering

511

Table 4: Mixing and re-ranking example.

mix

Rank RE id Score RE id Score RE id Score

1 14641 5,23 17961 222,61 17961 13,13

2 15850 4,73 15426 222,08 15426 12,98

3 16374 2,57 13975 213,66 14641 10,61

4 15470 1,29 14722 193,69 8958 6,66

5 8214 1,00 5047 191,87 10198 5,25

maximum scores found in the set RS

; d is a coefﬁ-

cient to avoid values equal 0 and boost is the impulse

factor necessary to controlling the resources relevance

in the ranking process. It’s a value given by the search

engine to OERs depending on the occurrence of the

exact searched terms (higher value) or syntactically

close terms (lower value).

n se

= boost ×



sc × (1 + d) − min sc

max sc −min sc



(4)

The normalization of the resulting set RS

gene-

rated by the support of the terms clustering is made by

Equation (5), where min sc and max sc are respecti-

vely the minimum and maximum scores found in the

set RS

; d is a coefﬁcient to avoid values equal 0 and

m boost is the maximum boosting value boost from

the set RS

. The major differential of this proposal is

situated at this point, since the maximum boosting va-

lue (m boost) is applied in the second set too, to boost

the score of its relevant OERs, just like it is done in the

search engine. Based on the premise that the OERs of

the RS

set were returned only because they are con-

sidered similar by the use of correlated terms, so it is

reasonable to apply m boost to the OERs from RS

so that there is no harm in their relevance in relation

to the items from RS

set.

n tc

= m boost ×



sc × (1 + d) − min sc

max sc −min sc



(5)

Next, another important measure adopted is based

on other research ﬁndings: resources returned by both

the search engine and the terms clustering should be

considered more relevant. So the ﬁnal OER score for

OER that occurs in both RS

and RS

is given by the

sum of the scores assigned to the OER in these both

sets.

Finally, the ﬁnal result set RS

mix

, that merges re-

sults from RS

and RS

, with a new ranking can be

returned to the user. Table 4 shows a comparative ex-

ample, where we can see the original ranking from

the resulting sets RS

and RS

, as well the mixed and

re-ranked ﬁnal set RS

mix

To summarize, the presented model increases the

search results through the expansion of the original

search terms given by the correlated terms identiﬁed

by the clustered co-occurrent terms. In addition it

combines the results found via terms clustering with

the results from the traditional search engine. All the

results are reclassiﬁed, so that greater relevance is at-

tributed to the results that appear in both search appro-

aches, as well as boosting the results obtained through

the correlated terms.

4 EXPERIMENTS

The presented solution was implemented using the in-

frastructure of the MEC RED web portal of educati-

onal objects with mechanisms of social network, sen-

ding, searching and ranking objects, as well as me-

chanisms to follow collections and authors. At the

experimental phase of this work, the portal repository

contained 19,159 OERs and 23,808 terms. This por-

tal uses only free and open source software

, in order

to guarantee the dissemination of the knowledge pro-

duced and the possibility of cooperation in the con-

struction of the platform itself

. OERs are stored in

a DSpace

portal and the social network information

is stored in an instance of PostgreSQL

. The main se-

arch is performed by the Elasticsearch

engine. The

front end layer receives user connections and com-

municates with a Ruby/Rails API providing informa-

tion needed by the users, and communicating with the

Elasticsearch engine through the SearchKick API.

To obtain the cluster of terms in the task Terms

clustering, the Mapequation framework

(Bohlin

et al., 2014) was adopted. It is a set of tools for data

clustering and visualization. From the graph genera-

ted in task Graph generation, represented in the spe-

ciﬁc format called PAJEK (.net), we used the Infomap

tool to calculate and generate the clusters. Infomap,

besides generating the clusters, provides the ranking

of the terms of each cluster. The result is stored in the

output ﬁle (.ftree), being the basis of information to

support the Searching via terms clustering task. Of

the total of 23,807 terms and 173,038 identiﬁed co-

occurrences, Infomap generated 8,568 clusters. Table

5 shows a sample of clustered terms with respective

weights.

It is important to highlight the use of the ex-

plain parameter in Elasticsearch execution, because

https://gitlab.c3sl.ufpr.br/portalmec/

Component sources: https://gitlab.c3sl.ufpr.br/

portalmec/portalmec/tree/tag-clustering-task

www.dspace.org

www.postresql.org

elasticsearch.co

www.mapequation.org

ICEIS 2018 - 20th International Conference on Enterprise Information Systems

512

Table 5: Term clustering sample.

Cluster terms Weight

DNA

RNA

Guanine

Thymine

Nucleotide

Nucleoside

Protein translation

enzymes restriction endonucleases

Homologous protein

Nucleic acid

Double helix

Capsid protein

1.00

0.91

0.82

0.77

0.67

0.62

0.61

0.59

0.54

0.50

Gravitacional forcePtolomeu Model

Retrograde movement

Position of the planets

Epicycle

Deferent

luminosity

Einstein

Greater circumference

1.00

0.94

0.87

0.66

0.64

0.50

Corrosion

Electrochemistry

Oxide-reduction

Concentration cell

1.00

0.97

0.95

0.50

this way we can capture the boost value applied in

the ranking process performed by the search engine.

Remembering that this value is important to be app-

lied also in the task OER mix and reclassiﬁcation to

boost relevant OERs found via terms clustering.

All experiments were performed with terms rand-

omly chosen and were performed considering the re-

trieval of a list of at most ten results, because accor-

ding to (Silverstein et al., 1999), users usually consi-

der only the ﬁrst page or the ﬁrst ten results.

Table 6 shows the resulting set for the sear-

ching term “Sagittarius” performed via Searching via

terms clustering. The column Term id represents the

terms from the Table 3 owned by each OER. These

terms are used to calculate the total weight of each

OER, that is used to rank the OER resulting set. It is

worth mentioning that in the Equation (3), according

to our experiments, the value of a set to 0.5 provided

satisfactory results.

Table 7 represents the resulting set of OERs found

and ranked via Elasticsearch search engine. The

columns Weight and Boost shows respectively the

weight and the boost value assigned to the OER from

the search engine. The maximum boost value retur-

ned was equal 10.

Considering results from Table 6 and 7, the ﬁnal

resulting set after performing the task OER mix and

reclassiﬁcation is showed in Table 8. In this expe-

riment, only the ﬁrst OER found via Elasticsearch

can be considered relevant, therefore the ﬁnal mixed

Table 6: Searching “Sagittarius” via terms clustering.

Search term = Sagittarius

OER id OER Weight Term id

2095 Stars and HR Diagram 3,1812 2,3,11,12

10667 Peony star 2,3670 4,5,12

16289 Milky way 2 1,5000 1,12

10837 W5 (Allen) 1,4114 6,12

557 W-5 Star-Forming Region 1,4114 6,12

2642 Daytime Motion of the Stars... 1,3978 12

11324 Cartwheel galaxy 1,3496 8,12

7105 Robot Astronomy... 1,3373 9,12

5482 Inner Gap in Circumstellar... 1,2147 12

11438 Space Trash 0,8373 9

Table 7: Searching “Sagittarius” via Elasticsearch.

Search term = Sagittarius

OER id OER Weight Boost

16289 Milky way 2 147,6802 10

2538 Sanitary landﬁll 11,1470 1

1917 Sound Almanac of Chemistry... 10,6484 1

3091 Periodical Talk - Trash 10,3336 1

17001 Sanitary landﬁll 9,9435 1

17393 Sanitary landﬁll 9,9435 1

3987 Mines without dumps 9,5448 1

6078 Slurry treatment pond 9,5448 1

15537 Mines without dumps 9,5448 1

9508 Slurry treatment 9,1596 1

resulting set, column Mixed Result, is composed by

only one item from Elasticsearch and all other from

the items found via terms clustering approach.

Table 8: Mixing and re-ranking OERs related to “Sagitta-

rius”.

Search term = Sagittarius

Terms clustering Elasticsearch Mixed Result

Rank OER id Weight OER id Weight OER id Weight

1 2095 3,18 16289 147,68 16289 13,68

2 10667 2,36 2538 11,14 2095 10,67

3 16289 1,50 1917 10,64 10667 7,03

4 10837 1,41 3091 10,33 10837 2,75

5 557 1,41 17001 9,94 557 2,75

6 2642 1,39 17393 9,94 2642 2,68

7 11324 1,34 3987 9,54 11324 2,47

8 7105 1,33 6078 9,54 7105 2,41

9 5482 1,21 15537 9,54 5482 1,86

10 11438 0,83 9508 9,15 11438 0,17

Table 9 shows the consolidated results of 10 expe-

riments performed with terms randomly chosen. The

ﬁrst column shows the search terms used to evaluate

the proposed model. The Original result column is

composed by TC (number of OERs found via terms

clustering) and SE (number of OERs found via se-

arch engine). The column Final result composition

shows the composition of the ﬁnal mixed result for the

search. The column TC’ shows the number of OERs

from column TC that compose the ﬁnal result, and

the column SE’ the number considered from SE. The

Searching and Ranking Educational Resources based on Terms Clustering

513

column TC+SE refers to the number of OERs that are

returned by both (TC and SE).

Analyzing the search term corrosion from Table

9, we can interpret that 4 OERs were found via terms

clustering, of which 1 compose the ﬁnal mixed result;

10 OERs were found via search engine, of which 7

compose the ﬁnal mixed result; and from the total 10

ﬁnal result set, 2 were found by both, via terms cluste-

ring and search engine. In this case, we can consider

that 30% (3 = 1 + 2) of the OERs came from terms

clustering. In 60% of the cases, the ﬁnal mixed re-

sult is composed of at least half of the items returned

via terms clustering (considering TC’ and TC+SE).

In 40% of the cases, where the search engine reco-

vers few relevant results (because it considers only

the main search term), the results via terms clustering

compose more than 80% of the ﬁnal result.

Considering the correlated terms to carry out the

expansion of the original query made it possible, in

some cases, to more than double the percentage of re-

levant results, as the experiments with term “Sustai-

nable development”, “Phylogeny”, “Morphine” and

“Sagittarius”. For other cases, where the search en-

gine itself returns a good amount of relevant results,

the evaluation is even more empirical and subjective,

since only a specialist or a user with speciﬁc search

purposes could evaluate with greater accuracy the re-

levance of the OERs as ranked.

(Knautz et al., 2010) presents a model based on

the presentation of a tag cloud, where the user must

click on the terms or the edges to access the docu-

ments related to the speciﬁc tag. In this proposal, a

teacher would need to spend much more time and ef-

fort to get the results that in our approach are returned

with just one query. Taking the example of the expe-

riment with the term “DNA”, which has 11 correlated

terms, the user would need to perform 12 queries in

the model proposed by Knautz et al. to obtain similar

results to those obtained by our model.

The ranking process, simply summing the scores

of correlated terms, was also viable and presented

good results. Less relevant results returned by the se-

arch engine were treated with little relevance in the ﬁ-

nal classiﬁcation in relation to OERs considered more

relevant because of the correlated terms.

5 RELATED WORK

(de Souza et al., 2008)(Patrocinio and Ishitani,

2009)(Costa et al., 2013) report some difﬁculties in

the OER search process in digital repositories, such

as searching process with syntactic restrictions, ma-

king it difﬁcult to ﬁnd relevant results. (de Souza

Table 9: Searching results composition.

Original

result

Final result composition

Search term TC SE TC’ SE’ TC+SE

corrosion 4 10 1 7 2

DNA 10 10 3 7 0

Discovery

of Brazil

4 8 0 4 4

Galileu Galilei 10 10 2 6 2

Regionalism 10 10 3 5 2

Gravitational

force

10 10 2 5 3

Sustainable

development

10 10 8 2 0

Phylogeny 10 2 8 2 0

Morphine 10 1 9 1 0

Sagittarius 10 10 9 0 1

et al., 2008) proposes a general purpose thesauri-

based approach to semantic retrieval of learning ob-

jects. This model faces a practical limitation, which

is the scarcity of thesauri. Using more generic the-

sauri, not speciﬁc to a particular knowledge area, of-

ten require the implementation of semantic similarity

analysis techniques or the combination of the use of

thesauri with ontologies.

(Patrocinio and Ishitani, 2009) proposes a mecha-

nism for learning objects recovery, based on a direc-

tory service that integrates metadata used by the main

Brazilian repositories and social annotation resources.

The proposed model does not address the question of

the ranking of the OERs.

A clustering framework called RankClus is propo-

sed in (Sun et al., 2009) that generates clusters inte-

grated with ranking. This work shows that ranking

objects globally without considering which clusters

they belong to often leads to dumb results.

The design of an information retrieval system ba-

sed on tag co-occurrence and subsequent clustering is

presented in the work of (Knautz et al., 2010). This

system allows users to access digital data through a

graphical/visual retrieval interface, providing an ela-

borate alternative to the conventional tag clouds. In

addition, for these authors, tag clusters represent a

new form of visualization-driven query expansion and

thus to a new possibility of the application of human-

computer interaction research in web-based informa-

tion retrieval. This expansion happens as the user na-

vigates through the vertices (tags) or the edges (relati-

onship between tags) of the tag cluster. This need for

interaction to compose the query may require a lot of

time and effort from the user.

The ranking in (Knautz et al., 2010) is calculated

in two ways: (i) absolute frequency of all tags is accu-

mulated creating the ranking; (ii) with the Within Do-

cument Frequency, which takes the logarithms of the

ICEIS 2018 - 20th International Conference on Enterprise Information Systems

514

relative occurrences is multiplied with the Inverse Tag

Frequency, a text statistical value which refers to the

total number of tags in the data set. The two approach

or ranking calculation provide very similar results.

The universe of OER and their assigned terms

or keywords can be mapped as a large network, and

strongly interconnected groups (clusters) can be map-

ped (Bohlin et al., 2014). The terms clusters give the

semantic potential necessary to combat the restricti-

ons imposed by the syntactic search process (Hassan-

Montero and Herrero-Solana, 2006)(Knautz et al.,

2010)(Saoud and Kechid, 2016).

According to (Li et al., 2016), access to the se-

mantics of visual content has been improved by ad-

ding relevant new tags, reﬁning existing ones and

using them in resource retrieval. The article presents

a research on assignment, reﬁnement and retrieval of

tags in images. A selected set of eleven representative

works for assignment, reﬁnement and/or retrieval of

tags were implemented and evaluated, presenting the

best performances in each speciﬁc task. For exam-

ple, retrieving images using the learned tag relevance

produces more accurate results compared to retrieving

images using original tags. For assignment and retrie-

val of tags, methods that explore tags together with

image media through instance-based learning take the

leading position.

(Lancichinetti and Fortunato, 2009) carried out a

comparative analysis of the performances of some al-

gorithms for community detection on various graphs:

the Girvan and Newman benchmark (Girvan and

Newman, 2002), Lancichinetti-Fortunato-Radicchi

benchmark and random graphs. They conclude that

the Infomap method by Rosvall and Bergstrom (Boh-

lin et al., 2014) has the best performance.

6 CONCLUSIONS

We presented a novel solution for searching and ran-

king OERs, which integrates the ranking of search re-

sults from an existing search engine with the rankings

of OERs found via terms clustering. The mixed ran-

king is used to recalculate the terms return order.

We have implemented using the infrastructure of

an existing web portal, allowing us to carry out ex-

periments that show the feasibility of our approach.

Considering the correlated terms provided by the

clustered information to expand the original search

term made, it was possible to increase the number of

relevant correlated results. In addition, there was a

diversiﬁcation of the results, thanks to the integration

with the results of the correlated terms.

The ranking process presented good results with

the application of simple equations. Irrelevant results

returned by the search engine were properly treated

with little emphasis in the ﬁnal classiﬁcation, consi-

dering that other more relevant OERs were returned

by the search. This way, we have concluded that it

is not necessary to use complex models and calcula-

tions to obtain improvements in ranking. The equa-

tion results were normalized in order to not prioritize

some speciﬁc search results. The relevance of the ran-

king was based on empirical analysis of the returned

objects. Further analysis should be done to evaluate

through some existing data set, if available.

The main contribution of our presented approach

is the increment of the number of OERs found by a

searching process, as well as ranking the result set

considering the relevance of all correlated terms.

As future work we can mention the application of

Natural Language Processing techniques such as radi-

calization, lemmatization, removal of stopwords and

disambiguation to improve the quality of the terms

clustering and, consequently, to improve the search

results. Another point that deserves additional rese-

arch is the techniques to perform OER ranking, since

depending on the applied equations and methods one

can classify the ﬁnal results in many different ways.

ACKNOWLEDGEMENTS

This work was funded by project (Pesquisa de re-

des sociais em nuvem voltadas para objetos educaci-

onais), FNDE (Fundo Nacional de Desenvolvimento

da Educac¸

ao) and CNPq Universal.

REFERENCES

Aggarwal, C. C. and Reddy, C. K. (2013). Data clustering:

algorithms and applications. CRC press.

Aguiar, J. J., Santos, S. I., Fechine, J. M., and Costa, E. B.

(2014). Um mapeamento sistem

atico sobre iniciati-

vas brasileiras em sistemas de recomendac¸

ao educaci-

onais. SBIE, 1:1123–1132.

Benediktsson, J. A., Swain, P. H., and Ersoy, O. K. (1990).

Neural network approaches versus statistical methods

in classiﬁcation of multisource remote sensing data.

IEEE Transactions on Geoscience and Remote Sen-

sing, 28(4):540–552.

Blondel, V. D., Guillaume, J.-L., Lambiotte, R., and Le-

febvre, E. (2008). Fast unfolding of communities in

large networks. Journal of statistical mechanics: the-

ory and experiment, 2008(10):P10008.

Blosseville, M.-J., Hebrail, G., Monteil, M.-G., and Penot,

N. (1992). Automatic document classiﬁcation: natu-

ral language processing, statistical analysis, and ex-

pert system techniques used together. In Proceedings

Searching and Ranking Educational Resources based on Terms Clustering

515

of the 15th annual international ACM SIGIR, pages

51–58. ACM.

Bohlin, L., Edler, D., Lancichinetti, A., and Rosvall, M.

(2014). Community detection and visualization of net-

works with the map equation framework. In Measu-

ring Scholarly Impact, pages 3–34. Springer.

Butcher, N. (2015). A basic guide to open educational re-

sources (OER). Commonwealth of Learning (COL);.

Coelho, G. O., Ishitani, L., and Nelson, M. A. V. (2012).

Vitae: recuperac¸

ao de objetos de aprendizagem ba-

seada na web 2.0. ETD-Educac¸

ao Tem

atica Digital,

14(2):238–257.

Committee, L. T. S. et al. (2002). Ieee standard for learning

object metadata. IEEE standard, 1484(1):2007–04.

Costa, E., Aguiar, J., and Magalh

aes, J. (2013). Sistemas

de recomendac¸

ao de recursos educacionais: concei-

tos, t

ecnicas e aplicac¸

oes. In Jornada de Atualizac¸

em Inform

atica na Educac¸

ao, volume 1, pages 57–78,

Campinas - SP - Brazil.

de Souza, A. B., da Silva, J. P., de Oliveira, W. C. C.,

Kuma, T. H., and Silveira, I. F. (2008). Recuperac¸

sem

antica de objetos de aprendizagem: Uma abor-

dagem baseada em tesauros de prop

osito gen

erico.

In Brazilian Symposium on Computers in Education),

volume 1, pages 603–612, Fortaleza - CE - Brazil.

Fortunato, S. (2010). Community detection in graphs. Phy-

sics reports, 486(3):75–174.

Gemmell, J., Shepitsen, A., Mobasher, B., and Burke, R.

(2008). Personalization in folksonomies based on tag

clustering. Intelligent techniques for web personaliza-

tion & recommender systems, 12:37–48.

Girvan, M. and Newman, M. E. (2002). Community struc-

ture in social and biological networks. Proceedings of

the national academy of sciences, 99(12):7821–7826.

Goffman, W. (1964). A searching procedure for information

retrieval. Information Storage and Retrieval, 2(2):73–

78.

Hassan-Montero, Y. and Herrero-Solana, V. (2006). Impro-

ving tag-clouds as visual information retrieval interfa-

ces. In International conference on multidisciplinary

information sciences and technologies, pages 25–28,

erida - Spain.

Knautz, K., Soubusta, S., and Stock, W. G. (2010). Tag

clusters as information retrieval interfaces. In System

Sciences (43rd HICSS), 2010, pages 1–10, Honolulu -

HI - USA. IEEE.

Lagoze, C., Lynch, C., Waters, D., Van de Sompel, H., and

Hey, T. (2006). Augmenting interoperability across

scholarly repositories. In Proceedings of the 6th

ACM/IEEE-CS Joint Conference on Digital Libraries

(JCDL’06), page 85, Chapel Hill - NC - USA. IEEE.

Lancichinetti, A. and Fortunato, S. (2009). Community de-

tection algorithms: a comparative analysis. Physical

review E, 80(5):056117.

Lee, J. H., Kim, M. H., and Lee, Y. J. (1994). Ranking do-

cuments in thesaurus-based boolean retrieval systems.

Information Processing & Management, 30(1):79–91.

Li, X., Uricchio, T., Ballan, L., Bertini, M., Snoek, C. G.,

and Bimbo, A. D. (2016). Socializing the semantic

gap: A comparative survey on image tag assignment,

reﬁnement, and retrieval. ACM Computing Surveys

(CSUR), 49(1):14–53.

Liu, R. and Niu, Z. (2014). A collaborative ﬁltering recom-

mendation algorithm based on tag clustering. In Fu-

ture Information Technology, pages 177–183. Sprin-

ger, Zhangjiajie - China.

Manning, C. D., Raghavan, P., Sch

utze, H., et al. (2008).

Introduction to information retrieval, volume 1. Cam-

bridge university press Cambridge, England.

Patrocinio, M. and Ishitani, L. (2009). Associac¸

ao de recur-

sos sem

anticos para a anotac¸

ao de objetos de apren-

dizagem. In Brazilian Symposium on Computers in

Education-SBIE), volume 1, Florian

opolis-Brazil.

Pontes, W. L., Franc¸a, R. M., Costa, A. P. M., and Behar,

P. (2014). Filtragens de recomendac¸

ao de objetos de

aprendizagem: uma revis

ao sistem

atica do cbie. In

Brazilian Symposium on Computers in Educatio), vo-

lume 25, pages 549–558, Dourados - MS - Brazil.

Rafailidis, D. and Daras, P. (2013). The tfc model: Tensor

factorization and tag clustering for item recommenda-

tion in social tagging systems. IEEE Transactions on

SMC: Systems, 43(3):673–688.

Ramos, J. (2003). Using tf-idf to determine word relevance

in document queries. In Proceedings of the ﬁrst in-

structional conference on machine learning, volume

242, pages 133–142.

Saoud, Z. and Kechid, S. (2016). Integrating social proﬁle

to improve the source selection and the result merging

process in distributed information retrieval. Informa-

tion Sciences, 336:115–128.

Shepitsen, A., Gemmell, J., Mobasher, B., and Burke, R.

(2008). Personalized recommendation in social tag-

ging systems using hierarchical clustering. In In proc.

of 2008 ACM RecSys, pages 259–266, Lausanne -

Switzerland. ACM.

Silverstein, C., Marais, H., Henzinger, M., and Moricz, M.

(1999). Analysis of a very large web search engine

query log. In ACM SIGIR Forum, volume 33, pages

6–12. ACM.

Sun, Y., Han, J., Zhao, P., Yin, Z., Cheng, H., and Wu, T.

(2009). Rankclus: integrating clustering with ranking

for heterogeneous information network analysis. In

12th EDBT, pages 565–576, Saint-Petersburg - Rus-

sian Federation. ACM.

Thet, T. T., Na, J.-C., and Khoo, C. S. (2007). Filtering pro-

duct reviews from web search results. In Proceedings

of the 2007 ACM symposium on Document engineer-

ing, pages 196–198. ACM.

ICEIS 2018 - 20th International Conference on Enterprise Information Systems

516