Comparison Between Static and Dynamic Willingness to Interact in

Adaptive Autonomous Agents

Mirgita Frasheri, Baran C

ukl

u and Mikael Ekstr

alardalen University, V

aster

as, Sweden

Keywords:

Adaptive Autonomy, Multi-agent Systems, Collaborative Agents.

Abstract:

Adaptive autonomy (AA) is a behavior that allows agents to change their autonomy levels by reasoning on their

circumstances. Previous work has modeled AA through the willingness to interact, composed of willingness

to ask and give assistance. The aim of this paper is to investigate, through computer simulations, the behavior

of agents given the proposed computational model with respect to different initial conﬁgurations, and level of

dependencies between agents. Dependency refers to the need for help that one agent has. Such need can be

fulﬁlled by deciding to depend on other agents. Results show that, ﬁrstly, agents whose willingness to interact

changes during run-time perform better compared to those with static willingness parameters, i.e. willingness

with ﬁxed values. Secondly, two strategies for updating the willingness are compared, (i) the same ﬁxed value

is updated on each interaction, (ii) update is done on the previous calculated value. The maximum number of

completed tasks which need assistance is achieved for (i), given speciﬁc initial conﬁgurations.

1 INTRODUCTION

Adaptive autonomy enables software agents to de-

cide, on the ﬂy, on their autonomy levels, i.e. on

whether to be more or less autonomous in the context

of a task or a goal, with respect to other entities, such

as humans and other agents. There are several other

theories on autonomy and the way it can change (Ver-

non et al., 2007). Castelfranchi (Castelfranchi, 2000)

uses dependence theory to deﬁne autonomy. An agent

A which is trying to complete a task/goal x but lacks

any means to do so (e.g. knowledge, resources, or

functional ability), will depend on another agent B for

help, thus will become less-autonomous with respect

to task/goal x. Note that, this represents the social as-

pect of autonomy which deals with agent-agent inter-

action, and is to be distinguished from issues related

to an agent’s autonomy from an environment. John-

son et al. (Johnson et al., 2011) consider the descrip-

tive and prescriptive dimensions of autonomy, or also

referred to as self-sufﬁciency, i.e. being able to carry

out a task by oneself, and self-directedness, i.e. being

able to choose one’s own goals.

A 10 levels of autonomy model was proposed as

a guideline for understanding the concept of several

levels of autonomy which could be displayed by a sys-

tem in the context of human-robot interaction (Para-

suraman et al., 2000). This approach deﬁnes dis-

crete changes in the level of autonomy from tele-

operation to full autonomy. On the other hand, col-

laborative control (Fong et al., 2001) departed from

the dominant view of human/master - agent/slave, and

brought forward a perspective in which human and

agent are peers and use dialogue to resolve inconsis-

tencies. However, that is not to say that the agent is

able to decide on its own goals, it will still operate

under the goals deﬁned by a human. Adjustable au-

tonomy, in some cases, is used for a system in which

the human decides on the autonomy levels (Hardin

and Goodrich, 2009), and in others as an umbrella

term that covers different ways in which autonomy is

shared between humans and agents (Johnson et al.,

2011). Mixed-initiative interaction allows for both

agent and human operator to decide on autonomy,

whilst adaptive autonomy places the decision-making

on the agent (Hardin and Goodrich, 2009). Usually,

the difference in these concepts lies on the party that

is increasing or decreasing agent autonomy. In adap-

tive autonomy, this decision lies with the agent itself.

In this paper, it is assumed that autonomy changes

when agents decide to become dependent on one an-

other. These decisions are taken continuously, based

on the circumstances. The willingness to interact

models the two facets of these interactions, through

the willingness to give, and ask for help (Frasheri

et al., 2017a). The behavior of the agents with dy-

258

Frasheri, M., Cürüklü, B. and Ekström, M.

Comparison Between Static and Dynamic Willingness to Interact in Adaptive Autonomous Agents.

DOI: 10.5220/0006648002580267

In Proceedings of the 10th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2018) - Volume 1, pages 258-267

ISBN: 978-989-758-275-2

namic and static willingness to interact is compared.

The hypothesis is that agents with dynamic willing-

ness complete more tasks than agents with static will-

ingness. Moreover, two different strategies for up-

dating the willingness are considered in the dynamic

case, one in which the same initial value (base-line) is

updated on each interaction, and another in which the

update is done on the previous calculated value.

The rest of this paper is organized as follows. In

Section 2 related work found in the ﬁeld is discussed.

Section 3 describes the agent model and in particular

the willingness to interact. The simulation setup is

described in Section 4, whilst the results are discussed

in Section 5. Finally, Section 6 provides a discussion

and future work directions.

2 RELATED WORK

Related work in the area is quite vast with respect

to the different theories and approaches to autonomy.

Johnson et al. (Johnson et al., 2011) assert that inter-

dependencies in joint-activity should be at the heart

of designing (software) systems with adjustable au-

tonomy. In this model, agents are inter-dependent if

they rely on each other during the execution of their

goals/tasks. Moreover inter-dependencies could be

soft, i.e. they are not necessary for the successful

outcome of a task but can improve performance, and

hard, i.e. they are in fact necessary for the success-

ful outcome of a task. They further propose a de-

sign methodology (Johnson et al., 2014), which aims

to provide concrete tools that can be used while im-

plementing a system with adjustable autonomy. The

method covers the following steps. In the beginning,

possible inter-dependencies in the system (between

tasks, and between humans and agents) are identiﬁed.

Afterwards, different mechanisms are designed in or-

der to support them. Lastly, it is analyzed how these

mechanisms affect the existing inter-dependent rela-

tionships. In the paper presented here, a higher level

of abstraction is considered, in which tasks are ab-

stract. Their other work has focused on policy sys-

tems, such as Kaa (Bradshaw et al., 2005), which al-

lows a central agent to change policies for some of

the agents during run-time, depending on the circum-

stances. The human will be put in the loop if Kaa

cannot reach a decision. In the paper presented here,

there is no central solution. Each agent makes deci-

sions on its own autonomy.

Frameworks such as STEAM (Tambe, 1997), and

DEFACTO (Schurr et al., 2009), have been proposed

to target support for teamwork and adjustable auton-

omy, respectively. STEAM extends the Soar (Laird,

2012) by adding support for teamwork through team

operators. The agents also have their individual plans

which do not require teamwork. As a result, they

can reason for team and individual plans. The so-

lution covers a synchronization protocol, based on

whether communication is necessary (through the

likelihood that others have it already), the cost for

miss-coordination, and the threat that some event

poses to the joint plan. In the paper presented

here, the main assumption is that an activity (task)

that may start as an individual one, could turn out

to need support, thus it could become a team-task.

The DEFACTO framework aims at providing support

for transfers of control in continuous time, resolv-

ing human-agent inconsistencies, and making actions

interrupt-able for real-time systems.

Scenarios with static and dynamic autonomy are

compared (Martin and Barber, 2006). The authors use

different decision frameworks, such as master-slave,

peer to peer and locally autonomous, which are dy-

namically switched between each other based on the

speciﬁc conditions. The mapping between the right

decision framework and conditions is set in advance.

The authors aim to show the usefulness of dynamic

autonomy. Whereas, other work compares different

implementations (Hardin and Goodrich, 2009), such

as adaptive autonomy (agents change their own auton-

omy), mixed-initiative interaction (both human and

agent are able to change autonomy), and adjustable

autonomy (the human is able to change the auton-

omy). The implementation of mixed-initiative inter-

action performs better than the other two, measured

by the number of victims found in a search and res-

cue simulation environment. In their case, AA agents

would always try to maintain the highest-level auton-

omy. In the paper presented here, two different sce-

narios are considered. One in which, the agents go

back to a ﬁxed level after each interaction, and an-

other in which agents adapt continuously.

Speciﬁc reasoning mechanisms have been pro-

posed that weigh the inﬂuence of outside stimuli (e.g.

order of a superior) on the agent, by considering

task urgency and dedication level to the organiza-

tion(van der Vecht et al., 2009). This paper extends

on the factors that shape agent reasoning as is detailed

in the following sections. Others allow the change

in autonomy to happen at the individual task level

(Brookshire et al., 2004), i.e. the agent can execute a

task autonomously, whilst being tele-operated for an-

other one. The scenario in the current paper assumes

that agents perform tasks sequentially, and that they

can delegate when assistance is needed. Another ap-

proach is to categorize tasks in two groups, i.e. tasks

which the robot is able to perform by itself, and tasks

Comparison Between Static and Dynamic Willingness to Interact in Adaptive Autonomous Agents

259

that need human supervision/assistance (Kim et al.,

2016). Algorithms are designed based on this clas-

siﬁcation. The current paper does not assume such

categorization done before hand, and any task can

turn out to need assistance. Moreover, the presence

of the human operator is not modeled. Silva et al.

(da Silva et al., 2017) propose an agent framework

for when to ask for and give advice to others, in a

multi-agent learning environment. These two behav-

iors are shaped from the conﬁdence level an agent has

in its current state, i.e. an agent will ask for advise if

not conﬁdent in its current policies, or give advice if

it is conﬁdent in them. The concepts discussed in the

present paper are complementary to these ideas, but

the type of interactions assumed represent task dele-

gation from one agent to another.

3 THE AGENT MODEL

The agent model described in this section stems from

(Frasheri et al., 2017b), (Frasheri et al., 2017a). In

this model, the problem of embedding adaptive au-

tonomous behavior in an agent is addressed from two

perspectives. Firstly, a generic high-level agent model

models the internal operation of the agent. Secondly,

the willingness to interact is introduced, based on

which the agent can modify its autonomy as needed.

Willingness to interact is composed of two separate

relationships, to help and to ask for help. In order

to calculate the willingness, an initial computational

model has been proposed and is incorporated in the

general agent framework.

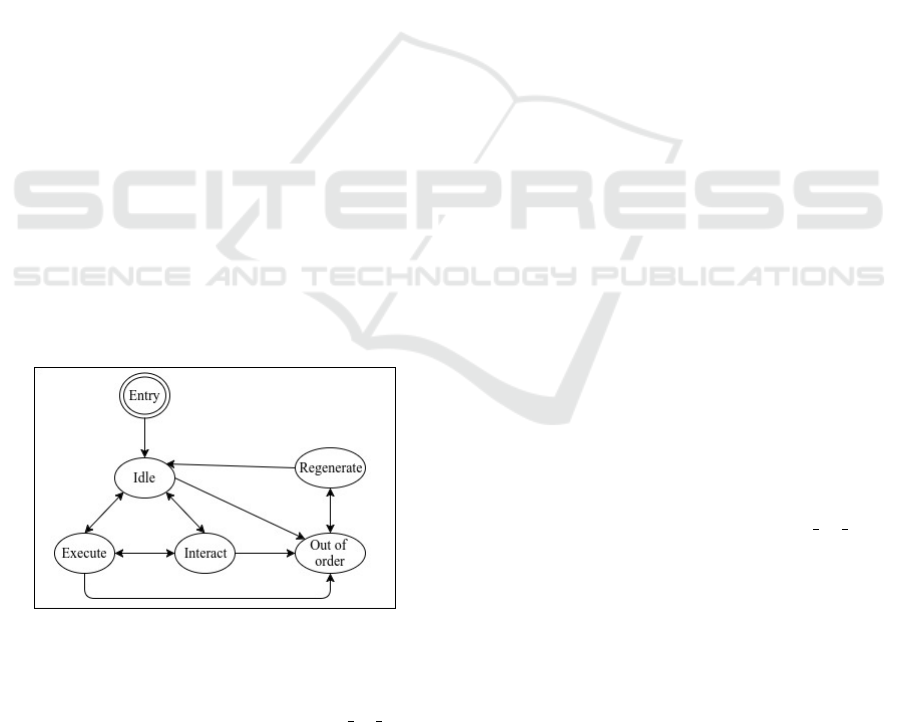
Figure 1: The proposed agent model composed of ﬁve

states.

The agent model is composed of ﬁve states, idle,

execute, interact, regenerative and out o f order

(Figure 1). It is also assumed to have the following

characteristics:

1. b: battery

2. e: equipment (sensors, motors, actuators)

3. a: abilities (2D vision, reasoning, planning, mov-

ing, object manipulation and so on)

4. t: tools

5. k: knowledge (with respect to a task, its environ-

ment, other agents)

These characteristics are implemented in an abstract

way, detailed in Section 4. Furthermore, the agent is

assumed to be able to estimate the following:

1. e

: environment risk factor

2. a

: potential collaborator risk

3. µ: its own performance

4. t

: progress of the task for which it is requiring

help (partially implemented)

5. t

: trade-off of adopting a new task and post-

poning/dropping the current task (not yet imple-

mented)

The general operation of the agent runs as follows.

The agent starts its operation in the idle state. In idle,

the agent has not committed to any goal. The impli-

cation of this is that the agent might be doing nothing

(simply waiting for a request), or it might decide to

adopt a goal. When an agent commits to a goal, it

is added into its FIFO queue, switches to the execute

state and performs the task related to that goal. Dur-

ing the execution, the agent will evaluate if it needs

to ask another agent for assistance (based on the will-

ingness to ask for help). When the task is complete,

the agent will return to idle. If the agent is in idle or

execute, when a request is received, it will switch to

the interact state. The latter is not possible to inter-

rupt, and by the end of this state the agent will decide

(based on the willingness to give help) whether to ac-

cept the received request. If accepted, the correspond-

ing task is put into the agent’s FIFO queue, otherwise

the request will be discarded. Multiple requests are

handled sequentially, depending on the incoming or-

der. If accepted they are put into the queue, otherwise

they are discarded. If an agent’s battery level goes

below the threshold, it will switch to out o f order.

Thresholds are taken the same for each agent for sim-

plicity, but it is not necessary that they are so. As a re-

sult, the agent will immediately switch to regenerate,

in which the recharge takes place. Afterwards the

agent returns to idle. The switch from regenerate

to idle happens immediately. Once more, this choice

was for simplicity. A time delay could be introduced

to make the process more realistic.

3.1 Willingness to Interact

In this paper an agent’s willingness to interact shapes

its autonomy and is composed of two elements which

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

260

are willingness to give help δ and willingness to ask

for help γ. The reasoning of the agent on its willing-

ness is explained in the following scenario.

Assume an agent A which decides to do a task

t. At ﬁrst, A will need to consider if it has enough

energy before continuing with the pursuit. Then, it

needs to make sure that it has all the required abili-

ties in its repertoire. Moreover, agent A might have

different levels of expertise for its abilities. After-

wards, the agent needs to make sure it has all the re-

quired resources, in the necessary quantity and qual-

ity. Resources are composed of internal and external

resources. Internal resources include energy/battery,

sensors, motors, actuators, knowledge that are part of

the agent. External resources include physical objects

in the environment and other agents (individually and

as groups). Whether the agent has the needed levels

of energy, abilities, and resources will depend upon

the speciﬁc requirements of the task. Assume that A

has an ability a

with level of expertise q. It might

be that even though the value of q is above a speciﬁc

threshold for a task t

, the same value may not be ac-

ceptable for another task t

. If agent A complies well

with what is needed for the task, it could in principle

conduct the activity autonomously on its own.

However, other factors might be taken into con-

sideration. Agent A has a performance value deter-

mined by its past successes and failures. The lower

the performance, the higher the inclination to ask for

help might be. Furthermore, the agent might be more

inclined to ask for help if it has not progressed by it-

self with respect to the task, or if the environment it

is operating within is highly threatening. However, if

the agent knows no one, or if it lives among unhelpful

agents, it might be inclined otherwise. When agent

A decides to require assistance, it will forward its re-

quest to some agent B. It is reasonable to assume that

B is not chosen at random, but based on past history

of collaboration between A and B and the correspond-

ing successes. Naturally, when there is not any of the

latter, the agent might choose at random between the

agents it knows. Agent B will then need to process the

request of agent A. The reasoning of B will be similar,

with the added consideration of the trade-off between

dropping or postponing its current activities in order

to help A. The inﬂuence of each of the factors on

the components of the willingness is captured in Fig-

ures 2 and 3. In Figure 2 it is shown that if the agent

misses any of the required internal resources, then it

cannot perform the task, thus it will ask for help. This

is deterministic. On the other hand, the other factors

model the probabilistic nature of the willingness to

ask for help. If the perceived environmental risk in-

creases, then the willingness to ask increases, other-

Figure 2: Inﬂuence diagram for the willingness to ask for

help, γ.

wise it decreases. If the perceived risk from another

agent increases, then the willingness to ask decreases,

otherwise it increases. If the agent’s own performance

increases, then the willingness increases, otherwise it

decreases. Finally, if the task progress increases, the

willingness to ask decreases (if the agent progresses,

the need for assistance decreases), otherwise it in-

creases. In Figure 3 it is shown that missing the in-

Figure 3: Inﬂuence diagram for the willingness to give help,

δ.

ternal resources will decrease the willingness to give

help, otherwise the willingness increases. It is clear

in this case, that if the agent still accepts to help, it

will in turn ask for help another agent, thus creating

a chain reaction (Frasheri et al., 2017b). Another ap-

proach could be to have the agent directly reject any

request if it misses any of the internal resources, and

let the agent in need ﬁgure out what to do next. If the

environmental risk decreases, then the willingness to

give increases, otherwise it decreases. If the agent risk

increases, then the willingness decreases, otherwise it

increases. If the agent’s own performance increases,

then the willingness increases, otherwise it decreases.

Comparison Between Static and Dynamic Willingness to Interact in Adaptive Autonomous Agents

261

Finally, if the task trade-off is in favor of the new task,

then the willingness will increase, otherwise it will

decrease.

Agents are assumed to start their operation with

predeﬁned values hδ

, γ

i, and corresponding chang-

ing steps h∆δ, ∆γi. Moreover, they are equipped with

a set of abstract sensors, actuators, motors, knowledge

and abilities. Also, there are no restrictions assumed

as to whether they change in time, e.g. an agent could

have an initial minimal amount of knowledge which

expands during the operation through learning, or the

agent might be updated to support new abilities and

so on. Agents are assumed to be able to compute a

risk factor for the environment they operate in and for

each other agent in that environment. In addition, they

are able to compute a performance measure for them-

selves. An agent can generate a task t

to do, or can

receive a request from another agent for another task

. The task comes with speciﬁc execution require-

ments such as: estimated amount of energy required,

equipment, knowledge, abilities, tools. It is worth

noting that the functions used to determine each of

the variables that affect willingness may vary. For the

purposes of this paper, they are computed in simple

terms (Section 4). Currently the following limitations

hold. (i) The degree to which an agent has an ability,

or a resource is not considered, i.e. these properties

take binary values. (ii) An agent checks if it needs

assistance at the beginning of each task. (iii) A task

is simulated as an atomic step, as such the trade-off

between tasks is not simulated in the current work.

4 SIMULATIONS

The behavior of the agents was investigated through

computer simulations. One trial was conducted, and

is composed of two separate computer simulations,

referred to as phases. In the ﬁrst phase, the values of

δ and γ are static throughout the whole time. Sim-

ulations are repeated for the following combinations

of hδ,γi: h0.0,0.0i h0.5,0.0i, h1.0,0.0i, h0.0,0.5i,

h0.5,0.5i, h1.0,0.5i, h0.0, 1.0i, h0.5,1.0i, h1.0,1.0i,

h0.2,0.2i h0.5, 0.2i, h0.8,0.2i, h0.2,0.5i, h0.8,0.5i,

h0.2,1.0i, h0.5,0.8i, and h0.8,0.8i. These values are

chosen as representatives of extreme and average self-

ish/unselﬁsh agent behavior. In the second phase,

their values will change during run-time according to

the scheme shown in Figures 2 and 3 with ∆δ = ∆γ =

0.05. Simulations are repeated for all combinations

of hδ

,γ

i: h0.0,0.0i h0.5,0.0i, h1.0,0.0i, h0.0,0.5i,

h0.5,0.5i, h1.0,0.5i, h0.0, 1.0i, h0.5,1.0i, h1.0,1.0i,

h0.2,0.2i h0.5, 0.2i, h0.8,0.2i, h0.2,0.5i, h0.8,0.5i,

h0.2,1.0i, h0.5,0.8i, and h0.8,0.8i, in which δ

and

are the initial values for δ and γ. Moreover, for the

second phase of simulations, two update strategies for

δ and γ are investigated. In one strategy, the values

for δ and γ will always be calculated from δ

and γ

In the other strategy, the values for δ and γ will be

calculated based on values calculated on the previous

interaction.

All experiments are repeated for three levels of

difﬁculty. Difﬁculty refers to the probability (P

) that

an agent lacks any of the abilities, knowledge, equip-

ment, or tools. The higher this probability, the higher

the chances that an agent will ask for help. The val-

ues taken for P

are 0.2,0.5,0.8, which means that

for P

= 0.2, the probability that the agent will ask

for help is 0.2, and the difﬁculty of the simulation is

low. The size of the population is 30, and remains

ﬁxed across phases.

Each simulation runs for circa 20 minutes. Within

this amount of time, the agents are able to attempt and

complete a considerable amount of tasks, in the range

of hundreds. Consequently, it is possible to identify

a trend for the number of tasks completed over those

attempted. This choice was considered adequate for

the purposes of this paper. Naturally, it is possible to

let the agents run for a longer time.

Each agent is composed of a set of ROS (Quigley

et al., 2009) nodes. The communication between

agents happens by broadcast (when agents make

themselves known to each other), and by a tailored

action-server mechanism (when agents make one to

one help requests to each other). All agents in the

simulation start in their idle state. Each time they are

in this state, a task could be generated with a proba-

bility P = 0.6.

In the current state of the implementation an agent

reasons at the beginning of each task on whether it

needs assistance. If it does not, then it is supposed to

always succeed by itself. Moreover, the execution of

each task is simulated by having the system pause for

a speciﬁc amount of time ∆t which corresponds to a

predeﬁned completion time of a task. This is a sim-

pliﬁed scenario that was deemed adequate for the pur-

poses of the simulations described here. The success

criterion for the static case is deﬁned as follows. An

agent fails when it attempts a task while lacking any

of the following internal resources: abilities, knowl-

edge, battery, equipment, and tools. Otherwise it will

succeed. The presence of any of the abilities, knowl-

edge, equipment, and tools, is decided by the difﬁ-

culty of the simulation.

All agents start with the same level of battery

b = 4000 of energy units, which decreases after every

ﬁnished task by the amount of energy required by that

task. If b becomes lower than a threshold b

low

= 300,

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

262

then the agent goes into the out o f order state. Pa-

rameters b and b

low

are not bound to these speciﬁc

values. These were chosen for running the simula-

tion. The energy level required by tasks is generated

at random at task generation as follows. First, a task

difﬁculty is selected randomly between low, medium,

and high. If the task is of low difﬁculty, then the en-

ergy required for it, is chosen randomly in the range

1 − 30. Whereas, if the difﬁculty is medium, then the

energy is taken in the range 31 − 60. Finally, for the

high difﬁculty, energy is chosen in the range 61 − 90.

When giving help, the agent always checks whether

its current battery level minus the energy required by

the task is above the threshold b

low

The agent to ask for help is the one with the high-

est perceived helpfulness with probability p = 0.6 and

randomly otherwise. Perceived helpfulness in this

case is interpreted as the least amount of risk, calcu-

lated as in Equation 1.

β = max({ph

,...ph

}) (1)

where ph

- perceived helpfulness of agent i, n - num-

ber of agents.

Agents keep track of how many tasks they are at-

tempting, completing, and also whether they needed

help for a task or not. Tasks for which help is ei-

ther needed or asked for, are called dependent tasks.

A task is by default dependent if the agent lacks any

of the following: battery, abilities, resources, knowl-

edge, external resources. The performance for each

agent is expressed in terms of completed tasks over

attempted tasks, as follows.

µ =

Tasks Completed

Tasks Attempted

(2)

Factors such as environmental risk and task

progress are kept constant throughout the simulation,

therefore they affect the willingness to interact in the

same way on each interaction. The environmental risk

is ﬁxed to a low value equal to 0.2, and affects γ by

−∆γ, and δ by +∆δ. This means that, when environ-

mental risk is perceived as low, the willingness to ask

for help will get lower, whilst the willingness to give

help will get higher. Furthermore, since the reasoning

for asking for help is done at the beginning of the task

and the agent cannot yet have a sense of progress, the

task-progress affect is by −∆γ over γ.

5 RESULTS

The simulations were run in order to investigate the

following hypothesis. Agents which change their

willingness to interact during run-time are able to

h0.0, 0.0i

h0.5, 0.0i

h1.0, 0.0i

h0.0, 0.5i

h0.5, 0.5i

h1.0, 0.5i

h0.0, 1.0i

h0.5, 1.0i

h1.0, 1.0i

h0.2, 0.2i

h0.5, 0.2i

h0.8, 0.2i

h0.2, 0.5i

h0.8, 0.5i

h0.2, 0.8i

h0.5, 0.8i

h0.8, 0.8i

0.2

0.4

0.6

0.8

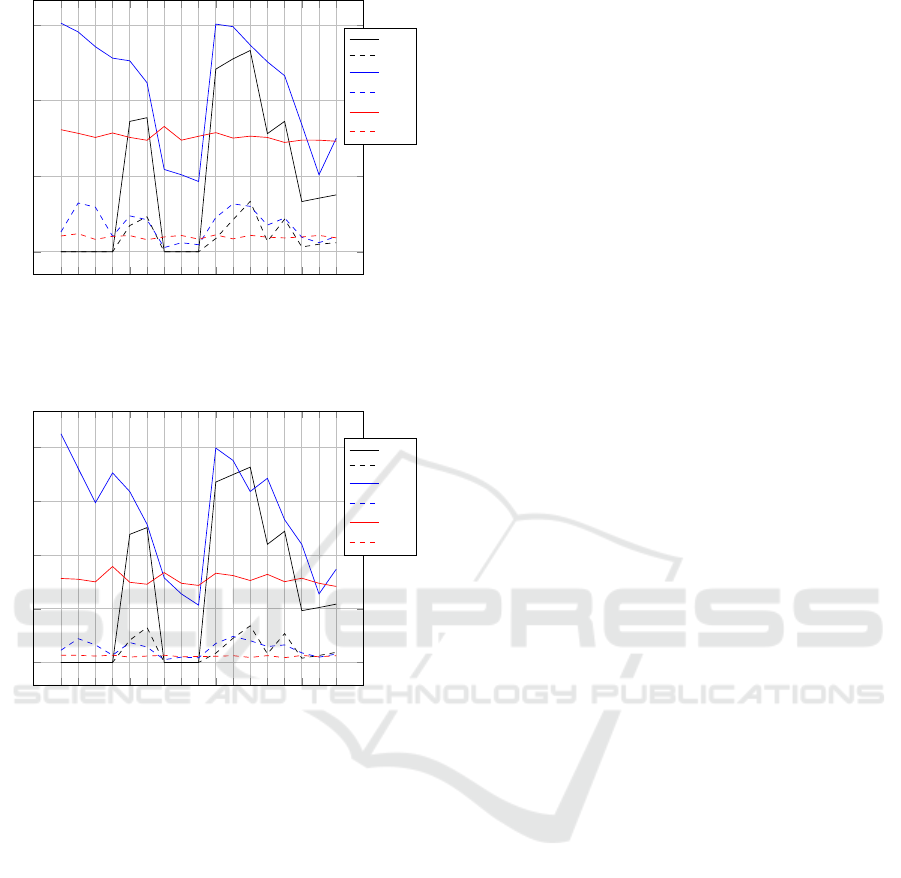
Figure 4: Task completion percentages for P

= 0.2. The

x-axis contains different conﬁgurations for hδ, γi. s

refers

to the completion degree for all tasks in the static phase,

whereas s

corresponds to completion degree of dependent

tasks. The interpretation of the subscript is the same for d1

and d2. Both refer to the dynamic case, d1 to the base-line

update, and d2 to the continuous update respectively.

complete more tasks (as a population) compared to

the agent population with static willingness. This

problem was partially targeted in (Frasheri et al.,

2017b) by considering only the willingness to give

help. Moreover, two different methods of updat-

ing the willingness are compared, (i) agents update

their willingness based on previous calculated values,

(ii) agent update their willingness from ﬁxed base-

line values. Each separate simulation was run 10

times, thereafter the mean and standard deviation val-

ues were calculated.

The results are shown in graphic, Figures 4-6, and

tabular form, Tables 1-3, (where the standard devi-

ation values are shown as well in round brackets).

In each graph, the different combinations hδ

,γ

i are

displayed along the x-axis, whereas the percentages

of completed tasks are along the y-axis (results corre-

spond to the population as a whole). Two completion

degrees are considered: on one hand the one with re-

spect to all tasks computed as in Equation 2, on the

other hand the one with respect to dependent tasks

(tasks that cannot be achieved without help) com-

puted as in Equation 3.

Dependent Tasks Completed

Dependent Tasks Attempted

(3)

5.1 Static vs. Dynamic Willingness

It is possible to observe from Figures 4-6 that agents

with dynamic willingness perform better in most

Comparison Between Static and Dynamic Willingness to Interact in Adaptive Autonomous Agents

263

h0.0, 0.0i

h0.5, 0.0i

h1.0, 0.0i

h0.0, 0.5i

h0.5, 0.5i

h1.0, 0.5i

h0.0, 1.0i

h0.5, 1.0i

h1.0, 1.0i

h0.2, 0.2i

h0.5, 0.2i

h0.8, 0.2i

h0.2, 0.5i

h0.8, 0.5i

h0.2, 0.8i

h0.5, 0.8i

h0.8, 0.8i

0.2

0.4

0.6

Figure 5: Task completion percentages for P

= 0.5. Nota-

tion interpretation as in Figure 4.

h0.0, 0.0i

h0.5, 0.0i

h1.0, 0.0i

h0.0, 0.5i

h0.5, 0.5i

h1.0, 0.5i

h0.0, 1.0i

h0.5, 1.0i

h1.0, 1.0i

h0.2, 0.2i

h0.5, 0.2i

h0.8, 0.2i

h0.2, 0.5i

h0.8, 0.5i

h0.2, 0.8i

h0.5, 0.8i

h0.8, 0.8i

0.1

0.2

0.3

0.4

Figure 6: Task completion percentages for P

= 0.8. Nota-

tion interpretation as in Figure 4.

cases than their static counterpart. Thus the hypoth-

esis holds across the three difﬁculty levels for most

combinations of hδ, γi, considering the completion of

both dependent and all tasks. Obviously, as the proba-

bility of failure (P

) increases, the performance of the

agents degrades independently of whether the will-

ingness is static or dynamic. Moreover, in Figure

6, it is also possible to observe that static combina-

tions of willingness such as h1.0,0.5i, h0.8, 0.2i, and

h0.8,0.5i perform slightly better than the dynamic

counterparts.

In the static scenario, it is clear that for δ = 0.0, the

agents will never help one another, thus no dependent

tasks will be achieved. Also, for γ = 1.0, all agents

will always ask one another, and will not accomplish

any tasks. When γ = 0.0, agents will never ask, so the

outcome will be the same as in the previous cases. For

other combinations, some dependent tasks are accom-

plished. As mentioned previously, if the agent does

not ask for help when a task is necessarily dependent

(i.e. either battery, ability, knowledge, equipment, or

external resources lack), then it will fail. Asking for

help is determined with ﬁxed probabilities, which are

the initial values for γ. In the dynamic case, this is

not probabilistic. If an agent determines a task to be

dependent (based on the difﬁculty level of the simu-

lation P

), then it will for sure ask for help, thus in-

creasing the chances of the task being completed.

5.2 Base-line Update vs. Continuous

The comparison between the cases with base-line up-

date and continuous update can be made from sev-

eral perspectives. For low difﬁculty of the simulation

(Figure 4), it is possible to observe that the best per-

formance (dependent tasks) is achieved in the base-

line update for the conﬁguration hδ

= 0.8,γ

= 0.2i,

followed by hδ

= 1.0, γ

= 0.0i.

In Figure 5, best performance in base-line up-

date is achieved for the conﬁgurations hδ

= 0.5,γ

0.0i, hδ

= 0.5,γ

= 0.2i, and hδ

= 0.8,γ

= 0.2i.

Whereas, in the static update, the performance peaks

are for hδ

= 0.8,γ

= 0.2i, and hδ

= 1.0,γ

= 0.5i.

The maximum performance, with respect to depen-

dent tasks, is achieved for static update with hδ

0.8,γ

= 0.2i. Nevertheless, with respect to all con-

ﬁgurations the base-line update does slightly better.

In Figure 6, there are three peaks for static up-

date, hδ

= 1.0,γ

= 0.5i, hδ

= 0.8,γ

= 0.2i, and

hδ

= 0.8,γ

= 0.5i. The difference with the base-

line update is higher than in Figure 5. The base-line

update does better for other conﬁgurations.

The continuous case does always worse, and is

overall better than the static case only for P

0.2, (Figure 4), with maximums achieved for hδ

0.5,γ

= 0.0i, hδ

= 0.5, γ

= 1.0i, and hδ

0.5,γ

= 0.8i. For the other values of P

, the con-

tinuous update has overall the worst performance out-

comes, with no clear peaks. It is also noticeable

that for the continuous update, all the agents, inde-

pendently of their start seem to reach a stable state,

i.e. the range of values for the performance is small,

around 0.2% for low difﬁculty level of the simulation.

This phenomenon is true for both dependent and total

tasks completed rates (Figure 4).

Finally, it is possible to observe that the same pat-

terns for static, base-line, and continuous update, hold

across difﬁculty levels. Furthermore, the base-line

and static updates follow similar patterns across dif-

ferent combinations of hδ,γi.

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

264

Table 1: Task completion percentages for P

= 0.2. s

refers to the completion degree for all tasks in the static phase, whereas

corresponds to completion degree of dependent tasks. The interpretation of the subscript is the same for d1 and d2. Both

refer to the dynamic case, d1 to the base-line update, and d2 to the continuous update respectively.

Static Base-line Continuous

hδ

,γ

i s

<0.0,0.0> na 0 0.833 (0.005) 0.158 (0.009) 0.711 (0.023) 0.203 (0.050)

<0.5,0.0> na 0 0.877 (0.016) 0.430 (0.062) 0.742 (0.024) 0.249 (0.049)

<1.0,0.0> na 0 0.882 (0.017) 0.483 (0.068) 0.687 (0.031) 0.191 (0.044)

<0.0,0.5> na 0 0.726 (0.009) 0.111 (0.017) 0.718 (0.020) 0.216 (0.050)

<0.5,0.5> 0.477 (0.015) 0.113 (0.010) 0.829 (0.009) 0.344 (0.022) 0.727 (0.017) 0.223 (0.024)

<1.0,0.5> 0.493 (0.012) 0.146 (0.017) 0.754 (0.013) 0.296 (0.032) 0.696 (0.031) 0.211 (0.049)

<0.0,1.0> na 0 0.311 (0.016) 0.027 (0.005) 0.709 (0.021) 0.216 (0.046)

<0.5,1.0> na 0 0.323 (0.019) 0.062 (0.010) 0.732 (0.021) 0.243 (0.041)

<1.0,1.0> na 0 0.306 (0.029) 0.046 (0.009) 0.695 (0.023) 0.223 (0.040)

<0.2,0.2> 0.673 (0.008) 0.067 (0.008) 0.861 (0.006) 0.326 (0.019) 0.704 (0.022) 0.193 (0.028)

<0.5,0.2> 0.701 (0.006) 0.166 (0.008) 0.908 (0.008) 0.581 (0.033) 0.722 (0.022) 0.215 (0.032)

<0.8,0.2> 0.731 (0.006) 0.258 (0.014) 0.920 (0.013) 0.654 (0.051) 0.697 (0.025) 0.201 (0.034)

<0.2,0.5> 0.435 (0.014) 0.049 (0.008) 0.756 (0.009) 0.207 (0.015) 0.700 (0.014) 0.203 (0.017)

<0.8,0.5> 0.488 (0.008) 0.136 (0.008) 0.776 (0.019) 0.303 (0.024) 0.703 (0.019) 0.206 (0.032)

<0.2,1.0> 0.193 (0.017) 0.019 (0.005) 0.492 (0.015) 0.086 (0.011) 0.696 (0.022) 0.200 (0.027)

<0.5,0.8> 0.199 (0.017) 0.032 (0.006) 0.525 (0.015) 0.133 (0.012) 0.734 (0.026) 0.243 (0.064)

<0.8,0.8> 0.208 (0.015) 0.033 (0.006) 0.492 (0.015) 0.118 (0.018) 0.691 (0.028) 0.202 (0.052)

Table 2: Task completion percentages for P

= 0.5. Notation interpretation as in Table 1.

Static Base-line Continuous

hδ

,γ

i s

<0.0,0.0> na 0 0.605 (0.016) 0.053 (0.009) 0.323 (0.021) 0.042 (0.008)

<0.5,0.0> na 0 0.581 (0.015) 0.129 (0.017) 0.313 (0.033) 0.048 (0.012)

<1.0,0.0> na 0 0.542 (0.016) 0.118 (0.014) 0.302 (0.019) 0.033 (0.015)

<0.0,0.5> na 0 0.512 (0.019) 0.041 (0.007) 0.314 (0.012) 0.041 (0.016)

<0.5,0.5> 0.345 (0.019) 0.070 (0.013) 0.505 (0.021) 0.095 (0.010) 0.302 (0.025) 0.043 (0.013)

<1.0,0.5> 0.355 (0.017) 0.092 (0.012) 0.447 (0.024) 0.085 (0.012) 0.295 (0.054) 0.032 (0.008)

<0.0,1.0> na 0 0.218 (0.016) 0.011 (0.003) 0.331 (0.051) 0.039 (0.007)

<0.5,1.0> na 0 0.204 (0.023) 0.024 (0.004) 0.295 (0.022) 0.043 (0.012)

<1.0,1.0> na 0 0.186 (0.018) 0.019 (0.004) 0.306 (0.034) 0.033 (0.010)

<0.2,0.2> 0.483 (0.009) 0.035 (0.004) 0.602 (0.019) 0.091 (0.011) 0.315 (0.030) 0.045 (0.016)

<0.5,0.2> 0.510 (0.008) 0.085 (0.007) 0.595 (0.023) 0.127 (0.020) 0.301 (0.030) 0.034 (0.011)

<0.8,0.2> 0.532 (0.005) 0.133 (0.009) 0.547 (0.023) 0.120 (0.022) 0.306 (0.017) 0.044 (0.015)

<0.2,0.5> 0.312 (0.013) 0.027 (0.003) 0.502 (0.023) 0.071 (0.009) 0.302 (0.018) 0.039 (0.012)

<0.8,0.5> 0.345 (0.011) 0.086 (0.009) 0.466 (0.033) 0.089 (0.017) 0.289 (0.024) 0.037 (0.011)

<0.2,1.0> 0.133 (0.019) 0.013 (0.004) 0.336 (0.021) 0.039 (0.007) 0.295 (0.024) 0.039 (0.011)

<0.5,0.8> 0.142 (0.014) 0.020 (0.006) 0.204 (0.023) 0.024 (0.004) 0.295 (0.022) 0.043 (0.012)

<0.8,0.8> 0.151 (0.023) 0.024 (0.008) 0.300 (0.037) 0.041 (0.005) 0.292 (0.037) 0.037 (0.008)

6 DISCUSSION

In this paper, the feature deﬁned as willingness to in-

teract has been investigated through multi-agent sim-

ulations. The evaluation is deﬁned as the percent-

age of completed tasks. The results show the beneﬁt

of dynamic willingness to interact, using a base-line

update strategy, as compared to its static counterpart

in the implemented scenario. Thus, the simulations

show that the performance of the agents improves, i.e.

percentage of completed tasks, when willingness be-

comes a dynamic function, in all difﬁculty levels. In

this context, difﬁculty level refers to the fraction of

tasks that require assistance from other agents to be

ﬁnished. Moreover, the effects of the update strat-

egy on the dynamic willingness to interact were in-

vestigated. The results show that, in the case of base-

line update, it is possible to reach a maximum perfor-

mance under speciﬁc initial conditions. Whilst in the

case of continuous update, the performance is con-

Comparison Between Static and Dynamic Willingness to Interact in Adaptive Autonomous Agents

265

Table 3: Task completion percentages for P

= 0.8. Notation interpretation as in Table 1.

Static Base-line Continuous

hδ

,γ

i s

<0.0,0.0> na 0 0.425 (0.019) 0.023 (0.005) 0.156 (0.017) 0.014 (0.006)

<0.5,0.0> na 0 0.361 (0.019) 0.044 (0.008) 0.155 (0.021) 0.013 (0.004)

<1.0,0.0> na 0 0.297 (0.025) 0.033 (0.002) 0.150 (0.022) 0.012 (0.006)

<0.0,0.5> na 0 0.353 (0.015) 0.013 (0.004) 0.179 (0.038) 0.013 (0.007)

<0.5,0.5> 0.238 (0.017) 0.041 (0.008) 0.318 (0.022) 0.037 (0.006) 0.149 (0.033) 0.010 (0.004)

<1.0,0.5> 0.251 (0.016) 0.065 (0.011) 0.257 (0.021) 0.029 (0.008) 0.146 (0.024) 0.012 (0.004)

<0.0,1.0> na 0 0.157 (0.024) 0.005 (0.003) 0.167 (0.039) 0.013 (0.004)

<0.5,1.0> na 0 0.127 (0.017) 0.010 (0.002) 0.147 (0.035) 0.011 (0.004)

<1.0,1.0> na 0 0.107 (0.012) 0.009 (0.003) 0.143 (0.022) 0.011 (0.004)

<0.2,0.2> 0.336 (0.005) 0.017 (0.002) 0.399 (0.018) 0.035 (0.005) 0.166 (0.030) 0.011 (0.006)

<0.5,0.2> 0.350 (0.010) 0.045 (0.005) 0.376 (0.013) 0.048 (0.007) 0.162 (0.033) 0.013 (0.003)

<0.8,0.2> 0.363 (0.013) 0.068 (0.005) 0.318 (0.018) 0.041 (0.008) 0.152 (0.027) 0.009 (0.004)

<0.2,0.5> 0.220 (0.009) 0.016 (0.004) 0.343 (0.016) 0.030 (0.005) 0.164 (0.029) 0.013 (0.006)

<0.8,0.5> 0.244 (0.014) 0.054 (0.009) 0.266 (0.024) 0.033 (0.006) 0.150 (0.026) 0.009 (0.005)

<0.2,1.0> 0.096 (0.008) 0.008 (0.002) 0.220 (0.013) 0.018 (0.006) 0.157 (0.024) 0.013 (0.004)

<0.5,0.8> 0.102 (0.015) 0.013 (0.005) 0.127 (0.017) 0.010 (0.002) 0.147 (0.035) 0.011 (0.004)

<0.8,0.8> 0.108 (0.011) 0.019 (0.003) 0.174 (0.016) 0.016 (0.005) 0.141 (0.019) 0.012 (0.004)

sistently worse. The simulation results seem to point

to the conclusion that a high willingness to ask for

help hinders the performance of the agents. Thus, the

best conﬁguration for the agents is the one in which

hδ

= 0.8, γ

= 0.2i, and hδ

= 1.0, γ

= 0.0i (for

low difﬁculty level), which change on run-time with a

base-line update strategy. If all agents start with these

conﬁgurations, it is possible to predict results similar

to the ones presented here.

The agent model discussed in this paper is rele-

vant for different application domains, both as soft-

ware (distributed software services, social/behavioral

population models), and hardware solutions (search

and rescue, precision agriculture, collaborative indus-

trial robots). The latter explains why battery is taken

as a factor in the reasoning of the agent, which could

be a robot. Thus, the intention is to keep the model

as general as possible. In these scenarios heteroge-

neous agents/robots need to interact to exchange in-

formation or assist each other. It might not always

be the case that human operators are available to take

control or give advice. When agents/robots are dis-

patched far from the operators, communication links

can become unreliable. In such cases, the agents will

need to solve the problems by relying and helping one

another in order to complete their tasks. Adaptive au-

tonomy, realized through the willingness to interact,

can be a mean to approach the issues of when and

with whom to interact, given speciﬁc circumstances.

Future work will address the following issues.

First, the computational model of the willingness to

interact needs to be reﬁned in order to include dif-

ferent weights for the different factors. It might

be that different application domains, require differ-

ent weights for these factors. This paper consid-

ered such weights to be equal to each other for the

sake of simplicity. Secondly, as mentioned in Sec-

tion 3, an agent could map an ability to a value be-

tween 0 and 1, which could reﬂect the accuracy for

such ability (similar reasoning could be applied to re-

sources as well). This means that, either the agent

has an ability which it can use with accuracy x%, or

it does not have the ability at all. Whether the x%

value is acceptable depends on the particular task, and

it should have an appropriate inﬂuence on the will-

ingness to interact. Therefore, this granularity needs

to be taken into account. Also, the impact of fac-

tors such as: environmental risk, task trade-off, and

task progress need to be investigated further with ded-

icated simulations, while keeping the other factors

ﬁxed.

ACKNOWLEDGMENTS

The research leading to the presented results has

been undertaken within the research proﬁle DPAC –

Dependable Platforms for Autonomous Systems and

Control project, funded by the Swedish Knowledge

Foundation (the second and third authors). In part it

is also funded by the Erasmus Mundus scheme EU-

ROWEB+ (the ﬁrst author).

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

266

APPENDIX

The source code to reproduce the simulations

described in this paper is publicly available

on github: htt ps : //github.com/gitting −

around/gitagent 18.git. The simulations were

conducted using the Microsoft Azure Cloud services,

with machines with the following characteristics:

Ubuntu 14.04 LTS, Standard B4ms (4 vcpus, 16 GB

memory).

REFERENCES

Bradshaw, J. M., Jung, H., Kulkarni, S., Johnson, M.,

Feltovich, P., Allen, J., Bunch, L., Chambers, N.,

Galescu, L., Jeffers, R., et al. (2005). Kaa: policy-

based explorations of a richer model for adjustable

autonomy. In Proceedings of the fourth international

joint conference on Autonomous agents and multia-

gent systems, pages 214–221. ACM.

Brookshire, J., Singh, S., and Simmons, R. (2004). Pre-

liminary results in sliding autonomy for assembly by

coordinated teams. In Intelligent Robots and Systems,

2004.(IROS 2004). Proceedings. 2004 IEEE/RSJ In-

ternational Conference on, volume 1, pages 706–711.

IEEE.

Castelfranchi, C. (2000). Founding agent’s ’autonomy’ on

dependence theory. In Proceedings of the 14th Euro-

pean Conference on Artiﬁcial Intelligence, pages 353–

357. IOS Press.

da Silva, F. L., Glatt, R., and Costa, A. H. R. (2017). Si-

multaneously learning and advising in multiagent re-

inforcement learning. In Proceedings of the 16th Con-

ference on Autonomous Agents and MultiAgent Sys-

tems, pages 1100–1108. International Foundation for

Autonomous Agents and Multiagent Systems.

Fong, T., Thorpe, C., and Baur, C. (2001). Collaborative

control: A robot-centric model for vehicle teleoper-

ation, volume 1. Carnegie Mellon University, The

Robotics Institute.

Frasheri, M., C¸

ukl

u, B., and Ekstr

om, M. (2017a). Anal-

ysis of perceived helpfulness in adaptive autonomous

agent populations. LNCS Transactions on Computa-

tional Collective Intelligence.

Frasheri, M., C¸

ukl

u, B., and Ekstr

om, M. (2017b). To-

wards collaborative adaptive autonomous agents. In

9th International Conference on Agents and Artiﬁcial

Intelligence 2017 ICAART, 24 Feb 2017, Porto, Por-

tugal.

Hardin, B. and Goodrich, M. A. (2009). On using mixed-

initiative control: A perspective for managing large-

scale robotic teams. In Proceedings of the 4th

ACM/IEEE international conference on Human robot

interaction, pages 165–172. ACM.

Johnson, M., Bradshaw, J. M., Feltovich, P. J., Jonker,

C. M., Van Riemsdijk, B., and Sierhuis, M. (2011).

The fundamental principle of coactive design: Inter-

dependence must shape autonomy. In Coordination,

organizations, institutions, and norms in agent sys-

tems VI, pages 172–191. Springer.

Johnson, M., Bradshaw, J. M., Feltovich, P. J., Jonker,

C. M., Van Riemsdijk, M. B., and Sierhuis, M. (2014).

Coactive design: Designing support for interdepen-

dence in joint activity. Journal of Human-Robot In-

teraction, 3 (1), 2014.

Kim, S., Kim, M., Lee, J., Hwang, S., Chae, J., Park, B.,

Cho, H., Sim, J., Jung, J., Lee, H., et al. (2016). Team

snu’s control strategies for enhancing a robot’s capa-

bility: Lessons from the 2015 darpa robotics challenge

ﬁnals. Journal of Field Robotics.

Laird, J. E. (2012). The Soar cognitive architecture. MIT

Press.

Martin, C. and Barber, K. S. (2006). Adaptive decision-

making frameworks for dynamic multi-agent organi-

zational change. Autonomous Agents and Multi-Agent

Systems, 13(3):391–428.

Parasuraman, R., Sheridan, T. B., and Wickens, C. D.

(2000). A model for types and levels of human in-

teraction with automation. IEEE Transactions on sys-

tems, man, and cybernetics-Part A: Systems and Hu-

mans, 30(3):286–297.

Quigley, M., Conley, K., Gerkey, B., Faust, J., Foote, T.,

Leibs, J., Wheeler, R., and Ng, A. Y. (2009). Ros: an

open-source robot operating system. In ICRA work-

shop on open source software, volume 3, page 5.

Kobe.

Schurr, N., Marecki, J., and Tambe, M. (2009). Im-

proving adjustable autonomy strategies for time-

critical domains. In Proceedings of The 8th Interna-

tional Conference on Autonomous Agents and Multia-

gent Systems-Volume 1, pages 353–360. International

Foundation for Autonomous Agents and Multiagent

Systems.

Tambe, M. (1997). Agent architectures for ﬂexible. In Proc.

of the 14th National Conf. on AI, USA: AAAI press,

pages 22–28.

van der Vecht, B., Dignum, F., and Meyer, J. C. (2009).

Autonomy and coordination: Controlling external in-

ﬂuences on decision making. In Web Intelligence

and Intelligent Agent Technologies, 2009. WI-IAT’09.

IEEE/WIC/ACM International Joint Conferences on,

volume 2, pages 92–95. IEEE.

Vernon, D., Metta, G., and Sandini, G. (2007). A survey of

artiﬁcial cognitive systems: Implications for the au-

tonomous development of mental capabilities in com-

putational agents. IEEE transactions on evolutionary

computation, 11(2):151–180.

Comparison Between Static and Dynamic Willingness to Interact in Adaptive Autonomous Agents

267