Towards a Stable Quantized Convolutional Neural Networks:

An Embedded Perspective

Motaz Al-Hami

1,3

, Marcin Pietron

2,3

, Raul Casas

, Samer Hijazi

and Piyush Kaul

Department of Computer Information Systems, Hashemite University, Zarqa 13133, Jordan

Department of Computer Computer Science and Electrical Engineering, AGH University, Cracow, Poland

Cadence Design Systems, San Jose, California, U.S.A.

Keywords:

Deep Learning, Quantization, Convolutional Neural Networks.

Abstract:

Nowadays, convolutional neural network (CNN) plays a major role in the embedded computing environment.

Ability to enhance the CNN implementation and performance for embedded devices is an urgent demand.

Compressing the network layers parameters and outputs into a suitable precision formats would reduce the

required storage and computation cycles in embedded devices. Such enhancement can drastically reduce the

consumed power and the required resources, and ultimately reduces cost. In this article, we propose several

quantization techniques for quantizing several CNN networks. With a minor degradation of the ﬂoating-point

performance, the presented quantization methods are able to produce a stable performance ﬁxed-point net-

works. A precise ﬁxed point calculation for coefﬁcients, input/output signals and accumulators are considered

in the quantization process.

1 INTRODUCTION

CNN paradigm architecture has shown a state-of-art

performance in the ﬁeld of image recognition bench-

marks (Ciresan et al., 2011). Studying other differ-

ent aspects of this network would enhance the net-

work use and implementation in embedded devices.

The underlying architecture of the CNN might vary

from one network to another, and recent architectures

have shown large number of layers. Some architec-

tures might include hundreds of layers, millions of co-

efﬁcients and even require billions of operations (He

et al., 2015).

CNN has different types of layers. Convolutional

layers are the ones that consume the majority of com-

putation. In these layers multiply-accumulate opera-

tions (MACs) are performed extensively, leading to

a large number of consumed MACs cycles. While

typical applications that use parallel GPUs perform

ﬂoating-point data format, the embedded systems and

specially the real-time ones require a ﬁxed-point for-

mat (Dipert et al., 2017).

A key property of CNN is its resistance to noise,

while keeping performance stable. Hence, treating

any degradation resulted from quantization process

as a new source of noise, makes CNN a preferable

choice to do this job. In this article, we focus on

quantizing the CNN for both coefﬁcients and (in-

put/ output) data with a reduced precision format

(8-bits). The quantization process can be applied

to both inference and training processes. Training

deep neural networks is done by applying many small

changes to the network coefﬁcients. These small ad-

justments utilize higher precision format which ac-

cumulate slowly over time and converge to optimal

values. There are research efforts to use quantized

representations for the training process, but in gen-

eral more bits are needed for training than for infer-

ence (Lin et al., 2016), (Hubara et al., 2016b), (Cour-

bariaux et al., 2014b), (Hubara et al., 2016a), (Gupta

et al., 2015), (Esser et al., 2015). Our work focuses

on quantization for inference as most real-time em-

bedded systems at the moment will only be deployed

with this mode of operations (Dipert et al., 2017).

This article introduces a novel hybrid quantization

(HQ) approach. (HQ) quantizes a network layer data

points (i.e. both coefﬁcients and data) at different lev-

els. Hence, the network performance stability might

be guaranteed using a speciﬁc HQ level.

In short, the Motivation is: Enhancing the CNN

capability to be implemented for embedded devices

by reducing the required storage for the network, and

the performed computations on these low powered de-

vices. Such enhancement should keep the CNN per-

Al-Hami, M., Pietron, M., Casas, R., Hijazi, S. and Kaul, P.

Towards a Stable Quantized Convolutional Neural Networks: An Embedded Perspective.

DOI: 10.5220/0006651305730580

In Proceedings of the 10th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2018) - Volume 2, pages 573-580

ISBN: 978-989-758-275-2

573

formance stable for the inference task. Our Contribu-

tion is: (1) We generate a stable CNN network with a

reduced precision format (8-bits) for both coefﬁcients

and (input/ output) data. (2) We apply a hybrid quan-

tization HQ approach. (3) We use a k-means quanti-

zation approach which reduces the network computa-

tion complexity.

A K-means approach for CNN compression has

been used in (Han et al., 2016b). A key difference be-

tween this compression method and our work is a di-

mensionality of the clusters. In (Han et al., 2016b) the

clustered points are single coefﬁcients which makes it

difﬁcult to achieve efﬁciency in an embedded proces-

sor, especially with vector processors that can handle

hundreds of coefﬁcients and data samples in parallel

with a single instruction.

The paper is organized as follows. The related

works is described in section 2. The ﬂoating-point

and ﬁxed-point representation and the mapping be-

tween them is discussed in Section 3. Additionally

it explains the CNN architecture and how complex-

ity of a CNN is measured. Section 4 reviews the

hybrid quantization approach. K-means quantization

approach is described in Section 6, and Finally con-

clusion remarks appear in Section 7.

2 RELATED WORKS

Many works have shown CNN quantization (An-

war et al., 2015), (Gysel et al., 2014), (Lin et al.,

2016). A common strategy is to quantize all coef-

ﬁcients in a single layer with speciﬁed number of

bits to represent the integer and fractional parts (An-

war et al., 2015), (Gysel et al., 2014) based on the

range of values of the coefﬁcients set. In (Van-

houcke et al., 2011) an 8-bits CNN implementation is

compared to an implementation with 32-bits ﬂoating-

point for speech recognition to speed-up throughput.

In (Hwang and Sung, 2014) a ﬁxed-point network

with ternary weights and 3-bits activations was pre-

sented. Several methods attempt to binarize weights

and the activations in neural networks (Hubara et al.,

2016a), (Courbariaux et al., 2015), (Soudry et al.,

2014), (Rastegari et al., 2016). All of them resulted

in signiﬁcant drop in accuracy relative to ﬂoating-

point performance. The most efﬁcient among them

is the XNOR-Net (Rastegari et al., 2016) architec-

ture which achieves comparable results to ﬂoating-

point format using only binary weights. Complex-

ity reduction of CNN can be achieved by several

other techniques (e.g. SVD reduction, reducing ﬁlter

sizes) (Han et al., 2016a), (Han et al., 2016b), (Hin-

ton and Salakhutdinov, 2006). SqueezeNet (Iandola

et al., 2016) is an example of compressed version

of AlexNet (Krizhevsky et al., 2012), reducing 60M

parameters to only 0.5M parameters while fully pre-

serving its accuracy. There are also other new ap-

proaches for image object recognition like Hierarchi-

cal Temporal Memory based on neocortex architec-

ture (Wielgosz and Pietron, 2017), (Wielgosz et al.,

2016), (Pietron et al., 2016a), (Pietron et al., 2016b)

which is suitable for embedded systems. A K-means

approach for CNN compression has been used in

(Han et al., 2016b). Recently, many tools have been

developed for CNN. Many of them take into account

the quantization of the networks. Ristretto tool quan-

tizes CNNs using two phases. In the ﬁrst phase con-

ventional quantization is used. In the second phase,

there is a ﬁne tuning process where the network is re-

trained using the reduced precision formats of the ﬁrst

phase (Gysel et al., 2014), (Gysel, 2016). The Tensor-

Flow (Google, 2017) learning framework now pro-

vides facilities for quantization where ﬂoating-point

numbers in a certain range are quantized/ dequantized

(to/ from) 8-bits precision format.

3 NETWORK QUANTIZATION

Quantization is the process of constraining values

from a continuous domain into discrete levels of val-

ues. As long as more bits are used in the quantization,

as long as the number of levels may increase. In our

case, the domain is ﬂoating-point representation (

f ).

A ﬂoating-point number can be represented as:

f = m · b

(1)

m ∈ Z is the mantissa, b = 2 is the base, and e ∈ Z is

the exponent value. In case of single precision ﬂoat-

ing point format according to the IEEE-754 standard,

the mantissa is assigned 23-bits, the exponent is as-

signed 8-bits, and 1-bit is assigned for the sign indi-

cator. Therefore, the set of values that can be deﬁned

by this format is described by:

single

: {±2

−126

,... ,±(2 −2

−23

) × 2

127

}. (2)

Similarly, a reduced precision IEEE-754 mini-ﬂoat

format assigns 10-bits of mantissa, 5-bits of exponent

and the sign bit.

Currently, GPUs with parallel processing being

applied to machine learning operate mainly using the

single precision format. In contrast, embedded DSPs

and the latest GPUs operate with 8-bit and 16-bit

ﬁxed-point (

f ) processing that restricts numbers to the

range:

f : 2

−F

· {−2

T −1

,. .. ,2

T −1

− 1} (3)

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

574

where T = {8,16} is the total used bits and represents

conventional bit-width. F is a shift down (or up) that

determines fractional length, or number of fractional

bits. I is the integer length, I = T −F − 1 for signed

numerical representation. When the fractional length

varies over individual coefﬁcients or data samples, or

over small groups of numbers this format is also re-

ferred to as dynamic ﬁxed-point (Courbariaux et al.,

2014b), (Gysel, 2016).

Assuming S is a dataset of points, it is possi-

ble to deﬁne a general mapping from a ﬂoating-point

data point x ∈ S to ﬁxed-point q as follows (assuming

signed representation)

fxp

= Q (x

ﬂp

) = µ + σ · round(σ

−1

· (x − µ)). (4)

To utilize the full range of the input, one can set:

µ =

(max

x∈S

x + min

x∈S

x),σ = 2

1−T

· max

x∈S

|x − µ| (5)

Alternatively, µ can be interpreted and measured as

the mean of a distribution of x and σ as the range

of the distribution to be represented before saturation.

Drawbacks of this approach are the need to calculate

and maintain the quantities µ, σ and to apply the nor-

malization procedure in (4).

A second simpler approach uses the magnitude of

values and assign int bits I to cover the maximum

absolute value such that:

I = d(log

(max

x∈S

|x|))e (6)

The rest of available bits are assigned to the fraction

bits F and the sign bit.

Yet another approach can deﬁne I and F based on

data points distribution histogram. Assuming a given

percentage (i.e a large portion of the histogram data

points like 99.9 %) to be covered in the quantization

assigned I and F . In this case, there will be a small

percentage of the data points considered as outliers.

To determine the effects of saturation (i.e. outliers),

one can experiment the performance with different

saturation levels.

3.1 Complexity Reduction Analysis

Typically, the layers of a CNN network have neurons

that generate outputs feature maps y

, i = 1...N as fol-

lows

= b

∑

j=1

i j

◦ x

) (7)

where F

i j

is a single two-dimensional (2D) convo-

lutional kernel with dimensions H × W . The op-

erator ◦ represents the convolution operation and

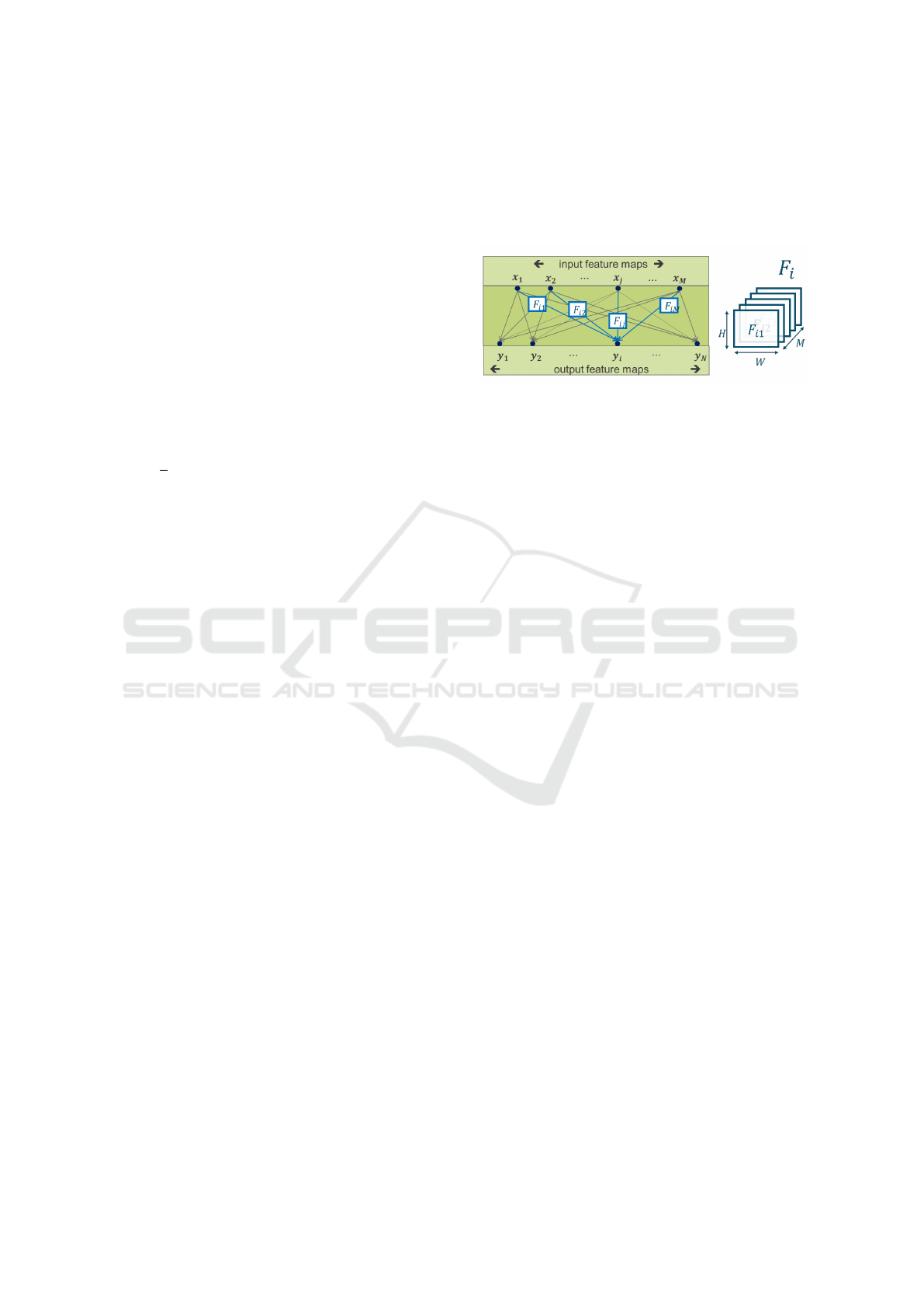
is the bias vector. Fig. 1 illustrates one three-

dimensional (3D) kernel

= (F

,..., F

) with di-

mensions H ×W × M. Altogether, the N three-

dimensional kernels form one four-dimensional (4D)

set of ﬁlter coefﬁcients.

Figure 1: Convolutional layer structure, and the order of a

layer kernels in the convolving process.

The number of multiply-accumulate (MAC) oper-

ations and cycles spent during the execution of Fig. 1

in a practical implementation is often used as the

metric for complexity of a CNN (Courbariaux et al.,

2014a). Assuming each output feature map y

has P

output pixels (i.e. image data) the total number of

MAC calculations for a convolutional ﬁltering opera-

tion is MACs = (P · H ·W · M · N).

Complexity may be interpreted in terms of the

size of the hardware blocks required to implement

the MAC operations or also in terms of the total

or average number of cycles required by a proces-

sor to perform these operations. In order to com-

pare the reduction in complexity across quantization,

we adopt the MAC complexity of 8-bits operations

with notation < coeff,data >=< 8b,8b > as a refer-

ence unit. Other quantization formats can be com-

pared relative to the complexity of < 8b, 8b > oper-

ations. For instance, if 4-bits representation is used

for both coefﬁcients and data < 4b, 4b > the relative

complexity is approximately 1/4 that of < 8b,8b >.

Similarly, ﬂoating-point operations < ﬂp,ﬂp > will

have approximately 9× to 10× of the complexity of

< 8b, 8b > since there are 3× the number of bits to

represent the mantissas plus the remaining work re-

quired to handle exponents. Table 1 calculates the

complexity for the 4

convolutional layer of AlexNet

for various quantization formats.

3.2 Convolutional Neural Network

Quantization Systems

This section reviews the TensorFlow and Ristretto

quantization systems and compares them to the quan-

tization system proposed in this work. The Tensor-

Flow system has an open source quantization mod-

ule (TensorFlow, 2017). The quantization process

uses min, max values (TensorFlow, 2017) to quantize

Towards a Stable Quantized Convolutional Neural Networks: An Embedded Perspective

575

Table 1: The parameters of 4

AlexNet convolutional layer

and its computational complexity in various quantization

formats.

Format

< coeff,data >

Relative Complexity

[M MACs]

< 8b,8b > 224 = HPWMN

< 4b,8b >

112 =

< 8b,8b >

< 4b,4b >

56 =

< 8b,8b >

< ﬂp,ﬂp > ≥ 2016 = 9 < 8b,8b >

N = 256,P = 27

,M = 48, H = W = 5

both data and coefﬁcients. The ﬂoating-point num-

bers uses buckets indices as a mapping to quantized

values. There is also Dequantization process where

the centers of the buckets are mapped back to ﬂoating-

point value as an approximate estimation for the orig-

inal values. The range of convolutional layers outputs

are estimated analytically.

Ristretto is a system developed by the Laboratory

for Embedded and Programmable Systems (LEPs) for

University of California, Davis (Gysel et al., 2014).

Ristretto is mainly based on dynamic ﬁxed-point and

mini-ﬂoat representation. However, a powers-of-two

mode is also available. Ristretto uses ﬁne tuning

to recover from any loss in accuracy after its initial

trimming phase of quantization. In this quantization

schema the quantization is based on ranges (max) of

data and coefﬁcients measured empirically. Also, no

support for accumulator quantization below 32-bits.

The main advantages of the Ristretto system are

its wide range of reduced representation formats and

ﬁne tuning approach. The drawback is lack of ac-

cumulator quantization. Our solution offers a wide

spectrum of layer quantization modes like 4D, 3D

and 2D quantization (Hybrid Quantization discussed

in the next section) and clustered kernels, or K-means

approach that allows advanced quantization based on

statistics and automatic tuning. The key feature in

TensorFlow is a new reduced format represented by

integer values. The drawback is that min and max

values must be known at each stage of CNN evalua-

tion.

4 HYBRID QUANTIZATION

This section explores Hybrid Quantization (HQ) of a

CNN network. In HQ coefﬁcients are represented in a

hybrid fashion by assigning different ﬁxed-point for-

matting to different partitions of convolutional layers

and feature maps. For instance, different precisions

(i.e. numbers of bits) and different formats (i.e. I ,

F ) can be assigned to each 2D ﬁlter or 3D kernel

of a convolutional layer. Fully connected layers are

only treated as 4D kernels. Similarly, different preci-

sions and formats can be assigned to different parti-

tions of the input and/or output feature maps. Deﬁn-

ing precisions and formats in a hybrid fashion adds

overhead for representation both in terms of storage

space and facilities to decode it. Nevertheless, it can

bring about a signiﬁcant improvement in CNN accu-

racy when compared to a homogeneous quantization

(i.e. 4D). Varying formats for intermediate accumu-

lated values can be speciﬁed in the same hybrid fash-

ion. There are three different formatting schemes are

summarized as follows:

(a) 4D-HQ (b) 3D-HQ (c) 2D-HQ

Figure 2: Different quantization schemes.

Figure 3: 4D quantization problem when outliers appears

in the data (Y axis - magnitudes of coeffs, X axis - id of

coeffs).

• Layer-based or 4D-HQ: Entire layer kernels are

quantized using the same precision format. In

Fig. 2(a) all coefﬁcients in the 4D convolutional

kernels F

i j

are quantized by the same F ,I preci-

sion format.

• Kernel-based or 3D-HQ:

Coefﬁcients in each 3D kernel in a layer are quan-

tized independently. In Fig. 2(b) each 3D kernel

with ﬁlters

= (F

,..., F

) is quantized inde-

pendently with precision format F [i], I [i] for each

• Filter-based or 2D-HQ:

Each 2D ﬁlter (each channel in a kernel) in each

kernel in a layer is quantized independently. In

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

576

Table 2: Comparison of quantization performance for 8-bits AlexNet.

Format < coeff,data > Quantization Top-1 Error[%] Complexity [M MACs]

Ristretto < ﬂp,ﬂp >

< 8b,8b > no Fine Tuning

with Fine Tuning

43.1

44.0

43.9

6516

724

TensorFlow < ﬂp,ﬂp >

< 8b,ﬂp >

< 8b,8b >

42.2

46.2

51.0

6512

2172

724

Ours < ﬂp, ﬂp >

< 8b,ﬂp >

< 8b,8b >

42.2

42.3

42.7

42.5

61.5

6516

2172

724

Figure 4: Automatic tuning. α is the reference Top-1 Er-

ror. f is the energy threshold. δ is the energy adjustment

amount.

Fig. 2(c) each ﬁlter F

i j

is quantized independently

with formatting F [i, j], I [i, j] for each pair i, j.

For large data precision, homogeneous quantization

(i.e. 4D) is sufﬁcient enough to quantize the data

points. The problem appears with low precision for-

mat, the assigned quantized levels are not sufﬁcient

enough to represent all data points in all layer ker-

nels with satisﬁed accuracy. In 3D quantization, the

maximum absolute value in each kernels controls the

kernel quantization format. Hence, it reduces the gap

between the data points and the maximum absolute

value. When using 2D quantization, the quantization

produces more efﬁcient quantization, where we re-

strict the maximum absolute value to each 2D ﬁlter

independently. This effect is described on Fig. 3. The

data point in the red circle (which might seem as an

outlier) affects the layer quantization format using the

homogeneous quantization (4D). However, using 3D

or 2D quantization this effect can be drastically re-

duced. Therefore kernel quantization (3D) were per-

formed in case of

<8b,8b > AlexNet quantization to

achieve 1% loss in accuracy in relative to ﬂoating-

point representation.

Next, we evaluate the performance of various HQ

modes and compare against Ristretto and TensorFlow

quantization of AlexNet of the the ImageNet valida-

tion set (ILSVRC2012 dataset), as shown in Table 2.

Our baseline ﬂoating-point AlexNet network (i.e. pre-

trained network in MatConvNet framework) (Vedaldi

and Lenc, 2015). This baseline is also ported to a

ﬁxed-point C-model. In the C-model, coefﬁcients and

input data in each layer are quantized to 8-bits while

intermediate accumulator values at the output of a

convolutional ﬁlter are quantized to 32-bits. Those

values are quantized back to 8-bits before being sent

to the next layer. Both 3D-HQ and Ristretto experi-

ence < 1.0% drop in accuracy relative to the ﬂoating-

point performance. The quantization in TensorFlow

experiences a much higher drop in accuracy (Ten-

sorFlow rounding mode), more than 4% despite the

use of ﬂoating-point to represent data. Our attempts

to quantize both data and coefﬁcients in TensorFlow

failed to produce reliable results.

Several networks have been tested against our pro-

posed quantization strategy. The goal is to quantize

the networks while keeping the performance within

the range less than 1% performance degradation rela-

tive to the ﬂoating-point performance (Table 5). We

applied <8b,8b > quantization precision to all net-

works. Hybrid quantization 4D and 3D are used in

the quantization.

5 ADVANCED AUTOMATIC

QUANTIZATION

Investigating the performance of mixing 8-bits and 4-

bits precision format on different network layers has

a lot of insights, specially for embedded devices. Uti-

lizing some statistics gathered during the evaluation

of the CNN, we can decide which parts of the net-

work should use (8-bits/ 4-bits) precision format. In

this quantization scheme, the energy contribution E

i j

of each 2D ﬁlter F

i j

is accumulated over a set of probe

Towards a Stable Quantized Convolutional Neural Networks: An Embedded Perspective

577

Table 3: Hybrid quantization of the 4

layer in AlexNet (40% of coefﬁcients are in 4-bits format), all biases are in 8-bits.

Experiment Layers: 1, 18 4 7, 9, 11, Top-1 Savings

14, 16 Error [%] [%]

Conservative Baseline < 8b, 8b > < 8b, 8b > < 8b,8b > 42.7 0

Moderate < 8b, 8b > < 4b, 8b > (40%) < 4b, 8b > 43.1 30

Aggressive < 8b, 8b > < 4b, 8b > (100%) < 4b, 8b > 64.1 44

Table 4: K-means quantization of Convolutional Layer 4 of AlexNet (all other layers are kept in < ﬂp,ﬂp >).

Quantization Base Residuals Top-1 Complexity Layer Network

Method Format Format Error [%] [M Macs] Savings Savings

2D-HQ Baseline < 8b, 8b > 42.7 224

2D-HQ < 4b, 8b > 65.9 112 50% 15%

K-means < 8b, 8b > < 8b,8b > 42.2 227 -2% -0.6%

K-means < 8b, 8b > < 4b,8b > 42.7 117 48% 15%

images as follows:

i j

∑

probe

images

∑

pixels

i j

(p)|

(8)

where y

i j

= F

i j

∗ x

are partial feature maps. Essen-

tially, the quantization scheme assigns baseline preci-

sion (i.e. 8-bits) to 2D ﬁlters with high energy con-

tribution and lower precision (i.e. 4-bits) to 2D ﬁlters

with low energy contribution based on some energy

threshold f. An automatic threshold tuning and quan-

tization procedure was developed to minimize com-

plexity through quantization while maintaining a ref-

erence level of Top-1 Error α. The procedure is illus-

trated in Fig. 4.

Table 3 shows the results of this quantization

scheme. The Conservative experiment utilizes 8b 2D-

HQ quantization throughout all layers. In the Mod-

erate experiment, the layers (1, 18) are quantized

to <8b,8b >. The most computationally expensive

Layer 4 is quantized with 40% of its 2D ﬁlters in

<4b,8b > format and all other layers use <4b, 8b >

quantization. The Moderate experiment suffers < 1%

loss in accuracy relative to ﬂoating-point but results

in 30% savings in complexity relative to the Conser-

vative experiment. The Aggressive experiment com-

pletely quantizes Layer 4 to <4b,8b > resulting in a

drastic loss in accuracy.

6 K-MEANS QUANTIZATION

K-means approach splits a layer coefﬁcients kernels

into two parts, basis ﬁlters G

`(i)

(i.e. approximations)

and residual ﬁlters

(i.e. differences) leading to

= G

`(i)

. The K-means clustering algorithm splits

a layer kernels into k centroids kernels serves as ap-

proximate kernels for their related cluster groups. The

residual kernels are the difference between the orig-

inal kernels and their corresponding approximation

centroids.

The base and residual ﬁlters are assigned differ-

ent quantization formats in order to reduce complex-

ity while maintaining accuracy. In this work we apply

K-means clustering to derive a set of K < N basis 3D

kernels. These kernels are formatted with <8b,8b >

precision. The residual kernels are assigned lower

precision, i.e. <4b, 8b > or <4b,4b >. The ﬁnal y

can be described as:

= b

∑

j=1

`(i), j

◦ x

| {z }

<8b,8b>

i j

◦ x

| {z }

<4b,8b>,<4b,4b>

(9)

where G

`(i), j

are the basis ﬁlters assigned to each 3D

kernel via some mapping `(·) : [1..N] 7→ [1..K]. The resid-

ual ﬁlters are given by

i j

= F

i j

− G

`(i), j

. Assuming the

base kernels use <8b,8b > precision and the residuals

use <4b,8b >, the effective complexity savings of this

approach is a factor of (0.5N −K)/N. The implementa-

tion is as follows: the input is convolved with K basis

kernels and generate K temporary feature maps. Next,

the output of the residual ﬁlters are added to their

corresponding base ﬁlter temporary feature maps to

yield the ﬁnal output of the convolutional layer. A

disadvantage of this approach is that the temporary

feature maps have to be stored. Table 4 shows the

performance of the K-means approach for convolu-

tional Layer 4 in AlexNet, the layer with the largest

complexity (all other layers are kept in ﬂoating-point

format). While 2D-HQ formatting to <4b,8b > re-

sults in 50% reduction in complexity of the layer, the

loss in accuracy is drastic. K-means quantization to

<8b,8b > format with K = 4 is attempted as a base-

line (i.e. K is chosen to be 4 based on empirical exper-

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

578

Table 5: Comparison of different CNN models using the proposed quantization approach (FLP - ﬂoating point, FXP - ﬁxed

point).

Top-5 Error [%] Top-1 Error [%] FXP Conﬁguration

FLP FXP FLP FXP Coeff Data

Caffe-AlexNet 20.33 20.51 43.35 43.64 8b, 4D 8b, 4D

20.33 20.43 43.35 43.52 8b, 3D 8b, 4D

MatConvNet-AlexNet 19.93 34.28 42.36 58.83 8b, 4D 8b, 4D

19.93 20.13 42.36 42.53 8b, 3D 8b, 4D

GoogleNet 13.54 13.60 34.89 34.90 8b, 4D 8b, 4D

13.54 13.58 34.89 35.09 8b, 3D 8b, 4D

Vgg-VeryDeep-19 10.64 10.72 29.48 29.93 8b, 4D 8b, 4D

10.64 10.61 29.48 29.62 8b, 3D 8b, 4D

Cactus-it6 8.05 9.34 25.26 27.48 8b, 3D 8b, 4D

ResNet-50 8.29 8.80 25.11 26.25 8b, 4D 8b, 4D

8.29 8.63 25.11 25.78 8b, 3D 8b, 4D

ResNet-101 7.61 8.36 23.96 25.69 8b, 4D 8b, 4D

8.61 7.91 23.96 24.59 8b, 3D 8b, 4D

ResNet-152 7.23 8.11 23.51 24.96 8b, 4D 8b, 4D

7.23 8.07 23.51 25.05 8b, 3D 8b, 4D

Table 6: Hybrid clustered quantization of AlexNet.

Base < 8b, 8b >

Residuals Layer 1: < 8b, 8b >

all others : < 4b, 8b >

Top-1 Error 44.1%

k - clusters k = 2 for layers 1, 4,

11, 14, 16

k = 3 for layer 7

k = 6 for layer 9

k = 4 for layer 18

Complexity [M MACs] 422

Network Savings 41.6%

iments), yielding a slight increase of 2% in complex-

ity and no signiﬁcant change in performance. Next,

K-means quantization to <4b,8b > format leads to

48% complexity reduction in the layer and no degra-

dation in accuracy relative to <8b,8b >. In Table 6 we

apply K-means quantization to <4b,8b > to all layers

of the network except Layer 1, which is the layer most

sensitive to perturbations. The net savings for the net-

work is > 40% with a degradation in accuracy < 2%.

In this experiment we chose different k values for dif-

ferent layers (i.e. based on empirical experiments).

7 CONCLUSIONS AND FURTHER

WORK

In this work we presented a novel quantization meth-

ods for deep convolutional neural networks. The sys-

tem reduces memory requirements, area for process-

ing elements and overall power consumption for hard-

ware accelerators. Our research shows that the most

popular CNN architectures can be quantized to 8-

bits for both coefﬁcients and data outputs with minor

degradation in accuracy compared to ﬂoating-point.

Hybrid quantization and clustered quantization al-

low the use of advanced quantization (e.g. <4b,8b >)

without signiﬁcant decrease in performance. Our sys-

tem is both fast and automated. It was implemented

in MatConvnet and ported to a C-model. We consider

adding new features in the future such as: exploit-

ing other statistics of the network in quantization pro-

cess, further optimizing the K-means approach, net-

work weights binarization (Rastegari et al., 2016) and

(Zhang and Liu, 2016), applying ﬁne-tuning and use

re-training in quantization process. These additional

features will help to reduce the bit-width even further,

and to reduce the computational complexity.

Towards a Stable Quantized Convolutional Neural Networks: An Embedded Perspective

579

REFERENCES

Anwar, S., Hwang, K., and Sung, W. (2015). Fixed point

optimization of deep convolutional neural networks

for object recognition. Speech and Signal Processing

IEEE International Conference.

Ciresan, D., Meier, U., M., G. L., and Schmidhuber, J.

(2011). Flexible, high performance convolutional neu-

ral networks for image classiﬁcation. Proceedings of

the Twenty-Second International Joint Conference on

Artiﬁcial Intelligence, 2:1237–1242.

Courbariaux, M., Bengio, Y., and David, J. (2015). Bina-

ryconnect: Training deep neural networks with binary

weights during propagations. Advances in Neural In-

formation Processing Systems.

Courbariaux, M., Bengio, Y., and Jean-Pierre, D. (2014a).

Training deep neural networks with low precision

multiplications. ArXiv e-prints, abs/1412.7024.

Courbariaux, M., David, J.-P., and Bengio, Y. (2014b).

Training deep neural networks with low precision

multiplications. arXiv preprint arXiv:1412.7024.

Dipert, B., Bier, J., Rowen, C., Dashwood, J., Laroche,

D., Ors, A., and Thompson, M. (2016 (accessed

February 20, 2017)). Deep learning for object

recognition: Dsp and specialized processor optimiza-

tions. http://www.embedded-vision.com/platinum-

members/embedded-vision-alliance/embedded-

vision-training/documents/pages/cnn-dsps.

Esser, S., Appuswamy, R., Merolla, P., Arthur, J., and

Modha, D. (2015). Backpropagation for energy-

efﬁcient neuromorphic computing. in: Advances in

neural information processing systems. Advances in

Neural Information Processing Systems.

Google (2016 (accessed February 22, 2017)). Tensorﬂow.

https://www.tensorﬂow.org.

Gupta, S., Agrawal, A., Gopalakrishnan, K., and

Narayanan, P. (2015). Deep learning with limited nu-

merical precision. Proceedings of the 32nd Interna-

tional Conference on Machine Learning.

Gysel, P. (2016). Ristretto: Hardware-oriented approxima-

tion of convolutional neural networks. arXiv preprint

arXiv:1605.06402.

Gysel, P., Motamedi, M., and Ghiasi, S. (2014). Hardware-

oriented approximation of convolutional neural net-

works. ArXiv e-prints, arXiv:1604.03168.

Han, S., Liu, X., Mao, H., Pu, J., Pedram, A., Horowitz,

M. A., and Dally, W. J. (2016a). Eie: Efﬁcient in-

ference engine on compressed deep neural network.

arXiv preprint arXiv:1602.01528.

Han, S., Mao, H., and Dally, W. J. (2016b). Deep compres-

sion: Compressing deep neural networks with prun-

ing, trained quantization and huffman coding. arXiv

preprint arXiv:1602.01528.

He, K., Zhang, X., Ren, S., and Sun, J. (2015). Deep resid-

ual learning for image recognition. arXiv:1512.03385.

Hinton, G. E. and Salakhutdinov, R. R. (2006). Reducing

the dimensionality of data with neural networks. Sci-

ence, 313(5786):504–507.

Hubara, I., Courbariaux, M., Soudry, D., El-Yaniv, R., and

Y., B. (2016a). Binarized neural networks: Train-

ing neural networks with weights and activations con-

strained to +1 or -1. arxiv 2016.

Hubara, I., Courbariaux, M., Soudry, D., El-Yaniv, R., and

Y., B. (2016b). Quantized neural networks: Training

neural networks with low precision weights and acti-

vations. arxiv 2016.

Hwang, K. and Sung, W. (2014). Fixed-point feedforward

deep neural network design using weights +1, 0, and

-1. Signal Processing Systems, 2014 IEEE Workshop

on, IEEE (2014).

Iandola, F. N., Moskewicz, M. W., Ashraf, K., Han, S.,

Dally, W. J., and Keutzer, K. (2016). Squeezenet:

Alexnet-level accuracy with 50x fewer parameters and

0.5mb model size. arXiv preprint arXiv:1602.07360.

Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2012). Im-

agenet classiﬁcation with deep convolutional neural

networks. In Advances in neural information process-

ing systems, pages 1097–1105.

Lin, D., Talathi, S., and Annapureddy, V. (2016). Fixed

point quantization of deep convolutional networks.

ICLR 2016.

Pietron, M., Wielgosz, M., and Wiatr, K. (2016a). Formal

analysis of htm spatial pooler performance under pre-

deﬁned operation condition. International Joint Con-

ference on Rough Sets.

Pietron, M., Wielgosz, M., and Wiatr, K. (2016b). Parallel

implementation of spatial pooler in hierarchical tem-

poral memory. International Conference on Agents

and Artiﬁcial Intelligence.

Rastegari, M., Ordonez, V., Redmon, J., and Farhadi, A.

(2016). Xnor-net: Imagenet classiﬁcation using bi-

nary convolutional neural networks. ArXiv e-prints,

arXiv:1603.05279.

Soudry, D., Hubara, I., and Meir, R. (2014). Expecta-

tion backpropagation: parameter-free training of mul-

tilayer neural networks with continuous or discrete

weights. Signal Processing Systems (SiPS), IEEE

Workshop.

TensorFlow (2017 (accessed July 12,

2017)). Tensorﬂow quantization.

http://www.tensorﬂow.org/performance/quantization.

Vanhoucke, V., Senior, A., and Mao, M. (2011). Improv-

ing the speed of neural networks on cpus. Proc. Deep

Learning and Unsupervised Feature Learning NIPS

Workshop.

Vedaldi, A. and Lenc, K. (2015). Matconvnet – convolu-

tional neural networks for matlab. In Proceeding of

the ACM Int. Conf. on Multimedia.

Wielgosz, M. and Pietron, M. (2017). Using spatial pooler

of hierarchical temporal memory to classify noisy

videos with predeﬁned complexity. Journal of Neu-

rocomputing.

Wielgosz, M., Pietron, M., and Wiatr, K. (2016). Opencl-

accelerated object classiﬁcation in video streams us-

ing spatial pooler of hierarchical temporal memory.

Journal IJACSA.

Zhang, L. and Liu, B. (2016). Ternary weight networks.

arXiv:1605.04711.

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

580