
Multi-server Marginal Allocation
With CVaR and Abandonment based QoS Measures
Per Enqvist
1
and G
¨
oran Svensson
1,2
1
Division of Optimization and Systems Theory, Kungliga Tekniska H
¨
ogskolan, Lindstedtsv 25, Stockholm, Sweden
2
Teleopti WFM, Teleopti AB, Sweden
Keywords:
Queueing, Queueing Networks, Marginal Allocation, Conditional Value-at-Risk, Abandonments.
Abstract:
Two multi-objective minimization problems are posed, one for Erlang-C queues and one for Erlang-A queues.
The objectives are to minimize the cost of added agents while also trying to optimize a quality of service
measure. For the Erlang-C system we propose using the Conditional Value-at-Risk measure with waiting time
as the loss function. We prove that this quality of service measure is integer convex in the number of servers.
For the Erlang-A system we use the fraction of abandoning customers and some rate based weighting function
as the service measure. Finally, a numerical comparison of the two system types is performed. The numerical
results show the similarities between the two systems in terms of optimal points.
1 INTRODUCTION
In this paper we investigate multi-class queueing net-
works and the optimal allocation of servers with re-
spect to a Quality of Service (QoS) measure. We con-
sider two types of queueing systems, one based on
the Erlang-C model with Conditional Value-at-Risk
(CVaR) (Rockafellar and Uryasev, 2000; Rockafellar
and Uryasev, 2002) on the waiting time as the QoS
measure. In the second system type we look at the
Erlang-A model and use the fraction of abandoning
customers as the basis of our QoS measure.
The basic model consists of a system of par-
allel server pools with a corresponding set of
agents(servers) that cater to customers(jobs), see Fig-
ure 1. Each server pool has a separate and infinite
first-come-first-serve (FCFS) buffer. The separate and
parallel queueing systems are bound together by a
common budget constraint.
The optimization problem is formulated and
solved in terms of the marginal allocation (MA) al-
gorithm (Fox, 1966). When varying the budget con-
straint the whole efficent front, consisting of efficient
solutions, can be found. The MA algorithm depends
on the costs per agent and the improvements of the
QoS measure, for the different queues, to be sepa-
rable and (integer) convex functions. In the tradi-
tion of (Rolfe, 1971; Dyer and Proll, 1977; Weber,
1980) we proceed to prove that the QoS measure, de-
termined by CVaR, is decreasing and convex in the
number of agents. In (Parlar and Sharafali, 2014) the
authors summarize other proofs of convexity for dif-
ferent QoS measures. In a similar fashion the system
of queues where abandonments are allowed is posed
and solved, using a QoS measure based on the frac-
tion of abandoning customers. The convexity of the
measure is posed as a conjecture.
2 MODEL DESCRIPTION AND
THE QoS MEASURES
We consider a system of N ∈ N queues of either
M/M/c or M/M/c + M type (using the notation of
(Baccelli and Hebuterne, 1981)), i.e., Erlang-C or
Erlang-A models, each with its own infinite queueing
buffer.
Introduce the index set I = {1,...,N}. Let c
i
, de-
note the number of servers in queue i, c = [c
1
... c
N
]
and let a
i
be the corresponding cost for each agent of
type i. The total cost of the agents is a separable and
integer convex function in c. Furthermore, assume
that the numbers of agents available for assignment to
the different demands are also limited. Let d
i
∈ N, be
the maximum number of available agents of type i.
The arrival process to queue i is a homogeneous
Poisson process with arrival rate parameter λ
i
. The
service rate of each server in pool i is denoted by µ
i
and service times are exponentially distributed. In the
case of the Erlang-A type systems the abandonment
Enqvist, P. and Svensson, G.
Multi-server Marginal Allocation - With CVaR and Abandonment based QoS Measures.
DOI: 10.5220/0006652602970303
In Proceedings of the 7th International Conference on Operations Research and Enterprise Systems (ICORES 2018), pages 297-303
ISBN: 978-989-758-285-1
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
297

rate of each customer is included. The time to aban-
donment of a customer in queue i is exponentially dis-
tributed with rate parameter θ
i
. Hence, the customer
may leave the system due to either service completion
or impatience, whichever occurs first. It is assumed
that customers being served do not defect.
Let b denote a budget constraint on the system,
meaning that the total cost of the assigned servers to
the queueing network must be within budget. The
model may be extended to include several budget con-
straints, affecting only a subset of the queues.
λ
1
.
.
.
λ
N
M/M/c
1
.
.
.
M/M/c
N
Figure 1: A system of N parallell M/M/c queues.
2.1 The Conditional Value-at-Risk
Measure
To promote a positive customer experience the queue-
ing system is endowed with a QoS measure. Typi-
cal QoS measures for contact centers include aver-
age speed of answer (ASA) and the telephone service
factor (TSF) (Gans et al., 2003), also known as ser-
vice level (SL). ASA measures the average time a cus-
tomer spends waiting on service while TSF considers
the acceptable waiting time (AWT) that a certain per-
centile of the customers have to wait before service.
The TSF type of QoS measure is also used in finance,
under the name of Value-at-Risk (VaR), to describe
the risk of (large) losses. The CVaR measure is of-
ten preferred to the VaR type measure due to its con-
vexity (Rockafellar and Uryasev, 2000; Rockafellar
and Uryasev, 2002) and coherent measure properties
(Artzner et al., 1999). In general CVaR offers a means
of controlling worst case outcomes, which might be of
great importance in fields like healthcare, as pointed
out in (Parlar and Sharafali, 2014). We consider the
QoS measure corresponding to CVaR where the loss
function is taken to be a customers waiting time in the
queue. We apply the CVaR measure to the system of
M/M/c queues.
First some preliminary results. The waiting time
distribution for a M/M/c queue is given by (Klein-
rock, 1996)
Pr(W
q
> t) = Π
q
(c,η)e
−(cµ−λ)t
= 1 − F
W
q
(t), (1)
where W
q
is the random variable representing the
waiting time and Π
q
(c,η) is the probability of delay,
i.e., of having to wait when there are c homogeneous
agents working under load η =
λ
µ
. This is given by
the Erlang-C formula (Kleinrock, 1996),
Π
q
(c,η) =
η
c
/c!
(1 − η/c)
c−1
∑
i=0
η
i
/i! + η
c
/c!
. (2)
It can be calculated efficiently via the following re-
cursion (Zeng, 2003)
Π
q
(c + 1,η) =
λ
µ
(cµ − λ)Π
q
(c,η)
(c + 1)µ − λ
c − λΠ
q
(c,η)
. (3)
This formula avoids numerical issues. We note that
the recursion is initiated by Π
q
(1,η) = η, and any
value larger than one should be interpreted as one,
since the larger values corresponds to unstable queues
when abandonments are excluded.
The different queues may have different QoS re-
quirements, thus let β
i
denote the quantile level for
queue i and t
i
be the VaR(AWT) value for queue i.
The QoS requirement for the VaR type measure is
then given by
Pr(W
q,i
≤ t
i
) ≥ β
i
, i ∈ I, (4)
and the corresponding β
i
-VaR is defined as
t
i
(c
i
) = min{t|F
W
q,i
(t) ≥ β
i
,c
i
}
=
logΠ
q
(c
i
,η
i
) − log(1 − β
i
)
c
i
µ
i
− λ
i
. (5)
We use the notation of t
i
to underscore that the VaR
value is measured in units of time, in this case.
The corresponding β-CVaR is defined by
φ
β
i
(c
i
) =
1
1 − β
i
∞
Z
t
i
(c
i
)
tdF
W
q,i
(t), i ∈ I, (6)
with explicit formulation for Π
q
(c
i
,η
i
) ≥ 1 − β
i
:
φ
β
i
(c
i
) =
1
c
i
µ
i
− λ
i
log
Π
q
(c
i
,η
i
)
1 − β
i
+ 1
= t
i
(c
i
) +
1
c
i
µ
i
− λ
i
, i ∈ I, (7)
where t
i
(c
i
) is given by (5).
Remark 1 (Probability atoms and CVaR). If β is
small then a probability atom might have to be han-
dled. To avoid such an atom it is required that Π
q
≥
1 − β holds. For a complete treatment of CVaR in
cases where there is a probability atom see (Rockafel-
lar and Uryasev, 2002). However, for most realistic
choices of parameters this is not an issue and will thus
be ignored throughout the rest of the paper.
The QoS measure given by this definition of the β-
CVaR is integer convex and decreasing in the number
of agents, c. The use of the MA algorithm rests on
this fact. This is formalized in Proposition 1.
ICORES 2018 - 7th International Conference on Operations Research and Enterprise Systems
298

Proposition 1 (Integer Convexity of β-CVaR). Con-
sider a M/M/c queue with constant rate parameters
µ,λ > 0 such that cµ > λ and that K < β ≤ 1, where
K is large enough that there is no probability atom.
Then
φ
β
i
(c
i
) = t
i
(c
i
) +
1
c
i
µ
i
− λ
i
, i ∈ I,
is decreasing and integer convex in c ∈ N.
The proof is given in the Appendix.
2.2 Probability of Abandonment
For a system of multi-server Erlang-A queues other
QoS measures are of interest. In (Garnett et al., 2002;
Mandelbaum and Zeltyn, 2007) different measures
for queueing systems with abandonments are consid-
ered. Erlang-A queues are stable for arbitrary loads
while Erlang-C queues are only stable when cµ > λ.
Here we consider systems in steady state, with con-
stant (random) demand. Perhaps the most obvious
measure is the probability that a customer will aban-
don (defect) the queue before recieving service. This
may occur if the arriving customer finds all servers
occupied and thus have to wait in queue. Then the
customer will abandon if his/her patience runs out be-
fore a server becomes available.
Let π
(i)
j
denote the probability of queue i being in
state j ∈ N, where the states are given by the number
of customers in queue i. Furthermore, let E
(i)
1,c
i
denote
the Erlang blocking formula of the i:th queue with c
i
servers. The incomplete Gamma function is defined
as
γ(x,y) =
y
Z
0
t
x−1
e
−t
dt, (8)
then, in accordance with (Mandelbaum and Zeltyn,
2007), let
A(x,y) =
xe
y
y
x
γ(x,y), x > 0,y ≥ 0. (9)
The probability of an arrival finding all servers busy
is given by
Pr(W
q
> 0) =
A(
cµ
θ
,
λ
θ
)E
1,c
1 +
A(
cµ
θ
,
λ
θ
) − 1
E
1,c
. (10)
The fraction of customers abandoning, conditioned
on having to wait on arrival, is given by
Pr(Ab|W
q
> 0) =
1
ρA(
cµ
θ
,
λ
θ
)
+ 1 −
1
ρ
, (11)
where ρ =
λ
cµ
, the offered load per agent. Then us-
ing the definition of conditional probability yields the
fraction of customers abandoning the queue.
The QoS measure given by the fraction of cus-
tomers abandoning is decreasing and integer convex
in the number of servers according to numerical tests
we performed. We are convinced it holds in general
and may be known. At this stage we pose it as a con-
jecture.
Conjecture 1 (Integer Convexity of Pr(Ab)). Con-
sider a M/M/c + M queue with constant rate param-
eters µ,λ > 0. Then
Pr(Ab) = Pr(Ab|W
q
> 0)Pr(W
q
> 0)
=
1
ρA(
cµ
θ
,
λ
θ
)
+
ρ − 1
ρ
!
A(
cµ
θ
,
λ
θ
)E
1,c
1 +
A(
cµ
θ
,
λ
θ
) − 1
E
1,c
(12)
is decreasing and integer convex in c ∈ N.
3 OPTIMIZATION
FORMULATION
Here we pose optimization formulations based on the
systems and QoS measures of Subsections 2.1 and
2.2. Since costs, CVaR and the probability to abandon
are integer convex functions in the number of servers,
the multi-objective solutions given by the MA algo-
rithm will be in terms of an efficient front.
First we will formulate the multi-objective prob-
lem that minimizes the total agent cost and β-CVaR
for all M/M/c queues. Then the following Optimiza-
tion problem can be formulated,
min
c
ϕ
N
∑
i=1
a
i
c
i
+ψ
N
∑
i=1
φ
(i)
β
i
(c
i
),
Sub. to
N
∑
i=1
a
i
c
i
≤ b,
c
i
≤ d
i
, ∀i ∈ I,
c
i
∈ N, a
i
,b,ϕ,ψ > 0, ∀i ∈ I,
(13)
where φ
(i)
β
i
(c
i
) denotes the QoS measure, for the i:th
queue, based on CVaR with waiting time as the loss
function. The weights ϕ and ψ are constant and de-
termine the relative importance of the two objectives.
Note that both functions in the objective are separable
functions.
In a similar fashion, we pose an optimization
problem minimizing the agent costs and the probabil-
ities to abandon modified by a weighting function for
the M/M/c + M queues. The optimization problem
Multi-server Marginal Allocation - With CVaR and Abandonment based QoS Measures
299

for a queue with abandonments can be formulated as
min
c
ϕ
N
∑
i=1
a
i
c
i
+ψ
N
∑
i=1
ω(λ
i
,µ
i
)Pr
i
{Ab|c
i
},
Sub. to
N
∑
i=1
a
i
c
i
≤ b,
c
i
≤ d
i
, ∀i ∈ I,
c
i
∈ N, a
i
,b,ϕ,ψ > 0, ∀i ∈ I,
(14)
where Pr
i
{Ab|c
i
} denotes the probability of abandon-
ment, for the i:th queue, given that there are c
i
servers
at work and ω(λ
i
,µ
i
) is some weight function that cor-
respond to some notion of the population of queue i.
We will use the offered load. Note that both functions
in the objective are separable functions.
The optimization problem formulated in (14) can
be extended to include a waiting time based QoS mea-
sure. Ideally we would like said condition to be the
CVaR measure with loss function in terms of the wait-
ing time under the condition that the waiting customer
gets served. This measure needs to be defined as of
yet. Instead we settle for average waiting time(mean
delay) under the condition that the demand eventu-
ally gets served. This result can be found in (Rior-
dan, 1962, p. 112, eq. 88). This condition forms
a lower bound on the number of agents and it is in-
cluded in the marginal allocation algorithm as the ini-
tiating number of agents of each type, thus guarantee-
ing that this QoS measure will be met.
3.1 The Marginal Allocation Algorithm
An efficient algorithm for finding the efficient points
for two integer convex and separable functions is the
MA algorithm, described in (Fox, 1966; Svanberg,
2009).
In general when minimizing the multi-objective
optimization problem for functions f ,g : N
N
→ R
where
∆ f
j
(x
j
) ≤ ∆ f
j
(x
j
+ 1) < 0 ∀ j,x
j
∈ N,
0 < ∆g
j
(x
j
) ≤ ∆g
j
(x
j
+ 1) ∀ j, x
j
∈ N,
(15)
the optimal vector x
∗
∈ N
N
minimizes ϕg(x) + ψ f (x)
if and only if the following conditions are satisfied for
each j = 1,...,N:
−∆ f
j
(x
∗
j
)
∆g
j
(x
∗
j
)
≤
ϕ
ψ
≤
−∆ f
j
(x
∗
j
−1)
∆g
j
(x
∗
j
−1)
if x
∗
j
> 0,
−∆ f
j
(0)
∆g
j
(0)
≤
ϕ
ψ
if x
∗
j
= 0.
(16)
x
∗
j
is an efficient solution if and only if there are con-
stants ϕ,ψ > 0 such that the conditions (16) are satis-
fied for each j = 1,...,N.
Marginal Allocation Algorithm
Step 0: Generate a table with N columns, fill the
columns with the quotients
−∆ f
j
(n)/∆g
j
(n) for n = 0,1,2,... where
n starts at zero. Set k = 0, x
(0)
= (0,...,0),
g(x
(0)
) = g(0) and f (x
(0)
) = f (0).
Step 1: Select the largest uncancelled quotient in
the table. Cancel it and let l be the
corresponding column number.
Step 2: Let k := k + 1 then let x
(k)
l
= x
(k−1)
l
and
x
(k)
j
= x
(k−1)
j
,∀ j 6= l.
Let f (x
(k)
) = f (x
(k−1)
) + ∆ f
l
(x
k−1
l
) and
g(x
(k)
) = g(x
(k−1)
) + ∆g
l
(x
k−1
l
).
Terminate algorithm if g(x
(k)
) ≥ g
max
;
otherwise go to Step 1.
We identify our budget constraint b to be g
max
and
the constraint on available agents, d
i
,i ∈ I, to be the
number of quotients to calculate for column i. This
algorithm can now be applied to (13) and (14), where
g(x) =
N
∑
i=1
a
i
c
i
(17)
f (x) =
N
∑
i=1
f
(i)
CVaR
(c
i
) for (13),
N
∑
i=1
ω(λ
i
,µ
i
)Pr
i
{Ab|c
i
} for (14).
(18)
4 NUMERICAL EXAMPLES
The main benefit of using the MA approach is that
huge systems can be optimized almost effortlessly.
An example of the efficient front of a system of 100
M/M/c queues, with a (maximal) budget constraint
of b = 4500, is shown in Fig 2. The input parame-
ters in terms of arrivals, service rates and more were
randomly generated. The optimal staffing calculation
took less than a second to perform on a laptop.
To compare the Erlang-C and the Erlang-A based
systems we look at a three class multi-server system
(i.e., three queues). First, find the efficient points for
the Erlang-C type system with CVaR as the service
measure. Then use those points in the solution of the
Erlang-A type system with fraction of abandonments
as basis for the service measure. These points are then
compared to the optimal points, shown in Figure 3.
The parameters used were β
β
β = [.95 .95 .95]
T
,λ
λ
λ =
[15 10 20]
T
,µ
µ
µ = [0.5 0.6 0.7]
T
and a = [12 15 18]
T
.
The procedure was repeated for two sets of im-
patience rates, θ
θ
θ = [0.25 0.25 0.25]
T
and θ
θ
θ =
[10 10 10]
T
, respectively. The weight function,
ω(λ
i
,µ
i
), in (14) is defined to be the offered load, η
i
.
ICORES 2018 - 7th International Conference on Operations Research and Enterprise Systems
300

Figure 2: Showing the efficient front for a system of 100
M/M/c-queues, using CVaR as QoS measure and with
a budget constraint of 4500. The parameters where ran-
domly generated. In the bottom figure some specific effi-
cient points are shown.
With respect to the patience parameter the two so-
lutions do not differ significantly. The given solutions
are very similar, which seem to hold for larger sys-
tems and for a wide range of parameter values. Even
though the probability of abandonment is very sim-
ilar for the two approaches, the optimal number of
agents may be different. Therefore, we consider the
optimal distributions in Table 1 to illustrate this for
the example seen in Figure 3. With abandonments
the first agent pool is prioritized over the second and
third, and recieves one or two more agents compared
to the CVaR assignment.
5 SUMMARY AND
CONCLUSIONS
The main objectives of this paper is to find an opti-
mal distribution of agents between N queues, bound
by budget constraints, via the MA algorithm. The
QoS measures used are CVaR, with waiting time as
the loss function, for the systems of M/M/c queues
and a weighted probability of abandonment for the
M/M/c + M queues. The advantage of using the MA
algorithm is that it can find the efficient points ex-
tremely fast. As can be seen from the numerical ex-
amples studying two different queueing networks give
similar solutions. The two QoS measures have rather
different shape, consider the curvature of the graphs
in Figure 3, but generate similar optimal points. We
Table 1: Showing the partial agent distributions for the
CVaR solution (left figure) and for the abandonment solu-
tion where θ = 0.25 (middle figure).
Agents
CVaR Ab
77 31 17 29 32 17 28
78 31 18 29 33 17 28
79 31 18 30 33 17 29
80 32 18 30 33 18 29
81 32 19 30 34 18 29
82 33 19 30 34 18 30
83 33 19 31 34 19 30
84 33 20 31 35 19 30
85 34 20 31 35 19 31
86 34 20 32 36 19 31
87 35 20 32 36 19 32
88 35 21 32 36 20 32
89 36 21 32 36 20 33
90 36 21 33 37 20 33
91 36 22 33 37 21 33
believe this is partly a consequence of the exponential
distributions of the service times. It may well diverge
for other service time distributions, e.g. lognormal
distributions.
ACKNOWLEDGEMENTS
The authors would like to thank Teleopti AB, Stock-
holm Sweden, for their support of our work.
REFERENCES
Artzner, P., Delbaen, F., Eber, J., and Heath, D. (1999).
Coherent measures of risk. Mathematical Finance,
9(3):203–228.
Baccelli, F. and Hebuterne, G. (1981). On queues with im-
patient customers. Research report, RR-0094, INRIA.
Dyer, M. and Proll, L. (1977). On the validity of marginal
analysis for allocating servers in M / M / c queues.
Management Science, 23(9).
Fox, B. (1966). Discrete optimization via marginal analysis.
Management Science, 13(3):210–216.
Gans, N., Koole, G., and Mandelbaum, A. (2003). Tele-
phone call centers: Tutorial, review, and research
prospects. Manufacturing Service Oper. Management.
Garnett, O., Mandelbaum, A., and M.Reiman (2002).
Manufacturing and Service Operations Management,
4:208–227.
Kleinrock, L. (1996). Queueing systems : problems and
solutions. Wiley, New York.
Mandelbaum, A. and Zeltyn, S. (2007). Service Engineer-
ing in Action: The Palm/Erlang-A Queue, with Appli-
Multi-server Marginal Allocation - With CVaR and Abandonment based QoS Measures
301
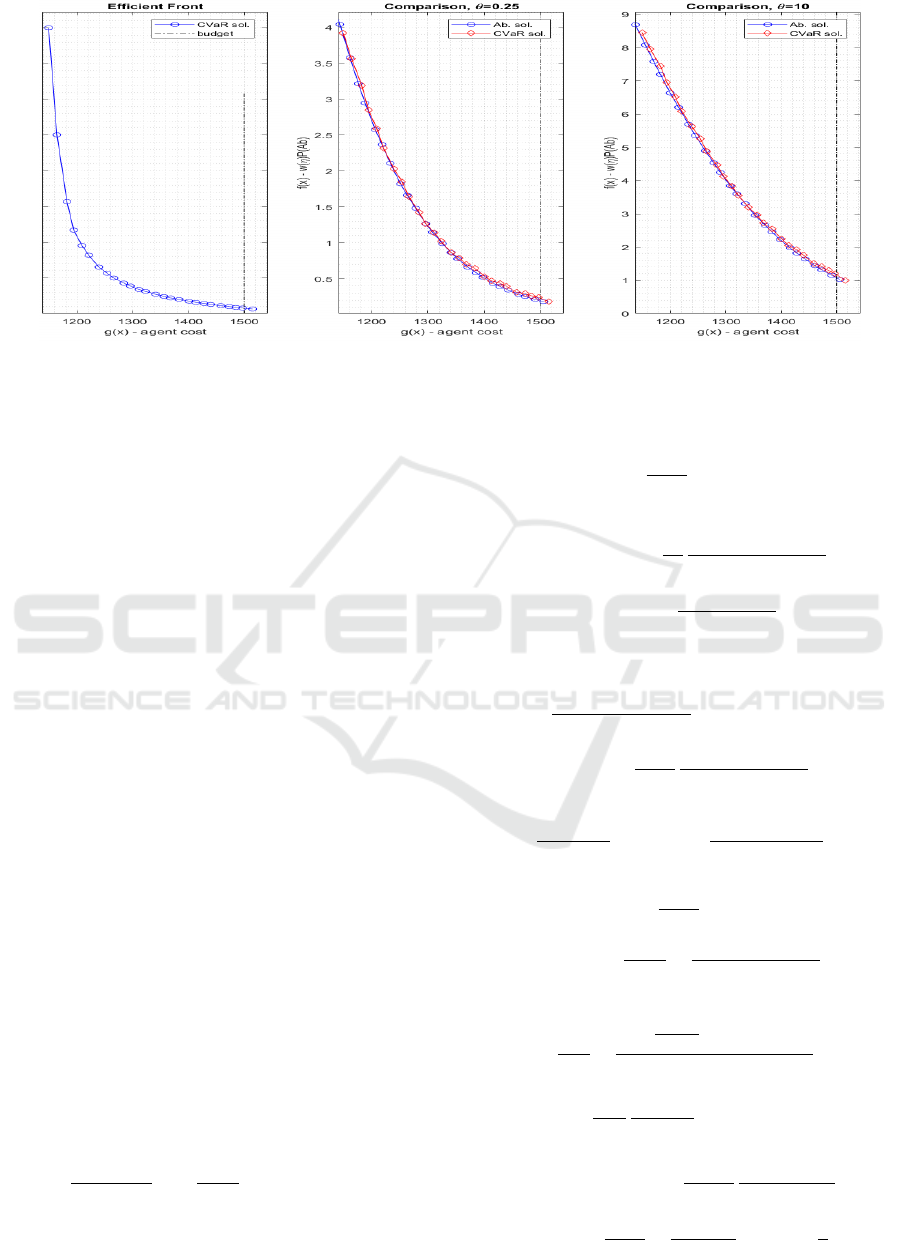
Figure 3: The left figure shows the CVaR solution for a system of three queues. In the middle and right figures the solution
under abandonments are shown, for θ = 0.25 and θ = 10. The MA solution for abandonments is compared to the CVaR
solution for abandonments.
cations to Call Centers, pages 17–45. Springer Berlin
Heidelberg, Berlin, Heidelberg.
Parlar, M. and Sharafali, M. (2014). Optimal design of multi
server markovian queues with polynomial waiting and
service costs. Applied Stochastic Models in Business
and Industry.
Riordan, J. (1962). Stochastic Service Systems. Wiley.
Rockafellar, R. and Uryasev, S. (2000). Optimization of
conditional value-at-risk. Journal of risk, 2.
Rockafellar, R. and Uryasev, S. (2002). Conditional value-
at-risk for general loss distributions. Journal of bank-
ing & Finance, 26:1443–1471.
Rolfe, A. J. (1971). A note on marginal allocation in
multiple-server service systems. Management Sci-
ence.
Svanberg, K. (2009). On marginal allocation. Dept. of
mathematics, KTH, Stockholm.
Weber, R. (1980). On the marginal benefit of adding servers
to G/GI/m queues. Management Science, 26(9).
Zeng, G. (2003). Two common properties of the Erlang-
B function, Erlang-C function, and Engset blocking
function. Mathematical and Computer Modelling,
37(12):1287–1296.
APPENDIX
Proof of Proposition 1
First note that β-CVaR satisfies φ
β
(c,λ,µ) =
(1/λ)Φ
β
(c,1,µ/λ), so we can without loss of gener-
ality assume that λ = 1 and µ < 1.
The forward difference ∆φ
β
(c) = φ
β
(c + 1)− φ
β
(c) is
given by
1
cµ + µ − 1
log
Π
c+1
Π
c
− µφ
β
(c)
≤ 0 (19)
since Π
c
is non-increasing, hence φ
β
(c) is non-
increasing.
The second forward difference is
∆
2
φ
β
(c) =
1
C
1
C
2
2µ
2
φ
β
(c) + G
(20)
where C
k
= (c + k)µ − 1, and
G = C
1
log
C
1
C
0
C
1
c − Π
c
C
2
(c + 1) − Π
c+1
−2µlog
C
0
(C
1
c − Π
c
)µ
. (21)
Convexity of β-CVaR follows by showing that G ≥ 0.
Using that x/(1 + x) ≤ log(1 + x) ≤ x we have that
log
C
1
C
2
(c + 1) − Π
c+1
≥ −log(c + 1) (22)
−
1
c + 1
µ(c + 1) − Π
c+1
C
1
, (23)
and
log
C
1
c − Π
c
C
0
≥ log(c) +
cµ − Π
c
cC
0
+ µc − Π
c
. (24)
Then
G ≥ C
1
log
c
c + 1
+ 2µ log(cµ) − µ
+
Π
c+1
c + 1
+
C
3
(cµ − Π
c
)
cC
0
+ (cµ − Π
c
)
. (25)
From (3), it follows that
G ≥
C
−1
c
+
Π
c
C
0
(c+1)µ
−C
2
+ 2µ
2
c
(cC
0
+ (cµ − Π
c
)
. (26)
Note that c(cµ − 1) + cµ − Π
c
> 0 since cµ > 1. Us-
ing that Π
c
≤
1
cµ+1
1
(c−1)µ+1
, G(c(cµ − 1) + cµ − Π
c
)
is bounded from below by
(cµ − 1)
2
+ µ
2
(2c − 1) −
1
cµ + 1
1
(c − 1)µ + 1
·
(cµ − 1)(
c + 1
c
−
1
(c + 1)µ
) + µ(2 −
1
c
)
(27)
ICORES 2018 - 7th International Conference on Operations Research and Enterprise Systems
302

Introduce ε =
cµ−1
µ
, and eliminate c in (27) to ob-
tain
µ
2
(ε
2
+ 2ε +
2
µ
− 1) −
H
(2 + µε)(2 + µε − µ)
, (28)
where H = µ(2 + ε) + µ
2
ε−1
1+µε
−
1
1+µ+µε
.
Consider two cases, ε ≥ 1 and ε < 1.
If ε ≥ 1, then (28) is greater than
µ
2
(ε
2
+ 2ε +
2
µ
− 1) − H/4 (29)
≥ (εµ +
7µ − 2
8
)
2
+
12 + 11µ + 97µ(1 − µ)
64
which is non-negative and we used that
1
1+µε
≤ 1 and
1
1+µ+µε
≥ 1 − µ − µε.
If ε < 1, then we write (28) on common denomi-
nator and use
1
1+µε
≥ 1 − µε and
1
1+µ+µε
≥ 1 − µ − µε,
we can show that the numerator is bounded below by
(1 − µ)
1 − εµ + µ
3
+ 5µ(1 − µ) + µ(1 − ε)
+4εµ
2
(13/4 − µ + ε(1 + µ)))
+µ
3
ε
3
(4ε + µε
2
+ 7) ≥ 0 (30)
for all ε,µ ∈ (0, 1).
Then ∆
2
φ
β
(c,1,µ) ≥
2µ
2
φ
β
(c,1,µ)
C
2
C
1
≥ 0, and φ
β
is
integer-convex.
Multi-server Marginal Allocation - With CVaR and Abandonment based QoS Measures
303
