
Transferring Information Across Medical Images of Different Modalities
Jakub Nalepa
1,2
, Piotr Mokry
1
, Janusz Szymanek
1
and Michael P. Hayball
1,3,4
1
Future Processing, Gliwice, Poland
2
Silesian University of Technology, Gliwice, Poland
3
Feedback PLC, Cambridge, U.K.
4
Cambridge Computed Imaging, Cambridge, U.K.
Keywords:
Multimodal Analysis, ROI Transfer, DICOM.
Abstract:
Multimodal analysis plays a pivotal role in medical imaging and has been recognized as an established tool
in clinical diagnosis. This joint investigation allows for extracting various bits of information from images of
different modalities, which can complement each other to provide a comprehensive view to the patient case.
Since those images may be acquired using different protocols, their synchronization and transferring infor-
mation, e.g., regions of interest (ROIs) between them is not trivial. In this paper, we derive the formulas for
mapping ROIs between different modalities and show a real-life PET/CT example of such image processing.
1 INTRODUCTION
Multimodal image information is useful not only for
visualization, analysis and interpretation of the ima-
ges, but also for undertaking multicenter clinical con-
sultations which allow for improving patient care
by designing better therapy and follow-up strategies.
Therefore, such approaches become common practice
in clinical and pre-clinical imaging, and they are a
very active research topic worldwide. In practical
scenarios, combining the structural (anatomical) in-
formation with the functional information is of the
biggest value. The ultimate goal of multimodal ima-
ging is to maximize the diagnostic (and very often
prognostic for several combinations (Greulich and
Sechtem, 2015)) value of differently acquired images
which may not be fully exploited otherwise.
There are numerous approaches for multimodal
analysis that couple different image modalities in both
side-by-side and fusion modes (Greulich and Sech-
tem, 2015). In the latter techniques, the images re-
quire further processing—they need to be registered,
due to potential misplacement caused by patient brea-
thing or motion (Deregnaucourt et al., 2016). Clinical
cases have shown that single-photon emission compu-
ted tomography/computed tomography (SPECT/CT)
and positron emission tomography/computed tomo-
graphy (PET/CT) are the established diagnostic tools
for radiologists (Pichler et al., 2008). An important
downside of CT imaging is a significant radiation
dose that affects the patient, and the limited soft tissue
contrast provided by CT. Therefore, coupling magne-
tic resonance imaging (MRI) with PET (in PET/MRI
systems) is being intensively developed—such sys-
tems can deliver morphologic, functional and mole-
cular information simultaneously (Estorch and Car-
rio, 2013; Vandenberghe and Marsden, 2015). The
current challenges in the multimodal imaging have
been summarized in several surveys and reviews (Es-
torch and Carrio, 2013; Mart
´
ı-Bonmat
´
ı et al., 2010;
Sui et al., 2012).
In this paper, we focus on the side-by-side analysis
of multimodal images. We derive formulas for trans-
ferring information between images, using only the
acquisition protocol information available in DICOM
(Digital Imaging and Communications in Medicine),
being a standard for exchanging medical image data.
The formulas can be easily applied to images of any
modalities in order to transfer annotated regions of
interests (ROIs) between them. This ROI transfer is
very useful in techniques for automated segmentation
and analysis of multimodal medical images—as alre-
ady mentioned, the structural information can be en-
hanced by the functional information in search of va-
rious tissues of interest (Nalepa et al., 2016).
Section 2 defines the prerequisites which are used
in Section 3 to derive formulas utilized for transfer-
ring ROIs across different modalities. In Sect. 4, we
show a real-life example of transferring information
between PET and CT. Section 5 concludes the paper.
526
Nalepa, J., Mokry, P., Szymanek, J. and Hayball, M.
Transferring Information Across Medical Images of Different Modalities.
DOI: 10.5220/0006653305260533
In Proceedings of the 7th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2018), pages 526-533
ISBN: 978-989-758-276-9
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

2 DEFINITIONS AND USEFUL
EQUALITIES
In this section, we gather the prerequisites, and derive
and prove useful equalities that will become handy in
Section 3—they will be exploited to retrieve the equa-
tions for mapping ROIs between images of different
modalities.
Definition 1. Consider the following orthonormal vectors:
~
F
1
= (F
11
,F
21
,F
31
) and
~
F
2
= (F
12
,F
22
,F
32
)
where
|
~
F
1
| = 1, |
~
F
2
| = 1 ⇒
⇒ F
2
11
+ F
2
21
+ F
2
31
= F
2
12
+ F
2
22
+ F
2
32
= 1 (1)
~
F
1
◦
~
F
2
= F
11
F
12
+ F
21
F
22
+ F
31
F
32
= 0 (2)
Additionally, let us introduce
~n = (n
1
,n
2
,n
3
) =
~
F
1
×
~
F
2
. (3)
Expanding Eq. 3, we obtain:
~n =
n
1
n
2
n
3
T
=
~
i
~
j
~
k
F
11
F
21
F
31
F
12
F
22
F
32
=
F
21
· F
32
− F
22
· F
31
F
12
· F
31
− F
11
· F
32
F
11
· F
22
− F
12
· F
21
T
,
where
~
i,
~
j and
~
k are versors. According to this definition, we have |~n| = 1,
~
F
1
◦~n = 0, and
~
F
2
◦~n = 0. For
~
F
1
,
~
F
2
and ~n, the following theorem is true:
Theorem 1.
~
F
1
=
~
F
2
×~n and
~
F
2
=~n ×
~
F
1
.
Proof.
~
F
1
=
~
F
2
×~n =
~
i
~
j
~
k
F
12
F
22
F
32
n
1
n
2
n
3
Eq. 1
====
=
F
22
(F
11
F
22
− F
21
F
12
) − F
32
(F
31
F
12
− F
11
F
32
)
F
32
(F
21
F
32
− F
31
F
22
) − F
12
(F
11
F
22
− F
21
F
12
)
F
12
(F
31
F
12
− F
11
F
32
) − F
22
(F
21
F
32
− F
31
F
22
)
T
=
=
F
2
22
F
11
− F
21
F
12
F
22
− F
31
F
32
F
12
+ F
11
F
2
32
F
2
32
F
21
− F
31
F
32
F
22
− F
11
F
12
F
22
+ F
21
F
2
12
F
2
12
F
31
− F
11
F
12
F
32
− F
21
F
22
F
32
+ F
31
F
2
22
T
=
=
F
11
(F
2
22
+ F
2
32
) − F
12
(F
21
F
22
+ F
31
F
32
)
F
21
(F
2
12
+ F
2
32
) − F
22
(F
31
F
32
+ F
11
F
12
)
F
31
(F
2
12
+ F
2
22
) − F
32
(F
11
F
12
+ F
21
F
22
)
T
Eq. 2
====
=
F
11
(F
2
22
+ F
2
32
) + F
12
F
11
F
12
F
21
(F
2
12
+ F
2
32
) + F
22
F
21
F
22
F
31
(F
2
12
+ F
2
22
) + F
32
F
31
F
32
T
Eq. 1
====
F
11
F
21
F
31
T
=
~
F
1
.
The second proof is analogous.
Remark 1. According to Theorem 1, the following formulas hold:
F
11
= F
22
n
3
− F
32
n
2
F
21
= F
32
n
1
− F
12
n
3
F
31
= F
12
n
2
− F
22
n
1
(4)
F
12
= F
31
n
2
− F
21
n
3
F
22
= F
11
n
3
− F
31
n
1
F
32
= F
21
n
1
− F
11
n
2
(5)
Transferring Information Across Medical Images of Different Modalities
527

Additionally, we can proof the following:
Theorem 2. The inverse matrix of
R =
F
11
F
12
n
1
0
F
21
F
22
n
2
0
F
31
F
32
n
3
0
0 0 0 1
constructed from
~
F
1
,
~
F
2
and ~n can be expressed as:
R
−1
=
F
11
F
21
F
31
0
F
12
F
22
F
32
0
n
1
n
2
n
3
0
0 0 0 1
.
Proof. The determinant of the R matrix is:
detR = F
11
(F
22
n
3
− F
32
n
2
) + F
21
(F
32
n
1
− F
12
n
3
) + F
31
(F
12
n
2
− F
22
n
1
)
Eq. 4
====
= F
2
11
+ F
2
21
+ F
2
31
Eq. 1
==== 1 (6)
Let us calculate the cofactor matrix R
D
:
R
D
=
F
22
n
3
− F
32
n
2
F
31
n
2
− F
21
n
3
F
21
F
32
− F
31
F
22
0
F
32
n
1
− F
12
n
3
F
11
n
3
− F
31
n
1
F
31
F
12
− F
11
F
32
0
F
12
n
2
− F
22
n
1
F
21
n
1
− F
11
n
2
F
11
F
22
− F
21
F
12
0
0 0 0 detR
Eq. 4, 5, 1
=======
=
F
11
F
12
n
1
0
F
21
F
22
n
2
0
F
31
F
32
n
3
0
0 0 0 1
.
Therefore—by the definition of the inverse matrix—we have:
R
−1
=
1
detR
(R
D
)
T
=
F
11
F
21
F
31
0
F
12
F
22
F
32
0
n
1
n
2
n
3
0
0 0 0 1
. (7)
3 TRANSFERRING ROIS ACROSS
MODALITIES
In this section, we derive the formulas for transfer-
ring ROIs across different modalities. We exploit
the expressions presented and proven in the previous
section, as well as the image information which can
be extracted from each DICOM file
1
. The derived
equations are independent from the underlying mo-
dality, and can be easily applied to process any pair of
modalities side-by-side.
Let
P
x
P
y
P
z
1
=
F
11
∆r F
12
∆c n
1
∆s S
x
F
21
∆r F
22
∆c n
2
∆s S
y
F
31
∆r F
32
∆c n
3
∆s S
z
0 0 0 1
r
c
s
1
= A
r
c
s
1
, (8)
where:
• P
xyz
—Coordinates of the voxel (c,r) in the image plane (in mm).
• S
xyz
—Image position (0020,0032 DICOM attribute). It is the location from the origin (in mm).
1
For more details see: http://nipy.org/nibabel/dicom/dicom orientation.html; last access date: Oct. 9, 2017.
ICPRAM 2018 - 7th International Conference on Pattern Recognition Applications and Methods
528

• F
:,1
, F
:,2
—Column (Y ) and row (X) direction cosine of the image orientation (0020,0037 DICOM attribute).
These vectors are normal, and F
:,1
◦ F
:,2
= 0.
• r—Row index to the image plane. The first row index is zero.
• ∆r, where ∆r 6= 0—Row pixel resolution of the pixel spacing (0028,0030 DICOM attribute) (in mm).
• c—Column index to the image plane. The first column index is zero.
• ∆c, where ∆c 6= 0—Column pixel resolution of the pixel spacing (0028,0030 DICOM attribute) (in mm).
• s—Slice index to the slice plane. The first slice index is zero.
• ∆s, where ∆s 6= 0—Spacing between the consecutive slices (in mm).
• n
i
, where i ∈ {1,2,3}—Vector orthogonal to F
:,1
and F
:,2
.
Taking into account the definition of ~n (see Eq. 3 and Def. 1, especially Eq. 1), the determinant of the A matrix
becomes:
detA =
F
11
∆r F
12
∆c n
1
∆s S
x
F
21
∆r F
22
∆c n
2
∆s S
y
F
31
∆r F
32
∆c n
3
∆s S
z
0 0 0 1
=
= ∆r∆c∆s ·
F
11
F
12
n
1
0
F
21
F
22
n
2
0
F
31
F
32
n
3
0
0 0 0 1
Eq. 6
==== ∆r∆c∆s · 1 6= 0.
Consider the following decomposition of the A matrix into the translation, rotation and scaling matrices:
A = T · R · S, (9)
(10)
where
T =
1 0 0 S
x
0 1 0 S
y
0 0 1 S
z
0 0 0 1
,R =
F
11
F
12
n
1
0
F
21
F
22
n
2
0
F
31
F
32
n
3
0
0 0 0 1
,S =
∆r 0 0 0
0 ∆c 0 0
0 0 ∆s 0
0 0 0 1
. (11)
Let us multiply the right side of Eq. 9:
T ·R · S =
1 0 0 S
x
0 1 0 S
y
0 0 1 S
z
0 0 0 1
F
11
F
12
n
1
0
F
21
F
22
n
2
0
F
31
F
32
n
3
0
0 0 0 1
∆r 0 0 0
0 ∆c 0 0
0 0 ∆s 0
0 0 0 1
=
=
1 0 0 S
x
0 1 0 S
y
0 0 1 S
z
0 0 0 1
F
11
∆r F
12
∆c n
1
∆s 0
F
21
∆r F
22
∆c n
2
∆s 0
F
31
∆r F
32
∆c n
3
∆s 0
0 0 0 1
=
=
F
11
∆r F
12
∆c n
1
∆s S
x
F
21
∆r F
22
∆c n
2
∆s S
y
F
31
∆r F
32
∆c n
3
∆s S
z
0 0 0 1
= A
Such decomposition helps find the inverse matrix of A.
Remark 2. Since detA = ∆r∆c∆s 6= 0, T , R and S are invertible (Theorem 2):
T
−1
=
1 0 0 −S
x
0 1 0 −S
y
0 0 1 −S
z
0 0 0 1
,R
−1
=
F
11
F
21
F
31
0
F
12
F
22
F
32
0
n
1
n
2
n
3
0
0 0 0 1
,S
−1
=
1
∆r
0 0 0
0
1
∆c
0 0
0 0
1
∆s
0
0 0 0 1
. (12)
Transferring Information Across Medical Images of Different Modalities
529

In order to transfer ROIs across images, P
xyz
values (in Eq. 8) should be the same for both of them (the d and
s subscripts denote the destination and source image, respectively). Therefore, we get:
P
x
P
y
P
z
1
= A
s
·V
s
=
F
s
11
∆r
s
F
s
12
∆c
s
n
s
1
∆s
s
S
s
x
F
s
21
∆r
s
F
s
22
∆c
s
n
s
2
∆s
s
S
s
y
F
s
31
∆r
s
F
s
32
∆c
s
n
s
3
∆s
s
S
s
z
0 0 0 1
r
s
c
s
s
s
1
P
x
P
y
P
z
1
= A
d
·V
d
=
F
d
11
∆r
d
F
d
12
∆c
d
n
d
1
∆s
d
S
d
x
F
d
21
∆r
d
F
d
22
∆c
d
n
d
2
∆s
d
S
d
y
F
d
31
∆r
d
F
d
32
∆c
d
n
d
3
∆s
d
S
d
z
0 0 0 1
r
d
c
d
s
d
1
d
Then:
T
s
· R
s
· S
s
· V
s
= T
d
· R
d
· S
d
· V
d
|
→
T
−1
d
(13)
T
−1
d
· T
s
· R
s
· S
s
· V
s
= R
d
· S
d
· V
d
|
→
R
−1
d
(14)
R
−1
d
· T
−1
d
· T
s
· R
s
· S
s
· V
s
= S
d
· V
d
|
→
S
−1
d
(15)
S
−1
d
· R
−1
d
· T
−1
d
· T
s
· R
s
· S
s
· V
s
= V
d
(16)
(S
−1
d
· R
−1
d
) · (T
−1
d
· A
s
) · V
s
= V
d
(17)
V
d
= A
−1
d
· A
s
· V
s
(18)
Let us continue with Eq. 17:
(S
−1
d
· R
−1
d
) =
1
∆r
d
0 0 0
0
1
∆c
d
0 0
0 0
1
∆s
d
0
0 0 0 1
·
F
d
11
F
d
21
F
d
31
0
F
d
12
F
d
22
F
d
32
0
n
d
1
n
d
2
n
d
3
0
0 0 0 1
⇒
(S
−1
d
· R
−1
d
) =
1
∆r
d
F
d
11
1
∆r
d
F
d
21
1
∆r
d
F
d
31
0
1
∆c
d
F
d
12
1
∆c
d
F
d
22
1
∆c
d
F
d
32
0
1
∆s
d
n
d
1
1
∆s
d
n
d
2
1
∆s
d
n
d
3
0
0 0 0 1
(19)
(T
−1
d
· A
s
) =
1 0 0 −S
d
x
0 1 0 −S
d
y
0 0 1 −S
d
z
0 0 0 1
·
∆r
s
F
s
11
∆c
s
F
s
12
∆s
s
n
s
1
S
s
x
∆r
s
F
s
21
∆c
s
F
s
22
∆s
s
n
s
2
S
s
y
∆r
s
F
s
31
∆c
s
F
s
32
∆s
s
n
s
3
S
s
z
0 0 0 1
⇒
(T
−1
d
· A
s
) =
F
s
11
∆r
s
F
s
12
∆c
s
n
s
1
∆s
s
S
s
x
− S
d
x
F
s
21
∆r
s
F
s
22
∆c
s
n
s
2
∆s
s
S
s
y
− S
d
y
F
s
31
∆r
s
F
s
32
∆c
s
n
s
3
∆s
s
S
s
z
− S
d
z
0 0 0 1
. (20)
Let us introduce the vector
~
D, given as:
~
D =
D
x
D
y
D
z
T
=
S
s
x
− S
d
x
S
s
y
− S
d
y
S
s
z
− S
d
z
(21)
and:
(T
−1
d
· A
s
) =
F
s
11
∆r
s
F
s
12
∆c
s
n
s
1
∆s
s
D
x
F
s
21
∆r
s
F
s
22
∆c
s
n
s
2
∆s
s
D
y
F
s
31
∆r
s
F
s
32
∆c
s
n
s
3
∆s
s
D
z
0 0 0 1
(22)
ICPRAM 2018 - 7th International Conference on Pattern Recognition Applications and Methods
530

Combining Eq. 19 and Eq. 20, we obtain:
A
−1
d
· A
s
=
1
∆r
d
F
d
11
1
∆r
d
F
d
21
1
∆r
d
F
d
31
0
1
∆c
d
F
d
12
1
∆c
d
F
d
22
1
∆c
d
F
d
32
0
1
∆s
d
n
d
1
1
∆s
d
n
d
2
1
∆s
d
n
d
3
0
0 0 0 1
·
F
s
11
∆r
s
F
s
12
∆c
s
n
s
1
∆s
s
D
x
F
s
21
∆r
s
F
s
22
∆c
s
n
s
2
∆s
s
D
y
F
s
31
∆r
s
F
s
32
∆c
s
n
s
3
∆s
s
D
z
0 0 0 1
=
=
∆r
s
∆r
d
(F
d
11
F
s
11
+ F
d
21
F
s
21
+ F
d
31
F
s
31
)
∆c
s
∆r
d
(F
d
11
F
s
12
+ F
d
21
F
s
22
+ F
d
31
F
s
32
)
∆r
s
∆c
d
(F
d
12
F
s
11
+ F
d
22
F
s
21
+ F
d
32
F
s
31
)
∆c
s
∆c
d
(F
d
12
F
s
12
+ F
d
22
F
s
22
+ F
d
32
F
s
32
)
∆r
s
∆s
d
(n
d
1
F
s
11
+ n
d
2
F
s
21
+ n
d
3
F
s
31
)
∆c
s
∆s
d
(n
d
1
F
s
12
+ n
d
2
F
s
22
+ n
d
3
F
s
32
)
0 0
∆s
s
∆r
d
(F
d
11
n
s
1
+ F
d
21
n
s
2
+ F
d
31
n
s
3
)
1
∆r
d
(F
d
11
D
x
+ F
d
21
D
y
+ F
d
31
D
z
)
∆s
s
∆c
d
(F
d
12
n
s
1
+ F
d
22
n
s
2
+ F
d
32
n
s
3
)
1
∆c
d
(F
d
12
D
x
+ F
d
22
D
y
+ F
d
32
D
z
)
∆s
s
∆s
d
(n
d
1
n
s
1
+ n
d
2
n
s
2
+ n
d
3
n
s
3
)
1
∆s
d
(n
d
1
D
x
+ n
d
2
D
y
+ n
d
3
D
z
)
0 1
.
From the definition of the dot product, we get:
A
−1
d
· A
s
=
∆r
s
∆r
d
(
~
F
d
1
◦
~
F
s
1
)
∆c
s
∆r
d
(
~
F
d
1
◦
~
F
s
2
)
∆s
s
∆r
d
(
~
F
d
1
◦ ~n
s
)
1
∆r
d
~
F
d
1
◦
~
D
∆r
s
∆c
d
(
~
F
d
2
◦
~
F
s
1
)
∆c
s
∆c
d
(
~
F
d
2
◦
~
F
s
2
)
∆s
s
∆c
d
(
~
F
d
2
◦ ~n
s
)
1
∆c
d
~
F
d
2
◦
~
D
∆r
s
∆s
d
(~n
d
◦
~
F
s
1
)
∆c
s
∆s
d
(~n
d
◦
~
F
s
2
)
∆s
s
∆s
d
(~n
d
◦ ~n
s
)
1
∆s
d
(~n
d
◦
~
D)
0 0 0 1
.
Using Eq. 18 gives:
V
d
=
r
d
c
d
s
d
1
= A
−1
d
· A
s
· V
s
=
=
∆r
s
∆r
d
(
~
F
d
1
◦
~
F
s
1
)
∆c
s
∆r
d
(
~
F
d
1
◦
~
F
s
2
)
∆s
s
∆r
d
(
~
F
d
1
◦ ~n
s
)
1
∆r
d
~
F
d
1
◦
~
D)
∆r
s
∆c
d
(
~
F
d
2
◦
~
F
s
1
)
∆c
s
∆c
d
(
~
F
d
2
◦
~
F
s
2
)
∆s
s
∆c
d
(
~
F
d
2
◦ ~n
s
)
1
∆c
d
(
~
F
d
2
◦
~
D)
∆r
s
∆s
d
(~n
d
◦
~
F
s
1
)
∆c
s
∆s
d
(~n
d
◦
~
F
s
2
)
∆s
s
∆s
d
(~n
d
◦ ~n
s
)
1
∆s
d
(~n
d
◦
~
D)
0 0 0 1
r
s
c
s
s
s
1
.
Finally, we have:
r
d
=
1
∆r
d
∆r
s
r
s
(
~
F
d
1
◦
~
F
s
1
) + ∆c
s
c
s
(
~
F
d
1
◦
~
F
s
2
) + ∆s
s
s
s
(
~
F
d
1
◦ ~n
s
) + (
~
F
d
1
◦
~
D)
c
d
=
1
∆c
d
∆r
s
r
s
(
~
F
d
2
◦
~
F
s
1
) + ∆c
s
c
s
(
~
F
d
2
◦
~
F
s
2
) + ∆s
s
s
s
(
~
F
d
2
◦ ~n
s
) + (
~
F
d
2
◦
~
D)
s
d
=
1
∆s
d
∆r
s
r
s
(~n
d
◦
~
F
s
1
) + ∆c
s
c
s
(~n
d
◦
~
F
s
2
) + ∆s
s
s
s
(~n
d
◦ ~n
s
) + (~n
d
◦
~
D)
(23)
Transferring Information Across Medical Images of Different Modalities
531

Eq. 23 can be used to transfer the information
(e.g., ROIs) across images.
4 CASE STUDY: PET/CT LUNG
SEGMENTATION AND
ANALYSIS
Lung cancer accounts for 12.7% of the world’s total
cancer incidence, and the PET/CT imaging plays a pi-
votal role in its diagnosis, staging and treatment, as it
provides both anatomical and functional information
about the patient. Therefore, automated PET/CT seg-
mentation and analysis techniques attracted research
attention and they are actively being developed (Mo-
kri et al., 2012; Zhao et al., 2015). In our very recent
work (Nalepa et al., 2016), we proposed an automa-
ted approach for PET/CT image analysis which does
not require any user intervention. The experimental
study (44 patients, age: 68.7 ± 10.3 years, 32 males
who underwent FDG-PET/CT using GE Discovery;
the clinical information was available for 42 patients:
I: 1, II: 9, III: 28, and IV: 4) revealed that our auto-
mated histogram-based texture analysis (Miles et al.,
2013) of filtered images
2
allowed for predicting sur-
vival (kurtosis, p = .028). Therefore, we showed that
using quantitative techniques (CT texture analysis) in
addition to existing measures, including size, density
and glucose uptake, can enhance the diagnostic effi-
ciency of PET/CT.
Algorithm 1: Hands-free PET/CT analysis algorithm.
1: Identify co-registered CT and PET series;
2: Segment lungs in CT;
3: Segment hot-spots in PET in the lung range;
4: Transfer hot-spot ROIs to CT;
5: Apply texture analysis algorithm in CT;
6: Generate report;
The high-level pseudo-code of our hands-free
PET/CT analysis algorithm is presented in Algo-
rithm 1 (we boldfaced the steps which require trans-
ferring information between modalities). After iden-
tifying the co-registered CT and PET series (line 1),
the CT frames are segmented in search of lungs (their
base and apex). Then, the PET images are processed
(line 3), only in the lung region (between base and
apex). First, a threshold is extracted (40% of the glo-
bal maximum pixel value, as suggested in (Win et al.,
2013)). This threshold is used to identify hot-spots in
2
We used our TexRAD software for texture analysis:
http://texrad.com/.
PET images (connected regions exceeding this value).
Hot-spots are transferred back to CT using Eq. 23 de-
rived in Section 3 (line 4). In the last step, we ap-
ply the TexRAD algorithm (line 5), and generate a
report (line 6) which is saved for review. TexRAD
is a filtration-histogram approach to texture analysis
which comprises image filtration performed to high-
light image features of a specified size. This proce-
dure is followed by the histogram analysis for quan-
tification of derived features using various measures
(e.g., kurtosis, skewness, standard deviation or en-
tropy). Such texture features were shown to be cor-
related with various clinical parameters (Weiss et al.,
2014; Parikh et al., 2014), not only in oncology (Ra-
dulescu et al., 2014).
Example images generated at the most important
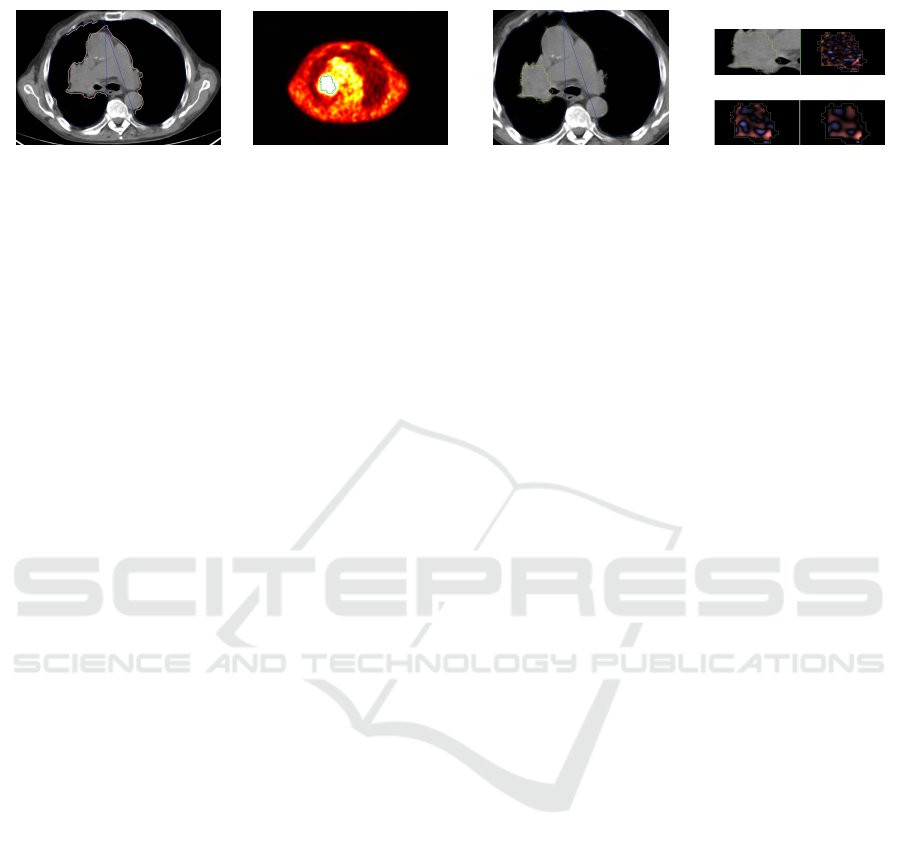
steps of the processing pipeline are shown in Figure 1.
The images are co-registered, and the CT frames are
segmented to find lungs (Figure 1a). Additionally, in
our approach the convex hulls of lungs are determined
(those regions are larger compared with the segmen-
ted lungs), since the tumors may be associated with
the lung wall or mediastinum. Then, the lung ROIs
are transferred to PET (using Eq. 23) to find the lo-
cation of lungs in PET series, and the hot-spots are
segmented (Figure 1b). Afterwards, the hot-spot ROI
is transferred back to the corresponding CT image (by
location), and it undergoes the texture analysis at vari-
ous spatial frequencies (scales). Finally, the extracted
texture features, along with the filtered images are sa-
ved in reports and can be further investigated. This
PET/CT analysis example shows how to efficiently
exploit the information (functional and anatomical)
about the patient exposed by two different modali-
ties. The key part of this analysis is concerned with
the possibility of transferring data (e.g., ROIs) across
the co-registered images, as presented in Section 3.
It is worth mentioning that the lung and hot-spot seg-
mentation algorithms can be easily replaced with new,
perhaps more efficient techniques without impacting
the entire hands-free processing pipeline. For more
details, see (Nalepa et al., 2016).
5 CONCLUSIONS
In this paper, we focused on the side-by-side analysis
of multimodal medical images, and derived formulas
which can be used to transfer information (e.g., ROIs)
across different modalities. Since the formulas are ge-
neric, they can be very easily applied to any pair of co-
registered images. Such multimodal analysis became
crucial in the clinical practice because it enhances the
diagnostic efficiency of this kind of imaging by cou-
ICPRAM 2018 - 7th International Conference on Pattern Recognition Applications and Methods
532
(a) Lungs in CT (b) Hot-spots in PET (c) Transfer (PET→CT) (d) Texture analysis
(i) Original
CT
(ii) Fine
texture
(iii) Medium
texture
(iv) Coarse
texture
Figure 1: Example images generated at the most important steps of the PET/CT analysis: (a) lungs segmented in CT (light
pink ROIs indicate lungs, whereas blue ROIs show their convex hulls), (b) hot-spot segmented in PET, (c) hot-spot transferred
from PET to CT (annotated in yellow), and (d) texture analysis at various scales (fine, medium and coarse) using the TexRAD
algorithm. We boldfaced the steps in which we benefit from transferring the information between two modalities.
pling complementary patient information (e.g., ana-
tomical and functional). It leads to extracting new in-
formation about the patient condition and treatment
response, which would not be revealed if the images
were processed separately.
ACKNOWLEDGEMENTS
This research was supported by the National
Centre for Research and Development under the
Innomed Research and Development Grant No.
POIR.01.02.00-00-0030/15.
REFERENCES
Deregnaucourt, T., Samir, C., and Yao, A.-F. (2016). A
regression model for registering multimodal images.
Procedia Computer Science (MIUA 2016), 90:42 – 47.
Estorch, M. and Carrio, I. (2013). Future challenges of mul-
timodality imaging. In Schober, O. and Riemann, B.,
editors, Mol. Imag. in Onc., pages 403–415, Heidel-
berg. Springer.
Greulich, S. and Sechtem, U. (2015). Multimodality ima-
ging in coronary artery disease – “the more the bet-
ter?”. Cor et Vasa, 57(6):e462 – e469.
Mart
´
ı-Bonmat
´
ı, L., Sopena, R., Bartumeus, P., and Sopena,
P. (2010). Multimodality imaging techniques. Con-
trast Media & Molecular Imaging, 5(4):180–189.
Miles, K., Ganeshan, B., and Hayball, M. (2013). CT
texture analysis using the filtration-histogram met-
hod: what do the measurements mean? Canc. Im.,
13(3):400–406.
Mokri, S. S., Saripan, M. I., Marhaban, M. H., and Nordin,
A. J. (2012). Lung segmentation in CT for thoracic
PET-CT registration through visual study. In Proc.
IEEE-EMBS, pages 550–554.
Nalepa, J., Szymanek, J., Mcquaid, S., Endozo, R., Pra-
kash, V., Ganeshan, B., Menys, A., Hayball, M. P.,
Ezhil, V., Bellamy, L., Crawshaw, J., Hall, J., Groves,
A. M., and Nisbet, A. (2016). PET/CT in lung cancer:
An automated imaging tool for decision support. In
Radiological Society of North America 2016 Scienti-
fic Assembly and Annual Meeting, pages 1–2, Chicago
IL, USA. RSNA.
Parikh, J., Selmi, M., Charles-Edwards, G., Glendenning,
J., Ganeshan, B., Verma, H., Mansi, J., Harries, M.,
Tutt, A., and Goh, V. (2014). Changes in primary bre-
ast cancer heterogeneity may augment midtreatment
MR imaging assessment of response to neoadjuvant
chemotherapy. Radiology, 272(1):100–112.
Pichler, B. J., Judenhofer, M. S., and Pfannenberg, C.
(2008). Multimodal imaging approaches: PET/CT
and PET/MRI. In Semmler, W. and Schwaiger, M.,
editors, Molecular Imaging I, pages 109–132, Heidel-
berg. Springer.
Radulescu, E., Ganeshan, B., Shergill, S. S., Medford,
N., Chatwin, C., Young, R. C., and Critchley, H. D.
(2014). Grey-matter texture abnormalities and redu-
ced hippocampal volume are distinguishing features
of schizophrenia. Psychiatry Research: Neuroima-
ging, 223(3):179 – 186.
Sui, J., Adali, T., Yu, Q., Chen, J., and Calhoun, V. D.
(2012). A review of multivariate methods for mul-
timodal fusion of brain data. J. of Neurosc. Met.,
204(1):68 – 81.
Vandenberghe, S. and Marsden, P. K. (2015). PET-MRI:
a review of challenges and solutions in the develop-
ment of integrated multimodality imaging. Physics in
Medicine and Biology, 60(4):R115.
Weiss, G. J., Ganeshan, B., Miles, K. A., Campbell, D. H.,
Cheung, P. Y., Frank, S., and Korn, R. L. (2014).
Noninvasive image texture analysis differentiates k-
ras mutation from pan-wildtype nsclc and is prognos-
tic. PLOS ONE, 9(7):1–9.
Win, T., Miles, K. A., Janes, S. M., Ganeshan, B., Shastry,
M., Endozo, R., Meagher, M., Shortman, R. I., Wan,
S., Kayani, I., Ell, P. J., and Groves, A. M. (2013).
Tumor heterogeneity and permeability as measured on
the ct component of PET/CT predict survival in pa-
tients with non–small cell lung cancer. Clin. Cancer
Res., 19(13):3591–3599.
Zhao, J., Ji, G., Qiang, Y., Han, X., Pei, B., and Shi, Z.
(2015). A new method of detecting pulmonary no-
dules with PET/CT based on an improved watershed
algorithm. PLOS ONE, 10(4):1–15.
Transferring Information Across Medical Images of Different Modalities
533
