A New Model Proposal for Integrated Satellite Constellation

Scheduling within a Planning Horizon given Operational Constraints

M. J. Pinto

1,2,4

, A. I. Barros

, R. Noomen

, P. H. A. J. M. van Gelder

and T. Lamballais Tessensohn

Geointelligence Division, Institute of Advanced Studies (IEAv), São José dos Campos, Brazil

Defence and Security, TNO, The Hague, The Netherlands

Faculty of Aerospace Engineering, Delft University of Technology, Delft, The Netherlands

Faculty of Technology, Policy and Management, Delft University of Technology, Delft, The Netherlands

Keywords: Scheduling, Satellite Constellation, Optimization Model, Operational Scenarios, Remote Sensing.

Abstract: The operational use of satellite systems has been increasing due to technological advances and the reduced

costs of satellites and their launching. As such it has become more relevant to determine how to better use

these new capabilities which is reflected in an increase in application studies in this area. This work focuses

on the problem of developing the scheduling of a constellation of satellites and associated ground stations to

monitor different types of locations (targets) with different priorities for a given planning horizon. In order

to address this problem we will propose a new model that considers explicitly the operational requirements

of Brazilian relevant scenarios for a given planning horizon and target priority list. The methodology to be

developed to solve this model will also be discussed.

1 INTRODUCTION

The rapid rate of technological advances in the area

of spaceflight and sensors combined with the

reduced costs of satellites and their launch yield

potential for applications in many areas like

navigation, communication, weather forecasting, and

also defense, safety and security, e.g. detecting oil

spilling, monitoring borders, etc. (IPIECA, 2006;

Brekke and Solberg, 2005; Gagne, 2017). As such

there is an increasing need for support during the

acquisition phase and planning of the use of these

new technologies.

As Brazil is in an emerging stage in terms of

management and development of satellite systems

technologies, there is a need for research focusing on

this context seeking a better management of satellite

services and products to increase the autonomy and

sovereignty of the country. Remote sensing using

satellites to acquire information on given areas of

the Earth´s surface are particularly interesting given

Brazil´s vast territory of more than 8.5 million

square kilometers. In order to contribute to this

challenge, this work focuses on the development of a

realistic optimization model that, given a planning

horizon and the specifications of different

satellites/sensors, can support the decision making

process on the best planning to monitor different

types of targets (high and low priority ones) taking

the mission requirements into account in a Brazilian

context.

As the mission requirements determine the type

of satellites/sensors that should be used, it is

important to define scenarios with logical

requirements. Brazil is confronted with several

environmental and security issues like drought,

deforestation, floods, landslides, dam ruptures, oil

spilling along the coast, border monitoring issues,

etc. For some of these situations satellite remote

sensing is an interesting option as sensors on-board

of such satellites can scan vast areas during day and

night and download this data to ground stations for

further processing and usage. However, the satellite

orbit and characteristics of the on-board sensor as

well as the location of the ground stations yield

limitations on the number of times and the duration

that a given area can be scanned by a particular

satellite and the time at which the collected

information can be downloaded to the ground

station. In this paper we will consider mostly

scenarios for which, regular monitoring can increase

the situation awareness and enable both early

detection of disasters and/or mitigation actions, like:

312

Pinto, M., Barros, A., Noomen, R., Gelder, P. and Tessensohn, T.

A New Model Proposal for Integrated Satellite Constellation Scheduling within a Planning Horizon given Operational Constraints.

DOI: 10.5220/0006655003120319

In Proceedings of the 7th International Conference on Operations Research and Enterprise Systems (ICORES 2018), pages 312-319

ISBN: 978-989-758-285-1

 Deforestation in the Amazon: a very extensive

inland region of difficult access that is often

victim of deforestation attempts. The detection of

small areas of deforestation at an early stage will

permit authorities to take mitigation measures to

contain this deforestation.

 Oil spilling along the extensive Brazilian coast

line: the extraction and transport of oil in this

vast area, which lies adjacent to some natural

reserves, poses environmental challenges. It is of

the utmost importance to detect oil spilling at an

early stage to contain any environmental disaster.

 Monitoring Brazil’s border: this border

incorporates parts of the world’s largest

rainforest, which are difficult to access.

Therefore remote sensing of this vast area is

required in order to identify activities like the

construction of alternative roads for smuggling

or transportation of drugs.

Figure 1 provides an idea of the location and area

extension of the scenarios described above, and the

positions of the Brazilian ground stations as well.

Figure 1: Brazilian scenarios information based on

Petrobrás (2007), Gagne (2017) and DPI (2017).

This paper is organized as follows. In Section 2,

we introduce the problem and provide a review of

related models proposed in recent literature. Next

the operational background on satellite remote

sensing as well as the MATLAB program that has

been developed to compute the satellite coverage is

described in Sections 3 and 4. This coverage will be

input to the optimization model that will be

discussed in Section 5. Section 6 presents further

research possibilities.

2 DATA ACQUISITION AND

DOWNLOAD SATELLITES

SCHEDULING PROBLEM

This section introduces the Data Acquisition and

Download Scheduling Satellite Problem (DADSSP)

and discusses related proposed models.

DADSSP considers the planning problem of

assigning a set of different data requests (targets)

with different values (priorities) to a constellation of

heterogeneous satellites and ground stations in such

a way that the value of the collected data is

maximized (as not all the targets might be

addressed), while dealing with time-windows

constraints and different operational restrictions.

DADSSP also takes mission requirements

constraints into account, like revisit time (the time

interval between successive observations of the

same target) and due time (the latest time for

reception at the ground station of the acquired new

imagery of the same target). This problem is related

to the heterogeneous fleet routing problem with time

window and capacities (Toth and Vigo, 2014).

Most of the existing literature takes only the

acquisition problem into account in a static (Sundar

et al., 2016) or dynamic way (Zhai et al., 2015; Niu

et al., 2015). Also literature can be found related to

the scheduling problem of downloading the acquired

imagery by a satellite constellation to several ground

stations (Marinelli et al., 2011). However, in this

paper we will focus on literature that addresses

problems similar to DADSSP (Wang and Reinelt,

2011; Wang et al., 2011; Kim and Chang, 2015).

These papers handle both the acquisition and the

download planning but report few or no details

about the data and do not devote attention to

operational constraints (related to orbit/sensors

characteristics like inclination, altitude, resolution,

etc) and/or to mission requirement constraints.

Wang and Reinelt (2011) consider the

acquisition and download planning aiming to

maximize the summed rewards of serviced requests

subject to acquisition/download constraints and

visibility time-windows constraints, taking transition

time between consecutive acquisitions/downloads

into account. The precedence of the acquisition and

the download of the same request and the capacity of

the satellite memory level are also modelled. Their

modelling approach has been tested considering

satellites from the First Chinese Environment

Monitoring Constellation and ground stations from

China, in a two-days planning horizon.

A New Model Proposal for Integrated Satellite Constellation Scheduling within a Planning Horizon given Operational Constraints

313

Wang and Reinelt (2011) randomly generated the

input and it is not clear how the satellite related data

was modelled. Wang et al., (2011) provided more

details about the satellite system and energy capacity

constraints are included in a nonlinear model. As

this model is not easy to apply in practice and since,

according to the author, the acquisition planning

plays a more decisive role than the download

planning, a priority-based heuristic with conflict-

avoidance and a decision support system based on

the model is provided. The methodology was tested

using the same set of satellites of Wang and Reinelt

(2011) but considering spot and/or polygon targets,

uniformly positioned inside and/or outside the

mainland of China. The target rewards were again

randomly generated. Their paper presents another

version model of DADSSP and takes into account

relevant space operational concepts like the sensor

agility (capability in both roll and pitch axes, i.e., it

can look to the left and to the right and image targets

ahead and behind). However, requirements like due

and revisit time are not considered in the model.

Kim and Chang (2015) also considered the

acquisition and download problem, but their

objective was to reduce the system response time

defined as the time between the image data request

and its final distribution (including on-orbit imaging,

download and image processing on Earth). A genetic

algorithm is proposed to solve the problem. The

paper shows that the mission planning using the

scheduler reduces the system response time. It also

shows that an increase in the number of satellites

decreases both the revisit time and the response time

yielding an increase of the overall mission cost.

Moreover, a higher number of satellites does not

result in a significant decrease in revisit time nor

response time. They considered a horizon planning

of two months and a 50 × 50 km arbitrarily selected

target area on the Korean Peninsula. Their paper

considers several details about the satellite system

but not in a generic way as only Synthetic Aperture

Radar (SAR) sensors are included in the

constellation; in particular, agile SAR sensors with

automatic change detection for abnormal activities,

strip map mode for a large coverage and, after,

spotlight mode for high resolution.

The above literature review has shown different

types of models (concerning associated variables,

constraints and/or objectives) and that the DADSSP

has not yet been tackled before. It also showed the

importance of deriving models that are operationally

relevant and that take into account the space

operations concept (orbit/sensors characteristics) and

the requirements of the scenario.

3 OPERATIONAL CONCEPTS

This section will summarize basic elements of the

concept: satellite orbits, imagery sensors and ground

stations.

3.1 Satellite Orbit

Satellite orbits depend largely on the altitude above

the Earth surface and can be categorized as

Geosynchronous Earth Orbits (GEO), Medium Earth

Orbits (MEO) and Low Earth Orbits (LEO).

GEO satellites orbit Earth at an altitude of about

35,800 km, and are known to cover about one-third

of the surface of Earth, which is a great advantage.

However, as a consequence of the large distances

involved, the resolution of remote-sensing pictures

taken from such a position is typically limited. LEO

satellites (at altitudes up to 1500 km) do offer

excellent resolutions, but their coverage area is

restricted, and because of the inherent motion of the

spacecraft with respect to Earth, they can observe

specific targets on Earth only with limited durations

(a so-called pass may take up to 15 minutes,

depending on altitude and other geometrical

aspects). Depending on the requirements of a

particular mission, a combination of GEO and LEO

satellites is used (Wertz and Larson, 1999).

3.2 Imagery Sensors

Two main categories of imagery sensors can be

identified: passive and active. Passive sensors

measure sunlight that is reflected by the targets or

radiation emitted by the target itself. Active sensors

have its own source radiation and its sensor

measures reflected energy. Examples of each sensor

with respective satellites (Reuner, 2017a) are:

a) Active: ASAR (ENVISAT); SAR (ERS-2,

RADARSAT-1 and RADARSAT-2).

b) Passive: OSA (IKONOS); ETM (LANDSAT-7).

The imagery collected by a given sensor is the result

of a combination of the area observed and the sensor

characteristics in terms of its spatial, temporal and

spectral resolutions. Spatial resolution specifies the

pixel size of satellite images covering the Earth

surface. Temporal resolution specifies the revisiting

frequency of a satellite for a specific location.

Spectral resolution specifies the number of spectral

bands in which the sensor can collect radiation and

its width that is related to the position of bands in the

electromagnetic spectrum (Reuner, 2017a).

In general, the field of view (FOV) and the

ICORES 2018 - 7th International Conference on Operations Research and Enterprise Systems

314

sensor altitude above the ground determine the size

of the imaged area (swath width). FOV describes the

opening angle of the sensor, as shown in Figure 2.

Figure 2: Illustration of FOV and sensor swath. Reuner

(2017b).

3.3 Ground Stations

Most satellites have a limited storage capacity and

therefore it is essential to download the information

collected to ground stations when possible (i.e.

within the associated visibility window).

The contact options depend on the relative

motion of the two elements involved: the ground

station (which is at a fixed position on Earth, and

which is rotating 360 degrees in a day), and the

satellite which is going about in its orbit around

Earth (for a LEO satellite, a full revolution takes

about 100 minutes or slightly more). Contact is

possible whenever the two players are in direct view

(starting with the handshake process), i.e. when the

satellite appears above the effective horizon of the

ground station. Ideally, this horizon could be the true

horizon at zero degrees elevation, but in practice the

viewing options will be limited by trees, buildings,

hills, etc., so a more realistic minimum elevation of

about 5

is required. The download capacity depends

on a large number of aspects, both at the satellite and

at the ground station such as broadcast power,

frequency of signal, size and shape of antenna, beam

width, size of picture (Wertz and Larson, 1999).

The Brazilian ground tracking system of INPE

(National Institute of Space Research) is named

Satellite Tracking and Control Centre (CRC) and is

composed of the Satellite Control Centre (SCC),

located in São José dos Campos, and two S-Band

ground stations located in Cuiabá and Alcântara

(Chiaradia et al., 2013), as shown in Figure 1.

4 OPTIMIZATION PROBLEM

INPUT

Before exploring the model for the DADSSP we will

first address how to derive the input for this model.

For this, a MATLAB program has been developed to

evaluate the coverage of a given satellite and

associated sensor and a more detailed description of

the scenarios will be presented to identify relevant

requirements.

4.1 Scenarios and Detection

Characteristics

This section will elaborate on the required input in

terms of the characteristics of the satellites and

sensors taking the scenarios requirements and their

detection characteristics into account.

4.1.1 Oil Spill Detection

Accidents at sea-based oil platforms can yield huge

environmental damage, as most of the Brazilian oil

reserves are in marine fields, in deep and ultra-deep

waters far away from the coastline. Since this

monitoring process needs to be done for a large area,

remote sensing offers a good option to uncover

possible oil spilling. When the surveillance area has

been reduced, other platforms can be deployed to

identify the polluter, the extent and the type of spill.

In order to distinguish a possible oil spilling the

following oil characteristics need to be considered

(Brekke and Solberg, 2005; IPIECA, 2006):

• absorbs solar radiation and re-emits a portion of

this energy as thermal energy;

• emits stronger microwave radiation than the

water and appears as bright objects on a dark sea

• at night, a thick spill can appear cooler than the

water since it releases heat quicker than its

surrounding water;

• can have strong surface-emissivity signatures.

As such, the detection of any oil spill will depend on

oil type, thickness of the spill, wind speed, sea

temperature and the target dimensions.

In terms of dimensions and locations we will

consider two Brazilian oil basins: Campos and

Santos Basins. Santos basin is the largest basin in

the country, with an area of more than 350,000 km

extending from Cabo Frio (RJ) to Florianópolis

(SC). Campos basin is the main area already

explored on the Brazilian coast, extending from

Vitória (ES) to Arraial do Cabo (RJ) with an area of

approximately 100,000 km

. Figure 1 provides an

idea of the Petrobrás Oil Basins location.

According to literature, this type of application

requires regular monitoring, preferably daily in order

to detect potential oil spills. The desirable spatial

resolution will depend on the needs of the mission.

For a general response, medium-to-high resolution

A New Model Proposal for Integrated Satellite Constellation Scheduling within a Planning Horizon given Operational Constraints

315

imagery will be required to distinguish different

slicks (IPIECA, 2006). SAR sensors are considered

as the best and most efficient satellite sensor for this

application (Brekke and Solberg, 2005).

4.1.2 Deforestation

The Amazon rainforest has been subject of

deforestation which is endangering this natural

reservoir. The Amazon covers an area of over 6.5

million square kilometers in the northern part of

South America that spreads across nine countries.

Brazil has 85% of this region (5.217.423 km²) which

occupies 61% of the national territory (see Figure 1).

According to Butler (2017) on average 15,000 km²

of the Amazon forest are deforested every year.

As the Amazon area is huge, dangerous and quite

inaccessible, remote sensing to monitor it offers an

efficient tool to provide early detection of

deforestation areas in order to be able to act and stop

the process. Deforestation detection requires the

following capabilities:

• monitoring a large area;

• detection of very small areas in a forest region;

• coping with cloudy and forested areas.

INPE in collaboration with the Ministry of the

Environment (MMA) and the Brazilian Institute of

Environment and Renewable Natural Resources

(IBAMA) uses DETER/PRODES systems to

monitor deforestation and forest degradation in the

Amazon. DETER uses data from the MODIS Terra

satellite sensor, with a 250 m spatial resolution that

makes it possible to detect deforestation polygons

with an area larger than 25 hectares. The high

revisiting time of MODIS of two days is used to

quickly inform deforestation to surveillance

authorities (INPE, 2012). PRODES monitors clear-

cut deforestation and has produced annual

deforestation rates for the region since 1988 (Global

Forest Watch, 2017). This system historically used

LANDSAT-5 images, but now is capable of

showing small clearings (larger than 6.25 hectares)

because it also incorporated imagery from

LANDSAT-7, LANDSAT-8, CBERS-2, CBERS-

2B, Resourcesat-1 and UK2-DMC. More

information (in Portuguese) about the

PRODES/DETER systems can be found on the

INPE website on Amazonia (INPE, 2017).

In this type of scenario both the spatial and the

temporal resolution are important because daily

information reduces the time to prevent the

deforestation and high resolution can be easier to

detect small-size deforestation areas. So our

constellation will contain the PRODES satellites

(LANDSAT-8, CBERS and UK2-DMC) and

SENTINEL. LANDSAT-8 and UK2-DMC have

good resolution and small revisit times and CBERS

is considered a Brazilian satellite because it was

born from a partnership between Brazil and China.

SENTINEL presents better resolution than the others

and could detect smaller areas in comparison to what

is now detected by Brazilian systems.

4.1.3 Illegal Border Activities

Brazil has a more than 6,500 km border with all

three major production sources of cocaine Colombia,

Bolivia and Peru, as shown in Figure 1. Remote

sensing provides an alternative to monitoring and

identifying drug smuggling activities along this large

area (which in some regions is quite inaccessible).

As intelligence reports indicate possible

transportation routes and border crossing points,

these areas can be monitored in order to collect high-

quality imagery. Moreover, by regularly comparing

imagery on border areas, it will be possible to

identify the opening of new smuggling routes.

The above suggests that a high-resolution

imagery and a regular revisit times should provide a

good view of what is happening on the ground and

improve the surveillance efficiency (SatCen, 2017).

4.2 Satellites Constellation

Considering satellites and sensor data available and

the requirements related to the detection

characteristics in each scenario, our constellation

(sensors and respective satellites) will be probably:

SAR (TERRASAR-X, SENTINEL 1, RADARSAT-

1 and RADARSAT-2), OLI+TIRS (LANDSAT-8),

DMC (UK-DMC2) and WFI (CBERS).

4.3 Satellite Coverage Modeling

The input for the optimization model will be derived

using a MATLAB program that computes for given

satellite/sensor parameters the target coverage over

different time periods.

A mathematical formulation is required to assess

the visibility options between a spacecraft and a

location on Earth (irrespective whether this is a

target or a ground station). Here, the satellite

position is described with respect to a uniformly

rotating Earth and a fixed location position. The

coverage model for the (circular) satellite orbit is

based on the so-called dual-axis description. A

summary of the essential expressions is given below,

full details can be found in Wertz (2009).

ICORES 2018 - 7th International Conference on Operations Research and Enterprise Systems

316

sin(



) = sin(i) cos(



2,0

+ nt)

(1)



1,0



t +

acos2









































 

(2)

where t is the independent parameter time, which

samples the spacecraft (index sc) position with an

arbitrary step size (e.g. once every second). The

latitude (measured with respect to the equator) and

longitude of the instantaneous satellite position are

expressed by δ

and α

, respectively. Parameter i is

the inclination of the orbit, n its mean motion, and

the rotational velocity of Earth. Parameters φ

1,0

and φ

2,0

are arbitrary initial values of the satellite

position and Earth orientation at the reference epoch,

respectively. H is the so-called hemisphere function,

needed to provide the proper four-quadrant answer

for the acos function (hence acos2, see Wertz, 2009).

Taking a location gs with position (δ

, α

) as an

arbitrary target for contact, the distance D between

the satellite and this target can be obtained from:

= R

+ a

- 2Ra[sin(



)sin(



) +

cos(



)cos(



)cos(α

- α

)]

(3)

where R is the Earth radius, and a the semi-major

axis of the satellite orbit.

Knowing D, one can readily determine the

elevation angle ε. This is the angle with respect to

the local horizon with which the satellite can be

observed from the target (for ε equal to 90°, the

satellite is at zenith, i.e. directly above the target,

and for ε equal to 0° it is exactly on the horizon).





  

















(4)

where



is the angle between the direction to the

satellite and to the target, as seen from the center of

Earth.

A direct link between the satellite and the target

is possible when the elevation is above a certain

minimum threshold (for communication with the

station, a representative value for ε

min

is 5°, whereas

for remote-sensing observations larger values are

typically required). When ε is negative, the satellite

is below the horizon as seen from the ground

component and it is invisible, obviously.

Basically, the coverage model uses the input:

• Satellite/sensor parameters: altitude; inclination;

spatial, temporal and spectral resolution; swath

width; field of view (FOV)

• horizon planning (time frame)

• target parameters: location; type (point or area)

Working our way through (1)-(4) for a series of

time-steps t will provide the time-window of contact

opportunities between the satellite and one

target/ground station. The resulting time-windows

can be represented in a coverage histogram for ease

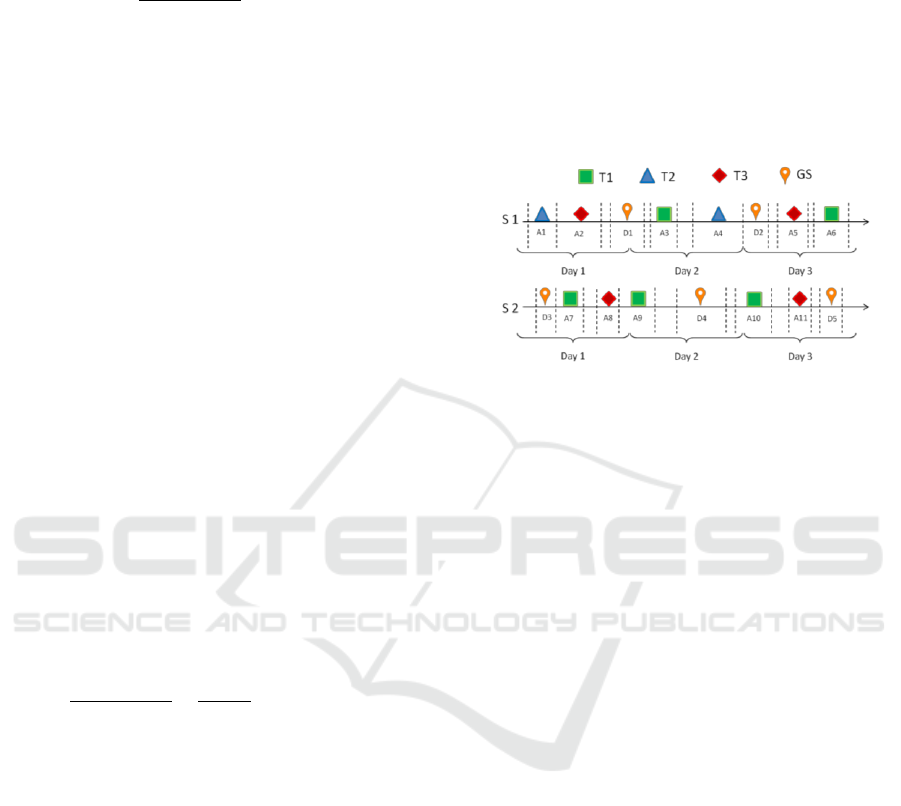
of interpretation, as shown in Figure 3. For a 3-days

horizon planning, three targets (T1, T2, T3), two

satellites (S1, S2) and one ground station (GS), 16

time-windows are derived: 11 acquisition time-

windows (A1 to A11) and 5 download time-

windows (D1 to D5).

Figure 3: Coverage histogram showing time-windows.

This coverage histogram and the scenario

requirements will define the input to the

optimization model. For instance, if satellite S1 has

a spatial resolution of 50 m and the requirement of

the target T2 is at most 30 m, then the acquisition

time-windows (A1 and A4) will not be considered as

input for the optimization model.

Results for the MATLAB analysis specifying the

Brazilian scenarios requirements in interaction with

required decision makers will be presented in a

follow-up paper.

5 OPTIMIZATION MODEL

We formulate the DADSSP as follows. Let H be the

planning horizon;  the set of targets; 



 the

priority of target i;  the set of heterogeneous

satellites in the constellation; S

the set of satellites

that can acquire target ; G the set of ground

stations; G

the set of ground stations that satellite j

has a visibility contact with; 



the set of

acquisition time-windows wherein target i can be

acquired during the planning horizon H by satellite

; 



the set of download time-windows wherein

the acquired data by satellite  can be downloaded to

the ground station  during the planning horizon H.

We are assuming that for a satellite its

acquisition/download time-windows do not overlap,

as the satellite will have to dedicate its time to a

single activity. Furthermore, let













be the start

and the end time of t-th acquisition time-window

A New Model Proposal for Integrated Satellite Constellation Scheduling within a Planning Horizon given Operational Constraints

317

and 









 the start and the end time of d-th

download time-window (

















 ); 





the required revisit time of target i (which implies

that in the given planning horizon H the target i will

be revisited at most 



 







, 



 ); 





 the required due time for the k-th download of

target i data In order to address the satellite

processing time capacity, let 



be the volume of

data of the target i (in MB); 



the acquisition

processing time of satellite j (in MB/sec); 



the

download processing time of satellite j to the ground

station g (in MB/sec); C

the maximum processing

time capacity of satellite j during the planning

horizon H. Assuming that acquisition and download

of target data depends mostly on the data size, the

satellite acquisition and download processing time

as well as of the ground station processing time, the

acquisition and download time will be defined,

respectively, as 



 









and 



 









Consider the following decision variables:





 

indicates whether satellite j will be

used for the k-th acquisition of target i in the

acquisition time-window t; 



  indicates

if satellite j will download the k-th data acquired on

target i to the ground station g in the time-window d.

We will also define the variables 



  as the

start time of the k-th acquisition of target i by

satellite j; 



 as the start time of the k-th

download of target i by satellite j to ground station g.





   

















(5)

s.t.:

  











    















 

    



(6)

  











   











    



 

(7)

 











 



  



 











    



  



(8)

 











 



  





 











    



  



  



(9)

 







 



 



 







    



   



(10)









 



    



  



  



(11)





 



 







  







    



  



(12)

   



















    





















 



  

(13)

The objective of DADSSP (5) is to maximize

the sum of the priorities of the target requests for

which all the required data was collected and

downloaded. Constraints (6) ensure that each target

request will be addressed at most once (by one

satellite and in one acquisition time-window). These

constraints also ensure that the target request is

completed only if the target data has been acquired

and downloaded to the ground station. Constraints

(7) enforce that targets that need to be revisited will

either be fully revisited or not at all. Constraints (8)

and (9) guarantee that the full acquisition and

download time required needs to fall within the

respective time-windows. Constraints (10) ensure

that for the targets that need to be revisited the

revisit time is respected. Constraints (11) ensure that

the acquired target data will be downloaded before

the required due time. Constraints (12) enforce the

acquisition/download precedence, i.e., the target data

can only be downloaded to a ground station if it was

fully acquired before by the same satellite. Finally,

Constraints (13) ensure that the satellite total

processing time will not exceed the satellite capacity

in the planning horizon.

To the best of our knowledge, revisit time and

due time have not yet been considered in the

literature. As these operational time scenario

requirements are extremely important in practice we

believe that they need to be addressed in order to

derive a model that can work in practice.

6 FINAL REMARKS

This paper proposes a new mathematical model to

DADSSP to find an optimal planning to acquire

different target data with different priorities taking

ICORES 2018 - 7th International Conference on Operations Research and Enterprise Systems

318

into account several operational constraints. Some of

these have not been addressed in literature before

but are required to realistically model mission

requirements. The model can be tackled with

optimization tools. Given its complexity heuristic

approaches should also be explored.

Further research also includes the extension of

the proposed model to consider polygon areas and to

model other constraints such as agility, storage

capacity and inherent uncertainties in the scenario.

Finally, if the considered satellite constellation

does not fulfill the scenario requirements it is

important to determine the best orbit/sensor

parameters to fill the identified gaps. The result is

expected to help Brazilian decision makers in future

acquisitions.

ACKNOWLEDGEMENTS

The authors would like to thank Harm-Pieter Gijsen

and Travis J. Pond for their collaboration in

developing the MATLAB program so far.

REFERENCES

DPI. AMBDATA: Administrative Units. In:

http://www.dpi.inpe.br/Ambdata/English/adm_units.p

hp. Accessed: September 2017.

Brekke, C., Solberg, A. H. S. Oil spill detection by

satellite remote sensing. Remote sensing of

environment, 95, 2005, p. 1-13.

Butler, R. Calculating deforestation figures for the

Amazon. 2017. In: http://rainforests.mongabay.

com/amazon/deforestation_calculations.html.

Accessed: August 2017.

Chiaradia, A. P. M, Kuga, H. K., Masago, B. Y. P. L.Short

arcs orbit determination using GPS. 11

International

Conference on Vibration Problems, Lisbon, Portugal,

September 2013.

Gagne, D., Lucrative Cocaine Trade Fuels Gang Presence

in Brazil's Amazon, 2017. In:

http://www.insightcrime.org/news-briefs/lucrative-

cocaine-trade-fuels-gang-presence-brazil-amazon.

Accessed: August 2017.

Global Forest Watch. Open data. 2017. In:

http://data.globalforestwatch.org/datasets/4160f715e12

d46a98c989bdbe7e5f4d6_1. Accessed: August 2017.

INPE. INPE releases DETER outcomes. 2012. In:

http://www.inpe.br/ingles/news/news.php?Cod_Notici

a=343. Accessed: August 2017.

INPE. National Institute for Space Research. 2017. In:

http://www.inpe.br/ingles/. Accessed: August 2017.

IPIECA. Satellite remote sensing of oil spills at sea. Good

practice guidelines for the application of satellite

remote sensing during oil spill response operations.

2016. In: http://www.oilspillresponseproject.org/wp-

content/uploads/2017/01/Satellite_remote_sensing_20

16.pdf. Accessed: August 2017.

Kim, H. and Chang, Y. K. Mission scheduling

optimization of SAR satellite constellation for

minimizing system response time. Aerospace Science

and Technology, v. 40, p. 17-32, 2015.

Marinelli, F., Nocella, S., Rossi, F. and Smriglio, S. A

Lagrangian heuristic for satellite range scheduling

with resource constraints. Computers & Operations

Research, v. 40, p. 1572-1583, 2011.

Niu, X., Tang, H., Wu, L., Deng, R, Zhai, X. Imaging-

duration embedded dynamic scheduling of Earth

observation satellites for emergent events.

Mathematical Problems in Engineering, v. 2015, 31

pages, 2015.

Petrobrás. Basin. 2017. In: http://www.petrobras.com.br/

en/our-activities/main-operations/basins/. Accessed:

August 2017.

Reuner, R. Introdution to Remote Sensing: Satellites and

Resolution. 2017a. In: http://lms.seos-

project.eu/learning_modules/remotesensing/remotesen

sing-c00-p01.html. Accessed: August 2017.

Reuner, R. Manine Pollution: Supplement 3.6: MERIS.

2017b. In: http://www.seos-project.eu/modules/

marinepollution/marinepollution-c03-s06-p01.html.

Accessed: August 2017.

SatCen. General crime and security surveillance. 2017. In:

https://www.satcen.europa.eu/services/general_crime_

and_security_surveillance. Accessed: September 2017.

Sundar, K., Qin, J., Rathinam, S., Ntaimo, L., Darbha, S.

and Valicka, C. Algorithms for a satellite constellation

scheduling problem. In: 2016 IEEE International

Conference on Automation Science and Engineering

(CASE), TX, USA, August 21-24, p. 373-378, 2016.

Toth, P., Vigo, D, eds. Vehicle routing: problems,

methods, and applications. Society for Industrial and

Applied Mathematics, 2

nd.

Edition, 2014.

Wang, P. and Reinelt, G. Solving the Earth Observing

Satellite Constellation Scheduling Problem by Branch-

and-Price. Operations Research Proceedings 2010.

Springer, Berlin, Heidelberg, p. 491-496, 2011.

Wang, P., Reinelt, G., Gao, P. and Tan, Y. A model, a

heuristic and a decision support system to solve the

scheduling problem of an earth observing satellite

constellation, Computers & Industrial Engineering, V.

61, p. 322-335, 2011.

Wertz, J. R. Orbit & Constellation, Design &

Management. Space Technology Library.

Microcosm/Kluwer, 2

print, 2009. 968 pages.

Wertz, J. R. and Larson, W. J. Space mission analysis and

design. Space Technology Library. 3

printa, 1999.

976 pages.

Zhai, X., Niu, X., Tang, H., Wu, L. and Shen, Y. Robust

satellite scheduling approach for dynamic emergency

tasks. Mathematical Problems in Engineering, v.

2015, 20 pages, 2015.

A New Model Proposal for Integrated Satellite Constellation Scheduling within a Planning Horizon given Operational Constraints

319