
Hydrodynamic Adaptive Routing Algorithm for Unstable Sensor
Networks with a Tsunami Model of Acute Events
Ekaterina V. Aleksandrova
1,2
and Vladimir A. Bashkin
1
1
P. G. Demidov Yaroslavl State University, 150003, Sovetskaja ul., 14, Yaroslavl, Russia
2
Yaroslavl State Technical University, 150023, Moskovsky pr., 88, Yaroslavl, Russia
Keywords:
Unstable Sensor Network, Adaptive Routing, Acute Event, Hydrodynamic Model, Tsunami Model, Seismic
Wave.
Abstract:
An algorithm of adaptive multi-path routing in unstable sensor networks with frequent reconfigurations is
presented. The model is based on the discrete imitation of water streams and water waves in the network of
river-connected reservoirs. The hydrodynamic phenomena of water currents, riverbed erosion and sediments
deposition are used as convenient models of different algorithmic features of the routing scheme. Acute
network events (topology changes, node failures, gateway migrations etc) are treated by imitating of such
natural phenomena as underwater seismic activities and surface tsunami waves.
1 INTRODUCTION
Nature-inspired heuristics such as directed diffusion
(Intanagowiwat et al., 2000), gradient-based routing
(Schurgers and Srivastava, 2001), thermal field rout-
ing (Baumann et al., 2008) and ant colony optimiza-
tion (DiCaro and Dorigo, 1998) have shown to be a
good technique for developing adaptive routing algo-
rithms for sensor networks.
In (Aleksandrova and Bashkin, 2016) we de-
scribed a novel approach, based on the discrete imi-
tation of water flow in the network of water reservoirs
(nodes), connected by rivers (links). The flow direc-
tion (data route direction) depends on the difference
of absolute water level (queue length) in neighboring
reservoirs. Some reservoirs may have additional un-
derwater springs (data sources), some others are wa-
ter drains (sinks, gateways). Different reservoirs may
have different absolute bottom levels, drains are al-
ways the deepest in the network. Constant transit wa-
ter flow deepens reservoirs that are located closer to
drains than others - a physical phenomenon, called
riverbed erosion (we use it as an adaptive preferred
routing). On the other hand, constant absence of wa-
ter outflow together with high water level imply de-
position of sediments and hence the rise of the bottom
level in the node (adaptive routing penalization).
The key features of our algorithm are its sim-
ple physical model and easy-to-understand multifac-
tor structure. It is possible to reconfigure a large
set of “real-world” parameters: frame size (“wa-
ter density”), link speed (“river width”), reconfig-
uration rates (“soil density” and “soil condensation
rate”), buffer speed/volume effectiveness (“surface
area of the reservoir”), etc. Moreover, the clear phys-
ical model can be easily enhanced with additional
naturally-inspired phenomena, such as surface waves
(data interference and multicast storms) and deepwa-
ter currents (control data flows). We believe that the
proposed concept may be used as a general base for a
wide range of proactive routing algorithms.
In this paper we present a modification of basic
algorithm for unstable networks with more frequent
acute events such as topology changes, node failures,
gateway migrations etc. Intuitively, all these events
require some abrupt changes in the routing scheme,
that is based primarily on the “water surface level” in
different nodes. Here we try to incorporate into our
model the closest natural phenomenon – a tsunami.
A tsunami is a natural “procedure” that stabilizes
water currents and waves after underwater seismic ac-
tivities: quakes, landslides and volcanic eruptions. In
our model we have an analogue of seabed relief –
the map of bottom levels of all nodes. So there is a
straightforward way to trigger the “tsunami” – it is
sufficient to apply some appropriate changes to the
bottom levels of nodes, adjacent to the node with an
acute “catastrophic” events (to trigger an appropriate
Aleksandrova, E. and Bashkin, V.
Hydrodynamic Adaptive Routing Algorithm for Unstable Sensor Networks with a Tsunami Model of Acute Events.
DOI: 10.5220/0006655901410146
In Proceedings of the 7th International Conference on Sensor Networks (SENSORNETS 2018), pages 141-146
ISBN: 978-989-758-284-4
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
141

“landslide” or “eruption”).
There may be different heuristics of seismic ef-
fects. In this paper we present a very simple concept:
a node monitors the bottom levels of its neighbors and
in the case of abrupt changes of the mean value ad-
justs its own bottom level. This can be interpreted as a
certain flowability of a sea bottom soil. Surprizingly,
such simple heuristic allows to adequately react to a
wide range of target events. For example, after the
shutdown of an important transit node (or a gateway)
we can observe both a seismic wave on the seabed
and a tsunami on the surface. The new model also
allows to accelerate the global balancing. For exam-
ple, after connection of two previously disconnected
subnets we can observe both landslides on the bottom
and waves on the surface, quickly reconfiguring the
routing “map” of an entire network.
The paper is organized as follows. In Section 2
the routing algorithm is presented. Informal examples
are given. We also consider and evaluate some key
properties of an algorithm. In Section 3 we briefly
describe preliminary results of imitational modeling.
Section 4 contains some conclusions.
2 ROUTING ALGORITHM
2.1 Informal Model – No Acute Events
In this subsection we describe the basic principles of
our hydrodinamic model for unstable sensor neworks,
as it was given in (Aleksandrova and Bashkin, 2016).
This concept is quite flexible and tuneable and can
be applied to a wide range of situations. However,
in our opinion, it is best suited for unstable networks
with a relatively “smooth” dynamics of changes (re-
locating nodes, energy consumption, moving subject
of surveillance, etc). The novel enhancement of this
algorithm, better suited for nets with more frequent
acute events will be given in a Subsection 2.2.
All hosts are synchronized, the global time is
quantified in “rounds”. The frame size is fixed.
A network consists of a fixed finite set of n hosts
H = {h
1
,... ,h
n
} and a variable finite set L of sym-
metric links. In any configuration (at any moment of
time), if L = {l
1
,. .. ,l
m
} then for all i ∈ {1,. .. ,m} we
have l
i
= (h,h
′
) with h,h
′
∈ H and h ̸= h
′
.
Each link l has its maximal transfer rate Width(l)
(“river width”), measured in “frames per round” (fpr).
Each host h has buffer effectiveness Area(h), mea-
sured in frames (“surface area of the reservoir”). It
also has four variable attributes: Top(h) — the ab-
solute “water surface level” (in frames), i.e. “Top
2
→
←
3
1
→
1→
←
1
1
→
1
→
1
→
Figure 1: Balancing queue lengths (“water waves stabiliza-
tion”).
level”; Low(h) — the absolute “bottom surface level”
(in frames), i.e. “Low level”; In(h) — the incom-
ing dataflow rate (in fpr, nonnegative); Out(h) —
the outgoing dataflow rate (in fpr, nonnegative). If
Out(h) > 0 then h is a sink (a drain) and we set
Low(h) = −n (hence all sinks are the deepest sites).
For the sake of shortness we describe here the sim-
plest variant of our model: all links have the same
maximal transfer rate (3 fpr in the examples), all hosts
have the same buffer effectiveness (1 frame in the fol-
lowing examples). Transfer rates and buffer sizes are
constant and never change (in contrast to water sur-
face level and bottom level, which are affected by
wave propagation and riverbed erosion).
Algorithm is proactive: we define the behavior of
a single node. The particular node h possesses all the
information about its local configuration and also the
top and low levels of all its neighboring nodes (nodes
with direct links to h). For a node h we denote the set
of its neighbors by N(h). Hence, for any h
′
∈ N(h)
the local node h knows values Top(h
′
) and Low(h
′
).
The model is based on several physical principles.
The first law defines the way, in which the exces-
sive frames (“extra water”) are distributed (“spread”)
among adjacent nodes (“on the surface”). The infor-
mal rule is very simple: we let the water flow to the
neighboring reservoirs with the lower water surface
level (frame-by-frame, starting from the node with the
lowest level, without exceeding the capacity of links
and reservoirs), while there exists such reservoirs.
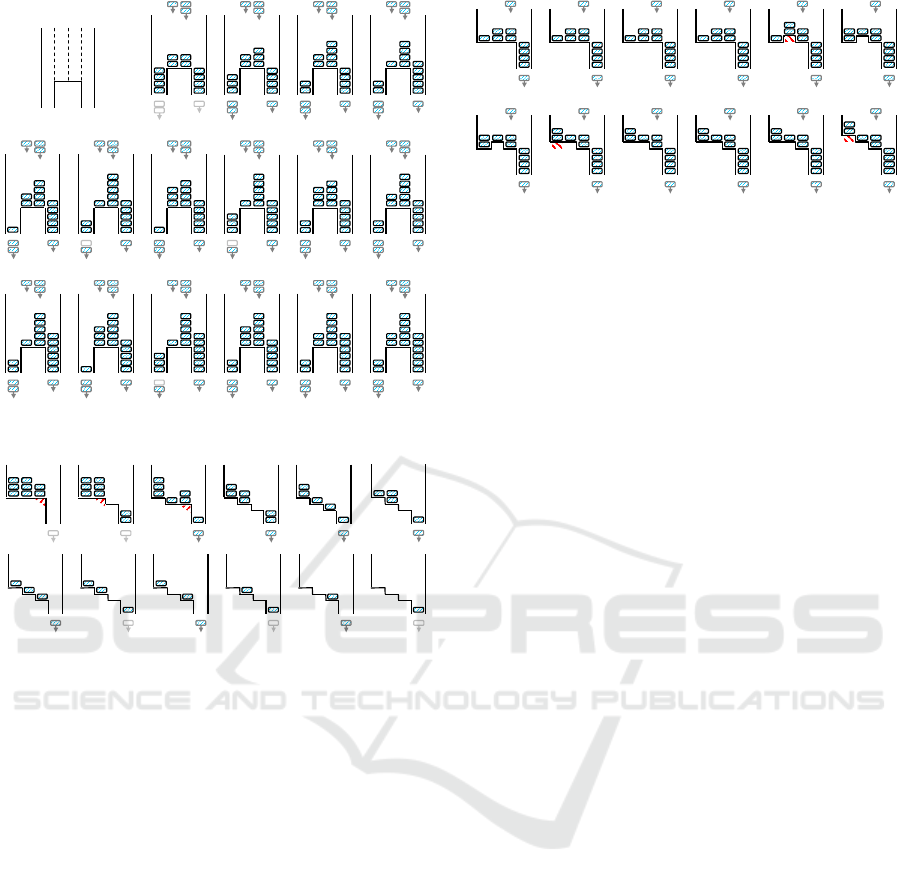
An example is given in Fig. 1. Here we depict a
time sequence (from left to right) of 5 successive con-
figurations (between time rounds) of a simple net. A
net in the example is a chain of 5 nodes, without in-
going and outgoing external links (a chain of 5 reser-
voirs without springs and sinks). In the initial config-
uration the first (from the left) node has 7 dataframes
(depicted by rounded rectangles), the second — 3, the
third — 9, and so on. The bottom levels are the same,
so the water surface levels are also 7–2–9–4–2. Each
round includes a set of data movements, depicted by
weighted arrows. For example, during the first round
2 frames moves from node #1 to node #2, 3 frames
from #3 to #2, 1 frame from #3 to #4 and 1 from #4
to #5. The “water levels” are stabilized after 4 rounds
– to the global configuration 6–6–5–4–4. Now “the
water is calm”.
The next example (Fig. 2) illustrates the same
SENSORNETS 2018 - 7th International Conference on Sensor Networks
142
←
1
1
→
←
1
1
→
←
2
2
→
←
1
1
→
←
1
←
2
1
→
←
1
1
→
←
2
←
3
1
→
←
1
1
→
←
2
←
2
1
→
←
2
2
→
←
1
←
2
←
3
2
→
←
1
←
2
←
2
2
→
←
2
1
→
←
1
←
2
1
→
←
1
←
1 fpr (in)
←
1 fpr (out)
←
2 fpr (in)
←
2 fpr (out)
Net configuration:
Figure 2: Balancing output (“water currents stabilization”).
2
→
2
→
1
→
2
→
1
→
1
→
1
→
1
→
1
→
1
→
1
→
1
→
1
→
1
→
Figure 3: Adaptive routing I (“riverbed erosion”).
physical law, but in a more comprehensive situation:
a net with incoming and outgoing data streams. Here
nodes #1 and #4 are gateways with maximal outgoing
transmission speed 2 fpr and 1 fpr respectively, nodes
#2 and #3 are sensors (data generators) with incom-
ing streams of 1 fpr and 2 fpr. As it can be seen, the
flow directions and rates stabilize after 14 rounds. The
physical analogy is the formation of stable currents in
the water system with constant inflow and outflow.
The other physical phenomenon is the erosion
of the river bottom. The more stable and powerful
stream produces the stronger soil erosion and hence
the resulting channel becomes a “mainstream” for fu-
ture transmissions. An example is given in Fig. 3.
Here we can see a chain of four nodes with a sin-
gle gateway (#4). The stream gradually cuts the bot-
tom “edge”, forming the slopes. The basic rule is
quite simple: the bottom level of current node is low-
ered if the accepting neighbor had surface level lower
than current node’s bottom level (“water is slopping
over”) and the corresponding flow is strong enough —
i.e., the number of moving frames exceeds a specific
ErosionParameter (we set it to 2 in the examples).
And the third key physical process is a deposi-
tion of sediments on the river bottom. If the flow
1
→
0
0
1
→
1
2
1
→
2
4
1
→
3
6
1
→
4
0
←
1
1
→
5
0
1
→
7
1
1
→
0
2
1
→
2
3
1
→
4
4
1
→
6
5
1
→
0
6
1
→
1
→
0
0
1
→
1
→
1
0
Figure 4: Adaptive routing II (“deposition of sediments”).
rate is low and the water column is high then the
bottom level rises. In our model we simplify both
these factors (time and volume) into a single “sedi-
ments counter” Sediments(h) that is incremented at
each round by a number of dataframes that lay immo-
bile in the node h. If any number of frames moves out
of the node then the counter is reset. If the counter
value exceeds a specific SedimentsParameter (we set
it to 6 in the examples) then the bottom level is raised
(and the counter is reset). An example is given in
Fig. 4. Here the counter values are depicted under the
corresponding nodes. With the lapse of time coun-
ters for nodes #1 and #2 are growing (the second one
grows two times faster because of 2 dataframes lo-
cated). So the bottom levels begin to rise and eventu-
ally the slopes are formed.
2.2 Informal Model of Acute Events
In this paper we want to show that the basic model
can be transparently enhanced to better handle such
acute events as node disconnection/reconnection and
gateway start/shutdown. Note that the causes of these
events may be of a different nature: fast moving
nodes, battery discharge, signal obstacles etc.
In fact, the basic model already handles all these
events quite successfully. For example, the switching-
on of a new gateway will cause the creation of new
riverbeds and (possibly) the silting of some old ones.
However, the reaction time may be substantially im-
proved by forced “deepening of the bottom” in some
of neighboring nodes. The closest natural models for
these events are quakes, landslides and other similar
seismic processes occuring at the “ocean floor”.
The main new idea of the algorithm is to model
a tsunami in the ocean. Tsunami often occurs as a
result of a sharp rise or fall of the sea bottom (over a
large area). In our model we have a bottom level —
so “seismic” features can be easily implemented.
Let’s consider several types of “catastrophic”
events in the sensor network and variants of their reso-
lution under the new scheme (with “earthquakes” and
“tsunami”). All situations are considered from the
point of view of a particular node:
Hydrodynamic Adaptive Routing Algorithm for Unstable Sensor Networks with a Tsunami Model of Acute Events
143

• The disappearance of a neighbor node whose bot-
tom level was below our bottom level (i.e., this
node in the recent past most likely was receiving
packets from us rather than sending them to us).
We believe that in the neighborhood a new “is-
land” was formed (“an earthquake has raised the
bottom”), so in our location the bottom level also
should slightly rise (and so a tsunami is formed).
How much to raise the bottom is determined by
the heuristic (see below).
• The disappearance of a neighbor node, which
transmitted packets to us (the level of its bottom
was higher than ours). We believe that the place of
the missing node has a “pit”, so we lower our local
level of the bottom a bit. A kind of a “whirlpool”
may be formed, making the node more attractive.
• The emergence of a neighbor node (consider both
a lower and a higher bottom). It’s one thing if
the node is completely new and just emerged from
nowhere, then, in principle, it can simply be em-
bedded into a network with an average bottom
value in a given “region” (taking the arithmetic
mean of the neighbors’ levels). Another thing is
if the node is already participating in some other
subnetwork with established levels (perhaps very
different from ours). Consider only the second sit-
uation. We propose to speed up the process of
leveling the bottom levels in subnets (raise if we
had lower, or deepen if we had higher ones), so
that the streams stabilize faster. In nature, this can
be compared with the rapid destruction of a thin
“dam” between two reservoirs with different lev-
els of bottom and water: simultaneously there will
be (1) a “waterfall” from a reservoir with a higher
water level to another one and (2) the landslide in
the area of the destroyed dam wall from the shal-
low reservoir to the deeper one.
•
Gateway switching off. Even in the basic ver-
sion of our algorithm there will be a fairly fast
(for a few time rounds) increase in the water level
at the former gateway node and all its neighbors
(the water “pouring”), so a kind of a big wave
will be formed. However, the bottom level will
change very slowly, because initially the gateway
was very deep. We propose to accelerate this pro-
cess: to raise the water level substantially and
rapidly by raising the bottom level to an average
value among all neighbors. Tsunami then will be
higher and more stable.
• Enabling the gateway role on the node. The bot-
tom level at the gateway instantly becomes very
low. For a few time rounds the water level will
drop at the gateway and all its neighbors and there
0
4
4
3
–
4
4
3
–
6
4
3
–
6
5
3
Figure 5: Acute event I — receiving node occlusion (“seis-
mic wave” and subsequent “tsunami”).
5
2
1
0
–
2
1
0
–
0
1
0
Figure 6: Acute event II — sending node shutdown (“land-
slide” and subsequent “whirlpool”).
0
1
2
5
4
3
0
1
2
5
4
3
0
1
4
4
4
3
0
2
4
4
4
3
→
→
Figure 7: Acute event III — connecting two subnets with
different levels (“landslide” and “waterfall”).
will be something like waves converging to a new
sink (a “whirlpool”). We speed up the process
by substantially deepening the bottom level at the
neighbors (“landslides” from the slopes).
Thus, the benefits of the introduction of the
“tsunami” are clearly visible. The problem is to come
up with an appropriate heuristic. The difficulty here
is that there can be several problematic neighbors. It
is necessary to take into account the possibility of the
emergence of various “catastrophic” changes for sev-
eral neighbors at once. We propose a simple solution:
to monitor the arithmetic mean of the bottom levels
of all neighbors. If the change is substantial (exceeds
some parameter) then we apply the same change to
our bottom level. Surprisingly, this simple heuristics
is adequate for all considered types of acute events.
Some examples are given below. We consider
the same chain-like topology as in the previous sub-
section, with simplest transfer rates and buffer sizes.
Moreover, for the sake of shortness we do not recalcu-
late water streams – only the bottom level dynamics
(“seismic activity”) is considered.
Consider Fig. 5. Here we depict a time sequence
of a net with a disconnected sink node (#1). At the
second round the node #2 finds out that the average
bottom level is raised from 2 to 4 (i.e. the delta is +2),
and hence at the third round it “lifts” its own bottom
from 4 to 6. Now, the node #3 is also affected (+1 at
the fourth round) – a fading seismic wave is formed.
At Fig. 6 we can see an opposite process – a land-
slide after the shutdown of an active sending node.
Here the node #2 discovers a gap and crumbles itself.
Fig. 7 depicts the emergence of a neighbor node
with a different bottom level.
SENSORNETS 2018 - 7th International Conference on Sensor Networks
144

2.3 Formal Definition
All nodes behave independently, the scheme is purely
proactive. We define a behavior of a single node
throughout a single time round. At the starting
moment of the round the node h knows every-
thing about itself (Top(h),Low(h), In(h), Out(h) and
Sediments(h)) and also knows levels and link band-
width of all it’s neighbors: Top(h
′
),Low(h
′
) and
Width(h,h
′
) for any h
′
∈ N(h).
An algorithm (in pseudocode) is given below.
For simplicity we denote N(h), In(h), Out(h) and
Sediments(h) by N,In,Out and Sediments.
Algorithm: 1 Behaviour of a single node h during a single
time round.
Constants (tuning parameters):
ErosionParam, SedimentsParam
: Nat
SeismicParam,IOFlowParam
: Nat
Persistent variables:
N
: set of Node
Top,Low
: map of (Node -> Int)
Width
: map of ((Node * Node) -> Nat)
In, Out,Sediments
: Nat
Round (local) variables:
h’ : Node
N’, Receivers, Above : set of Node
BufferTo : map of (Node -> Nat)
BufferOut, LowAvg, LowAvgNew : Nat
IOFlowDelta, LowAvgDelta : Int
Step 1
/* Computations */
N’, Receivers, Above :=
∅
BufferOut := 0
foreach h
′
∈ N let
BufferTo[h’] := 0
BufferOut :=
min{Out,Top[h] − Low[h]}
Top[h]
:=
Top[h]
-BufferOut
Iteration
:
if Top[h]
=
Low[h] goto
Final
Above :=
{x ∈ N : Top[x] > Top[h] + 1}
N’ :=
N \
Receivers
\
Above
if
N’
= ∅ goto
Final
take
h’
from N
′
s.t. Top[
h’
] = min
x∈N
′
Top[x]
BufferTo[h’] :=
min{ (Top[h] − Top[
h’
]) div 2,
Top[h] − Low[h],
Width[h,
h’
] }
Top[h]
:=
Top[h] − Bu f f erTo
[h’]
Receivers := Receivers
∪ {h
′
}
goto
Iteration
Final :
if
Receivers
̸= ∅
begin
take h
′
from
Receivers
s.t.
Low[h
′
] < Low[h] and
BufferTo[
h
′
]
≥ ErosionParam
if h
′
̸=
NULL
begin
Low[h]
:=
Low[h] − 1
Top[h]
:=
Top[h] − 1
end
Sediments
:= 0
end
else
begin
Sediments
:=
Sediments
+
(Top[h] − Low[h])
if Sediments
>
SedimentsParam
begin
Low[h]
:=
Low[h] + 1
Top[h]
:=
Top[h] + 1
Sediments
:= 0
end
end
Step 2
/* Data communications */
•
Try to
send
BufferOut dataframes to the
local gateway. In the case of failure
increase
Top[h]
accordingly.
•
Try to
send Bu f f erTo[h
′
]
dataframes to each
neighbor
h
′
.
In the case of failure increase
Top[h]
accordingly.
• Receive
some dataframes from each neighbor,
increase
Top[h]
accordingly.
• Receive In
dataframes from the local sensor,
increase
Top[h]
accordingly.
Step 3
/* Control communications */
(a)
Estimate
the new values of incoming and
outgoing flow (from the sensor and to the
local gateway)
InNew
and
OutNew
for the
next round.
IODelta := (Out − In) − (OutNew − InNew)
if |IODelta| > IOFlowParam
begin
Low[h] := Low[h] + IODelta
Top[h] := Top[h] + IODelta
end
In := InNew
;
Out := OutNew
(b)
Send
the new
Top[h]
and
Low[h]
to the
neighbors.
(c)
LowAvg := (
∑
h
′
∈N
Low[h
′
])/|N|
(d)
Receive
the new
Top[h
′
],Low[h
′
]
and
Width[h, h
′
]
from each neighbor
h
′
, calculate the value
of
N
for the next round.
(e)
LowAvgNew := (
∑
h
′
∈N
Low[h
′
])/|N|
LowDel ta := LowAvgNew − LowAvg
LowAvg := LowAvgNew
if |LowDelta| > SeismicParam
begin
Low[h] := Low[h] + LowDelta
Top[h] := Top[h] + LowDelta
end
Note that substeps of Step 2 may be executed in
any order (or in parallel). The same is not true for
the substeps of Step 3 ((c), (d), (e) must follow one
another sequentially). A substep 3(a) allows to react
to the abrupt changes of the dataflows from the lo-
cal sensor and to the outer network (through the local
gateway). This includes sensor activation, gateway
shutdown etc.
Hydrodynamic Adaptive Routing Algorithm for Unstable Sensor Networks with a Tsunami Model of Acute Events
145
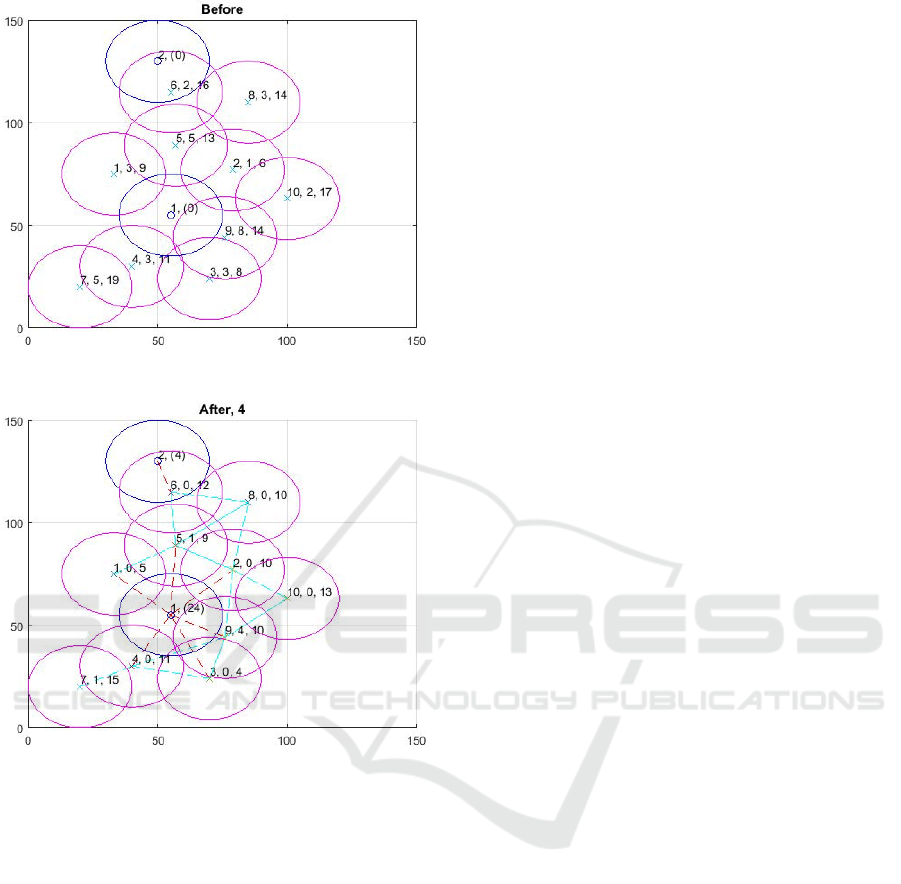
Figure 8: Initial configuration.
Figure 9: Configuration after 4 rounds.
2.4 Modeling
An example of routing scheme modeling is given in
Fig. 8 and Fig. 9. Here a simple sensor network
is modeled in MATLAB, consisting of eight sensors
(denoted by X-crosses) and two gateways (denoted by
small circles). Large circle denote the “transmitting
power” of the node. Each ordinary node is labeled
by a triple (node number, bottom level, surface level).
Gateways in this model are simple and can only re-
ceive frames. They are labeled by (sink number, re-
ceived frames). All frames will reach the gateways in
30 rounds.
The experiments were carried out in MATLAB for
the random arrangement of a fixed number of nodes.
Preliminary results show satisfactory routing and load
balancing rates.
3 CONCLUSION
Many approaches have been proposed for multiple-
path routing in sensor networks. Among them
there are a number of gradient-based and physi-
cally/biologically inspired algorithms. For a short
survey see (Aleksandrova and Bashkin, 2016).
The proposed routing algorithm is adaptive and scal-
able. We also believe that it can be further improved
by taking into consideration other important aspects
such as energy consumption. The key feature of the
model is its simple and natural interpretation, allow-
ing to implement purely “physical” reasoning without
any artificial heuristics.
We will explore the model in our future work.
In particular, further research will be concentrated
on the comparative study of our scheme with other
known routing algorithms in different network config-
urations. Another direction is the implementation of
new routing concepts in hardware and software wire-
less mesh network controllers (Sokolov et al., 2016).
ACKNOWLEDGEMENTS
This work was partially supported by Russian Fund
for Basic Research (project 17-07-00823) and YarSU
(project AAAA-A16-116070610022-6).
REFERENCES
Aleksandrova, E. V. and Bashkin, V. A. (2016). Hydrody-
namic model of adaptive routing for large-scale unsta-
ble sensor networks. In SIBCON, Int. Siberian Conf.
on Control and Communications. IEEE.
Baumann, R., Heimlicher, S., and Plattner, B. (2008). Rout-
ing in large-scale wireless mesh networks using tem-
perature fields. IEEE Network, 22(1):25–31.
DiCaro, G. and Dorigo, M. (1998). Antnet: Distributed stig-
mergetic control for communication networks. Jour-
nal of Artificial Intelligence Research, 9:317–365.
Intanagowiwat, C., Govindan, R., and Estrin, D. (2000).
Directed diffusion: A scalable and robust communi-
cation paradigm for sensor networks. In MOBICOM,
6th Int. Conf. on Mobile Comp., pages 56–67. ACM.
Schurgers, C. and Srivastava, M. B. (2001). Energy effi-
cient routing in wireless sensor networks. In MIL-
COM, Military Comm. Conf., pages 357–361.
Sokolov, V. A., Korsakov, S. V., Smirnov, A. V., Bashkin,
V. A., and Nikitin, E. S. (2016). Instrumental support-
ing system for developing and analysis of software-
defined networks of mobile objects. Automatic Con-
trol and Computer Sciences, 50(7):536–545.
SENSORNETS 2018 - 7th International Conference on Sensor Networks
146
