
Pipeline Pattern for Parallel MCTS
S. Ali Mirsoleimani
1,2
, Jaap van den Herik
1
, Aske Plaat
1
and Jos Vermaseren
2
1
Leiden Centre of Data Science, Leiden University, Niels Bohrweg 1, 2333 CA Leiden, The Netherlands
2
Nikhef Theory Group, Nikhef Science Park 105, 1098 XG Amsterdam, The Netherlands
Keywords:
MCTS, Parallelization, Pipeline Pattern, Search Overhead.
Abstract:
In this paper, we present a new algorithm for parallel Monte Carlo tree search (MCTS). It is based on the
pipeline pattern and allows flexible management of the control flow of the operations in parallel MCTS. The
pipeline pattern provides for the first structured parallel programming approach to MCTS. The Pipeline Pattern
for Parallel MCTS algorithm (called 3PMCTS) scales very well to a higher number of cores when compared
to the existing methods. The observed speedup is 21 on a 24-core machine.
1 INTRODUCTION
In recent years there has been much interest in the
Monte Carlo tree search (MCTS) algorithm. In 2006
it was a new, adaptive, randomized optimization algo-
rithm (Coulom, 2006; Kocsis and Szepesv´ari, 2006).
In fields as diverse as Artificial Intelligence, Opera-
tions Research, and High Energy Physics, research
has established that MCTS can find valuable approx-
imate answers without domain-dependent heuristics
(Kuipers et al., 2013). The strength of the MCTS
algorithm is that it provides answers with a random
amount of error for any fixed computational budget
(Goodfellow et al., 2016). Much effort has been
put into the development of parallel algorithms for
MCTS to reduce the running time. The efforts are
applied to a broad spectrum of parallel systems; rang-
ing from small shared-memory multicore machines
to large distributed-memory clusters. In the last two
years, parallel MCTS played a major role in the suc-
cess of AI by defeating humans in the game of Go
(Silver et al., 2016; Hassabis and Silver, 2017).
The general MCTS algorithm has four operations
inside its main loop (see Algorithm 1). This loop is
a good candidate for parallelization. Hence, a signif-
icant effort has been put into the development of par-
allelization methods for MCTS (Chaslot et al., 2008a;
Yoshizoe et al., 2011; Fern and Lewis, 2011; Schae-
fers and Platzner, 2014; Mirsoleimani et al., 2015b).
To implement these methods, the computation associ-
ated with each iteration is assumed to be independent
(Mirsoleimani et al., 2015a). Therefore, we can as-
sign a chunk of iterations as a separate task to each
parallel thread for execution on separate processors
(Chaslot et al., 2008a; Schaefers and Platzner, 2014;
Mirsoleimani et al., 2015a). This type of parallelism
is called iteration-level parallelism (ILP). Close anal-
ysis has learned us that each iteration in the chunk
can also be decomposed into separate operations for
parallelization. Based on this idea, we introduce
operation-level parallelism (OLP). The main point
is to assign each operation of MCTS to a separate
processing element for execution by separate proces-
sors. This leads to flexibility in managing the control
flow of operations in the MCTS algorithm. The main
contribution of this paper is introducing a new algo-
rithm based on the pipeline pattern for parallel MCTS
(3PMCTS) and showing its benefits.
The remainder of the paper is organized as fol-
lows. In section 2 the required background informa-
tion is briefly described. Section 3 provides necessary
definitions and explanations for the design of 3PM-
CTS. Section 4 gives the explanations for the imple-
mentation the 3PMCTS algorithm, Section 5 shows
the experimental setup, and Section 6 gives the exper-
imental results. Finally, in Section 7 we conclude the
paper.
2 BACKGROUND
Below we discuss MCTS in Section 2.1, in Section
2.2 the parallelization of MCTS is explained.
2.1 The MCTS Algorithm
The MCTS algorithm iteratively repeats four steps
or operations to construct a search tree until a pre-
defined computational budget (i.e., time or iteration
constraint) is reached (Chaslot et al., 2008b; Coulom,
614
Mirsoleimani, S., Herik, J., Plaat, A. and Vermaseren, J.
Pipeline Pattern for Parallel MCTS.
DOI: 10.5220/0006656306140621
In Proceedings of the 10th International Conference on Agents and Artificial Intelligence (ICAART 2018) - Volume 2, pages 614-621
ISBN: 978-989-758-275-2
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

v
0
v
1
v
4
v
5
v
8
v
2
v
3
v
6
v
7
(a) SELECT
v
0
v
1
v
4
v
5
v
8
v
2
v
3
v
6
v
9
v
7
(b) EXPAND
v
0
v
1
v
4
v
5
v
8
v
2
v
3
v
6
v
9
∆
v
7
(c) PLAYOUT
v
0
v
1
v
4
v
5
v
8
v
2
v
3
v
6
v
9
v
7
∆
∆
∆
(d) BACKUP
Figure 1: One iteration of MCTS.
2006). Algorithm 1 shows the general MCTS algo-
rithm.
In the beginning, the search tree has only a root
(v
0
) which represents the initial state in a domain.
Each node in the search tree resembles a state of the
domain, and directed edges to child nodes represent
actions leading to the succeeding states. Figure 1 il-
lustrates one iteration of the MCTS algorithm on a
search tree that already has nine nodes. The non-
terminal and internal nodes are represented by circles.
Squares show the terminal nodes.
1. SELECT: A path of nodes inside the search tree is
selected from the root node until a non-terminal
leaf with unvisited children is reached (v
6
). Each
of the nodes inside the path is selected based on a
predefined tree selection policy (see Figure 1a).
2. EXPAND: One of the children (v
9
) of the selected
non-terminal leaf (v
6
) is generated randomly and
added to the tree together with the selected path
(see Figure 1b).
3. PLAYOUT: From the given state of the newly
added node, a sequence of randomly simulated ac-
tions (i.e., RANDOMSIMULATION) is performed
until a terminal state in the domain is reached. The
terminal state is evaluated using a utility function
(i.e., EVALUATION) to produce a reward value ∆
(see Figure 1c).
4. BACKUP: For each node in the selected path, the
number N(v) of times it has been visited is incre-
mented by 1 and its total reward value Q(v) is up-
Algorithm 1: The general MCTS algorithm.
1 Function MCTS(s
0
)
2 v
0
:= creat root node with state s
0
;
3 while within search budget do
4 < v
l
,s
l
> := SELECT(v
0
,s
0
);
5 < v
l
,s
l
> := EXPAND(v
l
,s
l
);
6 ∆ := PLAYOUT(v
l
,s
l
);
7 BACKUP(v
l
,∆);
8 end
9 return action a for the best child of v
0
dated according to ∆ (Browne et al., 2012). These
values are required by the tree selection policy
(see Figure 1d).
As soon as the computational budget is exhausted, the
best child of the root node is returned (e.g., the one
with the maximum number of visits).
The purpose of MCTS is to approximate the
game-theoretic value of the actions that may be se-
lected from the current state by iteratively creating a
partial search tree (Browne et al., 2012). How the
search tree is built depends on how nodes in the tree
are selected (i.e., tree selection policy). In particular,
nodes in the tree are selected according to the esti-
mated probability that they are better than the current
best action. It is essential to reduce the estimation er-
ror of the nodes’ values as quickly as possible. There-
fore, the tree selection policy in the MCTS algorithm
aims at balancing exploitation (look in areas which
appear to be promising) and exploration (look in ar-
eas that have not been well sampled yet) (Kocsis and
Szepesv´ari, 2006).
The Upper Confidence Bounds for Trees (UCT)
algorithm addresses the exploitation-exploration
dilemma in the selection step of the MCTS algorithm
using the UCB1 policy (Kocsis and Szepesv´ari,
2006). A child node j is selected to maximize:
UCT( j) =
X
j
+ 2C
p
s
2ln(N(v))
N(v
j
)
(1)
where
X
j
=
Q(v
j
)
N(v
j
)
is an approximation of the game-
theoretic value of node j. Q(v
j
) is the total reward of
all playouts that passed through node j, N(v
j
) is the
number of times node j has been visited, N(v) is the
number of times the parent of node j has been vis-
ited, and C
p
≥ 0 is a constant. The left-hand term is
for exploitation and the right-hand term is for explo-
ration (Kocsis and Szepesv´ari, 2006). The decrease or
increase in the amount of exploration can be adjusted
by C
p
in the exploration term (see Section 6).
Pipeline Pattern for Parallel MCTS
615

2.2 Parallelization of MCTS
Parallelization of MCTS consists of a precise arrange-
ment of tasks and data dependencies. In section 2.2.1
we explain how to decompose MCTS into tasks. In
section 2.2.2 we investigate what types of data depen-
dencies exist among these tasks. In Section 2.2.3 the
existing parallelization methods for MCTS are dis-
cussed.
2.2.1 Decomposition into Tasks
The first step towards parallelizing MCTS is to find
concurrent tasks in MCTS. As stated above, there are
two levels of task decomposition in MCTS.
1. Iteration-level tasks (ILT): In MCTS the compu-
tation associated with each iteration is indepen-
dent. Therefore, these are candidates to guide a
task decomposition by mapping a chunk of itera-
tions onto a task.
2. Operation-level tasks (OLT): The task decom-
position for MCTS occurs inside each iteration.
Each of the four MCTS operations can be treated
as a separate task.
2.2.2 Data Dependencies
The second step is dealing adequately with the data
dependency. When a search tree is shared among mul-
tiple parallel threads, there are two levels of data de-
pendency.
1. Iteration-level dependencies (ILD): Strictly
speaking, in MCTS, iteration j has a soft de-
pendency to its predecessor iteration j − 1.
Obviously, to select an optimal path, it requires
updates on the search tree from the previous
iteration.
1
A parallel MCTS can ignore ILD and
then simply suffers from the search overhead.
2
2. Operation-level dependencies (OLD): Each of the
four operations in MCTS has a hard dependency
to its predecessor.
3
For example, the EXPAND op-
eration cannot start until the SELECT operation
has been completed.
1
i.e., a violation of ILD does not impact the correctness
of the algorithm.
2
It occurs when a parallel implementation in a search
algorithm searches more nodes of the search space than the
sequential version; for example, since the information to
guide the search is not yet available.
3
i.e., a violation of OLD yields an incorrect algorithm.
Figure 2: Tree parallelization. The curly arrows represent
threads. The rectangles are terminal leaf nodes.
2.2.3 Parallelization Methods
There are three parallelization methods for MCTS
(i.e., root parallelization, leaf parallelization, and tree
parallelization) that belong to two main categories:
(A) parallelization with an ensemble of trees, and (B)
parallelization with a single shared tree.
The root parallelization method belongs to cate-
gory (A). It creates an ensemble of search trees (i.e.,
one for each thread). The trees are independent of
each other. When the search is over, they are merged,
and the action of the best child of the root is selected.
The leaf parallelization and tree parallelization
methods belong to category (B). In the leaf par-
allelization, the parallel threads perform multiple
PLAYOUT operations from a non-terminal leaf node
of the shared tree. These PLAYOUT operations are in-
dependent of each other, and therefore there is no data
dependency. In tree parallelization, parallel threads
are potentially able to perform different MCTS op-
erations on a same node of the shared tree (Chaslot
et al., 2008a). Figure 2 shows the tree parallelization
where three threads simultaneously perform different
MCTS operations on the tree. This is the topic of our
research.
The existing parallel implementations for tree par-
allelization are based on ILP (Chaslot et al., 2008a;
Enzenberger and M¨uller, 2010; Mirsoleimani et al.,
2015b; Mirsoleimani et al., 2015a). The tasks are
of the type of ILT, and the only dependency that ex-
ists among them is ILD. The potential concurrency is
exploited by assigning a chunk of iterations to sepa-
rate parallel threads and having them work on sepa-
rate processors. Our proposed algorithm allows im-
plementation of tree parallelization based on OLP.
ICAART 2018 - 10th International Conference on Agents and Artificial Intelligence
616
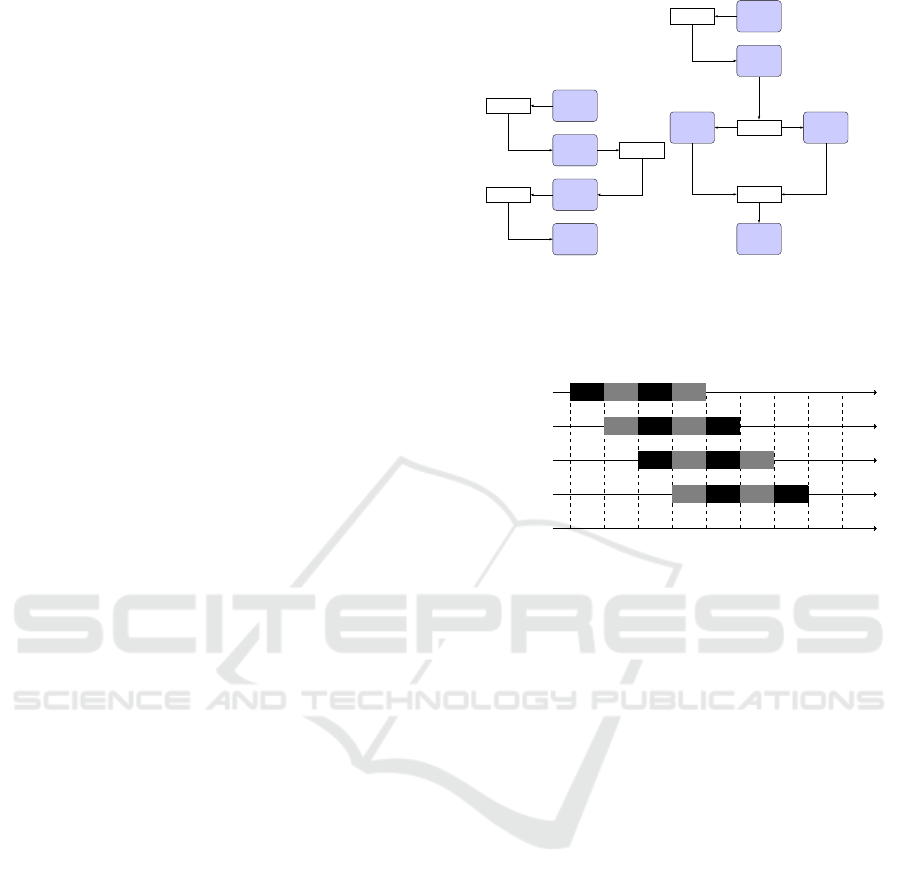
3 DESIGN OF 3PMCTS
In this section, we describe our proposed method for
parallelizing MCTS. Section 3.1 describes how the
pipeline pattern is applied in MCTS. Section 3.2 pro-
vides the 3PMCTS algorithm.
3.1 Pipeline Pattern for MCTS
Below we describe how the pipeline pattern is used
as a building block in the design of 3PMCTS. Figure
3 shows two types of pipelines for MCTS. The inter-
stage buffers are used to pass information between the
stages. When a stage of the pipeline completes its
computation; it sends a path of nodes from the search
to the next buffer. The subsequent stage picks a path
from the buffer and starts its computation. Here we
introduce two possible types of pipelines for MCTS.
1. Pipeline with sequential stages: Figure 3a shows
a pipeline with sequential stages for MCTS. The
idea is to map each MCTS operation to pipeline
stages so that each stage of the pipeline com-
putes one operation. Figure 4 illustrates how the
pipeline executes the MCTS operations over time.
Let C
i
represent a multiple-step computation on
path i. C
i
( j) is the jth step of the computation in
MCTS (i.e., j ∈ {S, E, P, and B}). Initially, the
first stage of the pipeline performs C
1
(S). After
the step has been completed, the second stage of
the pipeline receives the first path and computes
C
1
(E) while the first stage computes the first step
of the second path, C
2
(S). Next, the third stage
computesC
1
(P), while the second stage computes
C
2
(E) and the first stage C
3
(S). Each stage of the
pipeline takes the same amount of time to do its
work, say T. Figure 4 shows that the expected ex-
ecution time for 4 paths in an MCTS pipeline with
four stages is approximately 7 × T. In contrast,
the sequential version takes approximately 16× T
because each of the 4 paths must be processed
one after another. The pipeline pattern works best
if the operations performed by the various stages
of the pipeline are all about equally computation-
ally intensive. If the stages in the pipeline vary in
computational effort, the slowest stage creates a
bottleneck for the aggregate throughput. In other
words, when there are sufficient processors for
each pipeline stage, the speed of a pipeline is
approximately equal to the speed of its slowest
stage. For example, Figure 5 shows the schedul-
ing diagram that occurs when the PLAYOUT stage
takes 2×T units of time while others take T units
of time. Figure 5 shows that the expected execu-
tion time for 4 paths is approximately 11× T.
SelectBuffer
Expand
Buffer
Playout
Buffer
Backup
(a)
SelectBuffer
Expand
Buffer
Playout Playout
Buffer
Backup
(b)
Figure 3: (3a) Flowchart of a pipeline with sequential stages
for MCTS. (3b) Flowchart of a pipeline with parallel stages
for MCTS.
4: PE(B)
3: PE(P)
2: PE(E)
1: PE(S)
t
0
4: PE(B)
3: PE(P)
2: PE(E)
1: PE(S)
t
1
4: PE(B)
3: PE(P)
2: PE(E)
1: PE(S)
t
2
4: PE(B)
3: PE(P)
2: PE(E)
1: PE(S)
t
3
4: PE(B)
3: PE(P)
2: PE(E)
1: PE(S)
t
4
4: PE(B)
3: PE(P)
2: PE(E)
1: PE(S)
t
5
4: PE(B)
3: PE(P)
2: PE(E)
1: PE(S)
t
6
4: PE(B)
3: PE(P)
2: PE(E)
1: PE(S)
t
7
4: PE(B)
3: PE(P)
2: PE(E)
1: PE(S)
t
8
[T]
C
1
(S) C
2
(S) C
3
(S) C
4
(S)
C
1
(E) C
2
(E) C
3
(E) C
4
(E)
C
1
(P ) C
2
(P ) C
3
(P ) C
4
(P )
C
1
(B) C
2
(B) C
3
(B) C
4
(B)
Figure 4: Scheduling diagram of a pipeline with sequential
stages for MCTS. The computation for stages are equal.
2. Pipeline with parallel stages: Figure 3b shows a
pipeline for MCTS with two parallel PLAYOUT
stages. Using two PLAYOUT stages in the pipeline
results in an overall speed of approximately T
units of time per path as the number of paths
grows. Figure 6 shows that the MCTS pipeline is
perfectly balanced by using two PLAYOUT stages.
The expected execution time for 4 paths is ap-
proximately 8 × T. Therefore, introducing paral-
lel stages improves the scalability of the MCTS
pipeline.
3.2 Pipeline Construction
The pseudocode of MCTS is shown in Algorithm 1.
Each operation in MCTS constitutes a stage of the
pipeline in 3PMCTS. In contrast to the existing meth-
ods, our 3PMCTS algorithm is based on OLP for
parallelizing MCTS. The pipeline pattern can satisfy
the operation-level dependencies (OLDs) among the
iteration-level tasks (OLTs).
The potential concurrency is also exploited by as-
signing each stage of the pipeline to a separate pro-
cessing element for execution on separate processors.
If the pipeline has only sequential stages then the
speedup is limited to the number of stages.
Pipeline Pattern for Parallel MCTS
617

5: PE(B)
4: PE(Idle)
3: PE(P)
2: PE(E)
1: PE(S)
t
0
5: PE(B)
4: PE(Idle)
3: PE(P)
2: PE(E)
1: PE(S)
t
1
5: PE(B)
4: PE(Idle)
3: PE(P)
2: PE(E)
1: PE(S)
t
2
5: PE(B)
4: PE(Idle)
3: PE(P)
2: PE(E)
1: PE(S)
t
3
5: PE(B)
4: PE(Idle)
3: PE(P)
2: PE(E)
1: PE(S)
t
4
5: PE(B)
4: PE(Idle)
3: PE(P)
2: PE(E)
1: PE(S)
t
5
5: PE(B)
4: PE(Idle)
3: PE(P)
2: PE(E)
1: PE(S)
t
6
5: PE(B)
4: PE(Idle)
3: PE(P)
2: PE(E)
1: PE(S)
t
7
5: PE(B)
4: PE(Idle)
3: PE(P)
2: PE(E)
1: PE(S)
t
8
5: PE(B)
4: PE(Idle)
3: PE(P)
2: PE(E)
1: PE(S)
t
9
5: PE(B)
4: PE(Idle)
3: PE(P)
2: PE(E)
1: PE(S)
t
10
5: PE(B)
4: PE(Idle)
3: PE(P)
2: PE(E)
1: PE(S)
t
11
[T]
C
1
(S) C
2
(S) C
3
(S) C
4
(S)
C
1
(E) C
2
(E) C
3
(E) C
4
(E)
C
1
(P ) C
2
(P ) C
3
(P ) C
4
(P )
C
1
(B) C
2
(B) C
3
(B) C
4
(B)
Figure 5: Scheduling diagram of a pipeline with sequential
stages for MCTS. The computation for stages are not equal.
5:PE(B)
4:PE(P)
3:PE(P)
2:PE(E)
1:PE(S)
t
0
5:PE(B)
4:PE(P)
3:PE(P)
2:PE(E)
1:PE(S)
t
1
5:PE(B)
4:PE(P)
3:PE(P)
2:PE(E)
1:PE(S)
t
2
5:PE(B)
4:PE(P)
3:PE(P)
2:PE(E)
1:PE(S)
t
3
5:PE(B)
4:PE(P)
3:PE(P)
2:PE(E)
1:PE(S)
t
4
5:PE(B)
4:PE(P)
3:PE(P)
2:PE(E)
1:PE(S)
t
5
5:PE(B)
4:PE(P)
3:PE(P)
2:PE(E)
1:PE(S)
t
6
5:PE(B)
4:PE(P)
3:PE(P)
2:PE(E)
1:PE(S)
t
7
5:PE(B)
4:PE(P)
3:PE(P)
2:PE(E)
1:PE(S)
t
8
[T]
C
1
(S) C
2
(S) C
3
(S) C
4
(S)
C
1
(E) C
2
(E) C
3
(E) C
4
(E)
C
1
(P ) C
3
(P )
C
2
(P ) C
4
(P )
C
1
(B) C
2
(B) C
3
(B) C
4
(B)
Figure 6: Scheduling diagram of a pipeline with parallel
stages for MCTS. Using parallel stages create load balanc-
ing.
4
However in MCTS, the operations are not equally
computationally intensive, e.g., the PLAYOUT opera-
tion (random simulations plus evaluation of a terminal
state) could be more computationally expensive than
other operations. Therefore, our 3PMCTS algorithm
uses a pipeline with parallel stages. Introducing par-
allel stages makes 3PMCTS more scalable.
Figure 7 depicts one of the possible pipeline con-
structions for 3PMCTS. We split the PLAYOUT op-
eration into two stages to achieve more parallelism
(See Section 2.1). The five stages run the MCTS op-
erations SELECT, EXPAND, RANDOMSIMULATION,
EVALUATION, and BACKUP, in that order. The
SELECT stage and BACKUP stage are serial. The
three middle stages (EXPAND, RANDOMSIMULA-
TION, and EVALUATION) are parallel and do the most
time-consuming part of the search. A serial stage does
process one token at a time. A parallel stage is able
to process more than one token. Therefore, it needs
more than one in-flight token. A token represents a
path of nodes inside the search tree during the search.
The pipeline depicted in Figure 7 is one of the
possible constructions for 3PMCTS. Each of the five
stages could be either serial or parallel. Therefore,
3PMCTS provides a great level of flexibility. For ex-
ample, a pipeline could have a serial stage for the SE-
LECT operation and a parallel stage for the BACKUP
operation. In our experiments we use this construc-
tion (see Section 6).
4
This holds when the operations performed by the vari-
ous stages are all about equally computationally intensive.
Figure 7: The 3PMCTS algorithm with a pipeline that
has three parallel stages (i.e., EXPAND, RANDOMSIMULA-
TION, and EVALUATION).
4 IMPLEMENTATION
We have implemented the proposed 3PMCTS al-
gorithm in the ParallelUCT package (Mirsoleimani
et al., 2015a). The ParallelUCT package is an open
source tool for parallelization of the UCT algorithm.
5
It uses task-level parallelism to implement differ-
ent parallelization methods for MCTS. We have also
used an algorithm called grain-sized control paral-
lel MCTS (GSCPM) to measure the performance of
ILP for MCTS. The GSCPM algorithm creates tasks
based on the fork-join pattern (McCool et al., 2012).
More details about this algorithm can be found in
(Mirsoleimani et al., 2015a). Both 3PMCTS and
GSCPM are implemented by TBB parallel program-
ming library (Reinders, 2007) and they are available
online as part of the ParallelUCT package. In our im-
plementation for 3PMCTS, we can specify the num-
ber of in-flight tokens. This is equal to the number of
tasks for GSCPM algorithm.
5 EXPERIMENTAL SETUP
The performance of 3PMCTS is measured by using a
High Energy Physics (HEP) expression simplification
problem (Kuipers et al., 2013; Ruijl et al., 2014). Our
setup follows closely (Kuipers et al., 2013). We dis-
cuss the case study in 5.1, the hardware in 5.2, and the
performance metrics in 5.3.
5.1 Case Study
Our case study is in the field of Horner’s rule, which
is an algorithm for polynomial computation that re-
duces the number of multiplications and results in a
computationally efficient form. For a polynomial in
one variable
p(x) = a
n
x
n
+ a
n−1
x
n−1
+ ... + a
0
, (2)
5
https://github.com/mirsoleimani/paralleluct/
ICAART 2018 - 10th International Conference on Agents and Artificial Intelligence
618

the rule simply factors out powers of x. Thus, the
polynomial can be written in the form
p(x) = ((a
n
x+ a
n−1
)x+ ...)x+ a
0
. (3)
This representation reduces the number of multipli-
cations to n and has n additions. Therefore, the total
evaluation cost of the polynomial is 2n.
Horner’s rule can be generalized for multivariate
polynomials. Here, Eq. 3 applies on a polynomial
for each variable, treating the other variables as con-
stants. The order of choosing variables may be dif-
ferent, each order of the variables is called a Horner
scheme.
The number of operations can be reduced even
more by performing common subexpression elimi-
nation (CSE) after transforming a polynomial with
Horner’s rule. CSE creates new symbols for each
subexpression that appears twice or more and replaces
them inside the polynomial. Then, the subexpression
has to be computed only once.
We are using the HEP(σ) expression with 15 vari-
ables to study the results of 3PMCTS. The MCTS is
used to find an order of the variables that gives effi-
cient Horner schemes (Ruijl et al., 2014). The root
node has n children, with n the number of variables.
The children of other nodes represent the remaining
unchosen variables in the order. Starting at the root
node, a path of nodes (variables) inside the search tree
is selected. The incomplete order is completed with
the remaining variables added randomly (i.e., RAN-
DOMSIMULATION). The complete order is then used
for Horners method followed by CSE to optimize the
expression. The number of operations (i.e., ∆) in this
optimized expression is counted (i.e., EVALUATION).
5.2 Hardware
Our experiments were performed on a dual socket In-
tel machine with 2 Intel Xeon E5-2596v2 CPUs run-
ning at 2.4 GHz. Each CPU has 12 cores, 24 hyper-
threads, and 30 MB L3 cache. Each physical core has
256KB L2 cache. The peak TurboBoost frequency is
3.2 GHz. The machine has 192GB physical memory.
We compiled the code using the Intel C++ compiler
with a -O3 flag.
5.3 Performance Metrics
One important metric related to performance and par-
allelism is speedup. Speedup compares the time for
solving the identical computational problem on one
worker versus that on P workers:
speedup =
T
1
T
P
. (4)
Figure 8: Playout-speedup as function of the number of
tasks (tokens). Each data point is an average of 21 runs
for a search budget of 8192 playouts. The constant C
p
is
0.5. Here a higher value is better.
Where T
1
is the time of the program with one
worker and T
p
is the time of the program with P work-
ers. In our results we report the scalability of our par-
allelization as strong scalability which means that the
problem size remains fixed as P varies. The problem
size is the number of playouts (i.e., the search bud-
get) and P is the number of tasks. In the literature this
form of speedup is called playout-speedup (Chaslot
et al., 2008a).
The second important metric is the number of op-
erations in the optimized expression. A lower value
is desirable when higher number of tasks is used.
6 EXPERIMENTAL RESULTS
In this section, the performance of 3PMCTS is mea-
sured. Table 1 shows the sequential time to execute
the specified number of playouts.
Figure 8 shows the playout-speedup for both
3PMCTS and GSCPM, as a function of the number
of tasks (from 1 to 4096). The search budget for both
algorithms is 8192 playouts. The 3PMCTS algorithm
uses a pipeline with five stages for MCTS operations.
Four stages are parallel; the SELECT stage is chosen
to be serial (see the end of Section 3.2). A playout-
speedup close to 21 on a 24-core machine is observed
for both algorithms. From our results, we may pro-
visionally conclude that the 3PMCTS algorithm (a)
for 4 to 32 parallel tasks, shows a speedup less than
GSCPM and (b) for 64 to 512 parallel tasks, shows a
better speedup than the GSCPM algorithm (see Figure
8). At the same time, 3PMCTS also allows flexible
control of the parallel or serial execution of MCTS
Table 1: Sequential time in seconds when C
p
= 0.5.
Processor Num. Playouts Time (s)
CPU 8192 215.72 ± 4.12
Pipeline Pattern for Parallel MCTS
619
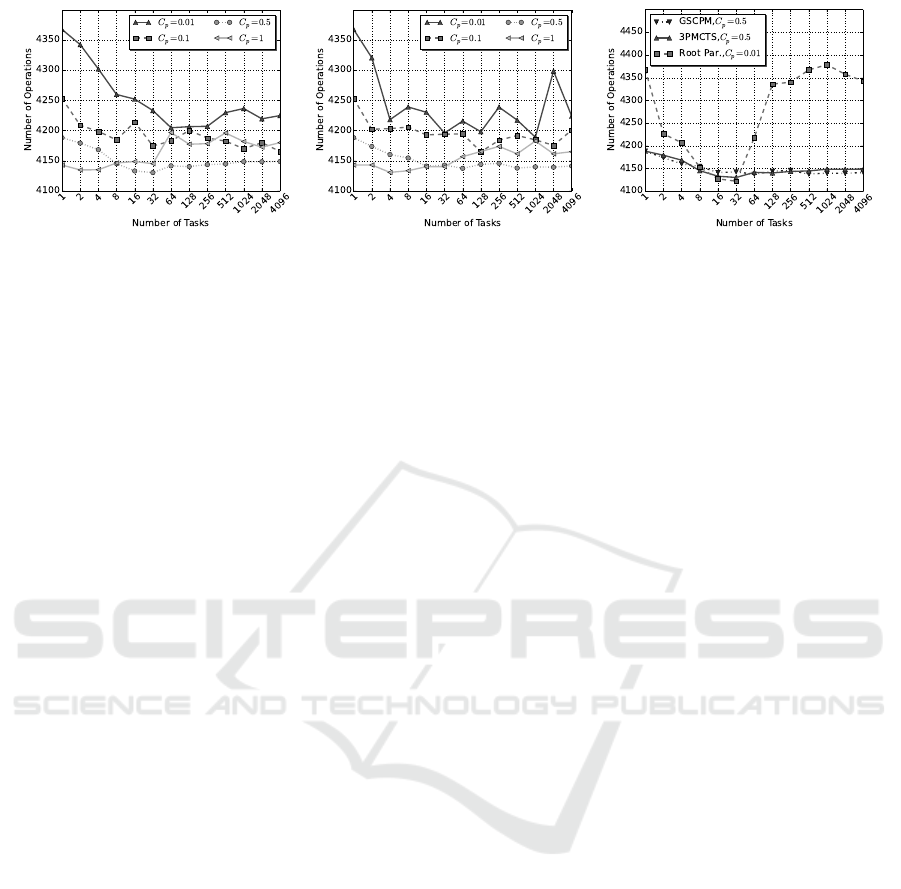
(a) 3PMCTS (b) GSCPM (c) Root Parallelization
Figure 9: Number of operations as function of the number of tasks (tokens). Each data point is an average of 21 runs for a
search budget of 8192 playouts. Here a lower value is better.
operations (e.g., the SELECT stage is sequential and
the BACKUP stage is parallel in our case), something
that GSCPM cannot provide.
Figure 9a and 9b show the results of the optimiza-
tion in the number of operations in the final expres-
sion for both algorithms. These results show consis-
tency with the findings in (Kuipers et al., 2013; Ruijl
et al., 2014). From our results, we may arrive at three
conclusions. (1) When MCTS is sequential (i.e., the
number of tasks is 1), for small values of C
p
, such that
MCTS behaves exploitively, the method gets trapped
in local minima, and the number of operations is high.
For larger values of C
p
, such that MCTS behaves ex-
ploratively, lower values for the number of operations
is found. (2) When MCTS is parallel, for small num-
bers of tasks (from 2 to 8), it turns out to be good to
choose a high value for the constant C
p
(e.g., 1) for
both 3PMCTS and GSCPM. With higher numbers of
tasks, a lower value for C
p
in the range [0.5; 1) seems
suitable for both algorithms. Figure 9c also shows
that 3PMCTS can find lower number of operations for
8, 16, and 32 tasks when C
p
= 0.5. (3) When both al-
gorithms find the same number of operations, the one
with higher speedup is better. For instance, the 3PM-
CTS algorithm finds the same number of operations
compared to GSCPM for 64 tasks, but it has higher
speedup when C
p
= 0.5. Note that these values hold
for a particular polynomial and that different polyno-
mials give different optimal values forC
p
and number
of tasks.
A comparison to root parallelization is illustrated
in Figure 9c. Both 3PMCTS and GSCPM belong to
the category of tree parallelization. For C
p
= 0.01,
root parallelization finds a lower number of opera-
tions for both 16 and 32 tasks compared to the two
other methods. However, increasing the number of
tasks causes root parallelization to provide a much
higher number of operations. From these results, we
may conclude that root parallelization could also be a
feasible choice in this domain.
Kuipers et al. remarked that tree parallelization
would give a result that is statistically a little bit in-
ferior to a run with sequential MCTS with the same
number of playouts due to the violation of iteration-
level dependency (ILD) that produces search over-
head (Kuipers et al., 2015). It is clear from our results
that the effectiveness of any parallelization method
for MCTS depends heavily on the choice of three
parameters: (1) the C
p
constant, (2) the number of
playouts, and (3) the number of tasks. If we select
these parameters carefully, it is possible to overcome
the search overhead to some extent. Furthermore, the
3PMCTS algorithm provides the flexibility of man-
aging the execution (serial or parallel) of different
MCTS operations that helps us even more to achieve
this goal.
7 CONCLUSION AND FUTURE
WORK
Monte Carlo Tree Search (MCTS) is a randomized
algorithm that is successful in a wide range of opti-
mization problems. The main loop in MCTS consists
of individual iterations, suggesting that the algorithm
is well suited for parallelization. The existing paral-
lelization methods, e.g., tree parallelization, straight
forwardly fans out the iterations over available cores.
In this paper, a new parallel algorithm based on
the pipeline pattern for MCTS is proposed. The idea
is to break-up the iterations themselves, splitting them
into individual operations, which are then parallelized
in a pipeline. Experiments with an application from
High Energy Physics show that our implementation of
3PMCTS scales well. Scalability is only one issue, al-
though it is an important one. The second issue is the
flexibility of task decomposition in parallelism. These
higher levels of flexibility allow fine-grained manag-
ICAART 2018 - 10th International Conference on Agents and Artificial Intelligence
620

ing of the execution of operations in MCTS which
provide different pipeline constructions. We consider
the flexibility an even more important characteristic
of 3PMCTS. For future work, we will study the ef-
fectiveness of 3PMCTS with regards to the different
pipeline constructions.
ACKNOWLEDGEMENTS
This work is supported in part by the ERC Advanced
Grant no. 320651, “HEPGAME.”
REFERENCES
Browne, C. B., Powley, E., Whitehouse, D., Lucas, S. M.,
Cowling, P. I., Rohlfshagen, P., Tavener, S., Perez, D.,
Samothrakis, S., and Colton, S. (2012). A Survey of
Monte Carlo Tree Search Methods. Computational
Intelligence and AI in Games, IEEE Transactions on,
4(1):1–43.
Chaslot, G., Winands, M., and van den Herik, J. (2008a).
Parallel Monte-Carlo Tree Search. In the 6th Interna-
tioal Conference on Computers and Games, volume
5131, pages 60–71. Springer Berlin Heidelberg.
Chaslot, G. M. J. B., Winands, M. H. M., van den Herik, J.,
Uiterwijk, J. W. H. M., and Bouzy, B. (2008b). Pro-
gressive strategies for Monte-Carlo tree search. New
Mathematics and Natural Computation, 4(03):343–
357.
Coulom, R. (2006). Efficient Selectivity and Backup Op-
erators in Monte-Carlo Tree Search. In Proceed-
ings of the 5th International Conference on Comput-
ers and Games, volume 4630 of CG’06, pages 72–83.
Springer-Verlag.
Enzenberger, M. and M¨uller, M. (2010). A lock-free mul-
tithreaded Monte-Carlo tree search algorithm. Ad-
vances in Computer Games, 6048:14–20.
Fern, A. and Lewis, P. (2011). Ensemble Monte-Carlo Plan-
ning: An Empirical Study. In ICAPS, pages 58–65.
Goodfellow, I., Bengio, Y., and Courville, A. (2016). Deep
Learning. Adaptive Computation and Machine Learn-
ing Series. MIT Press.
Hassabis, D. and Silver, D. (2017). Alphago’s next move.
Kocsis, L. and Szepesv´ari, C. (2006). Bandit based Monte-
Carlo Planning Levente. In F¨urnkranz, J., Scheffer, T.,
and Spiliopoulou, M., editors, ECML’06 Proceedings
of the 17th European conference on Machine Learn-
ing, volume 4212 of Lecture Notes in Computer Sci-
ence, pages 282–293. Springer Berlin Heidelberg.
Kuipers, J., Plaat, A., Vermaseren, J., and van den Herik, J.
(2013). Improving Multivariate Horner Schemes with
Monte Carlo Tree Search. Computer Physics Commu-
nications, 184(11):2391–2395.
Kuipers, J., Ueda, T., and Vermaseren, J. A. M. (2015).
Code optimization in FORM. Computer Physics Com-
munications, 189(October):1–19.
McCool, M., Reinders, J., and Robison, A. (2012). Struc-
tured Parallel Programming: Patterns for Efficient
Computation. Elsevier.
Mirsoleimani, S. A., Plaat, A., van den Herik, J., and Ver-
maseren, J. (2015a). Parallel Monte Carlo Tree Search
from Multi-core to Many-core Processors. In ISPA
2015 : The 13th IEEE International Symposium on
Parallel and Distributed Processing with Applications
(ISPA), pages 77–83, Helsinki.
Mirsoleimani, S. A., Plaat, A., van den Herik, J., and Ver-
maseren, J. (2015b). Scaling Monte Carlo Tree Search
on Intel Xeon Phi. In Parallel and Distributed Systems
(ICPADS), 2015 20th IEEE International Conference
on, pages 666–673.
Reinders, J. (2007). Intel threading building blocks: out-
fitting C++ for multi-core processor parallelism. ”
O’Reilly Media, Inc.”.
Ruijl, B., Vermaseren, J., Plaat, A., and van den Herik, J.
(2014). Combining Simulated Annealing and Monte
Carlo Tree Search for Expression Simplification. Pro-
ceedings of ICAART Conference 2014, 1(1):724–731.
Schaefers, L. and Platzner, M. (2014). Distributed Monte-
Carlo Tree Search : A Novel Technique and its Appli-
cation to Computer Go. IEEE Transactions on Com-
putational Intelligence and AI in Games, 6(3):1–15.
Silver, D., Huang, A., Maddison, C. J., Guez, A., Sifre, L.,
Van Den Driessche, G., Schrittwieser, J., Antonoglou,
I., Panneershelvam, V., Lanctot, M., et al. (2016).
Mastering the game of go with deep neural networks
and tree search. Nature, 529(7587):484–489.
Yoshizoe, K., Kishimoto, A., Kaneko, T., Yoshimoto, H.,
and Ishikawa, Y. (2011). Scalable Distributed Monte-
Carlo Tree Search. In Fourth Annual Symposium on
Combinatorial Search, pages 180–187.
Pipeline Pattern for Parallel MCTS
621
