Using Structure of Automata for Faster Synchronizing Heuristics
Berk Cirisci, Muhammed Kerem Kahraman, Cagri Uluc Yildirimoglu,
Kamer Kaya and Husnu Yenigun
Computer Science and Engineering, Faculty of Engineering and Natural Sciences, Sabanci University, Istanbul, Turkey
Keywords: Finite State Automata, Synchronizing Sequences, Strongly Connected Component.
Abstract: The problem of finding a synchronizing sequence for an automaton is an interesting problem studied widely
in the literature. Finding a shortest synchronizing sequence is an NP-Hard problem. Therefore, there are
heuristics to find short synchronizing sequences. Some heuristics work fast but produce long synchronizing
sequences, whereas some heuristics work slow but produce relatively shorter synchronizing sequences. In
this paper we propose a method for using these heuristics by considering the connectedness of automata.
Applying the proposed approach of using these heuristics make the heuristics work faster than their original
versions, without sacrificing the quality of the synchronizing sequences.
1 INTRODUCTION
A synchronizing sequence w for an automaton A is a
sequence of inputs such that without knowing the
current state of A, when w is applied to A, A reaches
to a particular final state, regardless of its initial
state. If an automaton A has a synchronizing
sequence, A is called as synchronizing automaton.
Synchronizing automata and synchronizing
sequences have various applications. One example
area of application is the model-based testing, in
particular Finite State Machine (FSM) based testing.
When the abstract behavior of an interactive system
is modeled by using an FSM, there are various
methods to derive test sequences with high fault
coverage (Chow, 1978; Lee and Yannakakis, 1996;
Hierons and Ural, 2006). These methods construct a
test sequence to be applied when the implementation
under test is at a certain state. Therefore, it is
required to bring the implementation under test to
this particular state, regardless of the initial state of
the implementation, which can be accomplished by
using a synchronizing sequence. Even when the
implementation has a reset input for this purpose,
there are cases where using a synchronizing
sequence is preferred (Jourdan et al., 2015). For
more examples of application areas of synchronizing
sequences and for an overview of the theoretical
results related to synchronizing sequences please see
(Volkov, 2008).
For practical purposes, e.g. the use of a
synchronizing sequence in model-based testing, one
is interested in finding synchronizing sequences as
short as possible. However, finding a shortest
synchronizing sequence is known to be a NP-hard
problem (Eppstein, 1990). Therefore, heuristic
algorithms, known as synchronizing heuristics, are
used to find short synchronizing sequences. Among
such heuristics are Greedy (Eppstein, 1990), Cycle
(Trahtman, 2004), SynchroP (Roman, 2009), and
SynchroPL (Kudlacik et al., 2012). In this paper, we
consider using the structure of an automaton while
applying a synchronizing heuristic to speed up the
execution of these heuristics. Namely, we consider
the connectedness of automata.
An automaton A is called strongly connected if
every state is reachable from every other state by
using at least one sequence of inputs. Otherwise, A is
called non-strongly connected and in this case A can
be represented as a set of strongly connected
automata. These automata are called as strongly
connected components (SCCs) of A.
In this paper, given a non-strongly connected
automaton A, we suggest a method to build a
synchronizing sequence for A by using the
synchronizing sequences of the SCCs of A. We
considered the application of Greedy and SynchroP
algorithms directly to an automaton, and to SCCs of
the automaton. We observe that, the suggested
methods improve the running time greatly, without
544
Cirisci, B., Kahraman, M., Yildirimoglu, C., Kaya, K. and Yenigun, H.
Using Structure of Automata for Faster Synchronizing Heuristics.
DOI: 10.5220/0006660805440551
In Proceedings of the 6th International Conference on Model-Driven Engineering and Software Development (MODELSWARD 2018), pages 544-551
ISBN: 978-989-758-283-7
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

extending the length of the synchronizing sequences
much.
The remaining part of the paper is organized as
follows. In Section 2, we introduce the notation and
briefly give the required background. In Section 3,
we introduce our approach. In Section 4, we talk
about the synchronizing heuristics that we have
worked on and their integration to our approach. In
Section 5, we compare the proposed approach with
the traditional one that performs synchronization
heuristics on full automata. In Section 6, we
conclude the paper and provide some future
directions for our work.
2 BACKGROUND AND
NOTATION
A (deterministic) automaton is defined by a tuple A
= (S, Σ, D, δ) where S is a finite set of n states, Σ is a
finite alphabet consisting of p input letters (or
simply letters). D  S × Σ is the called the domain
and δ: D → S is a transition function. When D = S ×
Σ, then A is called complete, otherwise A is called
partial. Below, we consider only complete automata,
unless otherwise stated.
An element of the set Σ
*
is called a sequence. For
a sequence w  Σ
*
, |w| denotes the length of w, and ε
is the empty sequence of length 0. For a complete
automaton, we extend the transition function δ to a
set of states and to a sequence in the usual way. For
a state s  S, we have δ(s, ε) = s, and for a sequence
w  Σ
*
and a letter x  Σ, we have δ(s, xw) = δ(δ(s,
x), w). For a set of states C  S, we have δ(C, w) =
{δ(s, w)|s  C}.
For a set of states C  S, let C
2
= {{s, s'}| s,
s'C} be the set of all multisets with cardinality 2
with elements from C, i.e. C
2
is the set of all subsets
of C with cardinality 2, where repetition is allowed.
An element {s, s'}  C
2
is called a pair.
Furthermore, it is called a singleton pair (or an s–
pair, or simply a singleton) if s = s', otherwise it is
called a different pair (or a d–pair). The set of s–
pairs and d–pairs in C
2
are denoted by C
2
s
and C
2
d
respectively. A sequence w is said to be a merging
sequence for a pair {s, s'}  S
2
if δ({s,s'},w) is
singleton. Note that, for an s-pair {s,s}, every
sequence (including ε) is a merging sequence. A
sequence w is called an S'-synchronizing sequence
for an automaton A = (S, Σ, SΣ, δ) and a subset of
states S'  S if δ(S', w) is singleton. When S' = S, w
is simply called a synchronizing sequence for A. An
automaton A is called S'-synchronizing if there exists
an S'-synchronizing sequence for A. An automaton
A is simply called synchronizing if there exists a
synchronizing sequence for A.
In this paper, we only consider synchronizing
automata. As shown by Eppstein (1990), deciding if
an automaton is synchronizing can be performed in
time O(pn
2
) by checking if there exists a merging
sequence for {s,s'}, for all {s,s'}  S
2
.
We write δ
−1
(s, x) to denote the set of states with
a transition to state s with letter x, i.e. δ
−1
(s, x) = {s'
 S | δ(s',x) = s}. We also define δ
−1
({s,s'}, x) =
{{p,p'} | p  δ
−1
(s, x)  p'  δ
−1
(s', x)}.
Given a partial automaton, we consider the
completion of this automaton by introducing a new
state, and adding the missing transitions of states to
this new state. Formally for a partial automaton
A=(S, Σ, D, δ) such that D  S×Σ, we define the
completion of A as A' = (S {*}, Σ, S×Σ, δ'), where
(i) the star state * is a new state which does not exist
in S, (ii)  (s, x)  D, δ'(s, x) = δ(s, x), (iii)  (s, x) 
D, δ'(s, x) = *, (iv)  x  Σ, δ'(*, x) = *.
An automaton A = (S, Σ, S×Σ, δ) is said to be
strongly connected if for every pair of states s, s' 
S, there exists a sequence w  Σ
*
such that δ(s, w)=
s'. Given an automaton A= (S, Σ, S×Σ, δ) and another
automaton B = (S', Σ, D, δ́), B is said to be a sub-
automaton of A if (i) S'  S, (ii) D = {(s,x)S' ×Σ |
Ǝs'  S' s.t. δ(s,x)= s' }, (iii) (s,x)  D, δ́(s,x) =
δ(s,x). Intuitively, the states of B consist of a subset
of states of A. Every transition in A from a state in B
to a state in B is preserved, and all the other
transitions are deleted.
A strongly connected component (SCC) of a
given automaton A = (S, Σ, S×Σ, δ), is a sub-
automaton B = (Ś, Σ, D, δ́) of A such that, B is
strongly connected, and there does not exist another
strongly connected sub-automaton C of A, where B
is a sub-automaton of C. When one considers an
automaton A as a graph (by representing the states of
A as the nodes, and the transition between the states
as the edges of the graph), B simply corresponds to a
strongly connected component of the graph of A.
For a set of SCCs {A
1
, A
2
, …, A
k
}, where A
i
= (S
i
,
Σ, D
i
, δ
i
), 1 ≤ i ≤ k, we have S
i
∩ S
j
= when i  j,
and S
1
 S
2
 …  S
k
= S. Please note here that k = 1
if and only if A is strongly connected.
An SCC A
i
= (S
i
, Σ, D
i
, δ
i
) is called a sink
component if D
i
= S
i
×Σ. In other words, for a sink
component, all the transitions of the states in S
i
in A
are preserved in A
i
. Therefore, if A
i
= (S
i
, Σ, D
i
, δ
i
) is
not a sink component, then some transitions of some
states will be missing. For this reason, A
i
is a
complete automaton if and only if A
i
is a sink
component.
Using Structure of Automata for Faster Synchronizing Heuristics
545

Figure 1: An automaton with 10 States, 2 inputs and 3
SCC's.
Figure 2: SCC
1
(A
1
) with additional star state.
3 SYNCHRONIZING
SEQUENCES FOR
NON-STRONGLY
CONNECTED
AUTOMATA
Consider an automaton A= (S, Σ, S×Σ, δ) and its
SCC decomposition {A
1
, A
2
, …, A
k
}.
Lemma 1: A is synchronizing iff there exists only
one sink component in A
i
in {A
1
, A
2
, …, A
k
} and A
i
is synchronizing.
Proof: If there are two distinct sink components A
i
and A
j
of A, a state s
i
in A
i
and a state s
j
in A
j
can
never be merged. If A
i
is the only sink component of
A and A
i
is not synchronizing, A is not synchronizing
as well.
Let A = (S, Σ, S×Σ, δ) be an automaton and {A
1
,
A
2
, …, A
k
} be the SCCs of A. We consider the SCCs
of A (topologically) sorted as  A
1
, A
2
, … , A
k
 such
that for any 1 ≤ i < j ≤ k, there do not exist s
i
 S
i
, s
j
 S
j
, w  Σ
*
where δ(s
j
, w) = s
i
. Note that in this case
A
k
must be a sink component and we have the
following result.
Lemma 2: Let  A
1
, A
2
, …, A
k
 be a topologically
sorted SCCs of an automaton A=(S, Σ, S×Σ, δ),
where A
i
= (S
i
, Σ, D
i
, δ
i
), 1  i  k. For any sequence
w  Σ
*
and for a state s  S
i
, 1  i  k, we have δ(s,
w)  (S
i
 S
i+1
 …  S
k
).
Proof: Since the components are topologically
sorted, states in A
i
can only move to a state in A
i
, or
to a state in A
i+1
, A
i+2
, …, A
k
.
Lemma 3: Let A
i
be an SCC of an automaton. If A
i
is a partial automaton, then the completion A'
i
of A
i
is a synchronizing automaton.
Proof: Since A
i
is an SCC, all states can be reached
from other states in A
i
. Also, we know that star state
is a state that can reach to only itself. When we
complete A
i
with a star state, every state can reach
the star state and star state can't reach to other state
then itself so that means other states should unite in
star state eventually and makes A'
i
a synchronizing
automaton.
3.1 An Initial Approach to Use SCCs
We now explain an initial idea to form a
synchronizing sequence for an automaton A by using
synchronizing sequences of the SCCs of A. Let A=
(S, Σ, S×Σ, δ) be an automaton and  A
1
, A
2
, …, A
k

be the topologically sorted SCCs of A, where A
i
= (S
i
,
Σ, D
i
, δ
i
). For 1 ≤ i < k, let β
i
be a synchronizing
sequence for the completion A'
i
of A
i
= (S
i
, Σ, D
i
, δ
i
).
Note that based on Lemma 2 one can always find a
synchronizing sequence for A
i
, 1  i < k. Let β
k
be a
synchronizing sequence for A
k
. Lemma 1 suggests
that A
k
always has a synchronizing sequence if A is
synchronizing.
We first claim that the sequence β
1
β
2
…β
k
is a
synchronizing sequence for A. In order to see this, it
is sufficient to observe the following.
Lemma 4: For any 0  i < k we have
δ(S, β
1
β
2
…β
i
)  (S
i+1
 S
i+2
…  S
k
)
Proof: By induction, where the base case i = 0 holds
trivially. Assume that the claim holds for i-1, i.e.
δ(S, β
1
β
2
…β
i-1
)  (S
i
 S
i+1
 …  S
k
). For a state s
 δ(S, β
1
β
2
…β
i-1
) such that s  (S
i+1
 S
i+2
… 
S
k
), then δ(s,β
i
) will also belong to (S
i+1
 S
i+2
…
 S
k
) based on Lemma 2. Hence it remains to show
that for any state s  δ(S, β
1
β
2
…β
i-1
) such that s  S
i,
MODELSWARD 2018 - 6th International Conference on Model-Driven Engineering and Software Development
546

δ(s,β
i
) is not in S
i
. The sequence β
i
is a synchronizing
sequence for the completion A'
i
of SCC A
i
. Since the
star state of A'
i
is the only state in which the states of
A'
i
can be synched, we must have δ'
i
(S
i
, β
i
) = {*}.
Note that the star state in A'
i
represents the states S\S
i
for A
i
. Hence the sequence β
i
is in fact a sequence
that pushes all the states in S
i
to the states in the
other components, i.e. δ(S
i
, β
i
) = . This implies that
for a state s  δ(S, β
1
β
2
…β
i-1
) such that s  S
i,
δ(s,β
i
)
is not in S
i
. Finally, we can state the following result.
Theorem 5: Let  A
1
, A
2
, …, A
k
 be a topologically
sorted SCCs of an automaton A = (S, Σ, D, δ), where
A
i
= (S
i
, Σ, D
i
, δ
i
), 1  i  k. Let β
i
be a synchronizing
sequence for the completion A'
i
of A
i
, 1  i < k , and
let β
k
be a synchronizing sequence for A
k
.
The sequence β
1
β
2
…β
k
is a synchronizing sequence
for A.
Proof: δ(S, β
1
β
2
…β
k-1
)  S
k
using Lemma 4. Since
β
k
is a synchronizing sequence for A
k
, δ(S
k
, β
k
) is
singleton. Combining these two results, we have
δ(δ(S, β
1
β
2
…β
k-1
), β
k
) = δ(S, β
1
β
2
…β
k-1
β
k
) as
singleton as well.
3.2 An Improvement on the Initial
Approach
Theorem 5 shows an easy way for constructing a
synchronizing sequence for an automaton A based
on its SCCs. As one may notice, though, the length
of the sequence to be constructed can be reduced
based on the following observation. Consider a
sequence β
i
, for some 1<i k, used in the sequence
β
1
β
2
…β
k-1
β
k
. The sequence β
i
is constructed to push
all the states in A
i
out of the component A
i
.
However, the sequence β
1
β
2
…β
i-1
applied before β
i
can already push some states in A
i
out of A
i
. On the
other hand, the sequence β
1
β
2
…β
i-1
can also move
some of the states in the components A
1,
A
2,
…, A
i-1
to a state in A
i
. Therefore, a more careful approach
can be taken considering which states in A
i
must
really be moved out of A
i
when constructing the
sequence to handle the component A
i
.
To take this into account, we define the
following sequences recursively. For the bases cases
we define α
0
= ε and σ
0
= ε. For 1 ≤ i < k, let S'
i
= S
i
∩ δ(S, σ
i-1
) and let α
i
be a S'
i
-synchronizing
sequence for A'
i
. For 1 ≤ i < k, let σ
i
= σ
i-1
α
i
.
Theorem 6: Let S'
k
= S
k
∩ δ(S, σ
k-1
) and α
k
be a S'
k
-
synchronizing sequence for A
k
. Then σ
k-1
α
k
is a
synchronizing sequence for A.
Proof: σ
k-1
is a synchronizing sequence for A
1
 A
2

A
3
...  A
k-1
and we know that they are
synchronized in the star state of A
k-1
which
represents the states that are outside of A
k-1
. These
states belong to A
k
because A
k
is ahead of A
k-1
in
topological sort and it is the only SCC left so we can
say that δ(S, σ
k-1
)  S
k
. In other words, σ
k-1
leaves us
with active states S'
k
 S
k
. Since α
k
synchronizes all
the states of S'
k
, σ
k-1
α
k
is a synchronizing sequence
for A.
Based on Theorem 6, the algorithm given in
Figure 3 can be used to construct a synchronizing
sequence for an automaton A.
Input: An automaton A = (S,Σ,D,δ)
Output: A synchronizing sequence for A
C = S; // All states are
// active initially
Г = ε ; // Г: synch. sequence to
// be constructed, initially
// empty
<A
1
, A
2
,…, A
k
> = find/sort SCCs of A
foreach i in {1, 2, …, k} do
// Consider A
i
= (S
i
,Σ,D
i
,δ
i
)
S’
i
= C ∩ S
i
;
// find active states
// of A
i
Г
i
= Heuristic( A’
i
,S’
i
);
// find S’
i
sync. sequence
// of completion A’
i
of A
i
Г = Г Г
i
;
// append Г
i
to sync. seq.
C = δ(C,Г
i
); // Update active
// states
return Г;
Figure 3: SCC algorithm to compute synchronizing
sequences.
Note that in the algorithm given in Figure 3, any
synchronizing heuristic can be used to compute Г
i
.
In the next section, we explain two different
algorithms from the literature that we used in our
experiments.
4 SYNCHRONIZING
HEURISTICS
As noted in Section 1, there are various
synchronizing heuristics. In this paper, we
considered and experimented with two of these
heuristics, Greedy and SynchroP. Both Greedy and
SynchroP heuristics have two phases. Phase 1 is
Using Structure of Automata for Faster Synchronizing Heuristics
547

common in these heuristics and given as Algorithm
1 below. In Phase 1, a shortest merging sequence
τ(i,j) for each {i, j}  S
2
is computed by using a
breadth first search. Note that τ(i,j) is not unique.
Input: An automaton A = (S,Σ,D,δ)
Output: A merging sequence for all
{i,j}  S
2
let Q be an initially empty queue
// Q: BFS frontier
P = Ø // P: keeps the set of nodes
// in the BFS forest
// constructed so far
foreach {i,j}  S
2
s
do
push {i,j} onto Q
insert {i,j} into P
set τ(i,j) = ɛ;
while P ≠ S
2
do
{i,j}= pop next item from Q;
foreach x  Σ do
foreach {k,l}  δ
-1
( {i,j},x) do
if {k,l} P then
τ(k,l)= x τ(i,j);
push {k,l} onto Q;
P = P  {{k,l}};
Figure 4: Phase 1 of Greedy and SynchroP.
Algorithm 1 performs a breadth first search
(BFS), and therefore constructs a BFS forest, rooted
at s–pairs {i, i}  S
2
s
, where these s–pairs are the
nodes at level 0 of the forest. A d–pair {i, j} appears
at level k of the BFS forest if |τ{i,j}| = k.
Algorithm 1 requires Ω(n
2
) time since each {i, j}
 S
2
is pushed to Q exactly once.
4.1 The Greedy Heuristic
Greedy’s Phase 2 (given as Algorithm 2 below)
constructs a synchronizing sequence by using the
information from Phase 1. Its main loop can iterate
at most n − 1 times, since in each iteration |C| is
reduced by at least one. The min operation at line 4
requires O(n
2
) time and line 5 takes constant time.
Line 6 can normally be handled in O(n
3
) time, but
using the information precomputed by the
intermediate stage between Phase 1 and Phase 2, line
6 can be handled in O(n) time. Therefore, Phase 2 of
Greedy requires O(n
3
) time. Note that Algorithm 2
finds an S-synchronizing sequence for a given
complete automaton A = (S, Σ, S×Σ, δ). However,
for our purposes we need to find an S'-synchronizing
sequence for a given subset S'  S of states.
Input: An automaton A = (S,Σ,D,δ),
τ(i,j) for all {i,j}  S
2
s
,
S’ to be synchronized
Output: An S’- synch. sequence Г for A
C = S’ // C: current state set
Г = ε // Г: synch. sequence to
// be constructed, initially
// empty
while |C| > 1 do // still not a
// singleton
{i,j} = arg min
<k,l>

2
d
| τ(k,l)|;
// decide the d-pair to be
// merged
Г = Г τ(i,j); // append τ(i,j)
// to the
// synchronizing
// sequence
C = δ(C,τ(i,j)); //update current
// state set
// with τ(i,j)
Figure 5: Phase 2 of Greedy.
4.2 The SynchroP Heuristic
Similar to the second phase of Greedy, the second
phase of SynchroP also constructs a synchronizing
sequence iteratively. The algorithms keep track of
the current set C of states, which is initially the
entire set of states S. In each iteration, the cardinality
of C is reduced at least by one. This is accomplished
by picking a d-pair {i, j}  C
2
d
in each iteration, and
considering δ(C, τ(i,j)) as the current set in the next
iteration. Since τ(i,j) is a merging sequence for the
states i and j, the cardinality of δ(C,τ(i,j)) is
guaranteed to be smaller than that of C.
For a set of states C  S, let the cost φ(C) of C be
defined as
    

φ(C) is a heuristic indication of how hard it is to
bring the set C to a singleton. The intuition here is
that, the larger the cost φ(C) is, the longer a
synchronizing sequence would be required to bring
C to a singleton set.
During the iterations of SynchroP, the selection
of {i, j}  C
2
d that will be used is performed by
considering the cost of the set δ(C,τ(i,j)). Based on
this cost function, the second phase of SynchroP is
given in Algorithm 2. Like in Greedy with SCC
Method, we also use a slightly modified version of
the second phase of SynchroP algorithm to find S'-
synchronizing sequence.
MODELSWARD 2018 - 6th International Conference on Model-Driven Engineering and Software Development
548

Input: An atomaton A = (S,Σ,D,δ),
τ(i,j) for all {i,j}  S
2
s
,
S’ to be synchronized
Output: An S’- synch. sequence Г for A
C = S’ // C: current state set
Г = ε // Г: synchronizing sequence to
// be constructed, initially
// empty
while |C| > 1 do // still not a
// singleton
minCost = ∞
foreach d-pair {i,j}  C
2
d
do
thisPairCost = ɸ ( δ(C,τ(i,j)))
if thisPairCost < minCost then
minCost = thisPairCost
τ’ = τ(i,j)
Г = Г τ’; // append τ’ to the
// synch. sequence
C = δ(C,τ’); // update current
// state set
// with τ’
Figure 6: Phase 2 of SynchroP.
5 EXPERIMENTAL RESULTS
The experiments were performed on a machine with
Intel Xeon E5-1650 CPU and 16GB of memory,
using Ubuntu 16.04.2. The code was written in
C/C++ and compiled using gcc with -o3 option
enabled.
In order to evaluate the performance of the
method suggested in this paper, we generated
random automata with n  {256, 512, 1024} states,
p  {2, 4, 8} inputs, k  {2, 4, 8} SCCs in the
following way. To construct a random automaton A
with a given number of states n, number of inputs p,
and number of SSCs k, we first construct k different
automata A
1
, A
2
, …, A
k
, where each A
i
is strongly
connected, has n/k states and p inputs. To construct
A
i
, we consider each state s in A
i
and each input x,
and assign (s,x) to be one of the states in A
i
randomly. If A
i
is not strongly connected after the
initial random assignment, we reassign (s,x) for
some of the states and inputs randomly again, and
keep repeating this process until A
i
becomes strongly
connected. Once we get A
i
strongly connected, we
identify those state s and input x pairs in A
i
(except
for the last SCC A
k
) such that A
i
stays strongly
connected even without using the transition of the
state s and with the input x. For these state/input
pairs in A
i
, we again assign (s,x) to be one of the
states in an automaton A
i+1
, A
i+2
, …, A
k
. For each n-
p-k combination we created 50 random automata.
The results given later in this section are the average
of these 50 automata.
For an automaton A= (S, Σ, S×Σ, δ) with n states,
p inputs and k SCCs A
1
, A
2
, …, A
k
 where A
i
= (S
i
,
Σ, D
i
, δ
i
), 1  i  k, we find a synchronizing (i.e. S-
synchronizing) sequence for A by using Greedy and
SynchroP algorithms given in Figure 5 and Figure 6,
respectively. We also find a synchronizing sequence
for A by using the SCC Algorithm given in Figure 3,
where for each A
i
= (S
i
, Σ, D
i
, δ
i
) we use Greedy and
SynchroP algorithms to find S'
i
-synchronizing
sequence as explained in Section 3.
Table 1 gives the running time and the
synchronizing sequence length for the direct
application of Greedy and SynchroP compared to the
SCC method suggested in this paper.
As expected, the running time is improved in all
the cases. The speed-up values (i.e. the time required
for the direct application of Greedy/SynchroP
divided by the time required for the application of
SCC method using Greedy/SynchroP) do not change
much based on the number of inputs of the
automata. However, the number of states and the
number of SCCs of the automata are very important
factors for the speed-up values. Figure 7 and Figure
8 display the speed-up values obtained in a more
explicit way. For the time performance, the SCC
method becomes more effective as the size of the
automaton and the number of SCCs increase.
For the length of the synchronizing sequences
found, the SCC method finds even shorter sequences
(5% shorter on the average) compared to the direct
application of Greedy. Although the direct
application of SynchroP yields shorter synchronizing
sequences in general, the increase in the length is not
large (3% longer on the average).
6 CONCLUSIONS
The SCC-based method suggested in this paper is a
method that can be used with any synchronizing
heuristic to make it run faster on non-strongly
connected automata. In case of Greedy, it can also
find shorter reset sequences in shorter time
compared to the application of Greedy directly.
SynchroP is a method which typically to finds
shorter reset sequences compared to Greedy but it
takes more time. With our method, we can use
SynchroP to find shorter reset sequences and also
SCC method will not take more time than the direct
application of Greedy.
Using Structure of Automata for Faster Synchronizing Heuristics
549

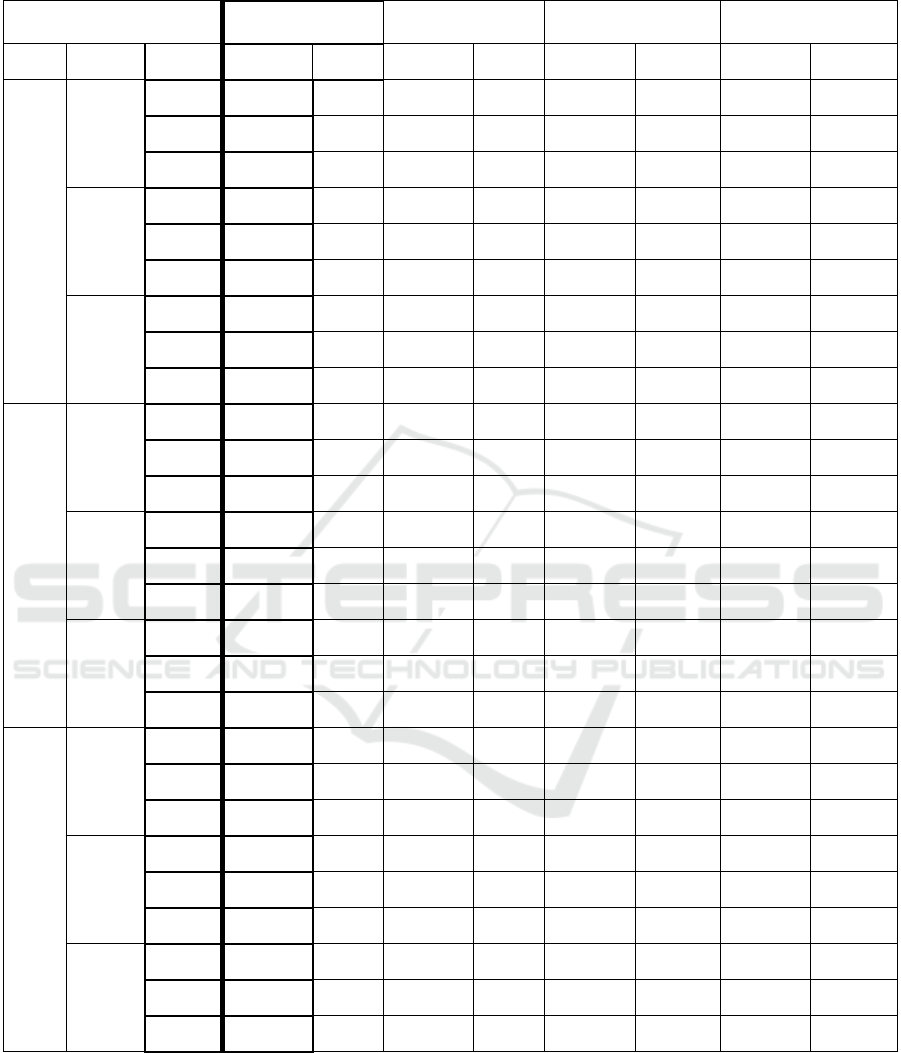
Table 1: Experimental results for Greedy and SynchroP.
Number of
Greedy with
SCC Method
Greedy
SynchroP with SCC
Method
SynchroP
States
SCCs
Inputs
Time(ms)
Length
Time(ms)
Length
Time(ms)
Length
Time(ms)
Length
256
2
2
3,12
35,84
5,71
38,08
60,39
32,18
388,23
31,92
4
4,06
20,66
7,66
22,22
46,88
17,94
373,22
17,9
8
6,72
29,64
12,72
29,94
53,68
24,54
495,94
23,74
4
2
2,02
31,96
6,617
36,47
5,26
30,6
380,11
29,38
4
2,38
22,26
8,66
23,72
5,78
19,2
405,3
18,58
8
3,1
23,9
11,82
23,76
7,92
19,86
487,72
19
8
2
1,21
30,15
6,71
36,40
1,44
28,52
405,35
27,71
4
1,62
19,4
10,08
21,64
1,76
17,9
422,72
16,6
8
2,7
19,82
17,58
20,5
2,42
17,48
477,72
15,7
512
2
2
13,8
44,88
23,52
46,18
472,28
38,7
4632,88
39,98
4
19,96
30,5
35,24
31,1
405,64
25,58
4968,16
25,56
8
27,88
45,36
48,66
46,2
485,92
37,04
6796,58
36,96
4
2
6,69
40,35
23,54
42,88
64,38
35,88
4704,10
34,67
4
8,46
23,7
33,08
24,74
50,36
20,3
4893,22
19,92
8
14,48
34,42
55,7
34,18
67
27,9
6023,2
26,98
8
2
3,79
35,542
24,48
41,83
7,98
33,94
4817,31
32,38
4
4,6
23,7
35
25,68
8,04
20,92
4920,16
20,42
8
7,56
25,8
59,34
26,58
11,16
22,02
5742,86
20,82
1024
2
2
48,88
47,22
73,86
46,78
6638,76
41,14
72047,02
41,32
4
65,16
32,36
101,26
32,8
5045,8
26,62
72164,72
26,42
8
96,94
62,7
141,84
62,46
6106,24
50,38
101063,7
49,94
4
2
26,08
46,74
81,56
49,18
510,16
41,92
69239,92
41,74
4
31,32
32,3
109,04
33,94
405,28
27,3
71939,54
26,86
8
46,96
46,08
160,54
47,2
467,24
38,62
85730
36,78
8
2
13,94
43,33
86,22
48,51
73,08
39,65
68696,92
39,31
4
15,88
24,42
115,74
26,72
62,94
22,08
72070,06
21,36
8
23,64
34,28
172,18
35,12
71,38
29,04
81185,02
28
The time improvements we obtain by using the
SCC method are expected. Greedy requires O(n
3
)
and SynchroP requires O(n
5
) time where n is the
number of states. Therefore, if one can divide the
automaton into pieces (components) in one way or
the other, and construct a synchronizing sequence
from the synchronizing sequences obtained for these
pieces, this approach would result in considerable
time savings. In this paper, we suggest that these
“pieces” can be the strongly connected components
MODELSWARD 2018 - 6th International Conference on Model-Driven Engineering and Software Development
550

Figure 7: SynchroP/SCC Method Time Ratio (Speedup)
Results of Automata’s with 256,512,1024 States and 2,4,8
SCC’s.
Figure 8: Greedy/SCC Method Time Ratio (Speedup)
Results of Automata’s with 256,512,1024 States and 2,4,8
SCC’s.
of the automaton. Because of the reasons above,
SCC method can make every heuristic faster as
shown in this paper. If there are k strongly connected
components with equal sizes, complexity of Greedy
and SynchroP becomes O(




 O(




,
respectively. Obviously, these are much faster
running times compared to original heuristics. In
practice, the running times differ as expected.
For future work, one direction is to improve our
synchronizing sequence lengths for the SCC method
when used with SynchroP. The direct application of
SynchroP algorithm performs a global analysis
compared to the local analysis performed when each
strongly connected component is analyzed
separately by our SCC method. Another direction of
research is to use the SCC method with other
synchronizing heuristics and to extend the
experiments to study the effects of aspects like
states, inputs, number of SCCs, and also the relative
size of SCCs, a factor which we did not take into
account in the experiments performed in this paper.
ACKNOWLEDGMENTS
This work was supported by The Scientific and
Technological Research Council of Turkey
(TUBITAK) [grant number 114E569].
REFERENCES
Chow, T.S., 1978. Testing software design modelled by
finite state machines. IEEE Transactions on Software
Engineering, 4:178-187.
Eppstein, D., 1990. Reset sequences for monotonic
automata. SIAM J. Comput. 19 (3), 500 - 510.
Hierons, R.M., Ural, H. 2006. Optimizing the length of
checking sequences. IEEE Transactions on
Computers. 55(5): 618-629.
Jourdan, G.V., Ural, H., Yenigün, H., 2015. Reduced
checking sequences using unreliable reset, Information
Processing Letters, 115(5), pp. 532-535.
Kudlacik, R., Roman, A., Wagner, H., 2012. Effective
synchronizing algorithms. Expert Systems with
Applications 39 (14), 11746-11757.
Lee, D., Yannakakis, M., 1996. Principles and methods of
testing finite state machines-a survey. Proceedings of
The IEEE, 84(8), 1090-1123.
Trahtman, A. N., 2004. Some results of implemented
algorithms of synchronization. In: 10th Journees
Montoises d'Inform.
Volkov, M.V., 2008. Synchronizing automata and the
Cerny conjecture. In Proceedings of the 3
rd
International Conference on Language and Automata
Theory and Applications, LATA’ 08, 11–27, 2008.
Using Structure of Automata for Faster Synchronizing Heuristics
551