Unbalanced Data Classification in Fraud Detection
by Introducing a Multidimensional Space Analysis
Roberto Saia
Department of Mathematics and Computer Science
University of Cagliari, Via Ospedale 72 - 09124 Cagliari, Italy
Keywords:
Business Intelligence, Fraud Detection, Data Imbalance, Pattern Mining, Metrics.
Abstract:
The problem of frauds is becoming increasingly important in this E-commerce age, where an enormous num-
ber of financial transactions are carried out by using electronic instruments of payment such as credit cards.
In this scenario it is not possible to adopt human-driven solutions due to the huge number of involved opera-
tions. The only approach is therefore to adopt automatic solutions able to discern the legitimate transactions
from the fraudulent ones. For this reason, today the development of techniques capable of carrying out this
task efficiently represents a very active research field that involves a large number of researchers around the
world. Unfortunately, this is not an easy task, since the definition of effective fraud detection approaches is
made difficult by a series of well-known problems, the most important of them being the non-balanced class
distribution of data that leads towards a significant reduction of the machine learning approaches performance.
Such limitation is addressed by the approach proposed in this paper, which exploits three different metrics of
similarity in order to define a three-dimensional space of evaluation. Its main objective is a better charac-
terization of the financial transactions in terms of the two possible target classes (legitimate or fraudulent),
facing the information asymmetry that gives rise to the problem previously exposed. A series of experiments
conducted by using real-world data with different size and imbalance level, demonstrate the effectiveness of
the proposed approach with regard to the state-of-the-art solutions.
1 INTRODUCTION
Many studies, such as those conducted by the
Euromonitor International
1
, indicate that the E-
commerce growth attracts fraudsters, as shown in Fig-
ure 1 that reports the total fraud levels in the Europe,
Middle East and Africa (EMEA) areas.
Considering the economic relevance of the frauds
events, is more and more crucial the research of ef-
fective fraud detection approaches able to face this
problem, reducing the economic losses as much as
possible. Unfortunately, the development of these ap-
proaches has to face some problems, the most impor-
tant of which is represented by the non-balanced dis-
tribution of data Japkowicz and Stephen (2002) that
characterizes the information usually available for the
definition of fraud detection models.
Other additional problems, such as the data
scarcity Assis et al. (2010); Ahmed et al. (2016), the
non-adaptability of the detection models Sorournejad
et al. (2016), the data heterogeneity Chatterjee and
1
http://www.euromonitor.com/
Segev (1991); Che et al. (2013), or the cold start Zhu
et al. (2008); Donmez et al. (2007) issue, contribute
to making the development of such approaches more
difficult.
The literature offers us a number of techniques
aimed to detect the fraudulent transactions in a fi-
nancial data flow. Some examples are those based
on the: Data Mining techniques to generate rules
on the basis of fraud patterns Lek et al. (2001); Ar-
tificial Intelligence techniques to detect anomalies
in the data Hoffman and Tessendorf (2005); Neu-
ral Networks techniques to design predictive mod-
els Gopinathan et al. (1998); Signature-based tech-
niques able to model the legitimate data Edge and
Sampaio (2009); Fuzzy Logic techniques that ex-
ploit the fuzzy analysis to perform fraud detection
tasks Lenard and Alam (2005); Decision Tree tech-
niques aimed to reduce the misclassifications Sahin
et al. (2013); Machine Learning techniques able to
generate predictions on the basis of multiple mod-
els Whiting et al. (2012); Zhang et al. (2011); Genetic
Programming techniques that exploit an Evolutionary
Saia, R.
Unbalanced Data Classification in Fraud Detection by Introducing a Multidimensional Space Analysis.
DOI: 10.5220/0006663000290040
In Proceedings of the 3rd International Conference on Internet of Things, Big Data and Security (IoTBDS 2018), pages 29-40
ISBN: 978-989-758-296-7
Copyright
c
 2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
29

2006 2008 2010 2012 2014 2016
1,250
1,500
1,750
Years
Millions o f euros
Figure 1: Total Fraud Level in EMEA.
Computation approach in order to detect frauds As-
sis et al. (2010); Statistical Inference techniques able
to detect frauds by adopting a Bayesian model Hooi
et al. (2016).
One of the limit shared by all these techniques is
the strategy they adopt to define an evaluation model,
which is usually based on an unique criterion applied
on the previous transactions collected by the fraud
detection systems. Such a way of proceeding leads
towards misclassifications, considering that the avail-
able data usually does not contain enough information
about all the transaction classes, due to the high level
of imbalance that characterizes them.
In several previous works Saia et al. (2015);
Saia and Carta (2017a); Saia (2017); Saia and Carta
(2017b) we studied the advantages and disadvantages
related to the adoption of proactive fraud detection
approaches as possible solution to mitigate the afore-
mentioned problems.
The main intuition on which this paper relies is
to perform the data analysis in a three-dimensional
space, which is given by three different metrics of
similarity. The objective we want to achieve is a better
characterization (with respect to the state-of-the-art
approaches) of each transaction in one of the two pos-
sible classes of destination (i.e., legitimate or fraudu-
lent).
The scientific contributions given by this paper are
as follows:
(i) formalization of three similarity metrics aimed
to compare different aspects of two transactions,
i.e., Transactions Global Similarity, Features
Local Similarity, and Features Global Similar-
ity metrics;
(ii) definition of a three-dimensional space given by
the aforementioned three metrics of similarity,
which allows us to well characterize each trans-
action with respect to the other ones;
(iii) formulation of an algorithm able to classify each
new transaction as legitimate or fraudulent by
performing its evaluation in the previously de-
fined three-dimensional space.
The paper is organized into the following sec-
tions: Section 2 introduces the background and re-
lated work; Section 3 provides a formal notation
and defines the faced problem; Section 4 describes
the proposed approach implementation; Section 5
gives details on the experimental environment, on the
adopted datasets and metrics, as well as on the used
strategy and the competitor approach, concluding by
discuss the experimental results; Section 6 provides
some concluding remarks and points to some further
directions for research.
2 BACKGROUND AND RELATED
WORK
This section introduces the fraud detection scenario
by starting with the description of strategies and ap-
proaches commonly used in this field, together with
the most important open problems. It continues by
exposing the idea that stands behind the proposed ap-
proach, concluding with a description of the state-of-
the-art competitor used to evaluate its performance.
2.1 Strategies and Approaches
A fraud detection system can operate by using two
different strategies Phua et al. (2010), supervised or
unsupervised:
• in the case of the supervised strategy, it takes into
account all the previous transactions (i.e., legiti-
mate and fraudulent) in the process of definition
of the evaluation model. Such strategy needs a
number of examples related to both the legitimate
and the fraudulent cases, and its capability is lim-
ited by the detection of patterns that were present
in the data used to train the evaluation model;
• the unsupervised strategy instead operates by
comparing the values of the features that com-
pose the transaction to evaluate to those present
in the legitimate cases previously collected by the
system. This strategy is often ineffective since
many fraudulent transactions do not have signifi-
cant variations in their feature values, with regard
to the legitimate ones. For this reason the develop-
ment of fraud detection approaches based on the
unsupervised strategy is not an easy task Gold-
stein and Uchida (2016).
Regardless of the adopted strategy, a fraud detec-
tion system can instead follow a static, updating, or
forgetting operative approach:
• the static approach Pozzolo et al. (2014) operates
by dividing the data into blocks of equal size and
IoTBDS 2018 - 3rd International Conference on Internet of Things, Big Data and Security
30

the evaluation model is defined by taking into ac-
count a certain number of initial and contiguous
blocks;
• the updating approach Wang et al. (2003) oper-
ates by updating the evaluation model at each new
block by using a defined number of latest and con-
tiguous blocks;
• the forgetting approach Gao et al. (2007) oper-
ates by updating the evaluation model when a new
block appears, by taking into account the legiti-
mate transactions in the last two blocks and all the
fraudulent transactions present in all the blocks.
The evaluation models defined by adopting the
aforementioned operative approaches can be used as
they are or they can be joined together in order to de-
fine a more complex evaluation model.
However, all the approaches lead toward several
issues, because the static approach is ineffective in
the modelization of the users behavior, the updat-
ing approach is ineffective when working with small
amounts of data, and the forgetting approach is char-
acterized by an excessive computational complexity.
2.2 Open Problems
This section reports the most common problems re-
lated to the fraud detection processes.
2.2.1 Data Scarcity
Frauds represent the biggest problem that affects the
E-commerce area, a problem worsened by the scarcity
of real-world datasets available for the research com-
munity Assis et al. (2010); Ahmed et al. (2016),
which are essential for the development of new fraud
detection techniques. This is a well-known problem
related to the restrictive policies commonly adopted
by those working in this field, financial operators that
for competitive or legal reasons do not want to release
information about their business and, above all, about
the frauds that they have suffered. It should be added
that such information is not even released in anony-
mous form, since even in this form they may reveal
potential vulnerabilities.
2.2.2 Model Non-adaptability
Another problem, which affect both the supervised
and unsupervised approaches, is related to the non-
adaptability of the detection models. This means that
the evaluation models do not lead toward good per-
formance when the transactions to evaluate are char-
acterized by unknown patterns (with regard to those
used to define the evaluation model) Sorournejad et al.
(2016).
2.2.3 Data Heterogeneity
The data heterogeneity problem is formally defined as
the incompatibility between similar features resulting
in the same data being represented differently in dif-
ferent datasets Chatterjee and Segev (1991); Che et al.
(2013), as it happens in the data involved in the fraud
detection processes.
2.2.4 Data Imbalance
Although the problems outlined above are also im-
portant, the crucial problem that has to be faced in
this field is the data imbalance. It is given by the
composition of the data available for the evaluation
model training, which is usually characterized by a
small number of fraudulent transactions and a large
number of legitimate ones.
This adversely affects the performance of the
canonical approaches of classification Japkowicz and
Stephen (2002); Brown and Mues (2012); He and
Garcia (2009), where such problem is usually faced
by performing a preliminary balance of data Vinciotti
and Hand (2003). It is performed by duplicating some
of the transactions that belong to the less numerous
class (over-sampling strategy) or by removing some
of the transactions that belong to the more numerous
class (under-sampling strategy). The effectiveness of
these balancing strategies is analyzed and discussed
in Marqu
´
es et al. (2013); Crone and Finlay (2012).
2.2.5 Cold-start
Another problem directly related to the data imbal-
ance is the cold-start one. It happens when the data
available for the definition of the evaluation model do
not contain enough information on all the classes of
data. This prevents the definition of an effective eval-
uation model, since the available information does not
represent all the possible classes of destinations (i.e.,
in our case, legitimate and fraudulent) Attenberg and
Provost (2010).
2.3 Proposed Approach
The proposed Multidimensional Similarity Space
(MSS) approach compares the transactions in a three-
dimensional space given by three different metrics of
similarity. The objective is to achieve a better char-
acterization of each transaction in the context of one
of the two possible classifications (i.e., legitimate or
fraudulent).
Unbalanced Data Classification in Fraud Detection by Introducing a Multidimensional Space Analysis
31

0.2
0.4
0.6
0.8
1.0
0.2
0.4
0.6
0.8
1.0
0.2
0.4
0.6
0.8
1.0
(0.5, 0.5, 0.5)
x
y
z
Figure 2: Three-dimensional Similarity Space.
Such metrics, described in detail later, allow us to
evaluate different aspects of the transactions, i.e., the
Transactions Global Similarity (T GS), the Features
Local Similarity (T LS), and the Features Global Sim-
ilarity (FLS).
They have been used to define, respectively, the X,
Y, and Z dimensions of our three-dimensional space,
where the similarity between two transactions is rep-
resented as a point placed at the X, Y, and Z coordi-
nates. This is shown in Figure 2, where the multi-
dimensional similarity between two transactions has
generated a point at the (X=0.5, Y=0.5, Z=0.5) coor-
dinates.
2.4 Competitor Approach
The state-of-the-art competitor we chose to evaluate
the performance of the proposed approach is Ran-
dom Forests Breiman (2001), since it outperforms the
other ones Brown and Mues (2012); Bhattacharyya
et al. (2011) in the fraud detection field, as indeed ex-
perimentally verified in Section Competitor).
Briefly, it works by growing many classification
trees, classifying a new transaction (in terms of vec-
tor of its features) by putting it at the bottom of each
one of the trees in the forest. Each tree provides a
classification (votes) and the final classification of the
transaction is given by the classification having the
most votes in the context of all the trees in the forest.
3 PRELIMINARIES
This section formalizes the notation used in this paper
and the problem faced by our approach.
3.1 Formal Notation
Given a set of classified transactions T =
{t
1
,t
2
, . . . ,t
N
}, we denote as T
+
the subset of le-
gitimate ones (then T
+
⊆ T ), and as T
−
the subset of
fraudulent ones (then T
−
⊆ T ).
Each transaction t ∈ T is composed by a set of
features V = {v
1
, v
2
, . . . , v
M
} and each transaction
can belong only to one class c ∈ C, where C =
{legitimate, f raudulent}.
We also denote a set of unclassified transactions
ˆ
T = {
ˆ
t
1
,
ˆ
t
2
, . . . ,
ˆ
t
U
}.
The aforementioned notation is for convenience
summarized in Table 1.
Table 1: Formal Notation.
Notation Description
T = {t
1
,t
2
, . . . , t
N
} Set of classified transactions
T
+
, with T
+
⊆ T Subset of legitimate transactions
T
−
, with T
−
⊆ T Subset of fraudulent transactions
V = {v
1
, v
2
, . . . , v
M
} Set of transaction features
ˆ
T = {
ˆ
t
1
,
ˆ
t
2
, . . . ,
ˆ
t
U
} Set of unclassified transactions
C = {legitimate, f raudulent} Set of possible classifications
3.2 Problem Definition
Initially, we denote as Φ the process of classification
made by our approach, which is aimed to classify an
unevaluated transaction
ˆ
t ∈
ˆ
T as legitimate or fraudu-
lent.
Subsequently, we define a function
Classi f icator(
ˆ
t, Φ) that returns a boolean value
β that indicates the correctness of the performed
classification made by Φ for the transaction
ˆ
t
(0=misclassification, 1=correct classification).
Finally, we formalize our problem as maximiza-
tion of the sum of the values returned by the
Classi f icator function, as shown in Equation 1.
max
0≤β≤|
ˆ
T |
β =
|
ˆ
T |
∑
u=1
Classi f icator(
ˆ
t
u
, Φ) (1)
4 PROPOSED APPROACH
Our approach has been implemented by following the
three steps summarized below and detailed later:
1. Metrics Definition: definition of three metrics
aimed to compare two transactions in terms of dif-
ferent similarity aspects, after we define the nature
of the data to be evaluated;
IoTBDS 2018 - 3rd International Conference on Internet of Things, Big Data and Security
32

2. Criteria Formalization: formalization of crite-
ria used to evaluate a new transaction in a three-
dimensional space given by the three metrics of
similarity previously defined;
3. Algorithm Formulation: formulation of an al-
gorithm based on our Multidimensional Similarity
Space (MSS) approach, able to classify each new
transaction as legitimate or fraudulent.
4.1 Metrics Definition
This section starts by defining the nature of the data
vectors taken into account during the evaluation pro-
cess, continuing by formalizing the three metrics in-
volved in such process. As introduced in Section 2.3,
these metrics give rise to the three-dimensional space
used to evaluated the similarity between two transac-
tions, as shown in Figure 2. They represent, respec-
tively, the X, Y, and Z dimensions of this space (i.e.,
X=TGS, Y=FLS, and Z=FGS).
4.1.1 Data Vectors
Equation 2 shows the matrix given by a series of trans-
actions, which in this case are those in the set T (i.e.,
then |T | = N). With regard to the first transaction,
we highlighted the vector of data (i.e., values in the
set V ) that will represent it in our Multidimensional
Similarity Space.
T =







v
1,1
v
1,2
. .. v
1,M
v
2,1
v
2,2
. .. v
2,M
.
.
.
.
.
.
.
.
.
.
.
.
v
N,1
v
N,2
. .. v
N,M







(2)
4.1.2 Transactions Global Similarity Metric
The first metric used in our approach is the Transac-
tions Global Similarity (T GS). It is not a novel metric,
since it coincides with the well known cosine similar-
ity metric, which is used to measure the global simi-
larity between two transaction vectors V
1
and V
2
(with
size larger than zero). More formally, given two trans-
action vectors V
1
and V
2
, it is calculated as shown in
the Equation 3. We normalized the result in a range
[0, 1], where 0 indicates two completely different vec-
tors and 1 two equal vectors.
T GS(V
1
,V
2
) =
V
1
·V
2
kV
1
k·kV
2
k
(3)
4.1.3 Features Local Similarity Metric
The Features Local Similarity (FLS) metric has been
designed in the context of the proposed approach in
order to measure the similarity between transactions
in terms of the weighted sequence of their features.
It relies on the consideration that similar transactions
are characterized by a similar weighted sequences of
features. This means that, if we sort their features on
the basis of their values, the obtained sequences of
their original indexes will be similar in terms of T GS
metric (i.e., cosine similarity). More formally, given
two transactions t
(1)
and t
(2)
we calculate the FLS
as shown in Equation 4, where V
(1)
and V
(2)
are the
transaction vectors to compare and the idx function re-
turns the sorted V in terms of former element indexes
(i.e., the indexes of the V elements before sorting).
FLS(V
(1)
,V
(2)
) = T GS

idx

V
(1)

, idx

V
(2)

with
V = {|v
1
| ≤ |v
2
| ≤ . . . ≤ |v
M
|}
(4)
4.1.4 Features Global Similarity Metric
The Features Global Similarity (FGS) is another met-
ric defined in the context of the proposed approach.
Its aim is the evaluation of the global difference be-
tween two transactions in terms of their feature val-
ues, measured between corresponding features of the
two transactions. It operates by following the same
criterion of the RMSE
2
metric, but in our metric the
obtained result has been normalized in a range [0, 1].
More formally, given two transactions
ˆ
t
(1)
and t
(2)
, the
FGS is calculated by considering the corresponding
vectors V
(1)
and V
(2)
, as shown in Equation 5, where
max(RMSE) is the maximum value assumed by RMSE in
the context of all the comparisons between V
(1)
and
all other vectors corresponding to all the transactions
in the set T .
FGS(V
(1)
,V
(2)
) = 1 −
RMSE
max(RMSE)
with
RMSE =
s
M
∑
m=1

v
(1)
m
− v
(2)
m

2
(5)
4.2 Criteria Formalization
A new transaction
ˆ
t ∈
ˆ
T is classified as legitimate or
fraudulent on the basis of a comparison process be-
tween it and all the transactions in the set T. Such
process is performed by using a threefold criterion of
similarity evaluation based on the three metrics previ-
ously described in Section 4.1 and a r value exper-
imentally defined in Section 5.4.2. More in detail,
2
Root Mean Squared Error
Unbalanced Data Classification in Fraud Detection by Introducing a Multidimensional Space Analysis
33

c
r
x (TGS)
y (FLS)
z (FGS)
legitimate cases fraudulent cases
Figure 3: Evaluation Space.
each new transaction
ˆ
t ∈
ˆ
T is classified on the basis
of the following three criteria:
(i) we define a center c in our three-dimensional
space, as shown in Figure 3, by using as coor-
dinates X, Y, and Z, respectively, max(T GS) −r,
max(FLS) − r, and max(FGS) − r, all of them
calculated between the transaction
ˆ
t to evaluate
and all the transactions in the set T ;
(ii) the classification of the transaction
ˆ
t depends on
the nature (legitimate or fraudulent) of the trans-
actions in the set T bounded by the sphere of
radius r and center c;
(iii) a new transaction is classified as legitimate if the
number of legitimate transactions in T
+
bounded
by this sphere is greater than that of the fraud-
ulent ones in T
−
, otherwise it is classified as
fraudulent.
By way of example, Figure 3 shows a case where
the evaluated transaction
ˆ
t has been classified as
fraudulent, because the number of fraudulent trans-
actions in T
−
bounded by the sphere of radius r and
center c is greater than that of the legitimate ones in
T
+
.
It should be noted that such evaluation process
adopts a prudential criterion, since the cases with
equal number of legitimate and fraudulent transac-
tions bounded by the sphere lead toward a classifi-
cation of the
ˆ
t transaction as fraudulent.
4.3 Algorithm Formulation
The classification Algorithm 1 takes as input the set
of previous transactions T , an unevaluated transac-
tion
ˆ
t ∈
ˆ
T , and the radius value r. It returns as
output a result value that provides the classification
given to the transaction
ˆ
i (i.e., a boolean value, with
true=legitimate and false=fraudulent).
It should be observed that when we refer to trans-
actions in the
ˆ
T and T sets, we refer to their respective
vectors composed by the values of the features (i.e.,
set V ).
Algorithm 1: Transaction classification.
Input: T =Previous transactions,
ˆ
t=Unevaluated transaction, r=Radius
Output: result=Transaction
ˆ
t classification
1: procedure CLASSIFICATION(T ,
ˆ
t, r)
2: cx ← (getMaxTGS(T,
ˆ
t) −r)
3: cy ← (getMaxF LS(T,
ˆ
t) −r)
4: cz ← (getMaxF GS(T,
ˆ
t) −r)
5: for each t in T do
6: s1 ← getT GS(
ˆ
t, t)
7: s2 ← getFLS(
ˆ
t, t)
8: s3 ← getFGS(
ˆ
t, t)
9: if (s1 ≥ (cx −r) ∧ s1 ≤ (cx + r)) ∧
10: (s2 ≥ (cy −r) ∧ s2 ≤ (cy + r)) ∧
11: (s3 ≥ (cz −r) ∧ s3 ≤ (cz + r)) then
12: if getClass(t) == legitimate then
13: lclass ← lclass + 1
14: else
15: f class ← f class +1
16: end if
17: end if
18: end for
19: if lclass > f class then
20: result ← true
21: else
22: result ← f alse
23: end if
24: return result
25: end procedure
The classification process is performed through
the Algorithm 1. It starts by calculating the max value
of the TGS, FLS, and FGT, between the transaction
ˆ
t and those of all the transactions in T, defining the
cx, cy, and cz centers to use in our evaluation process
(steps from 2 to 4).
From step 5 to 18 it calculates TGS, FLS, and FGT
between each transaction t ∈ T and the transaction
ˆ
t
under evaluation.
If the obtained values are, respectively, within the
cx ± r, cy ± r, and cz ± r bounds, in the steps from
12 to 16 it increases the lclass (if the instance t is
classified as legitimate) or the fclass (if the instance t
is classified as fraudulent) by one unit.
At the end of the previous process, in the steps
from 19 to 23 the transaction
ˆ
i is classified as legiti-
mate (true value) if the value of lclass is greater than
fclass, otherwise the transaction is classified as fraud-
ulent (false value).
The algorithm returns the classification at the step
24 through the boolean value result.
IoTBDS 2018 - 3rd International Conference on Internet of Things, Big Data and Security
34

5 EXPERIMENTS
This section provides information on the development
environment, on the adopted real-world dataset, as
well as on the evaluation metrics, the followed strat-
egy, and the state-of-the-art approach used as com-
petitor, reporting and discussing the experimental re-
sults at the end.
5.1 Environment
Our approach has been developed in Java by us-
ing the Waikato Environment for Knowledge Analysis
(W EKA)
3
library to implement the competitor state-
of-the-art approaches.
5.2 DataSet
This section describes the real-world dataset used for
the experiments, together with the criteria used to per-
form this operation.
5.2.1 Description
The adopted dataset is composed by a series of credit
card transactions made by European cardholders
4
.
It contains the transactions made in two days of
September 2013, i.e., 492 fraudulent transactions and
284,807 legitimate ones, and it represents an highly
unbalanced dataset Pozzolo et al. (2015), considering
that the fraudulent transactions are only the 0.0017%
of the total.
All dataset features are provided in an anonymous
form for privacy reasons, except the Amount and Time
ones. The first one indicates the total amount of
the transaction, while the second one the number of
seconds elapsed between it and the first transaction
stored in the dataset. We chose not to use the Time
information in order to operate without any reference
to the original transaction sequence.
5.2.2 Criteria
By keeping the number of fraudulent transactions
fixed (i.e., all of them), we create several subsets with
10000, 20000, . . . ,240000 legitimate transactions, in
order to reproduce several real-world scenarios with
different levels of data imbalance. Each dataset
has been randomly shuffled before its use and all
the experiments have been performed by following
the k-fold cross-validation criterion described in Sec-
tion 5.4.
3
http://www.cs.waikato.ac.nz/ml/weka/
4
https://www.kaggle.com/dalpozz/creditcardfraud
The characteristics of each dataset are reported
in Table 2, where the size indicates the number
of legitimate transactions and the data imbalance
is expressed in terms of percentage of fraudulent
transactions.
Table 2: Datasets.
Dataset Fraudulent Dataset Fraudulent Dataset Fraudulent
size cases (%) size cases (%) size cases (%)
10K 0.04920 90K 0.00547 170K 0.00289
20K 0.02460 100K 0.00492 180K 0.00273
30K 0.01640 110K 0.00447 190K 0.00259
40K 0.01230 120K 0.00410 200K 0.00246
50K 0.00984 130K 0.00378 210K 0.00234
60K 0.00820 140K 0.00351 220K 0.00224
70K 0.00703 150K 0.00328 230K 0.00214
80K 0.00615 160K 0.00289 240K 0.00205
5.3 Metrics
This section introduces and explains the metrics
adopted to evaluate the performance of our approach
and that of its competitor.
5.3.1 Specificity
The Specificity metric, also known as True Negative
Rate (T NR), is mainly driven by the number of trans-
actions correctly classified as fraudulent. More for-
mally, it is calculated as shown in Equation 6, where
ˆ
T , T N, and FP are, respectively, the set of new
transactions to classify, the number of transactions
correctly classified as fraudulent, and the number of
fraudulent transactions erroneously classified as legit-
imate).
Speci f icity(
ˆ
T ) =
T N
(T N + FP)
(6)
5.3.2 F-score
The F-score metric represents the weighted average
of the precision and recall metrics. It is largely used to
evaluate the binary classifiers performance when they
work with unbalanced datasets Pozzolo et al. (2015).
Its result is in the range [0, 1], where 1 denotes the
best performance. More formally, it is calculated as
shown in Equation 7, where the set
ˆ
T
1
contains the
predicted classifications and the set
ˆ
T
2
contains the
actual classifications of them.
F-score(
ˆ
T
1
,
ˆ
T
2
) = 2 ·
(precision(
ˆ
T
1
,
ˆ
T
2
) ·recall(
ˆ
T
1
,
ˆ
T
2
))
(precision(
ˆ
T
1
,
ˆ
T
2
) +recall(
ˆ
T
1
,
ˆ
T
2
))
with
precision(
ˆ
T
1
,
ˆ
T
2
) =
|
ˆ
T
2
∩
ˆ
T
1
|
|
ˆ
T
1
|
, recall(
ˆ
T
1
,
ˆ
T
2
) =
|
ˆ
T
2
∩
ˆ
T
1
|
|
ˆ
T
2
|
(7)
Unbalanced Data Classification in Fraud Detection by Introducing a Multidimensional Space Analysis
35

5.3.3 Area Under ROC Curve
The Area Under the Receiver Operating Character-
istic curve (AUC) is a metric used to evaluate the
performance of a classification model Powers (2011);
Faraggi and Reiser (2002). More formally, given the
subsets of the previous legitimate transactions T
+
and
the previous fraudulent ones I
−
, it works as shown in
Equation 8, where Ψ denotes all the possible compar-
isons between the transactions in the subsets T
+
and
T
−
. The result is in the range [0, 1] (where 1 indicates
the best performance) and it is obtained by the aver-
age of all these comparisons.
Ψ(i
+
, i
−
) =









1, i f i
+
> i
−
0.5, i f i
+
= i
−
0, i f i
+
< i
−
AUC =
1
|I
+
|·|I
−
|
|I
+
|
∑
1
|I
−
|
∑
1
Ψ(i
+
, i
−
) (8)
5.4 Strategy
This section gives some details about the criterion
adopted to evaluate our approach, defining also the
optimal value of the sphere radius r .
5.4.1 Cross-validation
All the performed experiments have been conducted
by adopting the k-fold cross-validation criterion, with
k=10. The dataset has been divided in k subsets, and
each k subset has been used as test set, while the other
k-1 subsets have been used as training set, considering
as final result the average of all the obtained results.
It was made to improve the worth of the obtained
results, since through this criterion we reduce the im-
pact of data dependency. The original dataset has
been divided into k subset by using an R
5
script, and
the obtained training and test sets have been used to
evaluate both our approach and its competitor RF.
The experimental results have been analyzed by
using the independent-samples two-tailed Student's t-
tests (p < 0.05), in order to verify the existence of a
statistical significance between them.
5.4.2 Sphere Radius Definition
The Algorithm 1 previously formalized in Section 4.3
needs the definition of the radius r value, since its per-
formance depends on it.
We obtained it by performing a series of experi-
ments where we tested a wide range of possible values
in the context of the set T , by adopting during this op-
eration the k-fold cross-validation criterion described
in Section 5.4.1.
5
https://www.r-project.org/
The results indicate 0.026 as the optimal value of
r, since it leads towards the best performance in terms
of Specificity, F-score, and AUC metrics.
5.5 Competitor
We use Random Forest as the competitor approach,
because the literature indicates it as the most per-
forming one for binary classification tasks with unbal-
anced data Brown and Mues (2012); Bhattacharyya
et al. (2011). In any case, we have nevertheless car-
ried out a preliminary study by involving ten differ-
ent state-of-the-art approaches designed to perform
binary classification tasks, i.e., Naive Bayes, Logit
Boost, Logistic Regression, Stochastic Gradient De-
scent, Multilayer Perceptron, Voted Perceptron, Ran-
dom Tree, K-nearest, Decision Tree, and Random
Forests.
The results shown in Table 3 confirm Random
Forests as the most performing approach in terms
of AUC metric, a metric able to evaluate the overall
performance of the evaluation model Sobehart and
Keenan (2001).
Table 3: Competitors Performance.
Approach AUC Approach AUC
Naive Bayes 0.789 Logit Boost 0.796
Logistic Regression 0.794 SGD 0.747
Multilayer Perceptron 0.792 Voted Perceptron 0.713
Random Tree 0.751 K-nearest 0.764
Decision Tree 0.761 Random Forests 0.799
5.5.1 Parameter Tuning
Despite the fact that Random Forests usually gets
better performance also without a preliminary tuning
process, we preferred to perform this activity in order
to maximize its performance.
Considering that, with respect to the WEKA de-
fault parameters, we get significant variations of the
Random Forests performance only by varying the
number of randomly chosen attributes, we tuned only
this parameter.
Such activity involved both the training and test
sets in order to overcome the overfitting problem,
adopting the cross-validation criterion previous ex-
posed in Section 5.4.1. The results indicates 8 as the
optimal number of randomly chosen attributes.
IoTBDS 2018 - 3rd International Conference on Internet of Things, Big Data and Security
36

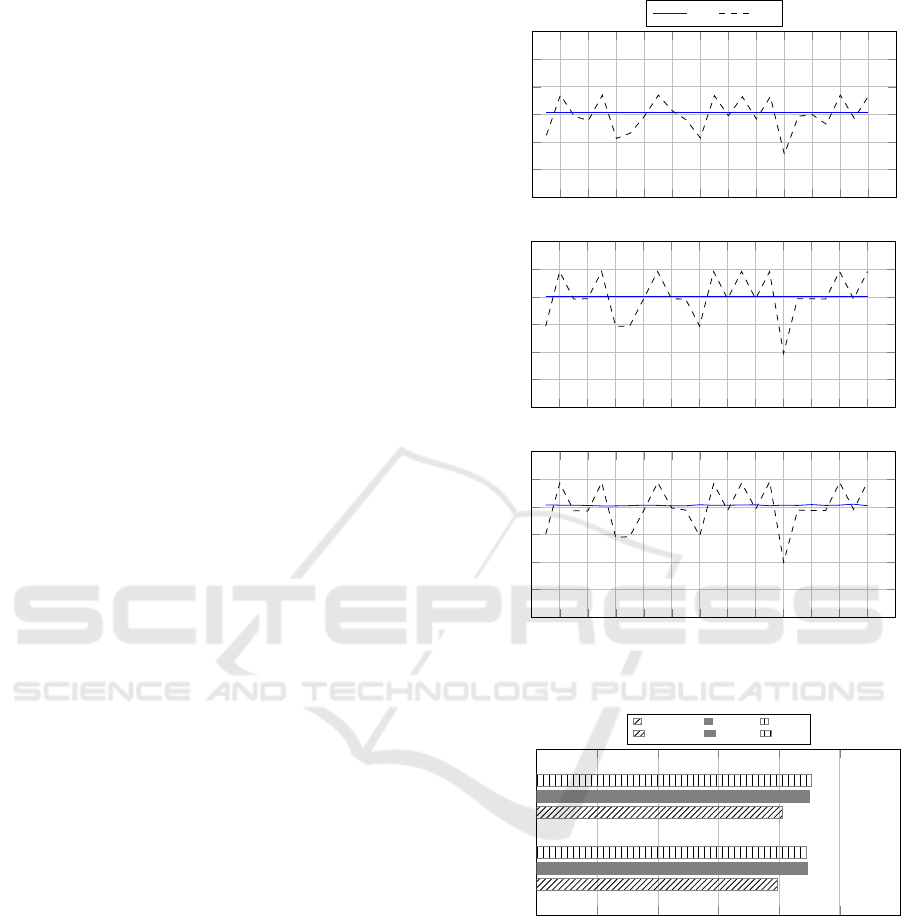
5.6 Results
The experimental results are presented and discussed
in this section, initially through a brief description and
then with a more in-depth analysis.
5.6.1 Overview
From a first analysis of the results reported in Figure 4
arises the following general considerations:
• Figure 4.a shows that, in comparison to its com-
petitor RF, the proposed MSS approach con-
stantly maintains good performance in terms of
Specificity. This indicates its capability in the de-
tection of the fraudulent transactions, regardless
of the number of transactions involved in the eval-
uation model definition and the level of data im-
balance;
• Figure 4.b shows that the proposed MSS approach
constantly maintains good performance in terms
of F-score, differently from its competitor RF.
This indicates its capability to reach a good bal-
ance between Precision and Recall performances,
regardless of the size of data and the level of im-
balance of them;
• Figure 4.c shows that also in terms of AUC the
proposed MSS approach reaches and maintains
good performance, with regard to its competitor
RF. This indicates the capability of its evaluation
model to work well with different data configura-
tions, in terms of their size and level of imbalance.
5.6.2 Discussion
An in-depth analysis of the results introduced in the
previous Section 5.6.1 has given rise to the following
observations:
• the first observation is tied to the capability shown
by our MSS approach to keep constant its perfor-
mance, regardless of the size and the level of data
imbalance. This mainly depends on its operative
strategy, which is able to better characterize the
transactions through a multidimensional space of
evaluation less influenced by the size and the level
of data imbalance;
• the second observation is closely related to the
first one, because the MSS constancy in the per-
formance is related to all the metrics taken into
account (i.e., Specificity, F-score, and AUC). This
represents an additional confirmation of the MSS
capability to better characterize the transactions
in our multidimensional space of evaluation based
on three different similarity metrics;
20 40
60
80 100 120 140
160
180 200 220 240
0.60
0.70
0.80
0.90
1.00
(a)
Dataset size (×1000)
Speci f icity
MSS
RF
20 40
60
80 100 120 140
160
180 200 220 240
0.60
0.70
0.80
0.90
1.00
(b)
Dataset size (×1000)
F-score
20 40
60
80 100 120 140
160
180 200 220 240
0.60
0.70
0.80
0.90
1.00
(c)
Dataset size (×1000)
AUC
Figure 4: Speci f icity, F-score, and AUC Per f ormance.
0.20 0.40
0.60
0.80 1.00
RF
MSS
0.79
0.81
0.89
0.9
0.89
0.91
Value
Approaches
Specificity
F-score
AUC
Figure 5: Average Per f ormance.
• the results in terms of Specificity metric, shown
in Figure 4.a, indicate a better capability of the
proposed MSS approach (with respect to its com-
petitor RF) to operate in different real-world sce-
narios. This shows its ability to correctly clas-
sify the new fraudulent transactions, regardless
of the number of instances available to build its
evaluation model and their levels of imbalance. It
should be emphasized how this aspect is crucial in
a real-world scenario, where the capability to de-
tect fraudulent transactions represents the primary
Unbalanced Data Classification in Fraud Detection by Introducing a Multidimensional Space Analysis
37

objective of any fraud detection system;
• the results in terms of F-measure metric, shown in
Figure 4.b, give us an important information about
our MSS approach for what concerns its combined
performance in terms of precision and recall met-
rics. They indicate the MSS capability to prop-
erly classify the new transactions with regard to
both the number of all classifications made and
the number of them that should have been made;
• another observation is related to the AUC results.
This is a metric able to evaluate the performance
of a binary classifier and the results shown in
Figure 4.c indicate the effectiveness of the MSS
model of evaluation, compared to that of its com-
petitor RF. In fact, it leads towards good and
constant performance that is not influenced by the
size and degree of imbalance of data;
• the average performance reported in Figure 5
shows how our MSS approach outperform its
competitor RF in terms of all the three metrics
taken into account. It follows that its adoption in
real-world applications can reduce the losses re-
lated to the fraudulent use of credit cards, more
effectively than its state-of-the-art competitors.
6 CONCLUSIONS AND FUTURE
WORK
Nowadays, the fraud detection approaches play a cru-
cial role for many financial operators, since they allow
them to reduce the losses related to the fraudulent use
of the electronic instruments of payment, first of all
the credit cards.
This occurs because, unlike the past, the enormous
number of financial transactions carried out in the E-
commerce area by using such instruments of payment
no longer allows the use of manual approaches based
on the human intervention.
In this context, however, it should be observed
that the development of effective fraud detection ap-
proaches is not a simple task due to several well-
known problems, first of all, the data imbalance in the
information available to define their evaluation mod-
els.
The Multidimensional Similarity Space approach
proposed in this paper faces this problem by analyzing
the transactions in a three-dimensional space, which
is defined in terms of three different metrics of simi-
larity. Its objective is a better characterization of each
transaction in one of the two possible classes of des-
tination (i.e., legitimate or fraudulent).
The experimental results show that our approach
outperforms its state-of-the-art competitor in the con-
text of several real-world scenarios, which reproduce
different size and degree of data imbalance.
Considering that the credit card fraud detection
represents only one of the possible contexts where our
approach can operate, a future work will be oriented
to experiment it in other scenarios characterized by
a high degree of data imbalance. Another interest-
ing future work would be the experimentation of ad-
ditional metrics of similarity in order to improve the
effectiveness of our classification approach.
ACKNOWLEDGEMENTS
This research is partially funded by Regione Sardegna
under project Next generation Open Mobile Apps
Development (NOMAD), Pacchetti Integrati di
Agevolazione (PIA) - Industria Artigianato e Servizi -
Annualit
`
a 2013.
REFERENCES
Ahmed, M., Mahmood, A. N., and Islam, M. R. (2016).
A survey of anomaly detection techniques in finan-
cial domain. Future Generation Computer Systems,
55:278–288.
Assis, C., Pereira, A. M., de Arruda Pereira, M., and Car-
rano, E. G. (2010). Using genetic programming to
detect fraud in electronic transactions. In Prazeres,
C. V. S., Sampaio, P. N. M., Santanch
`
e, A., Santos, C.
A. S., and Goularte, R., editors, A Comprehensive Sur-
vey of Data Mining-based Fraud Detection Research,
volume abs/1009.6119, pages 337–340.
Attenberg, J. and Provost, F. J. (2010). Inactive learn-
ing?: difficulties employing active learning in prac-
tice. SIGKDD Explorations, 12(2):36–41.
Bhattacharyya, S., Jha, S., Tharakunnel, K. K., and West-
land, J. C. (2011). Data mining for credit card fraud:
A comparative study. Decision Support Systems,
50(3):602–613.
Breiman, L. (2001). Random forests. Machine Learning,
45(1):5–32.
Brown, I. and Mues, C. (2012). An experimental compari-
son of classification algorithms for imbalanced credit
scoring data sets. Expert Syst. Appl., 39(3):3446–
3453.
Chatterjee, A. and Segev, A. (1991). Data manipulation
in heterogeneous databases. ACM SIGMOD Record,
20(4):64–68.
Che, D., Safran, M. S., and Peng, Z. (2013). From big
data to big data mining: Challenges, issues, and op-
portunities. In Hong, B., Meng, X., Chen, L., Wini-
warter, W., and Song, W., editors, Database Sys-
tems for Advanced Applications - 18th International
IoTBDS 2018 - 3rd International Conference on Internet of Things, Big Data and Security
38

Conference, DASFAA 2013, International Workshops:
BDMA, SNSM, SeCoP, Wuhan, China, April 22-25,
2013. Proceedings, volume 7827 of Lecture Notes in
Computer Science, pages 1–15. Springer.
Crone, S. F. and Finlay, S. (2012). Instance sampling in
credit scoring: An empirical study of sample size
and balancing. International Journal of Forecasting,
28(1):224–238.
Donmez, P., Carbonell, J. G., and Bennett, P. N. (2007).
Dual strategy active learning. In ECML, volume 4701
of Lecture Notes in Computer Science, pages 116–
127. Springer.
Edge, M. E. and Sampaio, P. R. F. (2009). A survey of
signature based methods for financial fraud detection.
Computers & Security, 28(6):381–394.
Faraggi, D. and Reiser, B. (2002). Estimation of the area un-
der the roc curve. Statistics in medicine, 21(20):3093–
3106.
Gao, J., Fan, W., Han, J., and Yu, P. S. (2007). A general
framework for mining concept-drifting data streams
with skewed distributions. In Proceedings of the Sev-
enth SIAM International Conference on Data Min-
ing, April 26-28, 2007, Minneapolis, Minnesota, USA,
pages 3–14. SIAM.
Goldstein, M. and Uchida, S. (2016). A comparative eval-
uation of unsupervised anomaly detection algorithms
for multivariate data. PloS one, 11(4):e0152173.
Gopinathan, K. M., Biafore, L. S., Ferguson, W. M.,
Lazarus, M. A., Pathria, A. K., and Jost, A. (1998).
Fraud detection using predictive modeling. US Patent
5,819,226.
He, H. and Garcia, E. A. (2009). Learning from imbalanced
data. IEEE Trans. Knowl. Data Eng., 21(9):1263–
1284.
Hoffman, A. J. and Tessendorf, R. E. (2005). Artificial in-
telligence based fraud agent to identify supply chain
irregularities. In Hamza, M. H., editor, IASTED In-
ternational Conference on Artificial Intelligence and
Applications, part of the 23rd Multi-Conference on
Applied Informatics, Innsbruck, Austria, February 14-
16, 2005, pages 743–750. IASTED/ACTA Press.
Hooi, B., Shah, N., Beutel, A., G
¨
unnemann, S., Akoglu,
L., Kumar, M., Makhija, D., and Faloutsos, C. (2016).
BIRDNEST: bayesian inference for ratings-fraud de-
tection. In Venkatasubramanian, S. C. and Jr., W. M.,
editors, Proceedings of the 2016 SIAM International
Conference on Data Mining, Miami, Florida, USA,
May 5-7, 2016, pages 495–503. SIAM.
Japkowicz, N. and Stephen, S. (2002). The class imbal-
ance problem: A systematic study. Intell. Data Anal.,
6(5):429–449.
Lek, M., Anandarajah, B., Cerpa, N., and Jamieson, R.
(2001). Data mining prototype for detecting e-
commerce fraud. In Smithson, S., Gricar, J., Pod-
logar, M., and Avgerinou, S., editors, Proceedings of
the 9th European Conference on Information Systems,
Global Co-operation in the New Millennium, ECIS
2001, Bled, Slovenia, June 27-29, 2001, pages 160–
165.
Lenard, M. J. and Alam, P. (2005). Application of fuzzy
logic fraud detection. In Khosrow-Pour, M., editor,
Encyclopedia of Information Science and Technology
(5 Volumes), pages 135–139. Idea Group.
Marqu
´
es, A. I., Garc
´
ıa, V., and S
´
anchez, J. S. (2013). On the
suitability of resampling techniques for the class im-
balance problem in credit scoring. JORS, 64(7):1060–
1070.
Phua, C., Lee, V. C. S., Smith-Miles, K., and Gayler, R. W.
(2010). A comprehensive survey of data mining-based
fraud detection research. CoRR, abs/1009.6119.
Powers, D. M. (2011). Evaluation: from precision, recall
and f-measure to roc, informedness, markedness and
correlation.
Pozzolo, A. D., Caelen, O., Borgne, Y. L., Waterschoot, S.,
and Bontempi, G. (2014). Learned lessons in credit
card fraud detection from a practitioner perspective.
Expert Syst. Appl., 41(10):4915–4928.
Pozzolo, A. D., Caelen, O., Johnson, R. A., and Bontempi,
G. (2015). Calibrating probability with undersampling
for unbalanced classification. In IEEE Symposium Se-
ries on Computational Intelligence, SSCI 2015, Cape
Town, South Africa, December 7-10, 2015, pages
159–166. IEEE.
Sahin, Y., Bulkan, S., and Duman, E. (2013). A cost-
sensitive decision tree approach for fraud detection.
Expert Syst. Appl., 40(15):5916–5923.
Saia, R. (2017). A discrete wavelet transform approach to
fraud detection. In Yan, Z., Molva, R., Mazurczyk,
W., and Kantola, R., editors, Network and System
Security - 11th International Conference, NSS 2017,
Helsinki, Finland, August 21-23, 2017, Proceedings,
volume 10394 of Lecture Notes in Computer Science,
pages 464–474. Springer.
Saia, R., Boratto, L., and Carta, S. (2015). Multiple be-
havioral models: A divide and conquer strategy to
fraud detection in financial data streams. In Fred, A.
L. N., Dietz, J. L. G., Aveiro, D., Liu, K., and Fil-
ipe, J., editors, KDIR 2015 - Proceedings of the Inter-
national Conference on Knowledge Discovery and In-
formation Retrieval, part of the 7th International Joint
Conference on Knowledge Discovery, Knowledge En-
gineering and Knowledge Management (IC3K 2015),
Volume 1, Lisbon, Portugal, November 12-14, 2015,
pages 496–503. SciTePress.
Saia, R. and Carta, S. (2017a). Evaluating credit card trans-
actions in the frequency domain for a proactive fraud
detection approach. In Samarati, P., Obaidat, M. S.,
and Cabello, E., editors, Proceedings of the 14th Inter-
national Joint Conference on e-Business and Telecom-
munications (ICETE 2017) - Volume 4: SECRYPT,
Madrid, Spain, July 24-26, 2017., pages 335–342.
SciTePress.
Saia, R. and Carta, S. (2017b). A frequency-domain-based
pattern mining for credit card fraud detection. In Ra-
machandran, M., Mu
˜
noz, V. M., Kantere, V., Wills,
G., Walters, R. J., and Chang, V., editors, Proceed-
ings of the 2nd International Conference on Inter-
net of Things, Big Data and Security, IoTBDS 2017,
Porto, Portugal, April 24-26, 2017, pages 386–391.
SciTePress.
Unbalanced Data Classification in Fraud Detection by Introducing a Multidimensional Space Analysis
39

Sobehart, J. and Keenan, S. (2001). Measuring default ac-
curately. Risk Magazine.
Sorournejad, S., Zojaji, Z., Atani, R. E., and Monadjemi,
A. H. (2016). A survey of credit card fraud detection
techniques: Data and technique oriented perspective.
CoRR, abs/1611.06439.
Vinciotti, V. and Hand, D. J. (2003). Scorecard construc-
tion with unbalanced class sizes. Journal of Iranian
Statistical Society, 2(2):189–205.
Wang, H., Fan, W., Yu, P. S., and Han, J. (2003). Mining
concept-drifting data streams using ensemble classi-
fiers. In Getoor, L., Senator, T. E., Domingos, P. M.,
and Faloutsos, C., editors, Proceedings of the Ninth
ACM SIGKDD International Conference on Knowl-
edge Discovery and Data Mining, Washington, DC,
USA, August 24 - 27, 2003, pages 226–235. ACM.
Whiting, D. G., Hansen, J. V., McDonald, J. B., Albrecht,
C. C., and Albrecht, W. S. (2012). Machine learning
methods for detecting patterns of management fraud.
Computational Intelligence, 28(4):505–527.
Zhang, L., Yang, J., Chu, W., and Tseng, B. L. (2011).
A machine-learned proactive moderation system for
auction fraud detection. In Macdonald, C., Ounis, I.,
and Ruthven, I., editors, Proceedings of the 20th ACM
Conference on Information and Knowledge Manage-
ment, CIKM 2011, Glasgow, United Kingdom, Octo-
ber 24-28, 2011, pages 2501–2504. ACM.
Zhu, J., Wang, H., Yao, T., and Tsou, B. K. (2008). Active
learning with sampling by uncertainty and density for
word sense disambiguation and text classification. In
Scott, D. and Uszkoreit, H., editors, COLING 2008,
22nd International Conference on Computational Lin-
guistics, Proceedings of the Conference, 18-22 August
2008, Manchester, UK, pages 1137–1144.
IoTBDS 2018 - 3rd International Conference on Internet of Things, Big Data and Security
40