
Autonomous Vehicle Simulation Model to Assess Potential Collisions
to Reduce Severity of Impacts
Alex Gilbert
1
, Dobrila Petrovic
1
, Kevin Warwick
1
and Vasilis Serghi
2
1
Coventry University, Faculty of Engineering, Environment and Computing, U.K.
2
Jaguar Land Rover, Autonomous Vehicle Control, U.K.
Keywords: Autonomous Vehicles, Collision Avoidance/Mitigation, Lane-Change Manoeuvre, Simulation Model.
Abstract: Autonomous vehicle safety has received much attention in recent years. Autonomous vehicles will improve
road safety by eliminating human errors. However, not all automotive collisions can be avoided. A strategy
needs to be developed in the event when an autonomous vehicle encounters an unavoidable collision.
Furthermore, the vehicle will need to take responsibility for the safety of its occupants, as well as any other
individuals, who may be affected by the vehicle’s behaviour.
This paper proposes a control system to assist an autonomous vehicle to make a decision to reduce the risks
to occupants potentially involved in highway motorway collisions. Before any decision can be made, the
potential collisions need to be assessed for their effects. A quick and numerical method for evaluation of
impact of potential collisions was developed. Assessing the Kinetic Energy of the vehicles before and after
collisions is proposed as a method to assess the severity of collisions. A simulation model developed
calculates the kinetic energy values and recommends an autonomous vehicle the motorway lane to drive
into to cause the least severe collision impact. Different scenarios are defined and used to test the simulation
model. The results obtained are promising and in line with the decision made by the subject expert.
1 INTRODUCTION
Autonomous vehicles is a major research area in
automotive engineering, as research organisations
and manufacturers have devoted a significant
amount of attention to developing this subject.
Models based on Automatic Emergency Braking
have been developed and assessed, (Geronimi, S.,
Abadie, V., and Becker, N., (2016)). Furthermore,
there is a significant amount of research which has
been dedicated to collision avoidance (Harper, C. D.,
Hendrickson, C. T., and Samaras, C., (2016)). Lane-
change manoeuvres have been assessed in collision
avoidance methods (Cesari, G., et al. (2017)). It may
not be possible to prevent all collisions, so attention
needs to focus on what the vehicle can do when a
collision is unavoidable. A new simulation model is
developed which uses a simplified non-dynamic
vehicle modelling to recommend an appropriate
action to take to avoid or mitigate the collision. This
approach is developed as an evolution to current
Adaptive Cruise Control systems.
The paper is organised as follows. Section 2
discusses existing research in the field of
autonomous vehicle collision avoidance and
collision prediction simulation. Section 3 describes a
considered research problem. Section 4 includes the
calculations used by the simulation model while
Section 5 discusses the development and
implementation of the simulation model. Section 6
defines scenarios used to validate the model and
analyses the results obtained. Section 7 concludes
the results, and Section 8 highlights the next phase
of the research.
2 BACKGROUND
A number of different trajectory planning algorithms
have been developed. Anderson et al. (2010)
developed an iterative method to evaluate upcoming
hazards, and adjust vehicle control to produce the
“best-case” vehicle path through the environment.
The framework proposed is semi-autonomous and
includes a human driver. Ammoun and Nashashibi
(2009) developed a method for predicting the
severity of collisions at crossroad junctions by
calculating a time-to-collision, its duration and a
Gilbert, A., Petrovic, D., Warwick, K. and Serghi, V.
Autonomous Vehicle Simulation Model to Assess Potential Collisions to Reduce Severity of Impacts.
DOI: 10.5220/0006663102430250
In Proceedings of the 4th International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS 2018), pages 243-250
ISBN: 978-989-758-293-6
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
243

percentage of area of the vehicle that intersects with
another vehicle’s area, using a dynamic model to
assess vehicle behaviour in predicting the collision.
However, t a problem considered in this paper
requires the severity of the collision impact to be
calculated
. Ammoun and Nashashibi (2009) discuss
the use of a geometric approach to estimating
vehicle behaviour. This approach is suited for a
situation that needs reliable estimations quickly.
Eidehall et al. (2007) developed Emergency Lane
Assist (ELA), a safety function assessing dangers of
changing lane, and if needed autonomously prevent
dangerous manoeuvres. Vehicle position is
determined using Cartesian coordinates. An
evaluation of surrounding traffic defines points on
the road which define areas of danger. A time for the
Host Vehicle to reach these points is calculated. In
this paper we use a similar methodology to the ELA
system of assessing threats with the Cartesian
coordinate method, evaluating a lane-change
manoeuvre. However, Eidehall et al. presented a
system designed to prevent a dangerous situation
from occurring due to the manoeuvre. It does not
need to prepare for a mitigation action.
Hayashi et al. (2012) developed a collision
avoidance system which used both braking and
steering, similar to the simulation model presented
in this paper. Both systems included geometric
trajectory planners and have similar goals. However,
the system proposed by Hayashi et al. is limited in
its mitigation decision, which instructs the vehicle to
apply maximum braking only if it predicts an
unavoidable collision. Also, braking applied through
the steering manoeuvre is simply the maximum
braking. As investigated in this paper, maximum
braking through a steering manoeuvre at high speed
may not be possible, and could result in a loss of
control. The system proposed in this paper includes
avoidance in its calculation of mitigation, with
consideration of vehicle limitations on braking and
maximum yaw rate.
3 RESEARCH PROBLEM
A motorway is considered as a controlled access
highway where traffic directions are separated. The
speeds are usually at the nation’s maximum speed
limit which can lead to collisions which can be fatal
or result in a serious injury.
In the event of a hazard scenario on the motorway,
an autonomous control system is needed to select the
best course of action in such a way as to reduce the
risks to those involved in potential collisions.
A three-lane motorway is analysed, with the Host
Vehicle occupying the middle lane, as presented in
Figure 1. It is assumed that the Vehicle Ahead, in
the same lane as the Host Vehicle, stops suddenly,
and the vehicles in the other two lanes decelerate as
a reaction to the hazard in the middle lane. The Host
Vehicle needs to evaluate what the best course of
action is, whilst considering the potential collisions
it may cause with Vehicles Behind itself and a lane
change manoeuvre and a potential collision it can
cause.
Figure 1: 3 Lane Motorway with Imminent Collision
Ahead.
4 SIMULATION MODEL
This paper proposes a simulation model which can
quickly provide metrics on which to base a decision
for the Host Vehicle to assess which lane of a
motorway it should drive into to avoid or mitigate
potential collisions. The lane which would result in
the least severe collision is selected. The severity of
potential collisions is assessed by the following
parameters: Impact Velocity, Required Rate of
Deceleration to avoid the collisions, Kinetic Energy
of collisions, and Velocity after collisions. Each
metric has a single numerical value for each
collision in each motorway lane, which can be
calculated quickly and evaluated with other metrics
in order to make a decision on which vehicle the
Host Vehicle should collide with.
The Host Vehicle must apply braking to
decelerate before a potential collision in order to
limit any potential risk to those involved in the
collisions. Braking will mitigate even the most
severe collisions. For situations where no steering is
required, full braking can be applied. For steering
manoeuvres, more consideration is needed, as full
braking cannot be applied without potentially
destabilizing the vehicle.
The simulation model requires information about
all vehicles including Current Velocity, Position,
Rate of Deceleration and Mass. Rate of Deceleration
is a complicated parameter value to obtain due to the
speed at which the vehicles can receive and
VEHITS 2018 - 4th International Conference on Vehicle Technology and Intelligent Transport Systems
244

communicate their parameter values, as will be
discussed in Section 4.4. Mass is needed for the
Kinetic Energy calculations, which would only be
available with V2V communication.
The SUVAT kinematic equations of motion used
in the simulation model are as follows:
=+
(1)
=
+2
(2)
=
−
2
(3)
=
2
(+)
(4)
where is initial forward velocity, is final forward
velocity, is acceleration, is distance, and is
time.
Constant braking is used to test the proposed
algorithm. Dynamic braking will be considered in a
future development.
4.1 Lane Change Trajectory
If a lane-change manoeuvre is required, a trajectory
for the Host Vehicle is determined considering
lateral displacement which effectively means 1 lane
width. A sinusoidal wave is created for the
trajectory, because this approach can accomplish a
lateral manoeuvre whilst ending with an effective
orientation change of 0. Using just the longitudinal
distance to complete the manoeuvre, and lateral
distance to change lane, and coordinates can be
extrapolated from the sinusoidal wave. These
coordinates can then be used to calculate the Radius
of Curvature parametrically as follows:
=
(′
+′
)
/
|
.
−
.′′
|
(5)
which is then inverted to find Curvature of Radius :
=
1
(6)
Curvature of Radius is used to calculate a
required Yaw Rate
to complete this steering
manoeuvre, as given by Houenou, A. et al. (2013):
=.
(7)
where is vehicle speed. Another calculation for
Yaw Rate is carried out in the simulation model in
order to evaluate if a manoeuvre is possible given
the limitations of friction. Blundell and Harty (2004)
developed an equation for evaluating the maximum
Yaw Rate that can be achieved due to friction.
=
.
(8)
where is the Coefficient of Friction (CoF), and
is Acceleration due to Gravity. If the required Yaw
Rate exceeds the maximum Yaw Rate limited by
friction, a steering manoeuvre cannot proceed.
4.2 Lateral Manoeuvre Braking
As long as Velocity or Acceleration are constant
values, the kinematic equations of motion can be
applied. An average rate of deceleration is assumed
to be a constant value for a braking only manoeuvre,
where the Host Vehicle stays in its current lane. In
the case of the lane change manoeuvres, different
considerations need to be made for the braking.
Firstly, Tyre Saturation which describes
limitations of tyre performance laterally and
longitudinally is calculated. In essence full braking
cannot be applied if full steering is applied
simultaneously. The braking for a lateral manoeuvre
is calculated as follows (Rajamani, (2011))
:
=
+
(9)
where
is Lateral Acceleration, and
is Velocity
in direction only determined as follows:
=cos(+)
(10)
=sin(+)
(11)
where is the Yaw Angle, and is Vehicle Sideslip
Angle. can be 0, as all calculations are based on
the required Yaw Rate.
Further on, the maximum lateral acceleration
.
is equal to the maximum longitudinal
acceleration
.
, effectively creating a unit circle.
As long as the limits of maximum acceleration
are set, a resultant value can be calculated. With the
lateral acceleration calculated in (9), a resultant
longitudinal acceleration
can be calculated from
the unit circle using Pythagorean Theorem.
=
−
(12)
If
has unequal
and
is maximum,
has an elliptical shape, which is described by
.
+
.
=1
(13)
is calculated by solving the following
equations:
=
.
sin()
(14)
=
.
cos()
(15)
where is the angle subtended by the vector
and
.
is used in equation (2). However, the distance
the Host Vehicle travels is calculated based on
as
opposed to . This is longitudinal Velocity, needed
for calculating the longitudinal distance.
Longitudinal distances of all vehicles are compared
when points of impact are determined. In the case of
steering manoeuvres a greater overall distance to
travel is required than in the case of longitudinal
only manoeuvres.
Autonomous Vehicle Simulation Model to Assess Potential Collisions to Reduce Severity of Impacts
245

4.3 Vehicles Ahead and Behind
It is assumed that all Vehicles Ahead of the Host
Vehicle in the lanes adjacent to the Host Vehicle’s
lane are closer to the Hazardous Vehicle, and
therefore will have started decelerating. This
information needs to be communicated to the Host
Vehicle in the simulation model. The kinematic
equations (1-4) calculate speed and distance arrays
for all vehicles in the simulation.
The distances of the Vehicles Ahead have an
offset distance-headway. This is the distance each
Vehicle Ahead is from the Host Vehicle at the start
of the simulation. With these headway distances, a
separation distance between the Host Vehicle and
Vehicles Ahead is calculated. The point when the
separation distance becomes 0, is the point of impact
between the two vehicles. This Point of Impact is
recorded for all three potential collisions, and is used
to determine the speed of the Vehicles Ahead and
Host Vehicle, and the position of the Host Vehicle
for a safety concern discussed in Section 4.4.
In addition to evaluating the potential three
collisions ahead, the Host Vehicle needs to ensure it
does not ignore the risk of Vehicles Behind itself
from colliding into it. Therefore, calculations are
made for three Vehicles Behind the Host Vehicle,
but there is an added complexity.
The Vehicles Behind are further away from the
initial hazard. Even with V2V, the Host vehicle will
receive the information about the hazard and the
simulation can begin before the simulation of the
Vehicles Behind can start. If the vehicles were able
to communicate their rates of deceleration before a
decision had been made by the Host Vehicle then the
same reducing velocity calculations would be made
as for the Vehicles Ahead. However, it is assumed
that the closer a vehicle is to the hazard vehicle, the
earlier it will receive the necessary information and
begin necessary calculations. The velocity and
distance calculations need a rate of deceleration, as it
cannot be assumed that these Vehicles Behind just
proceed at their initial velocity. Therefore, a braking
value needs to be assumed.
Inspiration for this calculation is taken from the
UK Highway Code (Driving Standards Agency for
the Department for Transport (2007)). It states a
general guide to vehicle stopping distances. Modern
cars will almost certainly achieve greater rates of
deceleration, but these stopping distances do give a
standard which motor vehicles should be able to
match. For vehicles that have not communicated
their braking values a braking assumption given by
the Highway Code is used. In this way vehicles have
a reducing velocity for the Vehicles Behind is
calculated. Separation distances between the Host
Vehicle and Vehicles Behind are calculated using
the same approach as for the Vehicles Ahead.
4.4 Lateral Manoeuvre Safe Lanes
The decision modelling of the lane in which the
collision will happen must guarantee that any
collision that occurs has a zero-lateral offset. The
effect that the lane change manoeuvres might have
on a collision has to be accounted for. The point at
which the steering manoeuvre is complete, which
must occur before the point of impact, has to be
determined.
Calculation of velocity and distance is set to the
same time frame for each vehicle. This makes it
possible to find the distances of all Vehicles Ahead
and Behind at the time point when the Host Vehicle
completes its lane-change manoeuvre. If any
collision occurs before the lane-change manoeuvre
is complete, the corresponding lane will be
disqualified in the decision-making process.
4.5 Kinetic Energy
In order to determine and compare the kinetic
energy before and after a collision for each vehicle,
velocities of the vehicles need to be calculated.
Conservation of Linear Momentum for Inelastic
Collisions is used to find the velocity of the
vehicles which get impacted, where Vehicles Ahead
are impacted by the Host Vehicle, and Host Vehicle
is impacted by Vehicles Behind as follows:
=
,
=1,2
(16)
=
+
(17)
=
(18)
=
∑
+
(19)
where
denotes the vehicle mass, and subscript
denotes the vehicle number.
Whilst energy cannot be lost or destroyed, a
comparison of the difference between the Kinetic
Energy before the collision,
, and after the
collision,
, shows how much of the kinetic
energy will have been converted in the impact,
which would deform the vehicles:
=
1
2
+
1
2
(20)
=
1
2
(
+
)
(21)
∆ =
−
(22)
VEHITS 2018 - 4th International Conference on Vehicle Technology and Intelligent Transport Systems
246
5 SIMULATION DEVELOPMENT
5.1 Parameters
Motorway simulation is tested for different
motorway scenarios. Vehicles Ahead and Behind are
modelled using the following parameters:
• Longitudinal Distance from Host Vehicle (),
• Lateral Distance from Host Vehicle
(
)
,
• Velocity
(
⁄)
,
• Mass
(
)
,
• Rate of Deceleration (/
) for Vehicles
Ahead,
• Host Vehicle Velocity (
⁄
) set to be equal to
the velocity of the Vehicle Ahead in the same
lane,
• CoF,
• Host Vehicle Following Distance Time (),
• Host Vehicle Maximum Deceleration
,
• Host Vehicle Maximum Acceleration (/
).
5.2 Assumptions
We made a number of assumptions in the simulation
model to perform the algorithmic calculations. These
assumptions support the aims of the simulation
model, aiding in the reliability and relevance of the
outputs.
• All vehicles are assumed to be in the centre of
lane, to determine Lateral Distances.
• Motorway is assumed to be straight, no
directional control is required.
• All rates of deceleration are assumed to be
constant.
• To determine if a lane-change manoeuvre is safe
without causing a collision with Vehicles
Behind, it is assumed that Vehicles Behind do
not brake.
• The closer a vehicle is to another, the sooner it
will receive data about that vehicle.
• Highway Code braking distances are satisfactory
for the assumption of Vehicles Behind
deceleration.
5.3 Motorway Lanes and Traffic
A UK three-lane motorway simulation is carried out,
with a Vehicle Ahead and a Vehicle Behind
occupying each lane. This means that all vehicles are
initially set to a speed of 70miles/h (112.65km/h).
The lane width is set to 3.75 metres, which is
slightly larger than suggested in Leics.gov.uk
(2016), but justifies the use of the simulation model.
5.4 Simulation Flowchart
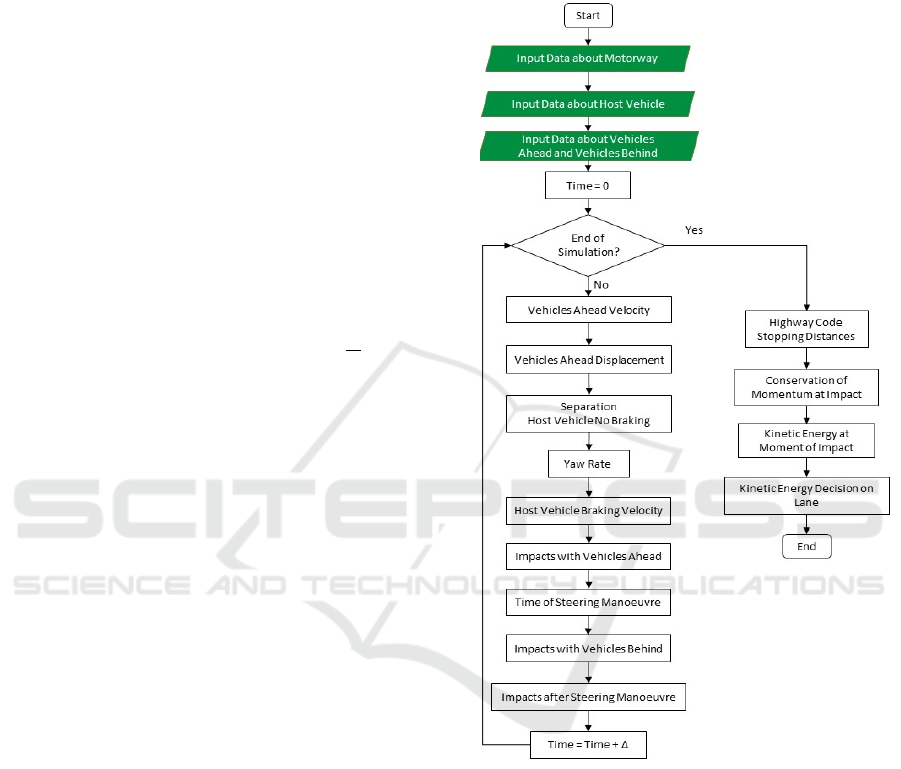
Figure 2: Simulation Model Flowchart.
The simulation model flowchart is given in Figure 2.
First vehicle velocities, displacements, and the Host
Vehicle’s steering trajectory are calculated. The
Kinetic Energy is determined based on the Highway
Code assumptions of braking used for calculating
the deceleration for the Vehicles Behind.
Once the Kinetic Energy values are calculated, a
decision on the best lane to drive into is made and
presented by the corresponding lane’s ID number.
The lane is selected following this procedure. Each
lane has 2 potential collisions which are independent
of one another. The two Kinetic Energy results, KE
i
and KE
f
, and Kinetic Energy difference, ∆KE, are
calculated for both Vehicles Ahead and Vehicles
Autonomous Vehicle Simulation Model to Assess Potential Collisions to Reduce Severity of Impacts
247

Behind, for each lane. A decision is based on
selecting the maximum of the kinetic energy
differences ∆KE obtained for each lane and then
selecting the lane with the smallest ∆KE, in order to
avoid the largest kinetic energy collisions. In the
event that multiple lanes have identical Maximum
∆KE values, a minimum value will be selected from
the Minimum ∆KE values of those lanes. If multiple
lanes have the same maximum and minimum ∆KE
values, the decision is made to progress to the lane
with the lower ID, as this refers to the lane with the
slower moving traffic.
The simulation is implemented using Matlab
2016a.
6 ANALYSIS OF RESULTS
Fifteen scenarios were defined to validate the
simulation model. A benchmark scenario with
parameters defined for each lane and both Vehicles
Ahead and Behind are given in Table 1.
Table 1: Benchmark Parameters.
Parameter Value
Mass of Vehicles Ahead 2000kg
Velocity of Vehicles Ahead 70mph
Headway Distance to Vehicles Ahead for
Lanes 1 and 3
15m
Braking Values of Vehicles Ahead
7/
Mass of Vehicles Behind 2000kg
Velocity of Vehicles Behind 70mph
Headway Distance of Vehicles Behind 20m
ACC Time Host Vehicle 1.4s
To evaluate how each parameter influences the
results, only one parameter was changed in each
simulation scenario compared to the benchmark
scenario. The results of all 16 simulations are
presented in Table 2.
Each lane was assigned an ID number and the
lane which was the best option for the Host Vehicle
to be in was selected. The decision made in each
scenario was in line with the subject expert decision.
In the event of equal values for both the minimum
and maximum kinetic energy values for multiple
lanes, such as in benchmark scenario 1, the decision
was to select the smallest ID lane number, as in
practise this should refer to the lane with the slowest
moving traffic and closest to the emergency lane.
In scenario 2, ΔKE_Ahead in Lane 1 was higher,
due to the difference in velocity at the point of
impact. The impact velocity is dependent on the
velocity of both the Vehicle Ahead and the Host
Vehicle. However, it is not the case that reducing the
Headway Distance always results in a higher ΔKE,
as demonstrated in scenario 3. Scenario 4 reduced
the velocity of the Vehicle Ahead in Lane 1, which
means the impact velocity was lower. This
difference resulted in a larger ΔKE, and is
reciprocated in scenario 5 as a smaller ΔKE resulted
from a higher initial velocity. In scenarios 6 and 7,
the Rate of Deceleration for the Vehicle Ahead in
Lane 3 was reduced, and in both scenarios this
resulted in a lower impact velocity. Scenario 7
demonstrated that no collision occurred as there was
no braking for the Vehicle Ahead in Lane 3.
Scenario 8 increased the initial Headway Distance
between the Host Vehicle and the Vehicle Behind in
Lane 2 giving greater distance to apply deceleration
and reduce the impact velocity. Scenario 9 reduced
this distance, and whilst the impact velocity was
reduced compared to the benchmark scenario, a
lane- change manoeuvre was selected.
The simulation model was able to identify lanes
where a lane-change manoeuvre was not feasible,
and to disqualify it from the decision (scenarios 10
and 14). Scenario 10 demonstrated that the Velocity,
of the Vehicle Behind in Lane 1 resulted in that
Lane being disqualified as a lane-change manoeuvre
cannot occur safely. Scenarios 11 and 12
demonstrated the effect Mass had on the Kinetic
Energy calculations, and an unfavourable “selfish”
decision made. This highlights the need for further
investigation as the effect of a collision on the other
vehicles would introduce a more altruistic decision.
Increasing the ACC time in scenario 13 did result in
Lanes 1 and 3 having a higher ΔKE_Ahead compared
to the benchmark scenario, but not considerably, and
lane 1 was selected. Reducing CoF in scenario 14
resulted in both Lanes 1 and 3 being disqualified,
causing a lower achievable maximum yaw rate, and
the lane-change manoeuvre was not possible.
Scenario 15 had the effect of reducing the braking for
the lane-change manoeuvre, increasing the
ΔKE_Ahead compared to the benchmark scenario.
Scenario 16 demonstrated a higher ΔKE_Ahead for
Lane 2 when the Deceleration was reduced, but did
result in a lower ΔKE_Behind.
It is worth noting that this decision process
resulted in an undesirable decision in scenarios 11
and 12. The only parameter changed was the mass of
one vehicle. The smallest mass vehicle was selected
in both scenarios. Using the conservation of
momentum in equations (16) to (19) this resulted in
a higher velocity after the impact with the vehicles.
This is not altruistic, and the decision made by the
Host Vehicle can be considered “selfish”.
VEHITS 2018 - 4th International Conference on Vehicle Technology and Intelligent Transport Systems
248
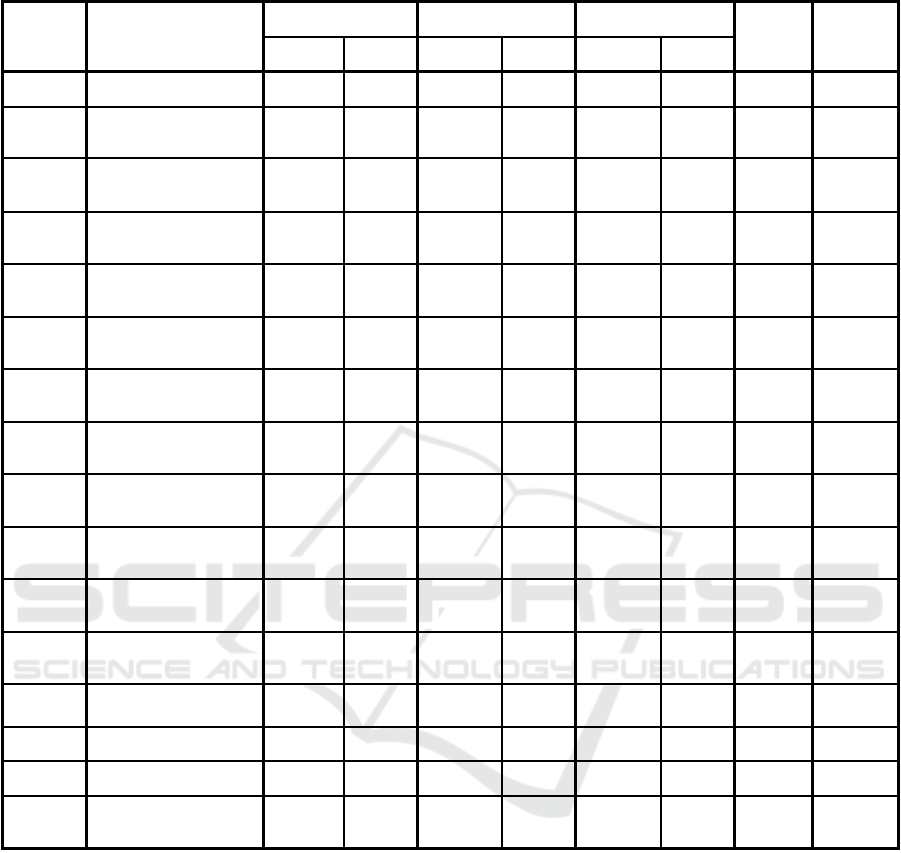
Table 2: Simulation Results and Decision. All Kinetic Energy Values are in 10^4 scale (J).
Scenario Parameter Changed
Lane 1 ΔKE Lane 2 ΔKE Lane 3 ΔKE
Lanes
Closed
Decision
Ahead Behind Ahead Behind Ahead Behind
1
Benchmark Scenario
1.6653 0
0.7178 5.236 1.6653 0 N/A Lane 1
2
Headway Ahead
Lane 1 - 14m
2.0062 0 0.7178 5.236 1.6653 0 N/A Lane 3
3
Headway Ahead
Lane 1 - 11m
1.5757 0 0.7178 5.236 1.6653 0 N/A Lane 1
4
Velocity Ahead Lane
1 - 69miles/h
2.1588 0 0.7178 5.236 1.6653 0 N/A Lane 3
5
Velocity Ahead Lane
1 - 71miles/h
0.5461 0 0.7178 5.236 1.6653 0 N/A Lane 1
6
Braking Ahead Lane
3 - 6.9m/s^2
1.6653 0 0.7178 5.236 1.1029 0 N/A Lane 3
7
Braking Ahead Lane
3 - 0m/s^2
1.6653 0 0.7178 5.236 0 0 N/A Lane 3
8
Headway Behind
Lane 2 - 43m
1.6653 0 0.7178 1.4692 1.6653 0 N/A Lane 2
9
Headway Behind
Lane 2 - 15m
1.6653 0 0.7178 4.0182 1.6653 0 N/A Lane 1
10
Velocity Behind
Lane 1 - 74miles/h
1.6653 0.182 0.7178 5.236 1.6653 0 1 Lane 3
11
Mass Ahead Lane 1 -
2100kg
1.706 0 0.7178 5.236 1.6653 0 N/A Lane 3
12
Mass Ahead Lane 3 -
1500kg
1.6653 0 0.7178 5.236 1.4274 0 N/A Lane 3
13
ACC Time -
1.5seconds
1.6837 0 0.0268 4.5815 1.6837 0 N/A Lane 1
14
CoF - 0.6 0 1.0415 0.7178 5.236 0 1.0415 1 and 3 Lane 2
15
Max Overall G - 0.8 4.7837 0 0.7178 5.236 4.7837 0 N/A Lane 1
16
Host Vehicle Max
Braking - 8m/s^2
1.6653 0 6.0729 3.4865 1.6653 0 N/A Lane 1
7 CONCLUSIONS
A novel simulation model is proposed to inform a
decision making process on the outcomes of several
potential collisions in a motorway situation. The
simulation model can be used when a hazardous
vehicle in the same lane as the Host Vehicle comes
to a sudden stop. This requires a fast simulation and
decision making process. The kinematic equations of
motion used simplify the complex task of assessing
the impact of a potential collision.
The developed decision process proved to be
satisfactory in all but two scenarios. A more
altruistic decision would be beneficial, where the
effect of the other vehicles and not just the Host
Vehicle needs to be considered.
The model is able to simulate the velocity and
displacements of 6 motorway vehicles in 3 lanes, as
well as the Host Vehicle. From this it can calculate
impact velocities which are then used to assess the
severity of the potential collisions. The simulation
model is also able to determine whether a potential
lane-change manoeuvre would result in a collision
before the manoeuvre is completed, and therefore
disqualifies that lane as being unsafe. The use of
Autonomous Vehicle Simulation Model to Assess Potential Collisions to Reduce Severity of Impacts
249

kinetic energy is suitable for the decision process,
and does give an indication to the severity of a
collision, but more in depth metrics can be
developed to evaluate the severity of the collision
such as deformation and passenger cell acceleration.
8 FUTURE WORK
This paper proposes numerical metrics to be
calculated and used to evaluate potential collisions,
and to select the best lane the autonomous Host
Vehicle should drive into. The simulation model and
decision process proposed rely on all required data
being available. This would rely heavily on V2V
communication. But V2V may not be widely
available, although a decision would still need to be
made. Without V2V communicating the masses of
each vehicle, a kinetic energy based decision is not
possible to make. However, the decision can be
made considering impact velocities and braking
distances, which could be obtained without V2V.
Further development will remove some of the
stated assumptions. Dynamic deceleration values to
include the effects of resistance forces would
improve the accuracy of calculating vehicle velocity.
Collision modelling will provide insight into
how automotive collisions can be assessed by the
simulation model. The kinetic energy calculations
proposed are suitable for the lane-change decision,
but could be further developed to introduce focused
metrics on assessing collision severity, such as
vehicle deformation and passenger cell acceleration.
Both decisions based on kinetic energy and
velocities can be considered by applying a Multi
Attribute Decision Making (MADM) method.
Different MADM methods will be analysed
including TOPSIS, Analytical Hierarchy Process
(AHP), and Analytical Network Process (ANP).
MADM will introduce altruism to the decision
process, considering the effects of the collision for
the Host Vehicle and the other vehicles in the
collision.
ACKNOWLEDGEMENTS
This research is supported by Engineering and
Physical Sciences Research Council (EPSRC),
Industrial Cooperative Awards in Science &
Technology (CASE) grant no. EP/L505614/1, and
the industrial collaborator Jaguar Land Rover. This
support is gratefully acknowledged.
REFERENCES
Ammoun, S. and Nashashibi, F. (2009). 'Real Time
Trajectory Prediction for Collision Risk Estimation
between Vehicles'. IEEE 5th International Conference
on Intelligent Computer Communication and
Processing ICCP. 27-29 August 2009 Cluj Napoca,
Romania: IEEE.
Anderson, S. J., Peters, S. C., Pilutti, T. E., and Iagnemma,
K. (2010). 'An Optimal-Control-Based Framework for
Trajectory Planning, Threat Assessment, and Semi-
Autonomous Control of Passenger Vehicles in Hazard
Avoidance Scenarios'. International Journal of
Vehicle Autonomous Systems 8 (2-4), 190-216.
Blundell, M. and Harty, D. (2004). The Multibody
Systems Approach to Vehicle Dynamics. 1st ed.
Oxford: Elsevier, 401-408.
Cesari, G., Schildbach, G., Carvalho, A., and Borrelli, F.
(2017). 'Scenario Model Predictive Control for Lane
Change Assistance and Autonomous Driving on
Highways '. IEEE Intelligent Transportation Systems
Magazine 9 (3), 23-35.
Driving Standards Agency for the Department for
Transport (2007). The Official Highway Code. 15th
ed. Norwich: Crown Copyright
Eidehall, A., Pohl, J., Gustafsson, F., and Ekmark,
J. (2007). 'Toward Autonomous Collision Avoidance
by Steering'. IEEE Transactions on Intelligent
Transportation Systems 8 (1), 84-94.
Geronimi, S., Abadie, V., and Becker, N. (2016).
'Methodology to Assess and to Validate the
Dependability of an Advanced Driver Assistance
System (ADAS) such as Automatic Emergency
Braking System (AEBS)'. in Langheim, J. (Ed.), Cham
Energy Consumption and Autonomous Driving.
Switzerland: Springer, 125-131.
Harper, C. D., Hendrickson, C. T., and Samaras,
C. (2016). 'Cost and Benefit Estimates of Partially-
Automated Vehicle Collision Avoidance
Technologies'. Accident Analysis & Prevention 95,
104-115.
Hayashi, R., Isogai, J., Raksincharoensak, P., and Nagai,
M. (2012). 'Autonomous Collision Avoidance System
by Combined Control of Steering and Braking using
Geometrically Optimised Vehicular Trajectory'.
Vehicle System Dynamics 50, 151-168.
Houenou, A., Bonnifait, P., Cherfaoui, V., and Yao, W.
(2013). 'Vehicle Trajectory Prediction Based on
Motion Model and Maneuver Recognition'. IEEE/RSJ
International Conference on Intelligent Robots and
Systems. 3-7 November. 2013, Tokyo, Japan: IEEE.
Leics.gov.uk (2016). Part 3 Design Guidance. Retrieved
December 14, 2016, from http://www.leics.gov.uk
/index/htd/highway_req_development_part3.html
Rajamani, R. (2011). Vehicle Dynamics and Control. 2nd
ed. New York, NY, USA: Springer.
VEHITS 2018 - 4th International Conference on Vehicle Technology and Intelligent Transport Systems
250
