Optimal Control for Energy Management of Connected Hybrid
Electrical Vehicles
Predictive Connectivity Compared to an Adaptive Algorithm
Hamza Idrissi Hassani Azami
1,2
, Stephane Caux
1
, Frederic Messine
1
and Mariano Sans
3
1
University of Toulouse, LAPLACE, INPT, 2 rue Charles Camichel B.P. 7122, 31071, Toulouse, France
2
French Environment and Energy Management Agency (ADEME), 20 avenue du Gresille-BP 90406, 49004,
Angers Cedex 01, France
3
Continental Automotive SaS, 1 avenue Paul Ourliac, 31100, Toulouse, France
Keywords:
Energy Management, Hybrid Electrical Vehicle, Optimal Control, Pontryagin Minimum Principle, Shooting
Algorithms.
Abstract:
For fuel consumption and CO
2
emissions reduction, an optimal predictive control strategy for connected hybrid
electrical vehicles is proposed, and evaluated through a comparison to an adaptive strategy. The predictive
strategy relies on the future driving conditions that can be predicted by intelligent navigation systems with real-
time connectivity. The theory proposed for such real-time optimal predictive algorithm is based on Pontryagin
minimum principle, a mathematical principle that provides general solutions for dynamic systems optimization
with integral criteria, under given constraints. In this work, the energy management problem is mathematically
modeled as an optimal control one, and optimal solutions are synthesized. The predictive optimal real-time
algorithm is confronted to the adaptive method. Both control strategies are simulated on different driving
cycles. The simulation results show the interest of predictive approaches for hybrid electrical vehicles energy
management.
1 INTRODUCTION
Hybridization has been introduced in car industry es-
sentially to reduce fuel consumption, which leads to a
reduction of CO
2
and pollutants emissions. The con-
cept of hybridization is to add another (clean) energy
source to the classical fossil fuel bringing another en-
ergy converter. In this paper, attention is focused on
Hybrid Electrical Vehicle where besides the Internal
Combustion Engine (ICE), the power-train is also me-
chanically connected to an electrical machine. One of
the major interests of electrical hybridization is the
reversible aspect of the energetic flow on the Electri-
cal Machine Actuator (EMA). The electrical machine
can convert the vehicle kinetic energy into electrical
energy stored in the battery. In a hybrid vehicle, the
combination of two energy sources creates a free en-
ergetic node. Regardless of the drivers behavior, the
combination ratio of the two energy sources is a new
degree of freedom which must be set by real-time em-
bedded control.
The question that constitutes the energy manage-
ment problem of this paper is : How can the fuel en-
ergy, consumed by ICE, be minimized in a way to ob-
tain a certain electrical energy balance over the trip?
In other words, knowing the future path, the objec-
tive is to use electrical on-board energy to minimize
the fuel consumption over the path, and at the same
time, retrieve a targeted state of charge of the battery.
A problem that is also referred to as the TorqueSplit
problem.
Researches on this energy management topic
started many years ago (Sciarretta and Guzzella,
2007). Two approaches have been adopted. First,
heuristic methods for real-time use, such as rule based
methods, fuzzy logic (Caux et al., 2010), stochastic
strategies or other strategies such as the equivalent
consumption minimization strategy (Sciarretta et al.,
2004). Although this type of methods has the advan-
tage of being compatible with real-time use, it does
not guarantee a rigorous optimal solution. On the
other hand, model-based methods using optimal con-
trol theory and dynamic programming algorithms, in
off-line computation (Tribioli and Onori, 2013), (Del-
prat et al., 2003), can guarantee optimal solutions
without being real-time compatible.
Idrissi Hassani Azami, H., Caux, S., Messine, F. and Sans, M.
Optimal Control for Energy Management of Connected Hybrid Electrical Vehicles.
DOI: 10.5220/0006668302610268
In Proceedings of the 4th International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS 2018), pages 261-268
ISBN: 978-989-758-293-6
Copyright
c
 2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
261

In strategies based on optimal control theory, a
calibration of the optimization parameters is neces-
sary. Existing real-time embedded strategies perform
this calibration either by using adaptive heuristics
(Kim et al., 2011), (Kermani et al., 2011), or by recal-
culating the optimal control periodically using short
term prediction, as in MPC (Model Predictive Con-
trol) methods (He et al., 2015). This on-line adap-
tation of the optimization parameters aims to avoid
unexpected scenarios which can yield high fuel con-
sumption. The drawback of these solutions is an alter-
ation of the time-global optimization over the whole
trip. They can only assure sub-optimal solution over
separated parts of the trip.
The purpose of this paper is to show the interest
of a predictive model based optimal control through a
comparison with an adaptive method. The gain from
such predictive method is evaluated in the context of a
connected vehicle which is able to acquire data about
the future circumstances. Both predictive and adap-
tive methods use the same on-line structure: the min-
imization of a weighted criteria of Fuel and Electrical
Power. The difference between these two methods is
the calibration of the weight coefficient. While the
adaptive method uses a rule based strategy to com-
pute this coefficient, the predictive method uses infor-
mation about the future path in a shooting algorithm
to determine the same coefficient.
Devices like Electronic-Horizon can be used to
provide a robust estimation of the necessary informa-
tion about the future trip. They can provide dynamic
information about red light stops, speed limitations,
traffic information etc... Using an embedded drivers
model (that could be shaped by AI algorithm), an es-
timation of torque demand and speed for the whole
future trip can be deduced. This gives the opportu-
nity of long prediction horizons, unlike existing MPC
methods where the prediction horizons are in an order
of magnitude of 10s. The prediction part is not in the
scope of the paper. We consider the vehicle equipped
with such a system, that provides reliable data.
In section 2, a mathematical modelling of the en-
ergy management problem into an optimal control
problem is exposed. Then its solution is developed
into a control structure that characterizes the two com-
pared methods. Section 3 opposes predictive and
adaptive methods by exposing the core practical dif-
ficulty of the problem which is the calibration of the
control structure. The predictive method is detailed,
and its differences with the adaptive heuristics are em-
phasized. An evaluation of the methods by simulation
results on different driving cycles is presented in sec-
tion 4. The conclusions of the paper are in section
5.
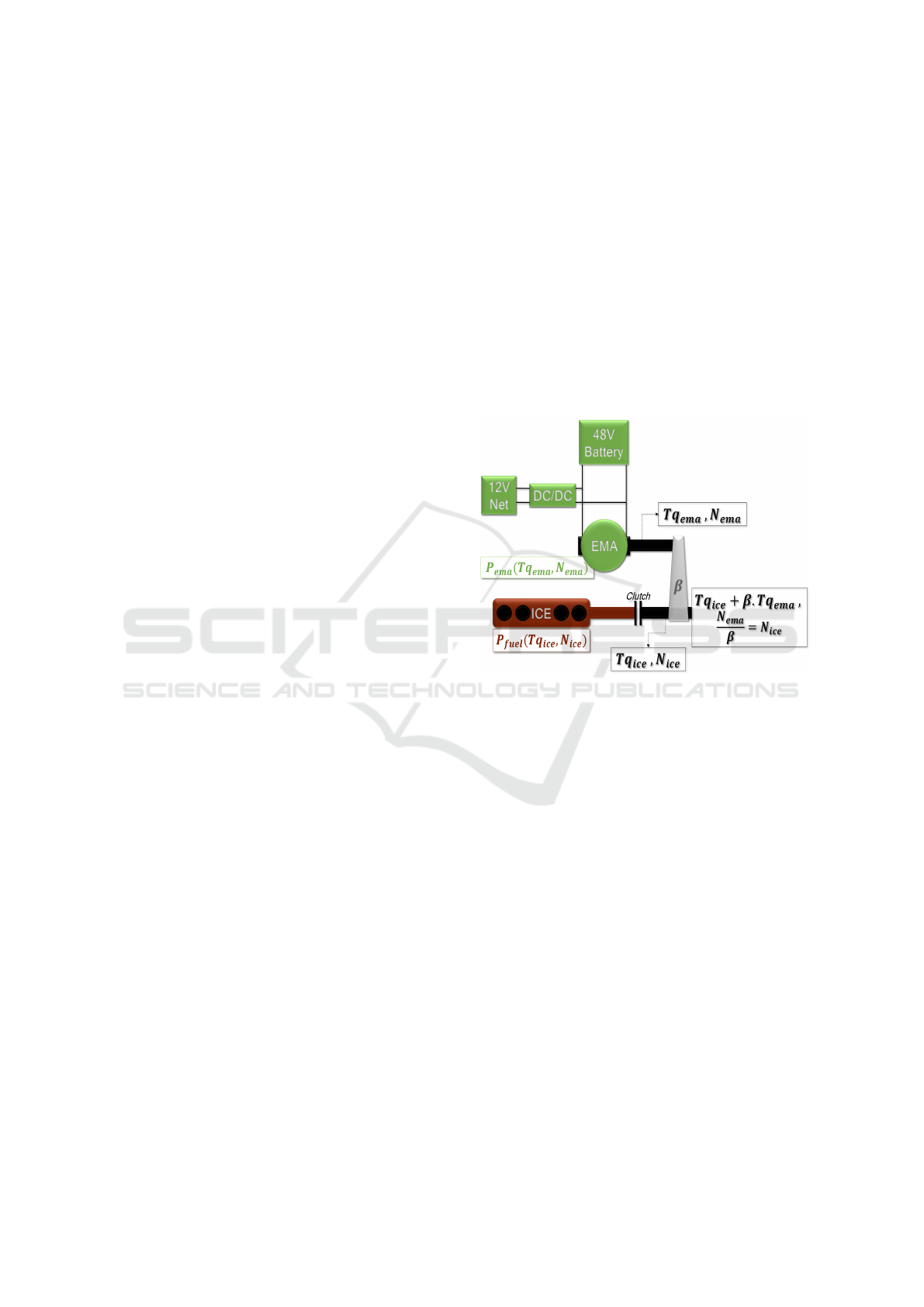
2 PROBLEM MODELLING
2.1 Hybrid Electrical Vehicle: 48V P2
Architecture
The vehicle considered is a 48V P2 Hybrid Ford Fo-
cus. The P2 architecture has the advantage of engine-
off electrical traction. The ICE is connected to the
power-train through a clutch that can be opened when
the engine is not required. The power-train is con-
nected to an electrical machine using a transmission
belt. A 48V Battery feeds the electrical machine, and
also an on-board 12V electrical net as shown in Fig-
ure 1.
Figure 1: Hybrid 48V P2 architecture.
The two electrical circuits are interfaced by a
DC/DC converter controlled using a PI controller.
The strategy proposed will not control this low volt-
age net. The power demand from the 12V net is writ-
ten P
12V
.
ICE consumes a power given by P
f uel
(T q
ice
, N
ice
)
to supply a torque T q
ice
at the speed N
ice
, a power
which is proportional to the necessary amount of fuel.
EMA takes P
elec
(T q
ema
, N
ema
) from the battery to
supply T q
ema
at the speed N
ema
. P
f uel
and P
elec
are
functions depending on respectively ICE and EMA
torque and speed. These functions are available as nu-
merical maps from experimental testing of ICE and
EMA over different operating points of the engines.
The electrical power is transmitted to the clutch using
a transmission belt. The belt ratio is considered to be
constant β. The mechanical transmission equations
are:
N
ema
= β.N
ice
= β.N
clu
(1)
T q
clu
= T q
ice
+ β.T q
ema
(2)
VEHITS 2018 - 4th International Conference on Vehicle Technology and Intelligent Transport Systems
262

The battery energy is characterized by its State of
Charge (SoC). SoC dynamic is:
dSoC
dt
=
I
bat
Q
max
(3)
Where I
bat
is the intput current of the battery, and
Q
max
is its maximum capacity. Knowing that: P
bat
=
I
bat
.V
bat
= −(P
elec
+ P
12V
), it can be concluded that:
dSoC
dt
= −
P
elec
+ P
12V
V
bat
.Q
max
(4)
Knowing the speed profile and the torque demand
from the driver over a future trip, the objective is to
minimize the fuel consumption under a constraint on
the SoC final value. The targeted SoC value is denoted
SoC
tg
.
2.2 Optimal Control Model
The equations developed in the subsection above are
already sufficient to synthesize an optimization prob-
lem that describes the needs of the energy manage-
ment problem:
min
T q
ice
,T q
ema
J =
R
T
0
P
f uel
(T q
ice
, N
ice
)dt
s.t. SoC(T ) = SoC
tg
T q
clu
= T q
ice
+ β.T q
ema
dSoC
dt
= −
P
elec
+ P
12V
V
bat
.Q
max
(5)
where T corresponds to the trip duration.
The battery voltage depends on SoC. Moreover,
V
bat
(SoC) is non-linear, which makes the battery
model difficult to manipulate and the analytic reso-
lution of this problem becomes difficult. Two simpli-
fications are introduced in order to deal with a more
affordable optimization problem for real-time use.
First, the power demand from the low-voltage on-
board net is considered as a constant, and null in the
following development P
12V
= 0 . The other assump-
tion concerns the voltage of the battery, which is con-
sidered constant V
bat
= 48V . Although the second as-
sumption is not realistic, it has been shown in previ-
ous studies that the effect of the internal dynamic of
the battery can be negligible for hybrid electrical ve-
hicles energy management, (Sciarretta and Guzzella,
2007) and (Steinmauer and del Re, 2001).
In addition to the two simplifications, equation (2)
shows that only one of the two torque set-points can
be used as decision variable or command. The SoC
dynamic equation can then be rewritten as a function
of the ICE torque:
dSoC
dt
= −
P
elec
(
T q
req
−T q
ice
β
, N
ema
)
V
bat
.Q
max
(6)
Accordingly, the optimization problem is rewrit-
ten :
min
T q
ice
J =
R
T
0
P
f uel
(T q
ice
, N
ice
)d t
s.t. SoC(T ) = SoC
tg
dSoC
dt
= −
P
elec
(T q
ice
, N
ema
)
V
bat
.Q
max
(7)
The control variable is the ICE torque T q
ice
(t),
and the state to control is SoC.
2.3 Solution of the Optimal Control
Problem
In optimal control theory, the purpose is to take a sys-
tem from an initial state A to a final state B, in a way
that minimizes an integral criterion. In this case, the
state would be the state of charge of the battery.
Optimal control theory (Pontryagin Minimum
Principle) is applied to the problem (7). SoC is the
state to control from an initial point Soc(0) to a final
point SoC
tg
.
Pontryagin principle asserts that the optimal so-
lution minimizes the Hamiltonian of the problem at
each instant. The Hamiltonian is constructed intro-
ducing the co-state variable λ which is a function de-
pending on time that verifies the following differential
equation:
∂H
∂SoC
= −
dλ
dt
(8)
The Hamiltonian of the problem is then written as
follows:
H
λ
(T q
ice
) = P
f uel
(T q
ice
, N
ice
)−λ.
P
elec
(T q
ice
, N
ema
)
V
bat
.Q
max
(9)
From the differential equation (8) of the co-state
variation, we obtain:
dλ
dt
= 0 (10)
Hence, λ is constant.
According to optimal control theory, the optimal
T q
ice
minimizes at each instant the Hamiltonian:
T q
opt
ice
= arg min
T q
ice
(H
λ
(T q
ice
)) (11)
At instant t, knowing the value of N
ice
and N
ema
,
and the functions P
f uel
and P
elec
, the solution is found
by minimizing the Hamiltonian (11). Only the co-
state variable λ needs to be determined. Its value will
determine the admissibility of the solution, or in other
words the final value of SoC.
Optimal Control for Energy Management of Connected Hybrid Electrical Vehicles
263

As a conclusion of these developments, we deduce
that the optimal control theory applied to the hybrid
energy management problem yields a very intuitive
solution. The result is to minimize, at each instant, a
criteria involving the two electrical and fuel powers,
with a pondering coefficient λ. Other types of strate-
gies do not directly use optimal control and Pontrya-
gin Maximum Principle. However, the most of them
minimize the same hybrid criteria by using a weight
coefficient that is adapted following the vehicle state.
It is the case of the adaptive method that we chose to
compare to the predictive optimal control approach.
In the following, we expose the two approaches of
calibration: predictive and adaptive.
3 ENERGY MANAGEMENT
CALIBRATION: PREDICTIVE
VS ADAPTIVE
3.1 Predictive Shooting Algorithm to
Find λ
The predictive method proposed in this paper, is a
continuity of the optimal control theory. Optimal con-
trol problems often imply high non-linearity which
makes the integration of the differential equations im-
possible. The classical solution to this problem is to
develop a shooting algorithm which is the predictive
approach proposed. It consists of doing iterations of
numerical integration of the system, until the targeted
SoC is reached with a satisfactory error.
It is necessary for this method to design a function
that, by integrating its equations, simulates the vehi-
cles behavior over some trip with some value of λ.
The simulation is based on the same model as the one
used to synthesize the optimal control problem in the
first section. Such function is called a shooting func-
tion. It takes for input, the predicted information from
the future path, as well as an entry value of λ.
The function computes the optimal T q
ice
by min-
imizing the expression (2.3) at each instant. Then the
optimal T q
ema
is deduced by fulfilling the torque de-
mand on the clutch, which allows the integration of
P
elec
(T q
ice
, N
ema
) over the time of the trip, to find the
corresponding final SoC.
The value of λ determines the value of the final
state SoC
tg
. A random value of λ would lead to a
random final value of the SoC. The idea of the shoot-
ing algorithm is to search for the constant value of λ
which renders the final state of charge targeted, by it-
erating the simulation of the system, using for each
iteration, a λ that is updated by the result of the previ-
ous simulation (see Figure 3).
This co-state can be seen from another point of
view: the minimization of the Hamiltonian (2.3) can
be understood as a weighted minimization of fuel en-
ergy and electrical energy. λ is then the weight of the
electrical energy in the minimization. This perspec-
tive of the problem gives an idea of the adequate opti-
mization method for the shooting algorithm to find λ:
the final state of charge grows as λ increases, which
means that the function, for which the shooting algo-
rithm is finding a zero, would be monotonous.
Figure 2: Variation of the SoC error: 50% SoC target on an
NEDC driving cycle.
As an example , on the NEDC driving cycle, with
SoC
tg
= 50%, an increasing, monotonous variation is
noticed, as illustrated in Figure 2. The final value of
SoC increases when λ increases.
The assumption that SoC(T ) = f (λ) is a
monotonous increasing function, allows the reduction
of the number of simulations to find the appropriate
λ. Finding the λ that guarantees SoC
tg
is equivalent
to finding the zero of the function S oC(T ) − SoC
tg
=
f (λ) − SoC
tg
= g(λ). Thanks to its monotonicity we
can use simple, fast, and efficient ways to find its zero.
The method used here is a simple bisection algorithm.
A shooting algorithm is designed under Matlab
R

as in Figure 3. The algorithm uses the shooting func-
tion previously designed to perform simulations using
a value of λ as an entry. The search of the appropriate
λ is done using bisection.
As an output of the shooting algorithm, the value
of λ that reaches the targeted final SoC is returned.
The embedded shooting algorithm is ran at the be-
ginning of a trip. It takes the predictions that connec-
tivity provides and returns the optimal λ which will
be used in real-time Hamiltonian minimization dur-
ing the trip.
VEHITS 2018 - 4th International Conference on Vehicle Technology and Intelligent Transport Systems
264

Figure 3: Shooting algorithm scheme.
3.2 Adaptive Costbased Tuning of λ
The adaptive method, that we chose to compare to
the predictive optimal control, has been developed by
Continental Automotive engineers. It is a rule based
strategy for Torque Split Energy management, and
does not use future predictions. This method is based
on an instantaneous minimization of a weighted cri-
terion combining electrical energy and fuel energy.
The weight coefficient λ is tuned on-line based on the
states of the vehicle, essentially the battery state of
charge. The coefficient varies with the state of charge
by using heuristic rules.
Although the method is not directly derived from
optimal control theory, it uses the same online control
structure: it is an on-line minimization of a pondered
criteria. The practical advantage of this method is its
independence from connectivity and prediction.
Figure 4: Calibration of the criteria using the CostBased
adaptive method.
λ is computed on-line using the value of
η
EMA
η
ICE
.
Where η
EMA
and η
ICE
are respectively the EMA and
ICE efficiency. The electrical machines efficiency
varies when the battery SoC varies. This variation de-
termines at each instant the value chosen for λ.
The value
η
EMA
η
ICE
represents a cost of electrical
power in terms of fuel power. The CostBased adaptive
method computes it off-line for all operating points of
the engine and all driving modes. The values of
η
EMA
η
ICE
are stored in maps and used in real-time to determine
λ.
The CostBased method is the most efficient
method developed by Continental Automotive for the
TorqueSplit problem, in terms of CO
2
emissions and
fuel consumption performance. It has been chosen
specifically for that reason as an adaptive method to
be compared to the predictive method proposed in this
paper, in order to demonstrate the possible gain from
such predictive methods.
4 SIMULATIONS ON FORD
FOCUS 48V P2 MODEL:
COMPARISON OF
PERFORMANCES
The model of Ford Focus P2 48V hybrid vehicle, fur-
nished by the CostBased method developers, is used
for the next validation. It is representative of all the
energetic flows on the vehicle which are not taken into
account in the optimization model developed in the
first section (such as thermal dynamics, mechanical
transmission losses,...). Note that P
12V
is not constant
in this reference model. The optimal control applied
here uses a constant value of P
12V
= 280W synthe-
sized as mean value from NEDC driving cycle simu-
lations.
The reference vehicle model was developed un-
der the modeling software AMESim
R

. The control
model using predictive and adaptive approaches is de-
veloped under Matlab/Simulink
R

. Therefore, a co-
simulation is performed, a real-time exchange of data
between AMESim and Simulink is implemented. The
simulation is performed on multiple driving cycles:
• NEDC (New European Driving Cycle): CO
2
emissions certification cycle of 11km.
• WLTP (Worldwide harmonized Light vehicles
Test Procedures): CO
2
emissions certification cy-
cle of 23km.
• RCC (Regensburg City Cycle): An urban driving
cycle recorded in Regensburg/Germany of 18km.
• Falkenstein Cycle: An extra-urban driving cycle
recorded in Regensburg/Germany of 59km.
The simulation results are summarized in Fig-
ure 5. The predictive shooting algorithm gives for
Optimal Control for Energy Management of Connected Hybrid Electrical Vehicles
265

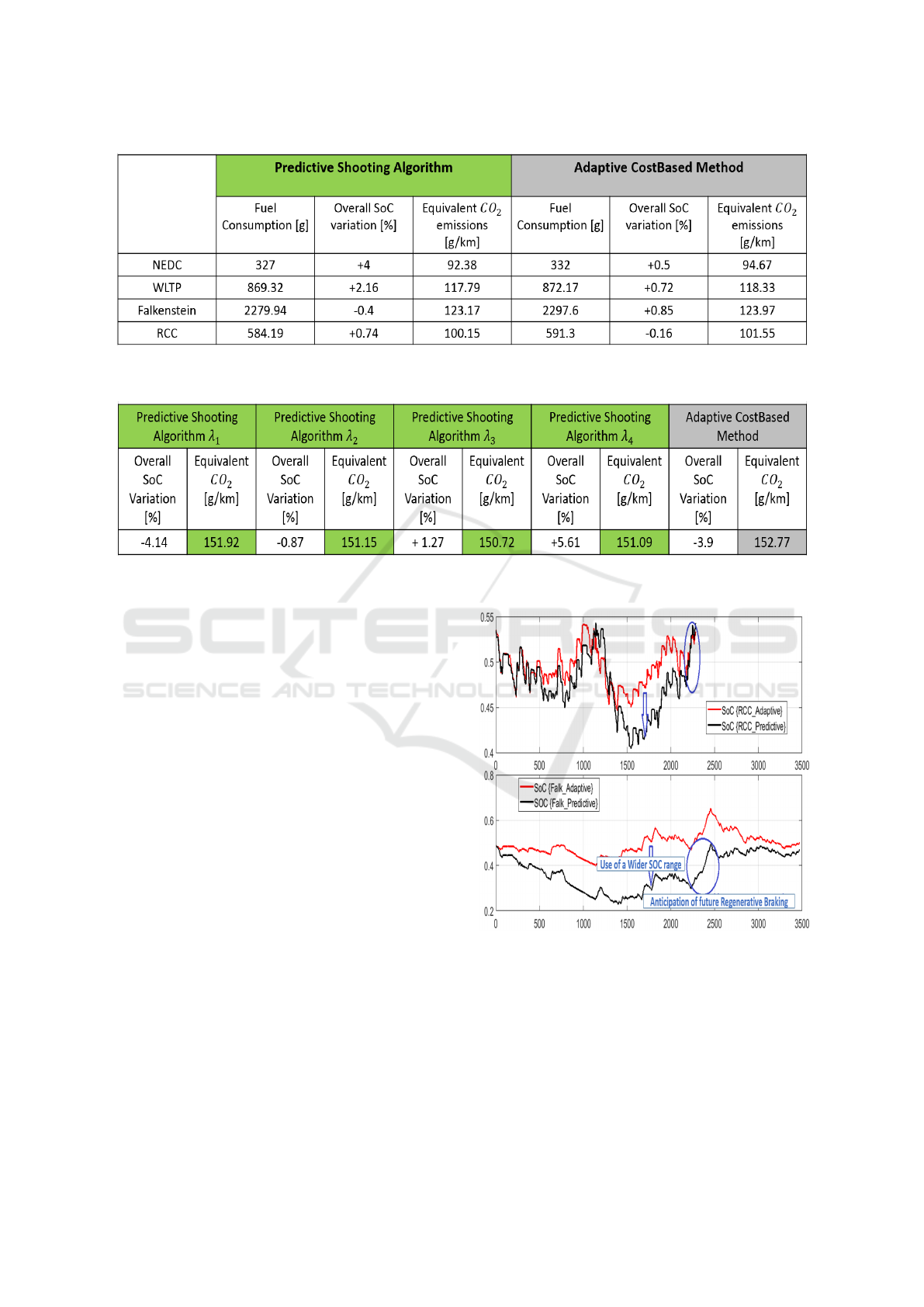
Figure 5: Simulation Results using 48V P2 Hybrid Ford Focus targeting a final SoC of 50% : Predictive TorqueSplit vs
Adaptive TorqueSplit.
Figure 6: Simulation Results using 48V P2 Hybrid Ford Focus targeting a final SoC of 50% with the predictive approach
using slightly different Predictions.
each cycle a better result in fuel consumption. Al-
though the adaptive CostBased method renders a bet-
ter state of charge over the Falkenstein cycle, the CO
2
equivalent is always better with the predictive shoot-
ing algorithm.
Note that the adaptive method is always closer to
the target state of charge while the predictive method
leads to more error. This is due to the fact that the
predictive method is a pure application of the optimal
control theory which is an open loop control. The
calibration of λ is calculated at the beginning of the
trip and is not updated on-line. This λ was calculated
using a prediction which is not 100% reliable. The
distance from the targeted final SoC reflects the ac-
curacy of the prediction: a more accurate prediction
gets closer to SoC
tg
. On the other hand, the adaptive
method keeps track of the SoC on-line and controls λ
to stay close to the targeted value.
However, even if the prediction is not completely
accurate, and the final state of charge obtained by the
open loop predictive approach deviates from the tar-
geted value, the predictive approach still has a better
CO
2
equivalent than the adaptive method. Simula-
tions on an urban cycle of 5km, with slightly different
predictions that render slightly different values of λ
yield the results in Figure 6.
Moreover, the SoC trajectories reveal an identifi-
able behavior of the predictive method: more battery
Figure 7: SoC trajectories (SoC vs Time) over the Falken-
stein cycle: Predictive anticipation of future recoverable en-
ergy VS Adaptive method.
energy is used and the SoC trajectory is wider. This
behavior is what is expected from the use of predic-
tion: the use of more electrical energy that is known to
be available in the future. This behavior is illustrated
in Figure 7, in which are illustrated the SoC trajecto-
ries from RCC and Falkenstein cycles using predic-
tive and adaptive methods. The results presented in
VEHITS 2018 - 4th International Conference on Vehicle Technology and Intelligent Transport Systems
266

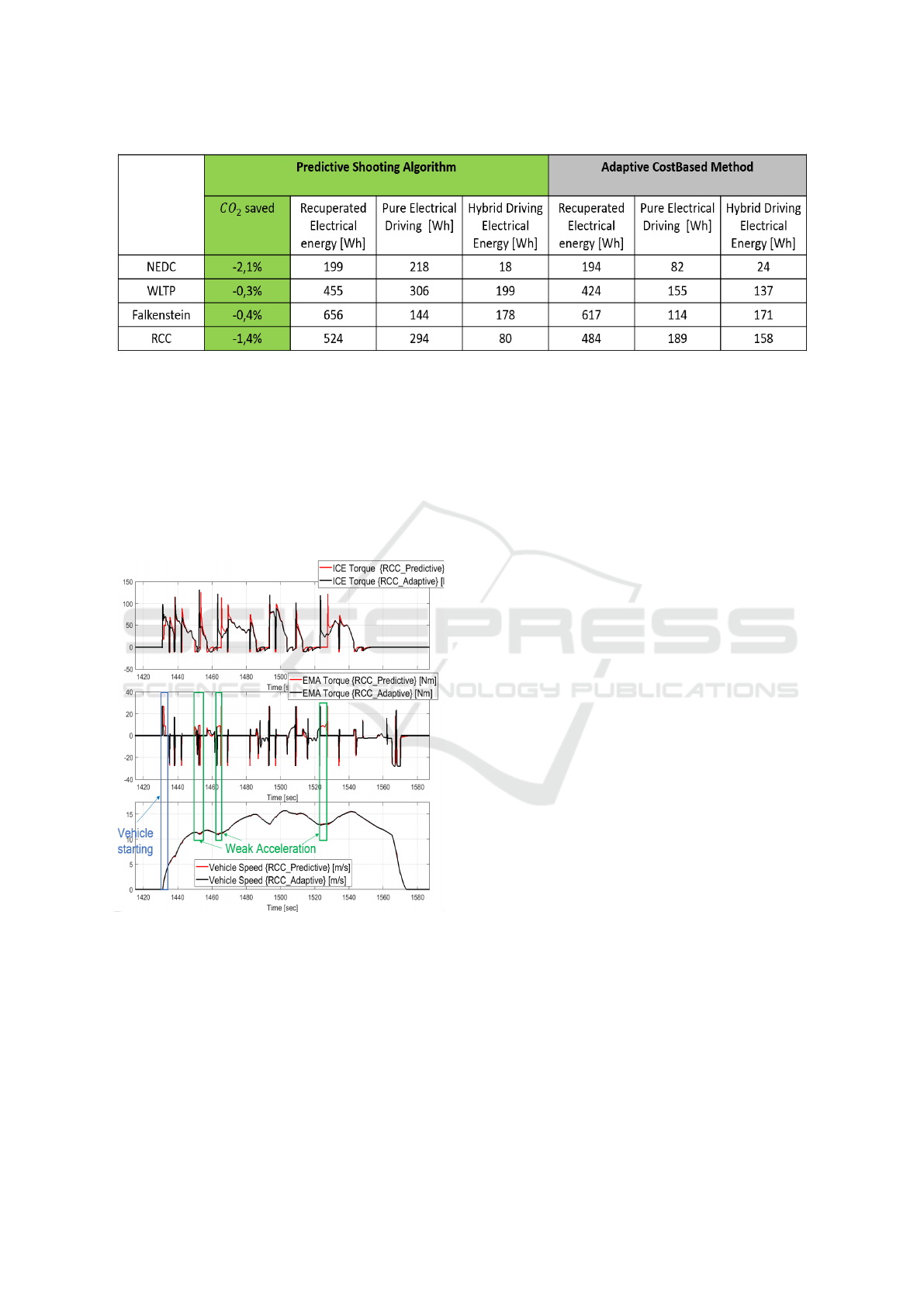
Figure 8: Simulation Results using 48V P2 Hybrid Ford Focus targeting a final SoC of 50% : Predictive TorqueSplit vs
Adaptive TorqueSplit. Analysis of electrical Energy usage.
the table in Figure 8 confirm that tendency, and show
that more electrical energy is used and recovered by
using the predictive approach.
On a local point of view, this tendency is often
translated into a longer pure electrical driving phases,
especially in weak acceleration phases. It also implies
longer use of electrical energy for the vehicle starting
phases, as illustrated in Figure 9.
Figure 9: Local behavior analysis in a part of the Regens-
burg City Cycle.
Nonetheless, the predictive shooting algorithm ap-
proach is not a rule based method and does not guar-
antee the same behavior in every situation. It mathe-
matically guarantees a time-global optimum for the
model based optimal control synthesized from the
TorqueSplit problem, without being predictable in
terms of local behavior. However, it is safe to assume
that the general behavior of anticipation will always
be present, since it represents the most important in-
terest of using predictions about the future path.
The predictive optimal control approach proves
itself to be more efficient than the adaptive one, in
terms of fuel consumption and CO
2
emissions. The
adaptive method has the advantage of a closed loop
on-line control, that makes sure to always reach the
targeted final SoC with a high precision. In addition,
it has a stable behavior, that is reproducible for ev-
ery driving cycle. The predictive approach adapts its
behavior to reach the targeted final S oC with the less
fuel possible, by using the results of optimal control
theory and the prediction of the road. Being an open
loop method, this method has the flaw of not reaching
the exact SoC target, but it still can guarantee an op-
timal equivalent CO
2
. However, if the deviation from
the targeted state of charge is too big, an increase of
fuel consumption may occur, and the CO
2
equivalent
may be worst.
5 CONCLUSIONS
Optimal control theory offers a simple control struc-
ture that guarantees a time-global minimization of the
fuel consumption over the whole trip. From a con-
trol point of view the ICE torque is used to control
the battery State of Charge while minimizing the fuel
mass consumed. Using this formalism, we obtain a
simple control structure that consists of an instanta-
neous minimization of a pondered criteria. The cal-
ibration of this criteria is what makes the difference
between the predictive and the adaptive approaches.
The predictive approach which is a continuity of the
application of optimal control theory to the Torque-
Split problem, fixes a calibration for each road via a
shooting algorithm. This shooting algorithm is fed
with a prediction of the trip. On the other hand, the
adaptive method updates this calibration using infor-
mation about the vehicles actual states.
The use of future information allows the con-
Optimal Control for Energy Management of Connected Hybrid Electrical Vehicles
267

trol to anticipate and use electrical power ranges that
are recoverable due to a future regenerative braking.
The adaptive method, as well as any non predictive
method, would not have the necessary information to
anticipate. Thus, the obtained solution could some-
times be wrongly careful when a recoverable amount
of electrical energy is available.
The predictive strategy yields better fuel con-
sumption and CO
2
emissions on 5 different cycles, in
comparison to the CostBased adaptive method. How-
ever, the method relies on the prediction to be close
enough to the real power demand in order to be able
to approach the targeted state of charge.
Future works will improve the efficiency of the
proposed predictive solution with less simplifications
in the optimization modelling. A more representative
model of the 12V net can be considered. The low volt-
age net model could be introduced in the optimal con-
trol modelling and the state of charge of the 12V bat-
tery can be controlled to reach a targeted final value.
Dynamics such as temperature, and mechanical trans-
mission losses can also be introduced to enhance the
optimal control problem, and make the model closer
to a real vehicle.
ACKNOWLEDGEMENTS
This work was supported by the French Environ-
ment and Energy Management Agency (ADEME)
and Continental Automotive. We also thank our col-
leagues from Continental Automotive who provided
insight and expertise that greatly assisted the research.
REFERENCES
Caux, S., Wanderley-Honda, D., Hissel, D., and Fadel, M.
(2010). On-line energy management for hev based on
particle swarm optimization. In IEEE Vehicle Power
and Propulsion (VPP) Conference, Lille, France.
Delprat, S., Guerra, T., and Rimaux, J. (2003). Control
strategies for hybrid vehicles: Synthesis and evalua-
tion. In Vehicular Technology Conference, 2003. VTC
2003-Fall. 2003 IEEE 58th, Orlando, FL, USA.
He, H., Zhang, J., and Li, G. (2015). Model predictive con-
trol for energy management of a plug-in hybrid elec-
tric bus. In CUE2015-Applied Energy Symposium and
Summit 2015: Low carbon cities and urban energy
systems, Fuzhou, China.
Kermani, S., Trigui, R., Delprat, S., Jeanneret, B., and
Guerra, T. M. (march 2011). Phil implementation of
energy management optimization for a parallel hev on
a predefined trip. In IEEE Transactions on vehicular
technology, Vol. 60, No. 3.
Kim, N., Cha, S., and Peng, H. (september 2011). Optimal
control of hybrid electric vehicles based on pontryagin
minimum principles. In IEEE Transactions on control
systems technology, Vol. 19, No. 5.
Sciarretta, A. and Guzzella, L. (april 2007). Control of
hybrid electric vehicles. optimal energy management
strategies. In IEEE Control Systems Magazine.
Sciarretta, A., Guzzella, L., and Back, M. (2004). A real-
time optimal control strategy for parallel hybrid vehi-
cles with on-board estimation of control parameters.
In in Proc. IFAC Symp. Advances Automotive Control,
Paper 136, pp. 502507, Salerno, Italy.
Steinmauer, G. and del Re, L. (2001). Optimal control of
dual power sources. In Proc. 2001 IEEE Int. Conf.
Control Applications, pp. 422-442, Mexico City, Mex-
ico.
Tribioli, L. and Onori, S. (June 17-19, 2013). Analysis of
energy management strategies in plug-in hybrid elec-
tric vehicles: application to the gm chevrolet volt. In
2013 American Control Conference (ACC), Washing-
ton, DC, USA.
VEHITS 2018 - 4th International Conference on Vehicle Technology and Intelligent Transport Systems
268