A Multi-Channel Software Decoder for the LoRa Modulation Scheme

Pieter Robyns

, Peter Quax

, Wim Lamotte

and William Thenaers

Hasselt University - tUL, Expertise Centre for Digital Media, Martelarenlaan 42, 3500 Hasselt, Belgium

Hasselt University - tUL - Flanders Make, Expertise Centre for Digital Media, Martelarenlaan 42, 3500 Hasselt, Belgium

Hasselt University - tUL, Martelarenlaan 42, 3500 Hasselt, Belgium

Keywords:

LoRa, Software Deﬁned Radio, PHY Layer, Decoder, Signal Processing, Reverse Engineering.

Abstract:

LoRa is a recently introduced modulation scheme speciﬁcally designed for Low-Power Wide-Area Networks.

In this paper, we provide the ﬁrst detailed and complete description of the LoRa PHY layer, and present a

novel methodology for detecting and decoding LoRa frames using Software Deﬁned Radios. Our proposed

decoding approach can efﬁciently decode multiple channels simultaneously in software due to an invariance

towards the signal frequency. Hence, our approach also removes the need for correcting frequency offset errors

imparted by the transmitter or receiver. We have evaluated our decoding technique in a lab setup using three

Software Deﬁned Radios (USRP B210, HackRF, and RTL-SDR) and three commercial off-the-shelf hardware

LoRa transceivers (Microchip RN2483, HopeRF RFM96, and Semtech SX1272). We show that our decoder

is fully compatible with all conﬁgurations of the RN2483 and SX1272, achieving an overall packet error rate

of 0 for a signal-to-noise ratio of 20 dB. The source code of the decoder and datasets used in the evaluation

are made available publicly.

1 INTRODUCTION

In coming years, the industry is expected to show

an increased interest in Low-Power Wide-Area Net-

works (LPWANs) and their applications, such as

smart metering, location tracking, Wireless Sensor

Networks (WSNs), smart transportation systems and

health monitoring (i-SCOOP, 2017). In such net-

works, several low-power embedded devices are typ-

ically deployed in areas of interest, and perform Ma-

chine to Machine (M2M) communication or interact

with services on the internet in order to complete a

certain computing task. For example, an internet-

connected embedded device may be distributed to in-

dividuals suffering from a cardiovascular disease, so

that their condition can be monitored in real time by

doctors.

The heightened attention for these use cases

sparked the creation of several Physical (PHY)-layer

modulation protocols that are optimized for LP-

WANs, i.e. for low power consumption and long

range communications. Examples of these proto-

cols are LoRa (LoRa Alliance, 2017), Sigfox (Sigfox,

2017), Wi-Fi HaLow (Wi-Fi Alliance, 2017), LTE-

M (3GPP, 2017), and Weightless (Weightless, 2017).

Out of those, LoRa is a proprietary, low-power, and

long-range modulation scheme developed by Cycleo

and acquired by Semtech in 2012 (Semtech, 2012).

It is currently among the more popular protocols,

with numerous gateways already deployed on a global

scale (The Things Network, 2017).

Due to its proprietary nature, specialized hard-

ware is required in order to transmit or receive

LoRa messages. Examples of such hardware are the

SX1272 transceiver developed by Semtech (Semtech,

2015b) and the RN2483 transceiver developed by Mi-

crochip (Microchip Technology Inc., 2015). Both

transceivers expose a serial interface to the user. The

serial interface can only be used to make high level

conﬁguration changes to the LoRa modem, and to

transmit or receive payloads using LoRa modulation.

Hence, the entire PHY layer of these transceivers is

abstracted in hardware, and therefore cannot be ac-

cessed or modiﬁed.

Having access to the PHY layer of a wireless

protocol is a desirable feature with many interesting

use cases for research and development. For exam-

ple, recent works have demonstrated the possibility

to ﬁngerprint individual transceivers using only PHY-

layer properties of the signal (Danev et al., 2012;

Robyns et al., 2017; Vo-Huu et al., 2016). This

could be useful for tracking devices or intrusion de-

Robyns, P., Quax, P., Lamotte, W. and Thenaers, W.

A Multi-Channel Software Decoder for the LoRa Modulation Scheme.

DOI: 10.5220/0006668400410051

In Proceedings of the 3rd International Conference on Internet of Things, Big Data and Security (IoTBDS 2018), pages 41-51

ISBN: 978-989-758-296-7

tection. Another use case could be to perform soft-

ware simulations of the PHY layer, e.g. to determine

the effect of various channel conditions without re-

quiring multiple physical deployments of hardware

transceivers (Ben Hamida et al., 2009; Mezzavilla

et al., 2015). As a ﬁnal example, enabling modiﬁca-

tions to the PHY layer allows for rapid prototyping

of improvements in terms of security, performance

or reliability (Bloessl et al., 2013a; Sklivanitis et al.,

2016).

In this paper, we provide several contributions that

aim to bring the advantages of PHY-layer access to

the LoRa modulation scheme. First, we provide a

detailed description of the LoRa PHY layer. This

description includes newly added and undocumented

features of the LoRa speciﬁcation that were reverse

engineered from hardware LoRa transceivers. To the

best of our knowledge, we are the ﬁrst to provide a

complete and validated overview. Second, we present

our algorithms for the detection, synchronization, and

decoding of raw PHY-layer LoRa frames using Soft-

ware Deﬁned Radios (SDRs). These algorithms in-

clude a novel decoding approach and a novel clock

drift correction approach for LoRa, both implemented

in a complete and open-source software LoRa de-

coder using the GNU Radio framework. Our decoder

is capable of decoding multiple channels simultane-

ously in real time regardless of the frame’s network

identiﬁer, similar to the capabilities of “monitoring

mode” devices in context of 802.11 (Wi-Fi). Finally,

we evaluate our decoder in a lab setup, and show that

it can interoperate with hardware LoRa transceivers,

using only inexpensive Commercial Off-The-Shelf

(COTS) SDRs such as the RTL-SDR.

The structure of this paper is as follows. In Sec-

tion 2, we will present an overview of the LoRa PHY

layer in consideration of our ﬁrst contribution. Sec-

tion 3 then shows how this knowledge can be applied

to build a complete software LoRa decoder. In addi-

tion, we detail our novel demodulation and clock drift

correction approaches. Our decoder will be compared

in terms of compatibility with existing LoRa hard-

ware and accuracy in Section 4, followed by a discus-

sion of these results. Works related to this research

will be discussed in Section 5. Finally, in Section 6,

we will make concluding remarks and give directions

for future work in this area of research.

2 LoRa PHY LAYER

In order to correctly decode LoRa-modulated data, a

receiver must sequentially perform seven operations

on the PHY layer, namely detection, synchroniza-

tion, demodulation, deinterleaving, dewhitening, de-

coding, and packet construction. A partial descrip-

tion of these operations can be found in several tech-

nical reports released by Semtech (Seller and Sornin,

2014; Semtech, 2015b; Sornin et al., 2015; Semtech,

2015a) and in the paper presented by Goursaud et al.

(Goursaud and Gorce, 2015). However, the informa-

tion contained within these works is insufﬁcient to

build a decoder that can interoperate with real hard-

ware LoRa transceivers. To this end, we have reverse

engineered a RN2483 LoRa transceiver, and provide

the ﬁrst complete overview of the LoRa PHY layer in

this section.

2.1 Modulation

The LoRa modulation scheme is based on Chirp

Spread Spectrum (CSS) modulation (Goursaud and

Gorce, 2015), and deﬁnes a “chirp” as a single sym-

bol (Semtech, 2015a). A standard, unmodulated lin-

ear chirp is called a “base chirp”, and can be math-

ematically described in function of the time t as fol-

lows (Mann and Haykin, 1991):

x(t) = e

i(ϕ

+2π(

+ f

t))

(1)

where ϕ

is the initial phase, k is the rate of frequency

change, and f

is the initial frequency. Given the

channel bandwidth BW , the parameters f

and k are

set so that the frequency increases from f

−

over the duration T of the chirp. Hence,

= −

and k =

. Here, the chirp duration T

depends on the bandwidth of the signal and on a pa-

rameter called the Spreading Factor (SF) according to

the relation T =

(Seller and Sornin, 2014).

Given that x(t + nT ) = x(t) with n ∈ N, an inte-

ger value i ∈ {0,1}

can be modulated onto the base

chirp by introducing a time shift of

t = Gray

−1

(i)

to the signal in Equation 1, where Gray

−1

stands for

a Gray decoding operation (Gray, 1953). This way,

a symbol is essentially quantized into 2

time shift

bins divided over the bandwidth, called “chips”, that

determine i. Upon reception of a modulated chirp

with an unknown time shift x(t +

t), the chip value

i can be recovered by sampling the signal at the chip

rate and calculating:

i = Gray(argmax(



FFT( x(t +

t)  x(t) )



) ) (2)

where x(t) denotes the conjugate of a base chirp,

the  operator indicates element-wise multiplication,



FFT(x)



signiﬁes the magnitude of the Fast Fourier

Transform (FFT) of x, and Gray stands for Gray en-

coding. Figure 1 shows an example where a value of

IoTBDS 2018 - 3rd International Conference on Internet of Things, Big Data and Security

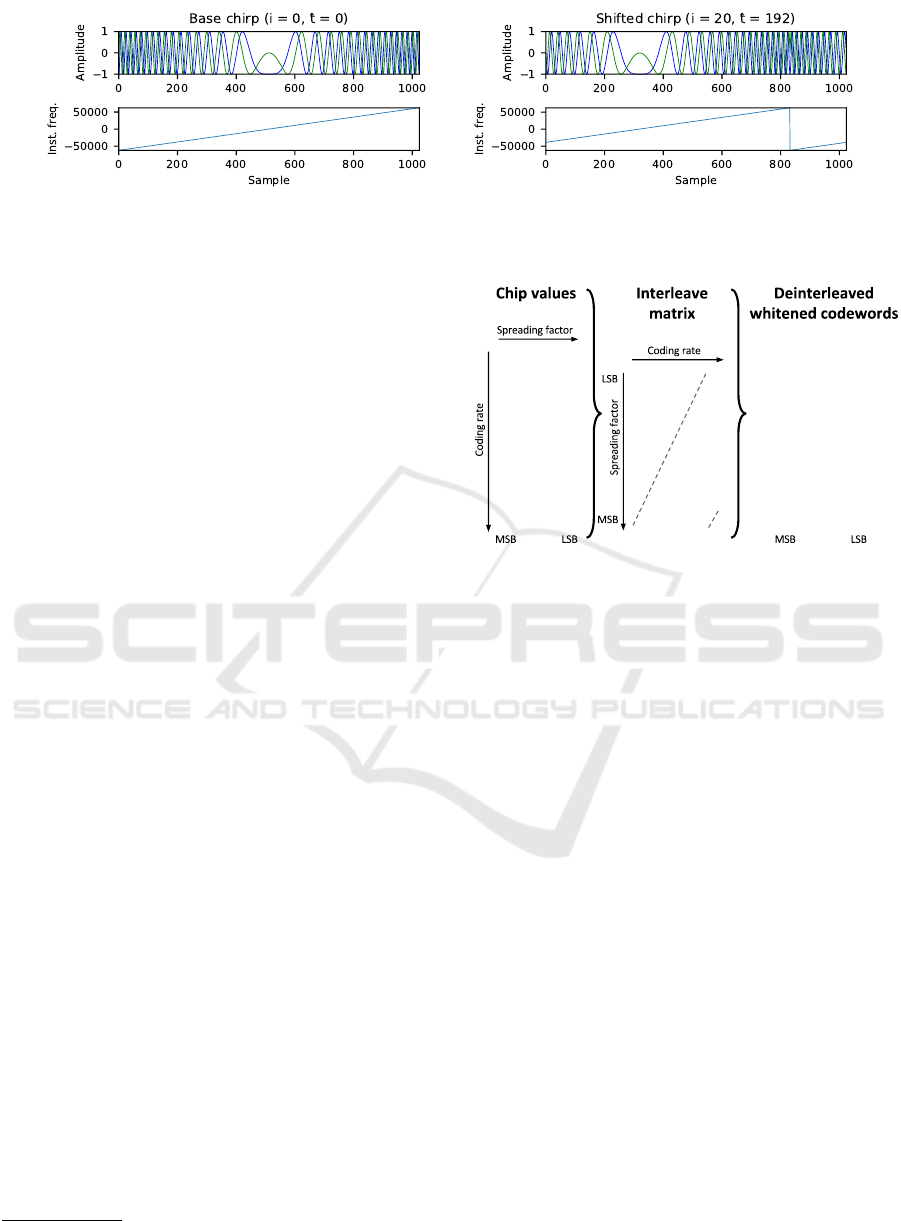
Figure 1: Example of an unmodulated LoRa base chirp and a chirp modulated with i = 20. The top row of ﬁgures shows the

time domain complex signal, whereas the bottom row of ﬁgures shows the instantaneous frequencies of the signals in Hz.

i = 20 is modulated onto the base chirp, shifting it by

192 samples.

2.2 Interleaving

When using the modulation approach described

above, errors can be introduced due to noise, inter-

ference, and time or frequency offsets. These errors

cause the receiver to derive an incorrect chip value

from the modulated symbol. For example, a burst of

noise could cause the peak of the FFT spectrum to ap-

pear at a different chip, therefore corrupting the entire

chip value.

In order to limit the impact of bursty noise to

a single bit error per symbol, multiple chip val-

ues are stacked together such that a bit matrix

{0,1}

SF×(4+CR)

is obtained. Here, the Coding Rate

(CR) or equivalently, the number of parity bits, can

range from 1 to 4. For example, when using SF = 7

and CR = 4, we obtain a matrix {0,1}

7×8

as shown in

Figure 2. A codeword of 4 +CR bits is then obtained

by diagonally deinterleaving the matrix. As such,

the ﬁrst chip value provides all ﬁrst Least Signiﬁcant

Bits (LSBs) of the codewords, the second chip value

provides all second bits of the codewords, etc. The

direction of the interleaving diagonal appears to be

upwards in practice, in contrast to the LoRa patent

where the interleaving diagonal direction is down-

wards

(Seller and Sornin, 2014). Observe that as a

result of the interleaving operation, an entirely cor-

rupted chip value now only affects one bit per code-

word.

The LoRa speciﬁcation also deﬁnes a “reduced

rate” mode, in which the top two rows of the inter-

leaving matrix are discarded. Consequently, the di-

mensions of the matrix become {0,1}

SF−2×(4+CR)

yielding two codewords less after deinterleaving. The

discarded rows correspond to the LSBs of the chip

values, which are more prone to errors because they

correspond to narrower frequency bins in the FFT

Note that this has no impact on the decoding perfor-

mance.

00000010

01011111

10101111

01011100

00100100

11010001

11000111

01110010

11101000

10100011

00000000

00101110

11010001

11111111

1100100

1101010

0010100

0101010

0001110

1011110

1000111

1100110

Figure 2: Diagonal deinterleaving with SF = 7 and CR = 4.

The bits of the third chip value are shown in bold.

spectrum. Therefore, in reduced rate mode, a de-

creased data rate is traded for an increased robust-

ness to noise. The PHY layer header of LoRa frames

is always transmitted in reduced rate mode, whereas

the payload bytes are only transmitted in reduced rate

mode when SF 11 or SF 12 is used (Semtech, 2015b,

p. 28, 112).

2.3 Coding

After deinterleaving, a number of codewords of size

4 +CR are obtained by the receiver. The codewords

of the frame payload are “whitened” in order to keep

the data Direct Current (DC)-free (Semtech, 2015b,

p. 75). Here, whitening is deﬁned as an opera-

tion where the data is XOR-ed with a 9-bit Linear

Feedback Shift Register (LFSR) after synchroniza-

tion (Semtech, 2015b, p. 72). The used coding al-

gorithm is not explicitly mentioned in the patent or

chipset datasheet (Seller and Sornin, 2014; Semtech,

2015b), leaving this an open choice to the vendor.

For the transceivers we considered during our tests

(see Section 3), we have reverse engineered the cod-

ing scheme and discovered that a modiﬁed version of

4/(4 + CR) Hamming coding is utilized in practice.

Hence, each codeword results in 4 data bits when de-

coded, which are subsequently parsed according to

A Multi-Channel Software Decoder for the LoRa Modulation Scheme

the LoRa frame structure. In Section 3.3, we will dis-

cuss our approach for decoding the data further.

2.4 Frame Structure

On the PHY layer, LoRa deﬁnes a frame struc-

ture with the following sequentially transmitted

ﬁelds (Semtech, 2015b, p. 27–29):

• Preamble: A variable-sized sequence of base

chirps that is used for time and frequency synchro-

nization.

• Frame synchronization symbols: Two modu-

lated chirps whose value can be used as a net-

work identiﬁer. A hardware LoRa transceiver will

drop frames containing synchronization symbols

that do not match a preconﬁgured value.

• Frequency synchronization symbols: Two con-

jugate base chirps followed by a conjugate chirp

with duration

, which can both be used for ﬁne

frequency synchronization.

• Header (optional): Field containing the payload

length, used data rate, a bit indicating the presence

of a payload Cyclic Redundancy Check (CRC),

and 1-byte header checksum. A CR of 4 is always

used in combination with reduced rate mode for

the header

(Seller and Sornin, 2014). The header

can be explicitly transmitted (explicit mode) or

left out of the frame (implicit mode). In the latter

case, the transmitter and receiver must conﬁgure

the coding rate and CRC presence bit beforehand.

• Payload: Variable-length ﬁeld containing the

transmitted Medium Access Control (MAC) layer

data and a 2-byte CRC of this data.

Figure 3 shows an example LoRa signal and its

frame structure.

2.4.1 Header Structure

The exact length and bit order of the ﬁelds in the PHY

layer header are not explicitly stated in the speciﬁca-

tions. However, since the transmission of an explicit

header requires a SF of at least 7, and the header is al-

ways transmitted with CR = 4 at a reduced rate (Seller

and Sornin, 2014), the header must ﬁt in an inter-

leaving matrix of {0,1}

(7−2)×8

. Therefore, the header

length must be equal to 5 codewords of 8 bits, i.e. 40

bits in total. Any remaining bits in the interleaving

matrix are used for the payload.

Since the header contains the payload length and cod-

ing rate, it is essential that these ﬁelds are decoded correctly.

Hence the increased robustness measures.

After decoding, the header data thus has a length

of 40 ·

= 20 bits or 2.5 bytes. We have experimen-

tally determined that when transmitting data using a

Microchip RN2483 LoRa transceiver, the left-to-right

order of the PHY header is as follows: a single pay-

load Length byte, followed by a nibble for the CR

and MAC CRC presence, the High Nibble (HN) of the

header checksum, and ﬁnally the Low Nibble (LN) of

the header checksum

. An overview of these ﬁelds is

given in Figure 4.

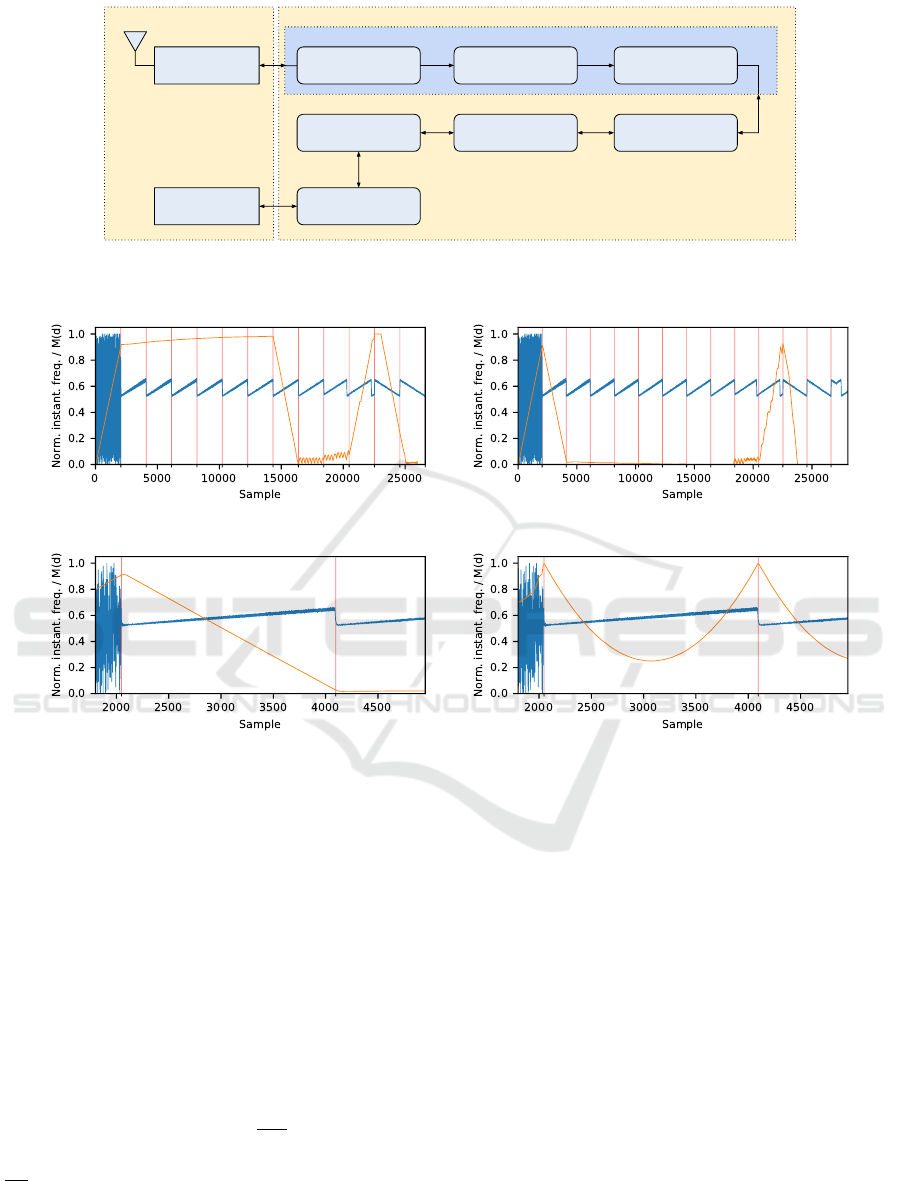
3 SOFTWARE DEMODULATOR

We have implemented the complete PHY layer of

LoRa in software, using the open source GNU Ra-

dio signal processing framework. The source code

of the decoder is publicly available on Github

. An

overview of the decoder components is given in Fig-

ure 5.

3.1 Detection and Synchronization

As a ﬁrst step in the demodulation process, the re-

ceiver must detect the LoRa preamble. To this end,

we exploit the repeating property of the preamble by

using the Schmidl-Cox algorithm, which deﬁnes two

quantities P(d) and R(d) as follows (Schmidl and

Cox, 1997):

P(d) =

L−1

∑

m=0

∗

t+m

t+m+L

) (3)

R(d) =

L−1

∑

m=0

t+m+L

(4)

where L is the length of a symbol, t is the sam-

ple index of the complex signal x, and x

∗

denotes the

complex conjugate of x. Next, P(d) and R(d) are used

to calculate a timing metric M(d):

M(d) =

|P(d)|

R(d)

(5)

The timing metric M(d) essentially calculates a

normalized autocorrelation of length L over two sym-

bols, which will be maximal when two consecutive

symbols are encountered in the signal. An added

advantage of this approach is that any errors intro-

duced by the channel or SDR (e.g. interference,

Carrier Frequency Offset (CFO) and Sampling Fre-

quency Offset (SFO) errors), consistently inﬂuence

Only the 5 LSBs of the checksum byte appear to be

used in practice.

https://github.com/rpp0/gr-lora

IoTBDS 2018 - 3rd International Conference on Internet of Things, Big Data and Security

Figure 3: Annotated spectogram of an example LoRa signal transmitted with the RN2483 LoRa transceiver using SF 11 and

CR 5, and received with a USRP B210 SDR.

Length Options

Chk.

(LN)

MAC Payload MAC CRC

Byte 0 1 2 3 n - 1

Bit 7 6 5 4 3 2 1 0

Has

CRC

Chk.

(HN)

Figure 4: The ﬁelds of the LoRa PHY layer.

both symbols and therefore minimally affect the result

of the correlation. To efﬁciently compute Equation 3

– 5 in software, we use Single Instruction, Multiple

Data (SIMD) instructions provided by Vector Opti-

mized Library of Kernels (VOLK). Figure 6 (a) shows

the resulting value of the timing metric M(d) when

evaluated for a complex LoRa signal. Observe that

the function reaches a plateau around sample 2,500,

which conﬁrms the presence of a preamble.

Although the Schmidl-Cox algorithm can deter-

mine the presence of a preamble effectively, the

plateau of the timing metric leads to uncertainty as

to the start of the symbol (Schmidl and Cox, 1997).

Wang et al. proposed a variation on the Schmidl-

Cox algorithm where M(d) is subtracted with a time-

delayed version M

(d) of itself (Wang et al., 2003).

Consequently, the plateau becomes a peak as shown

in Figure 6 (b), making it possible to take the argmax

of the timing metric in order to estimate the start of the

preamble. However, for LoRa signals, this estimate is

not sufﬁciently accurate, as shown in Figure 6 (c).

To solve this problem, we only use the standard

Schmidl-Cox metric with a threshold to assert that

the second symbol window is located anywhere in-

side the preamble. Next, we generate an ideal, lo-

cally synthesized base chirp and calculate its instan-

taneous frequency ω

(t), as well as the instantaneous

frequency of the received LoRa signal ω(t). Finally,

a sliding window normalized cross-correlation is per-

formed, and the index of the maximum value of the

cross-correlation is chosen as the starting point of the

symbol:

symbol start = argmax

i∈{0,1,...L}

(ω

? ω)(i) (6)

The result of this operation is visualized in Fig-

ure 6 (d). Note that by performing the cross-

correlation on the instantaneous frequency of the sig-

nals instead of their complex values, any CFO er-

rors imparted by the channel are automatically miti-

gated similarly to the Schmidl-Cox algorithm. Thus,

the accuracy of the synchronization is not affected

by the CFO. On the contrary, if one would consider

the complex-valued signals, a correction of frequency

errors introduced by the channel and SDR would

have to be performed before the signal can be cross-

correlated with the locally synthesized chirp.

At last, in order to verify the correctness of the

time synchronization, we threshold against the max-

imum correlation coefﬁcient between the instanta-

neous frequency of the locally generated chirp and re-

ceived chirp. The LoRa frame is rejected if the corre-

lation coefﬁcient falls below a certain tolerance value,

since this indicates a failed synchronization or false

positive during the detection stage (see Section 3.1).

3.2 Demodulation

Following synchronization, the receiver can demodu-

late the chip values as discussed in Section 2. How-

ever, the FFT-based demodulation approach speciﬁed

in (Seller and Sornin, 2014) is sensitive to frequency

offset errors, which cause the magnitudes of the FFT

(and thus the chip values) to shift. Therefore, an ac-

curate frequency synchronization is required. Fur-

thermore, this synchronization must be applied for

each LoRa channel separately in order to fulﬁll our

requirement of multi-channel decoding motivated in

Section 1.

Since channelization and separate processing of

each channel is an expensive operation to perform in

A Multi-Channel Software Decoder for the LoRa Modulation Scheme

Hardware

SDR

Sampling &

Filtering

Antenna

Preamble

detection

Synchronization

ModulationInterleavingWhitening

Coding

Host

Software

Receive chain specific

Figure 5: An overview of the LoRa decoder components, showing the various logical processing blocks required for the

transmission and reception of baseband I/Q samples with an SDR.

(a) Schmidl-Cox (b) Modiﬁed Schmidl-Cox

Figure 6: Normalized instantaneous frequency of a LoRa signal (blue) and the normalized Schmidl-Cox timing metric M(d)

(orange). The vertical red lines indicate the symbol window length L. In (a), the timing metric reaches a plateau upon

encountering two consecutive and identical symbols. A modiﬁed version (b) results in a single peak at the ﬁrst symbol, but is

insufﬁciently accurate to determine the start of the preamble (c). Our synchronization using the normalized cross-correlation

of the instantaneous frequency (d) shows a sharp peak at the start of each preamble symbol.

software, we have developed a novel demodulation

technique that is independent of the frequency. Our

technique removes the need for frequency corrections

and allows to decode LoRa frames in real time on all

channels and without additional processing overhead,

but at the cost of a reduced robustness compared to the

FFT approach discussed in Section 2.1. This tradeoff

will be discussed in Section 4.

In our methodology, we ﬁrst calculate the instanta-

neous angular frequency ω[t] =

dϕ[t]

. We then smooth

and decimate ω[t] with a constant decimation factor of

, where s

is the sampling frequency. This ensures

that the number of samples in ω[t] is equal to 2

Subsequently, the digital gradient of f is calculated:

[ω[t]] = ω[t + 1] − ω[t] (7)

This operation can be intuitively seen as a high

pass ﬁlter on the instantaneous frequency, or as the

second order derivative of the phase. Since the fre-

quency of a base chirp linearly increases with k, i.e.

ω(t) = kt + f

, its derivative ω

(t) is equal to k. For

a modulated chirp however, D

will exhibit a sharp

peak at the transition from high to low frequency. If

present, the position of the peak indicates the time

shift

t. Otherwise, the time shift is equal to 0 (base

chirp).

IoTBDS 2018 - 3rd International Conference on Internet of Things, Big Data and Security

p0 p1 p3 p2 d3 d2 d1 d0

1 1 0 1 0 0 0 1

p0 p1 d3 p2 d2 d1 d0 p3

1 1 0 1 0 0 1 0

Parity:

Data:

0111

0001

LSB

MSB

Bit 7 6 5 4 3 2 1 0

Figure 7: The bit mapping of an example Hamming code-

word used in LoRa (top) to a standard Hamming code (bot-

tom), for a CR of 4 and data 0x1.

3.3 Decoding

In the decoding stage, the chip values are deinter-

leaved to form codewords of 4 +CR bits. The ﬁrst 8

codewords of a frame can be directly decoded to form

the PHY-layer header. On the other hand, we found

that the payload symbols must be dewhitened ﬁrst.

Although the datasheet released by Semtech speciﬁes

the usage of a 9-bit LFSR, a different and unknown

whitening LFSR appears to be implemented in prac-

tice (Knight, 2016; Blum, 2017). We have reverse en-

gineered the whitening sequence using the following

approach.

If we represent the whitening process as c

( j)

⊕ w

( j)

with c

the whitened codeword, c the un-

whitened codeword, w the output of the LFSR and j

the byte index, we can determine w

( j)

by transmit-

ting a known codeword c

( j)

and calculating w

( j)

⊕c

( j)

. For example, a payload with all codewords

set to zero will result in w

( j)

= c

( j)

⊕0, or the whiten-

ing sequence itself. Hence, after transmitting a pay-

load consisting of all zeros, the resulting whitening

sequence can be retrieved and stored in a lookup ta-

ble.

With knowledge of the whitening sequence w,

the last step after dewhitening is to perform Ham-

ming decoding on the codewords. We found that in

LoRa transceivers, the data bits are positioned at bit

indices 0, 1, 2, and 3 of a byte. This is in contrast

to standard Hamming which uses indices 1, 2, 3, and

5 as data bits. This mapping is graphically depicted

in Figure 7. After extraction of the data bits and er-

ror correction or detection based on the present parity

bits, the demodulator outputs the data to a UDP socket

for further processing by higher-layer applications.

3.4 Clock Drift Correction

The crystal oscillators in the SDR and LoRa

transceiver inherently have a relative and unknown

clock drift, which causes a loss of synchronization

over time. This is especially problematic for long pay-

loads in combination with higher SFs due to the sym-

bol lengths in these conﬁgurations. To correct for the

clock drift, we propose a blind estimation technique

that exploits oversampling of the transmitted signal at

a rate of N.

As a ﬁrst step, our technique requires an accurate

initial acquisition of the timing offset using the algo-

rithm discussed in Section 3.1. Assuming that the

timing error per symbol ∆t, measured in number of

samples, satisﬁes the inequality |∆t| <

, we can de-

termine ∆t as follows:

1. The symbol is demodulated normally as described

in Section 3.2, in order to obtain the chip value i

and the time shift

2. At the receiver, a locally generated ideal upchirp

is now modulated using i, which introduces a time

shift of

on the local signal (see Section 2).

3. Since the locally generated chirp is not subject to

relative clock drift, the timing error is: ∆t =

−

The receiver can now correct

t by adding a time

offset of ∆t to the received signal.

Note that if the timing error for a single sym-

bol |∆t| ≥

, the decoder will incorrectly determine

the chip value i and therefore propagate the error to

subsequent symbols. For this reason, we interpo-

late from

t to

t + ∆t rather than setting the value di-

rectly. This mitigates the effect of single-symbol de-

modulation errors on the clock drift correction algo-

rithm. A higher oversampling rate N allows for more

ﬁne-grained timing error corrections at the cost of in-

creased processing overhead.

4 EVALUATION

Our demodulator was evaluated in a lab setup us-

ing different SDR models and LoRa hardware.

More speciﬁcally, we have performed tests with the

RN2483, SX1272 and RFM96 conﬁgured as trans-

mitters and the Ettus B210 USRP, HackRF, and RTL-

SDR conﬁgured as receivers. Each test was per-

formed using a carrier frequency of 868.1 MHz, a

sample rate of 1 Msps, and a distance between the

transmitter and receiver of about 1 meter. The source

code required for reproducing the test results and

datasets from the accuracy experiments are publicly

available on Github

Although the LoRa patent speciﬁes the usage of “pilot”

symbols for tracking timing (Seller and Sornin, 2014), these

symbols appear to be absent in practice. We therefore need

to make use of blind estimation techniques.

https://github.com/rpp0/lora-decoder-paper

A Multi-Channel Software Decoder for the LoRa Modulation Scheme

4.1 Compatibility

In a ﬁrst experiment, we evaluated the compatibil-

ity of our decoder with hardware LoRa transceivers.

Here, we used the USRP as the receiver and RN2483,

SX1272 and RFM96 as transmitters. The com-

patibility was evaluated by transmitting the pay-

load “0123456789abcdef” 100 times for all possible

combinations of CR and SF, and checking the number

of correctly decoded frames. A conﬁguration is con-

sidered compatible when transmitted LoRa frames are

consistently correctly decoded under ideal channel

conditions and a high Signal-to-Noise Ratio (SNR).

The results of this experiment are shown in Ta-

ble 1. Observe that the only incompatible con-

ﬁgurations are SF 11 and SF 12 for the RFM96

transceiver. After a manual inspection, we found that

the cause of this incompatibility is due to the fact that

the RFM96 transceiver does not enable the reduced

data rate mode as mandated in the LoRa speciﬁca-

tion (Semtech, 2015b, p. 28). In fact, even when

transmitting a message from the RFM96 to either the

hardware SX1272 or RN2483 hardware transceivers,

the resulting frame is always corrupted for SF 11 and

SF 12. When we manually disabled reduced data

rate mode in our decoder, we achieved full compat-

ibility with all devices. This conﬁrms that the is-

sue lies within the hardware implementation of the

RFM96, and shows that our decoder can be used to

troubleshoot incompatibilities between LoRa devices

from different vendors.

4.2 Accuracy

In the accuracy experiments, we measured the Packet

Error Rate (PER), i.e. the ratio of erroneous packets

received over the total number of packets transmitted,

for a fully compatible transmitter conﬁgured with SF

7 and CR 4. We also artiﬁcially introduce two types

of channel distortions to the I/Q signal at the receiver,

namely Gaussian white noise and CFOs.

Figure 8 shows the effect of artiﬁcial Gaussian

white noise on the decoding accuracy when using a

SF of 8 and CR of 4, the RN2483 as a transmitter,

and the HackRF, RTL-SDR and USRP SDRs as re-

ceivers. The receivers were each conﬁgured with a

receive gain of 10 dB, and the transmit power of the

RN2483 was conﬁgured to 1 dB. Note that even so,

the effective receive gain between the SDRs differs

due to their different hardware and antenna designs.

From the ﬁgure we can derive that a SNR around 20

dB is at least required in order to obtain a PER of 0

for all SDRs.

In Figure 9 (a), we used the USRP to add Gaus-

Figure 8: The effect of artiﬁcial Gaussian white noise on

the accuracy of the decoder. The PER of our decoder for all

evaluated SDRs approaches 0 around a SNR of 20 dB.

sian noise at the transmitter instead of the receiver

in order to compare our decoder (RTL-SDR) with a

hardware LoRa transceiver (RN2483). For this ex-

periment, both receivers were placed at an equal dis-

tance from the USRP, and 100 frames with a payload

of “0123456789abcdef” were transmitted to calcu-

late the PER. Observe that the RN2483 is still ca-

pable of receiving frames well below the noise ﬂoor,

whereas our decoder stops receiving any frames at 0

dB SNR. At this point, the transient of the gradient

cannot be detected by our gradient-based decoding al-

gorithm due to the presence of excess noise.

On the other hand, when we introduce a CFO in-

stead of Gaussian noise to the transmitted signal, our

decoder outperforms the hardware for a CFO larger

than 50 kHz or when transmitting at a different chan-

nel as shown in Figure 9 (b)

. The hardware device

must be retuned in order to capture frames from a dif-

ferent channel, whereas our decoder is capable of cap-

turing frames from multiple channels simultaneously.

Based on these observations, we conclude that our

decoding technique essentially trades ﬂexibility (i.e.,

being able to decode multiple channels simultane-

ously at no additional cost) for an increased sensitivity

to Gaussian noise. Although the increased sensitivity

to noise reduces the functioning range of the receiver,

the ﬂexibility of our approach allows for building a

fully compatible and multi-channel LoRa monitoring

device at a very low cost. We therefore believe our

software decoder is especially suited for research pur-

poses. In fact, in a previous work, the authors have

used the discussed techniques to extract PHY-layer

features from LoRa signals and ﬁngerprint individual

transceivers (Robyns et al., 2017).

Note that at 125 kHz, the PER of the RN2483 decreases

momentarily back to 0.2. This could possibly be explained

by the CFO causing the FFT peak to wrap back to an ap-

proximately correct position.

IoTBDS 2018 - 3rd International Conference on Internet of Things, Big Data and Security

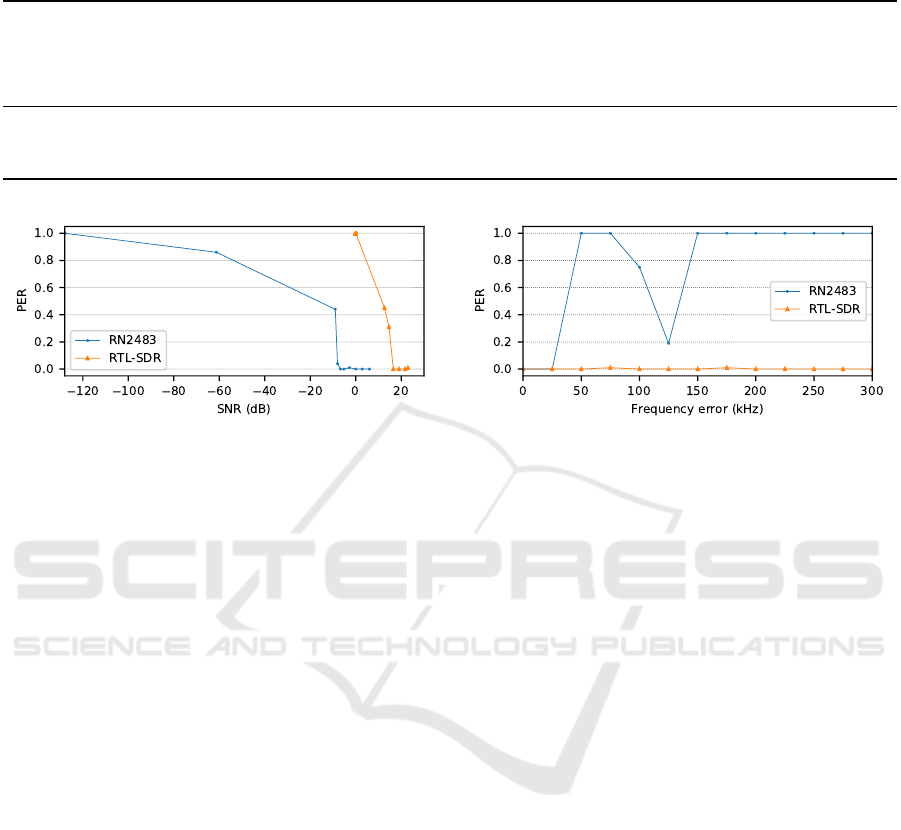
Table 1: Results of the compatibility experiment, showing the LoRa transceivers and conﬁgurations for which our decoder

was able to successfully decode frames.

Transceiver

SF 7, CR 1

SF 7, CR 2

SF 7, CR 3

SF 7, CR 4

SF 8, CR 1

SF 8, CR 2

SF 8, CR 3

SF 8, CR 4

SF 9, CR 1

SF 9, CR 2

SF 9, CR 3

SF 9, CR 4

SF 10, CR 1

SF 10, CR 2

SF 10, CR 3

SF 10, CR 4

SF 11, CR 1

SF 11, CR 2

SF 11, CR 3

SF 11, CR 4

SF 12, CR 1

SF 12, CR 2

SF 12, CR 3

SF 12, CR 4

Implicit

Custom module (RN2483) 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 N/A

Pycom LoPy (SX1272) 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 N/A

Dragino Pi HAT (RFM96) 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 7 7 7 7 7 7 7 7 3

Only device in our possession with an API for sending frames in implicit mode. A custom header appears to be transmitted by the RFM96 in this mode.

(a) (b)

Figure 9: Comparison between the RTL-SDR using our software decoder versus a hardware RN2486 LoRa transceiver in

terms of resistance to Gaussian noise (a) and resistance to frequency offset errors (b). Due to the properties of our gradient-

based decoding algorithm, our decoder is shown to be unaffected by frequency errors at the cost of a signiﬁcantly higher

sensitivity to Gaussian noise compared to the RN2483.

5 RELATED WORK

A high-level system architecture overview of LoRa is

given by Centenaro et al. (Centenaro et al., 2016).

Sikken has provided a general overview of the

LoRa frame structure and decoding stages, but does

not discuss the low level details of the modula-

tion (Sikken, 2017). Goursaud et al. have provided a

detailed and formal analysis of LoRa modulation, but

do not discuss the interleaving, whitening and cod-

ing (Goursaud and Gorce, 2015).

A ﬁrst complete analysis of the LoRa PHY was

presented by Knight (Knight, 2016). However, in

their work, it is assumed that the dewhitening op-

eration is performed before deinterleaving, that the

header is whitened, and that a different interleaving

pattern is used than the diagonal interleaving speci-

ﬁed in (Seller and Sornin, 2014). Based on our own

experiments, we concluded that these claims are in-

accurate. A decoder named gr-lora was developed

based on their analysis, but appears to only be able

to decode short frames transmitted without a header.

We believe this limitation is the result of errors made

during their reverse engineering process.

Other software LoRa decoders for SDRs have

been developed by Blum et al. (Blum, 2017) and

by Project Sdrangelove (RTL-SDRangelove, 2017).

However, we were unable to decode any frames trans-

mitted by hardware LoRa transceivers using these de-

coders. Finally, at the time of writing, none of the

decoders in other works have developed a clock drift

correction algorithm for decoding long LoRa frames.

Besides work on LoRa, GNU Radio based de-

coders have previously been developed to decode pro-

tocols such as Global System for Mobile Communi-

cations (GSM) (Alyafawi et al., 2014; Krysik, 2017),

Long Term Evolution (LTE) (Demel et al., 2015), and

802.11 (Bloessl et al., 2013b; Vo-Huu et al., 2016)

using SDRs.

6 CONCLUSIONS AND FUTURE

WORK

In this paper, we have provided an in-depth exami-

nation of the LoRa PHY layer, and demonstrated our

open source LoRa software decoder, which is imple-

mented using the GNU Radio framework. Our de-

coder can be used in real time with inexpensive SDRs

such as the RTL-SDR, and is able to interoperate with

existing LoRa transceivers. A set of frequency in-

variant techniques for the detection, demodulation,

A Multi-Channel Software Decoder for the LoRa Modulation Scheme

and clock drift correction of LoRa frames were intro-

duced, which result in the capability to decode mul-

tiple channels simultaneously in real time, at the cost

of an increased sensitivity to noise compared to COTS

LoRa radios. Our evaluation shows that a SNR of at

least 20 dB is required for the PER to approach 0.

In future work, a number of aspects of the decoder

can be further improved upon. Most importantly, the

robustness of the decoder could be improved to ap-

proach the performance of LoRa hardware, which is

a challenging problem given the limited available re-

sources and timing constraints in real-time software

decoders. Another scenario that was not yet consid-

ered in this work is the handling of collisions between

LoRa frames, which could occur on a busy channel.

Finally, we hope that the access to the PHY layer pro-

vided by our work will support the development of

future improvements in context of LoRa.

ACKNOWLEDGEMENTS

This research was funded by a Ph.D. Grant of the

Research Foundation Flanders (FWO), grant number

1S14916N.

REFERENCES

3GPP (2017). LTE Release 13. http://www.3gpp.org/

release-13. Accessed: 9 October 2017.

Alyafawi, I., Dimitrova, D. C., and Braun, T. (2014). Real-

time passive capturing of the GSM radio. In IEEE

International Conference on Communications (ICC),

pages 4401–4406. IEEE.

Ben Hamida, E., Chelius, G., and Gorce, J. M. (2009). Im-

pact of the physical layer modeling on the accuracy

and scalability of wireless network simulation. Simu-

lation, 85(9):574–588.

Bloessl, B., Leitner, C., Dressler, F., and Sommer, C.

(2013a). A GNU radio-based IEEE 802.15. 4 testbed.

12. GI/ITG KuVS Fachgespr

ach Drahtlose Sensor-

netze (FGSN 2013), pages 37–40.

Bloessl, B., Segata, M., Sommer, C., and Dressler, F.

(2013b). An IEEE 802.11 a/g/p OFDM Receiver for

GNU Radio. In Proceedings of the second workshop

on Software radio implementation forum, pages 9–16.

ACM.

Blum, J. (2017). LoRa SDR project. https://github.

com/myriadrf/LoRa-SDR. Accessed: 10 October

2017.

Centenaro, M., Vangelista, L., Zanella, A., and Zorzi, M.

(2016). Long-Range Communications in Unlicensed

Bands: the Rising Stars in the IoT and Smart City Sce-

narios. IEEE Wireless Communications, 23.

Danev, B., Zanetti, D., and Capkun, S. (2012). On physical-

layer identiﬁcation of wireless devices. ACM Comput-

ing Surveys (CSUR), 45(1):6.

Demel, J., Koslowski, S., and Jondral, F. K. (2015). A LTE

receiver framework using GNU Radio. Journal of Sig-

nal Processing Systems, 78(3):313–320.

Goursaud, C. and Gorce, J.-M. (2015). Dedicated networks

for IoT: PHY/MAC state of the art and challenges.

EAI endorsed transactions on Internet of Things.

Gray, F. (1953). Pulse code communication. US Patent

2,632,058.

i-SCOOP (2017). Wireless Internet of Things connec-

tivity: LPWAN IoT forecasts 2017. https://www.i-

scoop.eu/internet-of-things-guide/iot-spending-

2020/wireless-iot-lpwan-forecasts-predictions-2017/.

Accessed: 10 October 2017.

Knight, M. (2016). Reversing LoRa: Exploring Next-

Generation Wireless. GRCon.

Krysik, P. (2017). GNU Radio blocks and tools for

receiving GSM transmissions. https://github.com/

ptrkrysik/gr-gsm. Accessed: 10 October 2017.

LoRa Alliance (2017). LoRa Alliance home page.

https://www.lora-alliance.org/. Accessed: 9 October

2017.

Mann, S. and Haykin, S. (1991). The chirplet transform:

A generalization of Gabor’s logon transform. Vision

Interface ’91, pages 205–212. ISSN 0843-803X.

Mezzavilla, M., Dutta, S., Zhang, M., Akdeniz, M. R.,

and Rangan, S. (2015). 5G mmwave module for the

ns-3 network simulator. In Proceedings of the 18th

ACM International Conference on Modeling, Analysis

and Simulation of Wireless and Mobile Systems, pages

283–290. ACM.

Microchip Technology Inc. (2015). Low-Power Long

Range LoRa Technology Transceiver Module.

http://ww1.microchip.com/downloads/en/DeviceDoc/

50002346A.pdf. Accessed: 10 October 2017.

Robyns, P., Marin, E., Lamotte, W., Quax, P., Singel

ee,

D., and Preneel, B. (2017). Physical-layer ﬁngerprint-

ing of LoRa devices using supervised and zero-shot

learning. In Proceedings of the 10th ACM Conference

on Security and Privacy in Wireless and Mobile Net-

works, pages 58–63. ACM.

RTL-SDRangelove (2017). Github project page.

https://github.com/hexameron/rtl-sdrangelove.

Accessed: 10 October 2017.

Schmidl, T. M. and Cox, D. C. (1997). Robust frequency

and timing synchronization for OFDM. IEEE trans-

actions on communications, 45(12):1613–1621.

Seller, O. and Sornin, N. (2014). Low power long range

transmitter. EP Patent App. EP20,130,154,071.

Semtech (2012). Semtech Acquires Wireless Long Range

IP Provider Cycleo. http://investors.semtech.com/re

leasedetail.cfm?ReleaseID=655335. Accessed: 9 Oc-

tober 2017.

Semtech (2015a). LoRa Modulation Basics. http://www.

semtech.com/images/datasheet/an1200.22.pdf. Ac-

cessed: 9 October 2017.

Semtech (2015b). SX1272/73 - 860 MHz to 1020 MHz

Low Power Long Range Transceiver Datasheet. http://

IoTBDS 2018 - 3rd International Conference on Internet of Things, Big Data and Security

www.semtech.com/images/datasheet/sx1272.pdf. Ac-

cessed: 10 October 2017.

Sigfox (2017). Sigfox home page. https://www.sigfox.

com/. Accessed: 9 October 2017.

Sikken, B. (2017). Decoding LoRa. https://revspace.nl/ De-

codingLora. Accessed: 10 October 2017.

Sklivanitis, G., Gannon, A., Batalama, S. N., and Pa-

dos, D. A. (2016). Addressing next-generation wire-

less challenges with commercial software-deﬁned ra-

dio platforms. IEEE Communications Magazine,

54(1):59–67.

Sornin, N., Luis, M., Eirich, T., Kramp, T., and Hersent,

O. (2015). LoRaWAN

Speciﬁcations. LoRa

Al-

liance.

The Things Network (2017). Gateway coverage map.

https://www.thethingsnetwork.org/map. Accessed: 10

October 2017.

Vo-Huu, T. D., Vo-Huu, T. D., and Noubir, G. (2016). Fin-

gerprinting Wi-Fi Devices Using Software Deﬁned

Radios. In Proceedings of the 9th ACM Conference on

Security & Privacy in Wireless and Mobile Networks,

pages 3–14, New York, NY, USA. ACM.

Wang, K., Faulkner, M., Singh, J., and Tolochko, I. (2003).

Timing synchronization for 802.11 a WLANs under

multipath channels. In Proc. ATNAC, volume 2004.

Weightless (2017). Weightless home page.

http://www.weightless.org/. Accessed: 9 Octo-

ber 2017.

Wi-Fi Alliance (2017). Wi-Fi HaLow home page.

https://www.wi-ﬁ.org/discover-wi-ﬁ/wi-ﬁ-halow. Ac-

cessed: 9 October 2017.

A Multi-Channel Software Decoder for the LoRa Modulation Scheme