Eliminating Redundant and Irrelevant Association Rules in Large

Knowledge Bases

Rafael Garcia Leonel Miani

and Estevam Rafael Hruschka Junior

Department of Computing, Federal Institute of Sao Paulo, Votuporanka, Brazil

Department of Computing, Federal University of Sao Carlos, Sao Carlos, Brazil

Keywords:

Association Rules, Irrelevant Rules, Large Knowledge Bases, Redundant Rules.

Abstract:

Large growing knowledge bases are being an explored issue in the past few years. Most approaches focus

on developing techniques to increase their knowledge base. Association rule mining algorithms can also

be used for this purpose. A main problem on extracting association rules is the effort spent on evaluating

them. In order to reduce the number of association rules discovered, this paper presents ER component,

which eliminates the extracted rules in two ways at the post-processing step. The ﬁrst introduces the concept

of super antecedent rules and prunes the redundant ones. The second method brings the concept of super

consequent rules, eliminating those irrelevant. Experiments showed that both methods combined can decrease

the amount of rules in more than 30%. We also compared ER to FP-Growth, CHARM and FPMax algorithms.

ER generated more relevant and efﬁcient association rules to populate the knowledge base than FP-Growth,

CHARM and FPMax.

1 INTRODUCTION

Large growing knowledge bases construction are

being an explored issue in the past few years. Cyc

(Matuszek et al., 2006), DBpedia (Bizer et al., 2009),

NELL (Carlson et al., 2010a; Mitchell et al., 2015),

YAGO (Suchanek et al., 2007), Freebase (Bollacker

et al., 2008) and ReVerb (Etzioni et al., 2011) are

some examples of different approaches to build such

knowledge bases.

One important task in such approaches is to create

techniques to assist Knowledge Base (KB) population

and extension. Two common ways to achieve it are

by (i) ﬁlling in the KB with new instances and by

(ii) adding new relations among the KB categories.

In previous work, it was developed a system that

helps populating NELL’s KB with instances. It used

an association rule mining (Agrawal et al., 1993)

algorithm between the facts already stored on NELL’s

KB. For example, imagine the association rule AR1

AR1: athletePlaysLeague(X, nba) → athlete-

PlaysSport(X, basketball).

It means that if an athlete plays the league nba,

then he plays the basketball sport. The algorithm will

populate NELL’s KB with the value of basketball ever

time it ﬁnds nba, contributing to increasing the KB

and decrease the amount of missing values.

NELL (Never-Ending Language Learning) is a

computer system that runs 24 hours per day, 7 days

per week, extracting information from web text to

populate and extend its own KB. The main goal of

the system is to learn to read the web better each

day and to store the gathered knowledge in a never-

ending growing KB. The system takes advantage of

many different components like CPL (Carlson et al.,

2009), CSEAL (Carlson et al., 2010b), Prophet (Ap-

pel and Hruschka, 2011) and Conversing Learning

(CL) (Pedro and Hruschka Jr, 2012), in order to be

self-supervised and avoid semantic drifting.

NELL’s knowledge base is represented by an

ontology-based structure characterized by categories,

relations and their instances. This paper uses the data

already discovered by NELL’s components.

Such KBs gather data and increase their size con-

tinuously. Thus, they neither have all instances for

each category nor all relations between them, consis-

ting in a missing value dataset. To perform an asso-

ciation rule mining algorithm in KBs with such cha-

racteristic, the problem of missing values has to be

considered. In order to deal with this problem, a new

measure, called MSC, was created. Basically, MSC

discards an itemset if all items of each category are

Garcia Leonel Miani, R. and Rafael Hruschka Junior, E.

Eliminating Redundant and Irrelevant Association Rules in Large Knowledge Bases.

DOI: 10.5220/0006668800170028

In Proceedings of the 20th International Conference on Enterprise Information Systems (ICEIS 2018), pages 17-28

ISBN: 978-989-758-298-1

Table 1: Example of association rules.

Number Rule

1 athleteWinsAwardTrophyTournament(X, super bowl) → athletePlaysSport(X, Football)

2 athletePlaysLeague(X, nﬂ) → athletePlaysSport(X, Football)

3 athleteWinsAwardTrophyTournament(X, super bowl), athletePlaysLeague(X, nﬂ) → athletePlaysSport(X,Football)

4 athletePlaysSport(X, Football) → athletePlaysLeague(X, nﬂ)

5 athletePlaysSport(X, Football) → athletePlaysLeague(X ,nﬂ), athletePlaysForTeam (X, giants)

6 athletePlaysSport(X, Football), athletePlaysForTeam (X, giants) → athletePlaysLeague(X, nﬂ)

missing. This is a previous contribution and is better

explained in the Methodology section.

Nevertheless, association rule mining algorithms

usually bring a big quantity of rules to be evaluated,

and the effort spent on analyzing each one is an im-

portant problem. Thus, this paper presents ER (Elimi-

nating Rules) component, which has two methods at

post-processing step in order to reduce the amount of

association rules generated. The ﬁrst one introduces

the concept of super antecedent rules and eliminates

those redundant ones, keeping only the minimal as-

sociation rules needed to populate NELL’s KB. The

second method introduces the concept of super con-

sequent rules and prunes all the irrelevant ones, ba-

sed on those already discovered with higher minimum

support or in past iterations of the algorithm.

Consider the association rules in Table 1. By rules

1 and 2, the athlete who wins the super bowl tour-

nament (rule 1) or who plays in the nﬂ league (rule

2), also practices the football sport. However, in rule

3, both conditions (athlete wins super bowl and plays

nﬂ) need to be in the instance of the dataset so the

algorithm can be able to ﬁll the value of sport with

football. Thus, rule 3 is a redundant super antecedent

rule, and will be pruned off the ﬁnal set of generated

rules, preserving the minimal ones with the same con-

sequent, contributing to decrease the number of rules.

A super antecedent rule is only eliminated if the al-

gorithm ﬁnds all their minimal ones.

Imagine now that in an iteration with minimum

support degree of 0.2, the algorithm extracted the rule

4 of Table 1. This rule is evaluated and considered

irrelevant as not all football athletes play the nﬂ lea-

gue. In future iterations, all rules with the same ante-

cedent, having this consequent in their set are cut off

the amount of generated ones. By Table 1, rule 5 (an

irrelevant super consequent rule) is neither illustrated

nor evaluated in future iterations. To analyze and va-

lidate each rule extracted, Conversing Learning (CL),

a NELL component, is used.

Experiments were performed, comparing both ER

methods to the original algorithm (without ER), sho-

wing that ER can reduce the amount of rules in more

than 30%. It also ﬁlled the KB with the same amount

of values as the original algorithm, showing that all

eliminated association rules did not impact in the pro-

cess of populating the KB. This is the main contribu-

tion of this paper.

ER is also compared to FP-Growth (Han et al.,

2000), CHARM (Zaki and Hsiao, 2002) and FP-

Max (Grahne and Zhu, 2003) algorithms. FP-

Growth, CHARM and FPMax use the concepts of

Frequent Itemsets (FIs), Frequent Closed Itemsets

(FCIs) and Maximal Frequent Itemsets (MFIs), re-

spectively. FCIs e MFIs techniques have the goal

to decrease the set of frequent itemsets. However,

to generate the set of rules in this paper, it is ne-

cessary to use all FIs. We compared the number

of frequent itemsets generated by ER against those

algorithms, using the implementation provided by

(Fournier-Viger et al., 2014). The original implemen-

tation of CHARM and FPMax only generated FIs. In

(Fournier-Viger et al., 2014), they also generated as-

sociation rules from CHARM FCIs. In this way, ER

was compared to CHARM to check which one can ex-

tract more relevant rules in order to populate NELL’s

KB. Some simulations of possible associations rules

by FPMax MFIs were performed to analyze how it

could populate large KBs. ER generates more rele-

vant rules, contributing to populate the KB with more

facts than FP-Growth, CHARM and FPMax.

This paper aims to decrease the effort spent

on analyzing the association rules used to populate

NELL’s KB, presenting the following contributions:

• A new method to eliminate redundant association

rules;

• A new method to eliminate irrelevant association

rules;

• The deﬁnition of super antecedent rules;

• The deﬁnition of super consequent rules.

The remainder of this paper is organized as the

following: Section 2 brings some related work. The

complete description of our technique is depicted in

Section 3. Experiments are illustrated and discussed

in Section 4.

ICEIS 2018 - 20th International Conference on Enterprise Information Systems

2 RELATED WORK

Large growing KBs are being a very explored is-

sue in the past few years. Cyc (Matuszek et al.,

2006), DBpedia (Bizer et al., 2009), NELL (Carlson

et al., 2010a), ReVerb (Etzioni et al., 2011), Free-

base (Bollacker et al., 2008), YAGO (Suchanek et al.,

2007) and YAGO2 (Hoffart et al., 2013), which ex-

tend YAGO to deal with spatio-temporal dimension,

are examples of such systems.

Most works focus on increasing the KB by popu-

lating it with new instances or by enlarging the re-

lations between their categories or domains (Miani

et al., 2014), (Tamang and Ji, 2012), (Gal

Arraga et al.,

2013).

AMIE (Gal

Arraga et al., 2013) is a system that

extracts association rules like motherOf(m,c) ∧ mar-

riedTo(m,f) → fatherOf(f,c), which is pretty similar to

our system. However, besides the generalized asso-

ciation rules (Srikant and Agrawal, 1995) form, we

intended to get which fact is related to another one

in order to populate the KB. Considering the example

of Table 1 in Section 1, we are interested to know in

which league an athlete plays, so the algorithm can be

able to ﬁll with the corresponding sport (rule 2).

An important problem working with association

rule mining algorithms is the effort spent on evalua-

ting the amount of generated rules. To overcome that,

researches were performed in preprocessing or post-

processing step to reduce and facilitate the analysis of

each rule extracted. In order to cut off redundant item-

sets, many approaches have been developed, such as

Closed Itemsets and Maximal Itemsets, for example.

A Frequent Closed Itemset (FCI) is a Frequent

Itemset (FI) X such that there is no superset of X with

the same support count (Pasquier et al., 1999). (Zaki,

2000) used the concept of FCIs, reducing the number

of rules without any loss of information. CHARM

is an efﬁcient algorithm for mining FCIs, which enu-

merates closed sets using a dual itemset-tidset search

tree. It also uses a fast hash-based approach to re-

move any ”non-closed” sets found during computa-

tion (Zaki and Hsiao, 2002). Another algorithm that

used FCIs, called A-Close, was proposed by (Pasquier

et al., 1999). The number of rules decreased without

any loss of information, reducing the algorithm com-

putation cost. A-Close is one of the most known algo-

rithm to mine frequent closed itemsets.

A Maximal Frequent Itemset (MFI) is a frequent

itemset X with no frequent superset of X (Burdick

et al., 2001). According to the authors, the following

relationship holds: MFI ⊆ FCI ⊆ FI. They also propo-

sed an algorithm to mine MFIs, called MAFIA, which

integrates a variety of algorithms ideas into a practi-

cal algorithm. FPMax (Grahne and Zhu, 2003) uses a

FP-tree structure to store the frequency information

of the whole dataset. To test if a frequent itemset

is maximal, another tree structure, called a Maximal

Frequent Itemset tree (MFI-tree), is utilized to keep

track of all MFIs. GenMax (Gouda and Zaki, 2005)

and MaxMiner (Bayardo Jr, 1998) are also well-know

algorithms on this ﬁeld.

Both MFI and FCI techniques work during the

candidate generation step. Nevertheless, many appro-

aches developed post-processing mechanisms to re-

duce the number of redundant or irrelevant rules. In

(Marinica and Guillet, 2010), they proposed an inte-

ractive approach where human domain experts ﬁlter

the rules extracted in order to decrease the amount of

association rules. CoGAR (Baralis et al., 2012) is a

generalized association rule algorithm that introduced

two new measures: (i) a schema constraint is created

by an analyst and drives the itemset mining phase and

(ii) opportunistic conﬁdence constraint that identi-

ﬁes signiﬁcant and redundant rules at post-processing

phase.

PNAR IMLMS (Swesi et al., 2012) and MIP-

NAR GA (Rai et al., 2014) are algorithms that dis-

cover both positive itemsets (frequent itemsets) and

negative itemsets (infrequent itemsets). They created

some measures to prune rules and generate positive

and negative association rules.

(Djenouri et al., 2014) explored meta-rules ex-

traction in order to prune irrelevant rules. First, they

cluster association rules for large datasets. Then, dif-

ferent dependencies between rules of the same clus-

ter are extracted using meta-rules algorithms, and the

prune algorithm uses these dependencies to delete the

deductive rules and keep just the representative rules

for each cluster. The PVARM algorithm was propo-

sed by (Rameshkumar et al., 2013). It used the n-

cross validation technique to reduce the amount of ir-

relevant association rules.

This paper has the goal to reduce the amount of

association rules, decreasing the effort on evaluating

them. Thus, ER component has two methods to deal

with it at post-processing phase. One is by elimina-

ting the redundant association rules, pruning the re-

dundant super antecedent rules. The second one con-

sists on cutting out irrelevant super consequent rules.

3 METHODOLOGY

The main purpose of this paper is to reduce the ef-

fort on evaluating the generated association rules that

will be used to populate large KBs. In this way, ER

was developed, contributing to decreasing the amount

Eliminating Redundant and Irrelevant Association Rules in Large Knowledge Bases

Table 2: Dataset Example.

athlete sport league

awardTrophy

Tournament

sportsTeam

ben roethlisberger football nﬂ super bowl pittsburgh steelers

brian urlacher football nﬂ mv bears

favre football nﬂ mv jets

joe ﬂacco mv nﬂ mv mv

larry foote football nﬂ super bowl pittsburgh steelers

steve mcnair football nﬂ mv mv

tom brady football nﬂ super bowl new england patriots

drew bledsoe mv mv super bowl new england patriots

Figure 1: System Architecture.

of association rules in two ways at post-processing

phase:

• Pruning redundant association rules;

• Pruning irrelevant association rules.

Besides, in order to develop each method, this pa-

per introduces the concept of super antecedent rules

and super consequent rules, which are used by both

eliminating redundant and irrelevant rules methods,

respectively.

This section also discusses some basic ideas of

the association rule mining algorithm used. Figure

1 illustrates the system architecture. The highlighted

parts are the ones with contributions in this paper.

3.1 Association Rule Algorithm

The association rule mining algorithm used in this pa-

per is NARFO (Miani et al., 2009). It was chosen as it

is an available algorithm and has some important cha-

racteristics to this work. Its implementation is based

on Apriori. However, NARFO can navigates through

an ontology structure, being able to identify each fact

belongs to each category of the ontology. It also de-

als with generalized association rules, which are used

in another component of our system. We also modi-

ﬁed NARFO in the generating candidates step to deal

with the missing values problem (previous work), and

in the generating rules step (ER component) of the al-

gorithm.

3.2 Data Preparation

As it can be noticed in Figure 1, a subset of NELL’s

KB is selected and prepared to be used by the algo-

rithm. Each fact is associated to the corresponding

category. Figure 2 represents an ontology structure,

where the categories of the subset can be seen. For

each athlete selected, in this example, all his known

values for each category are ﬁlled. If NELL’s compo-

nents did not discover a speciﬁc fact to an athlete, the

correspondent cell is ﬁlled with a missing value. In

this work, missing values are represented by mv.

3.3 Generating Candidates

A large KB like NELL, as aforementioned, contains

many empty cells. To perform an association rule mi-

ning algorithm in such environment, a new parame-

ter, called MSC (Modiﬁed Support Calculation), was

created. To sum up, this technique disregards all tran-

sactions in which all items of the itemset, of which

the support is to be counted, are missing values. Con-

sidering Table 2 as an example and Table 3, which

brings the itemsets supports of Table 2. As you can

see, the itemsets supports by MSC is bigger than tra-

ditional support calculation. Consider the minimum

support set to 0.3, MSC measure generates one more

frequent itemset than traditional support calculation.

This may result in more signiﬁcant rules. The set of

Frequent Itemsets with Missing Values (FIMVs) is,

at least, equal to the set of FI. So, the following re-

lationship holds: MFI ⊆ FCI ⊆ FI ⊆ FIMV and is

illustrated in Figure 3. This paper does not focus on

MSC parameter as it is a previous contribution.

By Table 3, it can be observed the relationship

brought by the diagram in Figure 3. All MFIs (1) ⊆

FCIs (4) ⊆ FIs (7) ⊆ FIMVs (8). Using FIMVs, it

will generate more rules that might help populating

NELL’s KB. Considering the set of FCI and MFI, the

itemsets (football, super bowl) and (nﬂ, super bowl)

are not presented. So, association rules like AR1 and

ICEIS 2018 - 20th International Conference on Enterprise Information Systems

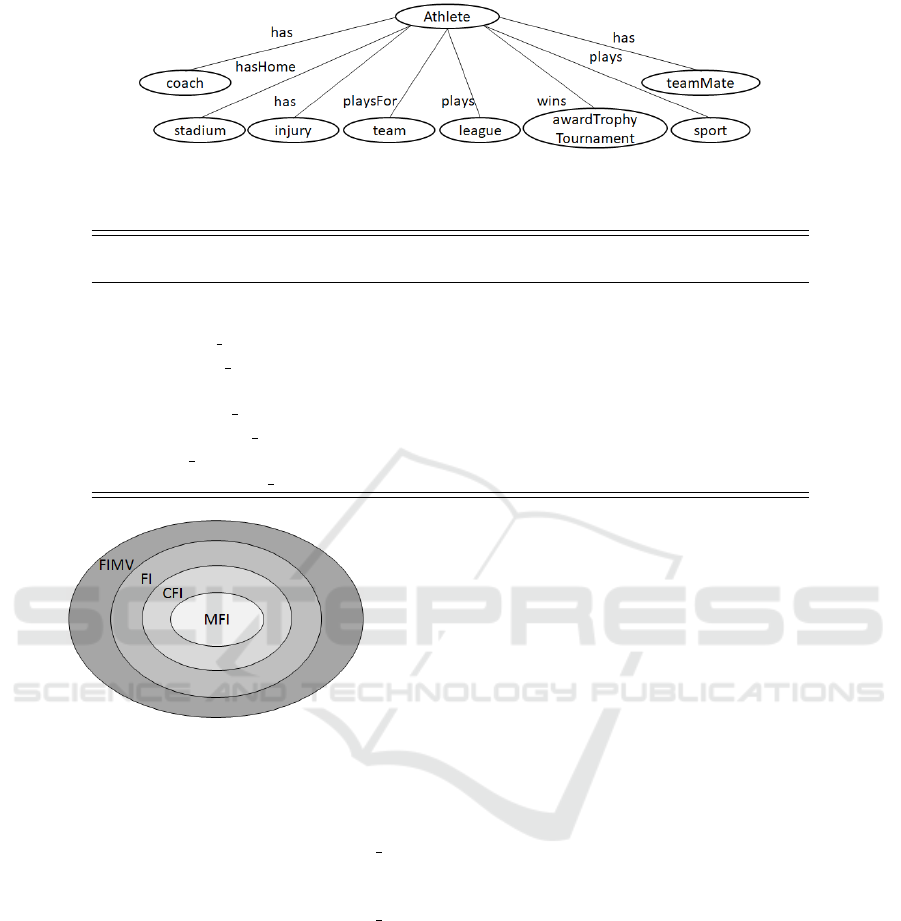
Figure 2: Ontology example.

Table 3: MSC Support x Traditional Support.

Itemset

Support by

MSC

Traditional

Support

FIMV FI FCI MFI

football 6/6 = 1 6/8 = 0.75 X X

nﬂ 7/7 = 1 7/8 = 0.87 X X X

super bowl 4/4 = 1 4/8 = 0.5 X X X

pittsburgh steelers 2/6 = 0.33 2/8 = 0.25 X

football, nﬂ 6/7 = 0.85 6/8 = 0.75 X X X

nﬂ, super bowl 3/8 = 0.37 3/8 = 0.37 X X

football, super bowl 3/7 = 0.42 3/8 = 0.37 X X

pittsburgh steelers, football 2/7 = 0.28 2/8 = 0.25

football, nﬂ, super bowl 3/8 = 0.37 3/8 = 0.37 X X X X

Figure 3: Relationship among FIMV x FI x FCI x MFI.

AR2 will not be generated, contributing to populate

the KB with less data if compared to our technique.

AR1: athleteWinTrophyTournament(X, super bowl)

→ athletePlaysSport(X, footbal), and

AR2: athleteWinTrophyTournament(X, super

bowl)

→ athletePlaysLeague(X, nﬂ).

3.4 Generating Rules: ER Component

The contributions of this paper are in the generating

rules step. The initial procedure is similar to Apri-

ori. Each frequent itemset is used to generate associ-

ation rules. ER component executes after the rules ex-

traction. First, it gets all extracted rules and eliminate

the redundant ones. Then, ER cuts off the irrelevant

ones, resulting in the ﬁnal set of generated rules.

3.4.1 Eliminating Redundant Rules

Let X → Y, X’ → Y be association rules, where X’ is

a superset of X.

Deﬁnition 1. An association rule X’ → Y is Super

Antecedent Rule (super AR) if it has the same conse-

quent items and if its antecedent X’ is a superset of

an antecedent X. In the other way, an association rule

X → Y is a Sub Antecedent Rule (sub AR) if there is

another rule with the same consequent and X is a sub-

set of X’.

All super antecedent rules are super rules, but not

all super rules are super antecedent rules.

Considering Table 1, rule 3 is a super AR of rules

1 and 2, and rule 6 is a super AR of rule 4. Rule 5 is a

super rule, but not a super AR.

The eliminating redundant rules algorithm con-

sists in removing super antecedent rules. But it only

prunes a rule from the set of association rules if it

ﬁnds all possibles sub antecedent rules of the super

antecedent one. By the example of Table 1, rule 3 can

be pruned as rules 1 and 2 are all possibles sub antece-

dent rules of it. Nevertheless, rule 6 is not eliminated

as only one of its sub antecedent rules was generated.

In order to populate the KB, a sub antecedent rule is

more efﬁcient than a super antecedent rule. Rule 3

can only populate a KB with the consequent value if

both antecedents are in an instance. This is the reason

that a super AR is pruned.

The examples brought by Table 1 represent super

ARs with antece dents having size 2, i.e., the antece-

Eliminating Redundant and Irrelevant Association Rules in Large Knowledge Bases

Algorithm 1: Eliminating Redundant Rules.

allCombinations = f alse;

for i = 0 to numberO f GeneratedRules − 1 do

currentRule = getAssociationRule(i);

allCombinations = f indAllComb(currentRule);

if NOT(allCombinations) then

f inalRules.add(currentRule);

end if

allCombinations = f alse;

end for

dent has 2 items (2-itemset). In this way, it looks for

sub ARs of 1-itemset in the antecedent. But what hap-

pens if a super AR has 3-itemset or more on its antece-

dent? There must be sub ARs of 1 or 2-itemsets in the

antecedent side, for example. To solve this issue, the

algorithm calculates all possible combinations of sub

antecedent rules as Equation 1. Algorithm 1 shows

the pseudo-code of this method.

Combination(n, k) =

k!(n − k)!

(1)

To a better comprehension, lets take Table 4 as

an example. In the ﬁrst line, there is a super AR of

4-itemset in the antecedent side. The algorithm be-

gins trying to ﬁnd all possibilities of sub ARs with

1-itemset. By Equation 1, n is the size of the antece-

dent of the super AR, and k is the size of the sub AR.

So, there are four possibles sub ARs of 1-itemset in

the antecedent. However, only 3 rules were genera-

ted. The super AR of 4-itemset in the antecedent can

not be pruned yet. Then, the algorithm looks for all

possible combinations of sub AR of size 2 in the an-

tecedent. It generated all the 6 possibilities, and the

rule from the ﬁrst line can be eliminated. The algo-

rithm will use the sub ARs of 2-itemset to populate

the KB, instead of the super AR.

Considering the rules from antecedent size 3 as

super ARs, both of them are eliminated. Rule a,b,c

→ e has all possibilities of sub AR of antecedent size

1, and a,b,d → e has all possibilities of size 2. In the

last column of Table 4 are the associations rule elimi-

nated. In this example, 6 (50%) rules were pruned.

The main task of the algorithm is to ﬁnd all pos-

sibilities of sub ARs from 1-itemset to (n-1)-itemset,

where n is the size of the antecedent of the current su-

per AR (ﬁndAllCombinations in Algorithm 1). If all

combinations are found with 1-itemset, the algorithm

prunes the rule. Otherwise, it tries to ﬁnd all of the

possibilities of 2-itemsets and so on.

By the set generated by FCI and MFI algorithms,

it is more probably to generate the super rules, instead

of pruning them and letting the minimal sub ARs as

our approach. For example, if FCI and MFI algo-

rithms discovered only the itemset (a,b,c,d,e) as clo-

sed and maximal, it can only populate the dataset with

the value e if all the other items appear in a instance in

the dataset. However, using the eliminating redundant

rules technique described in this paper, the rule a,b,c,d

→ e is pruned, letting only the sub ARs of size 2 in

the antecedent as described above. In this way, when

one of the 6 possibilities happens in a instance, it will

ﬁll the dataset with the value of e when necessary.

This contributes to populate large KBs compounded

by missing values more than using rules extracted by

FCI and MFI algorithms.

3.4.2 Eliminating Irrelevant Rules

At this point, all of the redundant super ARs to the

current algorithm iteration were eliminated. For each

iteration, the algorithm can generate a set of irrele-

vant rules, mostly in result of the KB characteristic.

In the ﬁrst iteration, no irrelevant association rule is

prior known. So, this procedure impacts the number

of rules from the second iteration of the ﬁrst cycle of

iterations. Each cycle is executed with different mi-

nimum support degrees. After the end of the cycle,

NELL’s KB subset is increased, and the next cycle

can be performed. All irrelevant rules discovered in

an iteration i will be used to help eliminating future

irrelevant rules in iterations i + n, with n ≥ 1.

Deﬁnition 2. An association rule is irrelevant if it can

populate a large growing KB with wrong data.

Table 3 brings some itemsets support values. Take

the 2-itemset football, nﬂ as an example. Imagine that

in the ﬁrst iteration, in the initial cycle, the minimum

support was 0.3, which make it a frequent itemset.

The following rules were generated:

1. athletePlaysLeague(X, nﬂ) → athletePlays-

Sport(X, Football);

2. athletePlaysSport(X, Football) → athletePlaysLe-

ague(X, nﬂ).

All generated rules are evaluated by NELL’s CL

component. The ﬁrst rule is considered relevant and

will be used to populate the KB. For example, in Ta-

ble 2 the line 4 has a missing value to the sport value,

and the corresponding value for league is nﬂ. So, the

algorithm ﬁlls it with football. In the other way, the

second association rule is an irrelevant one, once not

all athletes practicing football play the nﬂ league. Alt-

hough the table suggests this rule as a strong one, CL

evaluated it as irrelevant once a football athlete can

play in other leagues. In this way, this rule can not be

used to ﬁll NELL’s KB, once it will populate it with

incorrect information.

In the second iteration, the minimum support va-

lue was set to 0.2. Thus, the 3-itemset (football,

nﬂ, super bowl) is considered in the process of

ICEIS 2018 - 20th International Conference on Enterprise Information Systems

Table 4: Example to Eliminate Super Antecedent Rules.

Antecedent Size Association Rule

Number of

Combinations

Rule Eliminated

4 a,b,c,d → e - a,b,c,d → e

3 a,b,c → e / a,b,d → e 4 a,b,c → e / a,b,d → e

a,b → e / a,c → e / a,d → e /

b,c → e / b,d → e / c,d → e

a,b → e / a,c → e /

b,c → e

1 a → e / b → e / c → e 4 -

Algorithm 2: Eliminating Irrelevant Rules Algorithm.

isSuperIrrelRule = f alse;

for i = 0 to numberO f NonRedundantRules − 1 do

currentRule = getAssociationRule(i);

isSuperIrrelRule = f indSubIrrel(currentRule);

if NOT(hasSuperIrrelRule) then

f inalRules.add(currentRule);

end if

isSuperIrrelRule = f alse;

end for

generating rules. Consider the following association

rule:

3. athletePlaysSport(X, Football) → athletePlays

League(X,nﬂ), athleteWinTournament(X,super bowl).

This rule is also considered irrelevant. But there

is a sub rule (rule 2) that is irrelevant too, which was

discovered in a previous iteration. So, this rule will be

eliminated and will not be evaluated. It is important to

notice that a super rule must have the same antecedent

as the sub irrelevant rule. In this way, the algorithm

eliminates all super rules with the same antecedent of

an irrelevant sub rule.

A super rule with more antecedents can not be

pruned, as the addition of more antecedents can turn

it into a relevant rule. Consider the rule

4. athletePlaysSport(X, Football), athleteWinTourna-

ment(X, super bowl) → athletePlaysLeague(X, nﬂ).

This is a relevant rule, even having a sub irrelevant

one. The addition of the itemset super bowl (in the

antecedent side) turned it in a relevant rule.

Let X → Y, X → Y’ be association rules, where Y’

is a superset of Y.

Deﬁnition 3. An association rule X → Y’ is Super

Consequent Rule (super CR) if it has the same antece-

dent items and if its consequent Y’ is a superset of the

consequent Y. In the other way, an association rule

X → Y is a Sub Consequent Rule (sub CR) if there

is another rule with the same antecedent and Y is a

subset of Y’.

All super CRs of an irrelevant sub CR are also ir-

relevant. All super CRs are super rules, but not all

super rules are super CRs.

Algorithm 2 describes the procedure of elimina-

ting irrelevant rules. The set of non redundant produ-

ced by the eliminating redundant rules method is used

as an input. For each rule, the algorithm veriﬁes if it

has an irrelevant sub CR. If so, the rule is pruned of

the ﬁnal set of rules and will not be shown to analysis

in the end of the iteration.

3.5 Evaluating Rules

Traditional association rule mining algorithms con-

sider a rule strong that one with support and conﬁ-

dence values higher than the minimum support and

conﬁdence expected. So, those algorithms display the

strong association rules extracted. But this fact is not

entirely true in large growing KBs like NELL. Some

rules that have high conﬁdence, specially, could not

be good examples of rules to populate the KB, since

NELL’s KB did not contain all instances and relati-

ons yet. For instance, rules 2 and 3 from Subsection

3.4 are examples of such rules. They are strong, once

their support and conﬁdence are higher than the mini-

mum expected, but they are also irrelevant.

To analyze each rule extracted, NELL’s CL com-

ponent was used. To sum up, this component uses

Twitter and Yahoo Answers to validate rules. In this

work, however, only Twitter was used to evaluate ex-

tracted rules. With CL help, it is intended to automa-

tically evaluate extracted rules and increase NELL’s

KB with the useful ones.

3.6 Increase the KB

After the rules evaluation by CL, all relevant rules are

used to populate the KB, decreasing the amount of

missing values. For each one, the algorithm veriﬁes

its antecedent and ﬁlls the KB with the value of the

consequent whenever a missing value appears.

Eliminating Redundant and Irrelevant Association Rules in Large Knowledge Bases

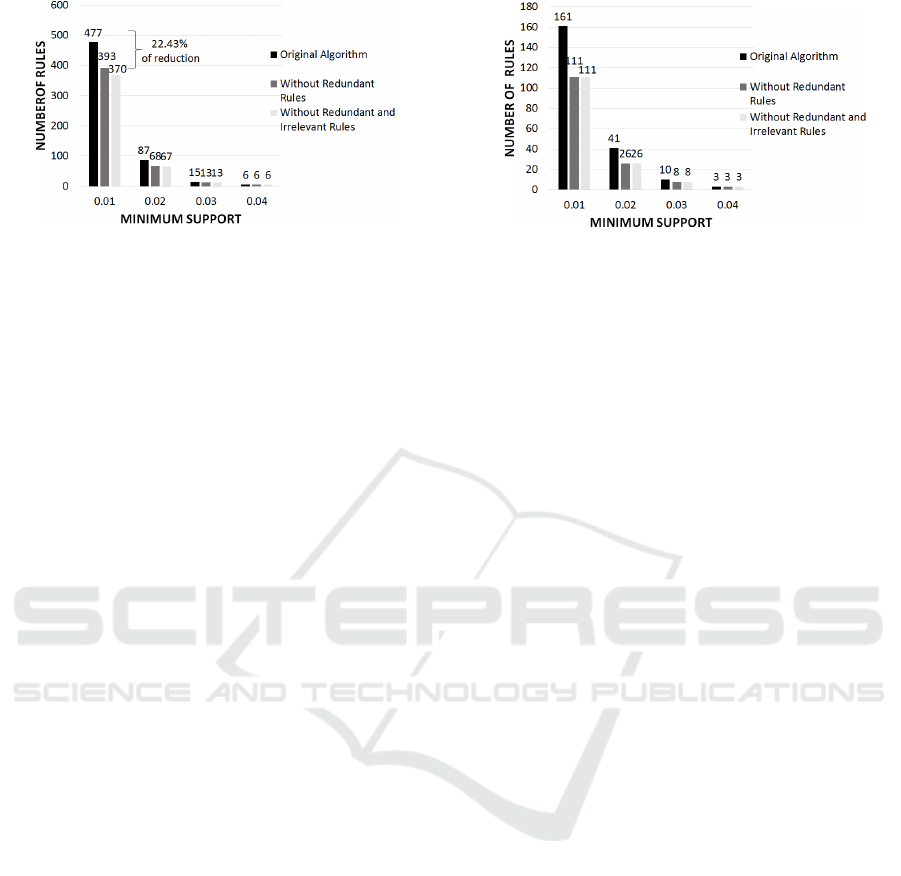
Figure 4: Number of Rules by Experiment 1.

4 EXPERIMENTS

The experiments were performed using a real data-

set extracted from NELL’s KB. It contains data from

athletes, sports, leagues and other categories related

to sports as represented by Figure 2. To run the ex-

periments, the minimum conﬁdence degree was set to

0.3 and the minimum support was, in each cycle of ite-

rations, set from 0.04 to 0.01, decreasing 0.01 in each

iteration. The minimum support was set with low va-

lues due to the characteristic of the KB that has a lot

of facts to each category. Also, with minimum support

set to 0.05, no association rule was generated.

The main goal of these experiments is to verify

how ER impacts the number of rules extracted. Three

iteration cycles were executed. Each one with a da-

taset increased with NELL’s KB facts to the corre-

spondent dataset. Lets call dataset 1, dataset 2, and

dataset 3 the ones used in the cycle 1, cycle 2, and

cycle 3, respectively. In this way, three experiments

were executed, comparing the amount of rules extrac-

ted by the original algorithm against the methods with

contribution:

• Experiment 1: dataset 1 and cycle 1;

• Experiment 2: dataset 2 and cycle 2;

• Experiment 3: dataset 3 and cycle 3.

We also compared ER against FP-Growth,

CHARM and FPMax algorithms in two aspects:

• The number of itemsets generated;

• The percentage of missing values ﬁlled (only

compared to FP-Growth and CHARM).

Figure 4 brings a comparison among the number

of association rules brought by our algorithm before

using ER component, and the amount of rules disco-

vered applying only the redundant and both redundant

and irrelevant methods. ER brought, approximately,

22.43% less rules than the original algorithm in Ex-

periment 1.

Figure 5: Number of Relevant Rules by Experiment 1.

As can be observed in Figure 4, the number of

association rules increased a lot whilst reducing the

minimum support degree. With the highest minimum

support (0.04), only rules with 2-itemsets were gene-

rated. In this way, the methods were not used to re-

duce the amount of rules, since they consist on elimi-

nating redundant super ARs and irrelevant super CRs,

which have at least two items in the antecedent and

in the consequent side, respectively. But, as the mini-

mum support decreases, ER component is used, con-

tributing to reduce the number of rules to be evalua-

ted.

The irrelevant rules discovered with minimum

support 0.04 are used in all the other iterations and

in the next cycles (Experiment 2 and 3). The same is

done to the irrelevant ones discovered with 0.03 and

0.02. Nevertheless, irrelevant rules discovered using

minimum support 0.01 will only be useful in futures

iteration cycles.

Figure 5 shows only the number of relevant ru-

les extracted by Experiment 1, after CL validation.

Notice that the original algorithm (without the new

methods) brought more relevant rules in comparison

to the redundant and irrelevant methods. This is result

of the amount of more redundant rules that the origi-

nal algorithm had (50) if compared to the approaches

introduced in this paper. You can also observe that

the number of relevant rules brought by eliminating

redundant and irrelevant rules methods is the same.

By Figure 4, the amount extracted by the eliminating

redundant rules method is a little bigger than the eli-

minating irrelevant rules, once the ﬁrst one did not

have eliminated the irrelevant association rules.

The results of Experiment 2 are in Figure 6. The

dataset used was increased in 10%, approximately,

once NELL is a growing KB. As in Experiment 1,

as the minimum support value reduces, the number

of rules rises. Most of the association rules extrac-

ted were also in Experiment 1. Both methods of ER

combined reduced in 33.60% the amount of rules in

comparison to the original algorithm.

The original algorithm generated 20 more rules

ICEIS 2018 - 20th International Conference on Enterprise Information Systems

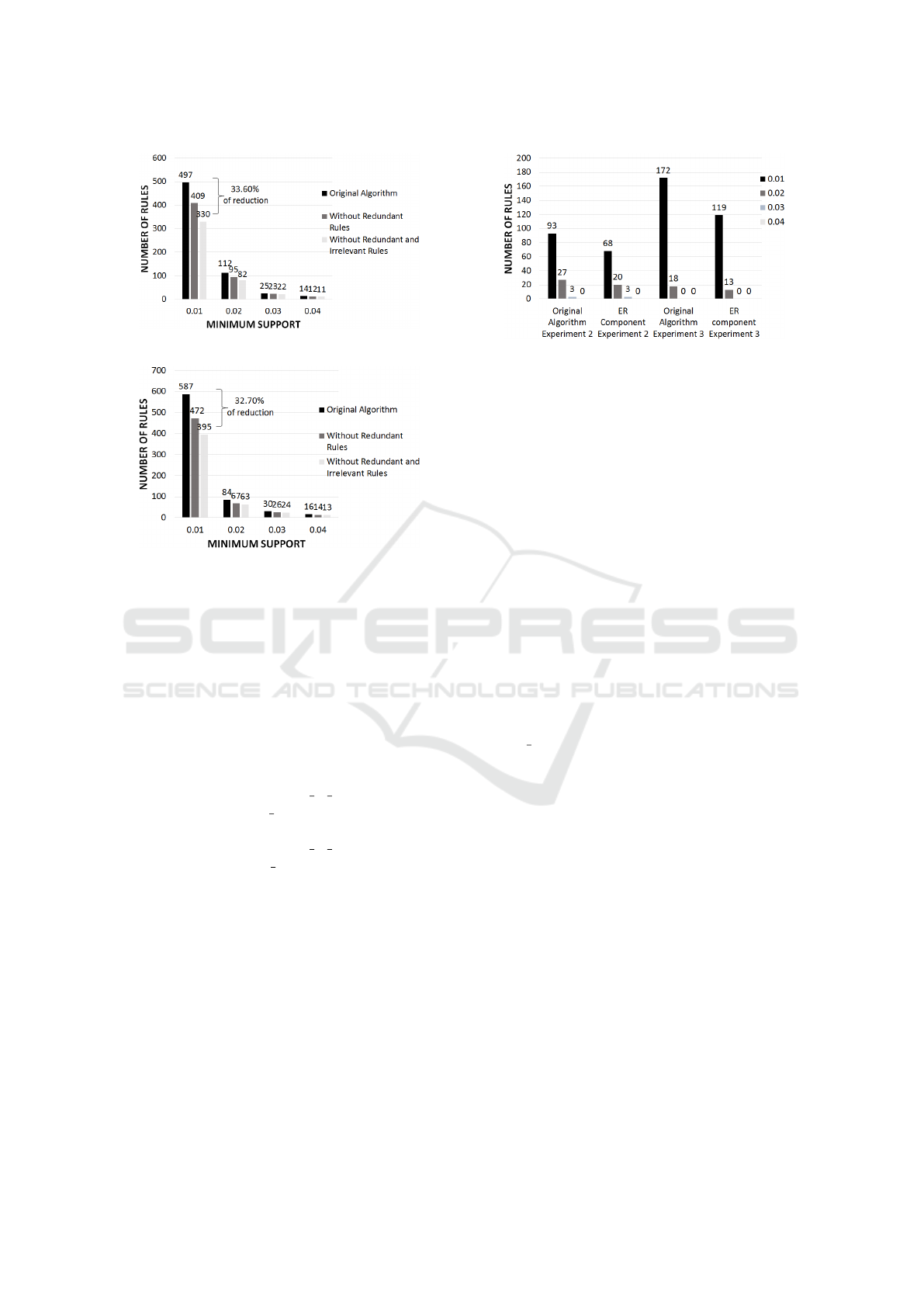
Figure 6: Number of Rules by Experiment 2.

Figure 7: Number of Rules by Experiment 3.

than in Experiment 1. But, observing the amount of

rules extracted by ER in Experiment 2, it reduced

in more than 10% (40 rules) due to the eliminating

irrelevant rules method. The explanation is on the

irrelevant association rules generated in the last

iteration of Experiment 1 (with minimum support

0.01). They could only be used in future iteration

cycles of the algorithm. For example, imagine that

the following irrelevant rules were generated in the

last iteration of Experiment 1:

1: athleteHasCoach(X, tony la russa) → athle-

tePlaysStadium(X, busch stadium)

2: athleteHasCoach(X, tony la russa) → athle-

tePlaysStadium(X, busch stadium), athletePlaysLea-

gue(X,mlb).

These rules are useful in future iteration cycles,

and the super CRs based on them will not be extrac-

ted. In fact, in Experiment 2, the second rule was not

generated, since its a super CR of the irrelevant as-

sociation rule number 1. This explains the reduction

of more than 30% of association rules with minimum

support of 0.01 in comparison to the original algo-

rithm, and why ER generated less rules in Experi-

ment 2 if compared to Experiment 1.

Experiment 3 is illustrated in Figure 7. The da-

taset used was also increased in 10%. ER extracted,

again, less association rules (32.70%) than the origi-

nal algorithm. Thus, these experiments demonstrated

Figure 8: New Rules extracted in Experiment 2 and 3.

how important and necessary ER component is to de-

crease the amount of redundant and irrelevant associ-

ation rules, without any lost in the process of popula-

ting large growing KBs.

However, if you compare the number of rules

brought by ER in Experiment 2 and Experiment 3,

you will notice that the last one extracted more rules.

The explanation to this behavior is on the kind of facts

added to the dataset on each iteration cycle. Figure 8

illustrates only the new rules extracted by the original

algorithm and ER in Experiment 2 and Experiment

3, and Table 5 shows some association rules extracted

by each experiment.

The dataset used in Experiment 1 and Experi-

ment 2 had sports facts related, mainly, to basketball,

football and baseball. Some new rules were disco-

vered by Experiment 2 due to the addition of new

teams, specially. For example, rules 3 and 4 only ap-

peared in Experiment 2, probably by the addition of

facts related to athletes that played for the teams spurs

and red sox.

In Experiment 3, more facts related to other

sports (soccer, for example) must have occurred, re-

sulting in more relevant and irrelevant rules, explai-

ning the behavior of ER, which brought more associ-

ation rules with minimum support of 0.01.

Nevertheless, comparing the number of rules ge-

nerated by the original algorithm against ER, the re-

dundant and irrelevant association rules were elimi-

nated by ER, specially with minimum support set to

0.01, demonstrating the importance and efﬁciency of

these approaches.

The second part of our experiments compares ER

to FP-Growth, CHARM and FPMax algorithms. The

objective is to check which algorithm is more efﬁcient

to populate a large KB, after eliminating redundant

and irrelevant rules. First, the amount of frequent

itemsets brought by ER, FP-Growth, CHARM and

FPMax is compared. Then a comparison is done with

ER, FP-Growth and CHARM in order to verify the

percentage of missing values replaced.

Figure 9 brings a comparison among the amount

Eliminating Redundant and Irrelevant Association Rules in Large Knowledge Bases

Table 5: Example of Rules Extracted on Each Experiment.

Number Rule Experiment

athleteWinsAwardTrophyTournament(X, super bowl) →

athletePlaysSport(X,Football)

2 athletePlaysLeague(X, nba) → athletePlaysSport(X, Basketball) 1

3 athletePlaysForTeam(X, spurs) → athletePlaysLeague(X, nba) 2

4 athletePlaysForTeam(X, red sox) → athletePlaysLeague(X, mlb) 2

5 athletePlaysForTeam(X, real madrid) → athletePlaysSport(X, Soccer) 3

6 athletePlaysLeague(X, champions league) → athletePlaysSport(X, Soccer) 3

Figure 9: Amount of FIMV, FI, FCI and MFI.

of frequent itemsets discovered by ER (FIMV), FP-

Growth (FI), CHARM (FCI) and FPMax (MFI). In

the ﬁgure, it is noticeable the relationship MFI ⊆ FCI

⊆ FI ⊆ FIMV described in Section 3.3. The discard

of items (parameter MSC) during the generating can-

didates step results in much more frequent itemsets

than those brought by FP-Growth, CHARM and FP-

Max algorithms. In this way, ER generates more as-

sociation rules (that might be used to help populating

NELL’s KB) than those algorithms. However, many

of those rules are redundant or irrelevant, making ER

component necessary in the process to reduce the ef-

fort on analyzing them.

CHARM and FPMax eliminate redundant item-

sets, generating only the frequent closed and maxi-

mal frequent itemsets, respectively. Unfortunately, it

can prune some itemsets that can be very useful in the

process of ﬁlling the KB. In this way, a classic associ-

ation rule mining algorithm (like FP-Growth) is more

efﬁcient to populate large KBs.

Table 6 shows the percentage of missing values

replaced by ER in comparison to FP-Growth and

CHARM algorithms in Experiment 1. Table 7 brings

some association rules extracted by ER, FP-Growth

and CHARM, and some possible association rules ge-

nerated from FPMax MFIs. It is not known any im-

plementation of an association rule mining algorithm

based on MFIs so far. The main reason is that there

is no way to quickly obtain the support of the antece-

dent/consequent of an association rule without scan-

ning the database again.

As can be observed in Table 6, even with minimum

support of 0.01, CHARM algorithm did not ﬁll the

same amount of missing values that ER did with mi-

nimum support of 0.04. This shows that using the mi-

nimal association rules, instead of pruning them, can

be more helpful to populate large KBs. Comparing

FP-Growth to CHARM, the ﬁrst one ﬁlled more mis-

sing values than CHARM only with minimum support

of 0.01. The main reason is due to the association

rules generated with minimum support of 0.02, 0.03

and 0.04, which has just two itemsets. The same be-

havior did not happen with minimum support of 0.01,

once FP-Growth used the minimal association and the

super rules to populate the KB, while CHARM used

only the association rules from FCIs. This shows,

once again, that minimal rules are more useful in the

process of populating large KBs.

If you compare FP-Growth to ER, some facts can

be observed. Firstly, the association rules generated

after applying ER methods help to populate the KB

with more facts than FP-Growth algorithm. This is

the result of MSC parameter, which generates more

frequent itemsets. Besides, as ER eliminates super

ARs and CRs, only the minimal association rules nee-

ded to feed the KB are used. FP-Growth extracts both

minimal and super association rules, which makes the

effort spent on evaluating them unnecessary.

Taking a look at Table 7, you can see that some as-

sociation rules were extracted only by ER (6 and 7),

due to MSC parameter. Other were extracted only by

FP-Growth and CHARM (1 and 4), once ER elimi-

nated them as it generated their sub ARs (rules 2 and

3). By rule 1 and 4, FP-Growth and CHARM would

populate the KB only if both antecedents are in an in-

stance. In the FP-Growth situation, it also generated

the two sub ARs of rule 1, which does not impact in

the KB population, but brings more redundant associ-

ation rules to be evaluated (rule 1). In this case, if only

nba or nba

championship values were in an instance,

the KB would be updated with basktball.

Performing a simple comparison with FP-

Max, consider the itemset (nba, basketball,

nba championship) that was generated with mi-

ICEIS 2018 - 20th International Conference on Enterprise Information Systems

Table 6: Percentage of Missing Values Replaced in Experiment 1.

Minimum Support ER FP-Growth CHARM

0.01 5.86% 3.09% 2.89%

0.02 5.58% 2.09% 2.09%

0.03 5.18% 1.4% 1.4%

0.04 3% 1.4% 1.4%

Table 7: Example of Rules Extracted by ER, FP-Growth, CHARM e FPMax.

Number Association Rule Method

athleteWinTrophyTournament(X, nba championship),

athletePlaysLeague(X, nba) → athletePlaysSport(X,Basketball)

FP-Growth /

CHARM / FPMax

2 athletePlaysLeague(X, nba) → athletePlaysSport(X, Basketball)

ER / FP-Growth /

CHARM

athleteWinTrophyTournament(X, nba championship) →

athletePlaysLeague(X, Basketball)

ER / FP-Growth

athletePlaysForTeam(X, cleveland cavalier), athletePlaysLeague(X, nba)

→ athletePlaysLeague(X, Basketball)

FP-Growth /

CHARM

athletePlaysForTeam(X, cleveland cavalier) → athletePlaysLeague(X,

Basketball)

ER / FP-Growth

6 athletePlaysForTeam(X, boston celtics) → athletePlaysSport(X, Basketball) ER

7 athletePlaysStadium(X, amway arena) → athletePlaysSport(X, Basketball) ER

nimum support of 0.01. No subset of it were

generated by FPMax. Rule 1 of Table 7 is one

possible association rule that could be generated by

MFI. As CHARM, it will only update the KB if both

antecedents are in an instance. Therefore, ER is an

efﬁcient system that prunes redundant and irrelevant

association rules, and also contributes to populate

better the KB in than CHARM and FPMax.

5 CONCLUSIONS AND FUTURE

WORKS

This paper introduced ER component, which has two

new methods that contributes to reduce the number

of association rules to be evaluated. The eliminating

redundant rules procedure consists in prune super an-

tecedent rules, and the irrelevant one eliminates super

consequent rules based on the previous discovered ir-

relevant association rules.

Both methods combined reduced the amount of

rules in more than 30%, without any lost on the pro-

cess of populating the KB. Consequently, the effort

on evaluating each rule extracted also decreased, sho-

wing the efﬁciency of ER component.

We also compared ER to FP-Growth, CHARM

and FPMax. Experiments showed that ER populated

NELL’s KB subset with more data than these algo-

rithms, without any lost of information.

In future works, it will be developed:

• An automatized process to discover irrelevant ru-

les without CL help;

• An improved process to prune irrelevant rules ba-

sed on the patterns already discovered.

REFERENCES

Agrawal, R., Imielinski, T., and Swami, A. (1993). Mining

association rules between sets of items in large databa-

ses. In IN: PROC. OF THE 1993 ACM SIGMOD INT.

CONF. ON MANAGEMENT OF DATA, WASHING-

TON DC (USA, pages 207–216.

Appel, A. P. and Hruschka, E. (2011). Prophet–a link-

predictor to learn new rules on nell. In Data Mining

Workshops (ICDMW), 2011 IEEE 11th International

Conference on, pages 917–924. IEEE.

Baralis, E., Cagliero, L., Cerquitelli, T., and Garza, P.

(2012). Generalized association rule mining with con-

straints. Information Sciences, 194:68–84.

Bayardo Jr, R. J. (1998). Efﬁciently mining long patterns

from databases. ACM Sigmod Record, 27(2):85–93.

Bizer, C., Lehmann, J., Kobilarov, G., Auer, S., Becker, C.,

Cyganiak, R., and Hellmann, S. (2009). Dbpedia - a

crystallization point for the web of data. Web Semant.,

7(3):154–165.

Bollacker, K., Evans, C., Paritosh, P., Sturge, T., and Taylor,

J. (2008). Freebase: a collaboratively created graph

database for structuring human knowledge. In Proc.

of the 2008 ACM SIGMOD int. conference on Mana-

gement of data, pages 1247–1250. AcM.

Burdick, D., Calimlim, M., and Gehrke, J. (2001). Maﬁa: A

maximal frequent itemset algorithm for transactional

Eliminating Redundant and Irrelevant Association Rules in Large Knowledge Bases

databases. In Data Engineering, 2001. Proc. 17th Int.

Conference on, pages 443–452. IEEE.

Carlson, A., Betteridge, J., Hruschka Jr, E. R., and Mitchell,

T. M. (2009). Coupling semi-supervised learning of

categories and relations. In Proceedings of the NAACL

HLT 2009 Workshop on Semi-supervised Learning for

Natural Language Processing, pages 1–9. Association

for Computational Linguistics.

Carlson, A., Betteridge, J., Kisiel, B., Settles, B., Hruschka,

E. R., and Mitchell, T. M. (2010a). Toward an ar-

chitecture for never-ending language learning. In In

AAAI.

Carlson, A., Betteridge, J., Wang, R. C., Hruschka Jr,

E. R., and Mitchell, T. M. (2010b). Coupled semi-

supervised learning for information extraction. In Pro-

ceedings of the third ACM international conference on

Web search and data mining, pages 101–110. ACM.

Djenouri, Y., Drias, H., and Bendjoudi, A. (2014). Pru-

ning irrelevant association rules using knowledge mi-

ning. International Journal of Business Intelligence

and Data Mining, 9(2):112–144.

Etzioni, O., Fader, A., Christensen, J., Soderland, S., et al.

(2011). Open information extraction: The second ge-

neration. In 22th Int. Joint Conf. on Artif. Intelligence.

Fournier-Viger, P., Gomariz, A., Gueniche, T., Soltani, A.,

Wu, C.-W., Tseng, V. S., et al. (2014). Spmf: a java

open-source pattern mining library. Journal of Ma-

chine Learning Research, 15(1):3389–3393.

Gal

Arraga, L. A., Teﬂioudi, C., Hose, K., and Suchanek,

F. (2013). Amie: Association rule mining under in-

complete evidence in ontological knowledge bases. In

Proc. of the 22Nd Int. Conf. on World Wide Web, pages

413–422, Republic and Canton of Geneva, Switzer-

land. Int. World Wide Web Conf. Steering Committee.

Gouda, K. and Zaki, M. J. (2005). Genmax: An efﬁcient

algorithm for mining maximal frequent itemsets. Data

Min. Knowl. Discov., 11(3):223–242.

Grahne, G. and Zhu, J. (2003). High performance mining

of maximal frequent itemsets. In 6th International

Workshop on High Performance Data Mining.

Han, J., Pei, J., and Yin, Y. (2000). Mining frequent patterns

without candidate generation. In ACM sigmod record,

volume 29, pages 1–12. ACM.

Hoffart, J., Suchanek, F. M., Berberich, K., and Weikum,

G. (2013). Yago2: A spatially and temporally en-

hanced knowledge base from wikipedia (extended ab-

stract). In Proceedings of the Twenty-Third Internatio-

nal Joint Conference on Artiﬁcial Intelligence, IJCAI

’13, pages 3161–3165. AAAI Press.

Marinica, C. and Guillet, F. (2010). Knowledge-based in-

teractive postmining of association rules using onto-

logies. IEEE Transactions on Knowledge and Data

Engineering, 22(6):784–797.

Matuszek, C., Cabral, J., Witbrock, M., and Deoliveira, J.

(2006). An introduction to the syntax and content of

cyc. In Proceedings of the 2006 AAAI Spring Sympo-

sium on Formalizing and Compiling Background Kno-

wledge and Its Applications to Knowledge Represen-

tation and Question Answering, pages 44–49.

Miani, R. G., Yaguinuma, C. A., Santos, M. T., and Biajiz,

M. (2009). Narfo algorithm: Mining non-redundant

and generalized association rules based on fuzzy on-

tologies. In Enterprise Inf. Systems, pages 415–426.

Springer.

Miani, R. G. L., Pedro, S. D. d. S., and Hruschla Jr, E. R.

(2014). Association rules to help populating a never-

ending growing knowledge base. In IBERAMIA 2014,

pages 169–181. Springer.

Mitchell, T. M., Cohen, W., Hruschka, E., Talukdar, P., Bet-

teridge, J., Carlson, A., Mishra, B. D., Gardner, M.,

Kisiel, B., Krishnamurthy, J., et al. (2015). Never-

ending learning. In 29th AAAI Conf. on Artiﬁcial In-

telligence.

Pasquier, N., Bastide, Y., Taouil, R., and Lakhal, L. (1999).

Discovering frequent closed itemsets for association

rules. In Proceedings of the 7th International Confe-

rence on Database Theory, ICDT ’99, pages 398–416,

London, UK, UK. Springer-Verlag.

Pedro, S. D. and Hruschka Jr, E. R. (2012). Conver-

sing learning: Active learning and active social in-

teraction for human supervision in never-ending lear-

ning systems. In Advances in Artiﬁcial Intelligence–

IBERAMIA 2012, pages 231–240. Springer.

Rai, N. S., Jain, S., and Jain, A. (2014). Mining interesting

positive and negative association rule based on impro-

ved genetic algorithm (mipnar

ga). In. Journal of Ad-

vanced Computer Science and Applications, 5(1).

Rameshkumar, K., Sambath, M., and Ravi, S. (2013). Re-

levant association rule mining from medical dataset

using new irrelevant rule elimination technique. In

Information Communication and Embedded Systems

(ICICES), 2013 Int. Conf. on, pages 300–304. IEEE.

Srikant, R. and Agrawal, R. (1995). Mining generalized as-

sociation rules. In Proceedings of the 21th Int. Conf.

on Very Large Data Bases, VLDB ’95, pages 407–

419, San Francisco, CA, USA. Morgan Kaufmann Pu-

blishers Inc.

Suchanek, F. M., Kasneci, G., and Weikum, G. (2007).

Yago: A core of semantic knowledge. In Proc. of the

16th Int. Conf. on World Wide Web, WWW ’07, pages

697–706, New York, NY, USA. ACM.

Swesi, I. M. A. O., Bakar, A. A., and Kadir, A. S. A. (2012).

Mining positive and negative association rules from

interesting frequent and infrequent itemsets. In Fuzzy

Systems and Knowledge Discovery (FSKD), 2012 9th

International Conference on, pages 650–655. IEEE.

Tamang, S. and Ji, H. (2012). Relabeling distantly supervi-

sed training data for temporal knowledge base popu-

lation. In Proceedings of the Joint Workshop on Au-

tomatic Knowledge Base Construction and Web-scale

Knowledge Extraction, pages 25–30. Association for

Computational Linguistics.

Zaki, M. J. (2000). Generating non-redundant association

rules. In Proc. of the 6th ACM SIGKDD Int. Con-

ference on Knowledge Discovery and Data Mining,

KDD ’00, pages 34–43, New York, NY, USA. ACM.

Zaki, M. J. and Hsiao, C.-J. (2002). Charm: An efﬁcient

algorithm for closed itemset mining. In Proc. of the

2002 SIAM int. conf. on data mining, pages 457–473.

SIAM.

ICEIS 2018 - 20th International Conference on Enterprise Information Systems